Spike Phase Locking in CA1 Pyramidal Neurons Depends on Background Conductance and Firing Rate

Abstract

Oscillatory activity in neuronal networks correlates with different behavioral states throughout the nervous system, and the frequency–response characteristics of individual neurons are believed to be critical for network oscillations. Recent in vivo studies suggest that neurons experience periods of high membrane conductance, and that action potentials are often driven by membrane potential fluctuations in the living animal. To investigate the frequency–response characteristics of CA1 pyramidal neurons in the presence of high conductance and voltage fluctuations, we performed dynamic-clamp experiments in rat hippocampal brain slices. We drove neurons with noisy stimuli that included a sinusoidal component ranging, in different trials, from 0.1 to 500 Hz. In subsequent data analysis, we determined action potential phase-locking profiles with respect to background conductance, average firing rate, and frequency of the sinusoidal component. We found that background conductance and firing rate qualitatively change the phase-locking profiles of CA1 pyramidal neurons versus frequency. In particular, higher average spiking rates promoted bandpass profiles, and the high-conductance state promoted phase-locking at frequencies well above what would be predicted from changes in the membrane time constant. Mechanistically, spike rate adaptation and frequency resonance in the spike-generating mechanism are implicated in shaping the different phase-locking profiles. Our results demonstrate that CA1 pyramidal cells can actively change their synchronization properties in response to global changes in activity associated with different behavioral states.

Introduction

Rhythmic activity in a wide range of frequencies has been observed in the CNS during different behavioral states (Engel et al., 2001; Buzsáki and Draguhn, 2004; Steriade, 2006). In rodents, hippocampal theta oscillations coincide with periods of active exploration and rapid eye movement sleep, and are involved in spatial information processing and memory formation (Buzsáki, 2002; Andersen et al., 2007). CA1 pyramidal neurons, which project the hippocampal output to the entorhinal cortex (Andersen et al., 2007), have a preferential theta phase of firing in vivo (Klausberger et al., 2003; Harvey et al., 2009). However, the network and cellular mechanisms involved in the generation and maintenance of hippocampal theta oscillations are still unclear. In particular, knowing how the firing rate of pyramidal neurons encodes time-varying stimuli requires understanding of the biophysical mechanisms governing their spiking activity.

In vitro experiments have shown that CA1 pyramidal cells have an intrinsic preference for theta frequency input (Leung and Yu, 1998; Pike et al., 2000; Hu et al., 2002; Narayanan and Johnston, 2007; Zemankovics et al., 2010). However, these works mostly focus on the entrainment of subthreshold membrane potentials, whose relationship to spike phase locking is undetermined. Moreover, recent work shows that the in vitro scenario differs considerably from the in vivo one: during active states neurons are bombarded with synaptic inputs (Penttonen et al., 1998; Henze and Buzsáki, 2001; Destexhe et al., 2003; Harvey et al., 2009; Epsztein et al., 2011); this bombardment leads to increased membrane conductance and highly irregular membrane potential fluctuations, which drive spiking. In CA1 pyramidal neurons, these effects alter basic electrophysiological properties and introduce changes in the input–output function (Prescott et al., 2006, 2008; Fernandez and White, 2010; Fernandez et al., 2011).

Dynamic-clamp technology allows the introduction of membrane voltage fluctuations and conductance to cells in vitro. Using this technique, we can create an in vivo-like state and investigate the action potential phase-locking profile of CA1 pyramidal neurons in response to a wide range of input frequencies. We performed recordings under low and high background conductance, at different firing rates, to account for in vivo data showing task-related variations in mean rates of CA1 pyramidal cells (Harvey et al., 2009; Epsztein et al., 2011). We here show that in CA1 pyramidal neurons spike frequency adaptation acts as a high-pass filter, which interacts with the cutoff frequency and an intrinsic frequency preference of the spike-generating mechanism, to set their phase-locking profile. The sensitivity of these properties to background conductance and firing rate accounts for the different locking profiles: this implies that pyramidal neurons are dynamic entities, changed by the state of their input.

Materials and Methods

Tissue preparation.

All experimental protocols were approved by the University of Utah Institutional Animal Care and Use Committee. Horizontal sections of hippocampus and entorhinal cortex were prepared from 21- to 36-d-old Long–Evans rats of either sex. All chemicals were obtained from Sigma-Aldrich unless otherwise noted. After anesthetization with isoflurane and decapitation, brains were removed and immersed in 0°C solution consisting of the following (in mm): 215 sucrose, 25 NaHCO₃, 20 d-glucose, 2.5 KCl, 0.5 CaCl₂, 1.25 NaH₂PO₄, 3 MgCl₂, buffered to pH 7.4 with 95% O₂/5% CO₂. Horizontal slices were cut to a thickness of 400 μm (Leica VT 1200; Leica Microsystems). After the cutting procedure, slices were incubated in artificial CSF (ACSF) at 30°C for 20 min before being cooled to room temperature (20°C). Slices were allowed to recover for at least 60 min before recordings commenced. The ACSF consisted of the following (in mm): 125 NaCl, 25 NaHCO₃, 25 d-glucose, 2 KCl, 2 CaCl₂, 1.25 NaH₂PO₄, 1 MgCl₂, and was buffered to pH 7.4 with 95% O₂/5% CO₂. After the incubation period, slices were moved to the stage of an infrared–differential interference contrast-equipped microscope (Axioscope 2+; Zeiss). ACSF contained 10 μm CNQX and 50 μm picrotoxin to block ionotropic synaptic activity. All recordings were conducted between 32 and 34°C.

Electrophysiology.

Electrodes were drawn on a horizontal puller (P97; Sutter Instruments) and filled with an intracellular solution consisting of the following (in mm): 120 K-gluconate, 20 KCl, 10 HEPES, 7 diTrisPhCr, 4 Na₂ATP, 2 MgCl₂, 0.3 Tris-GTP, 0.2 EGTA, and buffered to pH 7.3 with KOH. Final electrode resistances were between 1.5 and 3 MΩ, with access resistance values between 5 and 15 MΩ. Electrophysiological recordings were performed with a Multiclamp 700B amplifier (Molecular Devices), and data were acquired using pClamp 10 (version 10; Molecular Devices) or the Real-Time Experimental Interface software (RTXI; www.rtxi.org) (Bettencourt et al., 2008; Lin et al., 2010). In some experiments, tetrodotoxin (TTX) (5 nm) was bath-applied, and recordings were taken after a 10–15 min incubation period. For dynamic-clamp experiments, the patch-clamp amplifier was driven by an analog signal from a personal computer running RTXI. Membrane potential fluctuations (i.e., background noise) were introduced by two independent Poisson processes, triggering unitary artificial synaptic events. Frequency modulation was introduced by injection of a separate current-based cosine, or through manipulation of the rate of one of the two Poisson processes. One Poisson process triggered excitatory synaptic events at a rate of 600 Hz; the other process triggered inhibitory events at a rate of 1000 Hz. These rates were used to obtain membrane potential fluctuations consistent with in vivo results (Harvey et al., 2009; Epsztein et al., 2011). Individual synaptic waveforms were generated using a biexponential function. For both excitation and inhibition, the rise time constant was 0.5 ms. For excitation, the decay time constant was 2 ms, while it was 8 ms for inhibition. All synaptic events were modeled as currents. For both low- and high-conductance trials, the magnitude of the input current fluctuations was adjusted to yield subthreshold membrane potential fluctuations with a SD of 2 mV; for these measurements, neurons were held at mean membrane potentials close to −75 mV. This corresponded to high-conductance recordings having individual synaptic events of roughly twice the size as low-conductance recordings. In cases in which conductance was added, a linear leak conductance was introduced via dynamic clamp using the following equation: I_L = g_L(v − E_L), where v is the membrane voltage. For all experiments, E_L was set to −75 mV and g_L was set to 15 nS. Modulation amplitudes were tuned at 1 Hz modulation frequency at average rate of 2 spike/s in preceding experiments and chosen to yield spike phase-locking strengths of a given value (vector strength, ∼0.3) (see below, Analysis and statistics). Values used for the average firing rate and the magnitude of membrane potential fluctuations were chosen in accordance to in vivo recordings (Klausberger et al., 2003; Harvey et al., 2009; Epsztein et al., 2011). A measured junction potential of ∼10 mV was subtracted from all recordings and taken into account during dynamic-clamp experiments. The sample rate of the dynamic clamp was set to 20 kHz. Data were collected at 20 kHz and low-pass filtered at 3 kHz. When spike phase locking was recorded, firing rates were monitored on-line and DC injection was used to control the rates. We recorded four 1 min trials for low modulation frequencies (0.1 and 0.5 Hz) at an average firing rate of 2 spikes/s, and three 1 min trials for all other frequencies. For cases with an average firing rate of 8 spikes/s, we recorded three 1 min trials for 0.1 and 0.5 Hz modulations and two 1 min trials for all other frequencies. Fast-Fourier transforms of the membrane voltage and of the binary action potential trains revealed clear peaks at the modulation frequencies, confirming the effectiveness of our stimulus paradigm (data not shown). Spike trains were irregular and displayed CV values between 0.8 and 1 for 2 spikes/s average rate and between 0.5 and 0.7 at 8 spikes/s mean rate.

In the case of frequency modulation through current-based cosines, we used cosine amplitudes of 15 pA in the high-conductance (high g) and 7.5 pA in the low-conductance (low g) condition, except for the experiment shown in Figure 5, in which an amplitude of 5 pA was used. The modulation frequencies considered in the different experiments are always reported in the respective figure legends. When 5 nm TTX was applied, the high g condition was recorded at 1.5 spikes/s. This was due to the inability of some neurons to spike at 2 spikes/s in the presence of 5 nm TTX under high g.

Figure 5.

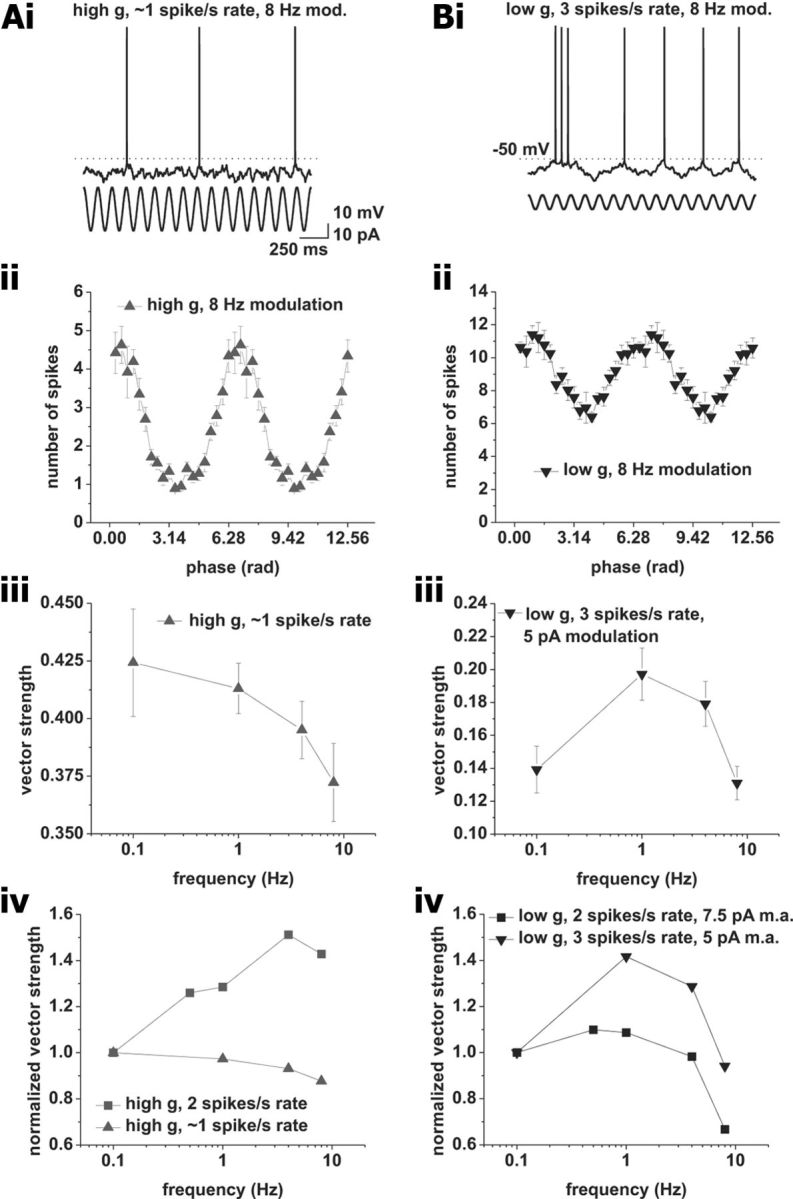
Action potential phase-locking peaks are sensitive to changes in firing rate. A, Phase locking at average firing rates of 1 spike/s under high conductance with a modulation amplitude of 15 pA. i, Example voltage trace. Sinusoidal modulation at 8 Hz is indicated below the voltage trace. ii, Average spike–phase histogram in response to 8 Hz modulation at an average spike rate of 1 spike/s. iii, Vector strength versus modulation frequency. Tested modulation frequencies were as follows: 0.1, 1, 4, and 8 Hz. iv, Comparison between vector strength at average firing rates of 1 (upward triangles) and 2 (squares) spikes/s. The vector strength normalized to 0.1 Hz modulation is plotted versus the modulation frequency. Note the change from low pass at 1 spike/s average rate to bandpass at 2 spikes/s mean rate. B, Phase locking at average firing rates of 3 spikes/s under low conductance with a modulation amplitude of 5 pA. i, Example voltage trace. Frequency modulation of 8 Hz is indicated by the sinusoid below the voltage trace. ii, Average spike–phase histogram in response to 8 Hz modulation at an average spike rate of 3 spikes/s. iii, Vector strength versus modulation frequency. Tested modulation frequencies were as follows: 0.1, 1, 4, and 8 Hz. iv, Comparison between vector strength at average firing rates of 3 (downward triangles) and 2 (squares) spikes/s. Vector strength normalized to 0.1 Hz modulation is plotted versus the modulation frequency. Modulation amplitude for 2 spikes/s mean rates was 7.5 pA; amplitude for 3 spikes/s mean rate was 5 pA. Note the change from low pass at 2 spikes/s average rate to bandpass at 3 spikes/s mean rate.

For introduction of an artificial adaptation current, we used a spike-triggered biexponential current with a rise time constant of 1 ms and a decay time constant of 500 ms. The adaptation current peak amplitude was set to 50 pA. The adaptation current was injected after every spike and summed with previously triggered injections. Introduction of the adaptation current required an increased DC injection to keep the average spike rate similar in control and adapting conditions.

When f–I relationships were measured, we used current steps whose amplitude covered twice the range of the modulatory cosines for high and low conductance (±15 pA for low g: range of 30 pA; ±30 pA for high g: range of 60 pA).

Analysis and statistics.

All analysis was performed in MATLAB (version 2010b; MathWorks) using custom software and/or built-in functions and/or Origin (version 7.5; OriginLab). Spike times were determined by finding the maxima of suprathreshold (>10 mV) intervals of membrane voltage. Phase locking to a given modulation frequency was determined by computing the vector strength, using the phases of individual spikes. Each spike t_k was treated as a unit vector with an angle φ_k corresponding to the phase of the modulation frequency. The vector strength |v⃗| is defined as the length of the normalized vector sum as follows:

for a total of N spikes. The current protocol for input impedance measurements consisted of a white-noise current input with a frequency cutoff of 100 Hz. Impedance [Z(f)] measures were calculated by taking the ratio of the Fourier transform of the membrane voltage response and current input stimulus. We evaluated the operating voltage as the mean membrane voltage from 500 to 475 ms preceding each spike. Statistical significance was determined using either a one-way ANOVA, or paired or unpaired t tests. For repeated measures, statistical difference was determined using Tukey's honestly significant criteria, which increases the threshold for significance. Means are presented with the SEM.

Relating gain to vector strength.

By definition, the vector strength |v⃗| is the modulus of the normalized vector sum of all the unit complex vectors with angles equal to the phase of each spike. The number of spikes per phase is given by the instantaneous firing rate f(φ), so that

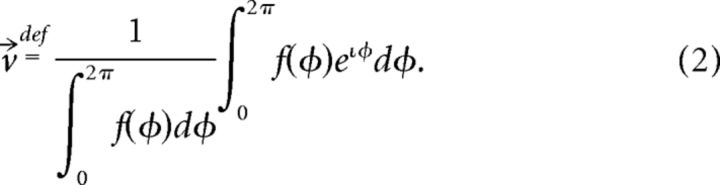When experimentally measured, f(φ) was found via spike–phase histograms, which appeared sinusoidal (see Fig. 1Aiii,Biii). If f(φ) was indeed sinusoidal, then it could be expressed as f(φ) = 〈f〉 + A cos(φ + φ₀), where 〈f〉 indicates the mean firing rate, and φ₀ is a phase shift induced by the integration time of the cell. We then embedded such expression for f(φ) in Equation 2; note that because the vector strength is invariant under rotation, it was sufficient to consider the case φ₀ = 0. From standard integration we have

The vector strength is computed as the length of v⃗; in our case, v⃗ is real, so the vector strength equals v⃗. We could then estimate the amplitude A of the histograms of firing phases as a function of the vector strength and mean firing rate, for each frequency modulation. When using those amplitudes to fit the f(φ) profiles, we had a good agreement for all frequency modulations <100 Hz (Pearson's correlation coefficient, >0.94). Thus, the instantaneous firing-rate histograms were well approximated by cosines.

Figure 1.

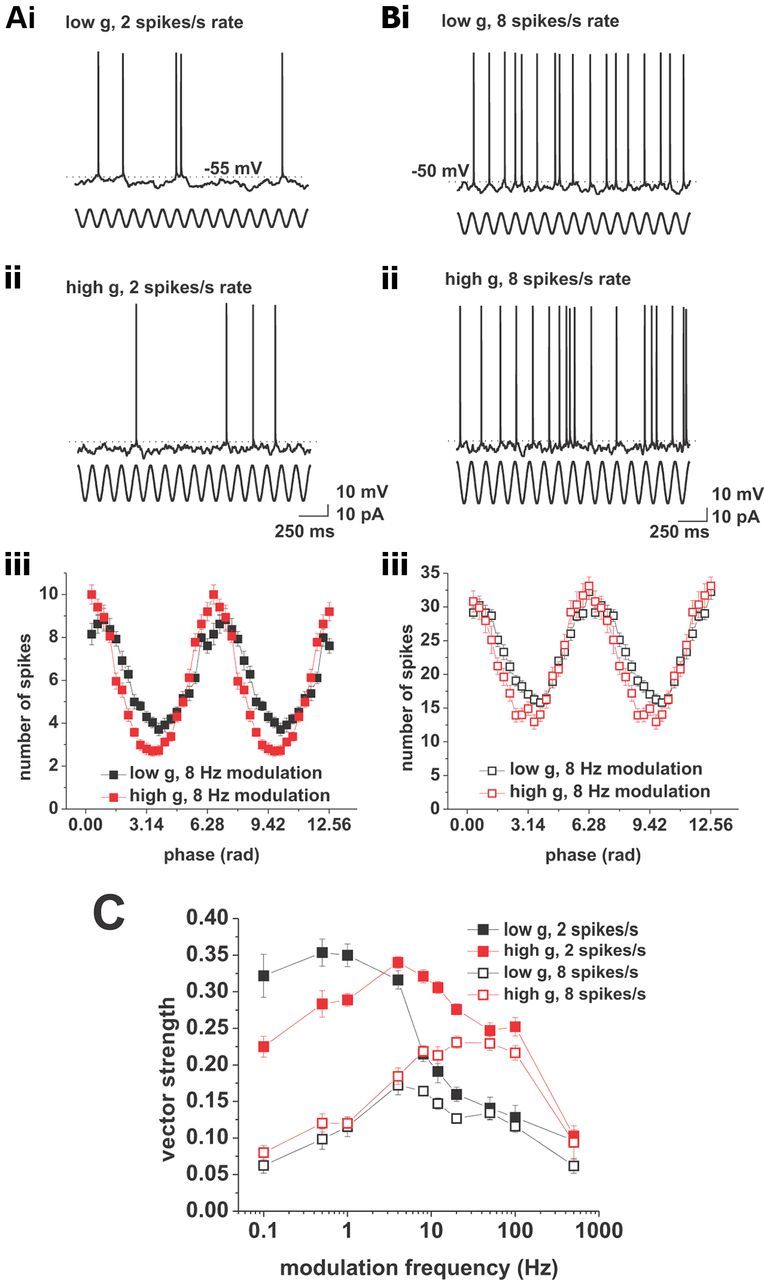
Action potential phase locking in response to current-based cosines. A, Response to current-based cosines at average firing rates of 2 spikes/s under low (i) and high (ii) conductance. Sinusoidal modulation at 8 Hz is indicated below the voltage traces. iii, Average spike–phase histogram in response to 8 Hz modulation at average spike rates of 2 spikes/s. Low conductance is shown in black, high conductance is shown in red. B, Response to current-based cosines at average firing rates of 8 spikes/s under low (i) and high (ii) conductance. Sinusoidal modulation at 8 Hz is indicated below the voltage traces. iii, Average spike–phase histogram in response to 8 Hz modulation at average spike rates of 8 spikes/s. Low conductance is shown in black; high conductance is shown in red. C, Vector strength versus modulation frequency plots for low (black) and high (red) conductance at average firing rates of 2 (solid squares) and 8 (open squares) spikes/s. Tested modulation frequencies were as follows: 0.1, 0.5, 1, 4, 8, 12, 20, 50, 100, and 500 Hz.

We then proceeded by incorporating the potential role of gain in the vector strength. The main assumption in this case was that, for slow frequency modulations, the amplitude of the instantaneous firing rate would be linear in the amplitude of the input current, scaled by gain. This assumption formalizes as f(φ) = 〈f〉 + mI_A cos(φ + φ₀), where m is the gain value and I_A is the amplitude of the input current. Thus, Equation 3 can be rewritten as follows:

Once we derived Equation 4, we compared the estimated vector strength to the vector strength measured in the experiments.

Principal-component analysis and frequency preference index.

In defining the principal components, we follow Jolliffe (1986). Given a finite number of sample observations of a random vector, looking for its principal components corresponds to identifying, in progressive ranking, the best fitting subspaces such that the distances between the samples and each subspace is minimized. Practically, this means decomposing the space according to the eigen-values and the eigen-directions of the covariance matrix of the given collection, and choosing only subspaces corresponding to higher spectral values. For each cell in a given condition (high or low conductance, 2 or 8 spikes/s firing rate, addition of TTX to the preparation), we use principal-component analysis (PCA) to identify a first-order linear kernel the cell might be using to filter the input it receives. We therefore performed experiments in which each pyramidal cell received the noise current but no cosine modulation, and its firing rate was controlled by DC. The exact noise realizations that the cell received in the experiment could then be used to extract its first-order kernel.

The input noise received by the cells during experiments had an autocorrelation timescale of ∼201 ms, which affected the shape of the kernel we were looking for. To remove the influence of the noise autocorrelation from this estimate of the linear filter, we deconvolved each noise realization by its autocorrelation. Our sample collection consisted of all the spike-triggering events (parts of the deconvolved input given to the cell in the experiments, each 200 ms long, ending at each spike time) and an equal number of randomly sampled parts of the deconvolved input (each sample 200 ms long as well). We constructed the covariance matrix of the sample, and diagonalized the matrix, selecting the eigen-vector of the highest eigen-value as the first principal component (PC1). We chose to use only one component once we verified that there was some distance between the maximum of the spectrum and the following values.

The first component PC1 (see Fig. 7Cii) was then considered the first-order kernel of a linear system. We tested whether such a system, when receiving inputs like the ones given to the pyramidal cells in our experiments, showed preferential frequency locking. Specifically, we considered as its input minutes of deconvolved noise traces plus cosine currents (with frequencies of 0.1, 0.5, 1, 2, 4, 8, 10, 20, 50, 100, and 500 Hz). Note that the amplitudes of the cosine currents used for the convolutions were scaled by the ratio of the SDs of the noise and its deconvolved version; this was done to preserve the relative size of the cosine currents and the SD of the noise. We then convolved such inputs with the filter (the PC1), to estimate instantaneous activity, consistent with the standard approach, which uses the spike-triggered average to predict the instantaneous firing rate of a cell given its input (Dayan and Abbott, 2001). The cycle-averaged activity profiles were cosine shaped (see Fig. 7Ciii), and we rescaled the amplitude in each experimental condition by its maximum across all modulation frequencies and cells in that condition, so that the activity would have a maximum of 1 spike/s. Modulation frequency significantly affected the activity amplitudes, in both the high- and low-conductance conditions (low g, p < 0.001, n = 10; high g, p < 0.001, n = 10; both one-way ANOVA). We consider the sum of the normalized activities and mean firing-rate values as instantaneous firing-rate distributions. We computed the frequency preference index as each amplitude divided by twice the mean firing rate, in agreement with Equation 3. The resulting frequency preference index is higher for normalized activities with higher amplitudes, and lower for those closer to a uniform distribution (i.e., a flat line). Overall, the frequency preference index profiles for cells spiking at 8 spikes/s mean firing rates are lower than for cells spiking at 2 spikes/s. Plots of the mean and SE of the frequency preference indices for cells in all experimental conditions are reported in Figures 7 and 8.

Figure 7.

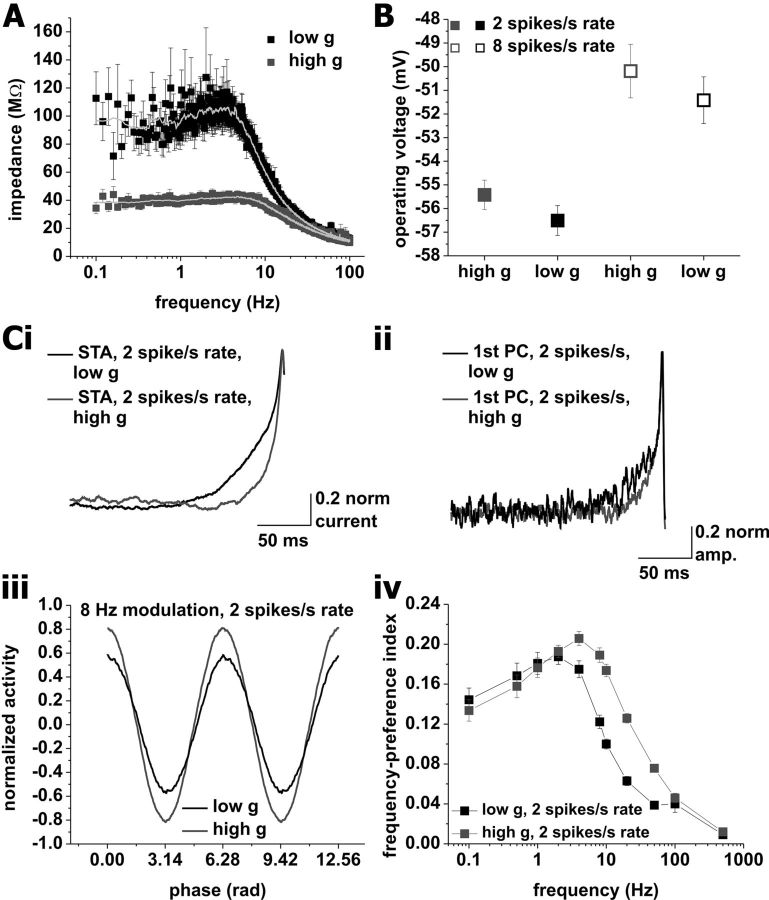
Evidence for an intrinsic frequency preference. A, Subthreshold impedance profile under low (black) and high (gray) conductance. The gray lines show sliding window averages. Note the reduced peak under high conductance. B, Mean operating voltages at average firing rates of 2 (solid squares) and 8 (open squares) spikes/s under low (black) and high (gray) conductance (values for 8 Hz modulation frequency are presented; we observed no significant differences between modulation frequencies; one-way ANOVA). C, Principal-component analysis of spike-triggering events at average firing rates of 2 spikes/s. i, Spike-triggered averages of the input current for mean firing rates of 2 spikes/s under low (black) and high (gray) conductance. Input currents used to measure spike-triggering events in neurons did not include any frequency modulation. ii, Average first principal components of the spike-triggering events under low (black) and high (gray) conductance at mean firing rates of 2 spikes/s. iii, Average normalized activity versus phase for a modulation frequency of 8 Hz. Activity for low conductance is shown in black; high conductance is shown in red. iv, Frequency preference index of the first principal components under low (black) and high (gray) conductance. Tested modulation frequencies were as follows: 0.1, 0.5, 1, 2, 4, 8, 10, 20, 50, 100, and 500 Hz.

Figure 8.

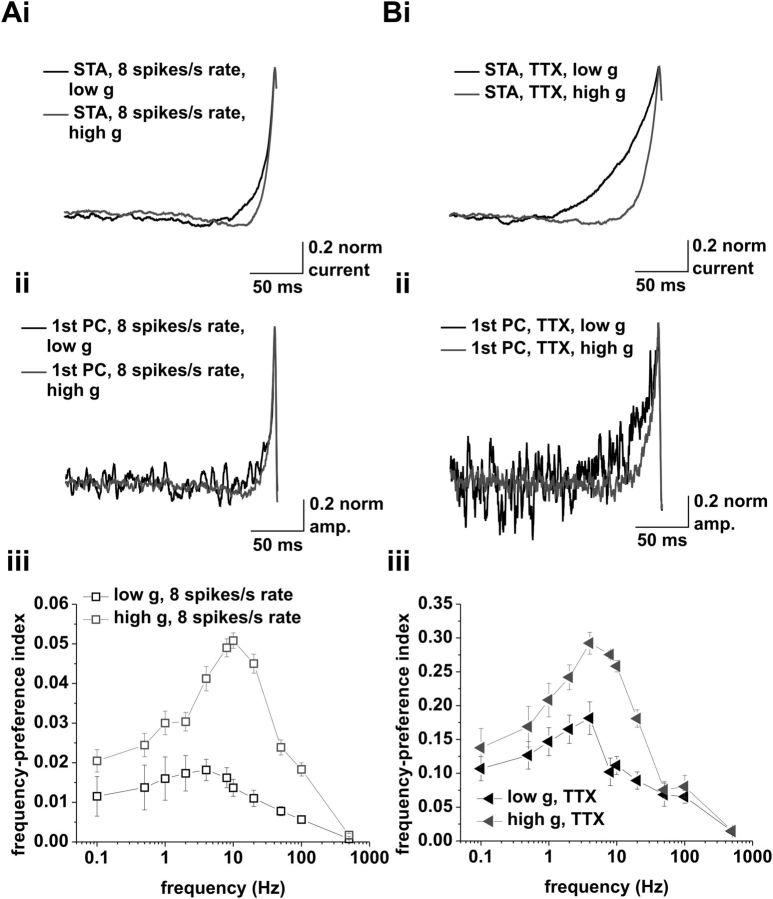
Principal-component analysis of spike-triggering events at 8 spikes/s mean rate under control conditions, and at 2 (low g) and 1.5 (high g) spikes/s mean rate in the presence of 5 nm TTX. Ai, Spike-triggered averages of the input current for mean firing rates of 8 spikes/s under low (black) and high (gray) conductance. Input currents used to measure spike-triggering events in neurons did not include any frequency modulation. ii, Average first principal components of the spike-triggering events under low (black) and high (gray) conductance at mean firing rates of 8 spikes/s. iii, Frequency preference index of the first principal components under low (black) and high (gray) conductance. Tested modulation frequencies were as follows: 0.1, 0.5, 1, 2, 4, 8, 10, 20, 50, 100, and 500 Hz. Bi, Spike-triggered averages of the input current for mean firing rates of 2 (low g; black) and 1.5 (high g; gray) spikes/s, in the presence of 5 nm TTX. Input currents used to measure spike-triggering events in neurons did not include any frequency modulation. ii, Average first principal components of the spike-triggering events under low (black) and high (gray) conductance in the presence of 5 nm TTX. iii, Frequency preference index of the first principal components under low (black) and high (gray) conductance. Tested modulation frequencies were as follows: 0.1, 0.5, 1, 2, 4, 8, 10, 20, 50, 100, and 500 Hz.

Simulations.

All simulations were run in MATLAB (MathWorks) using a fourth-order Runge–Kutta solver with a time step of 0.04 ms. The biophysical model is defined as follows:

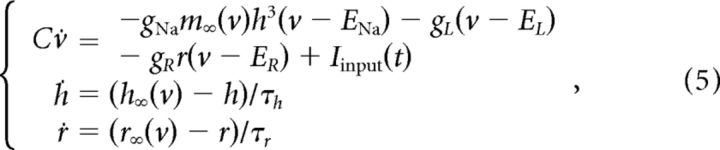where

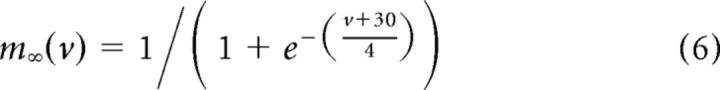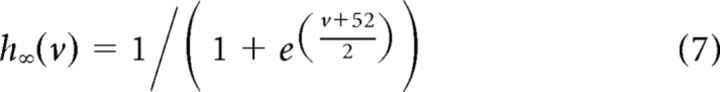and with

where I_DC is the constant drive used to tune the firing rate, I_A is the amplitude of the cosine modulation, with frequency f, g_n is a scaling factor for I(t), and I(t) is the noise input, introduced in Equations 12, 13, and 14. Note that, during each experiment, the input to the cell was scaled by a factor analogous to g_n (see above, Electrophysiology). In this work, we drove cells with either inhomogeneous Poisson stimuli or the sum of homogeneous Poisson processes and sinusoidal currents; we tested the model on the latter case. For spike repolarization, membrane voltage was reset to −65 mV subsequent to crossing 15 mV. Resonating properties are introduced by

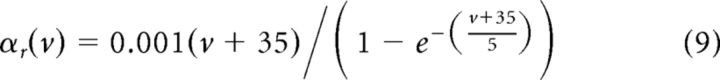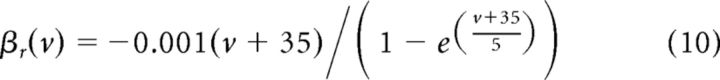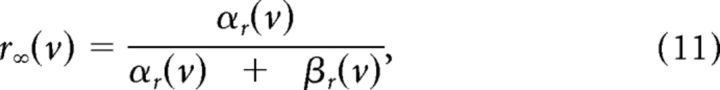where τ_r is constant at 125 ms.

Across the different conditions, the following parameters were kept constant: C = 1.5 μF/cm², g_Na = 6 mS/cm², τ_h = 200 ms, E_Na = 50 mV, E_L = −65 mV, E_R = −90 mV, g_R = 0.1 mS/cm². We approximated the activation variable associated with the sodium conductance m as instantaneous; therefore, it was modeled using only its steady-state function. Membrane voltage fluctuations were introduced in the same manner as in the experiments, and I(t) was scaled by g_n, to yield voltage fluctuations with ∼2 mV SD. The magnitude of the sinusoidal modulation current I_A was set to yield a vector strength value of ∼0.3 for a modulation frequency of 1 Hz at a firing rate of 2 spikes/s for each conductance condition, and held constant for different firing rates (see Fig. 9).

Figure 9.

Phase-locking profiles of CA1 pyramidal neurons can be qualitatively reproduced in a simple model incorporating spike frequency adaptation and a resonant current. A, Example of simulated voltage traces under low (top trace) and high (bottom trace) conductance, at mean rates of 1.5 spikes/s. B, Average spike–phase histogram in response to 8 Hz modulation at average spike rates of 1.5 spikes/s. Low conductance is shown in black; high conductance is shown in gray. C, Vector strength versus modulation frequency at a mean rate of 1.5 spikes/s under low (black) and high (gray) conductance. Model parameters were as follows: low g, g_L = 0.03 mS/cm², I_DC = −0.098 μA/cm², I_A = 0.018 μA/cm², g_n = 0.04 μA/cm ²; high g, g_L = 0.18 mS/cm², I_DC = 0.43 μA/cm², I_A = 0.098 μA/cm², g_n = 0.2 μA/cm². Tested modulation frequencies were as follows: 0.1, 0.5, 1, 2, 4, 8, 10, 20, and 100 Hz. D, Vector strength versus modulation frequency at a mean rate of 4 spikes/s under low (black) and high (gray) conductance. Model parameters were as follows: low g, g_L = 0.03 mS/cm², I_DC = −0.058 μA/cm², I_A = 0.018 μA/cm², g_n = 0.04 μA/cm²; high g, g_L = 0.18 mS/cm², I_DC = 0.68 μA/cm², I_A = 0.098 μA/cm², g_n = 0.2 μA/cm². Tested modulation frequencies were as follows: 0.1, 0.5, 1, 2, 4, 8, 10, 20, and 100 Hz.

Analytical derivation of the modulation amplitude of inhomogeneous Poisson noise.

In the last set of experiments, the input current was the sum of an inhibitory and an excitatory component,

where each component was given by the convolution of a Poisson process with an artificially designed synaptic wave, modeled as a biexponential. This can be written as follows:

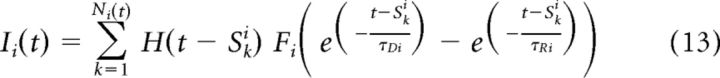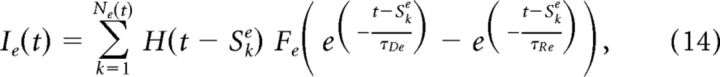where N_i(t) and N_e(t) are Poisson processes, S_k are the event times of the processes (with superscripts differentiating between excitatory and inhibitory), H(·) is the Heaviside function, τ_R and τ_D are the timescales of rise and decay of each artificial synaptic signal (with their own subscripts as well), and F_i and F_e are the normalization factors, which ensure that each synaptic event peaks at 1. We chose to introduce the frequency modulation by changing the rate of the Poisson processes. When excitation was modulated, we had N_i(t), a homogeneous Poisson process with rate λ̄_i = 1000 Hz, and N_e(t), an inhomogeneous Poisson process with rate λ̄_e(1 + c_ecos(2πft)), where λ̄_e = 600 Hz, f is the modulation frequency, and c_e is the strength of the modulation (c_e = 25%). When inhibition was modulated, we had N_e, a homogeneous Poisson process with rate λ̄_e, and N_i(t), inhomogeneous. The rate of N_i was λ̄_i(1 + c_i cos(2πft)), with c_i = 5%.

Intuitively, for each decay timescale, the biexponential artificial synaptic waveform acts as a filter over the instantaneous pulses of the Poisson process. Therefore, for rates modulated with progressively faster cosines, the trains of events are increasingly attenuated. Specifically, the trial average of the current input converges to its expected value, by the law of large numbers. The cycle average (i.e., the average over each cosine period) of this expectation can then be used to compute its amplitude as a function of the modulation frequency.

On average over many trials, the input signal defined by Equation 12 looks sinusoidal. In this section, we show how to derive analytically the amplitude of this average curve, which gives the magnitude of the frequency modulation in this signal. For clarity of reading, we will show the derivation only for the case in which inhibition is modulated. By the law of large numbers, the average of I(t) over m trials converges to its expected value

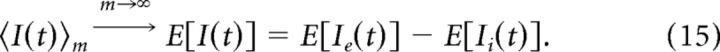We start from the inhibitory term. We derive the expectations by conditioning on the number of events up to time t, given E[I_i(t)] = E[E[I_i(t)|N(t)]]. So we consider

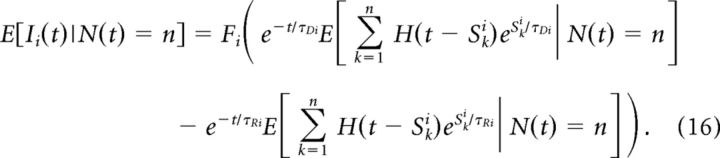It is known that for an inhomogeneous Poisson process of rate λ(t), given there are n events in the time interval [0, t), these points are independent and identically distributed with density $\lambda \left(t\right)/{\displaystyle {\int }_0^t\lambda \left(u\right)du}$ (Cox and Isham, 1980). We apply this fact to the S_kⁱ in the previous equation and find

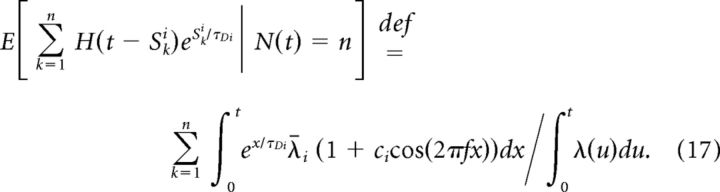We now can take the expectation of this conditioned expectation to find E[I_i(t)]:

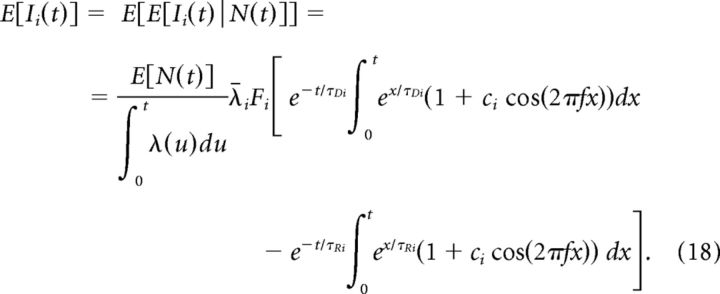Then standard calculus gives

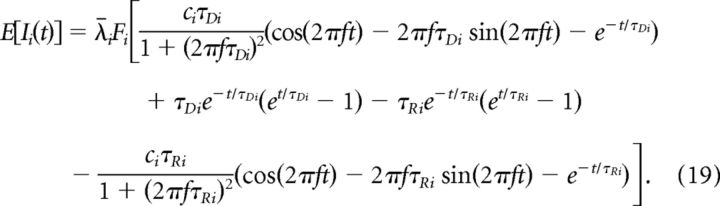The same derivation applied to the excitation (which is based on the homogeneous Poisson process N_e in this case) yields

Then, E[I(t)] is given by the difference between Equations 20 and 19.

To compute the amplitude of E[I(t)], which we will label Amp, consider the circular mean of E[I(t)]:

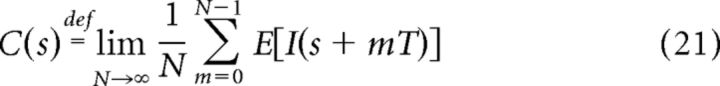with T = $\frac{1}{f}$, s ∈ [0, T). That gives

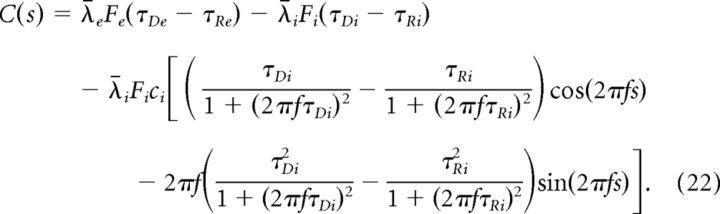Now Amp is equal to the amplitude of C(s). Given the amplitude of α cos(2πfx) + β sin(2πfx) is $\sqrt{{\alpha }^2+{\beta }^2}$, then the amplitude of C(s) is

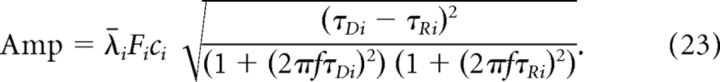Analogously, one can derive the amplitude for the excitation-modulated case, which will be exactly Amp, only with the excitation in the subscripts.

Results

Action potential phase-locking profile of CA1 pyramidal cells in response to current-based cosines

A widely used readout for the participation of a single neuron in a network rhythm is the relationship between its action potentials and the phase of the oscillation. In this study, our goal was to quantify the action potential phase locking of CA1 pyramidal neurons to an artificial oscillatory input, and to identify the underlying biophysical mechanisms. We stimulated the neurons with biexponential, current-based excitatory and inhibitory artificial synaptic inputs (see Materials and Methods) driven by separate Poisson processes. This replicated the membrane voltage fluctuations observed in awake behaving animals (Harvey et al., 2009; Epsztein et al., 2011). Frequency modulations were introduced via current-based sinusoids. We recorded the phases of action potentials with respect to the different modulation frequencies and quantified the degree of their phase locking.

In vivo work (Destexhe et al., 2003) also shows that neurons embedded in active networks have high membrane conductance. To investigate the effects of changes in membrane conductance on the phase-locking behavior of CA1 pyramidal neurons, experiments were performed in the control (low conductance, low g) condition and with increased background conductance (high conductance, high g), by injecting a linear leak of 15 nS. The added linear leak reduced the apparent input resistance from 84 ± 1 to 39 ± 0.3 MΩ (n = 353).

To span a wide frequency region above and below the delta, theta, beta, and gamma bands, we used modulation frequencies of 0.1, 0.5, 1, 4, 8, 12, 20, 50, 100, and 500 Hz (Fig. 1). The phases of individual action potentials were used to compute the vector strength for each frequency (see Materials and Methods). The vector strength is a measure of phase locking that yields values between 0 and 1, where 0 indicates a uniform distribution and 1 indicates perfect locking. At average firing rates of 2 spikes/s, we found that changes in background conductance induce qualitative differences in the phase-locking behavior in CA1 pyramidal cells. In the low-conductance case, we observed a low-pass-like phase-locking profile, while under high conductance the profile was bandpass, peaking at 4 Hz (Fig. 1C, solid symbols). In both cases, the modulation frequency significantly influenced the action potential phase locking (low g, n = 7–25, p < 0.001; high g, n = 8–22, p < 0.001, both one-way ANOVA).

The experiments described so far were performed at an average firing rate of 2 spikes/s, which matched observations in CA1 pyramidal neurons during exploratory behavior and under anesthesia (Klausberger et al., 2003; Harvey et al., 2009). In vivo data also indicate that the firing rate of CA1 pyramidal neurons increases under certain physiological conditions, for example, when the animal enters the place field of the neuron (O'Keefe, 1976; Harvey et al., 2009; Epsztein et al., 2011). We investigated the influence of an increased firing rate on the phase-locking profile by recording the responses of CA1 pyramidal cells to current cosines of varying frequencies at an average firing rate of 8 spikes/s (Fig. 1B). We found that an increase in firing rate qualitatively affected the phase-locking behavior: under low conductance the profile changed from low pass to bandpass, peaking at 4 Hz, while under high conductance the bandpass profile changed into a high-pass-like profile (Fig. 1C, open symbols). As before, the modulation frequency significantly influenced the phase-locking strength (low g, n = 6–17, p < 0.001; high g, n = 4–15, p < 0.001; both one-way ANOVA).

Overall, our data show a strong dependence of phase locking on both average firing rate and background conductance. With increasing firing rate, we observed an overall drop in phase-locking strength, under both high and low g. Moreover, an increase in background conductance shifted the cutoff frequency of action potential phase locking to a higher value. Note that this quantity is distinct from the cutoff frequency of the membrane potential (compare Figs. 1C, 7A). This discrepancy has been found in other cell types (du Lac and Lisberger, 1995; Carandini et al., 1996; Köndgen et al., 2008).

Gain of the f–I relationship can be used to predict the action potential phase-locking profile of CA1 pyramidal neurons for lower modulation frequencies

Our investigation so far revealed that pyramidal cells phase-locking behavior can display a variety of profiles depending on average firing rate and background conductance, and is more complex than previously suggested (Leung and Yu, 1998; Pike et al., 2000; Fellous et al., 2001; Hu et al., 2002; Narayanan and Johnston, 2007; Zemankovics et al., 2010). We were interested in identifying the biophysical mechanisms underlying such diversity of responses. In particular, the action potential phase locking to low modulation frequencies (<4 Hz) was different across conductance conditions at average firing rates of 2 spikes/s, but similar for average firing rates of 8 spikes/s (Fig. 1C). For slow enough input frequencies, we conjectured that variations of the cosine current in time could exert effects similar to DC variations. Consequently, we hypothesized that phase locking to low modulation frequencies may be approximated by the firing frequency versus injected current relationship (f–I curve), which can be derived from step responses. Previous work has shown that changes in background conductance change the slope (gain) of the f–I relationship of CA1 pyramidal neurons, and that gain is influenced by the mean operating voltage (Fernandez and White, 2010; Fernandez et al., 2011). We conjectured that, for low modulation frequencies, differences in gain across conductance conditions and mean firing rates may account for the observed differences in vector strength. To test this hypothesis, we held CA1 pyramidal neurons at average firing rates of 2 or 8 spikes/s and recorded action potentials evoked in response to depolarizing and hyperpolarizing current steps of 5 s duration (n = 11; Fig. 2). We chose the step length as one-half the slowest modulation period. In addition to the current steps, the neurons received the same fluctuating background current input generated using nonmodulated Poisson processes as before. Gain was computed as the slope of the linear fit to the f–I relationships (Fig. 2Bi,Bii,Ci). The gain values were then used to estimate the vector strength for a modulation frequency of 0.1 Hz.

Figure 2.

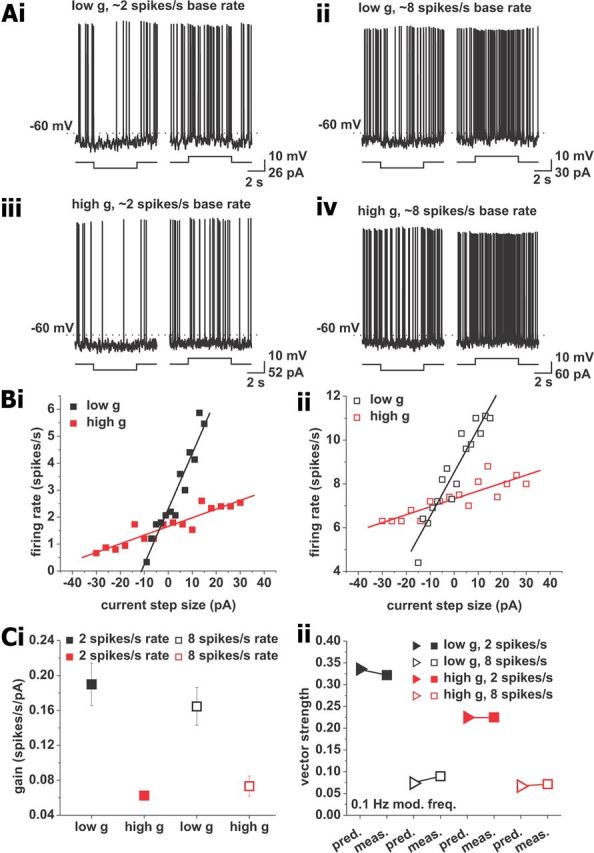
Prediction of vector strength for a modulation frequency of 0.1 Hz through gain measured using step responses. Neurons received step depolarizations and hyperpolarizations while held at baseline firing rates of 2 and 8 spikes/s. A, Example voltage traces showing responses to depolarizing (right traces in each panel) and hyperpolarizing (left traces in each panel) current steps from baseline firing rates of 2 (i, iii) and 8 (ii, iv) spikes/s. A recording under low conductance is shown in i and ii; a recording under high conductance is shown in iii and iv. B, Example plots of firing rate versus step size, at base firing rates of 2 (i) and 8 (ii) spikes/s. A step size of zero indicates the DC value used to keep the neuron at the respective firing rate. Recording under low conductance is shown in black; high conductance is shown in red. The solid lines indicate linear fits used to calculate the gain (slope of the linear fit). Ci, Average gain values for recordings at baseline firing rates of 2 (solid squares) and 8 (open squares) spikes/s. Low conductance is shown in black; high conductance is shown in red. ii, Comparison of measured and predicted vector strength. Predictions were derived using Equation 4 for a modulation frequency of 0.1 Hz and are denoted by triangles. Measured vector strengths are given for the same modulation frequency and are shown as squares. The closed symbols refer to 2 spikes/s average firing rate; open symbols refer to mean rates of 8 spikes/s. Low conductance is shown in black; high conductance is shown in red.

The phase-locking estimate was derived analytically (see Materials and Methods), yielding Equation 4, which was the basis to test whether gain regulated the response of the pyramidal cells at the slowest frequency modulation tested in the experiments. We found good agreement between the estimate and the experimental data for action potential phase locking to a modulation frequency of 0.1 Hz for all four experimental conditions (Fig. 2Cii). We thus concluded that the gain derived from step responses was sufficient to predict action potential phase locking to slow time-varying stimuli. Furthermore, Equation 4 shows that the vector strength is inversely proportional to the mean firing rate. This explains the small difference in vector strength values <1 Hz modulation observed for high and low g at average firing rates of 8 spikes/s. This relationship could also account for the overall drop in vector strength observed when firing rates were increased from 2 to 8 spikes/s in the experiments.

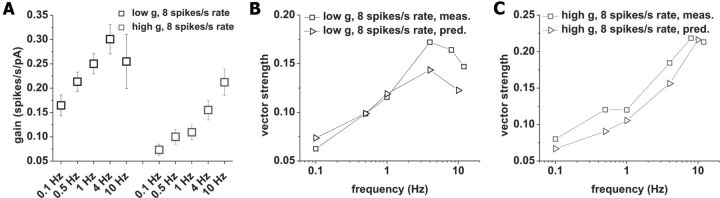
To investigate whether the accuracy of the estimate extended to higher frequencies, we compared the predicted and the measured vector strength for such frequencies. Except for one case (2 spikes/s firing rate, low g), we observed decreasing prediction accuracies with increasing modulation frequencies up to the peak or the plateau of the respective experimental condition. This indicated that the gain measured using 5 s current steps was most accurate for predictions of phase locking to a modulation frequency of 0.1 Hz. Given that spike frequency adaptation has been shown to be important for setting the gain of CA1 pyramidal neurons (Fernandez and White, 2010; Fernandez et al., 2011), and because the influence of spike frequency adaptation depends on the length of the step considered, we conjectured that shorter steps might be more accurate for predictions of phase locking to higher frequencies. To test this hypothesis, we chose modulation frequencies between 0.5 and 10 Hz, and considered step lengths of one-half their period. We then reanalyzed the same dataset, considering only spikes in the time windows corresponding to a given modulation frequency. Due to the low number of spikes in the shorter time windows in the 2 spikes/s mean firing rate condition, we restricted this analysis to 8 spikes/s mean firing rate. We found significant differences in gain with different step lengths (low g, p < 0.05, n = 11; high g, p < 0.001, n = 11, one-way ANOVA; Fig. 3A). For both high and low g, the gain increased as the step length was decreased from 5 s to 125 ms. This result indicated a contribution of spike frequency adaptation to establishing the gain of CA1 pyramidal neurons. We used Equation 4 to estimate the vector strength for faster modulation frequencies with the respective gain values. In the low-conductance condition, the prediction fitted the measured vector strength well up to 1 Hz, after which the estimates decreased in accuracy, but still captured the general trend (Fig. 3B). For high conductance, we found a good agreement from 0.1 to 10 Hz (Fig. 3C).

Figure 3.

Prediction of vector strength for higher modulation frequencies through gain measured using step responses at baseline firing rates of 8 spikes/s. Analysis was done on the same dataset shown in Figure 2. A, Gain for different step lengths associated with modulation frequencies of 0.1, 0.5, 1, 4, and 10 Hz. Step length was one-half the period of the respective frequency (5000, 1000, 500, 125, and 50 ms, respectively). B, Comparison of measured and predicted vector strength for different modulation frequencies under low conductance. Predictions are shown as triangles and were derived using Equation 4 and the frequency-specific gain shown in A. Measured vector strengths are shown as squares. C, Comparison of measured and predicted vector strength for different modulation frequencies under high conductance. Predictions are shown as triangles and were derived using Equation 4 and the frequency-specific gain shown in A. Measured vector strengths are shown as squares.

In summary, our gain data using different step lengths indicated a prominent influence of spike frequency adaptation on the phase-locking profiles at mean firing rates of 8 spikes/s. In agreement with the high-pass filter properties ascribed to spike frequency adaptation (Benda and Herz, 2003), lower modulation frequencies were associated with lower vector strengths. Different profiles were associated with different action potential cutoff frequencies, depending on background conductance. Under high conductance, the cutoff was located at high frequencies, thus revealing a phase-locking plateau, while the bandpass profile under low conductance was due to an earlier cutoff. Thus, at mean firing rates of 8 spikes/s, we could relate gain measured using current steps to responses to time-varying stimuli in CA1 pyramidal neurons, and show that the phase-locking strength is given by the combination of spike frequency adaptation, gain, and the action potential cutoff.

Spike frequency adaptation reduces phase locking to low frequencies

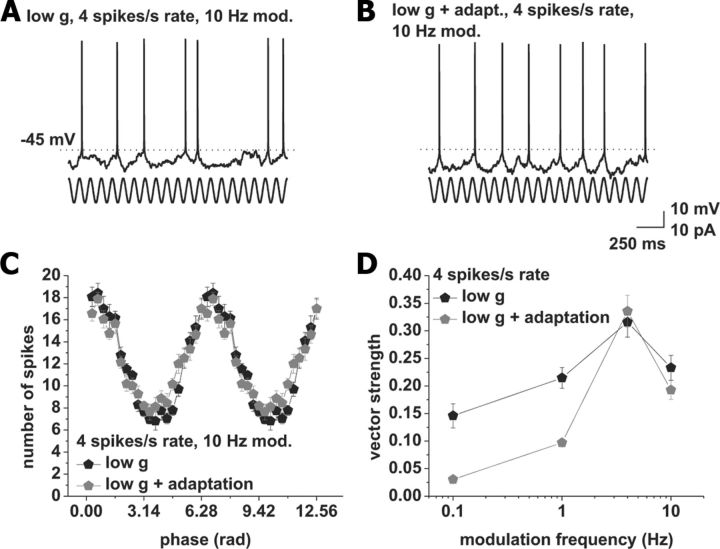
Based on results from Figures 1–3, we concluded that (1) differences at low modulation frequencies in Figure 1C are caused by differences in gain, and (2) the shape of the vector strength curve for the 8 spikes/s firing rate and modulation frequencies <10 Hz is dominated by stimulus-induced changes in spike frequency adaptation. To provide a proof of principle that adaptation reduces locking to low modulation frequencies, we introduced a spike-triggered adaptation current into CA1 pyramidal neurons via dynamic clamp (see Materials and Methods). We recorded phase-locking at an average rate of 4 spikes/s under low conductance (n = 8; Fig. 4). Confirming our predictions, introduction of the adaptation current selectively reduced locking to low modulation frequencies (0.1 and 1 Hz modulation frequency, control vs adaptation, both p < 0.001, 4 and 10 Hz modulation not significant, all paired t test).

Figure 4.

Introduction of an adaptation current selectively reduces action potential phase locking to lower modulation frequencies. A, Response to current-based cosines at average firing rates of 4 spikes/s under low conductance. Sinusoidal modulation at 10 Hz is indicated below the voltage traces. B, Response to current-based cosines at average firing rates of 4 spikes/s under low conductance with addition of an artificial adaptation current. Sinusoidal modulation at 10 Hz is indicated below the voltage traces. C, Average spike–phase histogram in response to 10 Hz modulation at average spike rates of 4 spikes/s. Low conductance is shown in black; low conductance with an additional adaptation current is shown in gray. D, Vector strength versus modulation frequency under low conductance (black) and low conductance with added adaptation current (gray); at average firing rates of 4 spikes/s. Tested modulation frequencies were as follows: 0.1, 1, 4, and 10 Hz. Note the decreased locking to 0.1 and 1 Hz with added adaptation current.

Action potential phase-locking peaks are sensitive to changes in firing rate

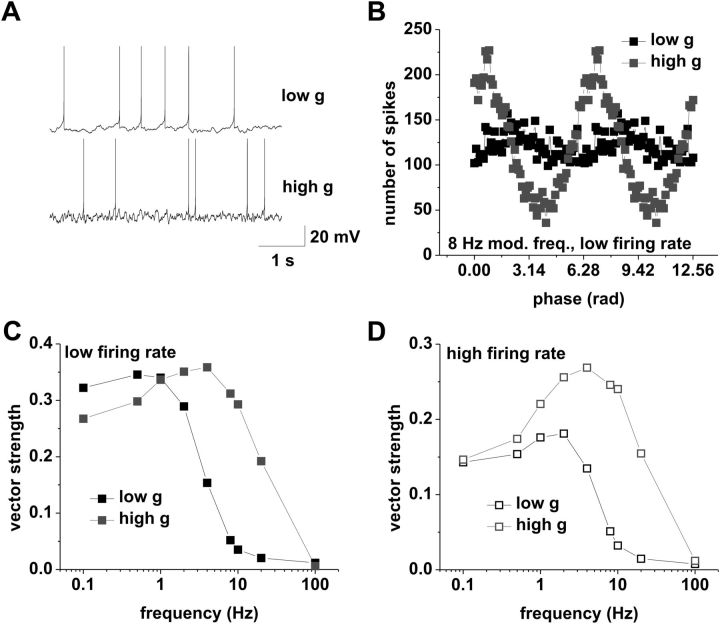
We used gain to establish the relationship between spike frequency adaptation and phase-locking profiles for higher firing rates. At average firing rates of 2 spikes/s, this was only possible for the modulation frequency of 0.1 Hz. To investigate the role of spike frequency adaptation in the locking profiles at low firing rates, we introduced a different approach. If spike frequency adaptation has a prominent influence on the action potential phase-locking profile at low mean firing rates, it should be possible to change it through manipulations likely to influence adaptation. It has been shown that increasing firing rate and conductance enhances spike frequency adaptation (Fernandez and White, 2010). Hence, the phase-locking profile at 2 spikes/s firing rate in high conductance should change from bandpass to low pass if spike frequency adaptation is decreased via a reduction in firing rate. Analogously, the phase-locking profile at 2 spikes/s firing rate under low conductance should change from low pass to bandpass when spike frequency adaptation increases by increasing the average firing rate.

To test these predictions, we first recorded the action potential phase-locking profile of CA1 pyramidal neurons under high conductance at an average firing rate of ∼1 spike/s, and observed a low-pass phase-locking profile (Fig. 5A; n = 8). We then recorded the action potential phase-locking profile at 3 spikes/s and observed a bandpass profile (Fig. 5B; n = 9, p < 0.05, one-way ANOVA, 0.1 vs 1 Hz modulation, p < 0.001, paired t test). These results confirmed our prediction that spike frequency adaptation is involved in shaping the locking profile at 2 spikes/s average firing rate under high and low conductance.

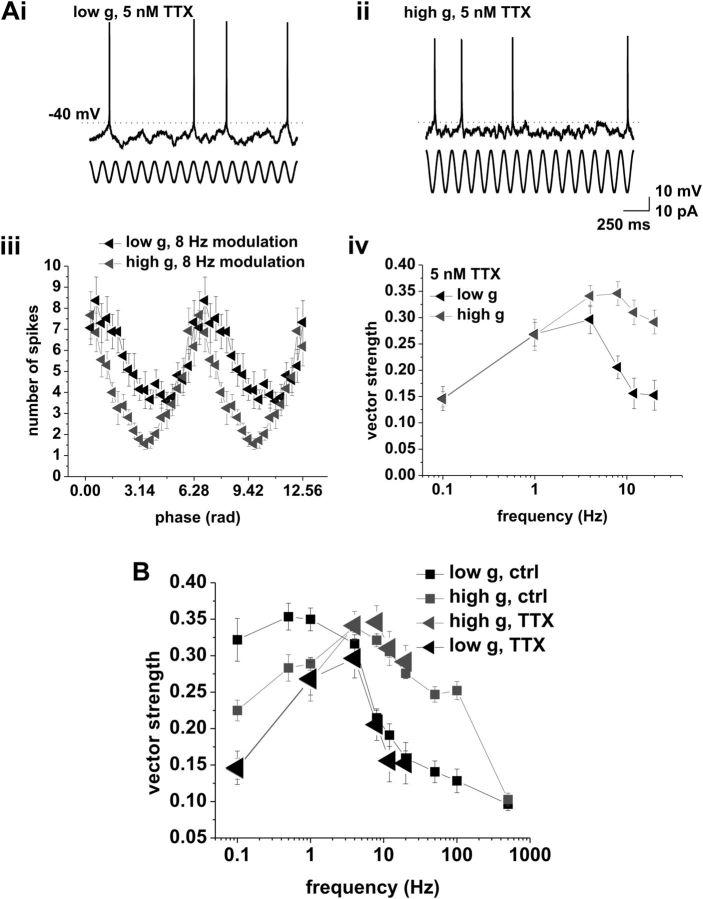
Low concentrations of TTX reduce phase locking to low modulation frequencies

Our results so far demonstrated the importance of spike frequency adaptation in shaping the phase-locking profiles of CA1 pyramidal cells. Previous work suggests the involvement of cumulative sodium current inactivation in setting spike frequency adaptation and gain in CA1 pyramidal neurons (Fernandez and White, 2010). In particular, our past work shows that low concentrations of TTX reduce the gain of CA1 pyramidal neurons through an increase of spike frequency adaptation (Fernandez et al., 2011). To test whether a reduction in gain through a reduction in sodium current availability would affect the action potential phase-locking profile, we recorded from CA1 pyramidal cells in the presence of 5 nm TTX (n = 8; Fig. 6). In both cases, the locking profile was bandpass, peaking at 4 Hz under low conductance and between 4 and 8 Hz under high conductance (influence of modulation was significant: low g, p < 0.001; high g, p < 0.001; both one-way ANOVA).

Figure 6.

Application of 5 nm TTX reduces phase locking to low frequencies. Ai, Response to current-based cosines at average firing rates of 2 spikes/s under low conductance. Modulation amplitude was 7.5 pA. ii, Response to current-based cosines at average firing rates of 1.5 spikes/s under high conductance. Modulation amplitude was 15 pA. Sinusoidal modulation at 8 Hz is indicated below the voltage traces in i and ii. iii, Average spike–phase histograms in response to 8 Hz modulation under low (black) and high (gray) conductance. iv, Vector strength versus modulation frequency under low (black) and high (gray) conductance. Tested modulation frequencies were as follows: 0.1, 1, 4, 8, 12, and 20 Hz. B, Comparison between vector strength in the presence (large triangles) and absence (small squares) of 5 nm TTX under low (black) and high (gray) conductance. Locking to low modulation frequencies is selectively reduced by TTX.

Comparing control and TTX conditions revealed a selective reduction of locking to low frequencies (0.1–1 Hz; Fig. 6B), consistent with a decrease in gain through an increased spike frequency adaptation, which only affects the locking strength at low frequencies. The enhanced adaptation was likely due to two factors. First, the reduced total sodium current available renders the neuron more susceptible to a further loss of sodium current caused by cumulative inactivation. Second, the mean operating voltage for a given firing rate in the presence of TTX was increased by 8–10 mV, thus augmenting cumulative inactivation.

In summary, our data show that sodium current is involved in setting the phase-locking profile of CA1 pyramidal neurons. This further supports our interpretation of the role of spike frequency adaptation in the locking behavior of these cells.

Evidence for an intrinsic frequency preference in the spike generation mechanism

We showed that spike frequency adaptation is a main factor in the phase locking of CA1 pyramidal neurons. Consistently, at an average firing rate of 8 spikes/s, we found a sustained plateau-like profile across a band of higher frequencies. If spike frequency adaptation was the only factor involved in setting the action potential phase-locking profile, a similar behavior should have been observed in the presence of TTX at low rates under high conductance, but this was not the case. Furthermore, spike frequency adaptation cannot account for the preference for modulation at 4 Hz in the high-conductance case at 2 spikes/s under control conditions. Given these results, we hypothesized that an intrinsic frequency preference could also be involved in shaping the phase-locking profiles (Brumberg and Gutkin, 2007). This would point to a scenario in which the overall behavior of CA1 pyramidal neurons firing at 2 spikes/s under high conductance would result from the combined influence of spike frequency adaptation, setting a plateau at higher modulation frequencies, and an additional intrinsic frequency preference at ∼4 Hz, resulting in a superimposed small peak. Hence, we continued by probing CA1 pyramidal neurons for a possible frequency preference in addition to spike frequency adaptation.

Previously, subthreshold resonance phenomena have been proposed to be involved in setting a frequency preference for CA1 pyramidal neurons in the theta band (Leung and Yu, 1998; Pike et al., 2000; Hu et al., 2002; Narayanan and Johnston, 2007; Zemankovics et al., 2010). If subthreshold resonant currents were the major cause for a phase-locking peak, increasing conductance should shunt these currents, reducing the subthreshold resonance (Hutcheon et al., 1996; Fernandez and White, 2008; Fernandez et al., 2011) and thus reducing the locking preference. To test this prediction, we recorded the impedance profile under low and high conductance (Fig. 7A) (see Materials and Methods). As expected, the Q value dropped under high conductance (p < 0.01, n = 12, paired t test; Q values: low g, 1.21 ± 0.03; high g, 1.12 ± 0.02). Therefore, increasing background conductance has opposite effects on the subthreshold impedance and the action potential phase-locking profile.

On the other end, a change in background conductance could affect the operating voltage, which in turn can influence the impedance profile (Hu et al., 2002; Narayanan and Johnston, 2007; Zemankovics et al., 2010). This effect could counteract the effect of background conductance shown in Figure 7A. We observed no significant difference in the operating voltage between high and low g at either a mean rate of 2 or 8 spikes/s (Fig. 7B). This argues against a differential activation of resonant properties between high and low conductance.

Our analysis suggests no strong relationship between the phase-locking profiles of CA1 pyramidal neurons and subthreshold resonance. For this reason, we investigated a possible frequency preference in the spike generation mechanism (Brumberg and Gutkin, 2007). To test whether the spike-triggering events derived from input without any frequency modulation showed any inherent preference, we recorded from CA1 pyramidal neurons firing at an average rate of 2 spikes/s under low and high conductance. The neurons received the same background current inputs as before, without any frequency modulation.

We performed principal-component analysis on the population of spike-triggering input events (PCA) (see Materials and Methods). We used the principal components to define a frequency preference index (Fig. 7Civ), which ranges between 0 and 1, where higher values represent increased locking (for details, see Materials and Methods). The index showed a bandpass profile in both low and high conductance, peaking at 2 and 4 Hz, respectively. These results indicated a frequency preference of the spike generation mechanism, which was sensitive to changes in background conductance, at mean firing rates of 2 spikes/s. Thus, we concluded that the low-pass phase-locking profile in the low-g case resulted from the absence of adaptation and the action potential cutoff frequency, which overrode the intrinsic frequency preference. In the high-conductance case, the cutoff shifted to higher frequencies, and the bandpass profile resulted from adaptation, and the intrinsic frequency preference, unmasked by the shifted cutoff.

Note that, given the absence of cosine modulation in the spike-triggering events used for the PCA, the effect of adaptation on the phase-locking profiles could not be evaluated by this analysis. In fact, the sinusoidal modulation itself recruits adaptation, which acts differently at different modulation frequencies. Furthermore, the voltage fluctuation induced irregularity of the spike trains (CVs between 0.8 and 1 for 2 spikes/s mean rate and between 0.5 and 0.7 for 8 spikes/s mean rate) in combination with the absence of cosine modulation in the input argues against a strong influence of firing-rate resonance (i.e., preferential locking to modulation frequency equal to firing rate) to the frequency preference described here (see below).

Next, we performed the same analysis on recordings at firing rates of 8 spikes/s. We found bandpass-like profiles for both conductance conditions (Fig. 8A), with peaks at 4 Hz under low g and between 8 and 10 Hz under high g. The higher mean rate led to an overall drop of the frequency preference index. This indicated that the intrinsic frequency preference of the spike generation mechanism was sensitive to the mean firing rate. Note that our analysis cannot address the relative importance of the different mechanisms involved in shaping the phase-locking profiles. Therefore, consistent with the lower indices found in this case, we think that, at firing rates of 8 spikes/s, the intrinsic frequency preference was overridden by spike frequency adaptation.

Finally, we performed the same analysis on recordings done in the presence of 5 nm TTX, without frequency modulation. The resultant frequency preference index was found to be bandpass for both high and low conductance (Fig. 8B), with peak frequency at 4 Hz in both conditions.

In summary, PCA provided evidence for the existence of an intrinsic frequency preference in the spike-generating mechanism across the different experimental conditions. In our interpretation of these results, the preference of the spike-generating mechanism acted in concert with adaptation, the cutoff, and possibly additional factors, to set the phase-locking profile of CA1 pyramidal neurons.

Action potential phase-locking profiles can be qualitatively reproduced in a simple model

Next, we tried to qualitatively reproduce the phase-locking behavior of CA1 pyramidal neurons in a computational model. We started from the simplest spiking model, the leaky integrate-and-fire (LIF), and found that it responded to inputs similar to the ones we presented to pyramidal cells with low-pass action potential phase-locking profiles, for high and low conductance, and high and low firing rates. Moreover, for reduced sizes of membrane potential fluctuations, the model responded with a phase-locking peak at the firing frequency. This behavior is consistent with the LIF receiving white noise (Tateno, 2002) and the generalized integrate-and-fire (GIF), which incorporates a resonant variable (Brunel et al., 2003). If the LIF or GIF were a good representation of our observations, CA1 pyramidal neurons should show firing-rate resonance. To test this, we recorded the phase locking to 4 Hz modulation frequency, in the presence of membrane potential fluctuations, at different average firing rates. No locking peak was present at an average firing rate of 4 spikes/s, under either high or low conductance. In fact, the vector strength decreased with increasing rate (low g, n = 5; high g, n = 6) (data not shown). We therefore conclude that firing-rate resonance does not play a major role in setting the spike phase locking under our recording conditions.

Our experiments indicated that changes in gain, through changes in spike frequency adaptation, in combination with an intrinsic frequency preference were crucial for obtaining different phase-locking profiles. To test this idea, we started from a previously published model, which reproduced changes in gain and spike frequency adaptation in response to increases in conductance due to sodium current inactivation (Fernandez and White, 2010). We adapted this model by incorporating a resonant current; frequency modulation and membrane potential fluctuations were introduced as before (see Materials and Methods).

The model qualitatively reproduced the effects of changes in background conductance and firing rate on the phase-locking profiles of CA1 pyramidal neurons (Fig. 9). In fact, under low conductance, increasing the firing rate changed the locking profile from low pass to bandpass. Under high conductance, the transition was more complex: at the lowest firing rates, the profile was low pass, changing to bandpass—with peaks in the theta range—for intermediate rates; at the highest rates tested, the peaks broadened into plateaus. While the curves reported in Figure 9 qualitatively reproduce the behavior shown in Figure 1C, the firing rates of model and cells are not an exact match. In addition, the apparent cutoff frequency for action potential phase locking was at lower frequencies in the model when compared with real neurons. However, the model reproduces the locking profiles with very steep voltage dependencies for sodium current inactivation, as well as activation and inactivation of the resonant current. As we have observed before, this is necessary because the changes in mean operating voltage with firing rate are much smaller in the model than in CA1 pyramidal neurons (Fernandez et al., 2011). Furthermore, having an artificial reset rule simplified the model at the expense of a full spike-generating mechanism, and served to highlight the role of the sodium current in the locking dynamics. Despite these discrepancies, our simulations indicate that the different action potential phase-locking profiles observed in CA1 pyramidal neurons can be qualitatively reproduced in a simple model incorporating spike frequency adaptation and a resonant property.

Modulation amplitude attenuates with inhomogeneous Poisson processes

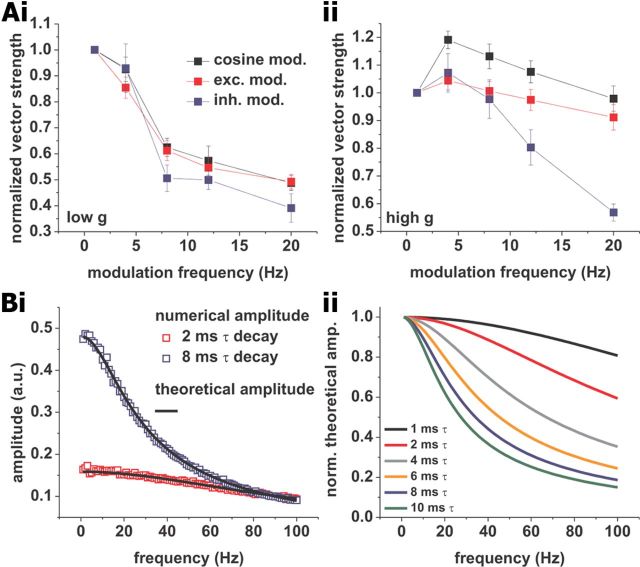
Rhythmic activity is likely experienced as synaptic input rate variation by a recipient neuron. To investigate the phase-locking profiles of CA1 pyramidal neurons in response to frequency modulation via synaptic input rate oscillation, we changed our experimental paradigm. In this series of experiments, we modulated the rate of either the excitatory or inhibitory Poisson process using a cosine function. We recorded phase locking at average firing rates of 2 spikes/s under low and high conductance. Under all conditions, phase locking was significantly affected by modulation frequency (excitation modulated: low g, p < 0.001; high g, p < 0.01; both one-way ANOVA, both n = 18; inhibition modulated: low g, p < 0.001; high g, p < 0.001; both one-way ANOVA, both n = 8). For both excitation and inhibition, we observed low-pass profiles under low g, and weakly bandpass profiles under high g. To directly compare the responses to current-based cosines and rate modulated synaptic events, we normalized profiles to their value at 1 Hz (Fig. 10Ai,Aii). While responses at low g were comparable, we observed a drop in vector strength with modulated inhibition at frequencies >10 Hz and a smaller peak at 4 Hz for both modulated excitation and inhibition under high g.

Figure 10.

Phase-locking of CA1 pyramidal neurons in response to rate-modulated Poisson processes driving artificial synaptic-current waveforms at 2 spikes/s average firing rate. A, Normalized vector strength versus modulation frequency for modulated excitation (red; 2 ms decay time constant), modulated inhibition (blue; 8 ms decay time constant), and modulation through current cosines (black; same dataset shown in Fig. 1) under low (i) and high (ii) conductance. B, Dependence of the modulation amplitude on the modulation frequency and the decay time constant of the artificial synaptic-current waveforms. i, Comparison of modulation amplitudes derived from the same Poisson processes used in the experiments with amplitudes derived analytically. For amplitudes derived numerically, the process driving the inhibitory artificial synaptic current waveforms was rate modulated with an amplitude of 5% and the decay time constant was varied. Results for decay time constants of 8 (open blue squares) and 2 ms (open red squares) are shown. Superposition of the analytical solution (black lines) shows a good agreement with the numerical results. Note the steeper drop in amplitude with the larger decay time constant. ii, Normalized analytical amplitudes for a range of decay time constants. Modulation amplitudes decreased with increasing modulation frequency. Attenuation for decay time constants ranging from 1 to 10 ms are shown. Note the stronger decrease with higher decay time constants.

We hypothesized that these effects could result from filtering of the input, with the time constants of the synaptic-like waveforms dampening the modulation at higher cosine frequencies. This attenuation would likely be different between the excitation-modulated and the inhibition-modulated case, because of the different τ_De and τ_Di. We quantified the average current injected per cycle and measured its amplitude (see Materials and Methods). We found significant differences in the average current amplitude for different frequencies in both the excitation-modulated and the inhibition-modulated inputs (excitation: low g, p < 0.05; high g, p < 0.001; n = 18; inhibition: low g, p < 0.01; high g, p < 0.001; n = 8; all one-way ANOVA). For both low- and high-conductance recordings, the average current amplitude decreased with increasing modulation frequency. The dependence on modulation frequency was greater for inhibition-modulated inputs than for excitation-modulated inputs (data not shown).

To highlight the mechanism underlying the decreasing per-cycle current amplitude with increasing modulation frequency, we derived this average analytically (see Eq. 23, Materials and Methods). The role the decay time constant plays in shaping this function is shown in Figure 10B: the larger the τ_D, the steeper the decay of the modulation amplitude with increasing frequency. Because the inhibitory decay timescale is larger than the decay timescale of excitation, their trends for the frequency dependence of the per-cycle current amplitude are different. It should be noted that, for synaptic time constants of ∼6–8 ms (commonly associated with GABA_A currents), the frequency-dependent attenuation was already ∼40% at 20 Hz modulation.

Discussion

This study demonstrates that CA1 pyramidal neurons dynamically change their frequency–response characteristics depending on background conductance and firing rate. We identify three main biophysical mechanisms underlying this phenomenon: spike frequency adaptation, the cutoff frequency of action potential phase locking, and an intrinsic frequency preference in the spike generation mechanism. We propose that these properties of CA1 pyramidal neurons may enable them to adjust the processing of time-varying stimuli in response to global changes in hippocampal activity.

Phase-locking profiles of CA1 pyramidal neurons

At low firing rates, increasing background conductance changes the locking profile from low pass to bandpass, peaking within the theta range. Increasing firing rate results in bandpass profiles, peaking in the theta band under low conductance, and in the beta–gamma band under high conductance. Firing rate affects phase locking mainly by altering the degree of spike rate adaptation, which implements a high-pass filter, as predicted by theoretical studies (Benda and Herz, 2003; Benda et al., 2010). While higher background conductance increases the high-frequency cutoff for action potential phase locking, the intrinsic frequency preference of spike generation has a more subtle effect, changing the peak of the frequency–response curve.

Implications for network function

Network oscillations of varying frequencies have been implicated in a plethora of systemic functions in animals and humans, ranging from sensory processing to memory formation (Engel et al., 2001; Buzsáki, 2002; Buzsáki and Draguhn, 2004; Steriade, 2006; Andersen et al., 2007). The overall network state translates into the drive, magnitude of voltage fluctuations, and total synaptic conductance a neuron will be exposed to (Destexhe et al., 2003; Destexhe and Contreras, 2006). We show the dependence of action potential phase locking on these parameters. In this context, our findings imply that the ability of CA1 pyramidal neurons to participate in a network rhythm of a given frequency depends on the overall network state. Thus, CA1 pyramidal neurons should not be thought of as invariable network elements, but rather as active units, able to modify their behavior according to global changes in hippocampal activity.

This work focuses on postsynaptic properties exclusively. Other network properties, including short- and long-term synaptic plasticity, also play a role in network rhythmogenesis. For example, recent theoretical work (Muller et al., 2011) shows that spike time-dependent plasticity (STDP), a form of long-term synaptic plasticity (Dan and Poo, 2004; Caporale and Dan, 2008), can induce synchrony in a population of neurons in response to oscillatory inputs. Cells with higher locking to a given input frequency will be more effectively synchronized by this kind of STDP mechanism. Here, we measure the spiking responses in relationship to oscillatory inputs with different frequencies and show that pyramidal cells change their locking preference depending on background conductance and firing rate. Given the dependence of STDP on neuromodulators and the general network state, it would be interesting to investigate whether the frequencies associated with higher locking as we measure it correlate with those inducing stronger plasticity across network conditions.

Evidence for the distinction of subthreshold and suprathreshold regimes

For the last few decades, subthreshold properties of neurons have been the subject of intensive investigation, under the natural, implicit or explicit assumption that observations made in the subthreshold regime are strongly predictive of neuronal spiking responses, especially in the context of network oscillations (Alonso and Llinás, 1989; McCormick and Pape, 1990; Llinás et al., 1991; McCormick and Bal, 1997; Leung and Yu, 1998; Pike et al., 2000; Hu et al., 2002; Narayanan and Johnston, 2007). Although subthreshold properties can influence neuronal firing properties and phase locking (Acker et al., 2003; Richardson et al., 2003; Gutkin et al., 2005), our data show that spike phase locking is not a simple reflection of the subthreshold impedance profile in CA1 pyramidal neurons. We find that the spike cutoff frequency is much greater than the cutoff of subthreshold membrane voltage, particularly in the high-conductance state. The cause for this behavior, which has also been observed in other cell types (Köndgen et al., 2008; Higgs and Spain, 2009), remains unclear. Theoretical work (Fourcaud-Trocmé et al., 2003; Wei and Wolf, 2011) suggests that the speed of spike initiation in combination with the firing rate and the spectral composition of the input noise are involved in setting the spike cutoff frequency. Furthermore, our data demonstrate that increasing background conductance has opposite effects on the subthreshold impedance and action potential phase-locking profiles at low firing rates: increasing background conductance greatly reduced the subthreshold resonant peak, while introducing a peak in the action potential locking profile. A discrepancy between subthreshold and spiking regimes has been observed before (Carandini et al., 1996; Brumberg and Gutkin, 2007; Haas et al., 2007; Fernandez and White, 2008; Kispersky et al., 2012), calling into question the general validity of predictions of the spiking regime based on subthreshold observations.

Representing in vivo inputs

Accumulating evidence suggests that CA1 pyramidal neurons in vivo experience periods of high membrane conductance associated with membrane voltage fluctuations (Penttonen et al., 1998; Henze and Buzsáki, 2001; Destexhe et al., 2003; Harvey et al., 2009; Epsztein et al., 2011). We introduced membrane voltage fluctuations by injecting artificial synaptic waveforms driven by Poisson processes: such inputs capture uncorrelated firing rates of individual neurons observed in vivo (Softky and Koch, 1993). However, this signal is still an imperfect representation of the actual in vivo input: for example, excitation–inhibition correlations (Okun and Lampl, 2008; Atallah and Scanziani, 2009; Gentet et al., 2010), and the variability within synaptic waveforms are not included. We found that introducing frequency modulation in the rate of the Poisson processes resulted in the dependence of its intensity on frequency. It can be expected that other more complex stimulation paradigms will display some form of nonuniform modulation strength across frequencies as well. To avoid this confound, we introduced frequency modulation via independent current-based cosine waveforms in the major part of this study. Spiking responses to this simple input can be used to predict the locking profiles to more complex inputs, once the dependence of their modulation strength on frequency is known. Furthermore, we believe the basic effects of changes in background conductance and firing rate on the phase-locking behavior can be observed more readily using this form of modulation. In the work presented here, we chose to simulate the high-conductance state by introducing a linear leak conductance instead of using conductance-based synaptic events. In preceding experiments, we found no obvious difference in phase-locking behavior between the two paradigms. We found a strong influence of firing rate on phase locking in our dataset, highlighting the importance of controlling this parameter.

Contribution of sodium current inactivation to adaptation and phase locking

Previous work has emphasized the contribution of M-type and Ca²⁺-activated potassium currents to spike frequency adaptation in CA1 pyramidal neurons (Madison and Nicoll, 1984; Pedarzani and Storm, 1993; Aiken et al., 1995; Peters et al., 2005; Otto et al., 2006). Although a contribution of these conductances cannot be ruled out, we are able to show that a reduction in sodium current availability can account for most of the effects of spike frequency adaptation on locking profiles.

The degree of spike frequency adaptation sets the gain of the input–output function of CA1 pyramidal neurons (Fernandez and White, 2010; Fernandez et al., 2011), and cumulative sodium current inactivation strongly affects adaptation in CA1 pyramidal neurons. For low to medium modulation frequencies, we relate gain to vector strength and show that the local linearization of the f–I relationship predicts the responses to time-varying stimuli. Moreover, reducing sodium current availability through TTX selectively reduces locking to low modulation frequencies. Together, this makes a strong argument for the role of sodium current inactivation in phase locking of CA1 pyramidal neurons.