Motor planning modulates sensory-motor control of collision avoidance behavior in the bullfrog, Rana catesbeiana

Summary

In this study, we examined the collision avoidance behavior of the frog, Rana catesbeiana to an approaching object in the upper visual field. The angular velocity of the frog's escape turn showed a significant positive correlation with the turn angle (r² = 0.5741, P<0.05). A similar mechanism of velocity control has been known in head movements of the owl and in human saccades. By analogy, this suggests that the frog planned its escape velocity in advance of executing the turn, to make the duration of the escape behavior relatively constant. For escape turns less than 60°, the positive correlation was very strong (r² = 0.7097, P<0.05). Thus, the frog controlled the angular velocity of small escape turns very accurately and completed the behavior within a constant time. On the other hand, for escape turns greater than 60°, the same correlation was not significant (r² = 0.065, P>0.05). Thus, the frog was not able to control the velocity of the large escape turns accurately and did not complete the behavior within a constant time. In the latter case, there was a small but significant positive correlation between the threshold angular size and the angular velocity (r² = 0.1459, P<0.05). This suggests that the threshold is controlled to compensate for the insufficient escape velocity achieved during large turn angles, and could explain a significant negative correlation between the turn angle and the threshold angular size (r² = 0.1145, P<0.05). Thus, it is likely that the threshold angular size is also controlled by the turn angle and is modulated by motor planning.

Introduction

We make many choices and decisions in daily life based upon both cognitive and unconscious processes. There has been a growing interest in understanding the neuronal mechanisms underlying such decision making in humans and non-human animals. Research on the neuronal basis of decision making has been largely driven by cortical recordings from single units in awake, behaving monkeys while they performed cognitive tasks. However, the complex multi-part structure of the primate brain precludes a detailed study of the neuronal circuitry and cellular mechanisms underlying decision making.

On the other hand, some invertebrate and lower vertebrate species perform human-like decision making and behavioral choice, thus providing useful model systems to study the relevant neuronal mechanisms. For example, appropriately placed tactile stimulation of a leech produces either swimming or crawling with nearly equal probability. During such responses, spatiotemporal patterns of activity of many individual neurons were examined simultaneously using voltage sensitive dyes. The results showed that decision making, the behavioral choice between swimming and crawling, is performed by co-varying activity of neuronal populations rather than by single neurons (Briggman et al., 2005; Kristan, 2008). Foraging juvenile crayfish respond to shadows that move toward them with one of two discrete and incompatible anti-predatory behaviors. They either freeze or produce powerful tail-flips thrusting them backwards. The behavioral choice is determined by a trade-off between the risk of predation which is evaluated by the speed of the moving shadow and the value of a food source. Thus, the crayfish makes a value-based decision and selects an adaptive behavioral output based on the interaction between medial giant neuron circuitry and unidentified freezing circuitry (Liden et al., 2010). In teleost fish, the final decision of whether or not to escape is made at the level of a single identified reticulospinal neuron, the Mauthner cell (M-cell) (Korn and Faber, 2005). Preuss et al. analyzed goldfish escapes in response to visual looming stimuli and compared them with intracellular responses of the M-cell to the same stimuli (Preuss et al., 2006). The results showed that feedforward inhibition mediated by midbrain interneurons influences both the time course and the magnitude of visually evoked excitation of the M-cell and thus the behavioral threshold and timing of escape.

Motor planning is closely related to decision making. As described above, decision making determines what kind of behavior the animal will perform (swimming or crawling, freeze or tail-flip) and whether or not the specific behavior will be carried out (escape or stay). On the other hand, motor planning determines how the animal will organize and perform forthcoming behavior. Thus, these two higher brain functions are thought to comprise different brain processes. Indeed a recent neurophysiological experiment showed that a perceptual decision and the associated oculomotor plan are represented in different manner in the monkey lateral intraparietal area (Bennur and Gold, 2011). Moreover, it was found that, in the rhesus monkey, the parietal reach region (PRR) is involved when the effector decision (saccade vs reach) is being made, while cells in dorsal area 5 in the posterior parietal cortex (PPC) encode the selected reach plans after the effector is unambiguously specified as the arm (Cui and Andersen, 2011).

Motor planning, as well as decision making, also has been studied mainly in primates including humans by means of behavioral experiments. In the monkey, it was found that the termination of head movement and the subsequent maintenance of posture are centrally preprogrammed and are not dependent upon the readout of proprioceptive afference generated during the movement (Bizzi et al., 1976). In humans, the peak velocity of an eye saccade is determined by the size of the actual eye movement rather than the size of target movement and is thus a ballistic movement generated without the need of sensory feedback during its execution (Bahill and Stark, 1979).

The neuronal correlates of motor planning also have been studied mainly in primates including humans. For example, planning or “set-related” activity in the monkey premotor cortex has been thought to be a neuronal correlate of motor planning. It is defined as neuronal activity that starts once a forthcoming movement is instructed and continues until the movement is executed (Weinrich and Wise, 1982; Wise, 1985). It was found that set-related activity reflects movement parameters, such as the direction and amplitude of arm movements (Fu et al., 1995; Kurata, 1993; Messier and Kalaska, 2000; O'Leary and Hatsopoulos, 2006). In further research on monkey arm movement, analysis of neural variability in the premotor cortex during the delay period, and of the effects of microstimulation of the premotor cortex, showed that the set-related preparatory activity in the premotor cortex facilitates the initiation of arm movement (Churchland et al., 2006b; Churchland and Shenoy, 2007). In the human brain, a non-invasive fMRI study revealed the neuronal correlate of motor planning in response to an approaching danger (Billington et al., 2011; Coull et al., 2008).

Recently, motor planning also has been studied in non-primate animals, including insects. It was shown that, approximately 200 ms before takeoff, both the fly and the locust begin a series of postural adjustments so that leg extension will push them away from a looming threat (Card and Dickinson, 2008; Santer et al., 2005). However, these preflight movements are different from motor planning observed in human and other primates since the former involves preparatory motor outputs for movements of the body itself while the latter is not accompanied by any body movement in advance of its possible execution.

Here we analyze a correlation between the turn angle and the angular velocity of frog collision avoidance behavior in response to an approaching object in the upper visual field. The results suggested that, without any movement of the body, frogs plan velocity control of collision avoidance behaviors in advance of their execution. This motor planning resembles that found in human saccadic eye movements and in owl saccadic head movements. So far, many behavioral experiments have shown that animals produce collision avoidance behavior to an approaching danger when the size of the retinal image subtended by the object reaches a constant threshold value (Fotowat and Gabbiani, 2011; Robertson and Johnson, 1993a; Robertson and Johnson, 1993b; Schiff, 1965; Yamamoto et al., 2003). However, due to the time required to turn through large angles, frogs should jump later when avoiding an approaching danger in a backward rather than forward escape behavior. The additional new finding in this study is that, unlike previous behavioral reports, the threshold angular size for the collision avoidance behavior varied depending on the upcoming behavior. Thus, we conclude that control of threshold angular size in collision avoidance behavior, like perisaccadic modulation of the lateral geniculate nucleus (LGN) activity in the monkey (Royal et al., 2006), would provide a very useful model to study the neuronal mechanisms underlying modulation of sensory information processing by motor planning.

Previous behavioural and electrophysiological research in our lab has shown that 1) the frog displays collision avoidance behavior in all or none fashion when the visual angle of a looming object reaches a constant value (Yamamoto et al., 2003), and 2) collision-sensitive neurons exist in the frog optic tectum and signal the retinal threshold size of an approaching object, in good agreement with the results from our behavioral experiments (Nakagawa and Hongjian, 2010). These findings provide the background for an analysis of subcortical neuronal mechanisms responsible for motor planning in this model animal.

Results

The angular velocity of escape behavior is controlled by the turn angle

To avoid an approaching danger, the frog jumps in various directions depending on the stimulus location and the position of barrier objects around the animal. Here, we examined the escape direction of the frog in response to looming objects which appeared in the upper visual field. In Fig. 1 the stimulus positions are represented by dots on concentric circles (vertical and horizontal eccentricity, ξ and Φ, respectively, relative to the animal, which is placed at the center of the concentric circles). The escape direction α was represented by a short bar extending from a dot. The bars seem to orient radially from the center of the concentric circles. This shows, unexpectedly, that the animals turned toward, not away from, the stimulus. The frog usually remained stationary, close to one of the walls or the corner of the experimental box. When the animal faced toward the center of the box, the wall or the corner was behind the animal and the looming stimulus was presented in the anterior upper visual field. In this case, the animal jumped forward in response to the stimulus instead of turning and colliding with the wall behind it. On the other hand, when the animal faced toward one of the walls, or the corner of the box, the looming stimulus was presented in the posterior upper visual field. In this case, the animal turned away from the wall and jumped in response to the stimulus. Thus the frog was actually jumping obliquely toward the stimulus. This is why the frog appeared to turn toward, rather than away from, an approaching danger in Fig. 1.

Fig. 1. Stimulus positions and escape directions.

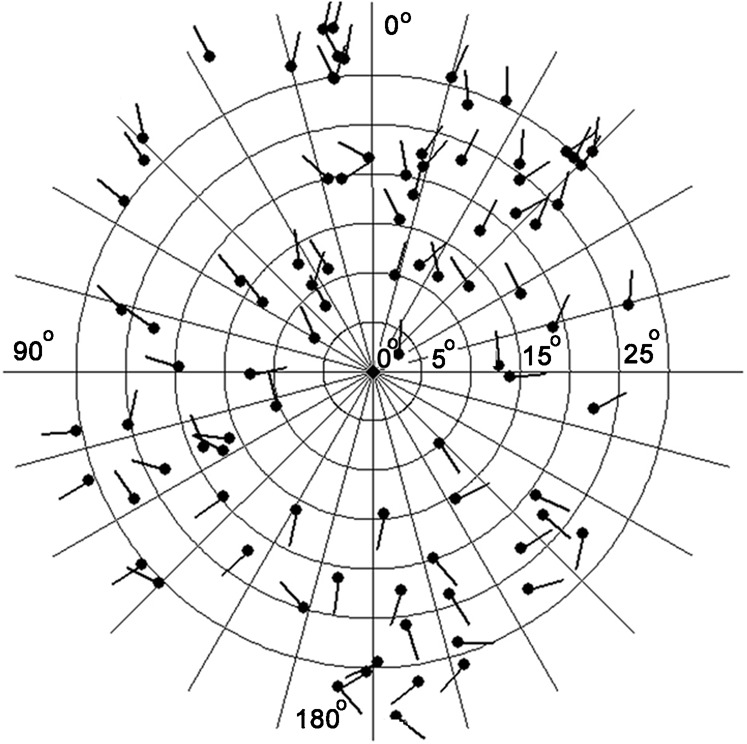
Vertical and horizontal eccentricities of the stimulus (ξ and Φ) are represented with concentric circles and radial lines, respectively. The frog is located at the center of the concentric circles facing 0° (upward on diagram). The stimulus position relative to the animal is represented by a large dot. The escape direction is represented by a bar extending from the dot. The bars seem to orient radially from the center of the concentric circles.

As shown in Fig. 1, the frog performed turns with various amplitudes during the collision avoidance behaviors. Does the velocity of the escape turn vary depending on the turn amplitude or is it constant? To clarify this, we examined the escape direction α and the angular velocity ω and found a significant (P<0.05) correlation between these variables (r² = 0.5741) (Fig. 2). This result suggests that the escape velocity was not constant but varied with the turn angle. Because the turn angle is not affected by visual feedback and must be determined in advance of its execution, it is likely that the frog had planned the escape velocity prior to executing the turn. Fig. 3 shows a correlation between α and behavioral duration τ. The slope of the regression line was very small (0.0026 s/deg, r² = 0.118), indicating that the behavioral duration was almost constant and independent of the escape direction. Thus, the frog increased the angular velocity of its escape turns to achieve greater turn angles, while the behavioral duration remained relatively constant.

Fig. 2. Scatter plot showing a significant positive correlation (P<0.05) between the escape direction α and the angular velocity ω of the escape behavior (r² = 0.5741).

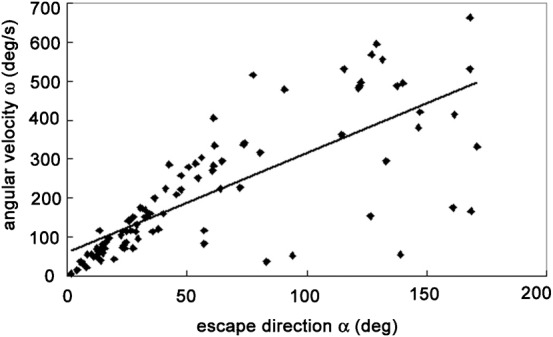
Data points obtained from right turns are shown as they would appear after reflection around the mid sagittal plane.

Fig. 3. Scatter plot showing a correlation between the escape direction α and behavioral duration τ of the escape behavior (r² = 0.118).

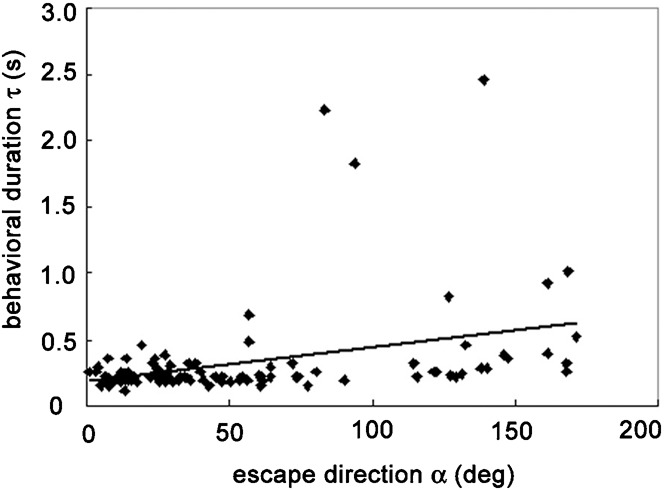
Data points obtained from right turns are shown as they would appear after reflection around the mid sagittal plane. The slope of the regression line is 0.0026 s/deg, suggesting almost constant behavioral duration.

The threshold angular size of escape behavior is affected by the turn angle

During collision avoidance behaviors, the frog jumps forward or makes turns depending on the experimental situation. So far, it has been believed that the animal produces collision avoidance behaviors when the size of the retinal image subtended by an object reaches a constant threshold value. However, if this hypothesis is correct, the frog should be late in jumping and could fail to avoid an approaching danger in backward escapes accompanied by a turn of large amplitude. Therefore, we examined the correlation between α and the angular threshold θth. We found a small but significant negative correlation (r² = 0.1145, P<0.05) (Fig. 4), which we confirmed by comparison of the mean θth values between forward (0°≤α≤90°, 270°≤α≤360°) and backward (90°≤α≤270°) escape jumps (Fig. 5). The mean value of θth for forward jumps (18.51 ± 8.58°, n = 67) was significantly larger (P<0.05) than that for backward jumps (13.95 ± 5.20°, n = 23). These results suggest that the threshold angular size is also controlled by the turn angle and is modified by motor planning.

Fig. 4. Scatter plot showing a significant negative correlation (P<0.05) between the escape direction α and the angular threshold θth of escape behavior (r² = 0.1145).

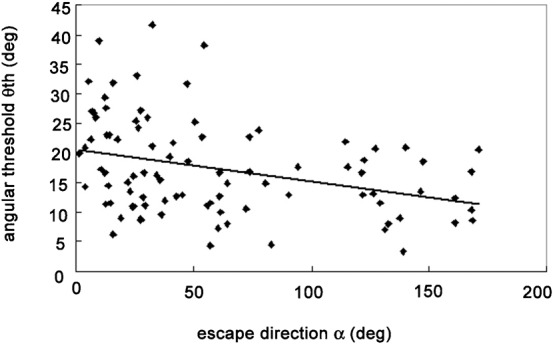
Data points obtained from right turns are shown as they would appear after reflection around the mid sagittal plane.

Fig. 5. Comparison between mean (± s.d.) angular thresholds (θth) triggering forward (0°≤α≤90°, 270°≤α≤360°) versus backward (90°≤α≤270°) escape jumps.

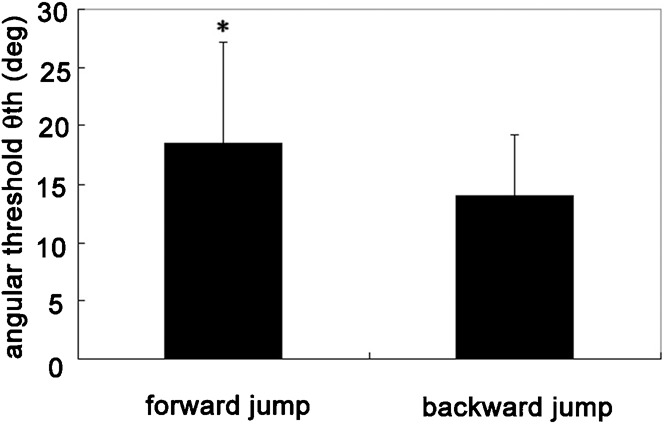
The former is significantly larger than the latter (P<0.05).

The frog changes escape strategy depending on turn amplitude

The dependence of the angular velocity ω, the behavioral duration τ and the angular threshold θth on the escape direction α is shown in Figs 2, 3, 4, respectively. In all three scatter plots, the distribution patterns of the data for escape turns less than 60° on either side of the midline seemed to differ from the patterns for escape turns greater than 60° from the midline. First, the mean θth of escape turns less than 60° on either side of the midline was 19.6 ± 8.73° (n = 55) while that of escape turns more than 60° from the midline was 13.81 ± 5.37° (n = 35). This confirmed the negative correlation between α and θth described above and also showed a larger variability in the former than the latter. Second, the mean ω of escape turns less than 60° on either side of the midline was 117.83 ± 77.62°/s (n = 55) while that of escape turns greater than 60° from the midline was 364.75 ± 161.41°/s (n = 35). This confirmed the positive correlation between α and ω described above. However, it is interesting that the correlation was much stronger in escape turns less than 60° than those greater than 60°. Thus, the r² value calculated for the data plots of escape turns less than 60° on either side of the midline was much larger than that calculated for all the data points (r² = 0.7097 and 0.5741, respectively). Furthermore, in escape turns greater than 60°, the correlation was not significant (r² = 0.065, P>0.05). Finally, the mean τ of escape turns less than 60° on either side of the midline was 0.24 ± 0.1 s (n = 55) while that of escape turns greater than 60° from the midline was 0.49 ± 0.56 s (n = 35). The very small variability in the former indicates that τ is kept almost completely constant in escape turns less than 60°.

Based on these observations, we propose a hypothetical control strategy for collision avoidance behavior depending on the turn angle executed by the frog. For escape turns less than 60° on either side of the midline, the positive correlation between α and ω was very strong and the variance of τ was very small. This shows that the frog controlled the angular velocity very accurately and completed escape turns within a constant time for the small turns. On the other hand, the variance of θth for small turns was quite large. The frog could successfully avoid an approaching danger with an accurate control of the angular velocity for escape turns of small amplitude on either side of the midline irrespective of the threshold angular size. For escape turns greater than 60° from the midline, the positive correlation between α and ω was not observed and the variability of τ was very large. This shows that the frog was not able to control the angular velocity accurately due to the large turn amplitude so that the animal did not complete escape turns within a constant time. On the other hand, the variability of θth for the large turns was quite small. Thus, the frog started to escape earlier, at smaller threshold angular sizes to compensate for its unsuccessful control of the turn velocity for turns greater than 60° from the midline.

Unsuccessful control of the escape angular velocity is compensated by control of the threshold angular size

To test our hypothetical behavioral strategy, we examined correlations between the angular velocity ω and the angular threshold θth in escape turns less than and greater than 60° on either side of the midline (Fig. 6). In the former, no significant correlation was found (r² = 0.0065, P>0.05) (Fig. 6A). On the other hand, in the latter, a significant positive correlation occurred (r² = 0.1459, P<0.05) (Fig. 6B). This suggests that the threshold is controlled to compensate for the insufficient escape velocity in large escape turns, but not in small escape turns where the animal can control the turn velocity accurately and successfully escape within a constant time.

Fig. 6.

(A) Scatter plot showing no significant correlation (P>0.05) between the angular velocity ω and the angular threshold θth of escape turns less than 60° on either side of the midline. (B) Scatter plot showing a correlation between ω and θth of escape turns of more than 60° from the midline. There is a significant positive correlation between them (P<0.05).

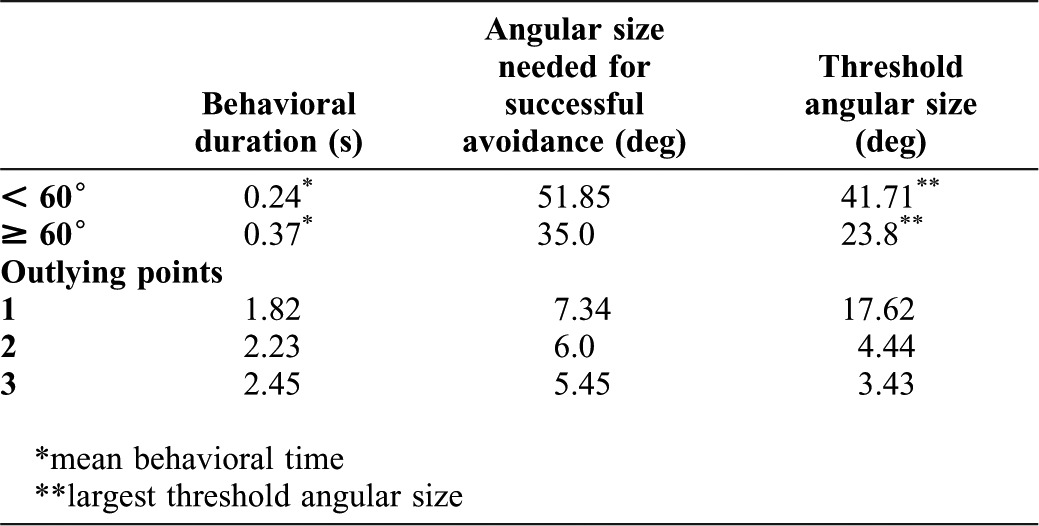
Finally, we tested theoretically whether the animal could succeed in avoiding an approaching danger with this behavioral strategy or not. The results are summarized in Table 1. The mean behavioral duration of escape turns less than 60° on either side of the midline was 0.24 s (n = 55). The calculated critical angular size needed for successful avoidance within the behavioral duration was 51.85°. The largest threshold angular size obtained from the experiment was 41.71°. Therefore, with small turns, the animals could avoid collisions successfully. On the other hand, the mean behavioral duration of escape turns greater than 60° from the midline, except for three outlying points, was 0.37 s (n = 32). The calculated critical angular size needed for successful avoidance within the observed behavioral duration was 35.0°. The largest threshold angular size obtained from the experiment was 23.8°. Therefore, also in large turns, the animal could avoid collisions successfully. As for the three outliers, the behavioral duration and the calculated critical angular sizes were 1.82 s and 7.34°, 2.23 s and 6.0°, 2.45 s and 5.45°, respectively. The corresponding angular threshold sizes obtained from the experiment were 17.62°, 4.44° and 3.43°, respectively. Thus, surprisingly, even in these trials with exceptionally long behavioral duration, the animals would have been able to avoid collisions successfully in two of the three trials.

Table 1. Comparison of calculated critical angular size needed for successful avoidance and the threshold angular size obtained from experiments.

Discussion

Control of behavioral output by motor planning

Unlike simple reflexes, the behavior studied here is not completely dependent on external stimuli, but is planned prior to execution for successful performance based on sensory information. Such motor planning requires sensory input as a trigger but does not rely on sensory input during the planning and behavioral phases. Related behaviors have been studied mainly in primates.

However, motor planning also has been observed in animals other than humans and primates. Such studies have uncovered different types of behaviors which appear to be motor planning but which may have different underlying control mechanisms. Some behaviors observed in non-primate animals can be controlled by sensory feedback, although they are seemingly planned in advance of execution. Here, we call such planning “apparent motor planning”. For example, some predators appear to control their flight trajectory to pursue and catch the prey animal at a point in front of the prey, thus predicting the flight path of the moving prey (Collett and Land, 1978; Ghose et al., 2006; Olberg et al., 2000). Dragonflies perching on the ground or on vegetation take off and pursue small flying insects as they pass. It was found that the dragonflies fly directly toward the point of prey interception by steering to minimize the movement of the prey's image on the retina during pursuit (Olberg et al., 2000). Echolocating bats rely on sonar to pursue and capture flying insects which often move unpredictably. The bat adjusts its direction of flight so as to maintain a constant absolute direction to the target to pursue such erratically moving prey (Ghose et al., 2006). In both cases, the dragonfly or the bat do not head for a predicted point of interception, but know how to get to that point simultaneously with the arrival of the prey animal, under control of visual, or vestibular and acoustic feedback, respectively.

On the other hand, recent papers have demonstrated that motor planning which does not comprise simple reflexes is indeed carried out in non-primate animals, even in insects with tiny nervous systems. The fruit fly can plan an escape trajectory that takes into account both its initial posture and the direction of approach of a looming stimulus. The fly repositions its legs and the center of mass during approach of the looming visual stimulus so that leg extension pushes it away from the threat successfully. The preparatory movements occur up to 200 ms prior to executing the main part of the jump (Card and Dickinson, 2008). The locusts can also direct their jumps away from looming threats, although their accuracy is much coarser than that of flies. The animals direct their jumps by rolling and yawing movements of the body that are controlled by the fore- and mid-legs prior to hind leg extension (Santer et al., 2005). In both cases, the motor planning involves some kind of movement of the body. In this sense, the motor planning observed in insects is different from that observed in humans. Here, we call such planning “motor planning in a wide sense”.

In primates, a motor action can be planned without any movement of the body in advance of its possible execution. Here, we call such planning “motor planning in a narrow sense”. In the present study, we have possibly found this type of motor planning in frog collision avoidance behavior. The escape direction and the angular velocity of turning showed a significant linear correlation (r² = 0.5741) (Fig. 2). Thus, the escape velocity was determined by the turn angle. Because the act of turning was ballistic and was not affected by visual feedback, this suggests that the frog planned the velocity of turning prior to its execution. A similar observation was reported in human saccadic eye movement. The peak velocity of saccades is determined by the size of actual eye movement rather than the size of target movement (Bahill and Stark, 1979).

We also showed that the behavioral duration was almost constant, and was independent of the escape direction (Fig. 3). This suggests that the frog planned the escape velocity so that the behavioral duration was maintained at a constant level independent of turn amplitude. A similar strategy has been reported in some orienting behaviors in other species. The peak velocity of human saccades increases with eye movement magnitude so that the movement duration is maintained at a relatively constant level (Bahill and Stark, 1979). The owl responds to a sound source with a quick, stereotyped head saccade. The owl rotates its head faster toward more peripheral targets so that total time to fixation is relatively constant. The owl rarely requires more than 400 ms to fixate on any target within 70° of the animal's front (Knudsen et al., 1979).

Thus, human saccades and some orienting behaviors of other animal species, including frog collision avoidance behavior, are produced in a similar way and may involve common neuronal mechanisms for control of the velocity prior to behavioral execution. Preparatory or “set-related” activity is well known to be a neuronal correlate of motor planning in the primate (Hoshi and Tanji, 2007; Weinrich and Wise, 1982; Wise, 1985). In the monkey, it was found that a forthcoming reaching movement is represented by set-related activity in the dorsal premotor cortex and primary motor cortex during an instructed-delay task. Churchland et al. found that the set-related activity is affected by the instructed speed as well as the direction and the distance (Churchland et al., 2006a). There is an overall tendency for the fast instructed speeds to evoke higher firing rates although the opposite effect is not uncommon. The same authors also showed that both the direction and distance tuning of the preparatory activity could vary with the instructed speed. Our new finding is that similar motor planning for velocity control is possibly carried out in much “simpler” animals, lacking an elaborated cortex. Further examination of frog collision avoidance behavior and the underlying neuronal mechanisms may thus give us new ways of identifying the subcortical neuronal structures and the functional organization responsible for motor planning.

Modulation of sensory processing by motor planning

Imagine the situation of a car entering an intersection with a traffic light. If driver sees the light turn yellow before entering the intersection, he/she does not cross the intersection. However, if the driver is already in the intersection and decides to continue crossing, he/she does so even while seeing the same yellow signal. Thus, motor planning sometimes affects not only motor control but also sensory information processing which is related to the forthcoming movement. The neuronal mechanisms underlying modulation of sensory processing have been examined in several animal species.

The idea of modulation of sensory processing exerted by internal collaterals of motor signals is well known (Sperry, 1950; Von Holst and Mittelstaedt, 1950). This kind of internal signal (corollary discharge or efference copy) plays an important role in the cancellation of self-generated sensory feedback during behaviors (McCloskey, 1981). In a mormyrid fish, a brief and precisely timed electric organ corollary discharge (EOCD)-driven inhibition blocks completely the afferent response evoked by the fish's own electric organ discharge (EOD), which greatly interferes with the detection of weak signals from other fish (Bell, 1989). The firing of crayfish giant axons inhibits extensor-muscle stretch receptors to prevent resistance reflexes from interfering with powerful tail flexion (Eckert, 1961). The giant axons also curtail their own inputs by inhibiting the terminals of the mechanosensory afferents presynaptically, thereby blocking an endless cycle of tail flexion evoked by reafferent stimulation (Kennedy et al., 1980). Furthermore, internal collaterals of motor commands also modulate active sensory systems. In a gymnotid fish, activation of the command neurons for escape responses (Mauthner cells) triggers an abrupt and prolonged increase in electric organ discharge rate. The Mauthner cell-initiated enhancement of electrosensory sampling is thought to be involved in the selection of the escape trajectory (Comas and Borde, 2010; Falconi et al., 1995; Morales et al., 1993).

However, modulation of sensory processing by corollary discharge is different from modulation by motor planning. In the former, the motor command and modulation of sensory processing are generated at the same time. On the other hand, in the latter, modulation of sensory processing should precede the possible execution of the forthcoming behavior and should be generated without any movement of the body. As described above, modulation by corollary discharge has been studied intensively, while the study of the neuronal mechanism of the modulation by motor planning has been limited so far.

In this sense, presaccadic suppression in the monkey LGN has been thought to be a neuronal correlate of modulation of sensory processing by motor planning (Royal et al., 2006). Due to these suppressive responses, we are completely unaware of the visual blur that should occur while our eyes sweep the visual field at remarkable speeds. About 25% of LGN cells demonstrate perisaccadic modulation consisting of presaccadic suppression and postsaccadic enhancement. Since the onset of the modulation precedes saccades by more than 100 ms, it is concluded that this modulation reflects higher order motor planning rather than corollary discharge derived from motor commands controlling eye movement themselves.

The limited knowledge about the neuronal mechanisms underlying the modulation of sensory processing by motor planning is due to lack of useful model systems. In this study, we provided an additional example of the modulation of sensory processing by motor planning. So far, it has been shown that animals produce escape responses to an approaching danger when the size of the retinal image subtended by the object reaches a constant threshold value (Fotowat and Gabbiani, 2011; Robertson and Johnson, 1993a; Robertson and Johnson, 1993b; Schiff, 1965; Yamamoto et al., 2003). However, in the real world, animals produce escape behaviors and avoid imminent dangers in complex environments. Just because the animals can detect the critical size of the retinal image of an approaching danger does not necessarily imply that the subsequent escape behavior is always performed in fixed pattern. For example, when a barrier object is placed in front of the animal, the frog should turn and then jump to avoid an approaching danger. Here, we for the first time showed that the threshold angular size varied depending on the behavioral context in an adaptive manner: that is, the threshold angular size decreased with the amplitude of the turn angle (Fig. 4).

It could be that the change of the threshold angular size at the time of behavior is not reflected at the time of detection by the collision-sensitive neurons. However, due to the following reasons, it is unlikely that the threshold angular size is constant at the time of detection, not at the time of escape behavior. The mean θth of escape turns less than 60° on either side of the midline was 19.6°. Because the threshold value was computed based on the distance between the computer monitor and the experimental stage, the height of the frog's eye of 5 cm would yield angular size threshold value of 26.2°. On the other hand, the threshold angular size for the collision-sensitive neurons revealed by fitting analysis or linear regression analysis were 24.2° and 21.2°, respectively (Nakagawa and Hongjian, 2010). Theoretical computation shows that the times during which the visual angle of the looming stimulus increases from 24.2° and 21.2° to 26.2° are 75 ms and 125 ms, respectively. These values show a good agreement with the average delay of 148 to 222 ms between the timing of DCMD peak and the takeoff of the locust escape jumps (Fotowat and Gabbiani, 2007), and the processing delay of 65 ms between detection of the object and behavioral reaction in obstacle avoidance in flying locusts (Robertson and Johnson, 1993a). Furthermore, these values are comparable to median reaction time of 175 and 200 ms measured in delayed saccade task in cue-delay-target paradigms in two monkeys (Snyder et al., 2006). Thus, for escape turns less than 60°, the threshold angular sizes at the time of detection and escape behavior can well explain the time course of collision avoidance behavior. The mean θth of escape turns more than 60° on either side of the midline was 13.8° and the height of the frog's eye of 5 cm would yield angular size threshold value of 18.2°. In contrast to the turns less than 60°, this value is smaller than the threshold angular sizes for the collision-sensitive neurons described above. Thus, the hypothesis of the constant threshold angular size at the time of detection is not consistent with the experimental result. Therefore, we conclude that, for the turns more than 60°, the change of threshold angular size should occur at the time of detection not at the time of escape behavior.

Furthermore, we suggested that the threshold angular size is controlled in a predictive manner to compensate for the inability to generate sufficiently high velocity if an upcoming turn will have a large amplitude (Fig. 6). Since for adaptive compensation the threshold angular size should be determined prior to the execution of the turn, this sensory modulation can not be explained by corollary discharge mechanisms. Thus, we conclude that this modulation reflects higher order motor planning as found in the perisaccadic modulation of the monkey LGN activity and frog escape behaviors to looming stimuli could be a useful model system to study the underlying neuronal mechanisms.

Materials and Methods

Animals

Adult bullfrogs, Rana catesbeiana, of either sex measuring about 10 cm in length, were used exclusively. Animals were obtained commercially and kept in laboratory tanks (10 animals in each tank) under a 12 h light/12 h dark cycle at 25°C before use. They were fed on chicken liver once a week. In preliminary escape testing, animals that responded at least once in four trials to the visual looming stimuli used in the following experiment (see below) were selected for experimental use. The test was performed at least one day before the behavioral experiments to avoid habituation to the visual stimulus.

Behavioral experiments

All experimental procedures were approved by the Kyushu Institute of Technology Animal Institutional Review Board and were in accordance with Kyushu Institute of Technology Animal Care Use Regulations and NIH Guidelines on the Care and Use of Animals in Research. A frog was placed on a transparent experimental stage and covered with a wooden box (27 cm long × 19.5 cm wide × 18 cm high) having white inner walls and a transparent upper surface. Before testing, the animal was allowed to acclimate for 3 min in the box. Looming visual stimuli generated by a computer were presented in the dorsal visual field of the animal on a computer display placed 20 cm above the experimental stage. The evoked escape behavior was recorded by a substage CCD camera (CSS110C; Tokyo Denshi Kogyo, Tokyo, Japan) and a videocassette recorder (SVO-2100; Sony, Tokyo, Japan) at 30 frames per second. A video timer (VTG-55; Houei, Tokyo, Japan) was used to show elapsed time (in ms) since the stimulus onset in the video frames. The PC generated a TTL signal at the stimulus onset. It was also recorded on a video tape through a D/A converter (PCI-3336; Interface, Hiroshima, Japan) and used to synchronize image capture to the stimulus onset. The behavior was also monitored simultaneously with another display (DTV-142G; Daewoo, Tokyo, Japan). Looming stimuli were presented to 42 animals. Each frog was presented with 6 successive visual stimuli at 3 min intervals, to avoid habituation. All experiments were carried out at room temperature (18–22°C).

Visual stimulation

Visual stimulation of an approaching object was produced by the 2-dimensional expansion of a stimulus square, as viewed by the animal. The animation was run on a PC Intel(R)Core(TM)2Quad CPU 2.4 GHz equipped with 2.0 GB of RAM, an ASUS EH8600GTS Graphics Controller and NEC model D-151 15-inch Multi-Scan Color Monitor set to a refresh rate of 60 Hz. It simulated the approach of a black square (35 × 35 cm) approaching at a velocity of 1.5 m/s through a path of 6 m. The background and the stimulus square had an average illuminance of 110 and 8 lux, respectively. The looming stimulus was presented at a distance of 1/3 of the display width from the left or the right margins of the display in random fashion. This allowed us to obtain data where the position of the stimulus relative to the animal changed extensively.

Analysis

Each video clip of avoidance behavior was fed into a computer through an NTSC video capture card (SIM-PCI; Ditect, Tokyo, Japan) and saved as 110–120 successive still video frames. Of these frames, the critical ones were de-interlaced into video fields separated by 16.6 ms. To measure the animal and the stimulus positions, the coordinates of the snout and the vent of the frog and the coordinates of the center of the looming stimulus were obtained by means of a custom VC++ program. Based on the coordinates and the calibration of body length, the following parameters were computed using the same program. 1) Vertical eccentricity of the stimulus (ξ) was represented with concentric circles where the center (vertical eccentricity of 0°) corresponded to the superior pole of the frog visual field. Thus, the horizontal plane passing through the experimental stage corresponded to 90°. But the maximal value in our experimental situation was limited by the display width and was less than 40°. 2) Horizontal eccentricity of the stimulus (Φ) was represented by a counterclockwise angle with respect to the sagittal plane of the animal. The stimulus position directly rostral to the frog's snout represented 0° and one directly caudal represented 180°. 3) The escape direction (α) was also represented by a counterclockwise angle with respect to the sagittal plane of the animal. If the animal turned directly toward the stimulus, the turn angle would be exactly equal to the stimulus angle Φ. The frog rarely makes a turn greater than 180°. Moreover, left and right turns are considered as symmetrical movements. Therefore, in some graphs (Figs 2, 3, 4), data points obtained from the right turn are shown as they would appear after reflection with respect to the mid sagittal plane. 4) Behavioral duration (τ) was the time between the onset of the animal's movement and the time when the animal completed the turn and stopped the movement. 5) The angular velocity of turning (ω) was computed with the following equation:

(1)

6) The threshold stimulus size on the screen triggering avoidance behavior (r) was calculated from the time when the animal started to move in response to the expanding stimulus by the following equation:

(2)

where h denotes the height of the display above the experimental stage (20 cm), l denotes the object size (35 cm), p denotes an initial distance of the simulated path (6 m), v denotes an approaching velocity (1.5 m/s) and t denotes the delay between the onset of stimulus and the time when the frog first moved (Fig. 7). Since the surface of the monitor is flat, the larger the distance between the animal and the stimulus became, the smaller the angular threshold (θth) for the same value of r became. Therefore, θth was calculated by different equations depending on the distance between the animal and the center of the stimulus projected on the experimental stage (d). If d > r/2, θth was calculated by the following equation:

(3)

If d ≤ r/2, θth was calculated by the following equation:

(4)

where h denotes a height of the display above the experimental stage (20 cm), r denotes the threshold of the stimulus size triggering avoidance behavior, and d denotes the distance between the animal and the center of the stimulus projected on the experimental stage.

Fig. 7. The stimulus simulated a black square approaching at a constant speed v with size l through a path of p.

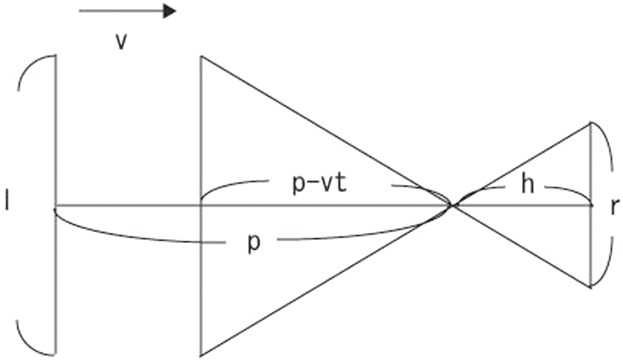
The threshold of the stimulus size on the screen placed h above the experimental stage was calculated by the equation, r  =  hl/(p − vt), where t denotes the delay between the onset of stimulus and the time when the frog start to move.

Statistics

Statistical analysis was performed with the aid of Excel 2003 (Microsoft, Tokyo, Japan). Scatter plots were used to examine the correlation between α and ω, α and θth, α and τ, θth and ω. Linear regression was used to calculate a measure of spread (r²) for these plots (significance level, P<0.05). Averages reported here were given as the mean ± the standard deviation. Student's t test for unpaired data sets was used to compare the means of threshold angular size between forward and backward escape behavior.