Further optimization of a hybrid united-atom and coarse-grained force field for folding simulations: Improved backbone hydration and interactions between charged side chains

Abstract

PACE, a hybrid force field which couples united-atom protein models with coarse-grained (CG) solvent, has been further optimized, aiming to improve itse ciency for folding simulations. Backbone hydration parameters have been re-optimized based on hydration free energies of polyalanyl peptides through atomistic simulations. Also, atomistic partial charges from all-atom force fields were combined with PACE in order to provide a more realistic description of interactions between charged groups. Using replica exchange molecular dynamics (REMD), ab initio folding using the new PACE has been achieved for seven small proteins (16 – 23 residues) with different structural motifs. Experimental data about folded states, such as their stability at room temperature, melting point and NMR NOE constraints, were also well reproduced. Moreover, a systematic comparison of folding kinetics at room temperature has been made with experiments, through standard MD simulations, showing that the new PACE may speed up the actual folding kinetics 5-10 times. Together with the computational speedup benefited from coarse-graining, the force field provides opportunities to study folding mechanisms. In particular, we used the new PACE to fold a 73-residue protein, 3D, in multiple 10 – 30 μs simulations, to its native states (C_α RMSD ~ 0.34 nm). Our results suggest the potential applicability of the new PACE for the study of folding and dynamics of proteins.

Introduction

Molecular dynamics (MD) has become an indispensable tool for revealing the molecular mechanism of biological processes.^1,2,3 Despite ever-growing computing power and better sampling methods,^4,5,6 all-atom MD simulation cannot achieve for the modeling of large biomolecular systems over time-scales long enough to be of biological interest. To overcome the challenge, coarse-grained (CG) models, in which multiple atomistic sites are grouped into one site, have been developed for proteins, solvent and membrane, significantly enhancing the speed of simulation.^7,8,9 However, due to inherent simplification, many CG simulations of proteins rely on information from native protein structures through biased methods such as elastic network models¹⁰ or Gõ-type potentials.¹¹ The CG models are limited, therefore, in their use in studies of folding, aggregation, large conformational change of proteins or conformational features of intrinsically disordered proteins.¹²

To alleviate the reliance on native structures, several CG protein models have been parameterized to reproduce peptide folding^13,14,15,16 or have been built on knowledge-based statistical potentials,^17,18,19,20 achieving even in some cases predictive capabilities.^{21,22,23,24,25} Nevertheless, it may be more advantageous to combine atomistic and CG models so that protein models contain enough atomistic detail to obviate the need for information on native structures while environments such as water and membrane are still coarse-grained. Such multiscale approaches have been practiced in numerous studies.^26,27 For example, in an early study,²⁸ a small portion of a protein was modeled with an all-atom force field while the rest of the protein was coarse-grained with a Gô model. The model developed by Shi and coworkers²⁹ combined all-atom protein force fields with multiple-site lipid and single-site water. A key element in their model is to parameterize interactions between sites of different resolutions by matching the forces calculated from actual atomistic simulations, allowing the model to maintain the stability of small membrane proteins without any biased constraint. Rzepiela and coworkers³⁰ have recently proposed a mixed model of all-atom and MARTINI CG force fields,^31,32 the latter of which has proven to be efficient for lipid and solvent simulations.^33,34 In their model, all-atom/CG interactions are replaced by CG interactions through dummy sites, such that need for re-parametrization of cross-resolution terms does not arise. The model has been tested for the case of partition of dialanine in different solvents, showing promising results.³⁰

In the present study we focus on another hybrid force field, namely PACE,³⁵ in which a unitedatom protein model has been developed in conjunction with MARTINI CG water^35,36,37 and re-cently also with some of MARTINI CG lipids.³⁸ In PACE, cross-resolution parameters were optimized through a thermodynamic-based approach, i.e., through reproducing experimental thermodynamic quantities, which is in line with the parameterization scheme of MARTINI. Moreover, in the context of the hybrid force field, the interactions of atomic sites in proteins were parameterized by using different data as references, such as potential of mean force (PMF) profiles of polar interactions from atomistic simulations and statistical backbone potentials from a PDB coil library.³⁹ Comprising such different ways of parametrization, PACE has successfully folded several model peptides, not relying on information of their native structures.⁴⁰ However, the stabilities of the native structures were generally underestimated by PACE, suggesting that further improvement of PACE is needed.

Hydration of the backbone is known to be critical for controlling the balance between unfolded and folded states of proteins.^41,42 In PACE, backbone and side-chain amide groups shared the same set of hydration parameters to describe interactions between amide groups and CG water, optimized by fitting hydration free energy of N-methylacetamide (NMA).³⁵ Although NMA was referred to as a model compound for amide groups in early studies,⁴³ both theoretical^44,45,46 and experimental⁴⁷ studies have demonstrated that NMA favors hydration too much to furnish a suitable model for an internal amide group in longer polypeptides, owing to the well-known end-group effects in polymers. It was assumed that in PACE the hydration parameters obtained with NMA could be used for peptide backbone hydration, but such an assumption had not been examined. Therefore, the hydration parameters need to be investigated and, very likely, re-optimized by using model compounds other than NMA. We chose polyalanyl peptides as model compounds, the hydration free energies of which are experimentally unavailable but can be obtained from atomistic simulations.

We also investigated the parameters for electrostatic interactions. In PACE, electrostatic interactions were modeled by effective potentials³⁵ other than Coulomb potentials. Such approach reduced the number of parameters needed for PACE, but renders PACE less compatible with MARTINI that uses Coulomb potentials for interactions between charged groups³¹ and, thereby, potentially complicates actual parametrization of cross-resolution terms. Also, the physical meaning of the approach is less clear, which may lead to difficulties in interpreting simulation results related to electrostatic interactions. Accordingly, we added Coulomb potentials back to PACE for interactions between charged groups. The parameters for Coulomb potentials, i.e., atomistic partial charges, were directly taken from all-atom force fields, as is done for most of the hybrid force fields.^28,29,30 The transferability of the atomistic charges was then evaluated through comparison between PMFs from PACE and atomistic simulations.

The new PACE was validated by ab initio folding simulations of a series of peptides and proteins, as summarized in Table 1. These peptides and proteins have a wide spectrum of structural motifs including α-helix (Fs^48,49,50), β-strands (GB1p⁵¹ and its mutants^52,53), α-PPII (Trp-cage⁵⁴), ββα (BBA5⁵⁵) and ααα (α3D⁵⁶) systems, providing a robust test of whether the force field is balanced among different structures. Using an enhanced sampling method, namely replica exchange molecu-lar dynamics (REMD),⁴ we were able to perform extensive conformational sampling and, thereby, could compare systematically the simulated results with thermodynamic and structural quantities measured in experiments. We show that the force field has been significantly improved in reproducing experimental observations. Also, standard MD simulations were carried out to demonstrate the ability of the force field to fold small peptides and proteins at physiological temperature, including the 73-residue α3D. Therefore, our force field is potentially useful to study folding and dynamics of whole protein systems.

Table 1.

Summary of peptides and proteins studied, including their sequences, melting temperatures T_m (K), folded populations near room temperature and RMSDs (nm) of representative structures from both experiments and current work, as well as respective representative computational studies by other groups.

Name	Sequence	Experiment		Current work			Refs
		Fold%	T m	Fold%	$T_m^g$	RMSD
AK17a	Ac-(AAKAA)3GY-NMe	30 – 35b		42 ± 5	N.D.h,i		57
Fs	Ac-A5(AARAA)3-NMe	~ 50b	~ 300	45 ± 2	N.D.h,i		58,59
GB1p	GEWTYDDATKTFTVTE	~ 30c	< 273	31 ± 9	N.D.h,i	0.11k	60,61,62 21,63,64 65,66
D47P	GEWTYDPATKTFTVTE	~ 50c	299-311	54 ± 7	300-308	0.12	63
GB1m2	GEWTYNPATGKFTVTE	~ 75c	318-322	79 ± 7	324-332	0.12	64
Trp-cage	NLYIQWLKDGGPSSG RPPPS	~ 70d	~ 315	68 ± 9	~ 324	0.13	63,64,67 21,68,69 70,71,72 73,74
BBA5	Ac-YRVpSYDFSRSDEL AKLLRQHAG-NMe	~ 20e	< 273	27 ± 9	N.D.h,i	0.19	75,76,77
α3D	MGSWAEFKQRLAAIK TRLQALGGSEAELAA FEKEIAAFESELQAY KGKGNPEVEALRKEA AAIRDELQAYRHN		> 363f		N.D.h,j	0.34	78,79

^aNote that as AK17 was used to parameterize the force field, it is not included in the test set.

^bHelical contents measured by CD at 300 K.^48,80

^cMeasured by NMR chemical shifts at 298 K.⁵³

^dEstimated from the melting curve at 300 K measured by NMR.⁵⁴

^eMeasured by CD and uorescence experiments at 293 K for its V3Y/F8W mutant.⁷⁵

^fMeasured by CD at pH 7.0.⁸¹

^gSimulated T_m values were determined by surveying all replicas in the REMD simulations for the one in which the probability of folded states is closest to 50%.

^hNot determined.

ⁱFor AK17, Fs, GB1p and BBA5, T_m values could not be determined because the probability of folded states was lower than 50% for all replicas with temperature above 300 K. Below 300 K, the CG water tends to freeze³¹ and, thus, simulations of protein folding become impossible.

^jIt is still difficult to achieve an equilibrium sampling of a protein of such size (73 a.a.), even through REMD, and, therefore, we were not able to determine T_m for α3D.

^kRMSDs were calculated based on backbone+C_β for GB1p, D47P and GB1m2, backbone (3-19) for Trp-cage, backbone (1-22) for BBA5 and Cα for α3D.

Models and Methods

In the following we introduce the terms in the PACE force field as well as describe briefly the simulation conditions and the secondary structure analysis applied to folding trajectories.

PACE force field

The details of PACE and its parametrization have been discussed in previous studies.^35,37 Only a brief introduction will be given here. PACE preserves all heavy atoms in proteins as well as their backbone and side-chain amide hydrogen atoms.³⁵ The overall potential energy of PACE is expressed as

$$E=E_{\text{bond}}+E_{\text{angle}}+E_{\text{dilhedral}}+E_{\text{improper}}+E_{\varphi ,\psi ,{\chi }_1}+E_{\text{CGW}-\text{CGW}}+E_{\text{CGW}-\text{UA}}+E_{\text{vdW}}+E_{\text{polar}},$$ (1)

where the first four terms account for generic bonded interactions (E_local) mediated through covalent bonds, E_{ϕ, ψ, χ1} accounts for local interactions involved with rotamers of backbone (ϕ, ψ) and side chains (χ₁), and the remaining terms account for non-bonded interactions. Specifically, the first four terms describe the energy associated with molecular geometries

$$\begin{array}{cc}\hfill E_{\text{local}}& =\sum _b\frac{1}{2}{K}_{\text{bond},\text{b}}{(r_b-r_{0,b})}^2+\sum _a\frac{1}{2}{K}_{\text{angle},\text{a}}{({\theta }_a-{\theta }_{0,a})}^2\hfill \\ \hfill & +\sum _d{K}_{\text{dih},d}[1+\cos (n_d{\zeta }_d-{\zeta }_{0,d})]+\sum _{1-4\text{pair}}4{∊}_{14,ij}\left(\frac{{\sigma }_{14,ij}^{12}}{r_{ij}^{12}}-\frac{{\sigma }_{14,ij}^6}{r_{ij}^6}\right)\hfill \\ \hfill & +\sum _i\frac{1}{2}{K}_{\text{imp},i}{({\xi }_i-{\xi }_{0,i})}^2.\hfill \end{array}$$ (2)

In Eq 2, bonds and angles are governed by harmonic potentials with respective force constants K_bond = 1.25×10⁵ kJ·nm⁻² and K_angle = 300 kJ·mol⁻¹rad⁻². The equilibrium bond lengths r₀ and angle values θ₀ were taken from optimized geometries by quantum mechanics (QM) calculations.³⁷ Dihedral potentials consist of both a cosine function of a dihedral, and the Lennard-Jones (LJ) potentials for 1-4 atom pairs associated with the dihedral. The dihedral parameters were obtained by fitting QM dihedral potential profiles of small molecules.³⁷ Improper terms, imposing constraints (K_imp = 300 kJ·mol⁻¹rad⁻²) on four sites of a dihedral angle, are used to maintain planarity or chirality of groups.

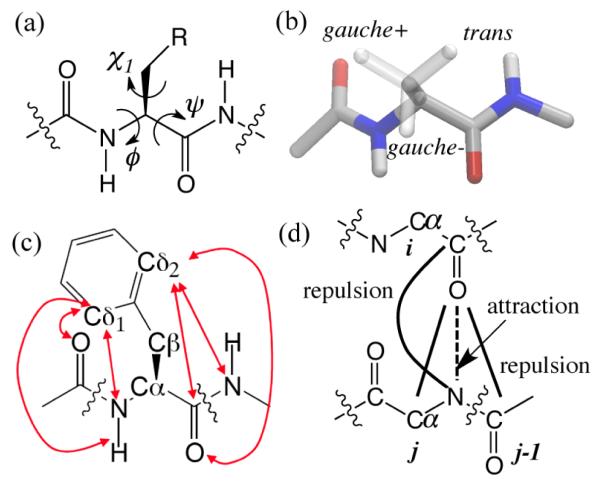
PACE is designed to provide correct description of conformational distributions of backbone (ϕ, ψ) and side chains (χ₁) (Figure 1a) for all amino acids. Previous statistical studies^39,82 have shown that the same amino acid assumes significantly different backbone (ϕ, ψ) conformations for distinctly different side chain conformations, such as rotamers gauche+, gauche− and trans (Figure 1b), the difference arising from conformationally specific interactions between side chain and adjacent backbone. The dependence between backbone and side-chain conformations is accounted for in PACE through the terms E_{ϕ, ψ, χ1},³⁵ which are expressed as

$$E_{\varphi ,\psi ,{\chi }_1}=\sum _d\sum _{n_d=1}^{N_d}{K}_{{\text{dih}}_{n_d},d}[1+\cos (n_d{\zeta }_d-{\zeta }_{0_{n_d},d})]+\sum _{\text{short}}4{∊}_{\text{short},ij}\left(\frac{{\sigma }_{\text{short},ij}^{12}}{r_{ij}^{12}}-\frac{{\sigma }_{\text{short},ij}^6}{r_{ij}^6}\right).$$ (3)

As shown in the equation, cosine functions with different multiplicities (n) are applied to the dihedral ϕ, ψ, or χ₁ for a more accurate description of dihedral potentials. Furthermore, certain short-range atom pairs, analogous to the pairs with 1-4 relationship, but separated by more than three covalent bonds, have separate parameters (ε_{short, ij} and σ_{short, ij}) to model the interactions between a side chain and its adjacent backbone. An example of such pairs in Phe is illustrated in Figure 1c, as indicated by arrows. The parameters K_dihn, ζ_0n, ε_{short, ij} and σ_{short, ij} in Eq 3 were optimized, through iterative equilibrium simulations,³⁵ against side-chain rotamer distributions and rotamer-dependent backbone conformations from a coil library.³⁹

Figure 1.

(a) Schematic representation of dihedral angles ϕ, ψ and χ. (b) Schematic representation of three side-chain rotamers gauche+, gauche− and trans. (c) Schematic representation of short-range pairs (arrows) in Phe for calculation of E_{ϕ, ψ, χ1}. (d) effective interaction potentials for backbone HB, with the dashed line for an attractive potential and the thick lines for the repulsive ones.

In PACE (Eq 1), LJ 12-6 potentials are used for the interactions E_CGW-CGW between CG water, E_CGW-UA between CG water and protein sites, and E_vdW between non-polar protein sites, namely,

$$E_{\text{A}-\text{B}}=\sum _{i\ne j}4{∊}_{\text{A}-\text{B},ij}\left(\frac{{\sigma }_{\text{A}-\text{B},ij}^{12}}{r_{ij}^{12}}-\frac{{\sigma }_{\text{A}-\text{B},ij}^6}{r_{ij}^6}\right).$$ (4)

The parameters of MARITINI water for E_CGW-CGW are ε_CGW-CGW = 5.0 kJ·mol⁻¹ and σ_CGW-CGW =0.47 nm; the cross-resolution terms E_CGW-UA were optimized by fitting experimental hydration free energies (HFE) of 35 compounds that cover 11 types of functional groups;³⁷ E_vdW parameters were optimized based on densities of liquid states and free energies of evaporation of eight organic compounds.³⁵

PACE handles polar interactions E_polar between protein sites through a set of effective LJ potentials which are necessary for directionality of polar interactions.³⁵ For example, Figure 1d illustrates the interaction scheme of backbone hydrogen bonds (HB), the potential energy functions of which are expressed as

$$E_{\text{HB,backbone}}=\sum _{\mid i-j\mid >2}4{∊}_{\text{attr},\text{O}-\text{N}}\left(\frac{{\sigma }_{\text{O}-\text{N}}^{12}}{r_{\text{O}-\text{N},ij}^{12}}-\frac{{\sigma }_{\text{O}-\text{N}}^6}{r_{\text{O}-\text{N},ij}^6}\right)+\sum _{\mid i-j\mid >2}\left(\frac{C_{\text{rep},\text{O}-{\text{C}}_{\alpha }}}{r_{\text{O}-{\text{C}}_{\alpha },ij}^{12}}+\frac{C_{\text{rep},\text{O}-\text{C}}}{r_{\text{O}-\text{C},ij}^{12}}+\frac{C_{\text{rep},\text{C}-\text{N}}}{r_{\text{C}-\text{N},ij}^{12}}\right),$$ (5)

where i and j denote reside numbers. The polar interaction parameters were optimized by fitting potential of mean force (PMF) profiles from atomistic simulations.³⁵ As pointed out already, we re-model polar interactions between charged groups with Coulomb potentials

$$E_{ele}=\sum _{i\ne j}\frac{q_i{q}_j}{4\pi {∊}_0{∊}_r{r}_{ij}},$$ (6)

where q_i and q_j are atomistic charges on atom pair i and j, r_ij is pair distance, and ε₀ and ε_r are vacuum permittivity and relative permittivity, respectively. ε_r takes the same value (15) as used for MARTINI.³¹

Finally, all the parameter files for the re-optimized PACE force field as well as the original PACE are available via http://www.ks.uiuc.edu/~whan/PACE/.

Simulation Details

NAMD 2.9,⁸³ with a minor modification for using PACE parameters, was used to conduct folding simulations. Switching functions were applied to Coulomb potentials from 0.0 to 1.2 nm, and to LJ potentials from 0.9 to 1.2 nm. We used a 4 – 5 fs timestep through increasing mass of hydro-gen atoms to 5 au by re-partitioning mass in H-containing groups, which should not a ect energy conservation.⁸⁴ Temperature was maintained by Langevin dynamics with a damping coe cient of 0.1 ps⁻¹; pressure was maintained by a Nosé-Hoover Langevin piston barostat⁸³ with period of 200 fs and decay rate of 100 fs. To study folding of peptides, PDB structures were solvated in cubic boxes of CG waters with 1.5 nm bu er clearance from the solutes, subject to 10-ns heating simulations at 700 K after optimization. The denatured structures, randomly selected from the heating simulations, were used for both standard MD and replica exchange MD (REMD) simulations.^4,85 REMD simulations were performed at constant NVT conditions. For each system, 18 replicas, ranging from 300 K to 480 K, started with different denatured structures. Attempts to exchange between replicas were made every 2 ps. The exchange ratio between the replica was on average 25 – 35%. All the folding simulations in this study are summarized in Table 2.

Table 2.

Summary of system size, simulation time, and MD methods used of folding simulations performed in this work.

System	Number of water molecules	Time (μs)b	MD methods
Dipeptidea	550	0.05	REMDc
AK17	1600	0.2	REMD
Fs	1850	0.2	REMD
	1850	3.0	MD
GB1p	1700	0.75	REMD
D47P	1700	0.35	REMD
	1800	1.3; 2.1; 3.5	MD
GB1m2	1700	0.35	REMD
Trp-cage	1800	0.2	REMD
	1800	3; 3	MD
BBA5	1800	0.5	REMD
	1800	8; 8	MD
α3D	4500	10; 20; 30	MD

^aREMD simulations were carried out for all 20 natural amino acids.

^bFor REMD simulations, the simulation time of each replica is listed. For standard MD simulations, the simulation time of each run is listed. Simulation times of multiple runs are all listed, separated by semi-colons.

^cEach REMD involved has 18 replicas with associated temperatures ranging from 300 K to 480 K.

Parameterization of PACE required calculation of hydration free energies (HFE) of solutes and potential of mean force (PMF) of interacting pairs. By following previous studies,^35,37 we cal-culated HFEs and PMFs through thermodynamic integration (TI) methods.⁸⁶ GROMACS 3.3⁸⁷ was used here in order to be consistent with the parametrization procedure employed previously for PACE.^35,37 Details about HFE and PMF calculations are presented in Supporting Information Figure S1 and Table S1.

Structure Analysis

Following Sorin and Pande,⁵⁹, we considered a residue to be α-helical only if this residue and both of its neighbors have their (ϕ, ψ) angles within (−60±30°, −47±30°). Similarly, we considered two residues to be involved in β-sheets if their (ϕ, ψ) angles are within (−135±45°, 135±45°), and also if there is at least a HB between the backbone amide groups adjacent to the two residues; we note that a HB is considered to be formed when a donor-acceptor distance is shorter than 0.35 nm and a donor-hydrogen-acceptor angle is larger than 120.0°.

An iterative clustering algorithm proposed by Daura et al.⁸⁸ was used to group conformations based on their root mean square distances of selected atoms. In each iteration, a cluster with the largest number of neighbors that are within a given cutoff of RMSD to the center of the cluster is removed from a pool of conformations. The remaining pool is used for the next iteration. The algorithm ends when the pool becomes empty.

Results and Discussions

In the following sections, we will first present how we improved the PACE force field by reoptimizing hydration parameters of protein backbones and incorporating Coulomb interactions into the force field. Then we will verify these improvements by examining performance of the new PACE in reproducing thermodynamics and kinetics in folding processes of series of small proteins.

Re-optimizing backbone hydration parameters

As models for backbone hydration, blocked polyalanyl peptides (Ace-Ala_n-NMe) have been investigated already in several computational studies.^44,45,46 Nevertheless, available HFE data from atomistic simulations were still inadequate for the purpose of parametrization. Therefore, we performed thermodynamic integration (TI) simulations⁸⁶ to calculate HFEs of polyalanyl peptides from 1 to 4 alanyl group long, using the OPLS-AA force field⁸⁹ and TIP3P water model.⁹⁰ An anti-parallel β-conformation (ϕ = −139°, ψ = 135°)⁴⁶ was chosen as a model for extended and exposed backbones of polypeptides (Table S1).

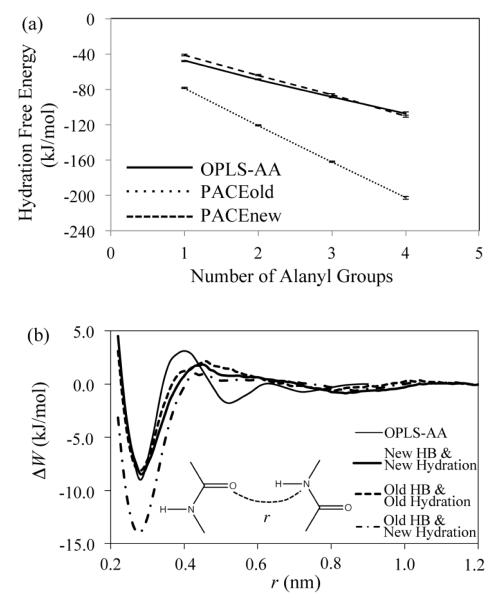
Figure 2a shows that HFEs of polyalanyl peptides, calculated with OPLS-AA, decreases linearly with the number of alanyl groups. Each individual internal amide group contributes similarly to overall HFEs of polypeptides, independent of peptide length, consistent with previous computational studies.^45,46,91 The HFE of an internal amide group was estimated, according to an average over all incremental change of the calculated HFEs, to be −20±2.3 kJ·mol⁻¹. Our result is comparable to the results from previous explicit-solvent simulations, such as −17 ± 1.3 kJ·mol⁻¹ for extended polyalanly peptides⁴⁶ and about −23 to −25 kJ·mol⁻¹ for extended polyglycyl peptides.^91,92

Figure 2.

(a) Hydration free energies of extended (ϕ = −139°, ψ = 135°) polyalanyl peptides having 1-4 alanyl groups, calculated with the OPLS-AA, the original PACE (PACEold) and the new PACE (PACEnew) force fields. The error bars are estimated with three independent simulations. (b) Potential mean force (PMF) profiles of two interacting amides in water, calculated with the OPLS-AA force field (thin line), the new PACE (thick line), the original PACE (dashed line) and the original HB potentials with the new hydration parameters (dot-dashed line).

In the original PACE, hydration parameters for amide groups were optimized based on methylacetamide (NMA), producing a HFE of −42 ± 1.5 kJ·mol⁻¹ for NMA,³⁵ close to the experimental value (~ −42 kJ·mol⁻¹).⁴³ However, our calculations (Figure 2a) show that these parameters lead to a HFE of −41.4 ± 1.4 kJ·mol⁻¹ for internal amide groups in peptide backbones, similar to the HFE of NMA, but significantly stronger than −20±2.3 kJ·mol⁻¹ for internal amide groups obtained from the atomistic simulations. Several factors may contribute to the discrepancy between HFEs of internal amide groups from the CG and atomistic simulations. 1) Previous Poisson-Boltzmann calculations⁴⁵ demonstrated that adjacent amide groups in peptide backbones could a ect electrostatic solvation free energies of each other, significantly reducing HFE of internal amide groups compared to an isolated amide group. However, the CG solvent here is lacking in regard to electro-static solvation. 2) Detailed amide-water hydrogen bonding (HB), which could also be important for backbone hydration,⁴⁶ is missing due to coarse-graining of the water model. 3) Comparative studies between CG and atomistic simulations⁹³ have shown that coarse-graining could lead to a considerable loss of configurational entropy associated with atomistic details. Thus, HFEs obtained with PACE may also be a ected by loss of entropy due to the CG water model. Considering the above factors, it is difficult to adopt only one set of hydration parameters for both internal and isolated amide groups in the current PACE. Therefore, we turned to different parameter sets for the two types of amide groups.

By fitting the HFEs of polyalanyl peptides from the atomistic simulations, we re-optimized the parameters for hydration of internal amid groups, including ε_CGW-H/O and σ_CGW-H/O for the interactions between CG water and backbone nitrogen and hydrogen atoms, assuming σ_CGW-O = σ_CGW-H (Eq 4) to simplify the optimization. The new parameters are listed in Table S2. The HFEs of polyalanyl peptides, calculated with the new parameters (Figure 2, the dashed line), deviate from the all-atom HFEs by ~ 3.8 kJ·mol⁻¹. With these parameters, the HFE of an internal amide group becomes −23 ± 2.0 kJ·mol⁻¹.

We also examined the effect of change of hydration parameters on HBs between backbone amide groups through comparison of potential mean force (PMF) profiles of interacting amide groups. As shown in Figure 2b, the interaction strength of backbone HBs, estimated as free energy minimum values in the PMFs, is ~ −8.2 kJ·mol⁻¹ for the original PACE, close to the value (~ −9 kJ·mol⁻¹) from atomistic simulations. Since the new parameters significantly reduce magnitude of backbone hydration, the desolvation penalty of backbone HBs should also be reduced. As expected, with the new parameters, the HB strength increases to ~ −14.0 kJ·mol⁻¹, indicating that backbone HBs become too strong. Therefore, we need to re-optimize the parameters for backbone HBs by referring to atomistic PMFs. For the same reason, the parameters for HBs involved with backbone amides also need to be examined and, if necessary, re-optimized. We also noticed that change of the backbone hydration parameters a ected backbone conformational distributions. Accordingly, we re-optimized the terms in Eq 3 to reproduce statistical (ϕ, ψ, χ₁)-distributions from a coil library.³⁹ The details of all the re-optimizations are discussed in Supplementary Information (Figures S2 and S3) and the new parameters are summarized in Tables S2 and S3. The new parameters were optimized in the same way as previous studies did,³⁵ except that parametrization for backbone amide HBs no longer relies on structural features of any specific peptide, but only on an amide-amide PMF obtained through atomistic simulation (Figure S4), thereby rendering the new parameters more general than the original ones.

Incorporation of all-atom charges in PACE for charged side chains

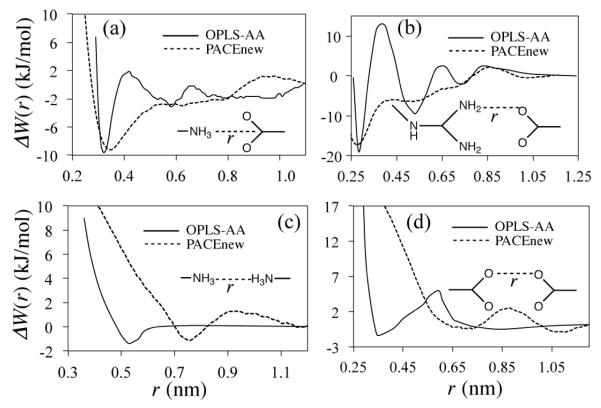
We combined atomistic partial charges, taken from OPLS-AA (Figure S5), with PACE to replace effective LJ potentials for interactions between charge pairs. The choice of atomistic force fields is not particularly important as other all-atom force fields, such as CHARMM22⁹⁴ and AMBER03,⁹⁵ have partial charges for charged groups very close to those of OPLS-AA. To calculate partial charges for PACE, we combined OPLS partial charges on a heavy atom and its attached hydrogen atoms and applied the sum to the corresponding atom in PACE. To see how well PACE and the atomistic partial charges work together, the PMFs of charge pairs, generated by the combined parameters, were compared with respective all-atom PMFs reported by Masunov and Lazaridis.⁹⁶

The comparisons (Figure 3) reveal four key features of charge interactions modeled by the combined parameters. First, the Lys⁺…Asp⁻/Glu⁻ PMF has a contact pair minimum (CPM) of −9.2 kJ·mol⁻¹ at r_N-C = 0.34 nm, matching the same minimum in the atomistic PMF (−9.6 kJ·mol⁻¹ at r_N-C = 0.32 nm) (Figure 3a). The charges on Lys⁺ and Asp⁻/Glu⁻ were repartitioned in sev-eral arbitrary ways (Figure S6a), but no better match could be obtained with the repartitioned charges than with those from OPLS-AA. Second, the atomistic CPM of Arg⁺…Glu⁻/Asp⁻ (Figure S6b) could not be reproduced by the combined parameters alone, no matter how the charges on Arg⁺ were rearranged, probably due to the lack of details of H atoms on Arg⁺. Thus, we turned to a set of effective LJ potentials (Figure S5 and Eq. S3) that had been used for this charge pair in the original PACE.³⁵ Together with the atomistic charges, these effective LJ potentials improve the description of the Arg⁺…Glu⁻/Asp⁻ CPM (Figure 3b). Third, despite electrostatic repulsion between a like-charge pair, such as Lys⁺…Lys⁺ and Glu⁻/Asp⁻…Glu⁻/Asp⁻, the combined parameters capture water-mediated minima present in the atomistic PMFs (Figures 3c and d). But the pairs at these minima are farther away by 0.2-0.3 nm than those in the atomistic PMFs, owing to the large size of CG water. Fourth, at intermediate distances (0.35 – 0.6 nm), the PACE PMFs, compared to their atomistic counterparts, are more attractive for opposite-charge pairs, and more repulsive for like-charge pairs (Figure 3).

Figure 3.

PMFs of Lys⁺…Asp⁻/Glu⁻ (a), Arg⁺…Asp⁻/Glu⁻ (b), Lys⁺…Lys⁺ (c) and Asp⁻/Glu⁻…Asp⁻/Glu⁻ (d). The solid lines denote PMFs by OPLS-AA force field in TIP3P water and the dashed lines (PACEnew) denote those by PACE with the all-atom charges.

As MARTINI CG water is unable to screen electrostatics through dielectric properties, an empirical dielectric constant ε_r = 15 is often introduced to account for dielectric screening.³¹ Also, solvation of charged solutes in CG water are parametrized to partly account for the screening. Considering the difference between the CG and all-atom water models, we do not expect a perfect match between the PMFs from PACE and all-atom simulations. For example, charge-pair interactions are overestimated by PACE when the pairs are separated at intermediate distances. However, even a more sophisticated solvent model, such as the Generalized Born (GB^HCT) model developed by Hawkins and coworkers,^97,98 renders, for example, Lys⁺…Lys⁺ and Glu⁻/Asp⁻…Glu⁻/Asp⁻ interactions too repulsive (cf. Figures 13a and 16 of ref⁹⁶). Accordingly, we need to further assess the applicability of the combined parameters. In this regard we note that peptide folding is sensitive to description of charge-charge interactions, incorrect description could significantly distort free energy landscapes of peptides, thereby leading to misfolding.^61,62,67,68 Indeed, peptide folding has been recognized as an important opportunity for improvement of force fields such as the GB model.^63,68 As will be shown later, the current charge parameters seem to be applicable for folding simulations, at least for the model peptides studied in this work.

Folding simulations of helical peptides AK17 and Fs

AK17 is a 17-residue polyalanine-based model peptide (Table 1), known through CD measurements⁴⁸ to have 30 – 35% helical content at 300 K. AK17 has been used to parametrize backbone HB in the original PACE.³⁵ A REMD simulation (200 ns/replica) for AK17 shows that the new PACE predicts too high a helical content (72 ± 2%) at 300 K. To reduce helical content of pep-tides, one approach is to adjust (ϕ, ψ) dihedral potentials in order to ameliorate the preference for α region in each residue, as done in previous development of AMBER-GS⁵⁸ and AMBER99ϕ⁵⁹ for helix folding. However, having been parameterized to fit the coil library, the (ϕ, ψ) dihedral parameters in the new PACE could not be altered further. We fine-tuned, therefore, the stability of local helical turns by changing the strength of all short-range backbone HBs between residue i and residue i + 3 or i + 4, while leaving the other HB parameters untouched. With a reduction of ε_{attr, Oi-Ni+3/i+4} (Eq 5 and Table S2), the new PACE produces 42 ± 5% helical content for AK17, comparable to experimental data. For consistency, all folding simulations below were performed with the same parameters, including the reduced ε_{attr, Oi-Ni+3/i+4} and all the new parameters discussed in previous sections.

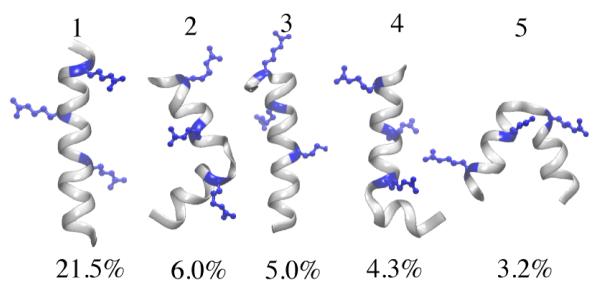
Another 20-residue helical peptide, known as Fs peptide^49,50 (Table 1), was used to examine the new PACE through a REMD simulation (200 ns/replica) and a 3-μs standard MD simulation at 300 K. The average helical contents from the 300 K replica and the standard simulation are 42±5% and 45 ± 1.8%, respectively, similar to ~ 43% of the original PACE; the result from the new PACE agrees with ~ 50% helical content of Fs found in CD measurement at 300 K.⁸⁰ The trajectory (t > 50 ns) from the standard simulation was clustered according to a 0.25 nm cutoff of backbone root mean square distance (RMSD) (see Methods). Top 5 clusters among 547 identified are shown in Figure 4. The most stable cluster (cluster 1, 21.5%) is a single full helix (SFH); in contrast, SFH was only marginally stable (~ 1%) in the simulation with original PACE.³⁵ On the other hand, the most stable cluster predicted by the original PACE is a reversed helix-turn-helix structure (HTH) with P_HTH = 14.6%,⁴⁰ but the same structure is much less stable with the new PACE (cluster 5). The new PACE results agree also more closely with previous all-atom simulations which showed that Fs has ~ 17% SFH.⁵⁹

Figure 4.

Structures of the first five of the most stable Fs clusters with their respective probability indicated below the structures. The structures were drawn by VMD¹¹³.

Since radii of gyration (R_g), which reflect overall shapes of proteins, are experimentally available for both AK17 and Fs,^57,59 we computed protein R_gs for both peptides to examine the ability of the new PACE to describe shapes. The average R_gs for AK17 and Fs are 0.78 ± 0.05 nm and 0.90 ± 0.06 nm, respectively, close to the experimental values (~ 0.82 nm and ~ 0.9 nm) and the values (0.78 ± 0.06 nm and 0.85 ± 0.07 nm) calculated with the original PACE.³⁵ The analysis of R_g suggests that the shapes of both helical peptides are described reasonably well by both the original and the new PACE.

Folding simulations of β-hairpin GB1p and its mutants

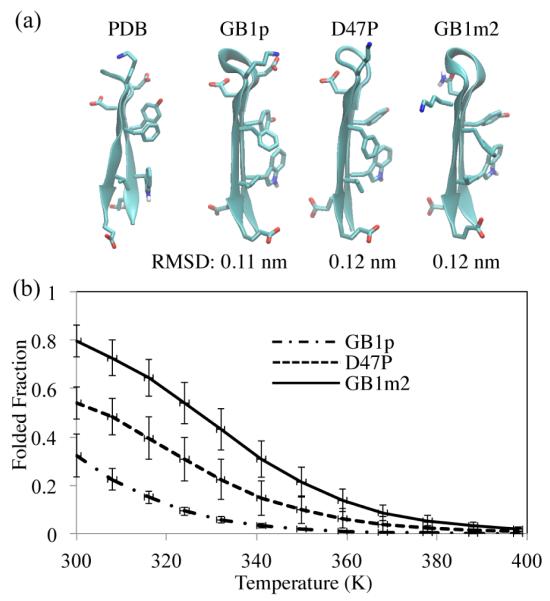
β-hairpin GB1p (Table 1), derived from residues 41-56 in the C-terminus of protein G B1 domain, has been well characterized experimentally.^51,52,53,99 Due to its fast folding kinetics (τ = 6 ~ 20 μs),^53,99 GB1p has also been intensively studied in folding simulations.^{21,40,60,61,62,63,64,66} GB1p is known to be marginally stable, having a melting temperature T_m < 273 K.⁵² The stability of GB1p can be increased to different extents through mutations in its loop such as D47P⁵³ or the replacement of DDATKT by NPATGK (GB1m2)⁵² (Table 1).

We performed REMD simulations for GB1p and its D47P and GB1m2 mutants with the new PACE. We took region 41-56 of the NMR structure (PDB ID: 1gb1) as a reference (Figure 5a) for a folded state. A simulated structure was considered folded if its RMSD of backbone and C_β atoms is less than a certain cutoff. To choose a proper cutoff, we calculated the folded populations of the three peptides by varying the RMSD cutoff from 0.1 to 0.34 nm (Figure S7), and looked for points after which the populations level off. Such points, as shown in the figure, turned out to be at 0.2 nm which was then chosen as the RMSD cutoff. For GB1m2 and D7P, the folded structures appeared early (t < 50 ns) in the REMD simulations and the population of folded peptides converged after t > 200 ns (Figure S8). Thus, we extended the simulations of GB1m2 and D47P to t = 350 ns and extracted the last 150 ns of simulations for analysis. On the other hand, GB1p was found to fold only after t > 400 ns; the percenage P_fold of folded states converged only after t > 600 ns. Indeed, a previous folding study with GB solvent involving REMD simulations also found that GB1p folded more slowly than its loop mutants.⁶³ Garcia and co-workers suggested that there are high barriers dividing folded and unfolded states for GB1p.¹⁰⁰ Therefore, we carried out extended (750 ns) REMD simulations for GB1p and analyzed the last 150 ns of simulations.

Figure 5.

(a) Representative structures of the most stable clusters in simulations of GB1p and its D47P and GB1m2 mutants with their respective RMSD values indicated below. (b) Melting curves obtained through REMD simulations of GB1p (dot-dashed), D47P (dashed) and GB1m2 (solid).

At 300 K, the folded populations P_fold of GB1p, D47P and GB1m2 were estimated to be 31 ± 9%, 54 ± 7% and 79 ± 7%, respectively, in good agreement with P_fold (~ 30%, ~ 50% and ~ 75%) measured at 298 K by NMR experiments.^52,53 In particular, the stability of folded GB1m2 is better reproduced by the new PACE than by the original one (P_fold =~ 40 - 45%).⁴⁰ The clustering (r_RMSD = 0.2 nm) results show that all the peptides have their most stable cluster folded (Figure 5a). The other clusters are only marginally stable (< 10%). Melting curves were plotted by calculating P_fold(T ) for all replicas (Figure 5a). The melting curves shows that the melting temperature T_m of GB1p should be below 300 K and that the T_ms of D47P and GB1m2 are 300 ~ 308 K and 324 ~ 332 K, respectively, in close agreement with the experimental T_m values (299 ~ 311 K and 318 ~ 322 K).^52,53 Therefore, the new PACE not only folds GB1p and its mutants into their native structures, but also reproduces the delicate stability difference among the peptides. Reproducing relative stabilities of GB1p and its mutants has also been reported by other groups. Chen and Brooks showed that their CHARMM22/GBSW force field was able to differentiate stabilities of GB1p and its β-hairpin enhancing or retarding mutants⁶³ as did the implicit solvent force field developed by Irback and Mohanty.⁶⁴ However, these force fields were optimized purposely for folding of GB1p and its mutants, which is in contrast to the new PACE here that did not incorporate any information of those β-hairpin peptides when it was optimized.

Folding simulations of Trp-cage

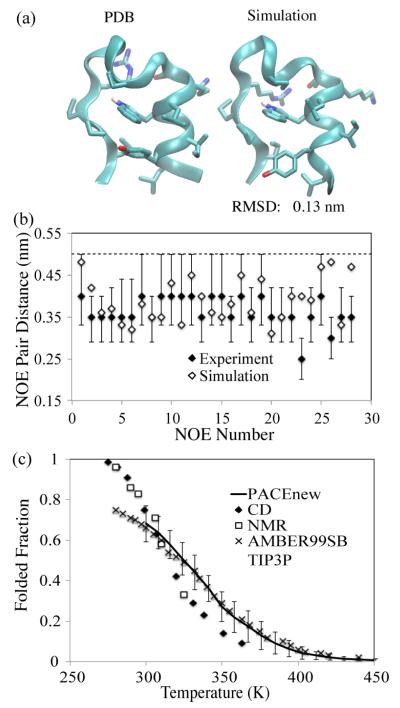
Trp-cage (Table 1) is a de novo designed 20-residue mini-protein which behaves in several respects like large globular proteins.⁵⁴ Tp-cage exhibits a compact hydrophobic core, centered around the Trp6 side chain that is caged by side chains of Tyr3, Leu7, Pro12 and Pro18 (Figure 6a). Due to its small size and fast kinetics (τ_f =~ 4.1 μs),⁶⁹ Trp-cage has been computationally studied in numerous folding simulations which reproduced its NMR structures with high accu-racy.^{21,63,64,67,68,69,70,71,72,73,74} The original PACE is also able to fold Trp-cage (P_fold = 30 - 35 %) with its representative folded structure exhibiting a backbone RMSD of 0.2 nm from the NMR structure.⁴⁰ But the original PACE underestimates P_fold of Trp-cage compared to P_fold (~ 70% with a 0.24 nm RMSD cutoff) measured by CD and NMR experiments.⁵⁴

Figure 6.

(a) NMR structure of Trp-cage (model 1 in PDB ID: 1L2Y) and representative structure of the most stable cluster in the 300K simulation. (b) NOE pair distances from NMR experiments (filled diamond)⁵⁴ and the simulation by the new PACE (empty diamod) for long-range pairs (i/i + n with i ≥ 5). Error bars show reported upper and lower bounds for NOE distance from NMR measurements. The dashed line denotes 0.5 nm distance. (c) Folded populations of Trp-cage against temperature, calculated with the new PACE (solid line) and AMBER99SB with TIP3P water (cross) and measured with NMR (filled diamond) and CD (empty square) methods. Error bars were estimated through block average with windows of 10 ns.

P_fold of Trp-cage with the new PACE was calculated through 200 ns REMD simulations, using a 0.24 nm RMSD cutoff of backbone (residue 3-19). This cutoff was calculated in the same way as earlier discussed (Figure S7). The second halves of simulations, which showed the converged P_fold (Figure S8), were used for analysis. P_fold at 300 K was estimated to be 68±9%, consistent with the experimental value (~ 70%). We clustered the 300 K ensemble with a RMSD cutoff of 0.2 nm. The representative structure of the most stable cluster (69%) has a RMSD of 0.13 nm, which is even better than the one (backbone-RMSD ~ 0.16 nm) from previous OPLS-AA/SPC simulations.⁷⁴

The melting curve of Trp-cage is plotted in Figure 6b. For comparison, we also plotted the melting data from NMR and CD experiments,⁵⁴ and from previous ~ 40 μs REMD simulations with AMBER99SB¹⁰¹ and TIP3P water for converged sampling.⁷⁰ As shown in Figure 6c, the melting curve generated by the new PACE agrees closely, for the entire temperature range of the REMD simulations, with that from the all-atom simulations. T_m measured from the PACE simulations is ~ 324 K, close to ~ 321 K from the all-atom simulations, and slightly higher than the experimental value (315 K), but much lower than those from other all-atom simulations with OPLS-AA in TIP3P (440 K)⁷⁴ and AMBER94¹⁰² in GB^HCT (~ 400 K).⁶⁷ Both the AMBER99SB melting curve and ours are in overall agreement with the experimental melting data, but depart noticeably (~ 15% folded population) from the experimental data for extreme temperatures.

We also calculated inter-proton NOE pair distances and compared them with the reported data from NMR experiments.⁵⁴ We first added all missing H atoms back to each frame of the simulations, and then evaluated NOE pair distances as $R_{\text{NOE}}={\langle R_{\text{HH}}^{-6}\rangle }^{-1∕6}$ which was averaged over the whole ensemble (t > 100 ns). As suggested by Zhou,⁷⁴ a simulated NOE pair was considered in disagreement with the NOE observations if its distance is 0.025 nm or more below the lower bound or beyond the upper bound in the NOE distance range.⁵⁴ For 83% of 169 reported NOE pairs, the simulated distances are within the NOE distance range, comparable to the results from OPLS-AA/SPC simulations in which 92% of NOE pairs showed correct distances.⁷⁴ Of 17% pairs in violation, only three had a distance > 0.5 nm, a typical distance limit for observing NOE signals. We further looked into 28 long-range NOE pairs which are separated by at least five residues (i/i + n with n ≥ 5). These long-range NOE pairs provided key constraints to define topology and tertiary structures of Trp-cage.⁵⁴ As shown in Figure 6b, only 3 of 28 long-range pairs violate NMR NOE distances, while there were also 4 long-range pair violation in the OPLS-AA/SPC simulations.⁷⁴ The three pairs with violation include: (1) the pair between Y3 HD1 and W6 HH2, suggesting a less tight packing between Y3 and W6 (Figure 6a); (2) pairs between W6 HZ2 and P12 HA and (3) between D9 HB1 and S14 HB2, which have also violated NOE distances in the OPLS-AA/SPC simulations.⁷⁴ Despite the three distance violations, all the long-range pair distances are still within the 0.5 nm limit. Therefore, we conclude that the PACE simulations reproduced well the NMR structures for Trp-cage.

Folding simulations of BBA5

De novo designed BBA5 (Table 1) is characteristic of globular proteins, namely having a well defined tertiary structure composed of all types of elementary structures, including a β-hairpin (residues 1-8), an α-helix (residues 12-20) and a connecting loop (Figure 7a).^55,103 Folding of BBA5 has been achieved in all-atom simulations with both explicit⁷⁶ or implicit^75,77,104 solvent models. We examined folding of BBA5 through REMD simulations with the new PACE. To achieve a converged sampling, the simulation lasted for 500 ns (Figure S8), the last 300 ns of which was taken for analysis.

Figure 7.

(a) NMR structure of BBA5 (PDB ID: 1T8J) and representative structure of the most stable cluster in the 300K simulation. (b) Overlay of randomly selected conformations from the most stable cluster (left), superimposed by residue 1-21 backbone, or from the entire simulations (right), superimposed by residue 12-19 backbone. (c) NOE pair distance upper and lower bounds from NMR experiments (vertical line)⁵⁴ and the simulated NOE distances by the new PACE (empty diamond) for long-range pairs (i/i + n with i ≥ 5). The dashed line denotes 0.5 nm distance.

We tried to use backbone RMSD to define folded states for calculation of P_fold, but we were unable to choose a definite RMSD cutoff as P_fold was found to increase linearly with RMSD cutoff, without any inflection point (Figure S7), unlike in the case of GB1p or Trp-cage. Thus, we set the cutoff as 0.3 nm, the same as used in previous simulations of BBA5,^76,77 and P_fold was calculated to be 27 ± 9% at 300 K. A BBA5 double mutant with enhanced stability, as shown in previous CD and fluorescence experiments,⁷⁵ has only P_fold of ~ 20%. Since the folded structures are marginally stable in the simulation, it is necessary to know if the lowest free energy minimum is still folded. The simulated ensemble was therefore clustered using a 0.25 nm backbone RMSD cutoff. The most stable cluster (28%) turned out to be folded, as reflected by a low RMSD (0.19 nm) for its representative structure (Figure 7a).

The β-hairpin and α-helix in BBA5, on the other hand, show considerable stabilities. The probability P_β of the β-hairpin is 77%. The helical content P_α in region 12-18 is 80%. The high P_β and P_α values agree with values determined in previous folding simulations of BBA5 with OPLS/GBSA.¹⁰⁴ Our results reveal that a large fraction of unfolded states have considerable native secondary structures. However, the hairpin adopts various orientations relative to the helix in the unfolded states, as demonstrated by a structural overlay of randomly selected conformations from the entire ensemble (Figure 7b). Previous simulations had shown that even at 278 K the relative orientation of the hairpin in the folded states is flexible.⁷⁵ NMR studies have also demonstrated that certain mutations on the BBA5 hairpin could alter relative orientation of the hairpin or even lead to multiple structures with different hairpin orientations.⁵⁵

To further validate the marginal stability of BBA5 and its flexibility, we calculated NOE pair distances for the entire ensemble and compared them with NMR data.⁵⁵ Of 347 reported NOE pairs, five pairs violate NMR NOE constraints. Of 60 long-range (i/i + n with n ≥ 5) NOE pairs, only one pair (R2 HA and D7 HB*) violates its constraint, showing a calculated NOE distance 0.03 nm above the experimental upper bound (0.34 nm) for this pair (Figure 7c). We noticed that the good agreement between the simulated and experimental NOE distances may be partly due to large upper bounds of certain experimental NOE constraints, some of which are even beyond 0.8 nm. To see if the good agreement relies on those large upper bounds, we also compared all the NOE pair distances with the 0.5 nm distance that is the typical distance limit for observing NMR signals. The comparison showed that 25 of 347 NOE pair distances exceed the 0.5 nm distance limit. Among the 25 NOE pairs, only six involve long-range NOE pairs, mainly between Y1 and L14 and between Y1 and A15. The majority of the experimental constraints are, according to the calculation, predicted to be observable in NOE spectrum. Therefore, the conformational ensemble of BBA5 generated by the new PACE reproduces the NMR structural data.

Folding Simulations of α3D

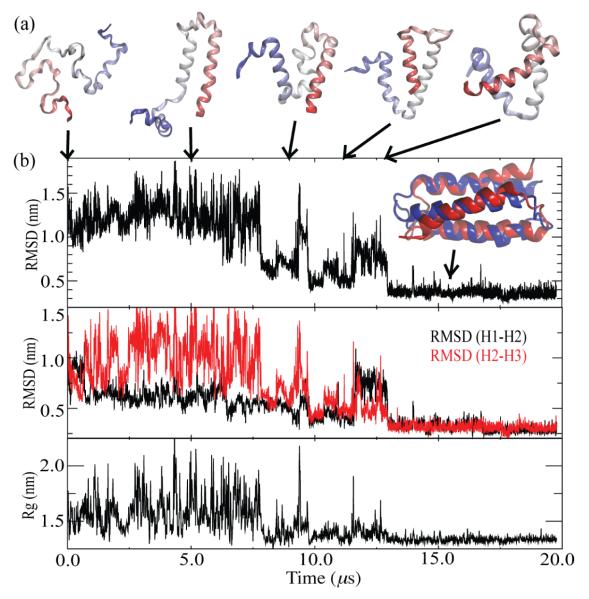
3D (Table 1) is a de novo designed three-helical-bundle protein that contains 73 residues.^56,105 Owing to its length folding of α3D requires tremendous conformational sampling such that ab initio folding with atomistic detail represents a great computational challenge. Indeed, computational folding of α3D has only been achieved in few studies. Using an AMBER96/GBSA model, Ozkan and coworkers folded α3D with a C_α RMSD of 0.46 nm by combining a conformational search algorithm with REMD.⁷⁸ Recently, Lindorff-Larsen and coworkers, using a modified CHARMM force field,¹⁰⁶ achieved ab initio folding of α3D for multiple times in a simulation extending beyond 700 μs.⁷⁹ As a final test, we employed the new PACE to fold α3D at T = 310 K. Starting with denatured α3D, folding of α3D was observed in three extended (10 – 30 μs) standard MD simulations. The average C_α RMSD of representative folded structures are 0.34 ± 0.02 nm for the three simulations, close to the result (0.31 nm) achieved by Lindorff-Larsen and coworkers.⁷⁹

Our α3D folding simulations lead to several interesting results. First, unfolded states of α3D were found to be disordered with radius of gyration exhibiting large fluctuations (Figures 8b and S9), yet these states exhibit significant (~ 25%) residual helical content. A residual helical content of 20% had also been reported for unfolded α3D in the atomistic simulations.⁷⁹ Second, for the three helices in α3D, namely H1 (residue 1-18), H2 (residue 28-44) and H3 (residue 54-73), H1 and H2 form the native two-helical bundle earlier than H2 and H3 do, as reflected by our RMSD calculation of H1-H2 and H2-H3 (Figures 8b and S9). Our results are in contrast to a previous folding study¹⁰⁷ which, using an Ising-like Gô model, suggested that H3 involves the native topology first. Third, in two of the simulations, folding completed after H3 packed itself to the pre-formed H1-H2 complex with correct native contacts (Figure S9); in a third simulation emerged intermediates with native-like topologies but a non-native hydrophobic core (8 μs < t < 13 μs, Figures 8b), which eventually transited to the folded structure. Such a scenario of multiple folding pathways is expected for α3D according to experiments.¹⁰⁵

Figure 8.

(a) Snapshots of the folding simulation of α3D. (b) C_α RMSD to the native structure (PDB ID: 2A3D) (top panels), C_α RMSDs of H1-H2 (black) and H2-H3 (red) (middle panels) and radius of gyration (bottom panels) of α3D in the folding simulations. Five fraying residues in each terminus were discarded when C_α RMSD was calculated. Superimposition of the representative folded structure (red) and the native structures (blue) is shown in the top panel.

Folding Kinetics with New PACE

Since several peptides have been folded successfully with the new PACE, it is natural to in-spect the kinetics of the simulated folding. For this purpose, additional multi-μs simulations were conducted for D47P, Trp-cage and BBA5. Alongside the simulations for Fs and α3D, these stan-dard MD simulations, summarized in Table 2, cover all the structural motif investigated in this work. The folding time τ_f was estimated as the average timespan of folding starting when the simulations began or when the peptides unfolded, and ending when the peptides reached folded states (Figures S9-13). As shown in Table 3, the simulated τ_f’s are 5-10 fold shorter than the experimental ones, except for the case of α3D which is probably due to different pH conditions, i.e., neutral pH in our simulations and pH 2.2 in the experiments.¹⁰⁵ Acidic pH can lower T_m of α3D from > 363 K to 343 K;¹⁰⁵ recent single-molecule FRET experiments also show that the folding kinetics of α3D around room temperature becomes ~ 10 folds faster at low pH compared to neutral pH.¹⁰⁸ Compared to τ_f from the atomistic simulations,⁷⁹ our τ_f is 2 – 3 times shorter (11 ± 4 μs vs. 27 ± 8 μs), though measured at a lower temperature (310 K vs. 370 K). Altogether, for the systems tested here, folding modeled by the new PACE is about 5-10 fold faster than seen in experimental measurements.

Table 3.

Number of folding events Nf in the standard MD simulations and comparison of folding time τ_f,sim (μs) with experimental τ_f,expt.

Peptidea	N f	τ f,sim	τ f,expt	τf,expt/τf,sim
Fs	45	0.04 ± 0.01	0.16 – 0.22b	~ 4.5 – 6.5
D47P	4	0.9 ± 0.3	~ 13c	~ 15
Trp-cage	7	0.4 ± 0.13	4.1d	~ 11
BBA5	13	0.8 ± 0.3	8 ± 3.5e	~ 9
α3D	3	11 ± 4	3 ± 1.2f	~ 0.3

^aStandard MD simulations were performed at 300 K for Fs, D47P and Trp-cage and at 310 K for BBA5 and α3D.

^bAt 301 K with T-jump CD.^109,110

^cAt 298 K with NMR.⁵³

^dAt 296 K with T-jump CD.⁶⁹

^eAt 298 K with T-jump uorescence.⁷⁵

^fAt 323 K and pH 2.2 with T-jump IR.¹⁰⁵

The 5-10 fold acceleration of folding by the new PACE could be attributed to multiple factors, such as coarse-graining of the solvent model and simplified potentials for protein-protein and protein-solvent interactions, both smoothing energy landscapes of folding. For instance, the CG water model becomes less viscous and allows solutes to diffuse faster by 4 – 5 times than atom-istic models, as demonstrated in previous studies.³¹ However, the observed factor of acceleration of folding may not be enough for estimation of the time scale of CG simulations since protein dynamics includes events on multiple time scales, each of which could be a ected to a different extent through coarse-graining of atomistic models. Also, we have re-distributed mass of hydrogen-containing groups for a larger time step, which could a ect hydrogen-bonding dynamics⁸⁴ and, thereby, complicate the meaning of the time scale of simulations. Therefore, one should be cautious to use the observed acceleration factor for folding to interpret the time scale of CG simulations.

Conclusion

We have presented a further optimization of the PACE multiscale model and validated it through folding several proteins. We demonstrated that the original PACE will overestimate backbone hydration and render small proteins, such as GB1m2, a GB1p mutant, and Trp-cage, less stable than seen in experiments. The new PACE, optimized for HFEs of peptide backbone, not only reproduces correct stabilities for GB1m2 and Trp-cage, but also for other proteins, such as GB1p and its D47P mutant and BBA5, bringing calculated T_m and NOE distances in close agreement with experiment. We also explored the possibility to combine atomistic charges from atomistic force fields with PACE for interactions between charged groups. We showed that with only minor modification of PACE, the combined parameters recall in satisfactory PMFs for charge pairs and work well in folding simulations. We expect that the treatment of electrostatic interactions will be significantly improved by further combining atomistic charges, PACE and recently developed polarizable CG water models.^111,112 The new PACE accelerates folding of the proteins tested by 5-10 times, as demonstrated in a systematic comparison between simulations and experiments. Finally, we were able to fold the 73-residue α3D into its native structure through standard MD simulations, indicating the potential of the new PACE for the study of protein folding and dynamics of large proteins.