Abstract
Plausibility of high variability in treatment effects across individuals has been recognized as an important consideration in clinical studies. Surprisingly, little attention has been given to evaluating this variability in design of clinical trials or analyses of resulting data. High variation in a treatment’s efficacy or safety across individuals (referred to herein as treatment heterogeneity) may have important consequences because the optimal treatment choice for an individual may be different from that suggested by a study of average effects. We call this an individual qualitative interaction (IQI), borrowing terminology from earlier work - referring to a qualitative interaction (QI) being present when the optimal treatment varies across a“groups” of individuals. At least three techniques have been proposed to investigate treatment heterogeneity: techniques to detect a QI, use of measures such as the density overlap of two outcome variables under different treatments, and use of cross-over designs to observe “individual effects.” We elucidate underlying connections among them, their limitations and some assumptions that may be required. We do so under a potential outcomes framework that can add insights to results from usual data analyses and to study design features that improve the capability to more directly assess treatment heterogeneity.
Keywords: Causation, Crossover interaction, Individual effects, Potential outcomes, Probability of similar response, Subject-treatment interaction
1. INTRODUCTION
“…,it appears that white sheep and pigs are injured by certain plants, whilst dark- coloured individuals escape.” ~ Charles Darwin
“What is food to one to some becomes Fierce poison” ~ Lucretius
The quotations above illustrate that individual differences in response to stimuli or ‘treatments’ have been the subject of interest throughout recorded history. They further illustrate two kinds of interactions. Darwin points out an interaction in which one type of animal is harmed by a certain treatment whereas other animals are not harmed, but are not necessarily helped. In contrast, Lucretius points out a more dramatic type of interaction in which what is helpful to some is actually harmful to others. More formally, treatment heterogeneity is present when the effect of a treatment, say T, with respect to a reference treatment, R, varies across subsets or individuals in a population. At the individual level, this variability is called subject-treatment interaction (Gadbury 2010). A consequence of this heterogeneity is that the effect of a treatment T with respect to R may be in opposite directions across different individuals or subsets, with treatment T having higher efficacy for some and treatment R having higher efficacy for others. The term qualitative interaction (QI) has been used to describe this situation at the subset level (Peto 1982; Gail and Simon 1985), and tests have been developed to detect a QI (Gail and Simon 1985; Silvapulle 2001; Li and Chan 2006). When such tests are significant, optimal treatments may differ among subsets (Byar and Corle 1977). A “quantitative” interaction (Peto 1982) exists when the magnitudes of the difference between treatment T and treatment R differ across subsets, but are in the same direction. Herein we refer to a “subset interaction” as a more general term that includes quantitative and/or qualitative interactions.
Taking the idea of subsets to its limit, we can recognize that each person is unique and can be considered their own subset. Then analogous to the QI described above, an individual qualitative interaction (IQI) is present when the difference between an outcome to treatment T and to treatment R have opposite signs for at least two individuals. A fact that initially seems counter-intuitive to many clinical investigators who are used to discussing “non-responders” in standard clinical trials (e.g., Inoue et al. 2010), is that individual effects of a treatment T with respect to R are inherently unobservable in a two treatment comparison study because only one of the two outcome variables is observable for each subject, depending on the treatment assigned to that subject. Let potential outcome variables (Rubin, 1974) to treatments T and R be given by X and Y, respectively, with an individual effect defined by the variable D = X – Y. Suppose, as in Gadbury and Iyer (2000), that the potential outcome variables, (X,Y)T are modeled by a bivariate population distribution with mean (μX,μY)T and covariance matrix , with the covariance σXY=σXσYρXY. The distribution of D then has mean μD = μX – μY and variance
| (1) |
In a two treatment comparison study where subjects are randomly assigned to treatments T and R, the mean treatment effect, μD, can be estimated but the variance, , cannot because there is no information in observable data to estimate the correlation, ρXY.
Assume throughout that μD = E(X – Y) = μX – μY > τ represents a beneficial average effect of T over R where τ is some threshold particular to the treatments being compared (that is, treatment T may have costs associated with it over treatment R that require a sufficiently positive value for μD before it is claimed that T is a preferred treatment over R). Hereafter, for convenience, we take τ = 0. Subject-treatment interaction is present in the population when . If there is no interaction at the individual level, and there is a constant treatment effect (Holland 1986). However, as individual treatment effects become more heterogeneous, gets larger, and a positive proportion of individuals in the population with a value of D less than zero (i.e., an IQI is present) becomes more plausible, despite μD > 0. We denote the proportion of individuals having an unfavorable outcome to treatment T versus R as PIQI. If the bivariate distribution given above is normal, then
| (2) |
where Φ(·) is the standard normal cumulative distribution function (CDF). Normality is assumed here for convenience, but other definitions for PIQI could be developed for non-normal distributions.
It has been remarked that medicine today generally makes use of statistical information gathered about the general population (often about the “average” subject) and then applies it to the individual (cf. Marshall, 1997). Some have suggested that information about a mean treatment effect be supplemented by information about treatment effect heterogeneity (cf., Longford, 1999). This paper explores methods to determine whether and/or PIQI are positive using observed data from a two treatment comparison study where treatments are randomly assigned. In particular, we discuss three approaches: tests for subset interaction, the proportion of similar responses (PSR), and cross-over designs. We review each method using the potential outcomes structure to highlight important connections and assumptions. A data example is used to illustrate the ideas. Though the focus here is a clinical setting, interest in other aspects of a treatment effect distribution besides the mean has emerged from other fields. For example, see Fan and Park, 2009, 2010, for application in econometrics.
It is recommended that new ideas for clinical trial designs and methodologies be pursued that may lead to further improvements in our ability to estimate and test aspects of individual treatment response heterogeneity. The potential outcomes framework helps to distinguish heterogeneity that is “explainable” in observed data from unexplained heterogeneity. Though subject-treatment interaction and the PIQI cannot be directly estimated in observed data without introducing additional assumptions, bounds can be estimated. Consequences of unexplained heterogeneity, reflected by estimable bounds for the PIQI, can alert investigators to the possible existence of an unobserved covariate that could be potentially predictive of individual success to a treatment application.
2. AN ILLUSTRATIVE EXAMPLE
Bookstores typically devote shelf space to a wide variety of dieting books, each book frequently containing anecdotes describing substantial weight loss and other remarkable improvements to health for particular individuals. Obesity researchers are cautious about embracing various new diets due to limited evidence that they outperform more traditional programs of weight loss. Two diets whose relative merits have been discussed are the low carbohydrate diet (sometimes called a reduced-glycemic-load diet) versus a more traditional portion controlled low-fat diet. Results from clinical studies comparing these two have been inconsistent, with some suggesting that one appears more effective for weight loss at some time points, on average, and others that show no significant difference. A March 4, 2010 article in the Wall Street Journal reported on an unpublished study by Stanford University researchers that suggested that individual differences in genetic predispositions contribute to substantial individual differences in the relative efficacy of one diet versus another (i.e., low fat versus low-carbohydrate) among overweight women.
Given the possibility of treatment heterogeneity in such a study as well as an IQI, we illustrate the ideas discussed here using a data set that compared a reduced-glycemic-load diet (RGL) and a portion controlled low fat diet. The data are a subset of data analyzed and reported in Maki et al., 2007. Subjects were randomized to two treatments: T = the RGL diet (n = 43) and R = the low fat diet (n = 43). A primary outcome variable was weight change from baseline at 12 weeks, measured in kilograms. Maki et al., 2007, also report analyses of other outcome variables such as waste circumference, fat free mass, and results from laboratory tests. Several covariates were measured such as baseline values of outcome variables, age, race, and gender. Using notation described earlier, we consider the outcomes X = weight change from baseline at 12 weeks for subjects assigned to treatment T, and Y = weight change from baseline at 12 weeks for subjects assigned to R. Positive values of X and Y are a weight “loss” (in kilograms) from baseline. We analyze data for the 69 subjects (out of 86) that remained in the study at 12 weeks (34 in treatment T and 35 in treatment R). For brevity and to focus on the topic presented herein, we do not consider issues related to compliance or drop out and initially, analyze data for only the two outcomes, X and Y.
The treatment T group had a mean weight loss of kg with a standard deviation of kg. The treatment R group had a mean weight loss of kg with a standard deviation of kg. An estimate of a mean treatment effect is kg, and a t-test of Ho: μD = 0 against an upper tailed alternative hypothesis gives a p-value of 0.003.
Sometimes investigators will interpret unequal variance of the outcome variables in each treatment group as evidence of treatment heterogeneity. This is, in fact, partially true because the minimum bound for the subject-treatment interaction standard deviation is , and this quantity can be large when σX and σY are very different. Estimable bounds for are obtained by setting the correlation equal to 1 and -1, respectively (Gadbury and Iyer, 2000). The maximum bound, , is not small unless both standard deviations of the potential outcome variables are small. From the example data, the estimated bounds are . The estimated standard errors obtained by 2000 bootstrap samples within treatment groups (cf., Gadbury et al., 2001) suggest that the lower bound is statistically very close to zero. The estimated standard error for is 0.59. Based on only these outcome variables and these estimated bounds, there is no clear and compelling evidence in the data that subject-treatment interaction ‘must’ be present, but there is evidence that it ‘could’ be.
Assuming as before a bivariate normal distribution for weight loss outcomes X,Y, bounds for the PIQI (Gadbury and Iyer, 2000) are given as and . The estimated bounds are,
| (3) |
The bootstrap standard error for the upper bound is 0.049. These results suggest that the estimated proportion of the population having an effect of treatment T versus R in the opposite direction from the mean effect could be negligible or as high as 0.37. One may argue that it is more plausible that this proportion is closer to zero rather than 0.37 because the nonestimable correlation between potential outcomes should be closer to 1 rather than -1. If one were to assume a lower bound for the correlation equal to 0, for instance, the estimated maximum PIQI decreases to 0.32. Yet without additional information or assumptions, little more can be said about treatment heterogeneity or its consequences based on these data alone.
3. METHODS FOR ASSESSING TREATMENT HETEROGENEITY AND ITS CONSEQUENCES
Other techniques have been developed for studying population treatment heterogeneity and its consequences under different assumptions and constraints. In this section we use potential outcomes to clarify the assumptions required to estimate and a PIQI under three different strategies. First we establish a connection between subset interaction and subject-treatment interaction and show how the former, with an appropriate design, is a detectable consequence of the latter. Second, we show that the proportion of similar response (PSR) or density overlap, though intuitively appealing, can be misleading when used as a proxy for treatment heterogeneity and, hence, the potential presence of IQI. Finally, we show that additional information becomes available in cross-over designs, but that direct estimation of the PIQI requires further assumptions.
3.1 Identification of Subsets
The study of subset interaction presupposes a covariate that is a “grouping variable” and some degree of homogeneity of treatment effects within groups, with QI then explained by differences in treatment effects seen across groups. If the grouping variable is continuous, then groups are subpopulations defined by values of the covariate. One reason for subset analysis then is to identify “which treatment is best for which kinds of patients,” (Byar and Corle 1997, p. 455). Standard methods seek to find such subsets through an investigation of interaction effects (Byar and Corle 1977; Simon 1982) or a direct test for a qualitative interaction (Gail and Simon 1985; Silvapulle 2001; Li and Chan 2006). In each case the interaction is detectable by changes in the mean response across subsets. Using potential outcomes, the subject-treatment interaction variance , can be decomposed into an explainable component (i.e., a component that is estimable) and an unexplainable component (remaining subject-treatment interaction within a subset).
3.1.1 A continuous covariate
First consider, as in Gadbury et al., (2001), a continuous covariate Z (i.e., not affected by the treatment) with mean μZ and variance that augments potential outcomes (X, Y). Assume the distribution of D given Z = z0 is normal with conditional mean
| (4) |
and conditional variance,
| (5) |
βXZ and βYZ in equation (4) are the slope coefficients between Z and X and Z and Y, respectively, and ρXY|Z in equation (5) is the partial correlation between X and Y, given Z. The conditional variances, and , are allowed to be different across the two treatment groups but are assumed to not depend on the value of Z. Gadbury et al. (2001) showed that,
| (6) |
So is comprised of two components, one that can be attributed to subset interaction (the second term in (6)) and one that can be attributed to subject-treatment interaction, within subsets (the first term in (6)). The quantity, , can be estimated using the observed data from a randomized trial. When βXZ ≠ βYZ, then within subpopulations is smaller than the unconditional subject-treatment interaction variance, . The conditional proportion of IQI within the subset (or subpopulation) defined by a value of the covariate Z, PIQIZ=z0, is given by a quantity analogous to that given in equation (2), except using the conditional mean and conditional variance of D, given Z. The two conditional variances, and , are not expected to be larger than their unconditional counterparts (e.g., in a regression setting where conditional variances are assumed to be constant over values of Z, then and . Thus, if βXZ ≠ βYZ then one could identify subsets of the population for which for values of Z0 for which μD|Z=Z0 is greater than μD.
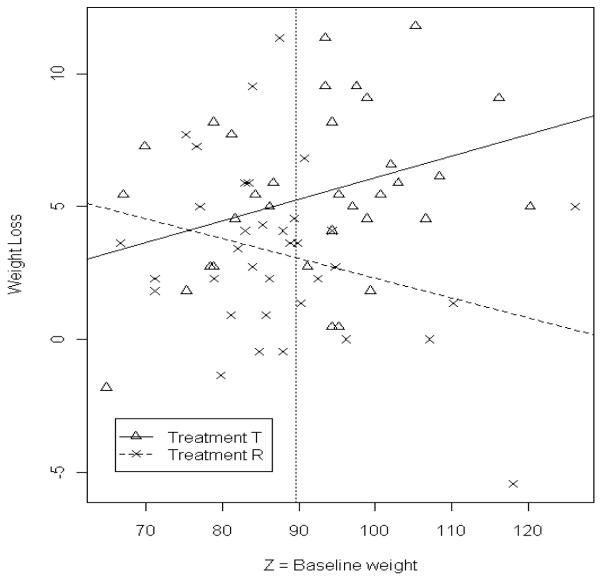
Returning to the data example, let Z = baseline weight. A test for a baseline-treatment interaction is significant (p-value = 0.007), , , and so that an estimated kg of σD is explained by the baseline weight covariate. Figure 1 is a plot of the data showing the interaction between treatment and baseline weight. The vertical line is plotted at kg, where is the mean of all 69 baseline weights. Estimable bounds for the remaining unexplained subject-treatment interaction standard deviation within subpopulations σD|Z can be bounded by quantities that are estimable by setting the nonestimable partial correlation in (6) equal to 1 and -1 respectively, and estimating the conditional variance of X and Y, given Z, using the mean squared error of models that regress X on Z and Y on Z. This gives estimated bounds and .
Figure 1.
Plot of weight loss in kilograms (kg) at 12 weeks (positive values are a weight loss) versus baseline weight in kg. The fitted lines are from regressing X on Z and Y on Z. The vertical dashed line is at the sample mean baseline weight.
If the distribution of D at a given value of Z is normal with mean and variance given by (4) and (5), then bounds for the PIQI at a given Z = z0 are given as
| (7) |
The quantities in (7) can be estimated from the regression of X on Z and of Y on Z.
Table 1 shows the estimated mean treatment effect for 3 values of baseline weight, the mean baseline weight and one and two standard deviation(s) above baseline weight. The standard deviation of baseline weight, sz, was computed from all 69 baseline weights. Estimates of the two conditional standard deviations in (7) are nearly the same, so that the estimated minimum PIQI is very close to zero. Estimated minimum and maximum PIQI are shown in Table 1 along with standard errors obtained from 2000 bootstrap samples within treatment groups. The last column in Table 1 for PSR will be discussed in section 3.
Table 1.
Estimated mean treatment effect and minimum and maximum PIQI (and standard error) at three different values of baseline weight.
| z 0 | ||||
|---|---|---|---|---|
| 89.61 | 2.16 (0.780) | 0 (0.052) | 0.363 (0.052) | 0.360 (0.050) |
| 102.52 | 4.16 (1.256) | 0 (0.006) | 0.248 (0.067) | 0.245 (0.064) |
| 115.43 | 6.17 (2.021) | 0 (0.009) | 0.156 (0.078) | 0.153 (0.074) |
The standard error estimates (se) are based on 2000 bootstrap samples.
Some conclusions can be summarized from the analysis of these data using baseline weight as a covariate.
Data suggest some evidence of subject – treatment interaction in the population as indicated by a significant treatment-covariate interaction.
Sometimes transformations are sought to remove interactions so that, on the transformed scale, more comprehensive statements about treatment effects can be made. However, if measurements are obtained on a clinically meaningful scale and subject-treatment interaction is present in the population on that scale, transforming the data with monotonic but non-linear transformations may eliminate such interactions. Doing so is not inherently correct or incorrect, but if subject-treatment interaction is present on a clinically meaningful scale of measurement, then using a transformation to remove it may change interpretation of the data in such a way that it is no longer so meaningful in the applied setting. Hence, with clinically meaningful scales, one might argue that any assessment of subject-treatment interaction should be done on the original scale of measurement.
Interactions like that shown above can highlight subpopulations that may respond differently to a treatment. The estimated lower bound for PIQI at the three values of baseline weight in Table 1 is very close to zero. The estimated upper bound is positive but decreases for larger values of baseline weight and, at two standard deviations above baseline, the estimate of the maximum PIQI is only two standard errors from zero. Table 1 illustrates a situation in which most individuals with a larger baseline weight would appear to benefit more from one treatment (i.e., the RGL diet) versus another (a more traditional low-fat diet) over the 12 week period. For individuals with an average baseline weight or less, which treatment is more effective is less clear. Again, this data example is focused on illustrating the concepts in this paper and is not intended to recommend a particular diet to anyone.
Covariates for which there is no interaction with treatment, but that are predictive of weight loss, can still be used to tighten estimable bounds for PIQI by tightening the bounds on σD, as shown in Gadbury and Iyer (2000).
3.1.2. A categorical covariate
Analogous results to those described above for a continuous covariate can be derived for a categorical one as well. In particular, the subject-treatment interaction variance decomposes into a covariate-treatment interaction term (the explainable component) and a within group variance (an unexplainable component).
A slightly different approach from that above helps facilitate the derivation. Suppose Z is a categorical covariate with g levels. A balanced design is considered here, so there are n units per group for a total of ng experimental units. Assume as before that a bivariate set of potential outcomes are randomly generated from a population model, and denote the set of potential outcomes as (Xij,Yij), i = 1,2,…,g,j = 1,2,…,n. From the set of potential outcomes, Dij = Xij – Yij is a individual treatment effect, is a mean treatment effect within the ith level of z, where and . Define the variance of these individual effects as,
| (8) |
where . The quantity in (8) can be thought of as a finite population version of from the prior section. If , then there is subject-treatment interaction present among the ng subjects in the sample. It can be shown that,
| (9) |
where represents a within group variance of individual treatment effects, pooled across groups. Equation (9) shows that the components of include both subject-treatment interaction within subsets, specified by , and a subset treatment interaction term that is a function of . When , the mean treatment effect within subsets varies across the subsets. In the case that , subject-treatment interaction in the set of ng subjects is completely explained by the interaction across subsets, which indicates a constant individual effect of treatment T relative to treatment R within subsets. If as given above is close to , then Z is less useful for predicting subsets of individuals (among the ng individuals) who may respond successfully to one treatment over the other (that is, the subset interaction term is small).
None of the quantities in equation (9) can be calculated from actual observed data post treatment assignment, because all potential outcomes are not observable. However, a post treatment assignment “estimate” for the second term in (9), , is a scalar of the usual sum of squares for the subset-treatment interaction term in a 2×g factorial analysis of variance computation with n/2 observations for each treatment group combination. Consequently, in an ANOVA model with weight loss as a response and treatment, Z, and a treatment-Z interaction as explanatory variables, an F-test for the contribution of the interaction term may not only be used to diagnose the degree of subset treatment interaction, but also provides an indication that some subject-treatment interaction is explained by the covariate.
, the first term in equation (9), may be used to evaluate the PIQI within groups, as before. If , j = 1,…,n, then bounds for the PIQI at a given Z = z0 are the same as those given in equation (7), and estimates for the parameters in these bounds, , and , can be estimated from sample statistics. One could estimate σX|Z and σY|Z by pooling sample variances of observed outcomes across groups or separately within each group. The latter approach is equivalent to conducting a separate analysis within each subset. It is possible that the bounds for PIQIzi vary widely across subsets, with some subsets exhibiting the plausibility of more treatment heterogeneity than others. Subsets with a positive estimated lower bound for the subject – treatment interaction variance (and/or PIQI), or a small estimated upper bound(s) may be particularly informative.
The categorical variable available in the illustrative data set is gender. A test for a gender-treatment interaction was not significant, indicating that the effect of the RGL diet with respect to the low fat diet was not estimated to be different across genders. This implies that either gender does not explain any treatment heterogeneity or that the study had insufficient power to detect the interaction. There is another technique that has been proposed to evaluate the potential presence of treatment heterogeneity. This is the proportion of similar response (Rom and Hwang 1996; Stine and Heyse 2001), discussed next.
3.2 Proportion of Similar Response
Inman and Bradley (1989) provide a comprehensive treatment of the PSR where its calculation is defined as a measurement of overlap between two probability density functions (pdfs), given as
| (10) |
where fX(x) and fY(x) are the pdfs of the outcome variables X and Y to treatments T and R, respectively. There has been some confusion regarding the interpretation of the PSR (Inman and Bradley 1989) and some disagreement over its usefulness as a measurement of treatment heterogeneity (Senn 1997, 2006b) and of a quantity similar to the PIQI (Gastwirth 1975). The pictorial overlap of the density curves shown by the PSR (e.g., see Figure 2) provides a natural way to think about treatment heterogeneity and IQI. The overlap seems to suggest that as the PSR increases, the potential for a value from fX(x) to be less than a value from fY(x) also increases. However, in an assessment of the PSR, Senn (2006b, pp. 3944-3945) points out, “If every patient benefits by having his or her outcome improved by the same amount [under treatment T] compared to what it would have been [under treatment R], then 100 percent of the patients have benefited” (brackets added to provide context for the notation herein). Thus Senn identifies what is clear using potential outcomes, which is, if D is a constant, both and PIQI equal 0, even when the PSR > 0.
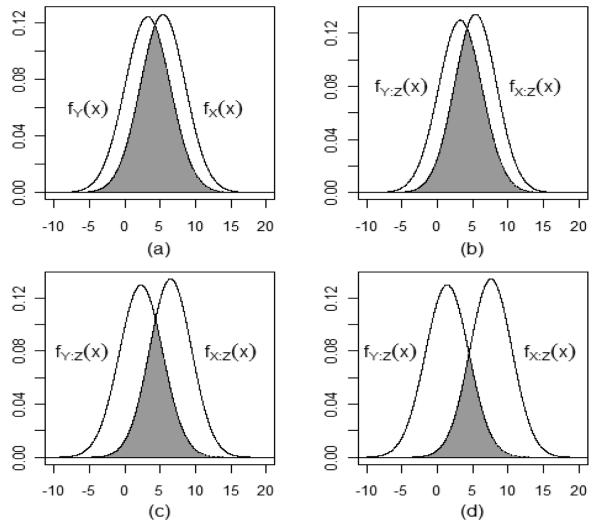
Figure 2.
Illustration of the PSR using only the marginal distributions of X and Y (panel (a)) and at three values of baseline weight given in Table 1 (panels b – d).
The calculation of the PSR depends on values of x such that fX(x) = fY(x). For clarity of illustration, assume that X and Y follow a bivariate normal distribution throughout, and, without loss of generality, assume μX > μY, , and for the remainder of this entry. When k ≠ 1 there will be exactly two finite points of equality, xL,xU with xL < xU, where fX(xL) = fY(xL) and fX(xU) = fY(xU). Both xL and xU result from
| (11) |
A similar representation for the points of equality can be found in Inman and Bradley (1989). When k > 1 the PSR can be calculated by adding three probabilities shown in equation (12),
| (12) |
When k < 1, equation (12) becomes PSR = P(Y ≤ xL) + P(xL ≤ X ≤ xU) + P(Y ≥ xU). When k = 1, fX(x) = fY(x) at a single value . The calculation of the PSR is then simplified to
| (14) |
The following proposition establishes a relationship between the PSR and the PIQI, with the details of the derivation given in the appendix.
Proposition 1
Assuming the bivariate normal distribution described earlier with μX > μY,
| (14) |
with equality at k = 1.
A similar result holds for subpopulations defined by either a continuous or a categorical covariate, Z. The conditional PSR is defined using the conditional distributions of X and Y given the observed covariate Z = z0 so that
| (15) |
As with the PSR, the relationship between PSRz0 and PIQIz0 depends on whether . Let . Given conditional distributions fX|z0) and fY|z0 at a finite value of z0, then
| (16) |
with equality holding at kZ = 1. This result follows directly from the proof of proposition 1.
Figure 2 illustrates the estimated PSR for the data example. The first panel shows the unconditional PSR and the other 3 show the estimated conditional PSR at the three values of z0 given in Table 1. Numerical estimates for (1/2)PSR (and standard errors) are given in Table 1, and they are very close to those reported earlier for the estimated maximum PIQI because the estimates for k (and kZ) are very close to 1. The estimated PSR decreases with increasing baseline weight – the result of the treatment-baseline weight interaction.
A connection between the maximum PIQI and PSR has been established under normality, as shown here. We are not aware of a similar result relating the PSR to the minimum bound for a PIQI. The connection between the bounds for PIQI and the PSR is likely to be less straightforward for non-normal distributions. For instance, some initial work with skew normal distributions (not reported here) suggests that there are connections, but they are less intuitively appealing than those made under normality. An advantage to the PSR is that it can be estimated nonparametrically, as reported by Stine and Heyse (2001). Exploring connections between the PSR and PIQI for non-normal data could be a subject of future work.
3.3 Cross-Over Designs
Perhaps the most straightforward design for estimating and the PIQI is a cross-over design. A large body of literature exists on estimating mean treatment effects, mean period effects, carry-over effects, etc. (e.g., Senn 2006a; Yang and Stufken 2008). Mixed-effects models fit to data from a cross-over design with a random subject effect may even compute what some have referred to as a “subject-treatment interaction variance” (e.g., Hauck et al. 2000; Endrenyi and Tothfalusi 1999). However, this variance computed from observed data may not equal a variance of true individual effects without certain assumptions and/or depending upon how one defines an individual effect in multiple period designs. We illustrate concepts for a two period two treatment cross-over design, assuming no carry over effects but that period effects may vary across individuals. Potential outcomes are (X1,Y1) at period 1 and (X2,Y2) at period 2, and these are rewritten as (X – t, Y – τ) at period 1 and (X + t, Y + τ) at period 2. The pair (X,Y) represents the average potential outcomes over the two periods for treatments T and R, respectively. The variables (t, τ) serve to quantify a deviation from the average potential outcomes at each time period for the two treatments. There are two “true” individual treatment effects given by D1 = (X – Y)—(t–τ) at period 1 and D2 = (X–Y)+(t–τ) at period 2. In some applications it may be D1 that is the effect of most interest. Another effect may be defined as the average over the two time periods, denoted as D = (D1 + D2)/2. The true individual effect is constant across the two time periods if t–τ = 0, an assumption that may be reasonable with no carry-over effects.
Since each individual is crossed over from one treatment to another after a washout period, an individual treatment effect may seem to be observable. Assume that n1 subjects are randomly assigned to the sequence, TR, where TR implies treatment T at time 1 and treatment R at time 2, and n2 subjects to the reverse sequence of treatments, RT, with n1 + n2 = n. The observed differences are dj, for j = 1,2,…,n and can be written as dj = (Xj – Yj)–(tj+τj) if the jth subject was assigned to sequence TR, and dj = (Xj – Yj)+(tj+τj) if assigned to sequence RT.
A straightforward naïve estimate of the PIQI may be obtained using equation (2), with to estimate to estimate . Following results analogous to Gadbury (2001) it can be shown that is positively biased for Var(D)= when an individual effect is defined by D = (D1 + D2)/2. The bias term involves the variance of (t + τ) which is not estimable in this design without assumptions. If (t + τ) is assumed to be constant in the population (i.e., a constant sequence effect), then the bias can be estimated from observed data. If this is not assumed, but it is assumed that the true individual effect is constant across periods, meaning that t = τ across the population, then the bias can be estimated if t (or τ) is a constant. If t = τ but Var(t)>0, then the bias can be estimated with an extension to the design such as the Balaam (Balaam 1968) design, where some subjects remain on the same treatment over the two periods (i.e., TR, RT, TT, and RR sequences).
Required assumptions for direct estimation of may be more plausible in certain applications than assumptions that are required without the multiple period feature of the design. Even with no additional assumptions, estimated bounds for (or PIQI) may be tighter than those obtained from single period designs. Repeated measures cross-over designs have advantages over single period designs for estimating subject-treatment interaction and its consequences (e.g., Senn 2001). More methodological development is needed to define the required assumptions and resulting estimators from different types of cross-over designs, and potential outcomes may be the best structure to use when doing this.
Cross-over designs, however, are not always practical to implement in many applications (cf., Brown 1980; Senn 2001). For instance, in applications like the data example used herein, there may be limitations in using cross-over designs when the primary outcome variable is weight loss. The true individual effect of a treatment at time 1 may be substantially larger than at time 2 because people tend to lose weight more rapidly at first, and substantial carry-over effects may be likely as well.
4. DISCUSSION AND CONCLUSIONS
In 1892 Sir William Osler stated, “If it were not for the great variability among individuals medicine might as well be a science and not an art” (extracted from Roses, 2000, page 857). Thus the topics discussed here have been long recognized as important considerations when selecting a “best” treatment for an individual. Individual treatment heterogeneity and its consequences should be an important consideration when designing clinical trials and interpreting treatment efficacy and safety for a target population. The quantities discussed herein may also inform the pursuit of pharmacogenetic research which seeks to identify genomic predictors of response to treatments (e.g., Hu et al. 2006). It is often poorly understood how much heterogeneity might be present in the first place and whether a search for such gene-treatment interactions that explain this heterogeneity will be fruitful (Senn 2001). Perhaps we should invest most readily in finding genetic factors influencing variability in treatment response for those treatments for which we have actually demonstrated, rather than merely presumed, large variability in response.
Evaluating the plausible variance in treatment effects, and even more so the proportion of a population with an IQI, has other applications as well. The Latin enjoinder primum non nocere (above all, do no harm) frequently (mis)attributed to Hippocrates (Smith 2005) remains a mainstay of medical thinking today. Thus, regulatory agencies such as the US Food and Drug Administration may wish to know not only the average effect of a drug compared to placebo, but the probability that it will have a poorer effect than no drug. Similarly, when faced with the possibility of approving a new drug that is no more efficacious on average than an existing drug which has been widely used and which has already survived the baptism of fire that is widespread clinical use, it is tempting to ask “why do we need to approve this new drug if it is no more efficacious than the old drug we know and trust?” A typical response is one voiced by the director of the UK’s National Institute for Health and Clinical Excellence’s health technology evaluation centre, who recently stated, “Different people respond in different ways to treatment, and the committee heard from clinical experts and patients about the importance of having multiple options available” (Mayor 2010). That is, it is often presumed that although drug A may be no better than drug B on average, for some persons, drug A works better than does drug B and vice versa for other persons. If this is the case, then having multiple drugs on the market may be important even if there is no difference in their effects on average and they cannot be used in combination. However, rather than accepting the premise as true a priori, the results shown herein may help lead to new ideas for the evaluation of the plausibility and frequency of such IQIs.
The ideas may also be useful in evaluating advertising claims. Consider the context of claims for weight loss products which can often be quite extravagant. The US Federal Trade Commission (FTC) states that “No [weight loss] product will work for everyone,” and therefore claims implying that a “product causes substantial weight loss for all users” is a likely sign of fraud (FTC statement). Is there evidence a company could provide to FTC to show that in their randomized clinical trial (RCT) showing a positive mean effect, the plausible proportion of people who will have an effect less than a threshold τ is negligible? Alternatively, is there evidence that the FTC could muster to show a company that their claim of a universal positive effect is almost certainly untrue despite their being a positive mean effect? Again, the results described herein may help clarify the issues involved when answering these questions.
Finally, one can imagine applications in legal settings (see, for example, Marchant 2001, 2010). Imagine that a plaintiff (e.g., a consumer) sues a defendant (e.g., a distributor of a drug, food, or pharmaceutical) claiming that use of defendant’s product caused a stroke secondary to markedly elevated blood pressure (BP) as a result of using the product. Imagine further that defense experts present evidence that well-designed RCTs show an average effect of the product on BP to be less than or equal to zero. Plaintiff’s experts reply that there is great interindividual variability in response and even though the average response is less than or equal to zero, some people will be hypersensitive hyper-responders with extreme BP increases. What evidence can the court bring to bear on the question of how probable it is that plaintiff was such a hyper-responder? The first question which must precede this is what evidence is there that hyper-responders in the opposite direction even exist and with what frequency? The techniques herein may provide a plausible range of answers.
Potential outcomes are a natural way to define individual treatment effects and metrics that quantify treatment heterogeneity as well as the risk of a qualitative interaction across individuals or groups of individuals. Existing techniques that seek to evaluate treatment heterogeneity have limitations, and these limitations are made clear by potential outcomes. The potential outcomes framework can delineate heterogeneity that is observable from that which is not, and unobservable heterogeneity can often be bounded by quantities that can be estimated in observed data. Thus, the potential outcomes framework is a useful complement to existing techniques to evaluate treatment heterogeneity and qualitative interactions, and they should be used as such when analyzing data from randomized trials. Their use may also suggest new directions in the design of randomized trials – directions that do not compromise estimation of mean effects but also allow for more direct evaluation of treatment heterogeneity. Eventually, perhaps, reporting of treatment heterogeneity and risks of qualitative interactions (at either the individual or group level), in addition to summary measures such as mean effects, will be a more standard practice, and a response to a perceived need that has been recognized by others in recent years (cf., Longford 1999).
Acknowledgments
Dr. Allison acknowledges research support from NIH R01DK078826. The authors are grateful to Kraft Foods for supplying the data for this paper. The authors acknowledge helpful comments from the editors and two referees.
APPENDIX.
Proof of Proposition 1
The equality at k = 1 is straightforward. Let k > 1. When ρXY = –1, the (x,y) pairs are constrained to the line y = μY + kμX – kx with probability one. Let x and y be equal and set to the common value . Note that the term under the square root in equation (11) is positive for any nonnegative k, and that the first term in equation (11), , is less than x–1. So it follows that xL < x–1. It can be further shown that xL < x–1 < μX < xU and
| (17) |
Therefore,
Thus, PIQImax ≥ PSR/2 because of the definitions of xL and xU. Proof for k < 1 is similar.
Contributor Information
Robert S. Poulson, Statistical Methods Group, Edwards Air Force Base Edwards, CA 93524 Robert.Poulson@edwards.af.mil
Gary L. Gadbury, Department of Statistics Kansas State University Manhattan, KS 66506 gadbury@ksu.edu
David B. Allison, Department of Biostatistics, Section on Statistical Genetics University of Alabama at Birmingham Birmingham, AL 35294 dallison@uab.edu
REFERENCES
- Balaam LN. A Two-period Design with t2 Experimental Units. Biometrics. 1968;24:61–73. [PubMed] [Google Scholar]
- Brown BW. The Crossover Experiment for Clinical Trials. Biometrics. 1980;36:69–79. [PubMed] [Google Scholar]
- Byar DP, Corle DK. Selecting Optimal Treatment in Clinical Trials Using Covariate Information. Journal of Chronic Diseases. 1977;30:445–459. doi: 10.1016/0021-9681(77)90037-6. [DOI] [PubMed] [Google Scholar]
- Darwin C. On the Origin of Species. 5th ed D. Appleton and Company; New York: 1871. p. 26. [Google Scholar]
- Endrenyi L, Tothfalusi L. Subject-by-Formulation Interaction in Determinations of Individual Bioequivalence: Bias and Prevalence. Pharmaceutical Research. 1999;16:186–190. doi: 10.1023/a:1018899504711. [DOI] [PubMed] [Google Scholar]
- Fan Y, Park SS. Partial Identification of the Distribution of Treatment Effects and its Confidence Sets. In: Li Qi, Racine Jeffrey., editors. Nonparametric Econometric Methods. Advances in Econometrics, Volume 25. Emerald Group Publishing Limited; 2009. pp. 3–70. [Google Scholar]
- Fan Y, Park SS. Sharp Bounds on the Distribution of Treatment Effects and Their Statistical Inference. Econometric Theory. 2010;26:931–951. [Google Scholar]
- [Retrieved on Sept. 10, 2010];FTC Statement. from http://www.ftc.gov/bcp/edu/pubs/business/adv/bus60.pdf.
- Gadbury GL, Iyer HK. Unit-Treatment Interaction and its Practical Consequences. Biometrics. 2000;56:882–885. doi: 10.1111/j.0006-341x.2000.00882.x. [DOI] [PubMed] [Google Scholar]
- Gadbury G. Randomization Inference and Bias of Standard Errors. The American Statistician. 2001;55:310–313. [Google Scholar]
- Gadbury GL, Iyer HK, Allison DB. Evaluating Subject-Treatment Interaction when Comparing Two Treatments. Journal of Biopharmaceutical Statistics. 2001;11:313–333. [PubMed] [Google Scholar]
- Gadbury GL. Subject-Treatment Interaction. In: Shein-Chung Chow., editor. Encyclopedia of Biopharmaceutical Statistics. Third Edition, Revised and Expanded Informa Healthcare; London: 2010. pp. 1316–1321. [Google Scholar]
- Gail M, Simon R. Testing for Qualitative Interactions Between Treatment Effects and Patient Subsets. Biometrics. 1985;41:361–372. [PubMed] [Google Scholar]
- Gastwirth JL. Statistical Measures of Earnings Differentials. The American Statistician. 1975;29:32–35. [Google Scholar]
- Hauck WW, Hyslop T, Mei-Ling C, Patnaik R, Williams RL. Subject-by-Formulation Interaction in Bioequivalence: Conceptual and Statistical Issues. Pharmaceutical Research. 2000;17:375–380. doi: 10.1023/a:1007508516231. [DOI] [PubMed] [Google Scholar]
- Holland PW. Statistics and Causal Inference. Journal of the American Statistical Association. 1986;81:945–960. [Google Scholar]
- Hu J, Redden DT, Berrettini WH, Shields PG, Restine SL, Pinto A, Lerman C, Allison DB. No Evidence for a Major Role of Polymorphisms During Bupropion Treatment. Obesity (Silver Spring) 2006;14:1863–1867. doi: 10.1038/oby.2006.215. [DOI] [PubMed] [Google Scholar]
- Inman HF, Bradley EL. The Overlapping Coefficient as a Measure of Agreement Between Probability Distributions and Point Estimation of the Overlap of Two Normal Densities. Communications in Statistics: Theory and Methods. 1989;18:3851–3874. [Google Scholar]
- Inoue J, Hoshino R, Nojima H, Ishida W, Okamoto N. Investigation of Responders and Non-responders to Long-Term Donepezil Treatment. Psychogeriatrics. 2010;10(2):53–61. doi: 10.1111/j.1479-8301.2010.00319.x. [DOI] [PubMed] [Google Scholar]
- Li J, Chan ISF. Detecting Qualitative Interactions in Clinical Trials: An Extension of Range Test. Journal of Biopharmaceutical statistics. 2006;16:831–841. doi: 10.1080/10543400600801588. [DOI] [PubMed] [Google Scholar]
- Longford NT. Selection Bias and Treatment Heterogeneity in Clinical Trials. Statistics in Medicine. 1999;18:1467–1474. doi: 10.1002/(sici)1097-0258(19990630)18:12<1467::aid-sim149>3.0.co;2-h. [DOI] [PubMed] [Google Scholar]
- [Retrieved Sept. 9, 2010];Lucretius. from http://classics.mit.edu/Carus/nature_things.4.iv.html.
- Maki KC, Rains TM, Kaden VN, Raneri KR, Davidson MH. Effects of a reduced-glycemic-load diet on body weight, body composition, and cardiovascular disease risk markers in overweight and obese adults. American Journal of Clinical Nutrition. 2007;85:724–734. doi: 10.1093/ajcn/85.3.724. [DOI] [PubMed] [Google Scholar]
- Marchant GE. Genetics and Toxic Torts. Seton Hall Law Review. 2001;31:949. [PubMed] [Google Scholar]
- Marchant GE. [Retrieved on Sept. 11, 2010];2010 from http://www.law.asu.edu/files/Programs/Sci-Tech/Commentaries/Marchant%20Formatted.rev.doc.
- Marshall A. Laying the foundations for personalized medicines. Nature Biotechnology. 1997;15:954–957. doi: 10.1038/nbt1097-954. [DOI] [PubMed] [Google Scholar]
- Mayor S. NICE Recommends Widening Choice of Biological Drugs for Patients with Rheumatoid Arthritis. BMJ. 2010;340:c3477. doi: 10.1136/bmj.c3477. [DOI] [PubMed] [Google Scholar]
- Peto R. Statistical Aspects of Cancer Trials. Chapman and Hall; 1982. pp. 867–871. [Google Scholar]
- Rom DM, Hwang E. Testing for Individual and Population Equivalence Based on the Proportion of Similar Responses. Statistics in Medicine. 1996;15:1489–1505. doi: 10.1002/(SICI)1097-0258(19960730)15:14<1489::AID-SIM293>3.0.CO;2-S. [DOI] [PubMed] [Google Scholar]
- Roses AD. Pharmacokinetics and the Practice of Medicine. Nature. 2000;405:857–865. doi: 10.1038/35015728. [DOI] [PubMed] [Google Scholar]
- Rubin DB. Estimating Causal Effects for Treatments in Randomized and Nonrandomized Studies. Journal of Educational Psychology. 1974;66:688–701. [Google Scholar]
- Senn S. Letter to the editor on “Testing for Individual and Population Equivalence Based on the Proportion of Similar Responses. Statistics in Medicine. 1997;16:1301–1306. doi: 10.1002/(sici)1097-0258(19970615)16:11<1303::aid-sim573>3.0.co;2-e. [DOI] [PubMed] [Google Scholar]
- Senn S. Individual Therapy: New Dawn or False Dawn? Drug Information Journal. 2001;35:1479–1494. [Google Scholar]
- Senn S. Cross-over Trials in Statistics in Medicine: The First ‘25′ Years. Statistics in Medicine. 2006a;25:3430–3442. doi: 10.1002/sim.2706. [DOI] [PubMed] [Google Scholar]
- Senn S. Letter to the editor on “Probability Index: An Intuitive Non-parametric Approach to Measuring the Size of Treatment Effects. Statistics in Medicine. 2006b;25:3944–3948. doi: 10.1002/sim.2587. [DOI] [PubMed] [Google Scholar]
- Simon R. Patient Subsets and Variation in Therapeutic Efficacy. British Journal of Pharmacology. 1982;14:473–482. doi: 10.1111/j.1365-2125.1982.tb02015.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith CM. Origin and Uses of Primum Non Nocere--Above All, Do No Harm! Journal of Clinical Pharmacology. 2005;45:371–377. doi: 10.1177/0091270004273680. [DOI] [PubMed] [Google Scholar]
- Stine RA, Heyse JF. Non-parametric Estimates of Overlap. Statistics in Medicine. 2001;20:215–236. doi: 10.1002/1097-0258(20010130)20:2<215::aid-sim642>3.0.co;2-x. [DOI] [PubMed] [Google Scholar]
- Silvapulle MJ. Tests for Qualitative Interaction: Exact Critical Values and Robust Tests. Biometrics. 2001;57:1157–1165. doi: 10.1111/j.0006-341x.2001.01157.x. [DOI] [PubMed] [Google Scholar]
- Yang M, Stufken J. Optimal and Efficient Crossover Designs for Comparing Test Treatments to a Control Treatment Under Various Models. Journal of Statistical Planning and Inference. 2008;138:278–285. [Google Scholar]