DNA Translocating Through a Carbon Nanotube Can Increase Ionic Current

Abstract

DNA translocation through a narrow, single-walled carbon nanotube can be accompanied by large increases of ion current, recently observed in contrast to the ion current blockade. We use molecular dynamics simulations to show large electro-osmotic flow can be turned into a large net current via ion-selective filtering by a DNA molecule inside the carbon nanotube.

1. Introduction

The next step in advances of DNA sequencing technology is third generation sequencing, based on the single-molecule, voltage-driven transport through biological and synthetic nanopores.¹ These nanopores provide a localization and controlled motion for sequence recognition of single DNA molecules. Typically, a DNA polymer, negatively charged in a solution, translocates through a nanopore under externally applied, electric field, caused by the electrophoretic voltage bias. The nanopore is sandwiched between two reservoirs, which supply ionic solution as well as the DNA segments for translocation.

DNA translocation through a nanopore is usually detected via a fall in ionic current, since DNA may mechanically block a number of charge carriers in the nanopore. Fan et al.² showed how small increases in nanopore current can occur at lower salt concentrations and be accounted for by the counterions pulled into a channel by translocating DNA. On the other hand, positively charged counterions can form an electrical double layer (EDL) around DNA, which exposed to the electrophoretic driving force may contribute to an increase of electro-osmotic current. There has been little discussion of the contribution of electro-osmosis to nanopore currents.^3,4,5 The electro-osmotic current of anions provides a drag which slows down the DNA translocation through the pore. This reduces the major drawback of the nanopore sequencing technology, the speed of translocation, which is often too fast to enable the detection of individual bases.^3,4 We show here that electro-osmotic flow can dominate signals of translocation, and that under some conditions DNA in a carbon nanotube (CNT) pores may lead to the enhancement of the ionic current rather than to its blockade.

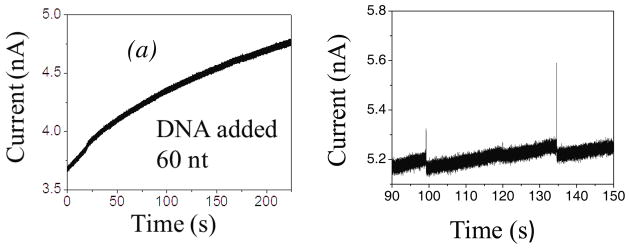
Single-walled carbon nanotubes (SWCNT) are excellent candidates for nanopore applications because they have attractive chemical, electronic, mechanical properties, and can be fabricated with various lengths and diameters. Significant advantages for nanofluidic applications are based on their hydrophobic, almost frictionless internal surface. As a consequence, ionic currents through an individual SWCNT⁵ is markedly different from those through other types solid-state nanopores (SSN)⁶ or through protein nanopores (e.g. α-hemolysin).⁷ Firstly, the magnitude of signal is much larger (nA) than in a conventional SSN (pA) due to a significant increase of electro-osmotic current caused by the perfect slip on the atomistically smooth internal surfaces,⁸ explaining, by more detailed modeling than in Ref. 5, the huge increase in the ionic current caused by surface charge at the SWCNT walls. Secondly, when DNA molecules are present in a narrow SWCNT, it is observed that the ionic current may increase, opposite to the expected ionic blockade in SSN^1,9,10 and in protein nanopores.⁷ In addition, a CNT may be much longer than the translocated DNA segments, opposite to the usual SSN applications.¹¹ For example, the length of the SWCNT in Ref. 5 was 2 μm, while the DNA segments were 60–120 nt, i.e only ~20–40 nm long. Therefore, the whole DNA segment typically stays inside the CNT during the translocation, which can also be related to the slow rise in ionic current (~ 5 pA/s), as shown in Figure 1(a)⁵, later followed by the random spikes in the current flow, Figure 1(b). This can be contrasted to the usual blockade which causes a decrease of the current in SSN and protein nanopores.

Figure 1.

Measured⁵ ionic current increase when ssDNA segments of ~60 nt translocate through the metallic SWCNT of much longer length (L=2μm), (a) immediately after the DNA addition, and (b) 5 min after the addition the current spikes appear.

It was speculated that the observed slow rise of the current in experiments of Liu et al.⁵ could come from a larger number of DNA molecules that slowly build up inside the nanotube, which are then released simultaneously in “spike” events. This raises the question of why the DNA does not swiftly translocate down the nanotube as it does in a conventional SSN. One possibility is that internal wall of the CNT get coated by DNA. In addition, discontinuous surface charges of the CNT wall, caused by fabrication defects, could provide regions of depleted and enriched volume charge of ions, defined by the difference in concentrations of cations and anions. The dominant sign and magnitude of this volume charge is determined by competition of the CNT surface charge density and the negative charge of the DNA in the tube. This may cause focusing of the charged DNA polymer inside the CNT, and rectification of ionic current. Formation of the DNA EDL and rearrangements of electrons at the surface of the metallic CNT are also attributed to the reduction of the electrophoretic driving force at the DNA and thus, to the suppression of its translocation speed.^11,12

The main purpose of this article is to offer, by performing all-atoms MD simulation, a quantitative rather than a speculative study of the conditions leading to the large enhancement of ionic current during already a single, short DNA translocation through a narrow, metallic SWCNT, distinctively from any conventional SSN. The long-time scale of the current increase in Figure 1, at the scale far beyond the ns time scale of MD, is then a consequence of a cumulative buildup of many DNA segments in time succession. This phenomenon rests on the huge variations of ionic current with electronic properties of CNT, surface charge, radius and material of the pores which we briefly review here. A significant contribution to understanding and control of the DNA translocation in the conventional SSN was given by research of Kawai and collaborators,^3,4 aimed both to reduce the DNA translocation speed and increase the DNA capture probability at the inlet of a SSN.

Volume exclusion of ions due to DNA and formation of counterions layer around DNA are competing effects: The former blocks the current, while the latter increases the number of ions available for the conductance. Even in a conventional SSN dominance of one of these effects can change the sign of the “blockade” effect,⁸ depending upon the pore diameter, its material, its charge, the electrolyte concentration, and the external electric field. In addition, the effective charge density of DNA could be suppressed by almost a factor 2 due to counterion screening.^3,4

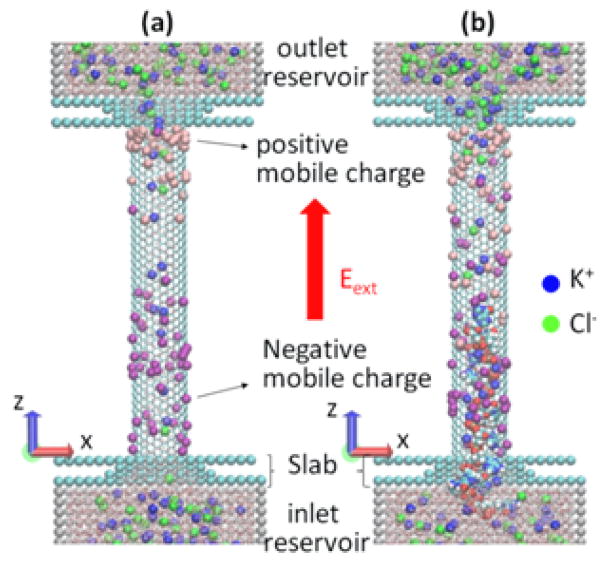
The modeled system is shown schematically in Figure 2. Two reservoirs are connected by a (12, 12) single-wall CNT whose wall-center-to-wall-center diameter is 1.628 nm, with a length of 10 nm, resulting in 1920 carbon atoms in the tube. The system is filled with 1 M KCl water solution. The ionic current is caused by the uniform electric longitudinal field E. All-atom MD simulations in the present study were performed using GROMACS 4.5.4 in an NVT ensemble.¹³ The details of MD simulation, including a description of charging and polarization of the CNT pore surface as well as the DNA modeling are described in the Section 2. Our results are presented and discussed in Section 3.

Figure 2.

Schematics of the MD simulation: SWCNT is connecting two reservoirs with solvated KCl; the system is embedded in electrophoretic field Eext; besides the fixed surface charge, CNT also contains mobile surface charges, to allow for the CNT polarization in the field. (a) Ionic current flows through CNT; (b) The ionic current while DNA is translocated through the CNT.

2. Computational MD Method

All MD simulations in present study were performed using GROMACS 4.5.4 in an NVT ensemble¹³. The Nośe–Hoover thermostat^14–16 was applied each 2.0 ps to maintain the system temperature at 300 K. The equations of motion were integrated using the leapfrog algorithm with the time step of 1.0 fs. The system is kept periodic only in axial, z-direction, to preserve the number of particles N, keeping a large size of the computation box of 20×20×22 nm³. Total number of water molecules was 11,000 which solvated 1 M of KCl electrolyte (more than 200 K⁺ and Cl⁻ ions each). The size of each reservoir is 6×6×6 nm³, and their walls are constituted of carbon atoms, in dense-packed single layer. All simulations are performed for 5.0 ns, with the sampling period of 4.0 ns (t=1 – 5 ns).

For the DNA, we use a 12-base ssDNA of 5′–CGCGAATTCGCG–3′, which is prepared by unzipping the well-known Dickerson’s B-DNA dodecamer (double stranded).¹⁷ The parameters (LJ parameter and atomic charge) in AMBER-99 force field¹⁸ are used for both non-bonding pairwise interactions and boding interactions in DNA. The nonbonding interactions consist of (6, 12) LJ potential and Columbic potential. The bonding interactions are modeled with stretching, bending, and torsion. The carbon atoms in CNT are assumed frozen and the LJ parameters are taken from Guo et al.¹⁹ The slab (see Figure 2) consists of united CH₂ segments and their LJ parameters are σ_S–S = 0.3871 nm and ε_S–S = 0.4909 kJ/mol.²⁰ Water molecules are modeled using the TIP3P model.²¹ In TIP3P model, the angle between hydrogen (H) – oxygen (O) vectors is fixed to 104.52 degree, while the distance between oxygen and hydrogen is held at 0.9572 Å. The hydrogen and oxygen charges are +0.417e and −0.834e, respectively. The LJ parameters for K⁺ and Cl⁻ were obtained from Koneshan et al.²² The electrostatic interactions between all charged particles (including solvated ions and DNA) use Coulomb cut-off radius of 7.5 nm.

The surface of the CNT was uniformly charged, resulting in the total surface charge Q. For example, choosing Q=−5e (= −16 mC/m²), the partial charge per carbon atom is −5e/1920 = −2.6×10⁻³e. In order to model the polarization of metallic CNT, due to the application of uniform external electric field E, we placed an equal number of mobile positively and negatively charged particles of 1 atomic mass unit on the surface. These are allowed to move only in the axial (z) direction, while constrained to the CNT surface. Motion of the particles in azimuthal direction is also constrained to avoid head-on collisions. These particles are mutually interacting only by Coulomb, electrostatic forces. At both ends of the tube (slabs) a strong repulsive potential barrier is set to prevent escape of the mobile charged particles from the CNT surface. The 45 positive and negative particles of the same charge q_p are initially randomly distributed at the surface, so that q=45q_p=0.4|Q|. Thus, for Q=±3e, q=1.20e and the charge of each mobile particle is q_p=1.20e/45=+0.0267e.

3. Results and Discussion

The DNA translocation event includes the capture phase of the polymer segment by the CNT, followed by the translocation through the tube (“retarded” phase^3,4), and exit phase, during which the polymer leaves the tube mouth and enters the outlet reservoir. All phases of the flow may be against the strong electro-osmotic current of cations, if the CNT is negatively charged. The capture phase evolves on a much slower time scale than the retarded phase, and is also determined by probability of finding the tube mouth, by the unfolding and the entropy barrier. The capture optimization requires somewhat opposite conditions from those optimal for slowing down translocation.^3,4 It determines frequency of the spikes in Figure 1(b), and is difficult to simulate by MD, because of the short time scale of the simulation. Therefore, in the present simulations we place the whole 11-segment DNA initially inside the tube³, enabling its immediate translocation, which is the focus of our study rather than capture dynamics, which requires a much longer time scale.

The ionic current is calculated by counting the ions that experience a complete transfer from one reservoir to another in the given time interval Δt = t₂ − t₁, where t₁ = 1 ns and t₂ = 5 ns. The total ionic current is computed by the total charge transversing the CNT, i.e. $I_{\mathit{tot}}=\frac{N_C-N_A}{\mathrm{\Delta }t}e$, where N_{C, A} are the signed numbers of cations and anions, respectively, which transfer ions from inlet to outlet reservoir. The N_{C, A} is positive when particles move in the direction of electric field vector, negative otherwise. Particles which do not finish travel from one reservoir to another are excluded. Those cations and anions which move opposite to and in the direction of the electric field, respectively, contribute a negative current.

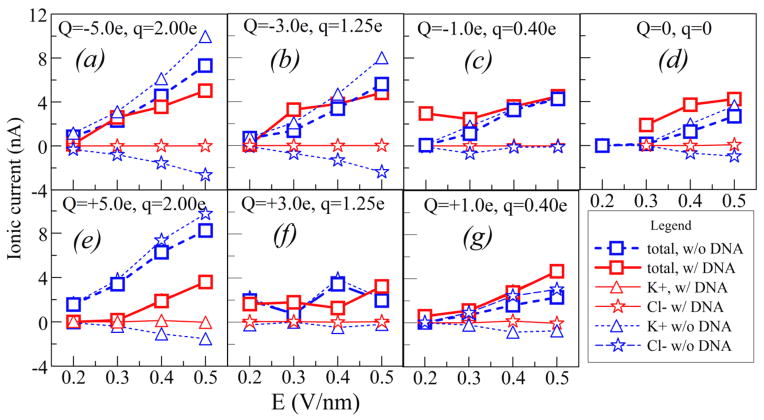
As found and extensively discussed by Liu et al.⁵ and Pang et al.,⁸ and also confirmed by the present MD simulations, when the tube wall is charged the ionic current is dominated by the electro-osmotic flow. The magnitude and sign of the charges at the walls are determined by external factors that are beyond the present simulation.⁸ Therefore, we vary these charges Q in the interval from −8 to +8×10⁻¹⁹ C, in form of a constant charge density, supplemented by about 40% of moving charges (q) of both signs to allow for the metallic tube polarization in the external driving field E (details in Section 2). The responses of ionic current to variation of E are shown in Figure 3. Although the chosen charge densities at the surface (<16 mC/m²) are small, these are compensated by the large driving fields E (0.2–0.5 V/nm), significantly higher than those reported in the Liu experiments⁵. These choices enable faster motion of ions through the tube and faster translocation, compatible with the MD (ns) time scales, providing statistically significant sampling of the ionic currents, while keeping them comparable with nA-range of measured values in Figure 1. As seen in Figure 3, in absence of DNA, the ionic current is dominated by cations (K⁺) when the CNT surface is negatively charged, and by anions (Cl⁻) when the surface is positively charged.

Figure 3.

Ionic currents through the narrow SWCNT (dashed, blue), for various CNT surface charges Q, and mobile surface charges q (see text). Ionic currents during the DNA translocation are shown by solid lines (red). The symbols in the legend represent various component of the ionic current.

For each set (Q,q) of surface charges, and for each value of the applied electric field E we performed two sets of MD calculations, with and without a DNA segment in the tube. Comparison of the two sets of results provides insight in conditions which may cause the ionic current increases in Figure 1.

The dominant electroosmotic flow is proportional to the driving field E and excess volume charges. The latter is induced and controlled by EDL close to the charged tube walls (with almost perfect slip features, and a Debye length of about 0.3 nm, when KCl concentration is 1M), and also by the EDL around the DNA. Due to the no-slip features of ions around DNA, these are mainly moving together with DNA during the translocation, unlike much faster ions close to the surface. However, since the CNT here and in Liu et al. experiment⁵ is narrow, an overlap and mutual interactions of the two EDLs, as well as of geometrical conformations of the DNA in the CNT can significantly influence the currents. Thus, generally, the negatively charged DNA in the tube attracts K⁺, depleting Cl⁻ ions, and this increases excess charge of positive ions. On the other hand, geometrical blocking i.e. volume expulsion of the DNA reduces the ionic current.

Coexistence and competition of the five effects explain the main features of the ionic currents in Figure 3. These are (A) increase of the ionic current with E, (B) increase of ionic current with Q, where the main carrier is regulated by the sign of Q, (C) the space charge induced by EDL of DNA, stimulating cation current, (D) volume expulsion by DNA, and (E) electrostatic repulsion of anions by DNA for positive Q.

For larger surface charges, Q= ± 5e at Figures 3a and 3e, the electroosmotic current is large and geometrical factor, the volume expulsion by DNA (effect D), is the dominant in blocking the ionic current, for both signs of Q. The blocking effect increases with electric field, i.e. with increase of ionic current due to effect A. Both in presence and absence of DNA, the counterions, determined by sign of Q, are the main carriers of the current. The volume expulsion of cations is significantly smaller for negative Q, due to the space-charge effect (C above), but larger for positive Q due to electrostatic repulsion (E above).

For intermediate surface charges, Q= ±3e, Figures 3b and 3f, the competition of all effects (A–E above) results in both positive and negative blockades of slight magnitude, depending on the driving electric field. However, interestingly, for both signs of Q, the cation electro-osmotic current, induced by negatively charged DNA, dominates the ionic current.

However, for small charges Q at the surface, Q= ±1e, DNA causes an increased ionic current for all considered values of E, as seen in Figures 3c and 3g. Like in the previous case, the current in presence of DNA is dominated by cations, irrespectively of the sign of Q. In other words, cation current caused by the EDL of DNA “normally” increases with E, playing more significant role in inducing volume charges than the surface charge Q. In case of positive Q, anions induced by Q are almost completely suppressed as the current carriers when DNA is present. For negative Q, the effect of enhancement is largely compensated by strong electro-osmotic current (in absence of DNA) due to Q. Interestingly, in absence of DNA the ionic currents are not the same for the two signs of Q. As a rule, in case when the current is dominated by cations (negative Q) the current is somewhat larger than when it is dominated by anions. This can be attributed to a larger (by about 40%) vdW radius of negative Cl⁻ ions in comparison to the positive K⁺ ions, which in case of a narrow tube may have effect to both efficiency of the DNA geometrical filtering and electroosmotic mobility in absence of DNA. This also explains slight asymmetry of cation and anion currents for Q=0 in Figure 3d. For that case, the cation current induced by the EDL of DNA causes a significant enhancement (negative blockade.) In spite of repeated calculations, we could not get satisfactory stability of the simulations for the point at E=0.2 V/m and Q=0. So we decided not to show the point which doesn’t meet the same standards of quality as the other points.

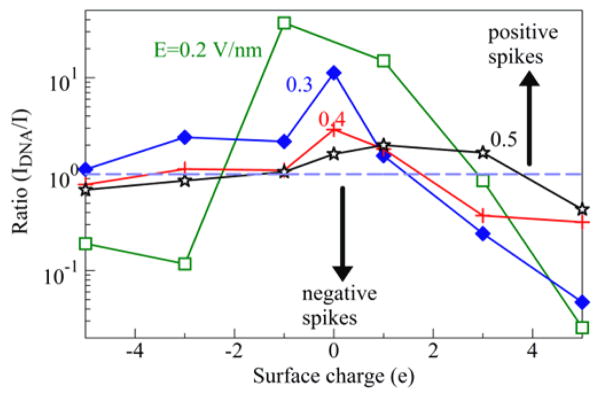
The DNA translocation effects in Figure 3 are summarized in Figure 4, which represents the ionic current enhancement factor due to the DNA translocation, I_DNA/I, as function of the surface charge Q, for various driving fields E. A significant current increase appears for smaller surface charges Q (including the case Q=0). The enhancement factors decreases with increase of E, and their peak value shifts toward positive Q.

Figure 4.

Ionic current enhancement factor due to the presence of a short DNA segment in the SWCNT.

The purpose of the present work is to show that “ion filtering” action of just one segment “sitting” at the exit of a narrow carbon nanotube may cause a significant ion current enhancement rather than the current blockade. This finding points out, though not conclusively, a possible mechanism for the measured increase of the current in Figure 1. However timescale of our modeling is 4 ns, while the measurements extends to seconds, so it is difficult to draw a clear equality of the two phenomena. Future modeling, using methods adequate to much longer time scales, could show whether the measured current increase is a consequence of the consecutive accumulation of the short-time effects obtained here. It might also show that the random current spikes⁵ (shown in Fig. 1(b)) are evolving over many orders of magnitude longer scale (seconds) through the buildup of the short DNA segments (60 nt in Figure 1) at the exit end of the long (2μm) SWCNT. The cation electro-osmotic current, caused by EDL of the negatively charged DNA and possibly of the charged SWCNT surface, as well as the electrostatic barrier⁸ at the tube end are opposing the DNA exit to the reservoir (Movie 2 of Supplementary Information), thus indicating the accumulation of the DNA segments at the exit.