A Method for Event-related Phase/Amplitude Coupling

Abstract

Phase/amplitude coupling (PAC) is emerging as an important electrophysiological measure of local and long-distance neuronal communication. Current techniques for calculating PAC provide a numerical index that represents an average value across an arbitrarily long time period. This requires researchers to rely on block design experiments and temporal concatenation at the cost of the sub-second temporal resolution afforded by electrophysiological recordings. Here we present a method for calculating event-related phase/amplitude coupling (ERPAC) designed to capture the temporal evolution of task-related changes in PAC across events or between distant brain regions that is applicable to human or animal electromagnetic recording.

1. Introduction

The mammalian neo- and archicortices generate electrophysiological oscillatory rhythms (Buzsáki and Draguhn, 2004; Engel et al., 2001) that interact to facilitate communication (Fries, 2005; Frolich and McCormick, 2010; Siorta et al., 2008). The amplitude and phase of these rhythms are typically assessed in an event-related manner across trials or subjects. There is emerging evidence that frequency-specific rhythms are often nested within other frequency bands (Kramer et al., 2008a; Roopun et al., 2008; Tort et al., 2009; see Canolty and Knight, 2010 for a review). There are multiple forms of coupling dynamics: phase/amplitude (Canolty et al., 2006; Cohen et al., 2009; Griesmayr et al., 2010; Lakatos et al., 2008; Osipova et al., 2008; Tort et al., 2009; Voytek et al., 2010a), phase/phase (Darvas et al., 2009; Palva et al., 2005; Tass et al., 1998), and amplitude-to-amplitude (Bruns and Eckhorn, 2004; Voytek et al., 2010b). It is proposed that phase/amplitude coupling (PAC) reflects interactions between local microscale (Colgin et al., 2009; Quilichini et al., 2010) and systems-level macroscale neuronal ensembles (Canolty et al., 2010; Fries 2005; Lisman and Idiart, 1995) that index cortical excitability and network interactions (Vanhatalo et al., 2004). From a behavioral viewpoint PAC has been shown to track learning and memory (Axmacher et al., 2010; Lisman and Idiart, 1995; Tort et al., 2009). PAC magnitude also fluctuates at an extremely low (<0.1 Hz) rate at rest (Foster and Parvizi, 2012).

Currently PAC calculation algorithms compute a value averaged across a semi-arbitrary time window (Canolty et al., 2006; Voytek et al., 2010a; Cohen and van Gaal, 2012) (see Cohen, 2008; Penny et al., 2008; and Tort et al., 2010 for methodological details). The minimum length of this time window is bounded by the frequency of the coupling phase, as at least one full cycle is needed to calculate the distribution of values of the coupling amplitude. However, the PAC metric is sensitive to noise, and recent simulations have made use of >200 cycles to get a reliable PAC estimate (Tort et al., 2010). This means, for example, that if one is investigating PAC between theta phase (4-8 Hz) and high gamma amplitude (80-150 Hz), the best temporal resolution one could achieve at 4 Hz would be 250 ms (one full cycle). However, 50 seconds or more might be required for reliable estimates (250 ms/cycle × 200 cycles). This requires researchers to use block designs (Voytek et al., 2010a), use long trial windows at the cost of temporal resolution (Tort et al., 2009), or to concatenate time series across trials (Tort et al., 2009) which could introduce spurious PAC due to edge artifacts (see Kramer et al., 2008b). These limitations present a problem for analyzing subcomponents of a task such as encoding, delay, and retrieval periods during working memory.

Here we demonstrate a novel approach for assessing time-resolved, event-related PAC (ERPAC). We provide results from subdural electrocorticographic (ECoG) data from three human subjects with implanted electrodes to demonstrate the utility of the ERPAC analysis procedure. We show that this method can be used to assess PAC both within local cortical regions as well as between distant sites. We observed couplings between multiple frequencies occurring at different time scales that evolved across trials and were independent of evoked responses. ERPAC provides a method for assessing sub-second coupling dynamics supporting cortical processing.

2. Methods

2.1. Data collection

We analyzed data from three patients with intractable epilepsy who were implanted with chronic subdural electrodes for approximately one week as part of a pre-operative procedure to localize the epileptogenic focus. Data were recorded at the Johns Hopkins School of Medicine where the surgeons determined electrode placement and treatment solely on the clinical needs of each patient. All subjects gave informed consent in accordance with the Johns Hopkins Medicine Institutional Review Boards. ECoG data were recorded at 1000 Hz using a Stellate Harmonie amplifier (Stellate Systems, Inc., Montreal, Canada). Signals were digitized for further analysis and referenced offline to the average potential of the electrodes included in analysis for each subject separately.

2.2. Behavioral tasks

We include data from one ECoG patient who performed a lateralized visual attention task and from three patients who performed a phoneme repetition task. The visual attention task is described in full in a previous manuscript (Voytek et al., 2010c). Briefly, the subject was rapidly presented (107 ms presentation; 800 or 1000 ms interstimulus interval (ISI)) with a series of non-target standard stimuli [p = 0.7], target stimuli [p = 0.2], or neutral novel stimuli [p = 0.1] to either the left or right visual field ([p = 0.5] for each hemifield). On separate blocks of trials, the subject manually responded to targets presented only to the left or only to the right visual hemifield. For the phoneme repetition task, the three ECoG subjects listened to a stream of vowel phonemes (e.g., “oo” as in “book”, “ee” as in “eel”, etc.) with an average 3000-ms ISI and were asked to repeat each of them aloud. For the visual task, there were 117 target trials and 380 standard non-target trials included in the analysis. For the three subjects who performed the phoneme task, 215 and 270 trials were included, respectively.

2.3. Data analysis

All electrophysiological data were put into a common average reference to avoid spatial bias due to the choice of intracranial reference electrode. All signals were analyzed in MATLAB® (R2009b, Natick, MA) using custom scripts. For ERSP and PAC figures (1, 3, 4, and 6) we corrected for multiple comparisons using a false discovery rate (FDR) method (fdr.m function in EEGLAB toolbox (Delorme and Makeig, 2004) in MATLAB). All analyses were done on an individual subject and electrode basis.

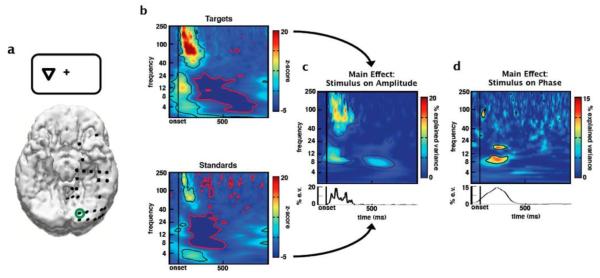
Fig. 1.

Event-related spectral responses to visual stimuli. (a) Reconstructed locations of electrodes on the inferior surface of the brain. In this example, the subject is viewing an attended target presented to the visual hemifield contralateral to hemisphere in which the electrodes are implanted. (b) ERSP plots (z-scores) for attended visual targets and attended visual non-target (standard) stimuli from an electrode over early visual cortex (green circle in a). Event-related amplitude increases can be seen in broadband γ (80-150 Hz) and lower-frequency θ (4-8 Hz) and α (8-12 Hz) bands. Black and red contours denote regions of significant event-related amplitude increases and decreases, respectively, after correcting for multiple comparisons (p < 0.001). Using a sliding ANOVA approach we calculated the percent of the variance explained in (c) amplitude or (d) phase by stimulus type. Color represents percent of variance explained by stimulus type, with significant regions outlined by contours (p < 0.001 after correcting for multiple comparisons). As suggested by the ERSPs, (c) standard ANOVA reveals a main effect of stimulus type on γ amplitude. However circular ANOVA (d) reveals a main effect of stimulus type on early α (8-12Hz) phase that provides information independent of amplitude. In order to calculate the effect of stimulus type on phase we used a circular ANOVA (see Methods). Line plots below c and d are similar as the spectral plots above, but for main effects of stimulus on a priori (c) γ amplitude and (d) α phase.

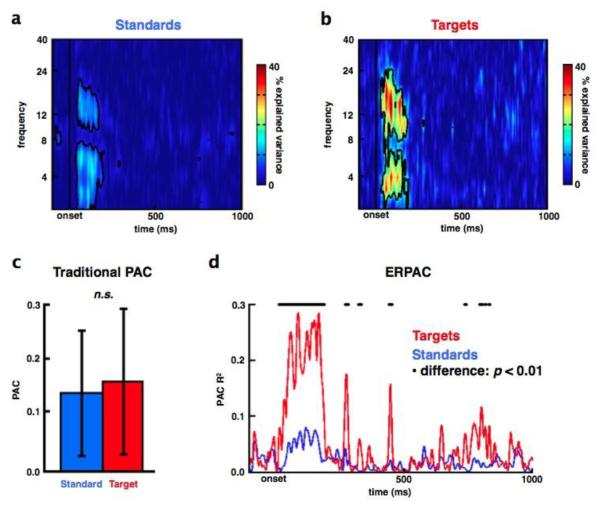
Fig. 3.

Event-related phase/amplitude coupling modulated by task demands. Trial-by-trial variance in low frequency phase explains a significant amount of the trial-by-trial variance in γ amplitude in visual cortex in response to (a) attended non-target standard and (b) attended target stimuli (data are from the same electrode as in Figure 1). (c) Traditional PAC for a priori α/γ coupling across the first 250 ms post-stimulus onset shows no significant difference between non-targets (blue) and targets (red). Note the lack of temporal resolution because PAC is calculated across time and averaged across trials. In contrast, ERPAC (d) is calculated across trials on a point-by-point basis in the time series. This shows that PAC in response to targets (red) is significantly higher compared to non-targets (blue) during the same 250 ms post-stimulus time window where traditional PAC showed no differences (black dots above ERPAC traces denote time points with a significant PAC difference between stimuli at p < 0.01; see Methods).

Error bars indicate SEM. (n.s.), not significant (p = 0.14)

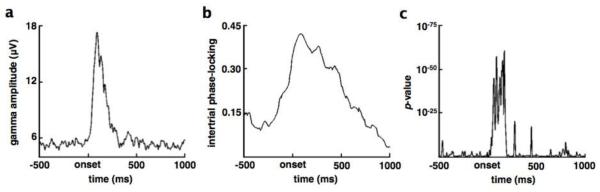
Fig. 4.

Event-related phase/amplitude coupling is not an artifact of stimulus-evoked responses. Target stimuli were associated with significant, transient changes in γ amplitude (a) and α IPL (b) during the same approximate time window where we observed significant ERPAC (Figure 3d). To assess whether ERPAC was an artifact of these stimulus-induced responses, we conducted a resampling analysis that preserves these induced changes but randomizes the inter-trial relationship between amplitude and phase. That is, for each time point, we shuffled the order of the trial-wise α phase values with respect to the γ amplitude values at that same time point and calculated the ERPAC between this shuffled α phase and γ amplitude. This keeps the distributions exactly the same, preserving the induced changes in frequency-specific analytic amplitude and phase, but randomizes the inter-trial relationship between them. This was done 1000 times at each time point to create a surrogate distribution of possible PAC values given the data. We then compared the real PAC value at each time point with the surrogate distribution to calculate the probability that the observed PAC is due to the exact trial-by-trial relationship between phase and amplitude, or whether the observed PAC arises naturally from the data. (c) We find that the likelihood of the observed PAC values occurring during the first 250 ms after stimulus onset, absent a specific trial-by-trial relationship between γ amplitude and α phase, is improbable (p < 10⁻²⁰).

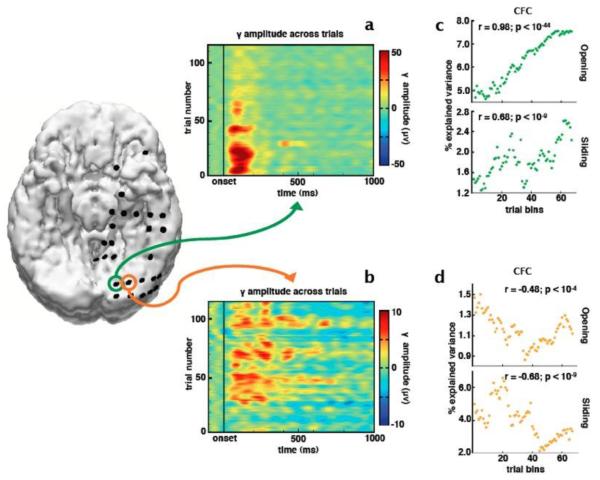
Fig. 6.

Relationship between phase/amplitude coupling and number of trials in the analysis. Two electrodes in the visual cortex show target-related γ responses with different trial-by-trial dynamics. γ amplitude between these electrodes is anti-correlated across trials (r = −0.26, p = 0.005) such that (a) the medial electrode (green) shows strong γ during early trials that diminishes across successive trials while (b) the neighboring electrode (orange) shows the opposite response. (c, d) We used two sliding-window techniques to calculate the effect of number of trials on ERPAC estimates. All plots show the percent of the variance in inter-trial γ amplitude explained by α phase. In the top plots we used an opening-window technique; for the bottom plots we used a sliding window technique (see Methods). Both methods show that ERPAC changes over time, independent of the changes in γ amplitude, such that in the medial electrode (green), even though γ amplitude decreases across trials, α/γ ERPAC increases, and vice versa for the more lateral electrode (orange).

2.4. Event-related spectral perturbations

For ERSP analyses, the data for each channel was first filtered in multiple, logarithmically-spaced pass bands using a two-way, zero phase-lag, finite impulse response filter (eegfilt.m function in EEGLAB) to prevent phase distortion. The filter order is defined as 3r where r is the ratio of the sampling rate to the low-frequency cutoff of the filter, rounded down. Data were filtered in partially overlapping bands from 0.5 to 250 Hz. We seeded the first pass band such that f_p(n) = [f_L(n) f_H(n)]; where for n = 1, f_L(n) = 0.5, and f_H(n) = 0.9. Successive bands were calculated such that f_L(n) = 0.85(f_H(n-1)) and f_H(n) = 1.1 + (f_H(n-1) – f_L(n-1))f_L(n). We then applied a Hilbert transform to each of these time-series (hilbert.m function) resulting in a complex time-series, h_x[n] = a_x[n]exp(iϕ_x[n]) where a_x[n] and ϕ_x[n] are the analytic amplitudes and phases, respectively, of a specific pass band f_p(n). The phase time-series ϕ_x assumes values within (−π, π] radians with a cosine phase such that −/+π radians correspond to the troughs and 0 radians to the peak. The Hilbert phase and amplitude estimation method yields results equivalent to sliding window FFT and wavelet approaches (Bruns, 2004).

From each trial the time-series of analytic amplitudes, a_x (the absolute value, or modulus, of h_x), was used to create an average event-related analytic amplitude (ERAA), an estimate of the band-specific signal energy. Each trial-specific epoch consisted of a 100-ms pre-stimulus period and a 1000ms post-stimulus period. To calculate the significance of any event-related changes in analytic amplitude under a given experimental condition, we used a standard resampling technique (see Voytek et al., 2010b) to assess whether any event-related changes in analytic amplitude occurred relative to stimulus onset. To statistically assess whether a change in analytic amplitude at a given latency was significantly different from the pre-stimulus baseline, we created 1000 surrogate ERAAs (sERAA). Each sERAA was calculated by taking the real stimulus onset times and shifting them randomly in time, keeping the relative timing between each event the same as the real timing, and then creating a new average sERAA. We chose this event-onset shifting method to account for any possible autocorrelation in the time series. From this, each time point in the ERAA was associated with a distribution of 1000 surrogate analytic amplitudes against which to compare the real ERAA.

The change from background activity was calculated with a z-score and associated p-value at each time point (t) where the z-score was calculated as z(t) = (a(t) – s(t))/σ(t), where a(t) is the real analytic amplitude at time (t), s(t) is the mean of the 1000 surrogate analytic amplitudes at time (t), and σ(t) is the standard deviation of that population of surrogate amplitudes. Because we are calculating a mean of means, the central limit theorem suggests that this distribution will be normal, and thus a z-score represents an estimate of the probability of observing a particular analytic amplitude given the distribution of the data. These methods were applied for each frequency band separately to construct the ERSP images.

Because all time-frequency amplitude, phase, and regression analyses were performed at each time point and across multiple frequency bands, we corrected for multiple comparisons using an FDR method to correct the raw p-values obtained from the analyses. We used no temporal binning or smoothing procedures, so we corrected for all 1000 post-stimulus time points and 45 frequency bins, to achieve a conservative and stringent correction procedure. The results we obtained were robust and survived multiple comparison correction, but statistical power could have been further increased using analyses restricted to a priori bands of interest, or through temporal downsampling. For example, rather than needing to correct for multiple comparisons for all time and frequency points, if the a priori hypothesis is that theta phase is coupled to gamma amplitude, one could restrict analyses to just those frequency bins.

2.5. Inter-trial phase locking (IPL)

For IPL analyses (Fig. 5b), each point in the Hilbert transform at a channel at each passband was divided by the absolute value of its amplitude to generate a signed, unit-length, complex-valued time series; epochs of these time series were then created as described above in 2.4. The absolute value of the mean of the complex-valued epochs is the frequency-specific IPL, which has a value from [0,1], where 0 represents total phase independence and 1 means all phase values are equal, similar to previous methods (Tallon-Baudry et al., 1996). The angle of the vector mean is the preferred phase. This method is equivalent to taking the circular mean angle and vector length of the phase distribution at each point across all trials, providing a metric of event-related phase locking across trials for a given frequency band. This can be accomplished using the CircStat toolbox (Berens, 2009) in MATLAB using circ_r.m).

Fig. 5.

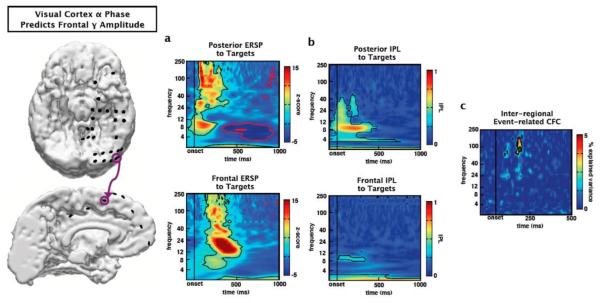
Inter-regional phase/amplitude coupling. The event-related PAC methods described are not limited to within-electrode effects. For example, θ phase from a visual cortical electrode (purple circle, top) correlates with γ amplitude at a target-responsive medial frontal site (purple circle, bottom). (a) Both the visual cortical and frontal sites exhibit strong event-related spectral perturbations (ERSPs) in response to attended targets. Both sites exhibit early (<250ms) target-related γ amplitude increases with the frontal site showing activity at a slightly longer latency. (b) Similarly, both sites show early inter-trial phase-locking (IPL) in the α band, though IPL is weaker at the frontal site (contours: p < 0.001 after correcting for multiple comparisons). (c) Interestingly, although visual cortical IPL is strongest in the α band, phase of the θ band within the visual cortex that predicts γ amplitude at the frontal site during the time-period of frontal event-related gamma γ increases (contour: p < 0.05 after correcting for multiple comparisons; α/γ PAC not shown).

2.6. Amplitude ANOVA

We used a sliding standard ANOVA to calculate the percent of the variance in the amplitude of each frequency band at each time point across trials (${\eta }_x^2\left[n\right]$) that is explained by the independent variables of interest (e.g., stimulus type). We restrict the explanation of our methods to a single frequency band in a single channel, though for the full analysis used to plot the figures this method was applied to all frequency bands. To calculate the standard ANOVA in Fig. 1c, the time series of analytic amplitudes (a_x) was divided into epochs relative to the onset of each of the stimuli (100-ms before and 1000-ms after stimulus onset). Each epoch was classified as belonging to a specific trial type for use in the ANOVA. For visual tasks, each trial type was encoded as being either a target or non-target standard. These coding variables were used in the ANOVA as independent variables; we then calculated the F-statistic and associated p-value for the main effects of stimulus on amplitude.

2.7. Circular ANOVA

For the sliding circular ANOVA, the same method was used as for the standard ANOVA. However, epochs were created around the phase time-series ϕ_x (the angle of h_x) and no baseline correction was performed. Circular statistics were performed using the CircStat toolbox making use of the circular equivalents of the one-way and two-way ANOVA (Watson-Williams test (circ_wwtest.m) and Harrison-Kanji test (circ_hktest.m), respectively). A circular ANOVA attempts to explain the amount of circular variance that is explained by task parameters (e.g., stimulus type; see Fig. 1d). This approach has recently been used to show that, during olfactory decision-making and response inhibition in rats, neurons in the OFC show differential phase-synchrony in the γ band (van Wingerden, 2010).

2.8. Traditional phase/amplitude coupling (PAC)

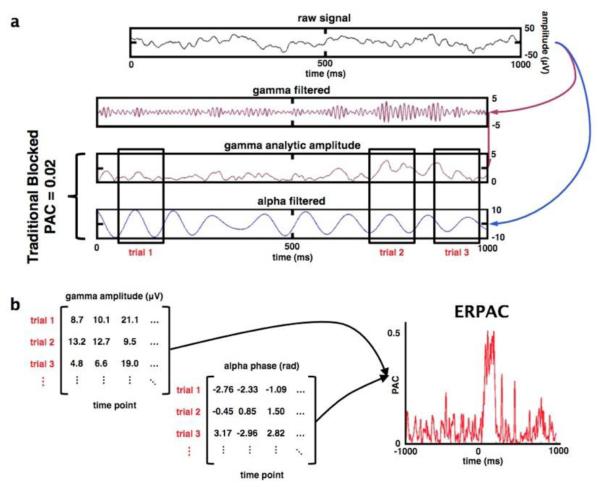
We calculated traditional PAC using a general linear model after Penny et al., 2008, where the gamma analytic amplitude (a_γ) is estimated from low-frequency phase (e.g. α) such that a_γ = X_αβ+ε where X_α is a three-column matrix composed of the sin and cos components of the phase h_α and a column of 1s; β are the regression coefficients, and ε is the error term. For Fig. 3c, we estimated a_γ from h_α for each trial separately. Because traditional PAC must be calculated across time, we estimated PAC across two cycles of the lower bound of α—(1000 ms/8 Hz) * 2 cycles)—or the first 250 ms of each trial. Note that 2 cycles is an arbitrary decision, as it is difficult to determine a priori how much data is needed to get an accurate PAC estimate. This loss of temporal resolution and the need for an arbitrary time window is one of the problems addressed by the ERPAC method.

2.9. Circular-linear correlation

We assessed circular-linear correlation after Berens, 2009 (circ_corrcl.m in the CircStat toolbox) which linearizes the phase variable into its sin and cos components and calculates a single correlation coefficient, ρ_ϕa such that

$${\rho }_{\varphi a}=\sqrt{\frac{r_{ca}^2+r_{sa}^2-2r_{ca}{r}_{sa}{r}_{cs}}{1-r_{cs}^2}}$$

where r_ca = c(cos ϕ[n], a[n]), r_sa = c(sin ϕ[n], a[n]), r_cs = c(sin ϕ[n], cos ϕ[n]) with c(x,y) equal to the Pearson correlation between x and y, ϕ[n] equal to the instantaneous phase, and a[n] equal to the instantaneous analytic amplitude. This method allows us to examine the relationship between a linear variable (such as γ amplitude) and a circular variable (such as α phase) across trials. This approach has recently been used to examine the relationship between scalp EEG θ phase and global field power during attention in humans (Busch and VanRullen, 2010).

We can compare the significance of the difference between correlation coefficients ρ₁ and ρ₂ by first applying Fisher’s z-transform to normalize correlation coefficients such that $z_{r_n}=\frac{1}{2}\ln \left(\frac{1+{\rho }_n}{1-{\rho }_n}\right)$ and calculating the difference Δρ_z = z(ρ₁)-z(ρ₂) and associated standard error $\sigma =\sqrt{\frac{1}{n_1-3}+\frac{1}{n_2-3}}$. From this we can calculate the z-score z = Δρ_z/σ and associated p-value.

2.10. Event-related phase/amplitude coupling (ERPAC)

We introduce a method for ERPAC making use of either the circular-linear correlation above or its more generalized form of a circular-linear regression. We calculated ERPAC using each channel’s frequency-dependent instantaneous amplitude as the regressand and the sin and cos components of the phase as the regressors (see Penny et al., 2008). For example, if we wish to determine the amount of trial-by-trial variance in the high frequency broadband γ amplitude (80-150 Hz; Miller et al., 2009) that can be explained by trial-by-trial variations in α phase (8-12 Hz), we can calculate the correlation between γ amplitude (a_γ) and α phase (ϕ_α) (or the regression between them) at each time point. This method is “event-related” in that we examine PAC at each time point, across trials, thus unmasking sub-second changes in PAC caused by an event of interest.

To examine the possibility that phase at one electrode correlates with amplitude at another, we calculated ERPAC between α and θ phase at four responsive visual cortical electrodes and the frontal electrode that showed the largest target-related γ amplitude response. While this type of selection may have the appearance of “double dipping” (Kriegeskorte et al., 2009), phase and amplitude are statistically independent, and phase information was not used in the frontal electrode selection analysis. We have made all ERPAC code available online as a resource for other researchers (http://darb.ketyov.com/professional/publications/erpac.zip).

2.11. Assessing possible ERPAC estimation artifacts

To examine the effect of stimulus-evoked amplitude changes or IPL on estimates of ERPAC, we performed a sliding window resampling analysis (Fig. 4c) to quantify the likelihood that the observed ERPAC is due to a specific statistical relationship between trial-by-trial amplitude and phase components, and not, for example, due to a possible spurious relationship induced by “sharp” artifacts (see Kramer et al., 2008b) or stimulus-induced. For normal ERPAC calculations, what is important is the trial-by-trial covariance between amplitude and phase. So for surrogate analyses we kept the actual analytic amplitude and phase values at each time point, but randomized the trial labels. This keeps the stimulus-evoked changes in amplitude or IPL intact while randomizing the relative trial structure between the two variables and is similar to methods used to calculate significance in e.g. phase synchrony (Lachaux et al., 1999). This was done 1000 times at each time point. If the observed ERPAC is caused by a spurious artifact then that value should not be improbable given the possible distribution of ERPAC values drawn from the permutation testing. In other words, at each time point we can compute the z-score and associated p-value of observing the real ERPAC value given the distribution of possible values.

To further examine the relationship between event-related changes in analytic amplitude and estimates of ERPAC, we performed a separate set of analyses (Fig. 6) to more directly test the effect of γ amplitude on ERPAC estimates by using two different, but related, sliding-window methods. The first is an “opening window” method where we use successively more trials in the α phase/γ amplitude ERPAC calculations (from 50 to all 117 attended target trials) at two neighboring electrodes that exhibit different trial-by-trial γ amplitude changes. The second method is a simple sliding-window technique calculating ERPAC on 50-trial bins with a one-trial increment.

3. Results

3.1. Event-related amplitude and phase changes

An analysis of of the effect of visual stimulus types (attended targets and standard non-targets) on event-related spectral perturbation (ERSP) in visual cortex (Fig. 1a) reveals an early latency (< 100 ms) increase in high frequency γ (80-150 Hz) and low frequency δ (1-4 Hz) and θ (4-8 Hz) activity for both stimulus types (Fig. 1b; p < 0.001, corrected for multiple comparisons). Upon visual inspection, it appears that γ and α (8-12 Hz) amplitudes are greater in response to targets compared to non-targets. A sliding-window standard ANOVA corroborates this observation, highlighting a main effect of stimulus type on γ and α amplitudes (Fig. 1c). However, what cannot be seen in the classic ERSP plot is also an effect of stimulus type on α phase distribution, revealed by circular ANOVA (Fig. 1d; p < 0.001, corrected; see Methods).

3.2. Event-related phase/amplitude coupling

By using a circular-linear correlation or regression analysis (see Fig. 2 and Methods), we find transient (< 250ms) effects of attention to visual stimulus (attended non-target standards and attended targets) on ERPAC over visual cortex (Fig. 3a and 3b; p < 0.001, corrected). We observe that variance in low frequency δ and α phases explain the trial-by-trial variance in γ amplitude, and that these effects are not seen using traditional PAC methods (Fig. 3c). ERPAC is significantly stronger for attended targets than for non-target stimuli (Fig. 3d), and this target-specific ERPAC effect is not an artifact caused by stimulus-related changes in amplitude or phase (Fig. 4a-c).

Fig. 2.

Comparison of phase/amplitude coupling methods. (a) Methods for calculating traditional blocked PAC and event-related PAC (ERPAC) begin similarly: the raw signal is filtered into separate amplitude and phase components (here broadband γ analytic amplitude and α phase). For traditional blocked PAC analyses, a single PAC index is calculated across an arbitrarily long time window at the cost of temporal resolution. (b) To calculate ERPAC, the phase and time series are broken into time windows of equal length around each trial, time-locked to the onset of stimulus presentation (example black rectangles in a). In contrast to blocked PAC, which is calculated across time, ERPAC is calculated across trials separately at each time point. In this example (from the electrode shown in Figure 1), trial-by-trial differences in α phase explain a significant amount of the inter-trial variability in broadband γ amplitude during a brief time window (50-250 ms) after stimulus onset. See Methods for full details.

Importantly, this ERPAC method assesses coupling between distant brain regions (Fig. 5). For example, in a midline frontal electrode that demonstrates significant (~200-400 ms) γ amplitude increases in response to targets we find that visual cortical θ phase correlates with frontal γ amplitude (Fig. 5). This technique might be useful for highlighting long-distance bottom-up and top-down interregional communication via neuronal synchrony (Engel et al., 2001; Fries, 2005; Womelsdorf and Fries, 2007).

We assessed the trial-by-trial evolution of ERPAC by examining two electrodes over visual cortex that exhibit strong γ activity in response to attended targets. We observe complex intertrial evolution of early (100-200ms) γ activity (Fig. 6). For example, across trials, at two neighboring electrodes, γ amplitude is anti-correlated (r = −0.26, p = 0.005) such that one electrode exhibits strong a γ during the first 20-30 target trials, but this response decreases or attenuates with successive trials. In contrast, γ activity at the neighboring electrode shows the opposite pattern. Furthermore, using separate sliding window techniques (see Methods), we show that α/γ ERPAC is not necessarily contingent upon γ amplitude. This is evident given that the electrode that shows decreasing γ activity across trials (green) also shows increasing α/γ ERPAC and the electrode that shows increasing γ across trials (orange) shows decreasing α/γ ERPAC.

3.3. Phoneme repetition

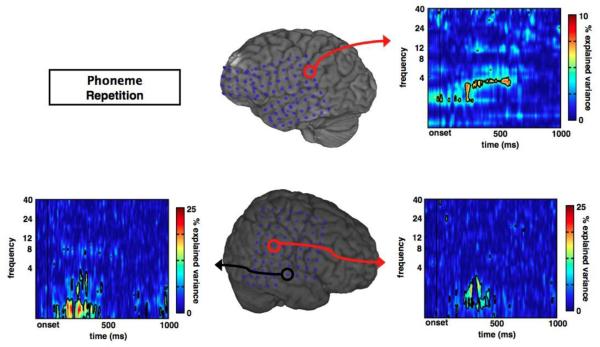
We extended the findings from our ECoG data in the visual target-detection task to the auditory modality and provide results from subjects with subdural ECoG performing a simple phoneme repetition task (see Methods). Similar to the visual attention data, subjects performing an auditory task also exhibit transient ERPAC. Consistent with previous reports of δ phase/γ amplitude relationships (Lakatos et al., 2008; Whittingstall and Logothetis, 2009), we show that δ phase correlates with γ amplitude in auditory cortical areas (Fig. 7). Notably one of the three subjects showed no significant δ phase/γ amplitude ERPAC effects. These findings illustrate that ERPAC is not limited to one subject, cortical region, or sensory modality, but rather might be a more broadly generalizable phenomenon.

Fig. 7.

Auditory cortex event-related phase/amplitude coupling in response to phonemes. In three separate subjects performing a phoneme repetition task, we observe significant, transient ERPAC between γ amplitude and δ phase (1-4 Hz) in auditory cortical regions for two subjects, illustrating the broad applicability of this method.

4. Discussion

We describe a PAC method that provides time-resolved calculation of event-related PAC (ERPAC). Because it is based on correlation and regression techniques, it is intuitive and straightforward to instantiate. While other methods exist for examining time-resolved phase/phase or amplitude/amplitude relationships (Bruns and Eckhorn, 2004; Darvas et al., 2009), this method combines a circular (phase) and linear (amplitude) variable with improved temporal resolution permitting within-trial changes in PAC.

As we show in Fig. 3c, traditional PAC measures miss temporally discrete phase/amplitude coupling effects that are observed when analyzed using our ERPAC technique. This is likely due to the underlying differences between what the two methods address: traditional PAC asks, “what is the statistical relationship between phase and amplitude across time?” at the expense of temporal resolution. In contrast, ERPAC asks, “what is the statistical relationship between phase and amplitude across trials, at each time point?” That is, with ERPAC we can examine sub-second changes in PAC related to the onset of an event of interest. This difference is analogous to the different inferences that can be drawn from event-related vs. block design fMRI studies and highlights the utility of this technique for assessing within-trial changes in PAC.

It is important to point out that we are not limited to using the phase at one channel to predict amplitude at that same channel (or vice versa). That is, we can use the phase of one channel to predict frequency band amplitudes at another (nearby or distant) channel (e.g., Fig. 5), which might be useful for examining the degree and timing of top-down or bottom-up communication between brain areas. An important caveat to consider is that cross-channel phase coupling or amplitude envelope correlations might have spurious effects on interregional coupling dynamics. For example, if two electrodes, A and B have correlated gamma amplitude envelopes, and theta phase in electrode A predicts gamma amplitude in A, the theta phase from A will also predict gamma amplitude in B. Note that recent new methods provide a multivariate solution to a network of coupled oscillators the diminishes the solution space (Canolty et al., 2010).

This technique provides a method for observing, quantifying, and statistically comparing ERPAC dynamics in a time-resolved and computationally tractable manner. Given that this method calculates PAC across trials at each time point it is likely capturing evoked (as opposed to induced) PAC effects (see David et al., 2006). This would provide complementary information to time-averaged PAC that would be better suited to capturing induced PAC. Here we use this method to analyze ECoG data from subdural recordings in humans, but the method can be applied to other forms of electromagnetic recordings in animals and man.