Measurement of Vocal Folds Elastic Properties For Continuum Modeling

Abstract

Objective

This study aimed to quantify the major elastic properties of human vocal fold lamina propria, including longitudinal and transverse Young's modulus, shear modulus and Poisson's ratio.

Methods

Samples were obtained from cadaveric human larynges that were snap frozen within 48 hours postmortem and kept at −82 degrees (F) and thawed overnight in saline solution. Once the sample was tested in the longitudinal direction, two special brackets were glued to the side of each sample and the sample was mounted with brackets in the transverse direction. The shear modulus was obtained from samples mounted between two parallel plates applying shear forces. The Poisson ratio was obtained using high-speed video imaging of two-dimensional samples with markers for longitudinal and transverse strain measurements.

Results

Results indicate that human vocal fold elasticity is very nonlinear with slope that increases 10–15 times from low strain to high strain values. Its average low-strain Young's modulus is about 30 kPa in the longitudinal direction and 1 kPa in the transverse direction. The vocal fold longitudinal shear modulus is in the same order of magnitude of its transverse shear modulus (less than 1 kPa). The average Poisson ratio is about 0.57.

Conclusions

The current study provides quantitative data for the longitudinal and transverse elastic properties of the human vocal fold tissue and indicates that nonlinear behavior and relative difference of these properties may lead to wide ranges of oscillation frequency and amplitude in human larynges.

INTRODUCTION

The phonation is a complex process, relying on several organs working in harmony in order to produce the many sounds used for communication and expression. Although small in size, the larynx is capable of producing a range of sounds to rival the most sophisticated musical instruments. To fully understand the kinematics and dynamics of the larynx, one must examine the larynx from several perspectives. These include the acoustics of the glottal region, the dynamics of the vocal folds as they oscillate to produce sound, and the material properties of the various regions of the larynx. An understanding of these material properties is important in many applications, including tissue engineering of replacement vocal folds, surgical training for vocal fold reconstruction, and modeling of the vocal folds using continuum mechanics to enable more accurate understanding of vocal fold dynamics.

During the vibration of the vocal folds, vocal tissue is deformed and experiences forces resulting from the airflow and tissue motion. These forces and deformations are related to each other through the tissues' elastic properties and can be described by the laws of continuum mechanics. A finite element model (FEM) is one such continuum model which can be used to study vocal fold vibration^1–2 and requires knowledge of the elastic properties of these tissues. These elastic properties are described by tissue-specific constants which vary by the type of the tissue and dimensionality of the problem. For example, Alipour et al¹ used a two-dimensional (plane strain) model of the vocal folds with three types of tissues, namely, vocal fold cover, vocal ligament, and vocal fold muscle. For such a 2D model, a constitutive equation for six stress and six strain components can be written as

$$\sigma =\left[S\right]\epsilon$$ (1)

where σ and ε are the stress and strain tensors and [S] is the stiffness matrix. For linear elastic materials, [S] is a 6 × 6 symmetric matrix, having 21 independent elastic constants in the most general case. However, for transversely isotropic materials such as vocal fold tissues, several elastic constants are dependent on each other, and many are zero. The total number of independent elastic constants for vocal fold tissues becomes five³. These are the Young's modulus and Poisson's ratio in the plane transverse to the fibers (E, ν), and the Young's modulus, shear modulus and Poisson's ratio along the longitudinal fiber axis (E', G', ν').

Knowledge of these elastic constants is prerequisite for successful modeling of the vocal folds. Due to the lack of complete set of elastic constants for human vocal folds, the continuum models such as Alipour et al¹ used the available animal elastic constants such as longitudinal Young's modulus and assumed some values for the unavailable constants such as transverse Young's modulus, shear modulus and Poisson's ratio that could give reasonable results. In the last few decades many experimental studies have been launched to measure these elastic properties. Elasticity of animal vocal fold tissues such as dog^4–5, pig, sheep, and cow⁶ are reported mostly due to their ease of availability and their freshness. Human cadaveric vocal fold tissues harvested from autopsy have also provided data for those vocal folds structures that are not available in animal vocal folds such vocal ligament Young's modulus⁷.

Most of the measurements on these constants were performed on the longitudinal Young's modulus or shear modulus of animal vocal folds except for Hirano et al⁸ who reported estimates of both longitudinal and transverse elastic moduli, and also the shear modulus for canine vocal folds. Some investigators studied the degree of stiffness of the vocal folds in elongation or shear though have not reported these elastic measures^9–11, while others have reported Young's and shear moduli from in vitro experiments on animal or human vocal fold tissues^{4–8,12–15}.

Hirano et al⁸ not only pioneered by identifying the vocal folds' layered structure, they also reported estimates of canine vocal folds elastic measures. By stretching the vocal folds samples using small weights attached at one end while it was mounted vertically from the other end, they measured longitudinal and transverse Young's moduli of vocal fold tissues. To measure the transverse modulus, they attached two pieces of wire on the sides of the sample (along the fibers) and used these wires for hanging the samples. They compared the order of magnitudes of Young's moduli for vocal folds body and cover and longitudinal and transverse and concluded that the transverse Young's modulus was one order of magnitude smaller than longitudinal value. This ratio was used in the Alipour et al¹continuum model.

A systematic and more detailed analysis of the longitudinal Young's modulus of canine vocal fold viable tissues (muscle and mucosa) was presented by Alipour and Titze⁵ through an in vitro measurement of vocal folds samples. By sinusoidal and slow (1 Hz) stretching of the vocal folds samples, they measured the stress-strain behavior of the tissue sample after few cycles of conditioning and when tissue was relaxed. They showed that the elastic behavior for vocal fold tissues was linear at low strains and exhibited an exponential profile at higher strain values. They reported average low strain Young's modulus of 21 kPa for the canine viable vocal fold body (muscle) and a value of 42 kPa for its viable cover. These values were used in Alipour et al¹ continuum model.

Unlike the canine tissue, the elastic properties of human vocal folds have not been measured as extensively from fresh tissue samples using comparable force-elongation tests. There have been some studies that reported tissue stiffness and spring constant from the resilience of the tissue to external excitation. For example, by applying a 1-mm diameter probe at various locations on the excised human vocal folds and measuring the force and displacements, Haji et al⁹ estimated the degree of stiffness for human true and false vocal folds from the inclination of force-displacement curve. They also defined a parameter of stiffness from the area of force-displacement hysteresis curve. Based on these techniques, they reported that stiffness is lower in the middle of membranous portion and higher at the vocal process and anterior commissure. They also reported that false vocal folds have the lowest stiffness than other portions of laryngeal structure.

Chan et al¹⁵ in a similar protocol to Alipour and Titze measured elastic properties vocal fold cover and ligament tissues from 20 human larynges obtained from autopsy within 27 hours postmortem. They elastic properties of male and female sample with particular emphasis on the effects of collagen and elastin. Based a linear model, they reported average Young's moduli of 15.35 kPa and 12.85 kPa for male and female cover samples, respectively. Also they reported average values of 11.66 kPa and 14.04 kPa for male and female ligament samples, which are much lower than the mean value of 33.1 kPa that was reported by Young et al⁷.

Shear properties of the human vocal folds have been reported by Chan and Titze¹², where they measured the complex shear modulus of human vocal fold mucosa within 18–20 hours postmortem, using a rheometer. Vocal fold tissue samples of about 0.1 grams were placed between two circular disks of 20 mm diameter and the oscillatory motion of one disk measured the complex shear modulus of the tissue sample with thickness of about 0.3 mm. They reported that at low frequency, the shear modulus was about 10–100 Pa for males and 3–20 Pa for female vocal folds. If these values of shear stress were the vocal folds transverse shears, they could be related to transverse Young's modulus through the relation

$$G=\frac{E}{2(1+\nu )}$$ (2)

Where E and G are Young's and shear modulus and ν is Poisson's ratio. With this relation and a value of 0.5 for Poisson's ratio (for incompressible tissues), one could estimate a low value for transverse Young's modulus of 30–300 Pa for human mucosa.

Thus the experimental data so far provided mostly canine longitudinal Young's modulus, relative order of magnitude of transverse Young's modulus and estimates of shear modulus. The available data on human elastic properties are either incomplete or speculated from the stiffness measures and not directly from stress-strain measurement. The purpose of this study was to measure some of these of elastic measures for human vocal folds that complement the available data. This include longitudinal and transverse Young's modulus, shear modulus and Poisson ratio.

METHODS

The most straightforward tissue mechanics test is the uniaxial extension test, in which a strip of tissue specimen is elongated using an ergometer or other material testing system and the force-extension relationship is measured and converted to a stress-strain curve. If this is performed in the primary fiber direction, one can establish a material property description of the behavior of the tissue in this direction. With two-dimensional information about a tissue's response to multi-axial deformation, a more sophisticated constitutive model can be developed to describe tissue behavior. Although biaxial stretching devices have been developed in which a tissue sample (typically square in shape) is obtained and subjected to stretching in two directions simultaneously, these devices require a minimum sample size of 3×3 cm^16–17. However, the size of the human vocal fold sample is about 15 mm long and 5 mm wide, which is not sufficient for those devices. Thus, separate experiments were performed in one-dimensional stretch fashion similar to those of Hirano et al⁸ and Alipour and Titze⁵.

Longitudinal sample preparation

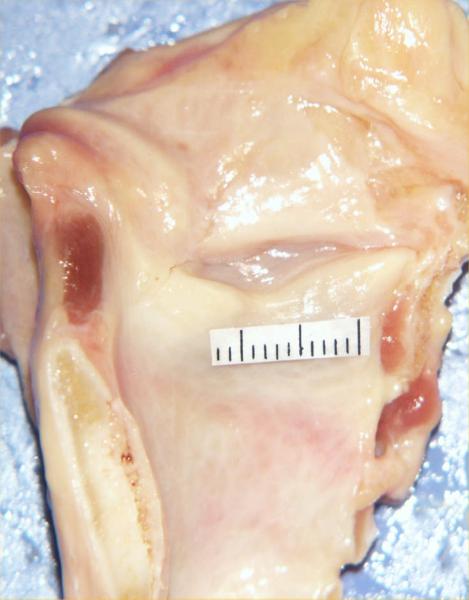
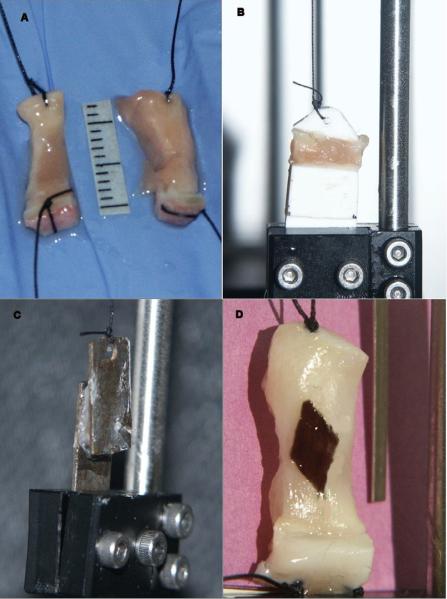
The experimental protocol used was similar to an earlier study by Alipour and Titze⁵. The frozen human larynx was slow thawed overnight in a saline jar within a refrigerator. The larynx was placed horizontally on a dissection tray and a midline longitudinal section was made in the posterior surface. The midline section extended from the superior margins of the arytenoid cartilage to the tracheal rings. Then a similar section was made anteriorly through the thyroid midline to divide it into two hemilarynges (Figure 1). The larynges used were from a geriatric group (age of donors ranged 53–82) that were stored in frozen condition for 3–4 years. These larynges were quick frozen first, hence it is expected that their elastic properties have been preserved¹⁸. Care was taken to maintain the vocal fold edges and cartilaginous connections intact. An effort was made to prepare two samples from each hemilarynx, one from the true vocal folds and one from the false vocal folds. Since the vibrating portion of the vocal is mostly the lamina propria, the true fold sample was made by removing 3–4 mm strips of lamina propria below the superior edge of the tissue, a segment that typically included ligament. Similarly, the false vocal fold sample was made from 3–4 mm strips of tissue above the ventricle. While the exact structure of the false fold sample has not been studied histologically to date, it is expected to have some glandular and connective tissues. The in situ lengths were measured for the true and false vocal folds. The false vocal fold samples were generally longer. A deep incision was made in the thyroid lamina around the anterior attachment point of the true vocal fold to carve out the cartilaginous ends of the sample. A transverse incision was similarly made through the portion of the arytenoid cartilage for other end cartilage of the sample. Once the cartilaginous ends were marked and excised, two lateral incisions were made on either side of the sample to extricate it from the surrounding tissue. The lamina propria was excised by gently teasing it out in the anterior-posterior direction from the underlying muscle fibers. A silk suture (#3.0 metric) attached to a curved needle was threaded through the cartilage ends of each tissue strip. Occasionally, the cartilage was too stiff or narrow for the needle to penetrate, in which case the suture was wrapped around the cartilage and tied (Figure 2A). The resulting sample was mounted in the ergometer using the cartilage sutures (Figure 3) and immersed in a temperature-controlled saline bath. The false fold sample was prepared and mounted in a similar fashion.

Figure 1.

Dissected view of a human hemilarynx with millimeter grids over true vocal fold. The false vocal fold is separated from the true fold with a laryngeal ventricle.

Figure 2.

Vocal fold samples. A: longitudinal samples with end cartilages and attached sutures; B: sample mounted for transverse experiment; C: sample mounted for shear experiment; D: sample with diamond shape spot for Poisson ratio experiment.

Figure 3.

Sample mounting apparatus with temperature controlled bath and adjustable brackets.

Transverse modulus sample mounting

Subsequent to the longitudinal experiments, the transverse measurements of a sample were performed. After removing the cartilage ends of each sample and measuring the sample's mass, two brackets made of hard plastic were attached to the sides of each sample in the anterior-posterior direction with super glue (Figure 2B). One bracket was fixed in the lower clamp of the ergometer and the other bracket was attached to the ergometer arm with a suture. The experiment for transverse samples was similar to the longitudinal samples.

Measurement of Young's modulus

To obtain the passive properties of these tissues, samples were stretched and released by applying a 1-Hz sinusoidal signal to the ergometer as described by Alipour and Titze⁵. The true vocal folds samples were subjected to about 40% elongation in this manner for 10 seconds. Because of their longer length, the false vocal fold samples that were longer elongated at 30% due to the elongation limitation of the device. The displacement of the ergometer arm and the force exerted by the tissue was measured electronically with a 300C-LR Dual-Mode System (Aurora Scientific, Ontario Canada). The analog signals of displacement and force of the ergometer were sent to a 16-bit A/D converter (PCI-6036E, National Instruments- Austin, TX) and acquired through the data acquisition toolbox in MATLAB. The force and displacement signals were calibrated and converted to stress and strain using the sample's cross-sectional area and length. Since the cross-sectional area changes during elongation, here the engineering definitions of stress and strain, which are based on the initial values of length and area are adopted. The average initial cross-sectional area (A₀) was obtained from the sample mass without cartilages (m), in situ length (L₀) and density (ρ) at the end of the experiment according to

$$A_0=\frac{m}{\rho L_0}$$ (3)

For the mass measurement, the attached cartilage ends were dissected out and the sample was dabbed with tissue paper to remove any extra moisture. After zeroing the balance with a small disposable cup, the sample's mass was measured in the cup with a digital balance (model AE100, Mettler Toledo, Columbus, OH) with a resolution of 0.1 milligram. The density was measured using a Mettler Density Kit by weighing the sample immersed in distilled water jar second time and using Archimedes law. Then, using force and length measures from the ergometer data and these reference length and area, one can estimate longitudinal stress and strain as

$$\sigma =\frac{F}{A_0}$$ (4)

and

$$\epsilon =\frac{L-L_0}{L_0}$$ (5)

Where σ and ε are stress and strain, F is the measured force and L is the measured length. The Young's modulus can be calculated from the slope of stress-strain curves. Once force and elongation data are converted to stress and strain, it would be possible to compare properties across the samples.

Shear modulus sample mounting

The shear experiment was performed by shearing each sample between two custom made metal plates with dimensions of approximately 7×20 mm and thickness of 0.6 mm. First one plate was glued to medial surface of the vocal fold and a rectangular piece of vocal fold was cut and separated from the underlying muscle. Then the second plate was glued to other side of sample (after being separated from adjacent muscle). This sample was mounted in the ergometer using its lower clamp and sutured as shown in Figure 2C. The thickness of the sample between the two plates and the area of the sample attached to the plates was measured with a caliper for the calculation of shear stress and shear strain from the force-extension data. The shear experiment was similar to the Young's modulus experiment except that the angular deformation applied was in proportion to the sample thickness. The sample was stretched and released at 1 Hz for 10 seconds. The shear strain γ was calculated from the angular deformation of two plates from shear motion (s) and plate distance (h) as

$$\gamma ={\text{tan}}^{-1}\left(\frac{s}{h}\right)$$ (6)

The shear stress τ was calculated by dividing ergometer force (F) by the sample area that was sheared by each plate (A) as

$$\tau =\frac{F}{A}$$ (7)

The shear modulus can be calculated from the slope of shear stress-shear strain curves.

Poisson's ratio measurement

Measurement of Poisson's ratio requires two-dimensional strain measurement. An optical method is used to achieve this goal. First a vocal fold sample with a width of 6–7 mm was prepared and mounted on the ergometer. Then a diamond shaped mark was made on the sample using a diamond stencil and black ink (Figure 2D). The sample was illuminated with intense light and video images were recorded with a high-speed camera system (Photron 1024 PCI, Motion Engineering, Indianapolis, IN). During a 1-Hz stretch and release experiment, images were acquired at 125 frames per second for 10 seconds. These images were processed for major and minor axis calculation with MATLAB image processing toolbox. The major and minor axis for each image frame were calculated and calibrated. Based on these measures, the axial and transverse strains were available and thus Poisson's ratio (the ratio of transverse strain to axial strain) was computed as

$$\nu =-\frac{{\epsilon }_y}{{\epsilon }_x}$$ (8)

Since the axial stretch of the tissue sample yields a positive axial strain and a negative transverse strain, the negative sign here results in a positive Poisson's ratio.

RESULTS

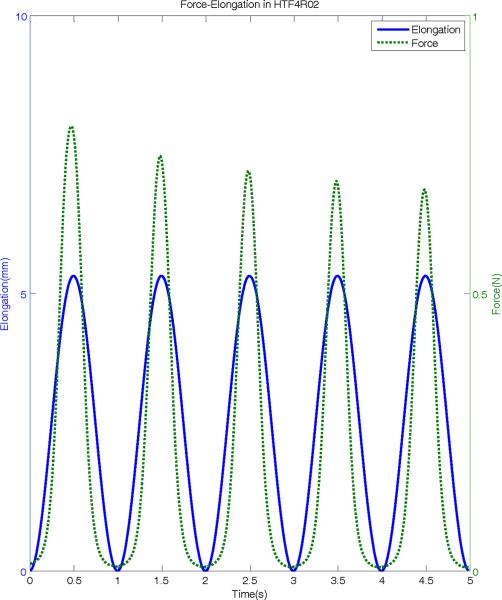
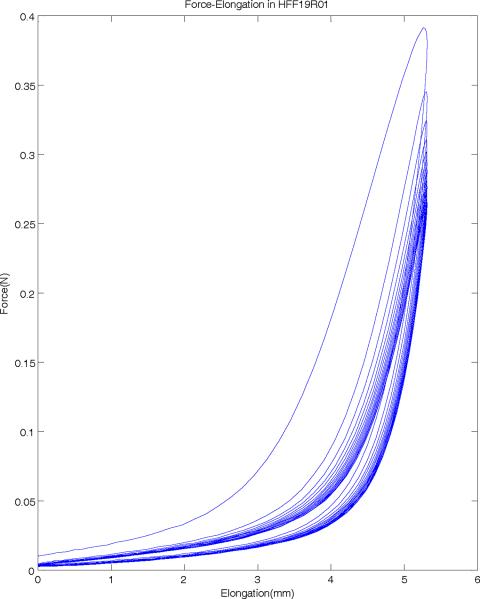
Figure 4 shows a portion of force-elongation used in this study to examine the elastic properties of human vocal folds. The ergometer arm is subjected to a prescribed cyclic elongation at a frequency of 1 Hz (solid line), and the resulting force in the tissue is measured (dotted line). While the displacement range stays constant throughout the protocol (as specified), the resulting peak force shows a clear decrease in subsequent cycles, indicating a stress-softening behavior. This is also shown in the force-position loop in Figure 5 for a sample of the false vocal folds, where initially, the force is shown to be higher and indicates the need for preconditioning. Over subsequent cycles, the force-elongation loops show consistent results (after 10 cycles) and the specimen is thus preconditioned. Also clear in Figure 5 is the hysteresis present in the tissue. As can be observed, stretching and relaxing the tissue represent different stress states at the same stretch (i.e. the same position or strain does not indicate the same force or stress when being pulled as when relaxing the tissue), a characteristic property of viscoelastic materials. Because of this relaxation, for each sample, the final three to four loops that are relaxed and preconditioned are averaged for stress-strain analysis.

Figure 4.

Typical force and elongation signals from a human true vocal fold sample. The solid line shows the sample elongation due to the sinusoidal stretch and release at 1-Hz. The dotted line shows the force response of the sample measured with ergometer.

Figure 5.

Force-elongation hysteresis loops of a human false vocal fold sample. Sample is stretched in the upper loops and released in the lower loops.

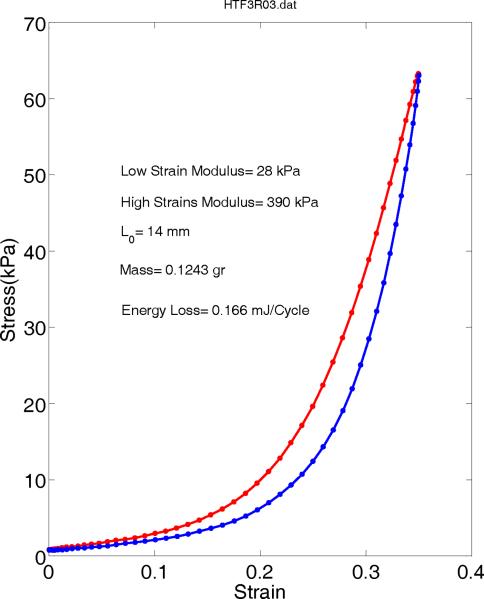
Figure 6 shows a typical true vocal fold longitudinal stress-strain behavior which is obtained from last few cycles of force elongation by averaging. The tangential Young's modulus during stretch changes drastically from the low strain to high strain values. The low strain portion (<0.15) can be assumed linear and its slope provides a low strain modulus of 28 kPa. Similarly the high strain portion (>0.3) yields a large modulus of 390 kPa which is about 14 times more than its low strain value. The energy loss due to hysteresis can be calculated as the area within this loop. For this true vocal fold sample, the energy loss is 0.16568 mJ/cycle.

Figure 6.

Stress-strain relations of a longitudinal true vocal fold sample averaged from last few relaxed cycles.

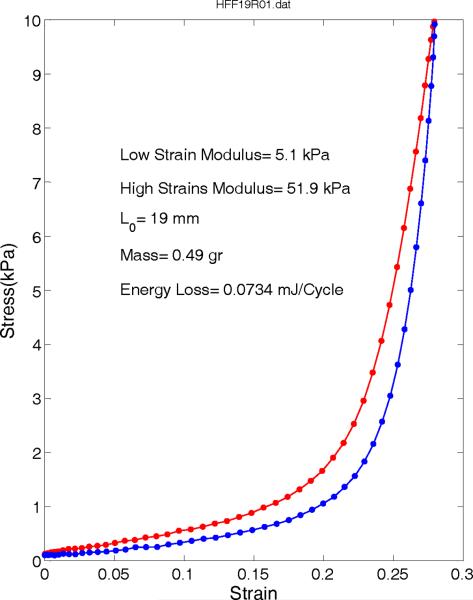
Similarly, a typical longitudinal stress-strain relationship of human false vocal folds is depicted in Figure 7. This sample is longer (19 mm instead of 14 mm) and with about 4 times larger mass, yet smaller moduli of 5.1 and 51.9 kPa at low and high strain ranges. This suggests that the false vocal fold is a softer tissue as reported by Haji et al⁹. The energy loss was computed to be 0.073435 mJ/cycle, almost half of the energy loss of true vocal folds, which suggests it takes less effort to deform the false vocal folds than the true vocal folds.

Figure 7.

Stress-strain relations of a longitudinal false vocal fold sample averaged from last few relaxed cycles.

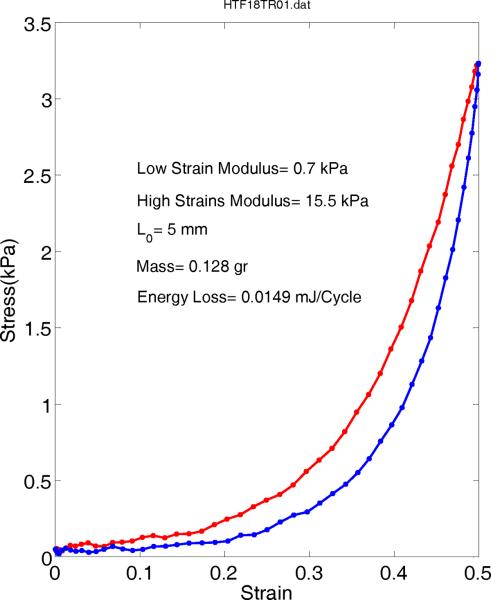
A typical transverse stress-strain behavior of human true vocal folds is shown in Figure 8. The range of stress values is considerably lower than the longitudinal values with low strain modulus of about 0.7 kPa and high strain modulus of 15.5 kPa. The energy loss is measured about 0.014891 mJ/cycle, which is about 5 times smaller than false vocal folds value. This indicates a very small resistance to the separation of tissue fibers in the transverse direction.

Figure 8.

Stress-strain relations of a transverse true vocal fold sample averaged from last few relaxed cycles.

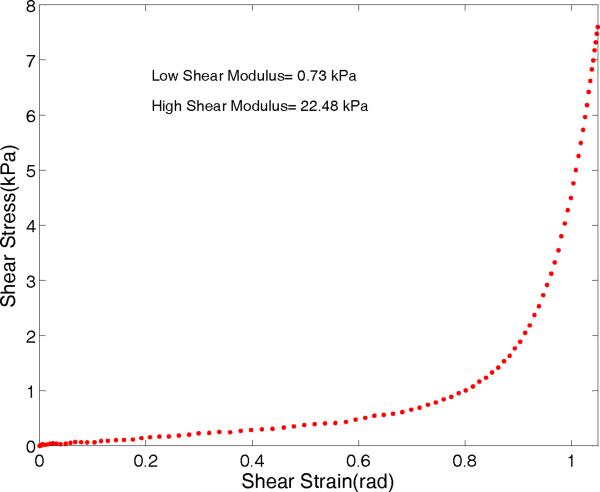
The measured shear stress (τ) versus shear strain (γ) for a true vocal fold sample is shown in Figure 9. The curve is almost linear up to the strain value of 0.7 radian. The low strain (<0.5 radian) shear modulus is about 0.73 kPa and the high strain modulus is about 22.5 kPa.

Figure 9.

Shear stress-shear strain relations for true vocal fold sample averaged from last few cycles.

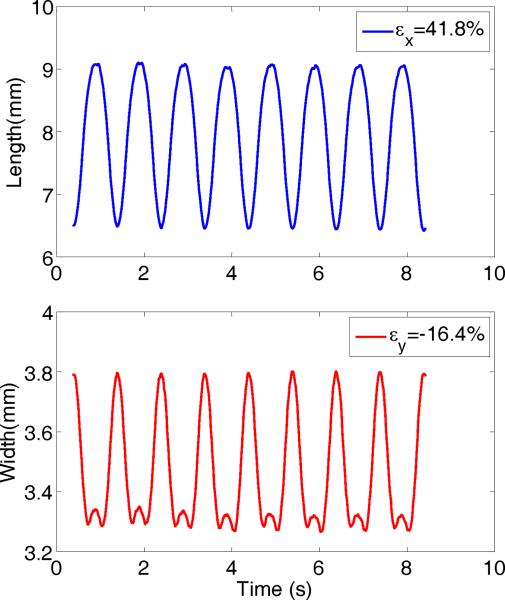
Figure 10 shows deformation waveforms of diamond spot in Figure 2D. In the top panel, the changes in diamond length or major axis is calculated with image processing software, which ranges from about 6.5 to about 9 mm, yielding a maximum axial strain of 41.8%. The bottom panel shows the variation in the diamond width or minor axis which is 180 degrees out of phase with the top panel waveform and ranges from about 3.8 to 3.3 mm (corresponding to minimum and maximum major axis), yielding a maximum lateral strain of −16.4%. Using these two strains one can estimate a Poisson's ratio of 0.392 from Eq. (8).

Figure 10.

Spot deformation waveforms of a vocal fold sample. The top panel shows the major axis (longitudinal) variation with time and the bottom panel shows the minor axis (transverse) variation. The corresponding strains are displayed in the upper right of each graph.

Table 1 shows the summary of results for the vocal fold samples used in this study, including their average, standard deviation, and the number of samples used. The true vocal folds represented by longitudinal, transverse, shear moduli, and also Poisson's ratio. The false vocal folds are represented by longitudinal Young's modulus only. The tissue density is measured for both tissues. It appears that the true vocal fold has its highest strength in the longitudinal direction, which is 30 times stronger than its transverse direction. Due to the assumption of transverse isotropy, the transverse shear modulus can be estimated as about 30% of transverse Young's modulus or about 300 Pa. However, the shear modulus in the longitudinal direction is not related to its Young's modulus in similar fashion due to the anisotropy, and has a much lower value, about twice the transverse shear modulus. Also, it is interesting to note that false vocal fold tissue has a lower density of 1.02 compared to that of the true vocal folds 1.03 gram/ml. A paired t-test results in a probability value of 0.0001, indicating a significant difference. The lower density of the false vocal fold samples may be attributed to the existence of glandular and adipose tissues in them.

Table 1.

Summary of elastic properties for vocal fold tissues.

	Average	STD	N
TF Longitudinal E'	30.0 kPa	13.4 kPa	8
TF Transverse E	1.0 kPa	0.5 kPa	5
FF Longitudinal E'	13.9 kPa	7.6 kPa	8
TF Longitudinal G'	0.67 kPa	0.31 kPa	9
TF Poisson's Ratio	0.57	0.17	8
TF density	1.0299	0.0051	10
FF density	1.0193	0.0046	10

TF: True vocal folds, FF: False vocal folds

DISCUSSION

While vocal fold tissue mechanics are not fully understood, there are general characteristics of physiologic soft tissues that apply to our understanding of voice dynamics. Physiologic soft tissues are typically comprised of two major stress-bearing proteins, elastin and collagen, with hyaluronic acid also playing an important role in the behavior of vocal fold tissue^19–21. Elastin is a highly elastic connective tissue, allowing tissues to easily return to their original shape when deformed. Collagen fibers are typically undulated in an unstretched tissue, so that as the tissue deforms, collagen fibers become taut and increase the stiffness of the tissue²². It is the sequential recruitment of additional collagen fibers under further strain that is primarily responsible for the nonlinear behavior of most soft tissues.

The stress-strain curves shown in Figures 6–9 provide important information about the elasticity of the tissue in low-strain and high-strain modes, which have implications in understanding the structure of the underlying proteins in the tissue. From the earlier described relationship between stress and strain in Equation (1), the elastic moduli can be computed as the slope of the stress-strain curve. In a non-homogenous, anisotropic material, such as the vocal folds, this slope changes as the material becomes further deformed, as is discussed in Alipour et al⁶. One can compute two moduli from this data, a low-strain elastic modulus and a high-strain elastic modulus. A third piece of information, the difference between low-strain and high strain moduli, or their ratio becomes important in inferring tissue structure, and has thus been computed as well. As can be seen in the figures, the elastic moduli varied between false and true folds, and between the longitudinal and transverse directions, which relates to tissue structures and fibers orientation.

As reported in previous histologic studies, elastin in the vocal fold tissue is found mostly in the superficial layer and collagen is in the deep layer^{8, 19–21}. Collagen is assumed to be the major load bearing component that allows better mucosal wave in the superficial layer during increased pitch. The stress-strain relationship presented in this study is the combined effects of both elastin and collagen, and both the superficial and deep layers of the vocal fold tissue. At low strain values, the effects of elastin dominates and while the effects of collagen is likely minimal, due to its highly wavy structure at low strain. The high strain modulus describes the response of the tissue when both elastin and collagen are engaged. This high value (13–15 times more than low strain values) might be due to the increased contribution of collagen. However, it is not easy to separate the elastic modulus of elastin and collagen from the current combined data.

A comparison of the longitudinal and transverse elastic moduli in the true vocal folds show significant differences in material properties in these two directions, with the longitudinal high-strain modulus being 25–30 times higher than the transverse direction. This indicates that true vocal folds clearly have a preferred fiber direction, as observed previously¹⁹. Other biological soft tissue also report preferred fiber orientations and structural orthotropy or anisotropy including aortic wall^23–24, heart valves^25–26, and left ventricle tissues²⁷. In all of these anisotropic tissues, the highest stiffness is always reported in the direction where collagen fibers predominate. This direction has also been reported to be the direction that the tissue is subjected to the highest stresses or deformation, hence the tissue is “reinforced” with more collagen.

The true vocal fold samples were made from lamina propria which included ligament. The value of 30 kPa for the low strain Young's modulus is in agreement with the values reported by Min et al⁷ for the human ligament. This is not surprising since the ligament is the load bearing component of the vocal folds and if our samples were prepared without ligament, a lower Young's modulus could have been expected.

A comparison between the longitudinal modulus of the true and false vocal folds indicates important differences in the elastic properties between the two. From this data, one can infer differences in the protein content between the tissues. The low strain and high strain elastic moduli are both significantly lower in the false vocal folds, indicating a lower elastin and collagen content, respectively. The average Young's modulus for the human false vocal folds reported in this study is almost half of the Young's modulus for the human true vocal folds. This is consistent with other studies such as Haji et al⁹ and Chan et al²⁸ that reported lower stiffness for the false vocal folds. But, the Young's modulus represented graphically in Chan et al²⁹ appears to be lower than this study. This might be due to the overloading of their samples with many stretching rates (1, 2, 3, 5, and 10 Hz) that could soften the tissues. However, there is a significant similarity between these data - in both cases, nonlinearity is observed which is attributed to fibrous structure of these tissues.

The average vocal folds shear modulus of 1.0 kPa reported in this study is similar to the value of 1.008 kPa reported by Goodyer et al¹¹ from their Linear Skin Rheometer measures and shear modeling. However, it is more than value of (10–100 Pa) reported by Chan & Titze¹² for human mucosa at frequencies of up to 15 Hz using rheometer. It is possible that their reported shear values are for transverse direction, although it is hard to establish any direction once a piece of vocal fold is squished between the two rheometer disks.

Preconditioning of the tissue was necessary in all of the experiments performed. During preconditioning, a stress-softening phenomenon was observed during force elongation which demonstrated as hysteresis loop (Figure 5). Other soft tissue studies have similarly reported the need for preconditioning, with anywhere from 3–15 cycles of preconditioning typically being necessary before the tissue displays a consistent force-extension relationship^{15, 22}. While preconditioning is quite often necessary in soft tissues, its physical meaning and relationship to in vivo tissue behavior remains largely unexplored. Nevertheless, hysteresis is a viscoelastic phenomenon observed in soft tissues. When a load is applied to a tissue, energy is lost, and thus when the tissue is unloaded, it can exhibit a different profile. This can be observed in Figures 6–8, where the loading and unloading curves are different. The area within the hysteresis loop is a measure of the energy lost, and is calculated for each tissue and displayed on the figures. While the energy loss is substantially higher for the longitudinal direction of the true vocal folds than that of the false vocal folds or the transverse direction of the true folds, they are within one order of magnitude of one another.

Viscoelastic tissues are strain-rate dependent, and thus it is important to note that the current study was performed under cyclic loading of 1 Hz. This is substantially lower than the loading rates experienced by vocal fold tissue during phonation. However, major length changes of the vocal folds (prephonatory adjustments) occurs at 10 Hz and below, the current cyclic rate was chosen for experimental consistency and practicality. In future studies, it would be interesting to further examine the rate-dependence of the observed material properties in true and false vocal folds. Additionally, a measure of hysteresis loss over subsequent cycles during is another important quantifier of viscoelasticity, and would be interesting to examine in detail for these tissues.

Most biomechanical model of the vocal folds such as Alipour et al¹ are based on small deformation and linear elasticity. However, these models may incorporate nonlinear elasticity later on with an exponential models of Young's moduli for the tissue components⁵. These exponential models should provide both low strain and high strain moduli during large deformations. The mean values of transverse Young's modulus, longitudinal shear modulus and Poisson's ratio of the true vocal folds should help to refine the biomechanical models of vocal folds, although these values are not available for all tissue component yet. But knowing the range of these properties for one tissue component may help us to estimate the other values based on the their histological structure better.

CONCLUSSIONS

The current study presents several new possibilities in the understanding of vocal fold dynamics. First, the nonlinear behavior of vocal fold tissues with increasing stiffness at higher strain can be related to the vast ranges of fundamental frequencies in human larynges where with an increasing vocal fold length, much stiffer vocal fold is expected that oscillate at higher pitch. Second, anisotropy of the vocal fold tissue is evident from their considerably different stiffness in longitudinal and transverse directions. Third, the vocal fold shear modulus in the longitudinal direction is almost as small as transverse direction allowing the easy rotation and bending of these tissues without much resistance. Fourth, the smaller energy loss in the false vocal folds confirms its softness.