Establishment of parameters for congenital stenosis of the cervical spine: an anatomic descriptive analysis of 1066 cadaveric specimens

Abstract

Purpose

Congenital cervical stenosis (CCS) occurs when the bony anatomy of the cervical canal is smaller than expected in the general population predisposing an individual to symptomatic neural compression. No studies have defined CCS based on the normal population. The diagnosis is currently made based on clinical impression from radiographic studies. The aim of this study is to establish parameters that are associated with CCS, based on anatomic measurements on a large sample of skeletal specimens.

Methods

From the Hamann-Todd collection at the Cleveland Museum of Natural History, 1,066 skeletal specimens were selected. Digital calipers were used to measure the sagittal canal diameter (SCD), interpedicular distance (IPD), and pedicle length. Canal area at each level was calculated using a geometric formula. A standard distribution was created and values that were 2 SD below mean were considered as congenitally stenotic. An analysis of deviance was performed to identify parameters that were associated with CCS. Regression analysis was used to determine odds ratios (OR) for CCS using these parameters.

Results

CCS was defined at each level as: C3/4 = 1.82 cm², C4/5 = 1.80 cm², C5/6 = 1.84 cm², C6/7 = 1.89 cm², C7/T1 = 1.88 cm². Values of SCD < 13 mm and IPD < 22.5 mm were associated with CCS and yielded sensitivities and specificities of 88–100 % at each level. Logistic regression demonstrated a significant association between these parameters and presence of CCS with OR > 18 at each level.

Conclusions

Based on our study of a large population of adult skeletal specimens, we have defined CCS at each level. Values of SCD < 13 mm and IPD < 23 mm are strongly associated with the presence of CCS at all levels.

Introduction

Congenital cervical stenosis (CCS) occurs when the bony anatomy of the cervical canal is smaller than expected in the general population. Stenosis at the cervical level is related to a wide array of clinical symptoms ranging from asymptomatic or mild neck pain to severe cervical myelopathy causing paralysis. Cervical stenosis has been a keen material for research studies since Gowers [1] successfully described the pathological changes in cervical spondylosis as vertebral exostoses. A total of 250,000–500,000 individuals in the US have symptoms of spinal stenosis, 20−25 % of which occur in cervical spine. The prevalence is expected to increase over the next decade to 18 million as the US population ages [2]. As the disease burden of cervical stenosis is large and increasing, it is necessary to define and establish definite criterion for cervical stenosis, which can help a physician with early diagnosis of the disease.

However, no studies have defined CCS based on morphoanatomic measurements in the normal American population. A number of studies have defined cervical stenosis based on sagittal diameter dimensions, which is only one of the many parameters involved in cervical stenosis [8, 9, 20, 24, 25]. The diagnosis is currently made based on clinical impression from radiographic studies, which is subjective at best. Investigative studies use differing eligibility standards, as there are no widely accepted diagnostic or classification criteria for the diagnosis, which further limit the interpretation of reported findings. Exact measurements are needed, which define this condition such as simple parameters that are associated with CCS.

The changes in interpedicular distance (IPD) and sagittal canal diameter (SCD) dimensions of vertebral canal are an indirect and simple measure of canal area. The main aim of this study is to determine the measure of canal area as a function of sagittal and interpedicular diameters and to define an anatomic lower limit of IPD and SCD associated with canal stenosis (as a measure of canal area) with high sensitivity and specificity. The main advantage of IPD and SCD measurements is that these can be easily measured on CT or MR as opposed to the canal area, which is technically demanding and has high interobserver variability.

Materials and methods

The Hamann-Todd Osteological Collection in Cleveland, Ohio contains more than 3,300 treated and dried specimens out of which 1,066 specimens were randomly chosen for examination in no particular order, with six teenage specimens being excluded from the study. This sample size gives 95 % confidence interval with a 3 % margin of error for a population size of 300 million (total US population) [16]. The specimens in the collection represent individuals who died in Cleveland, Ohio between the years 1893 and 1938. The present study included 879 men and 187 women, ranging in age from 20 to 105; 415 specimens were of African−American ancestry, and the remainder was Caucasian.

A number of studies have shown that cervical canal is narrowest in lower cervical levels [18–20]. Cervical stenosis does not occur at C1 and C2 levels as the canal is widest at these levels. As the objective of the study was to identify parameters associated with cervical stenosis, C1 and C2 were not included in the study. The gross specimens were measured subjectively by a single blinded examiner from C3 to C7.

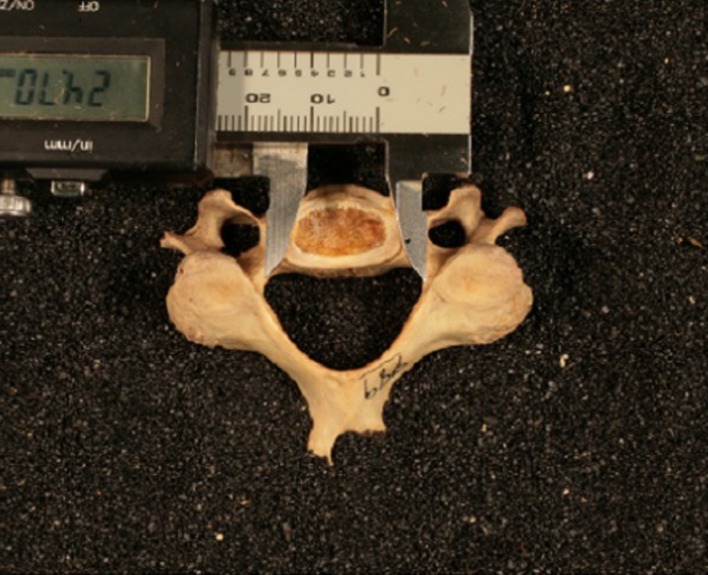
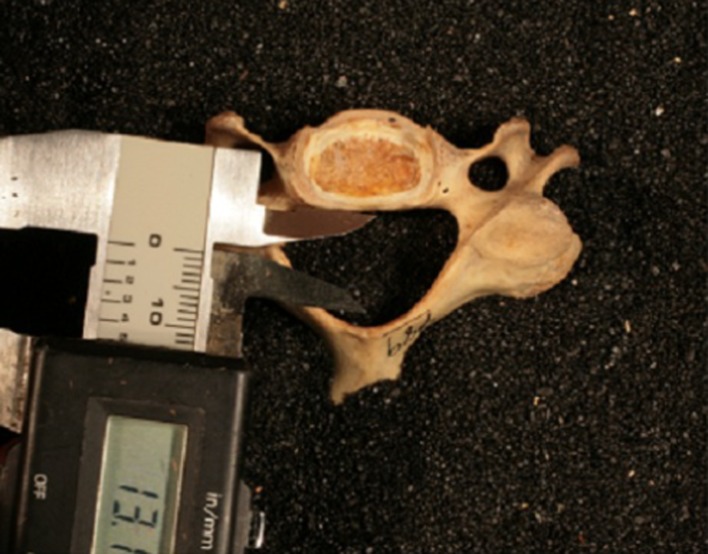
Digital caliper with precision of one-hundredth of a millimeter was used for all the measurements. The flat surface of the table edge was used to align each vertebra in the axial plane and all the measurements were taken from the superior aspect of the vertebrae. The interpedicular distance was measured as the maximal distance from the medial surface of the pedicles on either side (Fig. 1). The sagittal canal diameter was measured as the maximum anteroposterior distance of the spinal canal of each vertebrae (Fig. 2). Pedicle length (PL) was measured starting from the origin of pedicle from the body till the superior articular facet on either side (Fig. 3). The average was used as the pedicle length.

Fig. 1.

The measurement of interpedicular distance after proper alignment of the cervical vertebrae

Fig. 2.

Measuring the sagittal diameter from the superior surface of the cervical vertebrae

Fig. 3.

Pedicle length as measured from superior aspect of the cervical vertebrae. The average of both pedicles was used in the study

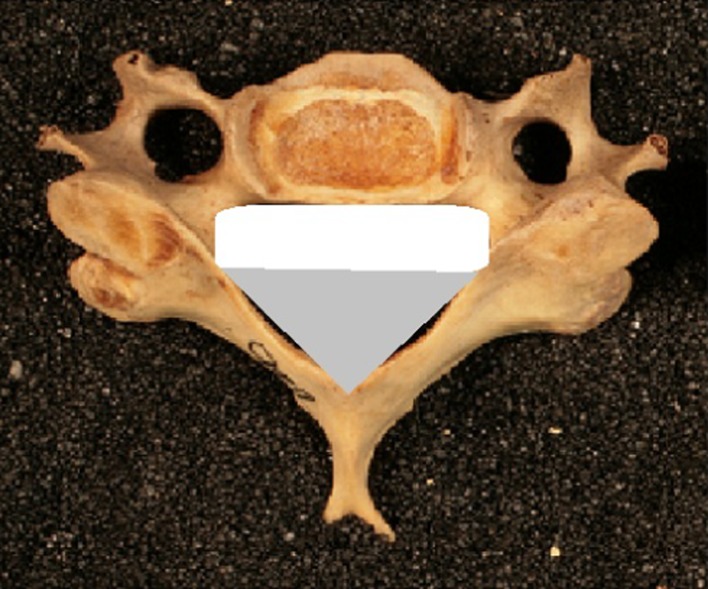
As it has already been established by Hashimoto et al. [18] that simple geometric measurements accurately predict canal area, area at each level was calculated using a standardized geometric formula (Fig. 4), i.e., Total area of canal = area of rectangle (IPD × PL) + area of isosceles triangle {IPD × (SCD−PL)/2}. Image J was used as a control standard to compare and verify the results of our geometric formula. To verify these calculations, computerized measurements were done using Image J (Image J 1.34, National Institutes of Health, USA) on a random sample of 20 cervical vertebrae. Our results were accurate within 10−13 % of the Image J calculations as shown in Table 1. As a result, our geometric formula measurements verified by Image J analysis constituted the control standard threshold for defining CCS as a canal area less than two standard deviations below the mean.

Fig. 4.

Calculation of the canal area. Total area of cervical canal was calculated as the sum of the area of the rectangle (shaded white) and the isosceles triangle (shaded grey). These measurements were further verified using Image J

Table 1.

Calculation of area by Image J and its comparison with geometric measurements (in mm²)

C3		C4		C5		C6		C7
Geometric*	Image J*	Geometric*	Image J*	Geometric*	Image J*	Geometric*	Image J*	Geometric*	Image J*
269	245	254	230	253	229	290	262	297	266
315	282	317	288	304	276	312	286	302	280
291	266	324	291	343	316	340	312	339	306
351	323	345	314	344	316	353	320	293	261

* p value <0.01 at all levels when comparing Image J with geometric measurements

Since the age, sex, and race of all the specimens at the time of death was known, the sagittal diameter, interpedicular distance, and pedicle length were linearly regressed with canal area using these variables to determine if there was a significant correlation between these anatomic parameters and canal area when corrected for these variables. A logistic regression analysis of sagittal and interpedicular diameters with stenotic canal area (2 SD below the mean) using the same covariates (age, sex, race) was conducted to calculate the odds ratio (OR), p value as well as the 95 % confidence intervals for both the sagittal and interpedicular distance at each cervical level.

The values of IPD and SCD which were associated with stenotic canal area with highest sensitivity and specificity at each level were tabulated. The standard p value cutoff (p < 0.05) was used in the study.

Results

A total of 1,072 specimens were examined. A full distribution of specimens by decade of life, sex, and race is given in Table 2. The canal area calculated using geometric formula was used to define CCS at each level. Lower limit of canal area defining CCS was calculated as C3/4 = 1.82 cm², C4/5 = 1.80 cm², C5/6 = 1.84 cm², C6/7 = 1.89 cm², C7/T1 = 1.88 cm². A stepwise linear regression analysis revealed that in all the specimens, the SCD and IPD had significant correlation with canal area (p < 0.01) at all cervical levels (C3−C7). The regression models revealed no significant correlation of sagittal and interpedicular diameters with specimen race and sex (p > 0.05). Logistic regression demonstrated a significant association between these parameters and presence of CCS with OR >18 at each level. These findings have been summarized in Tables 3 and 4. Interestingly, PL was not found to be associated with CCS at any of the cervical levels.

Table 2.

Age, sex, and racial breakdown of all the sampled specimens

Age (years)	Number of specimens	Females	Males	White	Black
20–24	52	15	37	08	44
25–34	129	42	87	46	83
35–44	233	44	189	120	113
45–54	260	35	225	163	97
55–64	191	15	176	146	45
65–74	127	18	109	107	20
75–84	60	12	48	53	07
85–94	12	6	6	07	05
95–104	01	0	01	01	0
105–114	01	0	01	0	01
Total	1,066	187	879	651	415

Table 3.

The odds ratio, p value, and the confidence interval data for the sagittal diameter

Cervical level	p value	95 % confidence interval	Odds ratio
C3	0.01	35–189	81
C4	0.01	12–796	101
C5	0.01	14–101	38
C6	0.01	12–116	38
C7	0.01	17–83	38

Table 4.

The odds ratio, p value, and the confidence interval data for the interpedicular distance

Cervical level	p value	95 % confidence interval	Odds ratio
C3	0.01	10–52	23
C4	0.01	6–130	28
C5	0.01	8–40	18
C6	0.01	21–262	75
C7	0.01	15–78	35

The IPD and SCD dimensions that are associated with CCS with highest sensitivities and specificities have been provided in Tables 5 and 6. In the transverse plane, C3 had the smallest dimension at 22 mm, which increased to 23 mm at C6 level. The sagittal diameter was smallest at C3 level (12.5 mm) and then remained constant from C4 to C7 at 13 mm.

Table 5.

The value of sagittal diameter dimensions associated with congenital cervical stenosis and its sensitivity and specificity at each level

Cervical level	Lower limit associated with cervical stenosis (mm)	Sensitivity (%)	Specificity (%)
C3	12.5	100	96.5
C4	13	90	90
C5	13	90	94
C6	13	85	93
C7	13	92	96.5

Table 6.

The value of interpedicular distance dimensions associated with congenital cervical stenosis and its sensitivity and specificity at each level

Cervical level	Lower limit associated with cervical stenosis (mm)	Sensitivity (%)	Specificity (%)
C3	22	89	88
C4	22.5	90	83
C5	22.5	100	90
C6	23	100	88
C7	22.5	92	90

Discussion

Cervical spine has been the interest of human research since late 19th century [4, 5] , but it was only in 1955 that the earliest detailed account of cervical vertebrae measurements were given by Carl C Francis [6]. In 1957, Payne and Spillane [7] described the relationship between developmental stenosis and canal size. Since then a number of anatomic and roentological studies on various cervical canal parameters to establish a standard for defining cervical stenosis have been done [8–11].

The anatomic narrowing of the neural pathway through the spine may be centrally located in the spinal canal or more laterally in the lateral recesses or neuroforamina [3, 12–14]. As a result, patients with cervical spinal stenosis can present with a variable spectrum of clinical presentations, ranging from intermittent neck and shoulder pain to cervical radiculopathy and myelopathy leading to paralysis. Patients with asymptomatic cervical lesions due to congenital stenosis are at high risk of developing myelopathies. The biomechanical characteristics of the spinal segments are altered in these patients, and as a result even minimal trauma can further perpetuate a cycle of degenerative changes causing the impingement of the spinal nerve. Over the years, the intervertebral discs also lose height and uncovertebral osteophyte formations occur which increase the risk of myelopathy even further in this subset of patients [13]. As a result, it is essential to diagnose these asymptomatic cervical stenosis lesions at the earliest so as to improve the prognosis and treatment of this disease. Thus the measurements of IPD and SCD on routine radiographs, which are simple and easy to perform, can be a helpful tool for the physician in diagnosing cervical stenosis.

Variable results have been reported in studies correlating cervical vertebral parameters with canal stenosis, irrespective of individual and exterior variables. A retrospective radiographic analysis of 47 intact cadaver pediatric cervical spines by Vara et al. [15] concluded that the pedicle length remained relatively constant throughout growth. The mean pedicle diameter width was 4.3 and 6.1 mm, respectively, at C3 and C7 at 18 years of age. The spinal canal sagittal diameter remained relatively constant with increasing age. Lee et al. [17] concluded that mid-sagittal diameter of the cervical spinal canal in the diagnosis of cervical spinal stenosis was not a reliable measurement. Another study by Hashimoto et al. [18] suggested good agreement between the radiographic measurements of cervical canal sagittal diameter with anatomic cadaveric measurements. The lower limit of sagittal diameter at all the cervical levels (C3–C7) was established at 10 mm. Tatarek et al. [19] morphometrically studied cervical canal narrowing using the sagittal and interpedicular diameters in 321 skeletons. It was concluded that sagittal diameter was narrowest at the C4 level for African–Americans and C6 for Caucasians. IPD was narrowest at the C2/C3 level for all groups. In another study [20] using CT myelography to perform morphological analysis of the cervical spinal canal reported that the spinal canal was narrowest at C4.

The cross-sectional area is reduced in stenotic canal due to reduced sagittal and interpedicular dimensions. As the levels of stenosis increase, the disease increases in severity. Patients with motor disturbances have a significantly smaller sagittal diameter of the bony spinal canal than patients without motor disturbances [21]. Mid-sagittal diameter has also been used as a measure of space available for the spinal cord in studies comparing normal control subjects with spinal cord-injured patients. Debois et al. [21] reported the mean sagittal diameter of cervical spinal canal at 12.9 mm in 100 consecutive patients, who underwent surgery because of soft cervical disc herniation, indicating a certain degree of developmental stenosis. The sagittal diameter was significantly smaller in patients with soft cervical disc herniation than in the control group. In another study by Kang et al. [9] reported the mean sagittal diameter of the canal at the uninjured levels was 16.1 mm for the patients who had a complete injury of the spinal cord and 18.1 mm for those who had no neurologic deficit. Matsuura et al. [22] concluded that the sagittal diameters of the spinal canal of the control group were significantly larger than those of the spinal cord-injured group while there was no significant difference present with regards to the cross-sectional area of the spinal canal between the two groups.

Only one-third of the cervical canal from C1 to C3 levels and three–fourths from C4 to C7 levels is occupied by spinal cord [7]. Therefore, a normal cervical canal can accommodate the changes of stenosis unless there is a congenital narrowing of canal. Inoue et al. [20] used CT myelography to perform morphological analysis of the cervical spinal canal and established the lower limit of normal of sagittal diameter on plain radiographs. He reported that compression of the spinal cord was expected whenever the sagittal diameter of the spinal canal in normal individuals was at or below 12 mm. Lee et al. [23] in their cadaveric study of 469 specimens reported the average anterior–posterior canal diameter at all levels at 14.1 ± 1.6 mm with men having significantly larger cervical spinal canals than women at all of the levels.

Various populations have been studied in establishing the criterion of cervical stenosis. A Korean population study [17] of 90 sets of cervical vertebrae reported average mid-sagittal canal diameters from C3 to C7 as 13.2 ± 1.3 mm in males and concluded that mid-sagittal diameter of the cervical spinal canal in the diagnosis of cervical spinal stenosis was not a reliable measurement. Another roentological study [24] in the Japanese population reported that 82 % of patients with value of sagittal diameter less than 14 mm for males and 13 mm for females had cervical spondylotic myelopathy. Sasaki et al. [25] studied the Japanese population and concluded that patients with a sagittal diameter of less than 12 mm have a high risk of cervical myelopathy. The cervical canal was found to be narrowest at the C4 level. No significant difference was found between values at the C4 and C5 levels.

Canal stenosis occurs when the area available to the cord is decreased, leading to pressure on the nerve roots and spinal cord. Thus it is very important to define all the morphological parameters of cervical spine in relation with canal area to correctly establish a criterion of cervical stenosis accurately, on a feasible sample size. Majority of these studies have been done on a relatively small sample size and as a result have been unable to establish a set standard or the definition of cervical spinal stenosis. Major emphasis in these studies have been on a single aspect of stenosis, i.e., either looking at the cross-sectional area alone or the sagittal diameter as itself.

Even when investigations done via radiologic techniques of MR or CT have defined cervical stenosis with reference to canal area, the major drawback of rater reliability cannot be ruled out. A set criterion can only be established in a normal population when the external variables have been ruled out. Thus a cadaveric study of a large sample size, studying each of the cervical vertebrae individually seems acceptable. Many previous studies have suggested one lower limit for the cervical spine as a whole. As the morphology of cervical spine varies considerably from one cervical level to another, this seems rather implausible. Majority of the anatomic studies have a Europe or Asian based population. As the morphology changes from one population set to another [8, 10, 22, 24, 25], the same criterion cannot be applied to different populations. Thus, it is pertinent to look at cervical stenosis in average American population.

In our study we have compared morphoanatomically, a much wider array of representative American population from adolescents to very old individuals. This study being a retrospective, cadaveric study presents with some inherent limitations in itself. Ideally we would require a prospective cohort study following a large group of patients with serial imaging studies and autopsy analysis after death. Such a study would provide the most satisfactory answers to the present questions. The problem is that such a study would be logistically difficult and financially prohibitive. There is always some component of soft tissue involved in the overall pathogenesis [3], which due to innate restrictions of this study, cannot be taken into account. Although from a biological standpoint, nutrients received from foods have not changed significantly over the past 100 years and the bone quality and structure have essentially remained the same [26], the last century has seen the emergence of obesity as a frequent cause of several significant health problems. Thus the findings of this study are limited in the context that obesity and its effect on the skeletal system, specially the spine, cannot be studied due to inherent restrictions of the study design.

The major percentage of total canal area is contributed by the isosceles triangle (>65 %), which is contributed by SCD and IPD. Furthermore, the area of rectangle (contributes <35 % to total area) is majorly influenced by IPD dimension and not PL. As a result, the biggest factor in deciding the canal area is IPD, followed by the SCD with minimum contribution from PL. The much wider variations in IPD and SCD dimensions (10–15 mm) compared to the variations in PL measurements (4 mm) mainly determine whether the canal is stenotic or not. So even if PL is congenitally small but the IPD and SCD are both normal, the total canal area is normal. These reasons may explain why pedicle length does not correlate well with the canal area.

In conclusion, based on our study of a large population of adult skeletal specimens, we have defined CCS at each level. As the morphology of cervical spine varies considerably even from one level to another, it seems impossible to set one lower limit for all the cervical vertebrae. Thus, the lower limits of SCD and IPD at each level have been defined which are strongly associated with the presence of CCS at all levels C3–C7. Our study encompasses a much greater and vast population of adult American individuals and the changes occurring in cervical region with regards to development of stenosis.

This anatomic study looks in totality at all the aspects of cervical stenosis, correlating the smaller cross-sectional area with the predictive parameters of bony anatomy, with a high sensitivity and specificity. This study takes care of the pitfalls of the previous studies with special emphasis on the diagnostic aspect of cervical spinal stenosis.