BTK: An Open-Source Toolkit for Fetal Brain MR Image Processing

Abstract

Studies about brain maturation aim at providing a better understanding of brain development and links between brain changes and cognitive development. Such studies are of great interest for diagnosis help and clinical course of development and treatment of illnesses. However, the processing of fetal brain MR images remains complicated which limits the translation from the research to the clinical domain. In this article, we describe an open-source image processing toolkit dedicated to these images. In this toolkit various tools are included such as: denoising, image reconstruction, super-resolution and tractography. The BTK resource program (distributed under CeCILL-B license) is developed in C++ and relies on common medical imaging libraries such as Insight Toolkit (ITK), Visualization Toolkit (VTK) and Open Multi-Processing (OpenMP).

1. Introduction

Brain maturation is one of the most captivating aspects of neuroimaging, particularly in the earliest phases of maturation of fetal development and childhood. The development of the human central nervous system begins in utero and continues until the end of adolescence. The maturation process is characterized by a spatio-temporal and very complex heterogeneity, which is likely to reflect the successive steps of psycho-motor and cognitive learning of the child (Lenroot and Giedd (2006)).

The non-invasive nature of magnetic resonance imaging (MRI) provides unique opportunities for in vivo investigation of the developing human brain. Fetal MRI is a valuable complement to prenatal sonography to confirm and characterize suspected brain abnormalities (see for instance Chung et al. (2009); Prayer and Baert (2011) for review on fetal imaging). Fetal brain maturation can be studied by MRI from the 18th gestational week to term, and relies primarily on T2-weighted and diffusion-weighted (DW) images. 3D detailed evaluation of the developing brain is crucial since the assessment of sulcation is often critical in identifying abnormalities. In addition, visualization of cortical development and maturational steps of the brain may benefit from information provided by DW sequences.

The development of ultrafast 2D acquisition sequences has led to significant improvements in the clinical application of fetal MRI (Glenn and Barkovich (2006)). However, the slice acquisition time is still very critical and has to be kept as short as possible to reduce the impact of fetal motion on the exam. As a result, a set of thick 2D slices are generally acquired in clinical studies, with motion commonly occurring between slices. Overall, the resulting image is limited in its geometric integrity between slices due to motion, and in its through plane spatial resolution.

Recently, several reconstruction methods have been proposed to cope with this issue for anatomical data (Rousseau et al. (2005, 2006); Jiang et al. (2007); Kim et al. (2010)) and DW data (Oubel et al. (2010)). Subsequently, super-resolution methods have been applied to fetal MRI to improve the quality of the reconstructed images (Rousseau et al. (2010); Gholipour-Baboli et al. (2010)). Such reconstruction methods are essential for fetal MRI analysis such as atlas building (Habas et al. (2010a)), and folding and growth pattern analysis (Habas et al. (2011); Rajagopalan et al. (2011)).

Moreover, it clearly appears that the currently existing open-source image processing softwares are not adapted to deal with fetal MRI. In addition to reconstruction algorithms, there is a need to develop new tools taking into account the specificities of fetal brain MR images for the entire processing pipeline such as, for instance, segmentation (handling changes in intensity and shape) and tractography (recovering weakly myelinated fiber bundles) (Studholme (2011)).

In this paper, we present an open-source image processing toolkit primarily dedicated to fetal brain MRI. It includes an image denoising algorithm (Coupe et al. (2008)), several image reconstruction methods (Oubel et al. (2010)) and a probabilistic tractography technique (Pontabry and Rousseau (2011)). After a brief technical overview of BTK (namely Baby Brain Toolkit), each algorithm is described with figures illustrating results on in-utero fetal brain MR data. Image processing pipelines combining BTK algorithms are presented in Section 4. Relying on common libraries (ITK, VTK, openMP), this proposed toolkit can be easily embedded into softwares which provide interactive processing tools.

2. Toolkit Implementation

To make it easily usable for the community, BTK depends on tools commonly used in medical image processing such as ITK (www.itk.org), VTK (www.vtk.org), OpenMP (www.openmp.org), Tclap (tclap.sourceforge.net) and ANN (www.cs.umd.edu/~mount/ANN). All these libraries can be easily installed through a package manager (for instance apt-get for Debian distribution or macports for MacOSX)¹.

The software compilation process is controlled using CMake (www.cmake.org). Documentation of the code can be obtained using Doxygen (www.doxygen.org). In order to provide the most versatile toolkit as possible, each image processing algorithm can be run separately from the command line. Although the library is based on the use of ITK, the image format used primarily by BTK is NIFTI (nifti.nimh.nih.gov).

BTK is governed by the CeCILL-B license under French law and abiding by the rules of distribution of free software. You can use, modify and/or redistribute the software under the terms of the CeCILL-B license as circulated by CEA, CNRS and INRIA at the following URL: www.cecill.info. The sources of BTK can be downloaded at this address: https://github.com/rousseau/fbrain

3. Algorithmic Content

The proposed image processing toolkit, namely Baby Brain Toolkit (BTK), contains the following image processing tools:

1. Non-local image denoising (Section 3.1),

2. 3D fetal T2-weighted image reconstruction (Section 3.2),

3. Super-resolution algorithm for T2-weighted images (Section 3.2),

4. 3D fetal diffusion weighted image reconstruction (Section 3.3),

5. Probabilistic tractography (Section 3.4).

Results obtained with each algorithm are illustrated with figures to show the ability of the proposed toolkit. Fetal MRI data have been obtained on a 1.5 T Siemens Avanto MRI Scanner (SIEMENS, Erlangen, Germany) using a 6-channel phased array coil combined to the spine array positioned around the mother abdomen. An axial spin echo single-shot echo-planar sequence was acquired in free breathing along 30 non-collinear diffusion gradient encoding directions with a b value of 700s/mm². The following pulse sequence parameters were used: TR=6800 ms; TE=99 ms; FOV=250 × 250 mm2; matrix = 128 × 128; 41 contiguous axial slices of 3.5mm thickness covering the whole fetal brain; no gap; number of excitations = 2. The resolution of the T2 weighted HASTE sequence (TE/TR = 147/3190 ms) is: 0.74 × 0.74 × 3.45mm.

3.1. Denoising

Recently, Buades et al. (2005) have proposed a very e cient denoising algorithm relying on a non-local framework. Let us consider, over the image domain Ω, a weighted graph w that links together the voxels of the input image I with a weight w(x, y), (x, y) ∈ Ω². This weighted graph w is a representation of non-local similarities in the input image I. In Buades et al. (2005), the non-local graph w is used for denoising purpose using a neighborhood averaging strategy (called non-local means (NLM)):

$$\forall \mathbf{x}\in \Omega ,I_{nlm}\left(\mathbf{x}\right)=\frac{{\Sigma }_{\mathbf{y}\in \Omega }w(\mathbf{x},\mathbf{y})I\left(\mathbf{y}\right)}{{\Sigma }_{\mathbf{y}\in \Omega }w(\mathbf{x},\mathbf{y})}$$ (1)

where w is the graph of self-similarity computed on the noisy image I, I(y) is the gray level value of the image I at the voxel y and I_nlm is a denoised version of I. The weighted graph reflects the similarities between voxels of the same image. It can be computed using an intensity-based distance between patches (see Coupe et al. (2008)):

$$w(\mathbf{x},\mathbf{y})=f\left(\frac{{\Sigma }_{\mathbf{x}\prime \in {\mathcal{P}}_I\left(\mathbf{x}\right),\mathbf{y}\prime \in {\mathcal{P}}_I\left(\mathbf{y}\right)}{(I(\mathbf{x}\prime )-I(\mathbf{y}\prime ))}^2}{2N\beta {\widehat{\sigma }}^2}\right)$$ (2)

where P_I(x) is a 3D patch of the image I centered at voxel x; f is a kernel function (f (x) = e^−x in Buades et al. (2005)), N is the number of voxels of a 3D patch; β is the standard deviation of the noise and is a smoothing parameter. Under the assumption of Gaussian noise in images, β can be set to 1 (see Buades et al. (2005) for theoretical justifications).

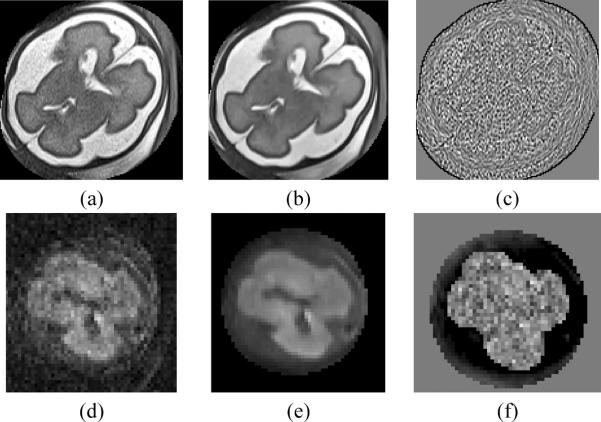
The implementation included in BTK is fully based on the method described in Coupe et al. (2008). This denoising algorithm is implemented for 3D images. The diffusion image sequences are denoised independently by applying this filter for each diffusion-weighted image (see Figure 1 for results on fetal brain MRI).

Figure 1.

Example of denoising result (the smoothing parameter β was set to 1). First row: a fetal MR brain T2-weighted image, second row: diffusion-weighted image. (a,d) original images, (b,e) denoised images, (c,f) difference image.

3.2. Anatomical Image Reconstruction

The first approach to form high resolution MR images of the fetal brain has been recently proposed by Rousseau et al. (2005, 2006) without modifying the acquisition protocol used in routine. This retrospective method is based on a registration refined compounding of multiple sets of orthogonal fast 2D MRI slices to address the key problem of fetal motion. This is achieved by first globally registering the low resolution images, and then applying an iterative slice alignment scheme which seeks to refine the 3D positioning of each slice to the current combined high resolution volume. This is driven by normalized mutual information to provide robustness to contrast variation induced by motion of the fetal brain with respect to the imaging coil in the magnet. This motion correction method has been implemented in BTK.

Moreover, a super-resolution (SR) technique for fetal brain MR data reconstruction (similar to Rousseau et al. (2010); Gholipour-Baboli et al. (2010)) is also present in the toolkit. As in most of common SR approaches, the image solution is computed by inverting this observation model:

$${\mathbf{Y}}_{r,s}=S_r{B}_r{W}_s{W}_r\mathbf{X}+{\mathbf{n}}_{\mathbf{r}}for1\le r\le n,1\le s\le m_r$$ (3)

where n is the number of low resolution (LR) images and m_r is the number of slices of the LR image r, Y_r,s denotes the slice s of the LR image r, X is the high resolution (HR) image, n_r represents the observation noise, S_r is the subsampling matrix, B_r a blur matrix, W_s and W_r are geometric transformations of sth slice of the y_r,s and of the rth low resolution image respectively.

The purpose of super-resolution is to remove the effects of the blurring convolution and to increase the voxel grid density (see Park et al. (2003); Ng and Bose (2003); Milanfar (2010) for technical overview on super-resolution). To estimate the high resolution image, the observation model is introduced into an inverse problem framework which is solved using a variational approach. The local regularization is performed by computing the sum of the square of the first derivatives of the reconstructed image. The overall cost function is minimized using a conjugate gradient descent (using the vnl library) where the parameter space dimension is the number of voxels of the reconstructed image.

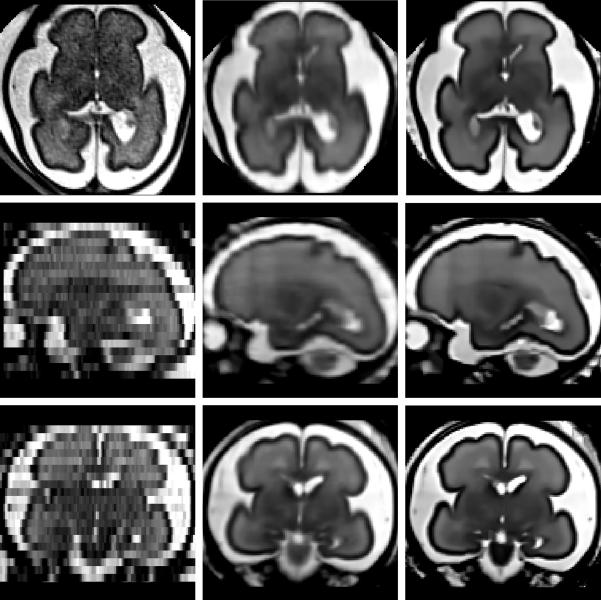
Incorporating a non-local regularization term into the SR framework can be done by iteratively performing the SR algorithm and the NLM denoising algorithm (as in Manjón et al. (2010)). Figure 2 shows image reconstruction results obtained with the two reconstruction methods implemented in BTK (local interpolation and super-resolution coupled with the non-local denoising procedure previously described). It shows one original low resolution image compared to the high resolution reconstructed images for axial, coronal, sagittal views. Results obtained with the SR approach compare favorably with the local sparse interpolation approach proposed by Rousseau et al. (2006). It can be especially noticed that the boundaries of brain structures (like the cortex) are better recovered.

Figure 2.

Details of a reconstructed fetal brain MR image using 3 orthogonal LR images. From left to right: A) original axial low resolution image, B) reconstructed image using local sparse interpolation similar to Rousseau et al. (2006), C) SR reconstruction coupled with non-local denoising (the non-local smoothing parameter β was set to 1 and the trade off parameter (between data fidelity and regularization) was set to 0.1).

3.3. Diffusion-weighted Image Reconstruction

A new technique has been recently proposed by Oubel et al. (2010) to extend the reconstruction method of T2-weighted MR images to DW sequences. This method aims at correcting geometrical distortions, fetal motion, and reconstructing a high resolution 3D DW image. The goal is to obtain isotropic images with resolution lower or equal to the in-plane resolution of the data currently acquired in routine. Contrary to the method proposed by Jiang et al. (2009), this method has the advantage that no specific diffusion model needs to be assumed. It relies on the use of a groupwise registration method, and a dual spatio-angular interpolation by using radial basis functions. We have implemented this algorithm into BTK.

Briefly, this method takes advantage of the intensity dependence between DW images to first obtain their joint alignment. To this end, the DW images are first registered to an arbitrary chosen reference by using a transformation model consisting of a set of full affine transformations applied to each slice independently, and mutual information as similarity metric. Then, a new reference is computed by averaging the transformed images and the process is repeated until the mean squared error between consecutive reference images is lower than a given threshold.

The final diffusion weighted sequence is obtained by applying an interpolation scheme relying on the use of a spatial (ϕ) and an angular (ψ) radial basis function:

$$Y(\mathbf{x},\Theta )=\sum _{i=0}^{N-1}{w}_i\varphi \left(\mid \mathbf{x}-{\mathbf{x}}_i^{\prime }\mid \right)\psi \left(\mid \Theta -{\Theta }_i^{\prime }\mid \right)$$ (4)

where x = (x, y, z) are the spatial coordinates, Θ = (ϕ, θ) the spherical coordinates, Y is the reconstructed signal and N is the number of points used for interpolation.

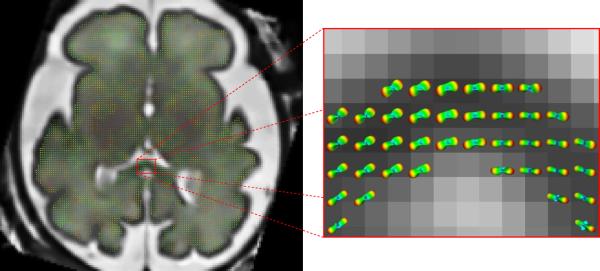
Figure 3 shows the estimated fiber orientation distribution functions (fODF) using such motion-corrected DW sequence, superimposed on the reconstructed anatomical T2-weighted image.

Figure 3.

Orientation distribution functions obtained from a reconstructed diffusion-weighted image sequence registered to reconstructed T2-weighted anatomical image.

3.4. Probabilistic Tractography

Tractography methods can be mainly categorized using the two following features: the way to use DW-MRI data (local vs global modeling) and the underlying mathematical framework (deterministic vs probabilistic approaches) (see Lazar (2010) for a recent review of tractography methods).

The tractography algorithm included in BTK is a probabilistic tractography technique (Pontabry and Rousseau (2011)) relying on the use of Q-ball based modeling (Tuch (2004)) within a particle filtering framework (Doucet et al. (2000, 2009)). The reliability of Q-Ball models allows us to extract more information from data, such as the ODF (Descoteaux et al. (2007)) which provides a precise idea of the underlying fiber architecture at every voxel (see Figure 3).

A non-linear state-model is used for the tracking modeling and the probabilistic maps of fibers are estimated using a particle filtering algorithm (see Pontabry and Rousseau (2011) for details). One of the outputs of the algorithm is an estimate of the posterior density of the white matter fibers. Fiber bundles are also provided by estimating the Maximum A Posteriori (MAP) from the posterior density map.

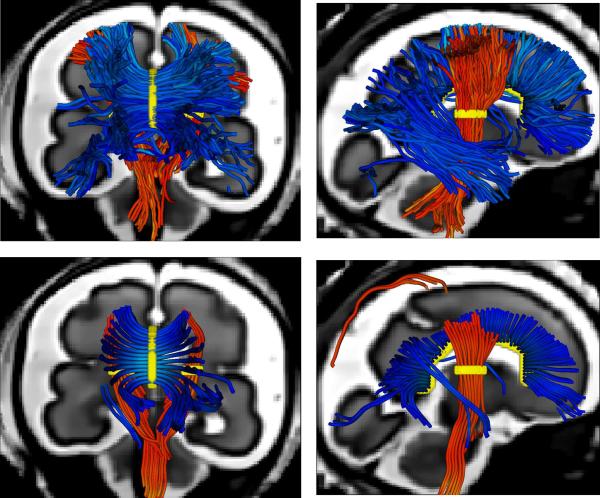
Figure 4 shows the estimated fiber bundles (fiber tracts in the corpus callosum and the pyramidal tracts) using the BTK tractography algorithm compared to the deterministic algorithm implemented in Slicer [www.slicer.org] (FA-based stopping criterion: 0.05, step size: 0.5mm). As in Kasprian et al. (2008) and Zanin et al., due to very low fractional anisotropy values in the fetal brain, the deterministic algorithm can only recover short fiber tracts, specially in the corpus callosum. The probabilistic aspect of the tractography method implemented in BTK leads to an increase of the algorithm robustness and allows to recover longer fibers.

Figure 4.

Example of tractography results of fiber tracts in the corpus callosum and the pyramidal tracts superimposed on a reconstructed 3D anatomical image. First row: BTK probabilistic algorithm, second row: Slicer deterministic algorithm (the FA-based stopping criterion was set to 0.05). In both cases, the maximum turning angle was set to $\frac{\pi }{3}$ and the step size was 0.5mm. The seed regions are shown in yellow.

4. Pipelines

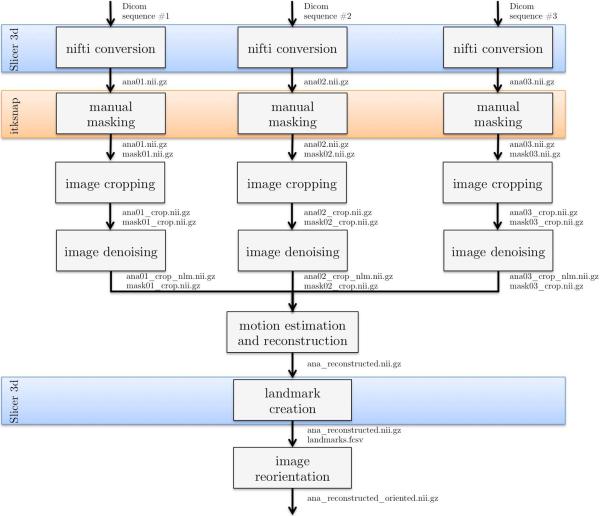
This section presents the two examples of image processing pipelines that can be built using BTK and other freely available softwares (Slicer, ITKSNAP, dcm2nii). The first one is dedicated to the reconstruction of anatomical fetal MRI data (depicted in Figure 5). The corresponding command lines are shown in Figure 6. This pipeline consists in: 1) converting the data from DICOM to NIFTI, 2) manual masking of the brain (optional step which can improve the reconstruction results) and image cropping (based on the size of the masks), 3) image denoising, 4) motion correction and super-resolution, 5) reorientation of the image using landmarks placed using Slicer. Figure 2 shows a reconstructed 3D image obtained using such a processing pipeline.

Figure 5.

Overview of the processing pipeline for anatomical data in BTK. Slicer3D (www.slicer.org) is used to convert the DICOM data to NIFTI format and for the placement of landmarks on which is based the reorientation of the 3D reconstructed image. The use of Slicer for these steps allows the user to check the orientation consistency between the three anatomical images (axial, coronal, sagittal for instance). ITKSNAP (www.itksnap.org) is used to create a rough mask of the brain (this step is optional).

Figure 6.

Command lines corresponding to the processing pipeline for anatomical data in BTK. On the left are shown the blocks used in the anatomical data pipeline (Figure 5) and on the right the correspond command lines.

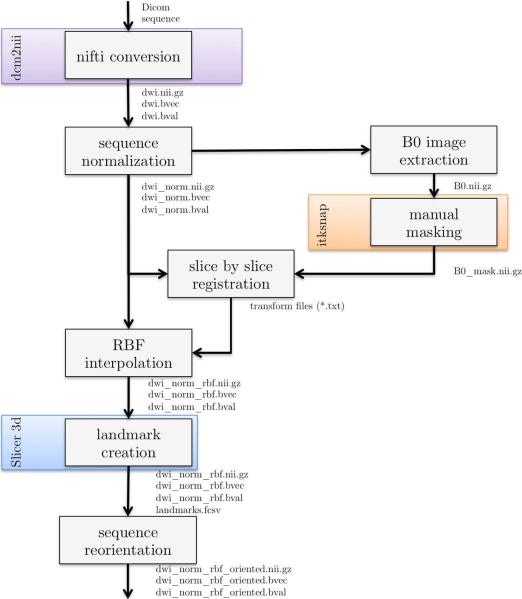
The second processing pipeline described in this section is dedicated to DWI of the fetal brain (depicted in Figure 7). The corresponding command lines are shown in Figure 8. It is similar to the previous but it includes processing tools dedicated to DWI: 1) data conversion using dcm2nii (www.cabiatl.com/mricro/mricron/dcm2nii.html), 2) sequence normalization (the B0 image are registered together using affine transforms and then averaged to produce one B0 image), 3) B0 image extraction and manual masking using ITKSNAP, 4) motion correction and RBF interpolation to compute the reconstructed DW sequence, 5) reorientation of the image using landmarks placed using Slicer. This final step (sequence reorientation) is very important since it allows the user to visualize the DW data using consistent color coding schemes. Figure 3 shows a superposition of estimated fiber orientation distribution functions (fODF) using a motion-corrected DW sequence with the corresponding reconstructed anatomical T2-weighted image.

Figure 7.

Overview of the processing pipeline for diffusion data in BTK. dcm2nii is used to convert the DICOM data to NIFTI format and Slicer for the placement of landmarks on which is based the reorientation of the 3D reconstructed image. ITKSNAP (www.itksnap.org) is used to create a rough mask of the brain.

Figure 8.

Command lines corresponding to the processing pipeline for diffusion data in BTK. On the left are shown the blocks used in the anatomical data pipeline (Figure 7) and on the right the correspond command lines.

5. Discussion

This article presents several image processing tools which have been put together into an open-source toolkit, called BTK, dedicated to fetal brain MRI. The results obtained in this work (in particular the super-resolution reconstruction and the tractography algorithm) show that such a toolkit might be very useful for the research community studying the early human brain development stage.

BTK is an on-going project and we expect to improve the robustness of the algorithms through the feedback of the community. Moreover, BTK is hosted on github (github.com) which combines some features of social networking sites with distributed source-control Git (git-scm.com). It makes this system highly suited to collaborative development projects.

Further work concerns outlier detections during the reconstruction process, such as the ones commonly known in diffusion tensor imaging (Jones and Cercignani (2010); Tournier et al. (2011)), or intensity bias in anatomical images (Rousseau et al. (2006); Kim et al. (2011)). We plan also to include in BTK automatic segmentation tools dedicated to fetal brain MRI such as the ones recently proposed in Habas et al. (2010b); Caldairou et al. (2011).

Finally, the image processing tools presented in this article may be also useful for studies of other populations such as newborns, infants or adults affected by pathologies (such as Parkinson disease) leading to involuntary movements during image acquisition. Furthermore, denoising and tractography algorithms are not specific to fetal brain MRI and it can be applied on any 3D MR image.