Class-Specific Weighting for Markov Random Field Estimation: Application to Medical Image Segmentation

Abstract

Many estimation tasks require Bayesian classifiers capable of adjusting their performance (e.g. sensitivity/Specificity). In situations where the optimal classification decision can be identified by an exhaustive search over all possible classes, means for adjusting classifier performance, such as probability thresholding or weighting the a posteriori probabilities, are well established. Unfortunately, analogous methods compatible with Markov random fields (i.e. large collections of dependent random variables) are noticeably absent from the literature. Consequently, most Markov random field (MRF) based classification systems typically restrict their performance to a single, static operating point (i.e. a paired sensitivity/Specificity). To address this deficiency, we previously introduced an extension of maximum posterior marginals (MPM) estimation that allows certain classes to be weighted more heavily than others, thus providing a means for varying classifier performance. However, this extension is not appropriate for the more popular maximum a posteriori (MAP) estimation. Thus, a strategy for varying the performance of MAP estimators is still needed. Such a strategy is essential for several reasons: 1) the MAP cost function may be more appropriate in certain classification tasks than the MPM cost function, 2) the literature provides a surfeit of MAP estimation implementations, several of which are considerably faster than the typical Markov Chain Monte Carlo methods used for MPM, and 3) MAP estimation is used far more often than MPM. Consequently, in this paper we introduce multiplicative weighted MAP (MWMAP) estimation — achieved via the incorporation of multiplicative weights into the MAP cost function — which allows certain classes to be preferred over others. This creates a natural bias for Specific classes, and consequently a means for adjusting classifier performance. Similarly, we show how this multiplicative weighting strategy can be applied to the MPM cost function (in place of the strategy we presented previously), yielding multiplicative weighted MPM (MWMPM) estimation. Furthermore, we describe how MWMAP and MWMPM can be implemented using adaptations of current estimation strategies such as iterated conditional modes and MPM Monte Carlo. To illustrate these implementations, we first integrate them into two separate MRF-based classification systems for detecting carcinoma of the prostate (CaP) on 1) digitized histological sections from radical prostatectomies and 2) T2-weighted 4 Tesla ex vivo prostate MRI. To highlight the extensibility of MWMAP and MWMPM to estimation tasks involving more than two classes, we also incorporate these estimation criteria into a MRF-based classifier used to segment synthetic brain MR images. In the context of these tasks, we show how our novel estimation criteria can be used to arbitrarily adjust the sensitivities of these systems, yielding receiver operator characteristic curves (and surfaces).

1. Introduction

The ability to classify multiple objects (e.g. pixels in an image) simultaneously is essential for certain estimation tasks. Within a Bayesian framework, each object (“site” in MRF nomenclature) is modeled as a random variable, and the collection of these random variables (under minor conditions) is called a Markov random field (MRF). If the random variables are assumed independent, we can estimate each in isolation. This estimation typically involves an exhaustive search. For example, obtaining the maximum a posteriori (MAP) estimate (of a single random variable) entails calculating the a posteriori probability for each possible class, and then choosing the class with the largest probability. However, if the random variables are not independent, the entire MRF must be estimated collectively. Since the number of possible states of the random field is prohibitively large, the exhaustive approach becomes untenable¹. Consequently, more sophisticated schemes, such as relaxation procedures (Geman and Geman, 1984; Besag, 1986), Monte Carlo methods (Marroquin et al., 1987), loopy belief propagation (Yedidia et al., 2000), and graph cuts (Boykov et al., 2001), become necessary. For a comparison of different estimation procedures see (Dubes et al., 1990; Szeliski et al., 2008).

The capability of adjusting classifier performance (e.g. sensitivity/Specificity) with respect to Specific classes is essential for many applications — especially in medical imaging. For example, misclassifying a malignant lesion is typically more egregious than misclassifying a benign lesion. In situations where the optimal classification decision can be identified by an exhaustive search, means for modifying classifier performance, such as probability thresholding or weighting the a posteriori probabilities, are well established (Duda et al., 2001). Unfortunately, analogous methods compatible with MRFs are noticeably absent in the literature. Consequently, most MRF-based classification systems restrict their performance to a single, static operating point (i.e. a paired sensitivity/Specificity).

Though MRFs are pervasive in the computer vision and medical imaging literature — addressing such tasks such as segmentation (Pappas, 1992; Farag et al., 2006; Awate et al., 2006; Liu et al., 2009; Scherrer et al., 2009; Marroquin et al., 2002; Bouman and Shapiro, 1994), denoising (Besag, 1986; Figueiredo and Leitao, 1997), and texture synthesis (Paget and Longstaff, 1998; Zalesny and Gool, 2001) — relatively little work has discussed means for varying the performance of MRF-based classification systems. To address this deficiency, we recently presented a generalization — and novel Markov Chain Monte Carlo realization — of the maximum posterior marginals (MPM) estimation criterion (Monaco and Madabhushi, 2011). This generalization allows certain classes to be weighted more heavily than others, thus providing a means for varying MRF-based classifier performance. Like all Bayesian estimation techniques, MPM estimation is derived by minimizing the expected value of an underlying cost function. For a given state of the random field, the MPM cost function is simply the sum of the number of sites that are misclassified. To generalize this cost function we weighted each misclassification by the type of classification error. Please see (Monaco and Madabhushi, 2011) for details.

However, this approach is Specific to MPM estimation, and is not appropriate for generalizing the very different MAP cost function. For unlike the MPM cost function that sums the site-wise misclassifications, the MAP cost function yields an identical cost for any number of misclassifications greater than zero. Thus, a strategy for varying the performance of MAP estimators is still needed. Such a strategy is essential for several reasons: 1) the MAP cost function may be more appropriate in certain classification tasks than the MPM cost function, 2) the literature provides a surfeit of MAP estimation implementations (Boykov et al., 2001; Dubes et al., 1990; Szeliski et al., 2008; Geman and Geman, 1984; Besag, 1986), several of which (e.g. graph cuts and ICM) are considerably faster than the typical Markov Chain Monte Carlo methods used for MPM (Marroquin et al., 1987; Monaco and Madabhushi, 2011), and 3) MAP estimation is far more prevalent than MPM. (Note that MAP and MPM should not be confused with the algorithms used to implement them, e.g. simulated annealing (Geman and Geman, 1984) for MAP and Markov Chain Monte Carlo (Marroquin et al., 1987) for MPM.)

Aside from our own work, we are aware of very few articles that discuss means for adjusting MRF-based classifier performance, whether using MPM or MAP estimation. In (Comer and Delp, 1999) Comer and Delp employed a Markov prior with a term that applied costs to specified classes. However, they did not discuss this term with respect to varying system performance, nor did they present it within the rigorous framework of Bayesian cost analysis (as we do here). In a seminal paper by Besag (Besag, 1986), the author suggested leveraging a unique property of iterated conditional modes (ICM) to adjust classification results. ICM is an iterative, deterministic procedure that converges to a local maximum of the a posteriori probability of a MRF. ICM requires the initial state of the MRF from which to begin the iteration; the choice of this state determines the local maximum to which ICM converges. Thus, varying the initial conditions can vary the classification results. However, the different modes of the a posteriori probability (to which ICM converges) do not necessarily correspond to meaningful classifications. Thus, this method, though intuitively appealing, lacks mathematical justification (from the perspective of Bayesian cost).

In this paper, we introduce a generalization of the MAP estimation criteria and present means for its implementation. Specifically, we demonstrate how multiplicative weights can be incorporated into the Bayesian cost function that leads to MAP estimation, thereby biasing the posterior probability to favor certain classes. We refer to estimation using this new cost function as multiplicative weighted MAP (MWMAP) estimation. Coincidentally, the same multiplicative weighting can also be applied to the MPM cost function, yielding multiplicative weighted MPM (MWMPM) estimation. In addition to introducing these novel estimation criteria, we demonstrate how they can be implemented by modifying existing estimation schemes (e.g. ICM). Furthermore, we highlight their significance by incorporating them into two separate classification systems based on MRFs: 1) a system for detecting cancerous glands in histological sections (HSs) from radical prostatectomies (Monaco et al., 2009a) and 2) a system for detecting cancerous regions in T2-weighted 4 Tesla ex vivo MRI of the prostate (Viswanath et al., 2012). Over a cohort of 40 digitized HSs and 15 2D MRI sections, respectively, we illustrate how MWMAP and MWMPM estimation can be used to vary classification performance, enabling the construction of receiver operator characteristic (ROC) curves. Finally, to demonstrate the extensibility of MWMAP and MWMPM to estimation tasks involving more than two classes, we incorporate these criteria into a MRF-based classifier used to segment synthetic brain MR images. In this instance, varying classifier performance results in ROC surfaces.

To summarize, the primary contributions of this work are as follows:

• By incorporating class Specific weights into the MAP and MPM estimation criteria, we introduce two novel estimation criteria capable of adjusting the performance of MRF-based classification systems.

• We develop implementations of these criteria by modifying existing realizations of MAP and MPM estimation (e.g. ICM and MPM Monte Carlo).

• We integrate the MWMAP and MWMPM estimation criteria into three MRF-based classification systems, demonstrating the ability of each criterion to arbitrarily adjust system performance.

The remainder of the paper is organized as follows: In Section 2 we review the Bayesian estimation of MRFs, deriving the MAP and MPM estimation criteria using Bayesian risk analysis. Section 3 discusses how class-Specific weights can be incorporated into MAP and MPM, yielding MWMAP and MWMPM. In Section 4 we present implementations of these novel criteria by modifying current MRF-compatible estimation strategies. In Section 5 we present experiments to demonstrate how the estimation criteria can be used to adjust the performance of our systems for detecting CaP (in HSs and MR images) and segmenting MR brain phantoms. Results of these experiments are provided in Section 6. Section 7 offers concluding remarks.

2. Review of Random Fields and Bayesian Risk

2.1. Random Field Definitions and Notation

Let the set S ={1, 2, …, N}reference N sites to be classified. Each site s∈S has two associated random variables: X_s ∈Λ ≡ {ω₁, ω₂, …, ω_L} indicating its state (class) and Y_s ∈ℝ^D representing its D-dimensional feature vector. Particular instances of X_s and Y_s are denoted by the lowercase variables x_s ∈ Λ and y_s ∈ ℝ^D. Let X = (X₁, X₂, …, X_N) and Y = (Y₁, Y₂, …, Y_N) refer to all random variables X_s and Y_s in aggregate. The state spaces of X and Y are the Cartesian products Ω = Λ^N and ℝ^D×N. Instances of X and Y are denoted by the lowercase variables x=(x₁, x₂, …, x_N) ∈ Ω and y =(y₁, y₂, …, y_N) ∈ ℝ^D×N. See Table 1 for a list and description of the commonly used notations and symbols in this paper.

Table 1.

List of notation and symbols.

Symbol	Description
S	Set referencing N sites
Λ	Range of Xs and xs: Λ ≡ {ω1, ω2, …, ωL}
Xs ∈ Λ	Random variable indicating state at site s
xs ∈ Λ	Instance of Xs
D	Number of features
Ys ∈ ℝD	Random variable indicating feature vector at site s
ys ∈ ℝD	Instance of Ys
x̂ ∈ Ω	Estimate of X
C(x, x̂)	Cost of choosing x̂ when the true labels are x
R(X|x̂, y)	Conditional risk: R(X|x̂, y) = E[C(X, x̂)|y]
X ∈ Ω	Collection of all Xs: X=(X1, X2, …, XN)
x ∈ Ω	Instance of X: x=(x1, x2, …, xN)
Ω	Range of X and x: Ω=ΛN
Y ∈ ℝ D×N	Collection of all Ys: Y =(Y1, Y2, …, YN)
y ∈ ℝ D×N	Instance of Y: y=(y1, y2, …, yN)
ηs	Set of sites that neighbor s ∈ S
x−s	x−s =(x1, …, xs−1, xs+1, …, xN)
xηs	xηs = xηs(1), …, xηs(|ηs|)
α(·)	Weighting function $\alpha :\mathrm{\Lambda }\to {\mathbb{R}}_0^{+}$
α(x)	α(x)=Πs∈S α (xs)

Let G = {S, E} establish an undirected graph structure on the sites, where S and E are the vertices (sites) and edges, respectively. A neighborhood η_s is the set containing all sites that share an edge with s, i.e. η_s = {r : r ∈ S, r ≠ s, {r, s}∈ E}. The random field X is a Markov random field if its local conditional probability functions satisfy the Markov property: P(X_s = x_s | X_−s = x_−s)= P(X_s = x_s|X_ηs = x_ηs), where x_−s = (x₁, …, x_s−1, x_s+1, …, x_N), x_ηs = (x_ηs(1), …, x_ηs(|ηs|)), and η_s(i) ∈ S is the i^th element of the set η_s. Note that in places where it does not create ambiguity, we will simplify the probabilistic notations by omitting the random variables, e.g. P(x) ≡ P(X=x).

2.2. Bayesian Risk

Given an observation of the feature vectors Y, we would like to estimate the states X. Bayesian estimation advocates selecting the estimate x̂ ∈ Ω that minimizes the conditional risk (expected cost)(Duda et al., 2001)

$$R(\mathbf{X}\mid \widehat{\mathbf{x}},\mathbf{y})=\text{E}[C(\mathbf{X},\widehat{\mathbf{x}})\mid \mathbf{y}]=\sum _{\mathbf{x}\in \mathrm{\Omega }}C(\mathbf{x},\widehat{\mathbf{x}})P(\mathbf{x}\mid \mathbf{y}),$$ (1)

where E indicates expected value and C(x, x̂) is the cost of selecting labels x̂ when the true labels are x. In the following subsections we will consider the two most prevalent cost functions used with MRFs.

2.3. Maximum a Posteriori Estimation

The most ubiquitous cost function (though this cost is rarely expressed explicitly) is

$$C_{\text{MAP}}(\mathbf{x},\widehat{\mathbf{x}})=1-\prod _{s\in S}\delta (x_s-{\widehat{x}}_s),$$ (2)

where δ is the Kronecker delta. Thus, a cost of 1 is incurred if one or more sites are labeled incorrectly. Inserting (2) into (1) yields

$$\begin{array}{l}{R}_{\text{MAP}}(\mathbf{X}\mid \widehat{\mathbf{x}},\mathbf{y})=\sum _{\mathbf{x}\in \mathrm{\Omega }}\left[1-\prod _{s\in S}\delta (x_s-{\widehat{x}}_s)\right]P(\mathbf{x}\mid \mathbf{y})\\ =1-P(\widehat{\mathbf{x}}\mid \mathbf{y}).\end{array}$$ (3)

Minimizing (3) over x̂ is equivalent to maximizing P(x̂|y). Thus, we have maximum a posteriori (MAP) estimation, which advocates selecting the x̂ that maximizes the a posteriori probability.

2.4. Maximum Posterior Marginals

As an alternative to MAP estimation, Marroquin et al. (Marroquin et al., 1987) suggested using the following cost function

$$C_{\text{MPM}}(\mathbf{x},\widehat{\mathbf{x}})=\sum _{s\in S}[1-\delta (x_s-{\widehat{x}}_s)].$$ (4)

This function counts the number of sites in x̂ that are labeled incorrectly. Inserting (4) into (1) yields

$$\begin{array}{l}{R}_{\text{MPM}}(\mathbf{X}\mid \widehat{\mathbf{x}},\mathbf{y})=\sum _{\mathbf{x}\in \mathrm{\Omega }}\left(\sum _{s\in S}[1-\delta (x_s-{\widehat{x}}_s)]\right)P(\mathbf{x}\mid \mathbf{y})\\ =\sum _{s\in S}\sum _{\mathbf{x}\in \mathrm{\Omega }}P(\mathbf{x}\mid \mathbf{y})-\sum _{s\in S}\sum _{\mathbf{x}\in \mathrm{\Omega }}\delta (x_s-{\widehat{x}}_s)P(\mathbf{x}\mid \mathbf{y})\\ =\mid S\mid -\sum _{s\in S}P({\widehat{x}}_s\mid \mathbf{y}).\end{array}$$ (5)

The distributions P(x̂_s|y) are called the posterior marginals. Minimizing (5) over x̂ is equivalent to independently maximizing each of these posterior marginals with respect to its corresponding x̂_s. Hence, this estimation criterion is termed maximum posterior marginals (MPM).

3. Class Weighted Cost Functions

Both the MAP and MPM cost functions weight each class equally. That is, the cost accrued from misclassification is identical across all classes. In this section we introduce generalizations of the MAP and MPM cost functions which provide a means for weighting certain classes more heavily than others. Specifically, we present the multiplicative weighted MAP (MWMAP) and MPM (MWMPM) estimation criteria.

3.1. Multiplicative Weighted Maximum a Posteriori (MWMAP) Estimation

To introduce the ability to favor Specific classes, C_MAP can be generalized as follows:

$$C_{\text{MWMAP}}(\mathbf{x},\widehat{\mathbf{x}})=\mathit{\alpha }(\mathbf{x})\left[1-\prod _{s\in S}\delta (x_s-{\widehat{x}}_s)\right],$$ (6)

where α(x) = Π_s∈S α (x_s) and $\alpha :\mathrm{\Lambda }\to {\mathbb{R}}_0^{+}$ are the class dependent weighting functions. Thus, if the estimate x̂ contains any erroneous labels it accrues a cost of α(x). Note that α(x) can not assume any arbitrary functional form, but is restricted to the product of the independent weighting functions α(x_s). This restriction is necessary for the tractability of subsequent derivations.

Before proceeding we introduce a Definition that will prove useful. Let X̃ be a random field that differs from X only with respect to the following probability measure:

$$P(\stackrel{\sim }{\mathbf{X}}=\mathbf{x})=\frac{1}{Z_{\alpha }}\mathit{\alpha }(\mathbf{x})P(\mathbf{X}=\mathbf{x}),$$ (7)

where Z_α = Σ_x−Ω α(x)P(X=x) is the normalizing constant. Note also that

$$P(\stackrel{\sim }{\mathbf{X}}=\mathbf{x}\mid \mathbf{y})=\frac{1}{Z_{\alpha }}\mathit{\alpha }(\mathbf{x})P(\mathbf{x}\mid \mathbf{y}).$$ (8)

We now insert (6) into (1) yielding

$$\begin{array}{l}{R}_{\text{MWMAP}}(\mathbf{X}\mid \widehat{\mathbf{x}},\mathbf{y})=\sum _{\mathbf{x}\in \mathrm{\Omega }}\mathit{\alpha }(\mathbf{x})\left[1-\prod _{s\in S}\delta (x_s-{\widehat{x}}_s)\right]P(\mathbf{x}\mid \mathbf{y})\\ =\sum _{\mathbf{x}\in \mathrm{\Omega }}\left[1-\prod _{s\in S}\delta (x_s-{\widehat{x}}_s)\right]\mathit{\alpha }(\mathbf{x})P(\mathbf{x}\mid \mathbf{y})\\ =\sum _{\mathbf{x}\in \mathrm{\Omega }}\left[1-\prod _{s\in S}\delta (x_s-{\widehat{x}}_s)\right]Z_{\alpha }·P\left(\stackrel{\sim }{\mathbf{X}}=\mathbf{x}\mid \mathbf{y}\right)\\ =Z_{\alpha }·R_{\text{MAP}}\left(\stackrel{\sim }{\mathbf{X}}\mid \widehat{\mathbf{x}},\mathbf{y}\right).\end{array}$$ (9)

Thus, minimizing R_MWMAP(X|x̂, y) is equivalent to minimizing R_MAP(X̃|x̂, y); and consequently, the optimal labeling is the MAP estimate of X̃. Since, as shown in (8), the a posteriori probability of X̃ corresponds to the weighted a posteriori probability of X, we refer to this type of estimation as multiplicative weighted MAP estimation. Note that if α (x_s) ≡ 1, MWMAP estimation reduces to MAP estimation.

3.2. Multiplicative Weighted Maximum Posterior Marginals (MWMPM)

Class-Specific weights can be similarly incorporated into the MPM cost function:

$$C_{\text{MWMPM}}(\mathbf{x},\widehat{\mathbf{x}})=\mathit{\alpha }(\mathbf{x})\sum _{s\in S}[1-\delta (x_s-{\widehat{x}}_s)].$$ (10)

Mislabeling a site whose true label is x_s has an associated cost of α(x). Consequently, the penalty for mislabeling the single site s depends upon the true labels of all sites s∈S. Inserting (10) into (1) yields

$$\begin{array}{l}{R}_{\text{MWMPM}}(\mathbf{X}\mid \widehat{\mathbf{x}},\mathbf{y})=\sum _{\mathbf{x}\in \mathrm{\Omega }}\left[\mathit{\alpha }(\mathbf{x})\sum _{s\in S}[1-\delta (x_s-{\widehat{x}}_s)]\right]P(\mathbf{x}\mid \mathbf{y})\\ =\sum _{\mathbf{x}\in \mathrm{\Omega }}\left[\sum _{s\in S}[1-\delta (x_s-{\widehat{x}}_s)]\right]\mathit{\alpha }(\mathbf{x})P(\mathbf{x}\mid \mathbf{y})\\ =\sum _{\mathbf{x}\in \mathrm{\Omega }}\left[\sum _{s\in S}[1-\delta (x_s-{\widehat{x}}_s)]\right]Z_{\alpha }·P\left(\stackrel{\sim }{\mathbf{X}}=\mathbf{x}\mid \mathbf{y}\right)\\ =Z_{\alpha }·R_{\text{MPM}}\left(\stackrel{\sim }{\mathbf{X}}\mid \widehat{\mathbf{x}},\mathbf{y}\right).\end{array}$$ (11)

Thus, this multiplicative weighted MPM (MWMPM) estimate of X is equivalent to the MPM estimate of X̃.

Note that in (Monaco and Madabhushi, 2011) we introduced another possible generalization of the MPM cost function. However, this generalization leads to a very different estimation strategy (see Appendix A). Also note that since the probability distribution of every MRF can be expressed using a Gibbs formulation (Besag, 1974), it is insightful to examine the Gibbs formulations of both P(X = x) and P(X̃= x). This examination is presented in Appendix B.

4. Implementations and Algorithms

In this section we demonstrate how MWMAP and MWMPM estimation can be performed using modifications of existing estimation strategies. As mentioned in Sections 3.1 and 3.2, the MWMAP and MWMPM estimates of a random field X are equivalent to the MAP and MPM estimates of the random field X̃, respectively. Consequently, we are free to realize these estimates using any existing MAP or MPM implementation. Though a variety of MAP estimation techniques exist (e.g. simulated annealing (Geman and Geman, 1984)), for MWMAP estimation we elect to employ iterated conditional modes (ICM) because of its popularity and simplicity. For MWMPM we select the Markov chain Monte Carlo (MCMC) method proposed by Marroquin et al. (Marroquin et al., 1987).

4.1. Weighted Maximum a Posteriori (MWMAP) Estimation with Iterated Conditional Modes

ICM is predicated on the following reformulation of the a posteriori probability (Besag, 1986):

$$P(\mathbf{x}\mid \mathbf{y})=P(x_s\mid {\mathbf{x}}_{-s},\mathbf{y})P({\mathbf{x}}_{-s}\mid \mathbf{y}).$$ (12)

Increasing P(x_s|x_−s, y) necessarily increases P (x|y). This suggests an optimization strategy that sequentially visits each site s ∈ S and determines the label x_s ∈ Λ that maximizes P (x_s|x_−s, y). The ICM algorithm is provided as Figure 1(a). Typically, the initial condition x⁰ is either a randomly selected element of Ω or the maximum likelihood estimate of P(y|x) (Pappas, 1992; Dubes et al., 1990). ICM converges to a local maximum of P(x|y).

Figure 1.

Algorithms for (a) iterated conditional modes and (b) weighted iterated conditional modes. Both algorithms are deterministic relaxation schemes that converge to a local maximum of P(x|y) and α(x)P(x|y), respectively.

Since the MWMAP estimate of X is equivalent to the MAP estimate of the X̃, modifying ICM to perform MWMAP estimation only requires replacing $P(X_s=\omega \mid {\mathbf{x}}_{-s}^k,\mathbf{y})$ with $P({\stackrel{\sim }{X}}_s=\omega \mid {\stackrel{\sim }{\mathbf{X}}}_{-s}={\mathbf{x}}_{-s}^k,\mathbf{y})$ in step 6, and then recognizing (see Appendix B) that $P({\stackrel{\sim }{X}}_s=\omega \mid {\stackrel{\sim }{\mathbf{X}}}_{-s}={\mathbf{x}}_{-s}^k,\mathbf{y})\propto \alpha (x_s)P(X_s=\omega \mid {\mathbf{x}}_{-s}^k,\mathbf{y})$. The resulting weighted ICM (WICM) algorithm is provided in Figure 1(b). Note that in practice, the computation of P(x_s|x_−s, y) is straight-forward. Consider that P(x_s|x_−s, y) reduces to P(x_s|x_ηs, y_s) by consequence of the Markov property and the typical assumption that the observations Y are conditionally independent given their associated states, i.e. P(y|x) = Π_s∈S P (y_s|x_s). Furthermore, P (x_s|x_ηs, y_s) ∝ P (y_s|x_s)P (x_s|x_ηs) by Bayes law.

4.2. Weighted Maximum Posterior Marginals (MWMPM) Using a Markov Chain Monte Carlo Simulation

MPM advocates selecting the estimate x that maximizes the marginal probabilities P(x_s|y) for all s ∈ S. To obtain these marginals Marroquin et al. proposed using the Gibbs sampler (Geman and Geman, 1984; Casella and George, 1992) or the Metropolis algorithm (Metropolis et al., 1953) to generate a Markov chain (X⁰, X¹, X², …) with equilibrium distribution P(x|y), where X^k is a random variable indicating the state of the chain at iteration k (see Figure 2(a)). Thus, the proportion of time the chain spends (after reaching equilibrium) in any state x is given by P(x|y), i.e. each state x^k represents a sample from the distribution P(x|y). The convergence to P(x|y) is independent of the starting conditions (Tierney, 1994); and consequently, x⁰ is typically selected at random from Ω. Determining the number of iterations l needed for the Markov chain to reach equilibrium is difficult, and depends upon the particular distribution P(x|y) and the initial conditions x⁰. Usually l is selected empirically.

Figure 2.

Algorithms for the Gibbs sampler and the weighted Gibbs sampler. These two Monte Carlo algorithms generate Markov chains with equilibrium distributions P(x|y) and P(X̃ =x|y), respectively.

Since the proportion of time the chain spends in any state x is given by P(x|y), the posterior marginal P(x_s|y) can be estimated as follows:

$$P(X_s=\omega \mid \mathbf{y})\approx \frac{1}{m-l}\sum _{k=l+1}^m\delta (x_s^k-\omega ),$$ (13)

where ω ∈ Λ and m−l is the number of iterations past equilibrium needed to generate an accurate estimate. The value for m, like l, is typically chosen empirically².

Since the MWMPM estimate of X is equivalent to the MPM estimate of X̃, modifying the previous MCMC method to explicitly perform MWMPM estimation only requires replacing $P(X_s=x_s^k\mid {\mathbf{x}}_{-s}^k,\mathbf{y})$ in step 6 of the Gibbs sampler (Figure 2(a)) with

$$P({\stackrel{\sim }{X}}_s=x_s^k\mid {\stackrel{\sim }{\mathbf{X}}}_{-s}={\mathbf{x}}_{-s}^k,\mathbf{y})=\frac{\alpha (x_s^k)}{A_{\alpha s}}P(X_s=x_s^k\mid {\mathbf{x}}_{-s}^k,\mathbf{y}),$$ (14)

where $A_{\alpha s}={\sum }_{\omega \in \mathrm{\Lambda }}\alpha (\omega )P(X_s=\omega \mid {\mathbf{x}}_{-s}^k,\mathbf{y})$. We refer to this modified version of the Gibbs sampler as the weighted Gibbs sampler (see Figure 2(b)). The remainder of the estimation procedure is identical to that used for MPM, i.e. for all s∈S we identify the ω∈Λ that maximizes the marginal distribution P(X̃_s = ω|y) obtained from (13).

5. Experimental Design

In this section, we begin by alternately incorporating the MWMAP and MWMPM estimation criteria into two MRF-based classification systems for detecting CaP: 1) a system for detecting CaP glands in HSs from radical prostatectomies and 2) a system for detecting CaP regions in T2-weighted 4 Telsa ex vivo prostate MRI. We then integrate these estimation criteria into a simple MRF-based classifier used to segment a two-dimensional synthetic brain MR image into regions containing cerebrospinal fluid (CSF), gray matter (GM), or white matter (WM). For each of these classification tasks, our goal is to demonstrate that by varying the class-Specific weights inherent in the MWMAP and MWMPM criteria, we can arbitrarily adjust their detection sensitivity/Specificity and generate ROC curves — or surfaces when the number of classes exceed two. To implement the MWMAP and MWMPM criteria, we employ the methods presented in Section 4, which we will refer to as MWMAP^ICM and MWMPM^MC. The superscripts ICM and MC (i.e. Monte Carlo) help describe the Specific approach, and hopefully, reemphasize that the estimation criteria and their Specific realizations should not be conflated. For convenience, the two estimation criteria and their associated implementations are listed in Table 2.

Table 2.

List of weighted estimation criteria and their associated implementations.

Estimation Criterion	Implementation
MWMAP	MWMAPICM
MWMPM	MWMPMMC

Before continuing, we should further clarify the difference between an estimation criterion and its associated implementation. In this paper, the MAP, MPM, MWMAP, and MWMPM estimation criteria are defined by equations (3), (5), (9), and (11), respectively. For a given estimation criterion, the “optimal” classification is the x̂ that minimizes that criterion. Solving for the optimal classification requires a Specific implementation. Because of complexity of MRFs, straightforward implementations that precisely minimize the estimation criteria do not exist; consequently, researchers have developed methods for yielding suboptimal classifications. For example, ICM (Besag, 1986), graph cuts (Boykov et al., 2001), and simulated annealing (Geman and Geman, 1984) are three approaches for approximating the MAP estimate, i.e. minimizing (3). That is, ICM, graph cuts, and simulated annealing are three possible implementations of the MAP estimation criterion. We should point out that each implementation is usually Specific to an estimation criteria; for example, ICM performs MAP estimation, and would not be used for MPM estimation.

5.1. Generating Receiver Operator Characteristic Curves and Surfaces

5.1.1. Binary Classes: ROC Curves

Both CaP detection systems are similar in the sense that they employ a MRF framework to classify their respective sites (i.e. glands or pixels) as either malignant ω₁ or benign ω₂. Assuming the systems use one of our two estimation criteria, the classification results will depend upon the choice of weights α(ω₁) and α(ω₂). Since only the ratio of weights, and not their Specific values, is relevant, they can be represented using a single, more intuitive threshold

$$T=\frac{\alpha ({\omega }_2)}{\alpha ({\omega }_1)+\alpha ({\omega }_2)},$$ (15)

where T ∈ [0, 1]. To see that applying the two weights is equivalent to thresholding (the Bayes factor (Kass and Raftery, 1995)), we need only rewrite step 6 in Figures 1(b) and 2(b) in terms of T (not shown).

To assess CaP detection performance, we define the following: true positives (TP) are those segmented objects (glands for HSs and pixels in the MRI) identified as cancerous by both the expert-provided ground-truth and the automated system; true negatives (TN) are those segmented objects identified as benign by both the truth and the automated system, false positives (FP) are those segmented objects identified as benign by the truth and malignant by the automated system; and false negatives (FN) are those segmented objects identified as malignant by the truth and benign by the automated system. The true positive rate (TPR) and false positive rate (FPR) are given by TP/(TP+FN) and FP/(TN+FP), respectively. Note that the TPR and FPR are synonymous with the sensitivity and one minus the Specificity, respectively. A ROC curve (Metz, 1978) is a plot of the TPR vs. FPR. For each estimation criterion, we can generate a ROC curve by varying T from zero to one, measuring the resulting TP/FP/FN/TN across all images, and then computing the TPR and FPR.

5.1.2. Ternary Classes: ROC Surfaces

The brain MR image, unlike the images for CaP detection, contain three classes: CSF (ω₁), GM (ω₂), and WM (ω₃). Segmentation performance depends upon the choice of weights α(ω₁), α(ω₂), and α(ω₃). Since only relative ratios of weights are relevant, we can, without loss of generality, restrict the weights as follows:

$$\alpha ({\omega }_1)+\alpha ({\omega }_2)+\alpha ({\omega }_3)=1\text{and}\alpha ({\omega }_1),\alpha ({\omega }_2),\alpha ({\omega }_2)\in [0,1].$$ (16)

Instead of the above restrictions, we could have employed two thresholds analogous to the T defined in (15); however, we found the representation in (16) to be more intuitive.

To assess segmentation performance, we define the class-Specific true positives TP_ωi for class ω_i, i ∈ {1, 2, 3} as the number of pixels labeled as ω_i by both the classifier and the ground-truth. The class-Specific true positive rate (TPR_ωi) for class ω_i is TP_ωi/Σ_iTP_ωi. The triplet (TPR_ω1, TPR_ω2, TPR_ω3) — which is a function of the weights — establishes an operating point on the associated three-dimensional ROC surface. We populate this surface (with unique operating points) by appropriately varying the weights in (16).

5.2. Experiment 1: Detection of CaP Glands in Digitized Radical Prostatectomy Sections

The analysis of HSs plays a significant role in the diagnosis and treatment of CaP (Kumar et al., 2004). The most salient information in these HSs is derived from the morphology and architecture of the glandular structures (Gleason, 1966). Since complex tasks such as Gleason grading (Tabesh et al., 2007; Doyle et al., In Press) consider only the cancerous glands, an initial process capable of rapidly identifying these glands is highly desirable. Thus, we introduced an automated system for detecting cancerous glands in Hematoxlyn and Eosin (H&E) stained tissue sections (Monaco et al., 2010). The primary goal of this algorithm is to eliminate regions of glands that are not likely to be cancerous, thereby reducing the computational load of further, more sophisticated analyses. Consequently, in a clinical setting the algorithm should operate at a high detection sensitivity, ensuring that very little CaP is discarded.

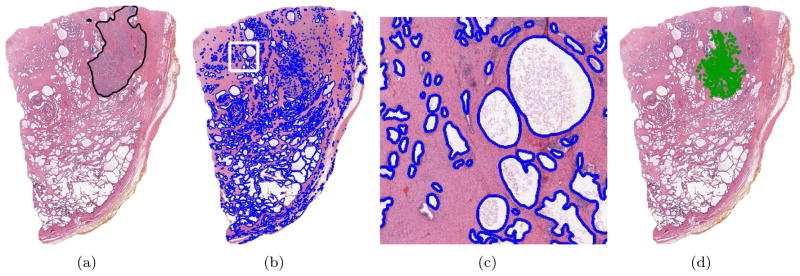
Figure 3(a) illustrates an H&E stained prostate histological (tissue) section. The superimposed black line delimits the spatial extent of CaP as determined by a pathologist. The numerous white regions are the gland lumens, i.e. cavities in the prostate through which fluid flows. Our system identifies CaP by leveraging two biological properties: 1) cancerous glands tend to be smaller in cancerous than benign regions and 2) malignant/benign glands tend to be proximate to other malignant/benign glands (Kumar et al., 2004). The basic algorithm proceeds as follows: Step 1) The glands (or, more precisely, the gland lumens) are identified and segmented. (Figure 3(b)–(c)). Step 2) Morphological features are extracted from the segmented boundaries. Currently, we consider only one feature: glandular area. Step 3) Using this feature and an MRF prior which encourages neighboring glands to share the same label, a Bayesian estimator classifies each gland as either malignant or benign (Figure 3(d)).

Figure 3.

(a) H&E stained prostate histology section; black ink mark indicates CaP extent as delineated by a pathologist. (b) Gland segmentation boundaries. (c) Magnified view of white box in (b). (d) Green dots indicate the centroids of those glands labeled as malignant.

We now formally express this CaP detection problem using the MRF nomenclature established in Section 2.1. Let the set S ={1, 2, …, N} reference the N segmented glands in a HS. Each site has an associated state X_s ∈ Λ ≡ {ω₁, ω₂}, where ω₁ and ω₂ indicate malignancy and benignity, respectively. The random variable Y_s ∈ ℝ indicates the area of gland s. All feature Y_s are assumed conditionally independent and identically distributed (i.i.d.) given their corresponding states. The conditional distributions P (y_s|x_s) are modeled parametrically using a mixture of Gamma distributions (Monaco et al., 2010); this distribution is fit from training samples using maximum likelihood estimation. The tendency for neighboring glands to share the same label is incorporated with a Markov prior P(x) modeled using probabilistic pairwise Markov models (PPMMs) (Monaco et al., 2010) (see Appendix C); the PPMM is trained using maximum pseudo-likelihood estimation (MPLE) (Besag, 1986). Two glands are considered neighbors if the distance between their centroids is less than 0.9 mm.

We construct two ROC curves by performing classification using MWMAP^ICM and MWMPM^MC. Since both require that T be specified before running the relaxation procedure, we evaluate these configurations at 21 predetermined thresholds: T ∈{0, 0.05, 0.1, … 0.95, 1}. The TP, FP, TN, and FN are generated over 40 HSs from 20 patients using leave-one-out cross-validation. Ground-truth for each HS was delineated by an expert pathologist using either the physical specimen or its digitized image. All glands whose centroids fall within the truth are considered malignant; otherwise they are benign. The parameters used by MWMPM^MC are as follows: m=30 and l=10.

5.3. Experiment 2: CaP Detection in MRI

Magnetic Resonance Imaging (MRI) has recently emerged as a promising modality for the non-invasive identification of CaP in vivo (Chelsky et al., 1993; Bloch et al., 2008). Because of it relatively high contrast and resolution it offers a possible means for guiding biopsies (Yu and Hricak, 2000), enhancing treatment (Yu and Hricak, 2000) (e.g. brachytherapy seed placement, high-focused ablation therapy), and improving screening for early detection. Motivated by these promising applications, we have developed automated systems for identifying CaP regions in MR images (Madabhushi et al., 2005; Tiwari et al., 2011; Viswanath et al., 2012; Monaco et al., 2009b).

For this experiment, we employ our system (Chappelow et al., 2008) for detecting CaP regions on T2-weighted 4 Tesla ex vivo prostate MR images. This detection occurs on a pixel-wise basis for each MR image. Figure 4(a) illustrates a typical MR image; the green overlay indicates the cancerous extent, determined by mapping pathologist-delineated CaP regions from a histological specimen onto a corresponding MRI section following the elastic registration (Chappelow et al., 2011) of the two modalities. The detection algorithm proceeds as follows: Step1) From each MRI section, we extract 21 gradient and statistical features at each pixel (Chappelow et al., 2008) (see Figures 4(b)–(c)). Step2) Using these features in combination with a Markov prior, which models the tendency for neighboring pixels to share the same class, each pixel is labeled as benign or malignant (Figure 4(d)).

Figure 4.

(a) T2-weighted 4 Tesla ex vivo MRI of an excised prostate gland with cancerous region (overlayed in green) determined by mapping pathologist-delineated CaP regions from an associated histological specimen onto the MR image after registering the two modalities. (b), (c) Images illustrating two of the 21 gradient and statistical features. (d) Result of automated CaP detection (malignant pixels in red).

This detection problem is recapitulated using the MRF terminology: Let the set S = {1, 2, …, N} reference the N pixels in the MR image that reside within the prostate. Each site has as associated state X_s ∈ Λ ≡ {ω₁, ω₂}, where ω₁ and ω₂ indicate malignancy and benignity, respectively. The random vector Y_s ∈ ℝ^D represents the D = 21 features associated with pixel s. All feature vectors Y_s are assumed conditionally independent and identically distributed (i.i.d.) given their corresponding states. Each multi-dimensional distribution P (y_s|x_s) (one for each class) is modeled as the product of 21 one-dimensional histograms (i.e. the individual features are assumed independent). The tendency for neighboring pixels to share the same class is incorporated using a PPMM trained using MPLE. The neighborhood η_s of a pixel s is the typical 8-connected region.

We construct two ROC curves by performing classification using MWMAP^ICM and MWMPM^MC. Both MWMAP^ICM and MWMPM^MC are evaluated at 21 thresholds: T ∈ {0, 0.05, 0.1, … 0.95, 1}. The TP, FP, TN, and FN are generated over 15 (256×256) MRI slices from a single patient using leave-one-out cross-validation. As previously mentioned, ground-truth for each slice was determined by mapping pathologist-delineated CaP regions from a histological specimen onto a corresponding MRI section following registration (Chappelow et al., 2011). All pixels lying within the pathologist-delineated CaP regions are considered malignant; otherwise they are benign. The parameters used by MWMPM^MC are as follows: m = 50 and l = 30.

5.4. Experiment 3: Segmentation of Brain MR Phantom

Experiments 1 and 2 both concern binary-class problems. We now present a task involving three-classes: segmenting brain MR images into regions of CSF, GM, and WM. Specifically, we consider a single two-dimensional brain MR phantom from the BrainWeb Simulated Brain Database (Collins et al., 1998). This image, as obtained from the database, has 9 percent additive noise and 40 percent intensity non-uniformity. To increase the difficultly of the segmentation task, we inserted an additional 10 percent additive Gaussian noise, creating the image shown in Figure 5(a). Figure 5(b), also obtained from BrainWeb, depicts the ground-truth, which partitions the image into its three constituent regions: CSF (black), GM (gray), and WM (white).

Figure 5.

(a) Two-dimensional simulated brain MR image (Collins et al., 1998) with 19 percent additive noise and 40 percent intensity non-uniformity. (b) Ground-truth image with ideal segmentation of CSF (black), GM (gray), and WM (white). (c) Automated segmentation results indicating CSF (red), GM (green), and WM (blue).

We now describe the Specific classification procedure. Let the set S = {1, 2, …, N} reference the N pixels in the MR image that reside within the brain. Each site has as associated state X_s ∈ Λ ≡ {ω₁, ω₂, ω₃}, where ω₁, ω₂, and ω₃ indicate CSF, GM, and WM, respectively. The random vector Y_s ∈ ℝ represents the MR intensity associated with pixel s. All random variables Y_s are assumed conditionally independent and identically distributed (i.i.d.) given their corresponding states. Each distribution P (y_s|x_s) (one for each class) is modeled as a Gaussian density; the mean and standard deviation were determined using MLE. The tendency for neighboring pixels to share the same class is incorporated using a Potts MRF prior with β =1. The neighborhood η_s of a pixel s is the typical 8-connected region. Note, an example of the automated classification results are shown in Figure 5(c).

We construct two ROC surfaces (He et al., 2006) by performing classification using MWMAP^ICM and MWMPM^MC on the single (181×217) brain MR phantom. Both MWMAP^ICM and MWMPM^MC are evaluated for all combinations of weights $\alpha ({\omega }_i)\in \{0,\frac{1}{100},\frac{2}{100},\dots \frac{99}{100},1\}$ that satisfy (16). (This yields 4831 unique combinations.) For each combination, we determine the the triplet (TPR_ω1, TPR_ω2, TPR_ω3). The parameters used by MWMPM^MC are m=20 and l = 10.

6. Results and Discussion

6.1. Experiment 1

Figure 6 illustrates the experimental results of the CaP gland detection system for the HSs. Figures 6(a) and 6(e) indicate the ROC curves when employing MWMAP^ICM and MWMPM^MC, respectively. The black dots indicate the performance at the 21 different T values. The connecting lines segments result from linearly interpolating between the points. Figures 6(b)–(d) and 6(f)–(h) provide qualitative examples of the final classification results for the estimation techniques at three different values of T. The green dots indicate the centroids of those glands labeled as malignant. The system performances at these T values are indicated with black circles in the corresponding ROC curves.

Figure 6.

(a), (e) ROC curves of CaP detection system on HSs using MWMAP^ICM and MWMPM^MC. The black dots in (a) and (e) indicate the performance at T ∈ {0,0.05, 0.1, … 0.95, 1}. (b)–(d) Centroids of the glands labeled as malignant (green dots) using MWMAP^ICM for T ∈{0.75, 0.6, 0.45}. System performances at these T values are indicated by the hollow black circles in (a). (f)–(h) Centroids of the glands labeled as malignant using MWMPM^MC for T ∈ {0.75, 0.6, 0.45}. Corresponding system performances at these T values are indicated by the hollow black circles in (e).

6.2. Experiment 2

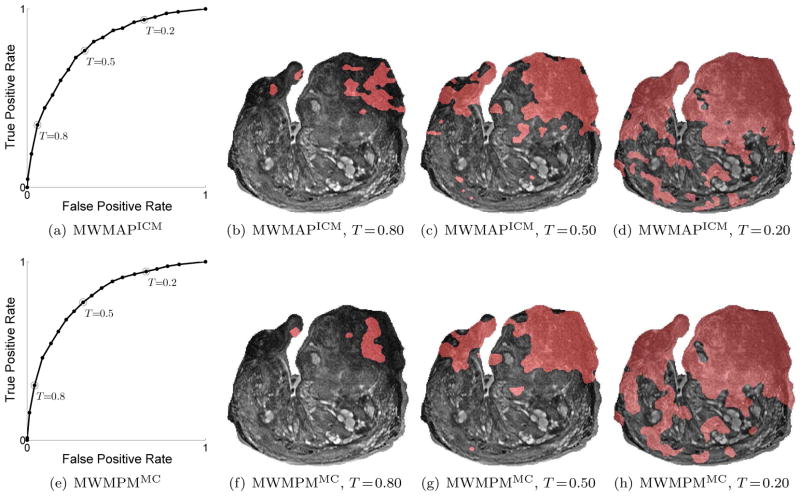
Figure 7 presents analogous results for the CaP detection system for MR images. Figures 7(a) and 7(e) indicate the ROC curves using MWMAP^ICM and MWMPM^MC. The figures in Figures 7(b)–(d) and 7(f)–(h) depict the qualitative classification results for these estimation schemes at different values of T. The pixels classified as malignant are overlaid in red. The system performances at these T values are indicated with black circles in the corresponding ROC curves.

Figure 7.

(a), (e) ROC curves of MRI CaP detection system using MWMAP^ICM and MWMPM^MC. The black dots in (a) and (e) indicate the performance for T ∈ {0, 0.05, 0.1, … 0.95, 1}. (b)–(d) Pixels labeled as malignant (overlayed in red) using MWMAP^ICM for T ∈{0.8, 0.5, 0.2}. The system performances at these T values are indicated by the hollow black circles in (a). (f)–(h) Pixels labeled as malignant using MWMPM^MC for T ∈{0.8, 0.5, 0.2}. The system performances for these values of T are indicated by the hollow black circles in (e).

6.3. Experiment 3

Figure 8 illustrates the results of brain segmentation. Figures 8(a) and 8(e) indicate the ROC surfaces when employing MWMAP^ICM and MWMPM^MC, respectively. Figures 8(b)–(d) and 8(f)–(h) provide qualitative examples of the final classification results for our two estimation techniques at three different combinations of weights.

Figure 8.

(a), (e) ROC surfaces depicting brain MRI segmentation performance using MWMAP^ICM and MWMPM^MC. The black dots in (a) and (e) indicate the performance for all α(ω₁), α(ω₂), $\alpha ({\omega }_3)\in \{0,\frac{1}{100},\frac{2}{100},\dots \frac{99}{100},1\}$ that satisfy (16). (b)–(d) Segmentations of MR image in Figure 5(a) using MWMAP^ICM for different combinations of weights [α(ω₁), α(ω₂), α(ω₃)]. Red, green, and blue colors indicate CSF, GM, and WM, respectively. The black dots in (f)–(h) indicate the performance for all α(ω₁), α(ω₂), $\alpha ({\omega }_3)\in \{0,\frac{1}{100},\frac{2}{100},\dots \frac{99}{100},1\}$ that satisfy (16). (b)–(d) Segmentations of MR image in Figure 5(a) using MWMPM^MC for different combinations of weights [α(ω₁), α(ω₂), α(ω₃)].

6.4. Discussion

Notice that the ROC curves/surfaces produced by MWMAP^ICM and MWMPM^MC are similar. This is not unexpected since both implementations have related underlying cost functions. Specifically, they identify the MAP and MPM estimates of the same random variable X̃ (see Section 3.1). It is important to point out that for the purposes of this paper the actual performances (e.g. the areas/volumes under the ROC curves/surfaces) of the classifiers are immaterial; the goal of this work is to demonstrate how the performance of any MRF-based classification system — that uses either MAP or MPM estimation — can be varied via the appropriate incorporation of multiplicative weights.

It is worth mentioning that our use of random initial conditions (x⁰) to begin each estimation technique is not optimal with respect to classification performance. We employed these conditions for two reasons: 1) to avoid any implication of a connection between the weights and the initial conditions and 2) to emphasize the importance of the estimation criteria (e.g. MWMAP) over any Specific implementation (e.g. MWMAP^ICM). Had we instead used the MLE of P(y|x), the resulting performance of both estimation schemes would have improved. With MWMAP^ICM, which converges to a local maximum of P(x|y), this is expected. However, even the Monte Carlo methods, whose convergence to P(x|y) is theoretically independent of the initial conditions, would benefit.

As is typical in ROC analysis, the curves/surfaces in Figures 6, 7, and 8 consist of a finite number of operating points. This discrete sampling is not a product of our novel weighting scheme, but results even when analyzing independent random variables for which likelihood ratios can be determined (He et al., 2006). However, producing ROC curves using our multiplicative weights — unlike the more familiar technique which employs likelihoods — requires rerunning the relaxation process (e.g. WICM) with every change in weights α. Thus, calculating each operating point can be a time-consuming process. (Note that using likelihoods to compute ROC curves is not straightforward with MRFs, and for MAP estimation it appears intractable.)

The need to perform multiple relaxations is a potential disadvantage of our proposed weighting scheme. However, this disadvantage only becomes problematic when the total time required to compute the necessary number of operating points is high. This computation time depends upon the total number of operating points — which is mostly a function of the number of classes — and the relaxation time — which is a function of the Specific classification system. Thus, it is difficult to predict the time needed to sufficiently sample ROC curves in absence of a definitive application. However, it is instructive to consider ROC construction for our three tasks.

Table 3 lists the total times needed to generate the ROC curves/surfaces depicted in Figures 6, 7, and 8. All times assume the use of single core of an Intel 2.5 GHz CPU. From these results, it becomes clear that both MWMAP^ICM and MWMPM^MC — at least for the three tasks presented in this paper — are computationally quite reasonable. However, extrapolating these results to predict time requirements for future applications should be done with care; as mentioned previously, total times will depend upon a host of factors such as the number of sites, number of images, algorithm implementations, convergence times for WICM, and the number of iterations specified for the Weighted Gibbs sampler.

Table 3.

Time required to populate ROC curves/surfaces.

	Implementation
Experiment (#)	MWMAPICM	MWMPMMC
Prostate HS (1)	0.33 hours	1.0 hours
Prostate MR (2)	0.66 hours	1.3 hours
Brain MR (3)	5.4 hours	14.8 hours

7. Concluding Remarks

Since MRFs typically contain large numbers of dependent random variables, estimating the state of the entire MRF is challenging, and requires sophisticated strategies. Currently these strategies weight each classification outcome equally, and consequently, provide no means for varying classifier performance. This is especially significant in medical image analysis, where certain errors (e.g. overlooking evidence of disease) are far more costly than others (e.g. further investigating an incorrect diagnosis of disease). Addressing this deficiency, we introduced MWMAP and MWMPM estimation, novel extensions of MAP and MPM estimation that allow certain classes to be favored more heavily than others. This creates a natural bias for Specific classes, and consequently a means for adjusting classifier performance. Additionally, we described how existing means for performing MAP and MPM estimation could be extended to obtain MWMAP and MWMPM estimates. To illustrate the value of our novel estimation criteria we incorporated them into two medically relevant MRF-based classification systems for detecting carcinoma of the prostate on 1) digitized HSs from radical prostatectomies and 2) T2-weighted 4 Tesla ex vivo prostate MRI. Furthermore, to underscore the extensibility of MWMAP and MWMPM to estimation tasks involving more than two classes, we also incorporated these estimation criteria into a MRF-based classifier used to segment synthetic brain MR images. In the context of these three tasks, we demonstrated how MWMAP and MWMPM estimation schemes could arbitrarily vary the cancer detection sensitivity of these systems, yielding receiver operator characteristic curves and surfaces.

Before concluding, it is worthwhile to briefly consider another technique that could be used to vary the performance of MRF-based classifiers: fuzzy MRFs (Ruan et al., 2002; Salzenstein and Collet, 2006). In theory, thresholds could be applied to each site’s fuzzy membership values, yielding different classifications. However, fuzzy membership was intended to indicate the degree to which a single site belongs to each of the possible classes (e.g. to account for partial volume effects), and not to reflect the probability of belonging to a Specific class. Thus, constructing ROC curves in this manner appears heuristic.

Highlights.

• We introduce estimation criteria for adjusting the performance of MRF-based classifiers.

• We implement these criteria adapting existing MRF algorithms (e.g. iterated conditional modes).

• We integrate the implementations into three classification systems for medical image analysis.

Appendix

A. Alternative Generalization of Maximum Posterior Marginals

In Section 3.2 we generalized the MPM cost function in (4) by incorporating multiplicative weights, yielding Equation (10). However, alternative generalizations are possible. In (Monaco and Madabhushi, 2011) we incorporated additive weights to produce the following cost function:

$$C_{\text{WMPM}}(\mathbf{x},\widehat{\mathbf{x}})=\sum _{s\in S}\alpha (x_s)[1-\delta (x_s-{\widehat{x}}_s)],$$ (17)

which leads to a Bayesian risk given by

$$\begin{array}{l}{R}_{\text{WMPM}}(\mathbf{X}\mid \widehat{\mathbf{x}},\mathbf{y})=\sum _{\mathbf{x}\in \mathrm{\Omega }}\left(\sum _{s\in S}\alpha (x_s)[1-\delta (x_s-{\widehat{x}}_s)]\right)P(\mathbf{x}\mid \mathbf{y})\\ =\sum _{s\in S}\sum _{\mathbf{x}\in \mathrm{\Omega }}\alpha (x_s)P(\mathbf{x}\mid \mathbf{y})-\sum _{s\in S}\alpha ({\widehat{x}}_s)P({\widehat{x}}_s\mid \mathbf{y}).\end{array}$$ (18)

Minimizing this risk function entails maximizing each of the weighted posterior marginals α(x̂_s)P (x̂_s|y), and thus — like MPM (and MWMPM) — requires estimates of these marginals. Unfortunately, the MCMC method (Marroquin et al., 1987) commonly used to estimate the posterior marginals — though sufficient for MPM (and MWMPM) estimation — is inadequate for this weighted extension of MPM. Consequently, in (Monaco and Madabhushi, 2011) we introduced a more appropriate estimation strategy.

B. Gibbs Formulation

The connection between the Markov property and the joint probability density function P of X is revealed by the Hammersley-Clifford (Gibbs-Markov equivalence) theorem (Besag, 1974). This theorem states that a random field (G, Ω, P) with P(x) >0 for all x ∈ Ω satisfies the Markov property if, and only if, it can be expressed as a Gibbs distribution:

$$P(\mathbf{x})=\frac{1}{Z}exp\left\{\sum _{c\in \mathcal{C}}{V}_c(\mathbf{x})\right\},$$ (19)

where Z = Σ_x∈Ω exp{Σ_c∈ V_c(x)} is the normalizing constant and V_c are functions, called clique potentials, that depend only on those x_s such that s ∈ c. A clique c is any subset of S which constitutes a fully connected subgraph of G; the set contains all possible cliques. Note that typically |Ω| = |Λ|^N is too large to directly evaluate Z. The following reveals the forms of the local conditional probability density functions:

$$P(x_s\mid {\mathbf{x}}_{{\eta }_s})=\frac{1}{Z_s}exp\left\{\sum _{c\in {\mathcal{C}}_s}{V}_c(\mathbf{x})\right\},$$ (20)

where 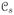represents {c ∈ 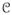: s ∈ c} and Z_s = Σ_xs∈Λexp{Σ_c∈ V_c(x)}. For proofs of Markov formulations and theorems, see Geman (Geman, 1991).

It is now useful to consider the Gibbs formulation of the weighted probability function in (7):

$$\begin{array}{l}P(\stackrel{\sim }{\mathbf{X}}=\mathbf{x})=\frac{1}{Z_{\alpha }}\mathit{\alpha }(\mathbf{x})exp\left\{\sum _{c\in \mathcal{C}}{V}_c(\mathbf{x})\right\}\\ =\frac{1}{Z_{\alpha }}exp\left\{\sum _{s\in S}ln\alpha (x_s)+\sum _{c\in \mathcal{C}}{V}_c(\mathbf{x})\right\}\\ =\frac{1}{Z_{\alpha }}exp\left\{\sum _{c\in \mathcal{C}}{\stackrel{\sim }{V}}_c(\mathbf{x})\right\},\end{array}$$ (21)

where Z_α = Σ_x∈Ω α(x) exp{Σ_c∈ 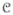V_c (x)}is the normalizing constant and Ṽ_c(x) is defined as follows: if c={s}, s∈S then Ṽ_c(x) = V_c(x)+ln α(x_s), otherwise Ṽ_c(x) = V_c(x). Thus, the weighting method proposed in this paper manifests as an increase of ln α(x_s) in each single element clique potential. The forms of the local conditional probability density functions are as follows:

$$\begin{array}{l}P\left({\stackrel{\sim }{X}}_s=x_s\mid {\stackrel{\sim }{\mathbf{X}}}_{\eta s}={\mathbf{x}}_{{\eta }_s}\right)=\frac{1}{Z_{\alpha s}}exp\left\{\sum _{c\in {\mathcal{C}}_s}{\stackrel{\sim }{V}}_c(\mathbf{x})\right\}\\ =\frac{1}{Z_{\alpha s}}exp\left\{ln\alpha (x_s)+\sum _{c\in {\mathcal{C}}_s}{V}_c(\mathbf{x})\right\}\\ =\frac{1}{Z_{\alpha s}}\alpha (x_s)exp\left\{\sum _{c\in {\mathcal{C}}_s}{V}_c(\mathbf{x})\right\}\\ =\frac{Z_s}{Z_{\alpha s}}\alpha (x_s)P(x_s\mid {\mathbf{x}}_{{\eta }_s}),\end{array}$$ (22)

where Z_αs = Σ_xs∈Λ α(x_s) exp{Σ _c∈ V_c(x)}.

C. Probabilistic Pairwise Markov Models

Before discussing probabilistic pairwise Markov models (PPMMs), we must first introduce additional notation. As discussed previously, P(·) indicates the probability of event {·}. For instance, P(X_s = x_s) and P(X=x) signify the probabilities of the events {X_s = x_s} and {X= x}. Note that we simplified such notations in the paper — when it did not cause ambiguity — by omitting the random variable, e.g. P(x)≡P(X=x). We now introduce p(·), which indicates a generic (discrete) probability function; for example, p_u might be a uniform distribution. The notations P (·) and p(·) are useful in differentiating P(x_s) which indicates the probability that {X_s = x_s} from p_u(x_s) which refers to the probability that a uniform random variable assumes the value x_s.

Continuing, in place of potential functions (i.e. a Gibbs formulation), PPMMs (Monaco et al., 2010) formulate the local conditional probability density functions (LCPDFs) P(x_s|x_ηs) of an MRF in terms of pairwise density functions, each of which models the interaction between two neighboring sites. This formulation facilitates the creation of relatively sophisticated LCPDFs (and hence priors), increasing our ability to model complex processes. Within the context of our CaP detection system, we previously demonstrated the superiority of PPMMs over the prevalent Potts model (Monaco et al., 2010). The PPMM formulation of the LCPDFs is as follows:

$$P(x_s\mid {\mathbf{x}}_{{\eta }_s})=\frac{1}{Z_s}{p}_0(x_s)\prod _{r\in {\eta }_s}{p}_{1\mid 0}(x_r\mid x_s),$$ (23)

where the normalizing constant Z_s ensures summation to one, p₀ is the probability density function (PDF) describing the stationary site s, and p_1|0 represents the conditional PDF describing the pairwise relationship between site s and its neighboring site r. The numbers 0 and 1 replace the letters s and r to indicate that the probabilities are identical across all sites, i.e. the MRF is stationary. Furthermore, p₀ and p_1|0 are related in the sense that they are a marginal and conditional distribution of the joint distribution p₀,₁, i.e. p_0.1(x_s, x_r) = p₀(x_s)p_1|0(x_r, x_s). We are free to choose any forms for p₀ and p_1|0, under the caveat that p_0,1 be symmetric to ensure stationarity. Please see (Monaco et al., 2010) for further details.