A prior feature SVM – MRF based method for mouse brain segmentation

Abstract

We introduce an automated method, called prior feature Support Vector Machine- Markov Random Field (pSVMRF), to segment three-dimensional mouse brain Magnetic Resonance Microscopy (MRM) images. Our earlier work, extended MRF (eMRF) integrated Support Vector Machine (SVM) and Markov Random Field (MRF) approaches, leading to improved segmentation accuracy; however, the computation of eMRF is very expensive, which may limit its performance on segmentation and robustness. In this study pSVMRF reduces training and testing time for SVM, while boosting segmentation performance. Unlike the eMRF approach, where MR intensity information and location priors are linearly combined, pSVMRF combines this information in a nonlinear fashion, and enhances the discriminative ability of the algorithm. We validate the proposed method using MR imaging of unstained and actively stained mouse brain specimens, and compare segmentation accuracy with two existing methods: eMRF and MRF. C57BL/6 mice are used for training and testing, using cross validation. For formalin fixed C57BL/6 specimens, pSVMRF outperforms both eMRF and MRF. The segmentation accuracy for C57BL/6 brains, stained or not, was similar for larger structures like hippocampus and caudate putamen, (~87%), but increased substantially for smaller regions like susbtantia nigra (from 78.36% to 91.55%), and anterior commissure (from ~50% to ~80%). To test segmentation robustness against increased anatomical variability we add two strains, BXD29 and a transgenic mouse model of Alzheimer’s Disease. Segmentation accuracy for new strains is 80% for hippocampus, and caudate putamen, indicating that pSVMRF is a promising approach for phenotyping mouse models of human brain disorders.

1. Introduction

Precise delineation of human neuroanatomical structures helps in the early diagnosis of a variety of neurodegenerative and psychiatric disorders (Fischl et al., 2002). The importance of human brain segmentation has given great momentum to the development of segmentation methods, and considerable progress has been made. In the meantime, the study of mouse models has also drawn substantial attention of the biomedical community due to the close evolutionary relationship between humans and mice, which enables scientists to use mouse mutants as models of human neurological disease, and to understand structural and functional changes of human brains (Kovacevic et al., 2005; Bock et al., 2006). For example, transgenic mouse models which mimic neurodegenerative diseases were investigated to study the functions of particular genes or other defects, and to test novel therapeutic interventions (McDaniel et al., 2001). However, developing automated segmentation methods for mouse brain MR images is a difficult task. First, the MR signal is proportional to the voxel volume (Edelstein et al, 1986), around 1 mm³ for the human brain, but more than 100,000 times smaller in higher resolution (21.5 µm) mouse brain images necessary to resolve detailed anatomical features. Improvements in imaging technology, complemented with the use of T1 shortening contrast agents (Johnson et al 2002, Badea et al 2007, Dorr et al, 2008) have allowed the segmentation of more than 30 mouse brain structures based on MR images (Ma et al, 2005; Kovacevic et al, 2005; Badea et al 2007; Dorr et al, 2008). These large image arrays (eg 1024×512×512 voxels, Badea et al 2007) pose increasing computational demands. Second, most studies using mouse models require large numbers of animals to achieve statistical power for detecting subtle variations in neuroanatomy. This requirement translates into a pressing need for the development of high-throughput segmentation methods for 3D brain images. The segmentation results should be robust, consistent and with acceptable computational time. To handle these challenges, we need to develop an automated mouse brain image segmentation method that is accurate, reliable and fast.

Previous research on developing automated segmentation method for human and mouse brain images includes the atlas based segmentation, the probabilistic information based segmentation, and the machine learning based segmentation. The atlas based segmentation method can involve nonlinear registration of a manually labeled atlas image to a new image set. The label of each voxel in the atlas image is elastically matched to the image being segmented. The segmentation performance can be improved by using an average atlas obtained from multiple subjects instead of a single subject (Rohlfing et al., 2004). Most existing methods for mouse brain segmentation have used the atlas based segmentation. Ma et al. (2005) used six-parameter rigid-body transformation and nonlinear registration to segment T2*-weighted MRM images of C57BL/6 mouse brains into 20 structures using an atlas image of a single mouse brain. Kovacevic et al. (2005) used an average atlas for atlas based segmentation of the MR images of 129S1/SvImJ mouse brain. The probabilistic atlas based segmentation incorporates different kinds of probabilistic information based on multi-spectral MR signals (Fischl et al., 2002). The probabilistic information on MR intensity is modeled as a Gaussian distribution. The prior probability of a label at one voxel location in the 3D image provides the location prior, and the pair wise probability of a labeling, given the labels of neighboring voxels is defined by the MRF theory. Ali et al. (2005) adapted Fischl’s method to segment T2, Proton Density (PD) and diffusion-weighted MRM images of the C57BL/6 mouse brain into 21 neuroanatomical structures.

Machine learning based segmentation was used in human brain segmentation, and uses various classifiers to assign each voxel to a number of classes. For example, Artificial Neural network (ANN) was used to segment MR images into three tissues types: white matter, gray matter and cerebrospinal fluid based on T1, T2 and PD-weighted MR signal intensity (Reddick et al., 1997). Powell et al. (2008) used probability map values, spherical coordinates, T1 and T2-weighted MR signal intensity as input features for ANN and SVM to segment MR images of human brains into eight structures. They showed that machine learning based segmentation outperforms the atlas or probability based segmentation methods. In our previous work (Bae et al., 2010), we segmented MRM images of the C57BL/6 mouse brain into 21 neuroanatomical structures using an enhanced SVM model, called Mix-Ratio sampling-based SVM (MRS-SVM), which relieved the data imbalance problem in multiclass classification. Only the location and MR intensity are used as features for the SVM model. The results showed much improved performance compared to the atlas-based method and comparable classification performance to the probabilistic information based method for larger structures (Bae et al., 2010).

Each segmentation method has its drawbacks. In the case of the atlas based segmentation, registration errors can severely hurt the overall segmentation performance (Sharief et al., 2008) since a poor registration can cause structure mismatches and boundary blurring. The probability information based segmentation uses MR intensity information and contextual information based on neighbors’ labels, as well as location information, which depend on the registration quality. The additional information -- MR intensity information and contextual information, could make up for the loss of segmentation performance resulting from imperfect registration. Therefore, the probability information based segmentation is less affected by the registration quality than the atlas based segmentation. This is why MRF, a class of probability theory modeling contextual dependencies has been widely applied for image segmentation (Li, 2009). However, the probability information based segmentation methods use a weak classifier, multivariate Gaussian distribution, to model the MR intensity information (Fischl et al., 2002; Ali et al., 2005). The contribution of MR intensity information to the segmentation is undermined due to the poor discriminative power of the classifier. We proposed a hybrid of probability information - machine learning based segmentation, termed eMRF (Bae et al., 2009) where SVM is employed to replace the weak classifier in the probability information based method. In the eMRF method, the overall segmentation performance was improved by employing SVM to model the MR intensity information instead of Gaussian distribution. Using manual labeling as golden standard, the eMRF method overall provides 10.05% higher percentage voxel overlap (VOP) and 23.84% less label volume difference (VDP) compared with the atlas based segmentation, and 2.79% higher percentage voxel overlap and 12.71% less label volume difference compared with the probability information based segmentation. Note for labeling overlap, higher is better, for label volume difference, less is better. While the machine learning based segmentation improves the segmentation accuracy, it requires enormous computation time. The long training and testing time and the difficulty in model parameter selection limit the practical application of the method to large data-sets and large samples. Powell et al. (2008) reported that it took a day to train a neural net for the classification of one structure from others even though they used a random sampled data (500,000 voxels per structure) instead of using the whole data set. It is known that the training time for SVM is approximated as O(N⁴) where N is the total number of training data points. For mouse MRM images (128×128×256), N is over 16 millions. Hence, in the eMRF study, it took ~ 7 days for training and the 4.82 hours for testing using a 3.4-GHz PC. The classification performance of classifiers largely depends on the selection of model parameters (e.g. kernel functions and related parameters for SVM). To find the best model parameters for a data set, additional large number of runs with different parameter settings should be conducted. However, the long training and testing time for the brain image segmentation make it prohibitive to run large number of experiments, which implies that the best performance of the machine learning based segmentation would be difficult to obtain due to computing concerns. The robustness of the algorithm for mutant mice which has large anatomical variability is also difficult to be assessed.

In this study, we develop a new algorithm that samples fewer voxels, enabling the identification of optimal parameters for the machine learning classifier. This new algorithm is called prior feature SVM-MRF (pSVMRF) which is robust and computational efficient. pSVMRF integrates the good classification ability of SVM into the MRF image segmentation framework. Both voxel location prior and MR intensity are used as input features for the training and testing of SVM. Adding the location prior as the input features is inspired by the previous work of Powell et al. (2008). The probabilistic outputs of the prior feature SVM (pSVM) are treated as inputs to the MRF segmentation formula. The contribution of the SVM and contextual information is controlled with two model parameters. This is different from the eMRF method, where the MR intensity information and location prior are combined linearly by weights that are tuned by grid-search. Since in the new approach the training sample size is small in each experiment, we can easily run a large number of experiments to find the best SVM parameters to give the best and robust classification performance.

We assess segmentation performance and compare the new segmentation method with two other methods: MRF (Ali et al. 2005), and eMRF (Bae et al., 2009) for the segmentation of MRM brain images of adult C57BL/6 mice. To test the robustness of the algorithm when faced with increased anatomical variability, we add two different strains: BXD29, a recombinant inbred strain derived from an intercross between C57BL/6 and DBA/2J, and a double transgenic mouse model of Alzheimer Disease (AD), overexpressing mutant amyloid precursor protein (Jankowsky, Slunt et al, 2005).

2. Methods

2.1. MRF based image segmentation

The contextual dependency is a general and meaningful way to model the spatial property (Zhang et al., 2001). MRF theory is a class of probability theory for modeling the contextual dependencies of physical phenomena such as image pixels and correlated features. It has become increasingly popular in many image segmentation problems and image reconstruction problems. In the field of medical image segmentation, MRF has been used for brain tissue segmentation (Held et al., 1997; Zhang et al., 2001; Awate et al., 2006), neuroanatomical structure segmentation (Fischl et al., 2002; Ali et al., 2005), detection of microcalcification in digital mammograms (Yu et al., 2006) and detection of multiple sclerosis lesions in MR images (Khayatia et al., 2008), etc.

Let S = {1,2, …, n} be the set of sites in a image, X be a vector of site’s signal, and Y be the associated labeling vector, that is, X = {x_i, i ∈ S} and Y = {y_i, i ∈ S}. Let N be a neighborhood system defined as N = {N_i, i ∈ S} where N_i denotes the set of sites neighboring site i. Y is said to be a MRF on S with respect to a neighborhood system N if and only if

$$P(Y)>0\mathit{\text{ and }}P(y_i|y_{S-\{i\}})=P(y_i|y_{N_i})$$ (1)

where S-{i} denotes the set difference. The condition of (1) means that only neighboring labels have direct interaction with each other, and the joint probability P(Y) can be uniquely determined by its local conditional probabilities.

According to Hammersley-Clifford theorem (Li, 2009), the probability P(Y) of an MRF can be equivalently specified by a Gibbs distribution as follows:

$$P(Y)=\frac{1}{Z}\text{exp }[-{\displaystyle \sum _{c\in C}}{V}_c(Y)]$$ (2)

where Z is a normalizing constant and V_c(Y) is a clique potential function over all cliques c ∈ C. A clique c is a subset of sites in S that are all neighbors of each other, and C is a set of cliques or the neighborhood of the clique under study. The value of V_c(Y) depends on a certain configuration of labels on the clique c. For the image segmentation problem, the posterior probability of the label of a site, given specific signal, can be formulated using Bayesian theorem and the Hammersley-Clifford theorem as:

$$P(Y|X)=\frac{1}{Z}\text{exp }[{\displaystyle \sum _{i\in S}}\text{log }P(x_i|y_i)+{\displaystyle \sum _{c\in C}}{V}_c(Y)]$$ (3)

${\displaystyle \sum _{i\in S}}\text{log }P(x_i|y_i)$ in the right hand side in (3) is the sum of the log likelihood function of the given labeling for the site's signal. Usually a multivariate Gaussian distribution is used for modeling P(X|Y) (Held et al., 1997; Zhang et al., 2001; Fischl et al., 2002; Ali et al., 2005), which is based on the assumption of Gaussian relationship between features and labels. This assumption is too restrictive to model the complex dependencies between features and labels in some cases. By employing a machine learning classifier, such as SVM, the performance of the MRF based image segmentation was improved since SVM is generally better at modeling the complex dependencies due to the virtue of the non-linear transformation (Lee et al., 2005; Bae et al., 2009). The well-accepted generalization ability of SVM is explained in next section.

2.2. Segmentation enhancement by SVM

SVM has received a lot of attention from the machine learning and pattern recognition community due to the following reasons (Abe, 2005). First, SVM works well for classifying objects which are not linearly separable. The objects are mapped from their input space into a high-dimensional feature space by kernel transformations; thus SVM can separate objects which are not linearly separable. Secondly, SVM has good generalization ability. SVM attempts to maximize the separation margin between the classes, so the generalization performance does not drop significantly even when the training data are scarce. In addition, SVM can achieve a global optimal solution because it is solved with quadratic programming. Because of the generalization ability of SVM, it has accomplished great success in a variety of applications including fault detection, fraud detection, handwritten character recognition, object detection and recognition, text classification. In the field of medical image classification, SVM has been used for brain tumor recognition (Luts et al., 2007), brain states classification of functional MRI (Mourao-Miranda et al., 2005), breast cancer detection in dynamic contrast-enhanced MRI (Levman et al., 2008), knee bone segmentation in MR images (Bourgeat et al., 2007).

The basic idea of SVM is to construct an optimal hyperplane which gives maximum separation margin between two classes. Assuming a binary classification problem with a n dimensional training set x_i ∈ Rⁿ with its label set y_i ∈ {+1,−1}, where i=1, 2, …, m. The hyperplane f(x), that separates the given data, is defined as:

$$f(\mathbf{x})={\mathbf{w}}^{\mathbf{T}}\mathrm{\Phi }(\mathbf{x})+b$$ (4)

where w is the n dimensional normal vector perpendicular to the hyperplane, b is a bias term and Φ(x_i) is a non-linear transformation which maps the samples into a higher-dimensional dot-product space called the feature space. The optimal hyperplane is obtained by solving the following optimization problem:

$$\mathit{\text{Min }}\frac{1}{2}{\mathbf{w}}^{\mathbf{T}}\mathbf{w}+C{\displaystyle \sum _{i=1}^m}{\xi }_{i}s.t.y_i(\mathbf{w}·\mathrm{\Phi }({\mathbf{x}}_i)+b)\ge 1-{\xi }_i,i=1,\dots ,m.{\xi }_i\ge 0,i=1,\dots ,m.$$ (5)

where ξ = {ξ₁, …, ξ_m} is a slack variable and C is the penalty parameter which controls the balance between the model complexity and classification error. The proper value of penalty parameter (C) is determined by the training set to avoid overfitting. The non-negative slack variable (ξ_i) allows (5) to always yield feasible solutions by relieving the constraint of maximum margin.

The constrained optimization problem in (5) can be converted to an unconstrained optimization problem by introducing the non-negative Lagrangian multipliers α_i, and the unconstrained optimization problem is converted to a Lagrangian dual problem by introducing the Karush-Kuhn-Tucker (KKT) condition. The optimal solution α_i^* of the dual problem yields the following optimal hyperplane:

$$f(x)=\mathit{\text{sign}}({\displaystyle \sum _{i=1}^m}{y}_i{\alpha }_i^{*}K(\mathbf{x}\mathbf{,}{\mathbf{x}}_{\mathbf{i}})+b^{*})$$ (6)

where x_i are support vectors and K(x, x_i) is a kernel function defined as K(x, x_i) = Φ(x)^T Φ(x_i). The kernel function performs the nonlinear mapping implicitly so that we can avoid the complexity of mapping and the curse of dimensionality resulted from the nonlinear mapping. Commonly used kernel functions are linear, polynomial and RBF among which nonlinear kernel function, RBF has been recommended in many studies. For example, a comparative study on SVM using fMRI to decipher brain patterns concludes RBF outperforms linear SVM significantly (Song et al., 2011). Our study on Alzheimer disease (AD) diagnosis using MRI imaging indicates that RBF kernel outperforms both linear and polynomial kernels for differentiating AD patients with normal individuals (Zhang et al., 2008). Therefore, in this study we used the Radial Basis Function (RBF) kernel, defined as follows:

$$K(\mathbf{x},{\mathbf{x}}_i)=\text{exp}(-\gamma {\Vert {\mathbf{x}}^T-{\mathbf{x}}_i\Vert }^2),\gamma >0$$ (7)

where γ in (7) is a parameter related to the span of an RBF kernel.

2.3. Brain image segmentation by eMRF

In our previous research (Bae et al., 2009) we proposed eMRF method, in which we integrate three different types of information – MR intensity, voxel location and contextual relationship with neighboring voxels’ labels –to improve the overall segmentation performance, and the MR intensity information is modeled by an enhanced SVM, which takes different sampling ratio for different brain structures. The three pieces of information are linearly combined with the model parameters which control their relative contributions. The model parameters are determined through a training process to maximize the segmentation performance. The experimental results from using the eMRF method showed that the integration of the probability information based segmentation and the machine learning based segmentation can improve the overall segmentation performance, compared with the atlas based segmentation method and the MRF method (Ali et al., 2005). This is because it takes advantage of the classification ability of machine learning classifiers, in addition to the virtue of the location information and the contextual information of the probability information based segmentation, which are critical information for classifying each voxel in a 3D image into the multiple classes.

Even though employing machine learning classifiers for brain image segmentation improves the overall segmentation performance, computation time remains a big challenge. As stated earlier, the eMRF method requires long training and testing times due to the difficulty in selection of SVM parameters. These drawbacks are mainly associated with the large data size. The number of data points in a 3D MRM images with the matrix of 128×128×256 is more than 4 million. Multiplied by the number of training sets this number is ~ 16 million. The number of data for training and testing directly affects the training and testing time of SVM. Therefore it is desirable to use the minimum number of data necessary to produce comparable classification performance. The key to solve the problem of the large data sets is to reduce the number of the training data while maintaining the classification performance of classifiers. The pSVMRF method proposed in the next section is built based on the eMRF method, but tries to reduce the training and testing time while maintaining the segmentation performance.

2.4. The proposed segmentation method: pSVMRF

Let S = {1,2, …, n} be the set of voxels in a 3D MR image, X be a vector of voxels signal intensity, and Y be the associated labeling vector, that is, X = {x_i, i ∈ S} and Y = {y_i, i ∈ S}. A location prior vector of a voxel, l_i, has m elements, where m is the number of structures to be segmented and ${\displaystyle \sum _{k=1}^m}{l}_i^k=1$. Let K be the set of the classes to which voxels will be assigned, i.e. K = {1,2, …, m}, and L = {l_i} is the collection of location prior vectors. The k^th element of the location prior vector of the voxel i is defined as:

$$l_i^k=\frac{{\displaystyle \sum _{j=1}^q}\#\mathit{\text{ of voxels labeled ask at location r}}(i)}{q}$$ (8)

where q is the number of the images in the training set and r(i) is location function which informs us the location of the voxel i in the 3D image. Using Hammersley-Clifford theorem and the assumption of P(Y)>0 and P(X,L)>0, the posterior probability of having a label configuration Y given a MR intensity vector X and a location prior vector L is formulated as follows:

$$P(Y|X,L)\propto \text{exp}\{w_1{\displaystyle \sum _{i\in S}}\text{log }{A}_i(y_i,x_i,l_i)+w_2{\displaystyle \sum _{i\in S}}{V}_i(y_i,y_{N_i})\}s.t.w_1+w_2=1$$ (9)

where w₁ and w₂ are model parameters which control the contribution of the two terms in (9) to the posterior probability P(Y|X,L). Based on the MRF theory, the prior probability of having a label at a given site i is determined by the label configuration of the neighborhood of the site i. The Hammersley-Clifford theorem enables us to calculate the joint probability P(Y) as a sum of the clique potential functions. We use a first order neighborhood system of a 3D image as a clique, which consists of the adjacent six voxels in the four cardinal directions in a plane and the front and back directions through the plane. The clique potential function V_i(y_i,y_Ni), called contextual potential function, in (9) will have a higher value when the number of neighbors that have the same label increases. This function is, thus, defined as

$$V_i(y_i,y_{N_i})=\frac{{\displaystyle \sum _{j\in N_i}}\delta (y_i,y_j)}{n(N_i)}\mathit{\text{ where }}\delta (y_i,y_j)=\{\begin{array}{ccc}1\hfill & \mathit{\text{if}}\hfill & y_i=y_j\hfill \\ 0\hfill & \mathit{\text{if}}\hfill & y_i\ne y_j\hfill \end{array}$$ (10)

where n(N_i) is the number of voxels in a neighborhood of site i.

The location information of a voxel in a 3D image after registration is important for classification of the voxel into the neuroanatomical structures. Fischl et al. (2002) pointed out that if the image registration does well, only small numbers of neuroanatomical structures are available at a given location in a 3D brain atlas and the location information have anatomical meaning so that it can help in classification. Powell et al. (2008) included probability map values as input features for the machine learning based segmentation. The probability map was created by calculating the probability of a neuroanatomical structure being located at a voxel location in the atlas space across all subjects in a training set. For example, given four subjects, if one out of four subjects labeled voxel i as structure k, and three out of four subjects labeled voxel i as structure l, in the probability map for structure k, the value for voxel i is 25% while the probability map for structure l will have 75% for voxel i. Separate probability maps for each structure were calculated and included as one of elements in the input vectors for the binary classification of ANN and SVM in Powell et al.’s experiment. Taking a similar approach, pSVMRF employs a prior feature SVM (pSVM), which includes the features from MR intensity and location prior vectors, for simultaneously modeling the MR intensity information and location information. Similar to eMRF, OAO (One-Against-One) method is applied to train SVM for classifying the k^th class against the l^th class since it is more efficient on large datasets than OAA (One-Against-All) and AAO (All-At-Once) (Hsu and Lin, 2002). Thus, overall n*(n−1)/2 models will be trained. In each SVM training, the location prior being derived from the specific probability map with respect to the specific structure together with MR intensity for each voxel are being the input features for the model.

Since pSVM performs a multiclass classification of SVM, the number of elements in the location prior vector is identical to the number of structures to be segmented. Each element of the location prior vector represents the number of times a particular structure occurs at a given location in all the brain images of the training set. The location prior vector defined in (8) can model all the probabilities of the m structures being located at a specific location and be used as a feature for the multiclass classification. As explained earlier, SVM can enhance linear separation by mapping the original input space into a high-dimensional feature space using the nonlinear transformation. By adding the MR intensity information and the location prior vector as input features, we anticipate that pSVM can boost the separability with the power of nonlinear transformation of SVM. The first term, A_i(y_i, x_i, l_i), in (9) is called as the observation potential function that models the MR intensity information and the location information. To be incorporated into pSVMRF, the decisions made by pSVM need to be probabilistic output. Platt (2000) proposed a method for mapping the SVM outputs into posterior probability by applying a sigmoid function. The observation potential function for voxel i is defined as follows, for class k:

$$A_i(y_i,x_i,l_i)=P_i(y_i=1|x_i,l_i)=\frac{1}{1+\text{exp}(\alpha f_k(x_i,l_i)+\beta )}$$ (11)

where f_k(x_i,l_i) is the SVM decision function for class k, α and β are the parameters estimated from the training data. That is, SVM model is trained using the MR intensity (x̱_i) and location (ḻ_i) to determine the belonging of voxel i to class k (y_i= −1, 1). Let us define a new training set (t_i, x̱_i, ḻ_i), where t_i here is the target probabilities defined as:

$$t_i=\frac{y_i+1}{2}$$ (12)

The parameters α and β can be found by solving the following minimization problem (Platt 2000):

$$\text{Min}-{\displaystyle \sum _i}{t}_i\text{ log}(p_i)+(1-t_i)\text{ log}(1-p_i)$$ (13)

where p_i is defined in (11). We used Matlab to solve the optimization problem (13) and obtain the values of α and β values for each class. The next step is to find the label configuration Y^* that maximizes the posterior probability P(Y|X,L) in (11), i.e., argmax $Y^{*}=\underset{Y}{\text{argmax}}P(Y|X,L)$. This is known as the maximum a posterior (MAP) solution. Because of the highly complicated interactions among multiple labels, it is very difficult to find the optimal solution of the joint probability P(Y|X,L). We adopt a local search method called iterated conditional modes (ICM), which maximize local conditional probabilities iteratively by using the greedy search in the local optimization. It is expressed as

$$y_i^{*}=\underset{y_i\in Y}{\text{argmax}}P(y_i|x_i,l_i)$$ (12)

The ICM algorithm sequentially updates $y_i^{(t)}\text{ into }{y}_i^{(t+1)}$ by switching the different labels to find the maximum value of P(y_i|x_i, l_i). We use the MAP solution based on the location prior vector as the initial estimator y⁽⁰⁾ of the ICM algorithm. In this study, the algorithm continues until no improvement is made and the iteration which gives the best solution and terminates the algorithm is the optimal terminating point. We estimate the optimal terminating point from the training process and apply the terminating points for predicting labels of new testing data.

3. Results and Discussion

3.1. Performance Measurements

To estimate the performance of segmentation methods, we use the two performance metrics: volume overlap percentage (VOP) and volume difference percentage (VDP) (Fischl et al., 2002; Ali et al., 2005). They are calculated by comparing the automated labeling with the manual labeling (gold standard) of each voxel. Denote L_A and L_M as labeling of the structure k by automated and manual segmentation respectively, and V(L) as a function which calculates the volume of the labeling. VOP and VDP for a structure k are defined as:

$${\mathit{\text{VOP}}}_k(L_A,L_M)=\frac{V(L_A\cap L_M)}{(V(L_A)+V(L_M))/2}\times 100\mathit{\text{ and }}{\mathit{\text{VDP}}}_k(L_A,L_M)=\frac{|V(L_A)-V(L_M)|}{(V(L_A)+V(L_M))/2}\times 100$$ (13)

VOP is the larger the better, VDP is the smaller the better. VOP is more sensitive to the spatial difference of the two labels than the volumetric difference, but VDP is more sensitive to the volumetric difference. To estimate the overall segmentation performance of a particular method, we use average VOP (AVOP) and average VDP (AVDP), which are calculated by dividing the sum of VOP or VDP for all structures by the number of structures.

3.2. Implementation of the segmentation method

We assessed the performance of pSVMRF using MRM images of mouse brains acquired by the Center for In Vivo Microscopy, at Duke University Medical Center, and previously used in Ali et al., (2005); Sharief et al., (2008); Badea et al. (2010). T2-weighted MRM mouse brain images from five formalin-fixed C57BL/6 male mice (approximately 9 weeks in age) were used. Image acquisition parameters were: TE/TR = 30/400 ms, bandwidth 62.5 kHz, field of view = 12×12×24 mm and matrix size = 128×128×256, 86 µm isotropic resolution. A 9-parameter affine registration was applied to each image. 21 manual labels were used as gold standard to evaluate segmentation accuracy. Table 1 presents the 21 neuroanatomical structures and abbreviations used in this study.

Table 1.

List of the 21 neuroanatomical structures and abbreviations

Cerebral cortex (CORT)	Inferior colliculus (INFC)	Pontine nuclei (PON)
Cerebral peduncle (CPED)	Medulla oblongata (MED)	Substantia nigra (SNR)
Hippocampus (HC)	Thalamus (THAL)	Interpeduncular nucleus (INTP)
Caudate putamen (CPU)	Midbrain (MIDB)	Olfactory bulb (OLFB)
Globus pallidus (GP)	Anterior commissure (AC)	Optic tract (OPT)
Internal capsule (ICAP)	Cerebellum (CBLM)	Trigeminal tract (TRI)
Periacqueductal gray (PAG)	Ventricular system (VEN)	Corpus callosum (CC)

Two different strains were introduced to test the segmentation, a BXD29 and an AD mouse models (Jankowsky et al, 2005). These mice and an additional set of five C57BL/6 were actively stained (Johnson et al, 2002), and imaged as described in Sharief et al., (2008). Imaging consisted of two protocols: T1 weighted (3D spin warp, TE/TR 5.2/50 ms, field of view 11×11×22 mm, matrix size 512×512×1024), and MEFIC enhanced T2 weighted acquisitions (3D CMPG, TR 400 ms, echo spacing 7 ms, 7 echoes, field of view 11×11×22 mm, matrix size 256×256×512) (Sharief and Johnson, 2006) were used to provide intensity priors. T1 images were re-sampled to match the resolution (43 microns) of the T2 weighted image set. Using both image channels, 33 manual labels were produced for the C57BL/6 brains, and a set of 7 labels was traced to test the BXD and AD segmentation.

The implementation of the pSVMRF method consists of two steps. The first step is to build the pSVM models and test the models. The pSVM models were trained using the randomly sampled training set, consisting of 300 randomly selected data points from each of the structures (all neuroanatomical structures to be defined, and one added miscellaneous structure). Each of the training and testing data has the input feature vector, which consists of one feature for T2-w MR signal intensity and additional N features (N=22 for the formalin fixed, N=34 for actively stained specimens) for the location prior. As mentioned earlier, the selection of the penalty parameter (C) and RBF kernel parameter (γ) greatly affects on the classification accuracy and the generalization ability of SVM. We conducted a grid search to find the best penalty parameter and the best RBF kernel parameter using the five-fold cross validation, which can help in avoiding the overfitting problem and estimating the generalization ability. Each of the trained pSVM models was tested on each of the testing data to calculate the observation potential function in (11). The training and testing time of the pSVM models for the randomly sampled mouse brain dataset (formalin fixed) were 1.12 minutes, and 14.24 minutes respectively, using a 3.4-GHz PC and LibSVM for Matlab (Chang and Lin, 2001). Since SVM can transform the linear combination of the MR intensity and location prior vector to a nonlinear combination that can help in classification, pSVM could train a better model using a small number of data (6,600 voxels for each formalin mouse, 10,200 voxels for each actively stained mouse). In the eMRF method (Bae et al., 2009), a large size of training set (472,100 voxels per a mouse), which is over-sampled from some classes, was needed for the SVM training. That results in a very long training and testing time: 7.56 days for training and 4.82 hours for testing.

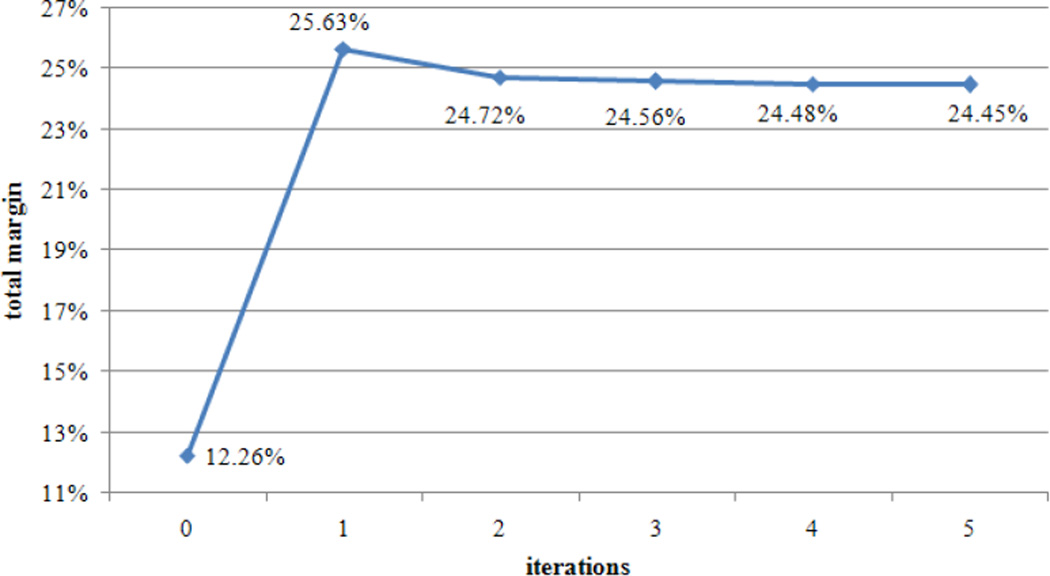
The second step was to implement the ICM algorithm to calculate the contextual potential function in (10) and the posterior probability P(Y|X,L) in (9). We did a grid search over the range $W=\{0.01\le w_i\le 0.99,{\displaystyle \sum _i}{w}_i=1\mathit{\text{ and }}i=1,2\}$ to find the best model parameters, which were chosen as w₁=0.89 and w₂=0.11 for observation and contextual functions, respectively. During the grid search for model parameters, a large number of the ICM implementations with the different parameter values were performed. Each of the ICM implementations run until there was no change in labels assignment, but the best solution was achieved at the first iteration from every ICM implementation. In this grid search, we tried to find the model that has the maximum AVOP and the minimum AVDP. Since one model has the maximum AVOP and the other model has the minimum AVDP, we could not find a best model which satisfied both criteria. Therefore, we calculated the margins of AVOP and AVDP compared with those of the MRF method (Ali et al., 2005). Total margin, which is sum of the two margins, was used as the criterion for selecting the best model. Fig. 1 provides the plot of the total margin vs. iterations of the ICM algorithm, with the best pSVMRF model of w₁=0.89 and w₂=0.11. The maximum of the total margin was achieved at the first iteration within 11.86 minutes using a 3.4-GHz PC. Therefore, we chose the first iteration as the optimal terminating point for this pSVMRF model. This optimal terminating point will then be used for testing new mouse brain images. Since the ICM algorithm is a local optimization algorithm and does not guarantee a global optimal, the optimal terminating point should be determinined based on the model and data set. Estimating and using the optimal termination point enables the ICM algorithm to converge much faster at better solution.

Fig. 1.

Convergence of the ICM algorithm with w₁=0.89 and w₂=0.11.

3.3. Validation of the segmentation method

To validate the proposed method, pSVMRF, we first test on MR images of five C57BL/6 mice using a five-fold cross validation. Each of the five mice was used as the testing set while the remaining four mice were used as the training set. The results are compared with two existing methods: the MRF method (Ali et al., 2005) and the eMRF method (Bae et al., 2009). In Table 2, the segmentation performances of the three automated mouse brain image segmentation method are estimated based on VOP and VDP. The performance estimates in Table 2 are based the average values from testing all the mice using the five-fold cross validation. The upper rows include VOP and the lower rows include VDP. A ‘+’ sign always means that pSVMRF method outperforms the other methods for the specific structure and ‘−’ means that pSVMRF underperforms. pSVMRF outperformed eMRF in 16 structures, there was no change in one structure and a slight underperformance in 4 structures. Major improvements in segmentation performance were noted for the olfactory bulbs (from 83% to 91%), pons (from 80% to 86%), and trigeminal tract (from 74% to 82%). In comparison to MRF, pSVMRF outperformed in 14 structures, most notable in the cases of optic tract (53% to 73%), trigeminal tract (from 64% to 82%), and pons (73% to 86%). Table 3 presents the comparisons of the overall segmentation performance and the computation time of the three automated segmentation methods. Overall pSVMRF outperforms the two existing methods. AVOP and AVDP of pSVMRF are improved by 2.55% and 9.57% compared with eMRF, and by 5.41% and 21.07% compared with MRF. The total testing time of pSVMRF in Matlab, which includes the testing time of pSVM testing and the ICM algorithm, was 26.10 minutes, which is improved by 92.85% compared with the testing time of eMRF (364.4 minutes). The testing time of MRF (15 minutes) is less than pSVMRF. However, pSVMRF can produce 26.48% (total margin from MRF) more accurate segmentation than MRF by spending 16 minutes more. The proposed method, pSVMRF, gives better segmentation than eMRF and MRF, within a short testing time.

Table 2.

Comparison of segmentation performance of the pSVMRF, eMRF and MRF methods based on VOP and VDP for 21 structures. A. pSVMRF vs. eMRF based on VOP; B. pSVMRF vs. eMRF based on VDP; C. pSVMRF vs. MRF based on VOP; D. pSVMRF vs. MRF based on VDP

A.
VOP	CORT.	CPED	HC	CPU	GP	ICAP	PAG	INFC	MED	THAL	MIDB
pSVMRF	94.08	74.22	87.07	87.67	79.49	73.33	90.16	88.40	93.27	94.18	93.81
eMRF	91.10	73.15	86.20	87.62	79.64	73.14	90.26	85.32	91.93	93.53	93.27
+/−	3.27	1.47	1.01	0.05	−0.19	0.26	−0.11	3.61	1.45	0.69	0.58
VOP	AC	CBLM	VEN	PON	SNR	INTP.	OLFB.	OPT	TRI	CC
pSVMRF	50.76	96.45	72.56	86.04	78.36	72.41	90.99	73.62	82.19	65.59
eMRF	50.76	92.68	71.83	80.03	78.98	71.61	82.50	68.67	73.83	65.75
+/−	0.00	4.06	1.01	7.50	−0.77	1.12	10.29	7.20	11.33	−0.23

B.
VDP	CORT.	CPED	HC	CPU	GP	ICAP	PAG	INFC	MED	THAL	MIDB
pSVMRF	3.69	2.31	5.13	3.57	9.34	11.03	4.01	4.93	7.62	2.34	3.08
eMRF	3.34	8.32	5.56	3.98	7.54	11.05	3.55	5.26	7.12	2.48	2.97
+/−	−10.52	72.27	7.72	10.19	−23.85	0.14	−12.93	6.33	−7.05	5.82	−3.72
VDP	AC	CBLM	VEN	PON	SNR	INTP.	OLFB.	OPT	TRI	CC
pSVMRF	25.16	3.34	14.26	7.28	9.05	19.71	7.30	12.52	9.87	15.67
eMRF	25.55	3.73	16.83	12.49	10.16	26.09	10.79	5.67	7.33	20.57
+/−	1.53	10.50	15.29	41.68	10.90	24.47	32.32	−120.91	−34.65	23.86

C.
VOP	CORT.	CPED	HC	CPU	GP	ICAP	PAG	INFC	MED	THAL	MIDB
pSVMRF	94.08	74.22	87.07	87.67	79.49	73.33	90.16	88.40	93.27	94.18	93.81
MRF	90.77	67.69	87.69	88.46	78.46	73.85	85.38	83.08	86.15	93.08	90.77
+/−	3.65	9.65	−0.71	−0.90	1.31	−0.70	5.59	6.41	8.26	1.19	3.35
VOP	AC	CBLM	VEN	PON	SNR	INTP.	OLFB.	OPT	TRI	CC
pSVMRF	50.76	96.45	72.56	86.04	78.36	72.41	90.99	73.62	82.19	65.59
MRF	55.38	93.08	70.77	73.08	68.46	76.92	84.62	53.08	63.85	71.54
+/−	−8.35	3.63	2.53	17.73	14.47	−5.87	7.53	38.70	28.73	−8.31

D.
VDP	CORT.	CPED	HC	CPU	GP	ICAP	PAG	INFC	MED	THAL	MIDB
pSVMRF	3.69	2.31	5.13	3.57	9.34	11.03	4.01	4.93	7.62	2.34	3.08
MRF	4.35	12.17	6.96	6.96	7.83	13.04	2.61	4.35	10.43	3.48	4.35
+/−	15.16	81.04	26.25	48.66	−19.38	15.43	−53.80	−13.39	26.95	32.73	29.14
VDP	AC	CBLM	VEN	PON	SNR	INTP.	OLFB.	OPT	TRI	CC
pSVMRF	25.16	3.34	14.26	7.28	9.05	19.71	7.30	12.52	9.87	15.67
MRF	19.13	3.48	19.13	17.39	15.65	13.91	16.52	14.78	10.43	22.61
+/−	−31.50	4.03	25.48	58.11	42.17	−41.66	55.79	15.34	5.44	−30.71

Table 3.

Comparisons of overall segmentation performances and computation time for the pSVMRF, eMRF and MRF methods.

	AVOP	AVDP	Testing Time (min)
pSVMRF	82.13	8.63	26.1
eMRF	80.09	9.54	364.4
MRF	77.91	10.93	15.0

Even though pSVMRF outperforms eMRF in 16 structures out of 21, eMRF is still better than pSVMRF in some small structures such as GP, PAG, OPT and TRI. This results from the fact that eMRF use Mix-ratio sampling based SVM (MRS-SVM; Bae et al., 2008) and an over-sampled training set for some smaller structures to improve the classification performance for these structures. In contrast pSVMRF uses the same number of training data from each of the structures regardless their size. MRF is also better than pSVMRF in some small structures such as GP, PAG, AC and INTP even though pSVMRF is better for most structures. That is because MRF relies more on the contextual information, which enhances the identification of the smaller structures, for segmentation than pSVMRF. The proposed method, pSVMRF, still needs to be improved for the smaller structures.

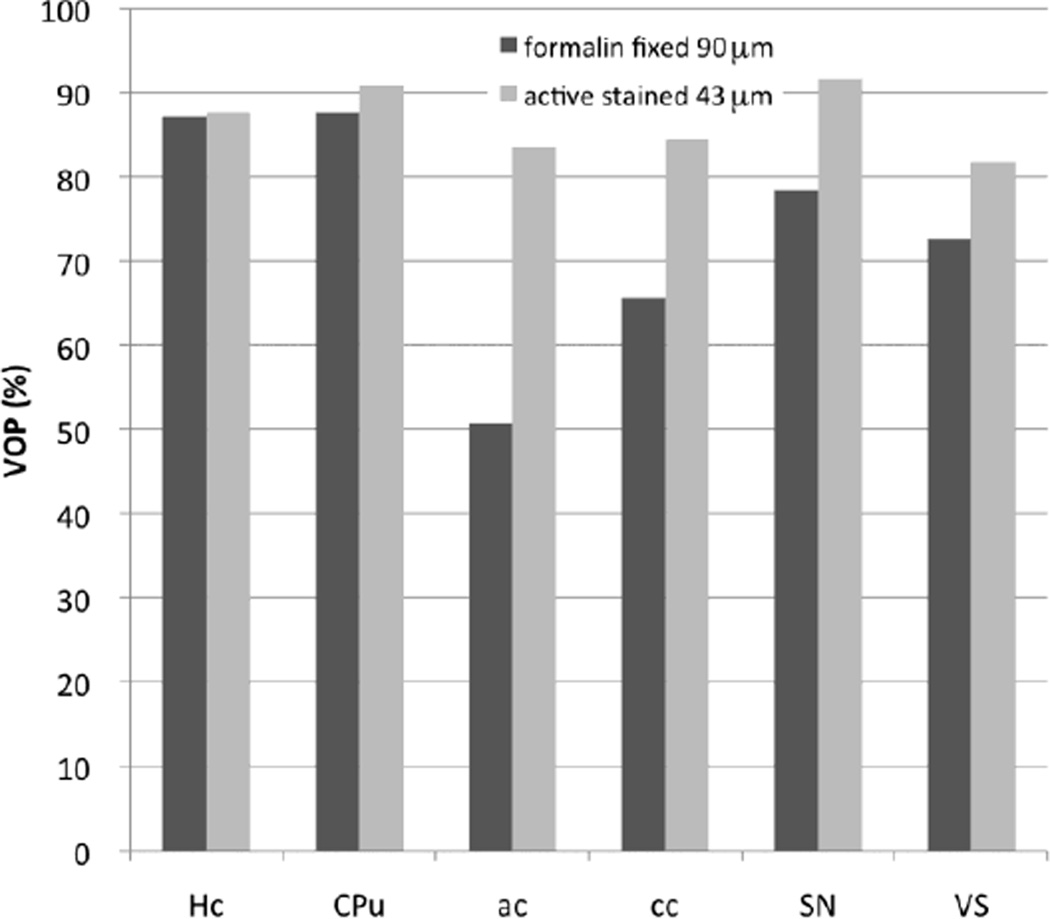
The combination of higher resolution imaging and higher contrast given by active staining boosted segmentation accuracy, relative to that obtained for the formalin fixed brains, as illustrated in Fig. 2 for adult C57BL/6 mice. The percent voxel overlap (VOP) increased substantially for smaller structures like the anterior commissure (from 50.76% to 83.5%), corpus callosum (from 65.59% to 85.44%), substantia nigra (78.36 to 91.55%) and ventricles (72.56 to 81.72%). For hippocampus and caudate putamen the VOP values were more similar. VOP changed from 87.07 o 87.67% for hippocampus, and increased from 97.67% to 90.87% for caudate putamen).

Fig. 2.

Increased segmentation accuracy was obtained for the higher resolution, actively stained sets, relative to the formalin fixed sets, particularly in smaller structures like the anterior commissure (ac: from 50.76% to 83.5%), corpus callosum (cc: 65.59% to 85.44%), substantia nigra (SN: 78.36 to 91.55%) and ventricles (VS: 72.56 to 81.72%). For hippocampus and caudate putamen the values are more similar (~87% for Hc, and increased from 87.67 to 90.87 % for CPu).

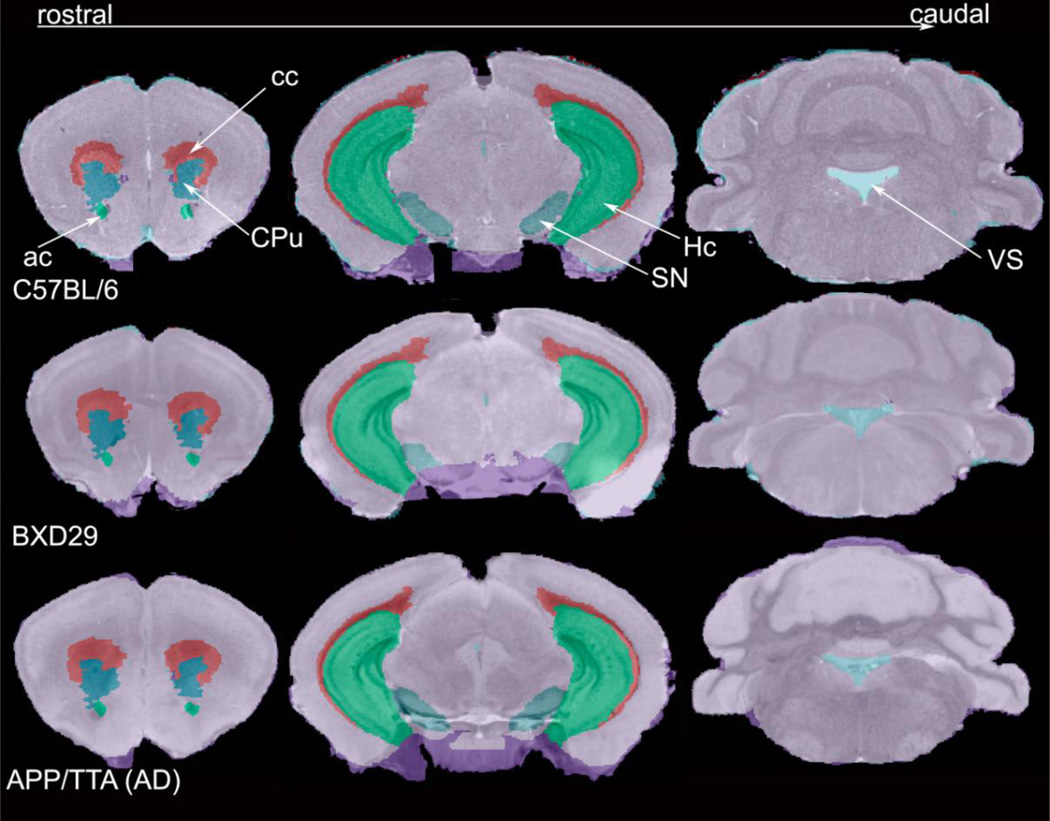
To test the robustness of the pSVMRF on mutant mice which has large anatomical variability, we examined the performance of the segmentation in two new strains, BXD29 the APP/TTA mouse model of AD, and contrasted it with the baseline accuracy for stained C57BL/6 mice, imaged using the same protocol, and using a full sampling strategy for training/classification. We evaluated the segmentation qualitatively (Fig. 3) and quantitatively (Fig. 4).

Fig. 3.

Visual assessment of comparable coronal levels through the brains C57BL/6, BXD29 and APP/TTA mouse model of AD, overlaid with automatically generated labels. The labeled regions are: anterior commisure (ac), corpus callosum (cc), caudate putamen (CPu), hippocampus (Hc), susbtantia nigra (SN) and the ventricular system (VS).

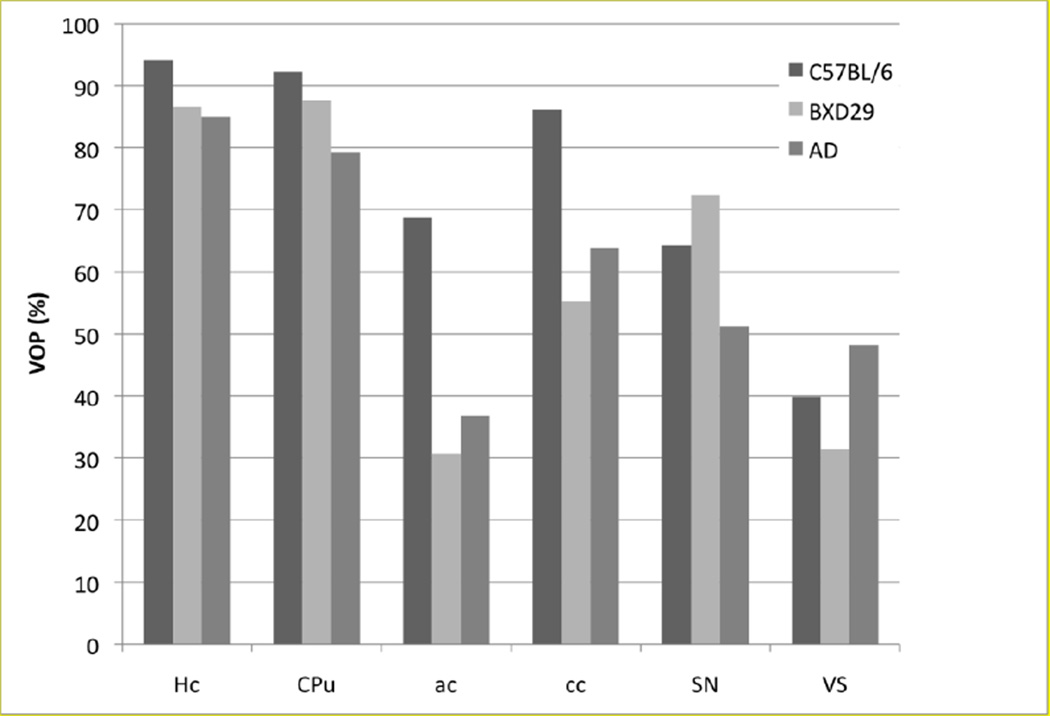
Fig. 4.

Segmenting strains other than the one used for generating the priors (C57BL/6) is a more challenging task, as illustrated by the examples of a BXD29 and an APP/TTA mouse model of AD. Using a full sampling strategy, but only a subset of 7 labels, yields VOP for hippocampus, ranging from 94.11±0.73% in the C57BL/6 (for the 5 specimens) to 86.65% for the BXD29 and 84.97% for APP/TTA mouse. For the caudate putamen VOP ranges from 92.21±0.71% for C57BL6, to 87.68% for BXD29 and 79.28% for APP/TTA. However smaller white matter tracts and nuclei, and especially the ventricles remain challenging for automated segmentation (eg. VOP for corpus callosum 86.11±2.12% in C57BL/6, 55.25% in BXD29, and 63.83% in APP/TTA).

Segmenting the overall brain is a very accurate process (>90% VOP), even in strains other than the C57BL6 used for generating priors. However, the increased anatomical variability introduced by new strains resulted in overall decreased performance for a subset of structures including: hippocampus, caudate putamen, anterior commisure, corpus callosum, substantia nigra and ventricles. When using 7 labels only during training, the larger structures such as hippocampus and caudate putamen could be segmented with accuracy of ~80% and greater. The hippocampus VOP was 94.11±0.73% for C57BL6, vs.: 85.81±1.19% for the other two strains, while for caudate putamen VOP was 92.21±0.71% for C57BL/6, and 83.48±5.93% for the new strains). Smaller white matter tracts and nuclei, and especially the widely variable ventricles remain challenging for the automated segmentation task. VOP for the corpus callosum was 86.11±10.06% for C57BL/6, but 59.54±6.06% for the additional strains, while for the substantia nigra VOP was 64.31±2.12% for C57BL/6, and 61.81±10.0% in the other strains.

Multiple avenues exist to increase accuracy of the segmentation. Improved registration, together with a denser sampling strategy, has the potential to increase segmentation accuracy, while increasing computational demands. For example the use of a full sampling strategy on C57BL/6 mice yielded VOP values of 92.38±0.20% for Hc, versus 87.67±0.86 for under-sampled data. Similarly for CPu the VOP was 94.58±0.9%, versus 90.87±0.16%. However the VOP for other structures, including ventricles did not increase using this strategy, e.g. VOP for ventricles was 81.72±0.19% for under-sampled strategy but only 75.92±4.33 for the full sampling strategy. We noted that a denser parcellation of the brain yields in general better segmentation results, compared to a reduced set of labels, embedded in the larger brain area, perhaps by more accurately constraining individual regions definition.

4. Conclusion

Given recent imaging technology development, we can acquire higher resolution mouse brain images which have eight times larger data than the current data. Hence, there has been a pressing need for computationally efficient segmentation method. We have presented an automated method for mouse brain images, pSVMRF, which is a computationally efficient. It integrates pSVM and MRF for a more accurate and faster segmentation by modeling the three kinds of information which are critical for the brain image segmentation. Even though eMRF produced a more accurate delineation of the mouse brain MRM images than the atlas based segmentation and the probability information based segmentation by integration of SVM and MRF, eMRF suffers from the long training and testing time due to the use of SVM which requires of the long training and testing time. To reduce the training and testing time of SVM, we use pSVM which relies on location priors as well as MR intensity information as input features. By the virtue of nonlinear transformation of these two critical pieces of information, pSVM can train better models with a small size of training sets and reduce the testing time by 92.85% compared with the SVM testing of eMRF. By using the optimal termination point for the ICM implementation, the ICM algorithm converges much faster with the better solution. The AVOP and AVDP of pSVMRF are improved by 2.55% and 9.57% compared with eMRF, and by 5.41% and 21.07% compared with MRF. In the future, we will make efforts to improve the performance of smaller structures in which pSVMRF still produces poorer performance than the other two methods.

The C57BL/6 is a widely used mouse strain, at the basis of a large number of derived strains, and therefore was chosen to create priors, and training the classifier. There is a wide interest in segmenting other mouse strains, many of them having a C57BL/6 background, to identify anatomical phenotypes. While more studies on larger groups of animals from different strains are required to validate and optimize a more general segmentation/anatomical phenotyping task in the future, we have shown the initial applicability of the method to other strains as well, including a recombinant inbred mouse strain derived from parental C57BL/6 and DBA2 (BXD29), and a model of Alzheimer’s disease (APP/TTA). The improvements in accuracy while reducing the computational time will allow us to address the issue of brain segmentation in larger population studies, and higher resolution images, therefore facilitating image based phenotyping of mouse models of neurological and psychiatric conditions.

Highlights.

1. A new method called pSVMRF is proposed for 3D mouse brain segmentation.

2. The proposed pSVMRF outperforms existing methods in terms of accuracy.

3. pSVMRF is more computationally efficient comparing to published eMRF.

4. pSVMRF has the potential to handle extra high resolution mouse brain images.

5. pSVMRF is capable to segment mutant mice brain images.