Abstract
Dynamic contrast-enhanced MRI has been used to quantify myocardial perfusion in recent years. Published results have varied widely, possibly depending on the method used to analyze the dynamic perfusion data. Here, four quantitative analysis methods (two-compartment modeling, Fermi function modeling, model-independent analysis, and Patlak plot analysis) were implemented and compared for quantifying myocardial perfusion. Dynamic contrast-enhanced MRI data were acquired in 20 human subjects at rest with low-dose (0.019 ± 0.005 mmol/kg) bolus injections of gadolinium. Fourteen of these subjects were also imaged at adenosine stress (0.021 ± 0.005 mmol/kg). Aggregate rest perfusion estimates were not significantly different between all four analysis methods. At stress, perfusion estimates were not significantly different between two-compartment modeling, model-independent analysis, and Patlak plot analysis. Stress estimates from the Fermi model were significantly higher (~20%) than the other three methods. Myocardial perfusion reserve values were not significantly different between all four methods. Model-independent analysis resulted in the lowest model curve-fit errors. When more than just the first pass of data was analyzed, perfusion estimates from two-compartment modeling and model-independent analysis did not change significantly, unlike results from Fermi function modeling.
Keywords: myocardial perfusion, DCE-MRI, kinetic modeling, quantitative, perfusion reserve
Estimates of myocardial perfusion from dynamic contrast-enhanced MRI (DCE-MRI) studies have been reported by a number of investigators (1–10). Despite validation with microspheres (2,3,6), or with other imaging modalities like positron emission tomography (5,6,8,10), and Doppler ultrasound (1,9), perfusion estimates from these and other studies have varied widely, likely depending on the population of subjects imaged and the image acquisition specifics and what analysis method was used to analyze the dynamic perfusion data. While some researchers have relied on physiologically derived or empiric kinetic analysis models for quantifying myocardial perfusion (1,6,11–13), other groups have used model-independent analysis (2,10,14) or Patlak plot analysis (8,9,15). There has been little published work to directly compare different models by applying the models to the same data. The objective of this work was to implement and compare four quantitative analysis methods for quantifying regional myocardial perfusion in 20 human subjects. The analysis methods used were two-compartment modeling, Fermi function modeling, model-independent analysis, and Patlak plot analysis.
THEORY
Most analysis methods used to quantify myocardial perfusion from DCE-MRI studies require that the measured blood and tissue enhancement data be accurately deconvolved to estimate the impulse response function, h(t) (1,2 6,10–12,15). For two-compartment modeling, Fermi function modeling, and model-independent analysis, the rate of perfusion to each region of the myocardium is proportional to the maximum amplitude of h(t) (11,12,16,17). The Patlak plot analysis method is based on compartment modeling and assumes there is an irreversible transfer of contrast agent (CA) into the myocardial tissue. Here, the basis for each of these four models is given, including some of the advantages and limitations of each.
Two-Compartment Modeling
Tofts et al. (12) presented a concise summary of two-compartment models that are used to estimate fluid flow into and out of a finite region of tissue. Equation 1 shows the standard differential equation given in Tofts et al. (12) for the two-compartment model. Ktrans represents the kinetic rate constant of CA flow from the vasculature into the extravascular, extracellular space within the myocardium; kep represents the kinetic rate constant of CA flow from the extravascular, extracellular space within the myocardium into the myocardial vasculature; Cbld(t) and Ctis(t) represent the blood and tissue enhancement signals measured with DCE-MRI. Equation 2 shows the analytical solution to Eq. 1, in which Ctis(t) is represented by the convolution (⊗) of Cbld(t) with the system impulse response function, h(t). As is shown in Eq. 2, h(t) is represented by a monotonically decaying exponential function: h(t) = Ktrans × exp(−kep × t).
| [1] |
| [2] |
While the complex processes of myocardial perfusion cannot be described exactly with a single exponential impulse response function, experimental studies have demonstrated that two-compartment modeling can yield enhancement curves that reasonably approximate the measured tissue enhancement data. Additional parameters can be included in the two-compartment model, as shown in Eq. 3 to account for variables such as the delay time (Δt) between blood and tissue enhancement and the component of tissue enhancement that is due to the fraction of myocardial vasculature (Vb) in the tissue.
| [3] |
In practice, Ctis(t) is deconvolved by Cbld(t) to solve for the unknown parameters Ktrans, kep, Vb, and Δt. While some groups directly report Ktrans as an index of myocardial perfusion, others report an estimate of total myocardial perfusion, F, which may be computed from the equation F = Ktrans/E. Here, E represents the extraction fraction, which represents a measure of the permeability of the myocardial vasculature that has been shown to vary nonlinearly as a function of the permeability-surface area product and the rate of perfusion in the myocardium (18,19). In this current study, Ktrans is reported. Estimates of Ktrans measured with DCE-MRI have been validated with dynamic positron emission tomography imaging (5,20) and fluorescent microspheres (21).
Fermi Function Modeling
The Fermi function model is an empiric model originally developed in the field of quantum mechanics (22). In 1983, Axel (23) used an analytical form of the Fermi function as a deconvolution constraint for estimating the mean transit time of CA flow through tissue with dynamic x-ray computed tomography. In 1998, Jerosch-Herold et al. (1) used a similar form of the Fermi function as a model for estimating myocardial blood flow by deconvolution of DCE-MRI perfusion data. Equation 4 shows the analytical expression of the Fermi function used in Jerosch-Herold et al. (1). G and k represent indices of the CA influx and efflux parameters, respectively; Δt represents the delay time between LV blood pool enhancement and myocardial tissue enhancement; τ controls the time duration of the plateau portion of the Fermi function, which may approximate the initial “filling” phase of CA influx into the myocardium; δ(t) represents a delta function, and ⊗ is the mathematical convolution operator. From Eq. 4, myocardial perfusion is calculated as hF(t = 0), when the data are adjusted for the time delay between blood and tissue enhancement (1,24,25).
| [4] |
Estimates of myocardial perfusion using the Fermi function model have been reported in several human and animal studies (1,3,4,26–28). Fluorescent microspheres were used to validate myocardial perfusion estimates in 12 dogs (3) and three pigs (1). Doppler ultrasound was used to validate perfusion estimates in nine humans with syndrome X (25).
Model-Independent Deconvolution
The theoretical framework for model-independent analysis was established by Zierler et al. (17) in 1962 based on the central volume principle. In that work, the authors concluded that the rate of fluid flow (perfusion) into a region of tissue can be determined by directly deconvolving the measured blood enhancement signal and the measured tissue enhancement signal to estimate the impulse response function, h(t). Once h(t) is known, a quantitative estimate of perfusion can be calculated from the maximum amplitude of h(t), scaled by the inverse of the sampling rate of the perfusion images: Flow = max[h(t)]/dt.
Model-independent analysis has been used with dynamic susceptibility MRI to estimate cerebral perfusion (29,30), and breast tumor perfusion (31). In 2002, Jerosch-Herold et al. (2) developed a model-independent deconvolution method that uses generalized singular value decomposition with temporal regularization to estimate myocardial perfusion with DCE-MRI. In that work, h(t) was parameterized as a sum of shifted B-spline functionals, in which temporal regularization was imposed on the scalar coefficients of the B-splines. This B-spline method has been used in several myocardial perfusion studies (2,14,32–34) and validation with fluorescent microspheres was performed in three pigs (2) and nine dogs (14). Goldstein et al.(14) used a similar model-independent deconvolution method to estimate myocardial blood flow, in which h(t) was parameterized as a “consolidated” set of gamma variate basis functions with temporal regularization.
Pack et al. (10) presented a model-independent analysis method that estimates h(t) without the use of B-splines or other polynomial functions. That method used iterative minimization with temporal gradient regularization to estimate myocardial perfusion. Temporal regularization similar to that used by other authors (2,10,14,32–34) has been shown to minimize the effects of noise and motion artifacts on the estimate of h(t) when the measured blood and tissue enhancement data are deconvolved (35,36).
The cost function that was used in (10) to estimate h(t) is shown in Eq. 5. Cbld(t) and Ctis(t) represent the blood and tissue enhancement data, respectively, and h(t) represents the system impulse response function; λ represents the regularization weight parameter; △ represents the first-order difference (gradient) operator and ||*|| denotes the Euclidean norm (L2 – norm) operator. For this iterative minimization problem, the fidelity of the h(t) estimate (without regularization) is balanced with the temporal smoothing constraint imposed by the first-order difference regularization operator, △. Gradient descent minimization (37) or other techniques can be used to solve for h(t). The value of λ can be optimally chosen using methods such as L-curve analysis or generalized cross-validation (38). Dynamic positron emission tomography imaging was used to validate myocardial perfusion estimates in one small study with five humans (10).
| [5] |
Patlak Plot Analysis
Patlak plot analysis is a graphical analysis method based on compartment modeling for estimating the unidirectional influx constant (Ktrans) of fluid or tracer flow into a region of tissue. This method was developed for estimating the accumulation of deoxyglucose across the blood-brain barrier in cerebral perfusion studies (15). Unlike the two-compartment model shown in Eq. 1, Patlak plot analysis requires that the system of interest have at least one compartment into which the CA is irreversibly transferred. For example, CA passes from one compartment (the blood vasculature) into the second compartment (the interstitial tissue space) and remains there.
Assuming the efflux constant (kep) is equal to zero, which may be a reasonable approximation only during the initial increasing uptake of CA in the myocardium, an estimate of the concentration of CA in the tissue can be approximated by integrating both sides of Eq. 1. Equation 6 shows the Patlak model after integration, which reveals that there is a linear relationship between Ctis(t) and the integral of Cbld(t) during the time of CA uptake in the myocardium.
| [6] |
Ktrans can be calculated from the slope of the correlation between Ctis(t) and the integral of Cbld(t). Estimates of myocardial perfusion using Patlak plot analysis have been reported in 10 human volunteers (8). Dynamic positron emission tomography imaging with 15O-labeled water was used to validate the perfusion estimates in that study. Myocardial perfusion reserve (MPR) estimates using the Patlak method were also reported in 20 patients with suspected coronary artery disease (9) and compared to Doppler flow wire measurements.
MATERIALS AND METHODS
To directly compare the four quantitative analysis methods outlined in this work, each model was implemented with DCE-MRI data acquired in 20 human subjects. Results of myocardial perfusion at rest and during adenosine stress, and the MPR—the ratio of hyperemic to resting perfusion—were calculated for each method.
Acquisition of MR Image Data
Twenty human subjects (18 males, ages 50 ± 13 years, two females, ages 39 ± 18 years) were imaged with DCE-MRI. Twelve subjects were imaged with a 1.5T MRI scanner (Avanto from Siemens, Erlangen, Germany) and eight subjects were imaged with a Siemens Trio 3T MRI scanner. Sixteen of the subjects were imaged with a saturation recovery fast low angle shot (SR-FLASH) pulse sequence and four subjects were imaged with a hybrid gradient echo-echo planar (GRE-EPI) pulse sequence. Imaging parameters were selected to acquire at least three short-axis slices of the LV during every heartbeat. Typical imaging parameters for the GRE-EPI sequence were delay after saturation pulse = 40–70 ms, pulse repetition time = 5.8–6.5 ms, echo time = 0.98–1.23 ms, echo train length (ETL) = 4, flip angle = 20–25°, band width (BW) = 650–1000 Hz, 8mm slice thickness, field of view = 360 × 270 with an image matrix = 160 × 90 and a symmetric k-space acquisition. Parameters for the SR-FLASH sequence were similar except that the delay after saturation pulse = 100–110 ms, pulse repetition time ~2 ms, flip angle = 12–16°, with GRAPPA, R~1.7. Because the primary goal of this work was to compare myocardial perfusion estimates from four quantitative analysis methods, identical acquisitions were not essential. Eight of the subjects were imaged at rest, after being given a low-dose (0.022 ± 0.007 mmol/kg) bolus injection of gadolinium diethylenetriamine pentaacetic acid (Gd-DTPA) (Omniscan; Amersham Health Inc., Princeton, NJ) at 5 mL/sec. The other 12 subjects were given a slightly lower dose (0.018 ± 0.003 mmol/kg) bolus injection of gadobenate dimeglumine (Gd-BOPTA) (Multihance; Bracco Diagnostics Inc., Princeton, NJ), due to its higher relaxivity (39). The change in CA was due to a change in internal policy (40,41).
Dynamic stress images were acquired in 14 of the subjects approximately 10 min after the rest scans with the same imaging sequences and parameters described above. These subjects abstained from caffeine for at least 12 h prior to imaging. During stress imaging, a continuous infusion of adenosine (140 μg/kg/min) (Adenoscan; Astellas Pharma US, Inc., Deerfield, IL) was administered to each subject via an antecubital vein to induce vasodilation. Approximately 3 min after the start of the adenosine infusion, images were acquired while a low-dose (0.020 ± 0.007 mmol/kg) bolus injection of Gd-DTPA was administered to six of these subjects and a low-dose (0.023 ± 0.002 mmol/kg) bolus injection of Gd-BOPTA was given to the other eight subjects. Each CA injection at rest and stress was followed by a saline flush of 15 mL at 5 mL/sec using a Medrad Spectris Solaris MR power-injector (Medrad, Inc., Indianola, PA) via an antecubital vein. During the dynamic rest and stress imaging, most of the subjects held their breath for approximately 10–20 sec during the first pass of CA through the LV and then breathed shallowly for the remainder of the scan. Approximately 1 minute’s worth of image data was obtained in all the subjects.
MR Image Processing
All MR image postprocessing was performed using Matlab (The MathWorks Inc., Natick, MA). The image frames for each short-axis slice of the LV were manually registered for in-plane rigid body motion, and endocardial and epicardial contours were manually and conservatively drawn to segment the LV myocardium for perfusion analysis. Next, two separate normalization steps were performed to correct for in-plane regional coil sensitivity and slice-to-slice coil sensitivity. The second normalization step is necessary when using a single blood enhancement curve (arterial input function) from one slice of the LV as the arterial input function for other slices of the LV.
To correct for in-plane regional coil sensitivity in the LV, each short-axis slice was divided into six equiangular sections and each section was normalized to the mean precontrast signal of the entire LV (2,10,42), which was assumed to have a uniform signal intensity before the injection of CA. Dynamic tissue enhancement curves, Ctis(t), were obtained from each LV region and a single dynamic blood enhancement curve, Cbld(t), was obtained from the mean signal intensity of a manually selected region of the LV blood pool in a midbasal short-axis slice.
To correct for slice-to-slice coil sensitivity, the tissue enhancement curves from each LV slice—which were already scaled for in-plane coil sensitivity variations— were scaled again to the mean precontrast signal from the LV slice with the desired arterial input function. As with the in-plane normalization, this scaling was based on the assumption that differences in the precontrast signal intensity in the tissue enhancement curves between slices are due to slice-to-slice variations in coil sensitivity and not due to differences in T1 values throughout the LV myocardium.
Next, prior to deconvolution analysis, the mean pre-contrast signal intensity of the blood and tissue enhancement curves was subtracted from each curve to normalize them to a baseline signal intensity of zero. Also, to reduce overestimation effects caused by noise in the precontrast frames of Ctis(t) and Cbld(t), the precontrast data prior to the onset of blood and tissue enhancement were not used in the fitting process for each of the deconvolution models.
For two-compartment modeling, Fermi function modeling, and model-independent analysis, perfusion estimates were computed by constrained deconvolution of all the measured blood and tissue enhancement data and then again using only the measured data during the first pass of CA through the myocardium. The first pass was manually identified for each subject as the lowest blood enhancement signal immediately following the first pass bolus of CA, prior to signal enhancement of the recirculation bolus. Prior to regional perfusion analysis with two-compartment modeling and Fermi function modeling, an average time delay, Δt, was computed for each LV slice of the myocardium, using the deconvolution models in Eq. 3 and Eq. 4, respectively. The average per-slice time delay parameter from these two models was then held fixed and the perfusion estimates were recomputed for each region in that slice.
For model-independent analysis, the delay time between blood and tissue enhancement was not explicitly modeled as a free parameter. In general this was not a problem, because perfusion estimates with the model-independent method are essentially invariant to positive increases of delay time (10,43). However, there were a few cases in which there appeared to be simultaneous enhancement of the LV blood pool and myocardium, or even noncausal enhancement, in which the myocardium enhanced before the LV blood pool. This noncausal enhancement is not physiologic and was related to noise and motion artifacts in the data. To correct for this problem, we added a time delay of approximately 2 sec to the tissue enhancement data. A time delay of 2 sec was chosen as the minimum to prevent the noise/artifact problems in all of the datasets; 0 or 1 sec gave the same results in the vast majority of curves.
For Patlak plot analysis, only the blood and tissue enhancement data during the initial phase of increasing CA uptake into the myocardium was used. For this analysis, the blood enhancement data were truncated to the time in which the LV blood pool enhancement was at a maximum and the delay time between the onset of blood and tissue enhancement was modeled in the same manner as the two-compartment model.
For all of the subjects in the study, regional perfusion estimates and MPR values were computed in six regions in three short-axis slices of the LV, similar to the American Heart Association 17-segment model (44). In this study the apical slice was divided into six regions instead of four regions. However, perfusion estimates from these regional segments were combined per American Heart Association standards and coronary artery territorial perfusion estimates were reported instead of regional perfusion estimates because the territories were assumed to be relatively independent regions. As part of the data analysis, it was assumed that the specific gravity of the myocardial tissue was equal to 1 g/mL. It was also assumed that for the relatively low doses of CA used, the change in signal intensity of Cbld(t) and Ctis(t) from the DCE-MRI perfusion images was linearly proportional to the change in local CA concentration within the LV blood pool and the myocardial tissue. Prior to deconvolution analysis, precise image acquisition times were obtained from the MRI scanner to interpolate the measured Cbld(t) and Ctis(t) data to account for each subject’s variable heart rate during imaging (45).
For two-compartment modeling, Ktrans, an index of the extravascular perfusion estimate, was reported at rest and stress. For Fermi function modeling, myocardial perfusion estimates were calculated as the amplitude of the Fermi impulse response function at time 0, hF(t = 0), when the data are adjusted for the time delay between blood and tissue enhancement. For model-independent analysis, the cost function shown in Eq. 5 was minimized to estimate h(t), from which myocardial perfusion was calculated as Flow = max[h(t)]/dt. As outlined in Pack et al. (10), gradient descent minimization (37) was used in the iterative minimization process to compute h(t), with an initial estimate of constant h(t) = 0.001.
Prior to model-independent deconvolution, L-curve analysis was performed to determine a single near-optimal regularization weight parameter (λ = 0.045) for all the subjects in the study. It was previously determined that this method is robust to large changes in the CNR of the dynamic perfusion data (10). The iterative minimization process was repeated until the curve-fit error—the square root of the sum of squared difference between the measured Ctis(t) data and the estimated Ctis(t) data, computed by convolving the measured Cbld(t) with the estimate of h(t)—was less than 5% or until n = 1200 iterations were completed. A fixed step size of γ = 1 × 10−9 was used in the minimization process for all 20 subjects in the study.
For Patlak plot analysis, the measured Ctis(t) data were plotted versus the integral of the accumulated Cbld(t) data as outlined in (8,9,15), after the data were truncated to ensure only the initial phase of increasing CA uptake was included in the analysis. Linear regression was then performed for each region of tissue enhancement to determine the equation of best fit and the correlation between Ctis(t) and the integral of Cbld(t). Ktrans was approximated as the slope of the line of best fit and was reported as the myocardial perfusion estimate for each region of tissue.
Statistical Analysis of Myocardial Perfusion Estimates
For the three deconvolution models, rest and stress perfusion estimates were computed using all time frames of the measured blood and tissue enhancement data. Perfusion was also estimated when only the first pass of contrast enhancement data was analyzed. Linear regression was performed to determine the correlation between the regional perfusion estimates from all four analysis methods.
Analysis of variance and Bland-Altman analysis were performed to determine whether there were significant differences in rest and stress perfusion estimates and the MPR between all four quantitative analysis models. Standard errors of the dependence of the perfusion estimates from each analysis model to the other models were also computed and shown on the linear regression plots. When significant differences in perfusion estimates were found, a pairwise Tukey’s statistical test was performed to determine which of the analysis methods were significantly different (46). For the three deconvolution analysis methods (not Patlak plot analysis), a curve-fit error—the square root of the sum of squared difference between the measured Ctis(t) data and the estimated Ctis(t) data—was computed for all 20 subjects in the study.
RESULTS
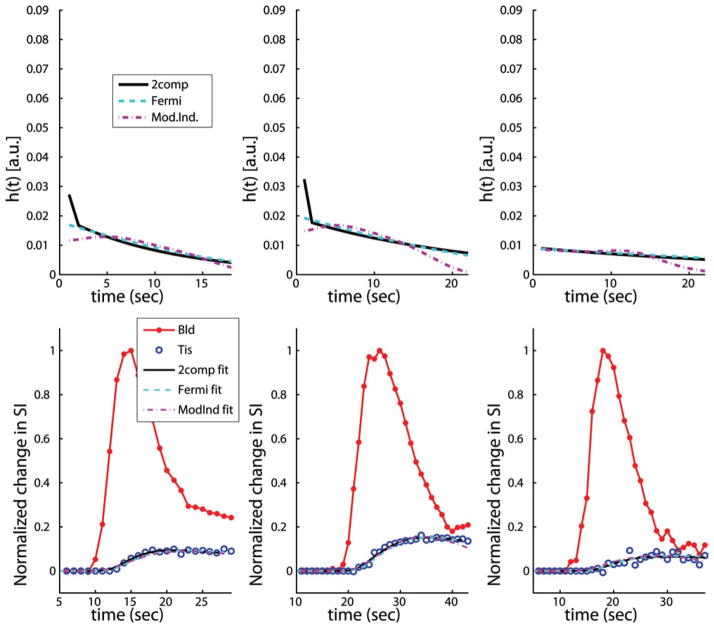
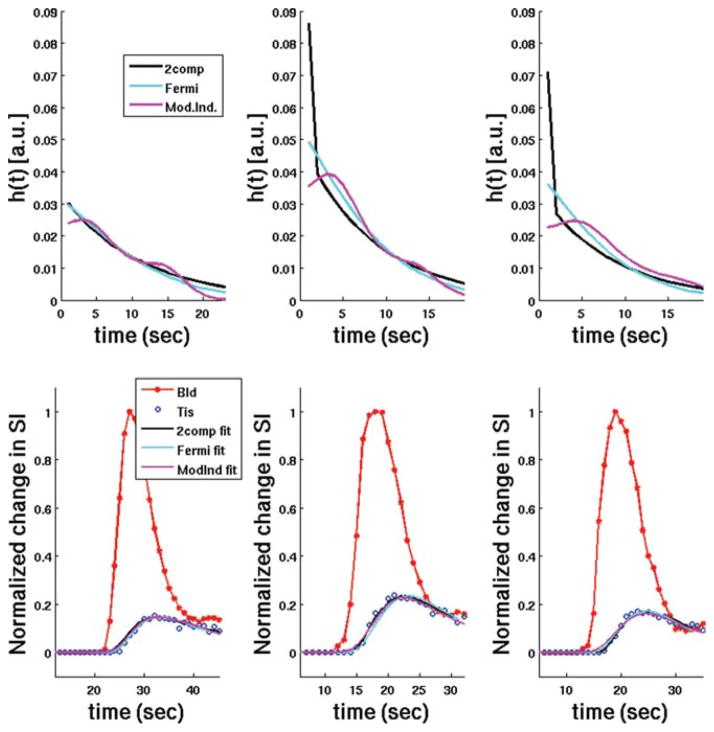
Figure 1 shows plots of typical h(t) curves from three subjects in the study at rest, along with the estimated tissue enhancement model fits using two-compartment modeling, Fermi function modeling, and model-independent analysis (not Patlak plot analysis). Figure 2 shows plots of typical h(t) curves from three subjects in the study at stress, along with the estimated tissue enhancement model fits using the same three models as in Fig. 1. In general, estimates of myocardial perfusion from all of these deconvolution models are proportional to the maximum amplitude of h(t). However, the two-compartment model includes a separate parameter to model the volume fraction of vasculature, Vb, in the myocardium, so an additional delta function, scaled by Vb, is added to h(t = 0).
FIG. 1.
Representative plots of typical h(t) curves (top row) from three subjects in the study at rest, along with the estimated tissue enhancement model fits (bottom row) using two-compartment modeling, Fermi function modeling, and model-independent analysis (not Patlak plot analysis). In general, estimates of myocardial perfusion from all three of these deconvolution models are proportional to the maximum amplitude of h(t). However, when Vb is nonzero in the two-compartment model an additional δ function, scaled by Vb, is added to h(t = 0).
FIG. 2.
Representative plots of typical h(t) curves (top row) from three subjects in the study at stress, along with the estimated tissue enhancement model fits (bottom row) using two-compartment modeling, Fermi function modeling, and model-independent analysis (not Patlak plot analysis). In general, estimates of myocardial perfusion from all three of these deconvolution models are proportional to the maximum amplitude of h(t). However, when Vb is nonzero in the two-compartment model an additional δ function, scaled by Vb, is added to h(t = 0).
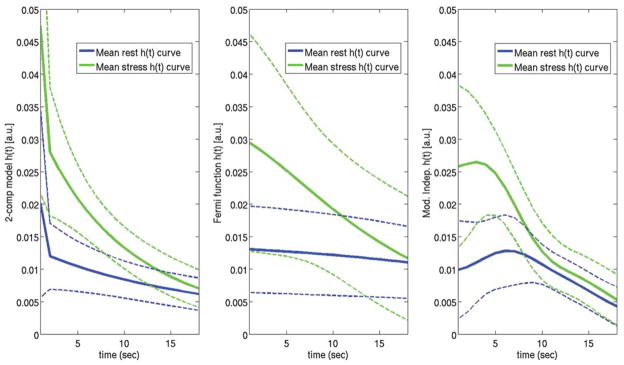
Figure 3 shows a plot of the aggregate rest and stress h(t) curves (mean ± standard deviation) for two-compartment modeling, Fermi function modeling, and model-independent analysis from all the subjects imaged in the study. The initial “shoulder” of h(t) that is present with the model-independent h(t) curves and to a lesser extent the Fermi function h(t) curves is assumed to represent the initial filling phase as CA enters the myocardial vasculature. With two-compartment modeling, this filling phase is approximated with the Vb term shown in Eq. 3, which is represented by a δ function in the impulse response. Because model-independent analysis does not explicitly fit the time delay, Δt, between blood and tissue enhancement as a free parameter like with two-compartment modeling and the Fermi function modeling, the mean maximum amplitude of the aggregate model-independent h(t) curves is more spread out and slightly reduced compared to the other models. The reduced mean maximal amplitude of the model-independent h(t) curves is due to averaging the curves from all the subjects in the study that generally have different time delays between blood and tissue enhancement. The maximum amplitude of the h(t) curves for two-compartment modeling and Fermi function modeling are shifted and plotted beginning at time t = 0 for easier visual comparison.
FIG. 3.
Plots of the aggregate rest and stress h(t) curves for two-compartment modeling (left), Fermi function modeling (center), and model-independent analysis (right) from all the subjects imaged in the study. The solid lines represent the mean h(t) curves for each model and the dashed lines represent the standard deviation of the estimated h(t) curves for each model. In general, estimates of myocardial perfusion from all three of these deconvolution models are proportional to the maximum amplitude of h(t). However, for the two-compartment model, an additional δ function scaled by Vb is added to h(t). The reduced mean maximal amplitude of the model-independent h(t) curves is due to averaging the curves from all the subjects in the study that generally have different time delays between blood and tissue enhancement. The maximum amplitudes of the h(t) curves for two-compartment modeling and Fermi function modeling are all aligned and plotted beginning at time t = 0 for easier visual comparison.
Myocardial perfusion estimates from two-compartment modeling and model-independent analysis were not significantly different when only the first pass of dynamic enhancement data (approximately 20 sec of data) was used in the analysis versus when all the measured data (approximately 1 min of data) was used in the analysis (P = 0.27 and P = 0.21, respectively). Perfusion estimates from the Fermi function model were significantly different (P = 0.016) and approximately 25% higher at rest and stress when all the measured data were used in the analysis versus when only the first pass of dynamic enhancement data was used.
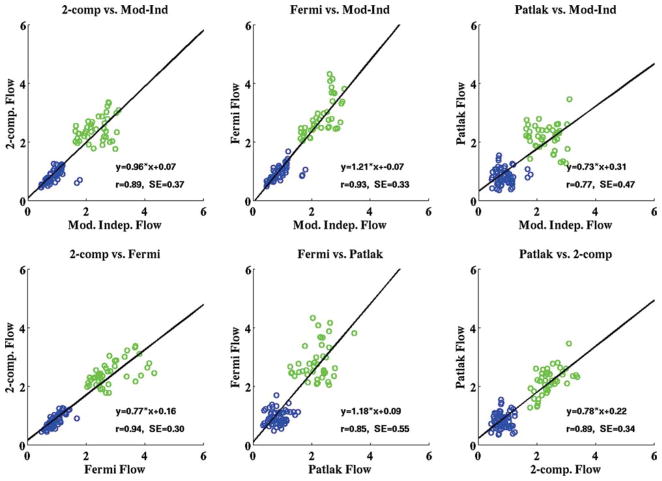
The aggregate rest and stress perfusion estimates and MPR values (mean ± standard deviation) for all the subjects in the study using all four quantitative analysis methods are shown in Table 1. Figure 4 shows the scatterplots of the American Heart Association regional rest and stress perfusion estimates from all four methods for the 20 subjects imaged in the study. The linear regression line representing the equation of best fit for each model comparison and the correlation associated with each fit are overlaid on the plots shown in Fig. 4. The standard error estimates for the correlations between perfusion estimates from each method are also shown on the plots.
Table 1.
A Summary of the Aggregate Myocardial Perfusion Estimates and MPR Values From All 20 Subjects Imaged at Rest and All 14 Subjects Imaged at Adenosine Stress in the Study†
| Rest perfusion (mL/min/g) | Stress perfusion (mL/min/g) | MPR values | |
|---|---|---|---|
| 2-Compartment modeling (Ktrans) | 0.82 ± 0.22 | 2.42 ± 0.42 | 3.06 ± 0.86 |
| Fermi function modeling | 0.93 ± 0.24 | 2.84 ± 0.63* | 3.09 ± 0.95 |
| Model-independent analysis | 0.88 ± 0.28 | 2.32 ± 0.46 | 2.90 ± 1.10 |
| Patlak plot analysis (Ktrans) | 0.83 ± 0.27 | 2.17 ± 0.44 | 2.90 ± 1.27 |
Indicates that myocardial perfusion estimates at stress were significantly different with Fermi function modeling than with the other three analysis methods.
Results are from the AHA coronary artery territory regions determined using two-compartment modeling, Fermi function modeling, model-independent analysis, and Patlak plot analysis.
FIG. 4.
Scatterplots from all four quantitative analysis methods used in the study showing the comparison of mean rest (blue) and adenosine stress (green) perfusion estimates in three coronary artery territory regions for all the subjects in the study (all units are in milliliters/minute/ gram). The line representing the equation of best fit for each model comparison and the correlation associated with each fit are overlaid on the plots. The aggregate rest and stress perfusion estimates for the four models are shown in Table 1. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
Aggregate perfusion estimates at rest were not significantly different between all four analysis methods (P = 0.06). The P value would likely be higher if the resting Fermi results were not considered. However, there were significant differences in aggregate perfusion estimates at stress (P < 0.00001). A post hoc Tukey’s test (46) revealed that the significant differences in perfusion estimates were between Fermi function modeling and the other three models: two-compartment modeling, model-independent analysis, and Patlak plot analysis. MPR values were not significantly different between all four methods (P = 0.84), suggesting that systematic differences between these methods are cancelled when the ratio of stress and rest perfusion is computed.
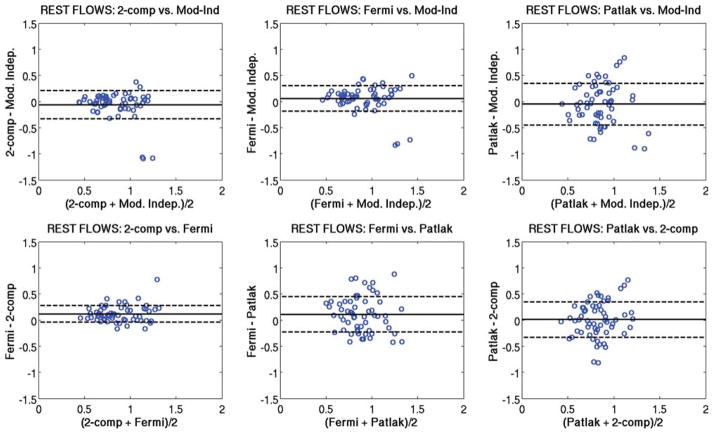
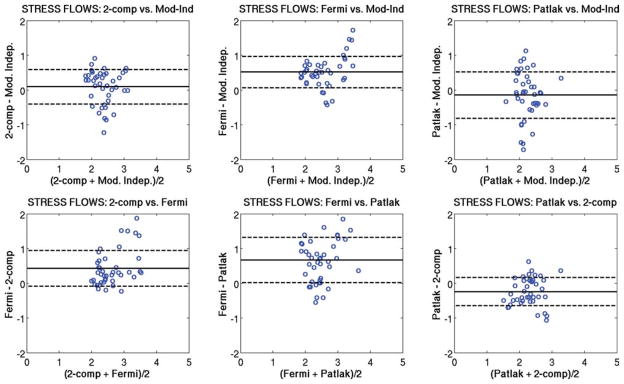
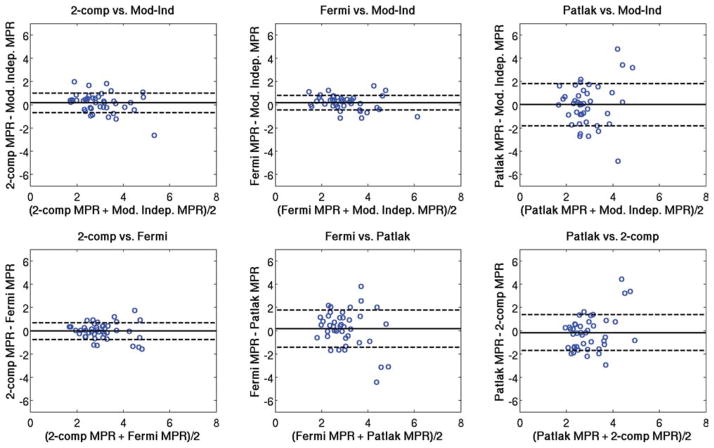
Figure 5 shows Bland-Altman plots comparing the regional rest perfusion estimates between each of the four quantitative analysis methods used in the study. Figure 6 shows Bland-Altman plots comparing the regional stress perfusion estimates between the four analysis methods used in the study. Figure 7 shows Bland-Altman plots comparing the regional MPR values between each of the four quantitative analysis methods used in the study. In general, the comparisons that included the Patlak method tended to have the largest variations. The most notable observation from these plots is that the largest bias between perfusion estimates between models occurs with the Fermi function model at stress versus the other three models, as also seen in Table 1.
FIG. 5.
Bland-Altman plots showing the comparison of mean rest perfusion estimates between each of the four quantitative analysis methods used in this study. The same axis value ranges were used in each case to facilitate comparisons. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
FIG. 6.
Bland-Altman plots showing the comparison of mean stress perfusion estimates between each of the four quantitative analysis methods used in this study. The same axis value ranges were used in each case to facilitate comparisons. The most notable observation from this plot is that the largest bias between perfusion estimates between models occurs with the Fermi function model at stress versus the other three models. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
FIG. 7.
Bland-Altman plots showing the comparison of mean MPR values between each of the four quantitative analysis methods used in this study. The same axis value ranges were used in each case to facilitate comparisons. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
The aggregate curve-fit errors at rest and stress were 0.13 ± 0.08 for two-compartment modeling, 0.11 ± 0.06 for model-independent analysis, and 0.14 ± 0.08 for Fermi function modeling. Although the mean curve-fit errors were similar at rest and stress for all three deconvolution models, they were significantly different for the three models separately when the enhancement curves were analyzed in aggregate (P < 0.0001 at rest and stress) and were slightly lower for model-independent analysis than with the other two analysis methods.
DISCUSSION
Findings From Published Studies
Quantitative estimates of myocardial perfusion using DCE-MRI have been reported by many investigators in recent years (Table 2). Several groups did not report rest and stress perfusion estimates explicitly and instead reported MPR values. Published resting perfusion estimates (and Ktrans values) range from 0.52 mL/min/g to 1.2 mL/min/g. Published stress perfusion estimates (and Ktrans values) range from 1.36 mL/min/g to 4.0 mL/min/ g. This broad range of absolute myocardial perfusion estimates at rest and stress likely reflects differences in the species and types of subjects imaged, the imaging sequence used to acquire the perfusion images, the dose and type of CA used, and the analysis method used in each study.
Table 2.
A Summary of Quantitative Myocardial Perfusion Estimates and MPR Values From Many Published DCE-MRI Studies (Including Results From This Work)*
| Author | Year | Ref. | Acquisition | Gd dose (mmol/kg) | Analysis method | Comparison | Rest perfusion (or Ktrans) (mL/min/g) | Stress perfusion (or Ktrans) (mL/min/g) | MPR |
|---|---|---|---|---|---|---|---|---|---|
| Jerosch-Herold et al. | 1998 | (1) | SR-FLASH | 0.025 | Fermi/ΔSI | 9 pts. vs. Doppler CFR | — | — | 2.14 ± .57 |
| Jerosch-Herold et al. | 2002 | (2) | SR-FLASH | 0.04 | Mod-Ind/ΔSI | 3 pigs vs. microspheres | ~1.0 | ~4.0 | — |
| Jerosch-Herold et al. | 2003 | (25) | SR-FLASH | 0.03 | Mod-Ind/ΔSI | 15 normals vs. 27 pts. | — | — | ~3.9 |
| Jerosch-Herold et al. | 2005 | (33) | SR-FLASH | 0.04 | Mod-Ind/ΔSI | MESA study | 1.2 ± .3 | — | — |
| Jerosch-Herold et al. | 2006 | (32) | SR-SSFP | 0.015 | Mod-Ind/ΔSI | 5 dogs vs. microspheres | ~1.3 | ~2.5 | — |
| Jerosch-Herold et al. | 2006 | (34) | SR-FLASH | 0.04 | Mod-Ind/ΔSI | MESA study | 1.01 ± .23 | 3.02 ± .84 | 3.05 ± .84 |
| Jerosch-Herold et al. | 2008 | (14) | SR-FLASH | 0.015 | Mod-Ind/ΔSI | 9 dogs vs. microspheres | ~1.0 | — | — |
| Jerosch-Herold et al. | 2008 | (53) | SR-FLASH | 0.04 | Mod-Ind/ΔSI | 30 adults, MESA study | ~0.95 | ~2.75 | — |
| Arai et al. | 2004 | (3) | SR-GRE/EPI | 0.0025/0.1 | Fermi/ΔSI | 16 dogs vs. microspheres | ~1.0 | — | — |
| Arai et al. | 2006 | (26) | SR-GRE/EPI | 0.005/0.1 | Fermi/ΔSI | 10 normals vs. upslope/MCE | 1.02 ± .22 | 3.39 ± .59 | 3.43 ± .71 |
| Arai et al. | 2008 | (4) | SR-GRE/EPI | 0.0025/0.1 | Fermi/ΔSI | 6 dogs vs. microspheres | 0.79 ± .21 | 2.04 ± 1.26 | — |
| Arai et al. | 2008 | (56) | SR-GRE/EPI | 0.005/0.1 | Fermi/[Gd] | 10 normals | ~1.0 | ~3.7 | ~3.8 |
| Vallee et al. | 1997 | (54) | IR-GRE | 0.04 | Two-comp/ΔSI | 6 dogs | — | — | 2.82 ± .72 |
| Vallee et al. | 1998 | (20) | IR-GRE | 0.03 | Two-comp/[Gd] | 4 dogs vs. microspheres and PET | ~0.55 | — | — |
| Vallee et al. | 1999 | (6) | SR-FLASH | 0.02 | Two-comp/ΔSI | 10 humans | 0.72 ± .22 | — | — |
| Larsson et al. | 1996 | (21) | IR-FLASH | 0.1 | Two-comp/ΔSI | 6 normals | 0.54 ± .10 | — | — |
| Larsson et al. | 1998 | (47) | IR-FLASH | 0.08 | Two-comp/ΔSI | 10 normals vs. 10 pts. | 0.55 ± .16 | 1.36 ± .46 | 2.5 ± 1.2 |
| Larsson et al. | 2004 | (48) | IR-FLASH | 0.08 | Two-comp/ΔSI | 6 dogs vs. microspheres | ~0.8 | — | — |
| Larsson et al. | 2008 | (5) | IR-FLASH | 0.08 | Two-comp/ΔSI | 10 normals | 0.80 ± .22 | 1.83 ± .56 | ~2.4 |
| Kostler et al. | 2004 | (57) | SR-SSFP | 1 mL/4 mL | Fermi/ΔSI | 11 normals | ~0.7 | — | — |
| Kostler et al. | 2006 | (7) | SR-SSFP | 1 mL/4 mL | Fermi/ΔSI | 12 normals | 0.52 ± .11 | 1.78 ± .53 | 3.59 ± 1.26 |
| Utz et al. | 2008 | (27) | SR-FLASH | 0.005/0.05 | Fermi/ΔSI | 19 normals | — | — | 2.5 ± 0.8 |
| Parkka et al. | 2006 | (55) | SR-FLASH | 0.05 | Two-comp/ΔSI | 10 males vs. PET | 0.71 ± .24 | 1.72 ± .67 | 2.51 ± 0.95 |
| Cullen et al. | 1999 | (58) | IR-FLASH | 0.05 | Two-comp/[Gd] | 5 normals vs. 20 pts. | 0.54 ± .13 | 2.29 ± .85 | 4.21 ± 1.16 |
| Ibrahim et al. | 2002 | (59) | GRE-EPI | 0.05 | Upslope/ΔSI | 25 normals vs. PET | — | — | ~2.1 |
| Gatehouse et al. | 2004 | (28) | SR-FLASH | 0.01/0.1 | Fermi/ΔSI | 15 normals | — | — | CFR ~1.8 |
| Ishida et al. | 2009 | (8) | SR-FLASH | 0.05 | Patlak/[Gd] | 10 normals vs. PET | 0.86 ± .25 | — | — |
| Ishida et al. | 2009 | (9) | SR-FLASH | 0.05 | Patlak/[Gd] | 20 humans vs. Doppler | — | — | 3.45 ± 0.78 |
| Pack et al. | 2008 | (10) | SR-FLASH | 0.017–0.025 | Mod-Ind/ΔSI | 5 humans vs. PET | 1.09 ± .80 | 3.14 ± 1.69 | 3.3 ± 1.0 |
| Current study | 2009 | — | SR-FLASH | 0.016–0.023 | Two-comp/ΔSI | 20 humans (14 at stress) | 0.82 ± .22 | 2.42 ± .42 | 3.06 ± 0.86 |
| Current study | 2009 | — | SR-FLASH | 0.016–0.023 | Fermi/ΔSI | 20 humans (14 at stress) | 0.93 ± .24 | 2.84 ± .63 | 3.09 ± 0.95 |
| Current study | 2009 | — | SR-FLASH | 0.016–0.023 | Mod-Ind/ΔSI | 20 humans (14 at stress) | 0.88 ± .28 | 2.32 ± 0.46 | 2.90 ± 1.10 |
| Current study | 2009 | — | SR-FLASH | 0.016–0.023 | Patlak/ΔSI | 20 humans (14 at stress) | 0.83 ± .27 | 2.17 ± .44 | 2.90 ± 1.27 |
Some differences in perfusion estimates are likely due to differences in the species that was imaged (dog, pig, or human), the imaging sequences used to acquire the perfusion images, the injection protocol of CA, the doses and types of CA used in each study, and the analysis method used to analyze the dynamic blood and tissue enhancement data.
From the published perfusion values shown in Table 2, the absolute perfusion estimates computed using two-compartment modeling (ranging from 0.52 mL/min/g at rest to 2.29 mL/min/g at stress) are lower than results published with Fermi function modeling (ranging from 0.79 mL/min/g at rest to 3.7 mL/min/g at stress) and model-independent analysis (ranging from 0.95 mL/min/ g at rest to 4.0 mL/min/g at stress). This finding may partially be rationalized by the fact that Ktrans is reported with two-compartment modeling, which accounts for the intravascular blood signal differently (with Vb) than Fermi modeling and model-independent analysis. Of the published results reported in Table 2 in which two-compartment modeling was used, only some of the studies included the Vb parameter (5,21,47,48) in the same way that it was modeled in this current study. When all of the data used in this paper were fit without the use of Vb, the rest and stress perfusion estimates were 20% and 25% higher, respectively. And although a slightly higher Ktrans estimate was reported in (8) with Patlak plot analysis (0.86 mL/min/g) versus groups that used two-compartment modeling, the MPR value reported using the Patlak method (9) was similar to results from the groups that used two-compartment modeling.
Findings From the Current Study: 20 Subjects and Four Quantitative Analysis Methods
All of the four modeling methods have been compared at some point to gold standards such as microspheres or dynamic positron emission tomography and were shown to have good correlations. Thus, it was anticipated that the models might give results that were similar when compared directly. It was found that at rest and stress, aggregate myocardial perfusion estimates were slightly lower for two-compartment modeling, model-independent analysis, and Patlak plot analysis than with Fermi function modeling (Table 1), although the differences were significant only for stress perfusion values from the Fermi model (Fig. 6). Additionally, there was no significant difference in aggregate MPR values (P = 0.84) between the four deconvolution models. This suggests that systematic differences in each of the models can cancel when the ratio of stress and rest perfusion is computed. Like the summary of other groups’ findings shown in Table 2, the aggregate perfusion estimates from the current study were slightly lower for two-compartment modeling than with Fermi function analysis, although they were fairly similar to results from model-independent analysis.
The aggregate Ktrans values from all 20 subjects estimated with two-compartment modeling and Patlak plot analysis were not significantly different (P = 0.79). However, Patlak plot analysis occasionally resulted in negative estimates of Ktrans, which cannot be rationalized physiologically. This error may have been caused by poor linear regression fits of the measured Ctis(t) data versus the integral of Cbld(t) data, due to the relatively small number of blood and tissue enhancement data points (approximately five data points each at rest and stress) acquired during the increasing uptake phase of CA in the myocardium. This effect may have been increased in Ichihara et al. (8), in which the images were only acquired every other heartbeat. Also, because Patlak plot analysis does not explicitly account for Vb, like two-compartment modeling, slightly higher Ktrans estimates than those from the two-compartment model were expected. This was not seen in the aggregate results from these datasets and may be related to the assumption of kep = 0, as nonzero kep would likely reduce the Ktrans estimates.
Myocardial Perfusion Estimates From First-Pass Enhancement Data Versus Longer Acquisitions
Although myocardial perfusion estimates from two-compartment modeling and model-independent analysis were not significantly different when only the first pass of dynamic enhancement data was used in the analysis versus when all the measured data were used in the analysis (P = 0.27 and P = 0.21, respectively), results from Fermi function model were significantly different and approximately 25% higher when all the measured data were used in the analysis versus when only the first pass of dynamic enhancement data was used (P = 0.016). This difference is expected and is why most investigators take an extra step to delineate only the first pass of contrast uptake for use with Fermi function modeling. Also, because only the first pass of perfusion data is used in the Fermi function model, the washout parameter, k, does not provide meaningful physiologic information about the delayed kinetics of CA efflux from the extravascular, extracellular tissue space, which can be informative when the two-compartment model is used (49).
MRI Pulse Sequences and CA Doses
Since the four analysis methods used in this study employed the same blood and tissue enhancement curves, it was hypothesized that identical image acquisitions between subjects were not critical. In support of this belief, no systematic differences in perfusion estimates were found between the 16 subjects imaged with an SR-FLASH pulse sequence versus the four subjects imaged with a hybrid GRE-EPI pulse sequence. Both sequences had similar low-dose (0.016–0.023 mmol/kg) bolus injections of CA, and both sequences have been shown by other groups to yield quantitative estimates of myocardial perfusion (1–4,6,10,14,50). There were also no systematic differences found in perfusion estimates between the 12 subjects imaged with a 1.5-T MRI scanner and the eight subjects imaged with a 3-T MRI scanner or for perfusion estimates using the Gd-DTPA or Gd-BOPTA.
Though the relationship between changes in image signal intensity and CA concentration has been studied (50), there is still debate about how large a CA dose can be used while retaining linearity between changes in signal intensity and CA concentration. Several groups have used single bolus CA doses ranging between 0.01 and 0.03 mmol/kg, assuming that changes in signal intensity are linearly proportional to changes in CA concentration (1,6,10,20,25,32). Others have demonstrated that single-bolus CA doses as high as 0.04–0.05 mmol/kg can result in blood and tissue enhancement data that are linearly proportional to changes in CA concentration, which can be used for quantifying myocardial perfusion (2,33,34,53–55).
Alternatively, some investigators have found that CA doses higher than 0.005 mmol/kg result in signal saturation and have instead used very small doses of CA as part of a dual-bolus or prebolus injection scheme to reduce the potential for signal saturation effects (7,26,27,56,57). Others have used larger single-bolus CA doses (ranging from 0.05–0.1 mmol/kg) in tandem with analytical MRI signal equations to correct for potential signal saturation effects (5,21,47,48). Given the uncertainty of signal saturation effects with large doses of CA, all the subjects in this work were given relatively low-dose single-bolus injections of CA ranging between 0.01 and 0.027 mmol/kg.
Model Comparisons and Curve-Fit Errors
All of the analysis methods used in this study fit the measured tissue enhancement data well. Curve-fit errors were not reported for Patlak plot analysis because no curve fitting was performed. The slightly lower curve-fit errors found with model-independent analysis are likely due to the larger number of independent parameters that can be simultaneously adjusted to estimate h(t).
In general, model-independent analysis allows for more flexibility in the estimate of h(t) than two-compartment modeling and Fermi function modeling. This is likely due to the fact that it has more free parameters and because it is not characterized by a single decaying exponential function. The latter two methods, which only include one decaying exponential function, may oversimplify the complex kinetics of CA transfer in the myocardium, although this simplification may be reasonable, given that the perfusion estimates reported here were not significantly different between these three models.
One notable difference between the Fermi function model and the two-compartment model is the inclusion of the “shoulder” portion of the Fermi h(t) curve, which is not included in the two-compartment model. The shoulder in the impulse response effectively delays the exponential decay of h(t) and may better model the filling phase of the myocardial vasculature with blood. It may also better model the dispersion of the arterial input function as blood is delivered to different regions of the myocardium. In aggregate, the Fermi h(t) curves appear slightly more similar to the model-independent h(t) curves than the two-compartment model h(t) curves (Fig. 3). Alternatively, the two-compartment model includes the Vb parameter, which may accurately account for arterial blood in the myocardium.
CONCLUSIONS
In this work, aggregate myocardial perfusion estimates at rest in relatively large (coronary artery territory) regions were not significantly different between all four of the analysis methods: two-compartment modeling, Fermi function modeling, model-independent analysis, and Patlak plot analysis, when only the first-pass portion of the data was analyzed with each model. At stress, perfusion estimates from Fermi function modeling were significantly higher than in all three of the other models. However, the aggregate MPR values for all four methods were not significantly different, which suggests that any of these four models are useful for MPR measurements.
Myocardial perfusion estimates from two-compartment modeling and model-independent analysis were not significantly different when all the measured blood and tissue enhancement data were used in the analysis compared to when the data were truncated to only include the first pass of blood and tissue enhancement. Thus, neither of these two analysis methods requires that the dynamic enhancement data be truncated prior to analysis. Perfusion estimates from Fermi function modeling were significantly different (P = 0.016) and nearly 25% higher when all the acquired data were used versus when only the first-pass enhancement data were analyzed.
With the exception of the Fermi model at stress, the good agreement between the methods is a useful finding that allows more focus on standardization of acquisition protocols to be able to compare results between studies from different groups.
Acknowledgments
The authors thank the Ben B. and Iris M. Margolis Foundation. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institute of Biomedical Imaging and Bioengineering or the National Institutes of Health. The authors also thank Dr. Christopher McGann, Dr. Brent Wilson, and Henry Buswell for assistance with acquiring the MRI data.
Grant sponsor: National Institute of Biomedical Imaging and Bioengineering; Grant number: NIH R01EB000177
References
- 1.Jerosch-Herold M, Wilke N, Stillman AE. Magnetic resonance quantification of the myocardial perfusion reserve with a Fermi function model for constrained deconvolution. Med Phys. 1998;25:73–84. doi: 10.1118/1.598163. [DOI] [PubMed] [Google Scholar]
- 2.Jerosch-Herold M, Swingen C, Seethamraju RT. Myocardial blood flow quantification with MRI by model-independent deconvolution. Med Phys. 2002;29:886–897. doi: 10.1118/1.1473135. [DOI] [PubMed] [Google Scholar]
- 3.Christian TF, Rettmann DW, Aletras AH, Liao SL, Taylor JL, Balaban RS, Arai AE. Absolute myocardial perfusion in canines measured by using dual-bolus first-pass MR imaging. Radiology. 2004;232:677–684. doi: 10.1148/radiol.2323030573. [DOI] [PubMed] [Google Scholar]
- 4.Christian TF, Aletras AH, Arai AE. Estimation of absolute myocardial blood flow during first-pass MR perfusion imaging using a dual-bolus injection technique: comparison to single-bolus injection method. J Magn Reson Imaging. 2008;27:1271–1277. doi: 10.1002/jmri.21383. [DOI] [PubMed] [Google Scholar]
- 5.Fritz-Hansen T, Hove JD, Kofoed KF, Henning K, Larsson HBW. Quantification of MRI measured myocardial perfusion reserve in healthy humans: a comparison with positron emission tomography. J Magn Reson Imaging. 2008;27:818–824. doi: 10.1002/jmri.21306. [DOI] [PubMed] [Google Scholar]
- 6.Vallee J-P, Lazeyras F, Kasuboski L, Chatelain P, Howarth N, Righetti A, Didier D. Quantification of myocardial perfusion with FAST sequence and Gd bolus in patients with normal cardiac function. J Magn Reson Imaging. 1999;9:197–203. doi: 10.1002/(sici)1522-2586(199902)9:2<197::aid-jmri7>3.0.co;2-x. [DOI] [PubMed] [Google Scholar]
- 7.Ritter C, Brackertz A, Sandstede JJ, Beer M, Hahn D, Kostler H. Absolute quantification of myocardial perfusion under adenosine stress. Magn Reson Med. 2006;56:844–849. doi: 10.1002/mrm.21020. [DOI] [PubMed] [Google Scholar]
- 8.Ichihara T, Kitagawa K, Ichikawa Y, Natsume T, Yamaki N, Maeda H, Takeda K, Sakuma H. Quantitative analysis of first-pass contrast-enhanced myocardial perfusion MRI using a Patlak plot method and blood saturation correction. Magn Reson Med. 2009;62:373–383. doi: 10.1002/mrm.22018. [DOI] [PubMed] [Google Scholar]
- 9.Kurita T, Sakuma H, Onishi K, Ishida M, Kitagawa K, Yamanaka T, Tanigawa T, Kitamura T, Takeda K, Ito M. Regional myocardial perfusion reserve determined using myocardial perfusion magnetic resonance imaging showed a direct correlation with coronary flow velocity reserve by Doppler flow wire. Eur Heart J. 2009;30:444–452. doi: 10.1093/eurheartj/ehn521. [DOI] [PubMed] [Google Scholar]
- 10.Pack NA, DiBella EVR, McGann CJ, Rust TC, Kadrmas DJ, Butterfield R, Christian PE, Hoffman JM. Estimating myocardial perfusion from dynamic contrast-enhanced CMR with a model-independent deconvolution method. J Cardiol Magn Reson. 2008;10:52. doi: 10.1186/1532-429X-10-52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Anderson DH. Compartmental modeling and tracer kinetics. Springer-Verlag; New York: 1983. p. 302. [Google Scholar]
- 12.Tofts PS, Brix G, Buckley DK, Evelhoch JL, Henderson E, Knopp MV, Larsson HBW, Lee T-Y, Mayr NA, Parker GJM, Port RE, Taylor J, Weisskoff RM. Estimating kinetic parameters from dynamic contrast-enhanced T1-weighted MRI of a diffusible tracer: standardized quantities and symbols. J Magn Reson Imaging. 1999;10:223–232. doi: 10.1002/(sici)1522-2586(199909)10:3<223::aid-jmri2>3.0.co;2-s. [DOI] [PubMed] [Google Scholar]
- 13.St Lawrence KS, Lee TY. An adiabatic approximation to the tissue homogeneity model for water exchange in the brain, I: theoretical derivation. J Cereb Blood Flow Metab. 1998;18:1365–1377. doi: 10.1097/00004647-199812000-00011. [DOI] [PubMed] [Google Scholar]
- 14.Goldstein TA, Jerosch-Herold M, Misselwitz B, Zhang H, Gropler RJ, Zheng J. Fast mapping of myocardial blood flow with MR first-pass perfusion imaging. Magn Reson Med. 2008;59:1394–1400. doi: 10.1002/mrm.21559. [DOI] [PubMed] [Google Scholar]
- 15.Patlak CS, Blasberg RG, Fenstermacher JD. Graphical evaluation of blood-to-brain transfer constants from multiple-time uptake data. J Cereb Blood Flow Metab. 1983;3:1–7. doi: 10.1038/jcbfm.1983.1. [DOI] [PubMed] [Google Scholar]
- 16.Kroll K, Wilke N, Jerosch-Herold M, Wang Y, Zhang Y, Bache RJ, Bassingthwaighte JB. Modeling regional myocardial flows from residue functions of an intravascular indicator. Am J Physiol. 1996;271(4 pt 2):H1643–1655. doi: 10.1152/ajpheart.1996.271.4.H1643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zierler KL. Theoretical basis of indicator-dilution methods. Circ Res. 1962;10:393–407. [Google Scholar]
- 18.Crone C. The permeability of capillaries in various organs as determined by the use of the “indicator diffusion” method. Acta Physiol Scand. 1963;58:292–305. doi: 10.1111/j.1748-1716.1963.tb02652.x. [DOI] [PubMed] [Google Scholar]
- 19.Tong CY, Prato FS, Wisenberg G, Lee TY, Carroll E, Sandler D, Wills J, Drost D. Measurement of the extraction efficiency and distribution volume for Gd-DTPA in normal and diseased canine myocardium. Magn Reson Med. 1993;30:337–346. doi: 10.1002/mrm.1910300310. [DOI] [PubMed] [Google Scholar]
- 20.Vallee J-P, Sostman HD, MacFall JR, DeGrado TR, Zhang J, Sebbag L, Cobb FR. Quantification of myocardial perfusion by MRI after coronary occlusion. Magn Reson Med. 1998;40:287–297. doi: 10.1002/mrm.1910400215. [DOI] [PubMed] [Google Scholar]
- 21.Larsson HBW, Fritz-Hansen T, Rostrup E, Sondergaard L, Ring P, Henriksen O. Myocardial perfusion modeling using MRI. Magn Reson Med. 1996;35:716–726. doi: 10.1002/mrm.1910350513. [DOI] [PubMed] [Google Scholar]
- 22.Reif F. Fundamentals of statistical and thermal physics. McGraw-Hill; 1965. [Google Scholar]
- 23.Axel L. Tissue mean transit time from dynamic computed tomography by a simple deconvolution technique. Invest Radiol. 1983;8:94–99. doi: 10.1097/00004424-198301000-00018. [DOI] [PubMed] [Google Scholar]
- 24.Clough AV, al-Tinawi A, Linehan JH, Dawson CA. Regional transit time estimation from image residue curves. Ann Biomed Eng. 1994;22:128–143. doi: 10.1007/BF02390371. [DOI] [PubMed] [Google Scholar]
- 25.Muehling OM, Wilke NM, Panse P, Jerosch-Herold M, Wilson BV, Wilson RF, Miller LW. Reduced myocardial perfusion reserve and transmural perfusion gradient in heart transplant arteriopathy assessed by magnetic resonance imaging. J Am Coll Cardiol. 2003;42:1054–1060. doi: 10.1016/s0735-1097(03)00924-0. [DOI] [PubMed] [Google Scholar]
- 26.Hsu LY, Rhoads KL, Holley JE, Kellman P, Aletras AH, Arai AE. Quantitative myocardial perfusion analysis with a dual-bolus contrast-enhanced first-pass MRI technique in humans. J Magn Reson Imaging. 2006;23:315–322. doi: 10.1002/jmri.20502. [DOI] [PubMed] [Google Scholar]
- 27.Utz W, Greiser A, Niendorf T, Dietz R, Schulz-Menger J. Single- or dual-bolus approach for the assessment of myocardial perfusion reserve in quantitative MR perfusion imaging. Magn Reson Imag. 2008;59:1373–1377. doi: 10.1002/mrm.21611. [DOI] [PubMed] [Google Scholar]
- 28.Gatehouse PD, Elkington AG, Ablitt NA, Yang GZ, Pennell DJ, Firmin DN. Accurate assessment of the arterial input function during high-dose myocardial perfusion cardiovascular magnetic resonance. J Magn Reson Imaging. 2004;20:39–45. doi: 10.1002/jmri.20054. [DOI] [PubMed] [Google Scholar]
- 29.Singer OC, de Rochemont RM, Foerch C, Stengel A, Lanfermann H, Sitzer M, Neumann-Haefelin T. Relation between relative cerebral blood flow, relative cerebral blood volume, and mean transit time in patients with acute ischemic stroke determined by perfusion-weighted MRI. J Cereb Blood Flow Metab. 2003;23:605–611. doi: 10.1097/01.WCB.0000062342.57257.28. [DOI] [PubMed] [Google Scholar]
- 30.Sourbron S, Dujardin M, Makkat S, Luypaert R. Pixel-by-pixel deconvolution of bolus tracking data: optimization and implementation. Phys Med Biol. 2007;52:429–447. doi: 10.1088/0031-9155/52/2/009. [DOI] [PubMed] [Google Scholar]
- 31.Makkat S, Luypaert R, Sourbron S, Stadnik T, DeMey J. Quantification of perfusion and permeability in breast tumors with a deconvolution-based analysis of second-bolus T1-DCE data. J Magn Reson Imaging. 2007;25:1159–1167. doi: 10.1002/jmri.20937. [DOI] [PubMed] [Google Scholar]
- 32.Goldstein TA, Zhang H, Misselwitz B, Gropler RG, Zheng J. Improvement of quantification of myocardial first-pass perfusion mapping: a temporal and spatial wavelet denoising method. Magn Reson Med. 2006;56:439–445. doi: 10.1002/mrm.20950. [DOI] [PubMed] [Google Scholar]
- 33.Selvanayagam JB, Jerosch-Herold M, Porto I, Sheridan D, Cheng AS, Petersen SE, Searle N, Channon KM, Banning AP, Neubauer S. Resting myocardial blood flow is impaired in hibernating myocardium: a magnetic resonance study of quantitative perfusion assessment. Circulation. 2005;112:3289–3296. doi: 10.1161/CIRCULATIONAHA.105.549170. [DOI] [PubMed] [Google Scholar]
- 34.Wang L, Jerosch-Herold M, Jacobs DR, Jr, Shahar E, Folsom AR. Coronary risk factors and myocardial perfusion in asymptomatic adults: the Multi-Ethnic Study of Atherosclerosis (MESA) J Am Coll Cardiol. 2006;47:565–572. doi: 10.1016/j.jacc.2005.09.036. [DOI] [PubMed] [Google Scholar]
- 35.Phillips DL. A technique for the numerical solution of certain integral equations of the first kind. J Assoc Comput Mach. 1962;9:84–97. [Google Scholar]
- 36.Tikhonov AN, Goncharsky AV, Stepanov VV, Yagola AG. Numerical methods for the solution of ill-posed problems. Dordrecht, The Netherlands: Kluwer; 1995. [Google Scholar]
- 37.Snyman JA. Practical mathematical optimization: an introduction to basic optimization theory and classical and new gradient-based algorithms. Springer Publishing; 2006. [Google Scholar]
- 38.Hansen PC. Analysis of discrete ill-posed problems by means of the L-curve. SIAM Rev. 1992;34:561–580. [Google Scholar]
- 39.Pintaske J, Martirosian P, Graf H, Erb G, Lodemann KP, Claussen CD, Schick F. Relaxivity of gadopentetate dimeglumine (Magnevist), gadobutrol (Gadovist), and gadobenate dimeglumine (MultiHance) in human blood plasma at 0.2, 1. 5, and 3 tesla. Invest Radiol. 2006;1:213–221. doi: 10.1097/01.rli.0000197668.44926.f7. [DOI] [PubMed] [Google Scholar]
- 40.Thomsen HS, Morcos SK, Dawson P. Is there a causal relation between the administration of gadolinium based contrast media and the development of nephrogenic systemic fibrosis (NSF)? Clin Radiol. 2006;61:905–906. doi: 10.1016/j.crad.2006.09.003. [DOI] [PubMed] [Google Scholar]
- 41.Shellock FG, Parker JR, Venetianer C, Pirovano G, Spinazzi A. Safety of gadobenate dimeglumine (MultiHance): summary of findings from clinical studies and postmarketing surveillance. Invest Radiol. 2006;41:500–509. doi: 10.1097/01.rli.0000209661.99225.c2. [DOI] [PubMed] [Google Scholar]
- 42.Gebker R, Schwitter J, Fleck E, Nagel E. How we perform myocardial perfusion with cardiovascular magnetic resonance. J Cardiovasc Magn Reson. 2007;9:539–547. doi: 10.1080/10976640600897286. [DOI] [PubMed] [Google Scholar]
- 43.Jerosch-Herold M, Hu X, Murthy NS, Seethamraju RT. Time delay for arrival of MR contrast agent in collateral-dependent myocardium. IEEE Trans Med Imaging. 2004;23:881–890. doi: 10.1109/TMI.2004.827969. [DOI] [PubMed] [Google Scholar]
- 44.Cerqueira MD, Weissman NJ, Dilsizian V, Jacobs AK, Kaul S, Laskey WK, Pennell DJ, Rumberger JA, Ryan T, Verani MS. Standardized myocardial segmentation and nomenclature for tomographic imaging of the heart: a statement for healthcare professionals from the Cardiac Imaging Committee of the Council on Clinical Cardiology of the American Heart Association. Circulation. 2002;105:539–542. doi: 10.1161/hc0402.102975. [DOI] [PubMed] [Google Scholar]
- 45.DiBella EVR, Kholmovski EG. Accuracy of assuming uniform temporal sampling in the analysis of cardiac perfusion MRI datasets. Proceedings of the 14th annual meeting of ISMRM; Seattle, WA, USA. 2006. p. 3577. [Google Scholar]
- 46.Zar JH. Biostatistical analysis. 5. Pearson Publishing; 1998. [Google Scholar]
- 47.Fritz-Hansen T, Rostrup E, Søndergaard L, Ring PB, Amtorp O, Larsson HBW. Capillary transfer constant of Gd-DTPA in the myocardium at rest and during vasodilation assessed by MRI. Magn Reson Med. 1998;40:922–929. doi: 10.1002/mrm.1910400619. [DOI] [PubMed] [Google Scholar]
- 48.Nielsen G, Fritz-Hansen T, Dirks CG, Jensen GB, Larsson HB. Evaluation of heart perfusion in patients with acute myocardial infarction using dynamic contrast-enhanced magnetic resonance imaging. J Magn Reson Imaging. 2004;20:403–410. doi: 10.1002/jmri.20142. [DOI] [PubMed] [Google Scholar]
- 49.Pack NA, DiBella EVR, Wilson BD, McGann CJ. Quantitative myocardial distribution volume from dynamic contrast-enhanced MRI. Magn Reson Imaging. 2008;26:532–542. doi: 10.1016/j.mri.2007.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Kellman P, Arai AE. Imaging sequences for first pass perfusion—a review. J Cardiovasc Magn Reson. 2007;9:525–537. doi: 10.1080/10976640601187604. [DOI] [PubMed] [Google Scholar]
- 51.Ivancevic MK, Zimine I, Lazeyras F, Foxall D, Vallee J-P. FAST sequences optimization for contrast media pharmacokinetic quantification in tissue. J Magn Reson Imaging. 2001;14:771–778. doi: 10.1002/jmri.10009. [DOI] [PubMed] [Google Scholar]
- 52.Epstein FH, London JF, Peters DC, Goncalves LM, Agyeman K, Taylor J, Balaban RS, Arai AE. Multislice first-pass cardiac perfusion MRI: validation in a model of myocardial infarction. Magn Reson Med. 2002;47:482–491. doi: 10.1002/mrm.10085. [DOI] [PubMed] [Google Scholar]
- 53.Jerosch-Herold M, Vazquez G, Wang L, Jacobs DR, Jr, Folsom AR. Variability of myocardial blood flow measurements by magnetic resonance imaging in the multi-ethnic study of atherosclerosis. Invest Radiol. 2008;43:155–161. doi: 10.1097/RLI.0b013e31815abebd. [DOI] [PubMed] [Google Scholar]
- 54.Vallee J-P, Sostman HD, MacFall JR, Wheeler T, Hedlund LW, Spritzer CE, Coleman RE. MRI quantitative myocardial perfusion with compartmental analysis: a rest and stress study. Magn Reson Med. 1997;38:981–989. doi: 10.1002/mrm.1910380618. [DOI] [PubMed] [Google Scholar]
- 55.Parkka JP, Niemi P, Saraste A, Koskenvuo JW, Komu M, Oikonen V, Toikka JO, Kiviniemi TO, Knuuti J, Sakuma H, Hartiala JJ. Comparison of MRI and positron emission tomography for measuring myocardial perfusion reserve in healthy humans. Magn Reson Med. 2006;55:772–779. doi: 10.1002/mrm.20833. [DOI] [PubMed] [Google Scholar]
- 56.Hsu LY, Kellman P, Arai AE. Nonlinear myocardial signal intensity correction improves quantification of contrast-enhanced first-pass MR perfusion in humans. J Magn Reson Imaging. 2008;27:793–801. doi: 10.1002/jmri.21286. [DOI] [PubMed] [Google Scholar]
- 57.Kostler H, Ritter C, Lipp M, Beer M, Hahn D, Sandstede J. Prebolus quantitative MR heart perfusion imaging. Magn Reson Med. 2004;52:296–299. doi: 10.1002/mrm.20160. [DOI] [PubMed] [Google Scholar]
- 58.Cullen JHS, Horsfield MA, Reek CR, Cherryman GR, Barnett DB, Samani NJ. A myocardial perfusion reserve index in humans using first-pass contrast-enhanced magnetic resonance imaging. J Am Coll Cardiol. 1999;33:1386–1394. doi: 10.1016/s0735-1097(99)00004-2. [DOI] [PubMed] [Google Scholar]
- 59.Ibrahim T, Nekolla SG, Schreiber K, Odaka K, Volz S, Mehilli J, Guthlin M, Delius W, Schwaiger M. Assessment of coronary flow reserve: comparison between contrast-enhanced magnetic resonance imaging and positron emission tomography. J Am Coll Cardiol. 2002;39:864–870. doi: 10.1016/s0735-1097(01)01829-0. [DOI] [PubMed] [Google Scholar]