Comparing Pre- and Post-Operative Fontan Hemodynamic Simulations: Implications for the Reliability of Surgical Planning

Abstract

Background

Virtual modeling of cardiothoracic surgery is a new paradigm that allows for systematic exploration of various operative strategies and uses engineering principles to predict the optimal patient-specific plan. This study investigates the predictive accuracy of such methods for the surgical palliation of single ventricle heart defects.

Methods

Computational fluid dynamics (CFD)-based surgical planning was used to model the Fontan procedure for four patients prior to surgery. The objective for each was to identify the operative strategy that best distributed hepatic blood flow to the pulmonary arteries. Post-operative magnetic resonance data were acquired to compare (via CFD) the post-operative hemodynamics with predictions.

Results

Despite variations in physiologic boundary conditions (e.g., cardiac output, venous flows) and the exact geometry of the surgical baffle, sufficient agreement was observed with respect to hepatic flow distribution (90% confidence interval-14 ± 4.3% difference). There was also good agreement of flow-normalized energetic efficiency predictions (19 ± 4.8% error).

Conclusions

The hemodynamic outcomes of prospective patient-specific surgical planning of the Fontan procedure are described for the first time with good quantitative comparisons between preoperatively predicted and postoperative simulations. These results demonstrate that surgical planning can be a useful tool for single ventricle cardiothoracic surgery with the ability to deliver significant clinical impact.

Introduction

The total cavopulmonary connection (TCPC), a variation of Fontan’s procedure¹¹, is the current surgical method of choice for the palliation of single ventricle congenital heart defects⁴. This staged series of operations ultimately creates a right-heart bypass via the direct connection of the superior and inferior vena cavae (SVC, IVC) to the pulmonary arteries (PA). While this intervention successfully restores a series configuration to the cardiovascular circuits, the resulting hemodynamics are severely altered given the need for systemic venous pressure to passively drive pulmonary flow. Therefore, despite improved surgical outcomes, numerous long-term complications have been documented^{17, 19}.

For a handful of these complications, there is strong evidence suggesting a link between the specific characteristics of blood flow through the TCPC and the cause or exacerbation of the complication. The most prominent example of such relationships is the development of pulmonary arteriovenous malformations (PAVM) (causing progressive hypoxia) because of the maldistribution of hepatic factors produced by the liver to the pulmonary vasculature⁹. Another example is impaired exercise capacity^{23, 26} due in part to non-linear increases in the energy dissipated through the TCPC pathway with increased cardiac output^{25, 31, 33}. Therefore, ensuring an efficient TCPC design with a balanced hepatic flow distribution (HFD) may yield long-term benefits for patient health and quality of life.

Virtual surgical planning of the Fontan procedure has been proposed to help achieve desired flow characteristics on a patient-specific basis²¹. Through this truly translational technique, the surgeon and clinical team are able to virtually mimic various surgical options on the medical imaging-derived patient anatomy, and then evaluate the hemodynamic consequences of each design using computational fluid dynamics (CFD). Previous reports have detailed the prospective use of such techniques for single ventricle patients and based the estimation of their effectiveness on measures such as improving arterial oxygen saturations, which are clinically meaningful yet inconclusive for confirming modeled predictions^{7, 28}. Thus, while a key assumption of these methods is the accuracy of preoperative predictions with respect to postoperative hemodynamic outcomes, detailed quantitative comparisons between pre- and post-operative hemodynamic metrics have not yet been reported.

The objective of this study is to quantify the impact of the numerous unknown variables inherent to prospective surgical modeling (e.g., geometric agreement, adaptation of input and output boundary conditions) to assess the predictive power of the virtual surgery paradigm. We present findings from a consecutive series of single ventricle patients for whom these techniques were employed and post-operative cardiac magnetic resonance (CMR) images were acquired.

Materials and Methods

Patients: The study was approved by the Institutional Review Boards at Georgia Tech, the Children’s Hospital of Philadelphia (CHOP), and Children’s Healthcare of Atlanta (CHOA). The characteristics of 4 single ventricle patients who underwent both preoperative surgical planning and postoperative CMR are provided in Table 1. Patient 1 was treated at CHOA, while patients 2-4 were treated at CHOP. PAVMs were present in each case and represented the primary reason for clinical referral for surgical planning. Patients 1-3 had an interrupted IVC, in which all inferior blood flow (except for the hepatic flow from the liver) was carried by an enlarged azygos vein, while the hepatic veins natively drained into the right atrium. Patient 4 had an intact IVC pathway and bilateral superior venae cavae (SVC). Patient 1 was recommended for surgical planning for the revision of a previous Fontan connection because of unilateral hepatic flow streaming, while for the three other cases (patients 2-4), the planned procedure was the initial Fontan. [TABLE 1]

Table 1.

Patient Characteristics and Imaging Details

				Image Detail
Pt	Age (yrs)	BSA (m2)*	PAVM Side	Pixel Size [mm2] (Scan 1/2)	Slice Thickness [mm] (Scan 1/2)	Pre-Op O2 Saturation (%)	Post-Op O2 Saturation (Follow-up duration in months)
1	18	1.49	Right	1.33/1.41	9/5	N/A	N/A†
2	2	0.59	Right	0.86	3	85	95 (16.5)
3	2.8	0.61	Left	0.7/0.86	3	61	72 (1)
4	2.3	0.46	Left	0.78	3	86	96 (8)

^*Body Surface Area (at pre-operative CMR)

^†N/A- Not available: Post-operative saturations not acquired under room air, less than 5 days post-operatively

Clinical Imaging and Reconstruction

The image resolution details are provided in Table 1. An axial stack of steady-state free precession images was acquired through the thorax to allow for anatomic segmentation and reconstruction¹². In addition, phase velocity measurements were acquired in a single plane perpendicular to all systemic venous pathway vessels (SVC and IVC (when present), azygos vein, branch pulmonary arteries), plus the aorta, to provide boundary conditions for the simulations²⁹. In all cases, post-operative imaging occurred in the hospital prior to discharge (5-10 days following surgery).

Virtual Surgery

The pre-operative patient reconstructions, inclusive of the ventricle, aorta, and pulmonary veins, were imported into the SURGEM virtual surgery interface²¹. At the guidance of the surgeon, and based on patient-specific anatomic landmarks and limitations, various surgical options were created for each patient (on average 4 to 5). These virtual models served as the basis for the pre-operative CFD-based evaluation.

Numerical Methods

Numerical simulations were conducted using a validated^{5, 6, 14, 28}, unstructured sharp-interface immersed-boundary method⁶ with a 2^nd order, unsteady fractional step implementation¹³. This approach is advantageous for surgical planning because it simplifies the meshing process required for simulating the various surgical options. Rather than creating a volume mesh for each case, only a triangular surface mesh (created in GAMBIT; Fluent, Inc., Lebanon, NH) was required before registration within the Cartesian grid. Grid spacing was set at 2% of IVC/hepatic vein diameter for each model, which has previously been shown to yield mesh independent results⁶. Resulting model element numbers ranged from 500k to 3.3 million. Blood was assumed to be incompressible (density=1060 kg/m³) and Newtonian (kinematic viscosity=3.5 cSt). In all cases, the boundary conditions (BCs) were imposed as flow rates at the inlets and outlets.

Simulations were conducted on a 64-bit Linux workstation with 2 Intel Xeon six core 3.33 GHz processors. Results were considered converged when the residual of the Poisson pressure solver at each time step reduced by 10⁻⁸ and either the running average of velocities at numerous monitor points in the domain converged to the instantaneous values (time-averaged simulations) or cycle-to-cycle consistency of instantaneous velocities at the monitor points was achieved (pulsatile simulations-usually requiring 4-5 cardiac cycles).

Surgical Planning Evaluation

BCs for the surgical planning analyses were all time-averaged because the IVC/hepatic vein connection to the contracting atrium pre-operatively (before surgical re-routing to the PAs) creates significant variations in pulsatile amplitude (as high as ± 2 L/min) that are not present in the post-operative measurements, once the IVC/hepatic vein is re-routed to the PAs. It was thus assumed that the time-averaged pre-operative flow conditions would better approximate the post-operative flows than the measured time-varying conditions. Figure 1 supports this rationale as the averaged pre-operative value (dashed line) is a closer match to the time-varying post-operative flows than are the pulsatile pre-operative measures. [FIGURE 1].

Figure 1.

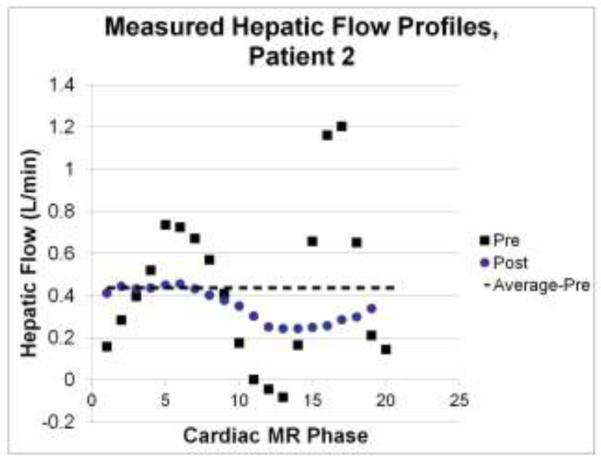
CMR phase velocity-derived flow rates for the hepatic vein in patient 2 both pre- and post-operatively. The time-average pre-operative value for this patient is clearly a better approximation of the post-operative conditions, thus justifying the use of time-averaged flow conditions for the pre-operative simulations.

Because the use of flow boundary conditions at the model outlets is not responsive to either physiologic changes in downstream pulmonary vascular resistance or small potential variations in the internal resistance of the TCPC as a function of connection design, each connection was parametrically evaluated at multiple outflow split conditions. This practice provides insight into the performance of the various connections under both the expected post-operative physiologic conditions, as well as potential variations thereof. That is one way in which unstable designs (i.e., those that only have desirable performance characteristics under a narrow range of operating characteristics) can be identified and discarded.

HFD and hemodynamic power loss are the most commonly used metrics for surgical planning studies, and TCPC modeling studies in general^{3, 8}. Per standard practice, the power loss (${\stackrel{.}{E}}_{\mathit{Loss}}$) was calculated using principles of control volume energy balance according to:

$${\stackrel{.}{E}}_{\mathit{Loss}}=\sum _{\text{inlets}}\underset{A}{\int }(p+\frac{1}{2}\rho {\nu }^2)\nu \cdot \mathit{dA}-\sum _{\text{outlets}}\underset{A}{\int }(p+\frac{1}{2}\rho {\nu }^2)\nu \cdot \mathit{dA}$$

where p is the static pressure, π is the blood density, A is area of the inlet/outlet, and v the velocity. When reported as connection resistance (R), an energy loss-based pressure drop ($\Delta {\mathrm{P}}_{\mathrm{TCPC}}=\frac{{\stackrel{.}{E}}_{\mathit{loss}}}{Q_{\mathit{VC}}}$) was normalized by the flow rate through the connection (Q_VC) and body surface area (BSA) as: $R=\frac{\Delta P_{\mathrm{TCPC}}}{Q_{\mathit{VC}}∕\mathit{BSA}}$.³¹ HFD was assessed by uniformly seeding velocity streamlines across the IVC or hepatic venous (HepV) cross-section and quantifying the percentage of blood flux through the LPA and RPA.

Post-operative Comparison

Because both patient-specific anatomy and flow conditions were variables in this analysis, multiple simulations were performed for each patient to isolate their effects. Specifically, in addition to the time-averaged pre-operative analysis, which is simulation (1a), four simulations were run for each patient after the surgery:

1. The retained surgical planning model under:

   1. time-averaged pre-operative BCs
   2. pulsatile post-operative BCs
   3. time-averaged pre-operative inflows and time-averaged post-operative PA outflow split BCs
2. In vivo post-operative anatomy under:

   1. time-averaged pre-op BCs
   2. pulsatile post-op BCs (i.e., actual outcome)

Comparison of 1a vs. 2b provides an assessment of the surgical planning predictive power with respect the primary planning endpoint of hepatic flow distribution. A comparison of 1c vs. 2b is instead used to assess connection resistance in order to remove the confounding effects of varying flow through a stenotic vessel (e.g., the LPA of patient 2). Comparing 1a vs. 2a and 1b vs. 2b provides insights into the impact of geometric variation; 1a vs. 1b vs. 1c and 2a vs. 2b was used to isolate the impact of the varying inflow and outflow BCs. Rigid vessel walls were assumed in all cases.

Unlike the time-averaged analyses, HFD for pulsatile simulations was assessed by uniformly seeding massless particles across an IVC/HepV cross-section at 50 evenly spaced time intervals throughout one cardiac cycle and advected through the time-varying velocity field using a fourth order Runge-Kutta scheme²⁰. The percentage distribution of the particles to the LPA and RPA were quantified once all particles had been completely washed through the connection during the subsequent cardiac cycles.

Geometric Analysis

TCPC geometric analysis was performed using the vascular modeling toolkit (VMTK; vmtk.org) to quantitatively compare anatomic features of the surgical planning and actual post-operative connections for each patient, and help explain hemodynamic differences. The centerlines of each vessel were automatically extracted from the geometry and used to calculate the mean and minimum radii.

Results

Pre-Operative Analysis

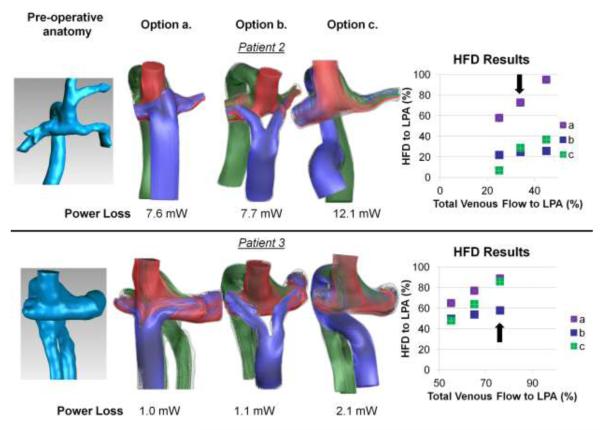
Representative pre-operative flow streaming, HFD, and power loss results for three different surgical options for patients 2 and 3 are shown in Figure 2. The envisioned options represented (a) traditional extracardiac, (b) bifurcated (Y-graft)^{15, 16, 27}, and (c) hepatic-to-azygos connections. The arrows in the HFD plots denote the pre-operatively measured flow split condition from which the included streamline and power loss results were derived. The additional points represent different post-operative evolutionary scenarios related to the effect of PAVM regression⁷ or growth-related factors on the total pulmonary distribution. [FIGURE 2]

Figure 2.

Results from pre-operative modeling of patients 2 and 3. Far left: pre-operative Kawashima connections (azygos vein and SVC connected to PAs); Middle panels: Flow streaming results for three of the surgical options investigated representing (a) extracardiac, (b) bifurcated (Y-Graft), and (c) hepatic-to-azygos approaches; Far right: HFD curves for each model of the range of outflow splits investigated. Arrow on HFD plot denotes the pre-operatively measured PA split, which correspond to the flow stream and power loss results shown. Streamlines are color-coded by vessel of origin (red-RSVC; blue-HepV/IVC; green-AZ)

Because of relatively low flow momentum through the hepatic venous baffle (blue streamlines), the distribution characteristics of extracardiac connections (Fig. 2a) are known to be extremely sensitive to baffle placement and offset in these patients⁷, which made them poorly suited, unrobust options for both cases. The impinging of SVC flow (red streamlines) into the hepatic baffle in pt. 3 demonstrates this point- the exact nature of the interaction between the colliding flows is tightly coupled to their relative geometric position. Conversely, the HFD results for the other two options were positive based on: 1) the majority of hepatic flow perfusing the diseased lung over the range of conditions investigated, and 2) relatively small distribution changes with varying outflow conditions. The distinguishing factors were therefore determined to be the relative insensitivity of the Y-graft distribution to changes in PA split, and the lower power loss of the Y-graft compared to the Hepatic-to-Azygos. Thus, the Y-graft option was recommended for use in both of these patients.

Post-Operative TCPC Geometry [FIGURE 3]

Figure 3.

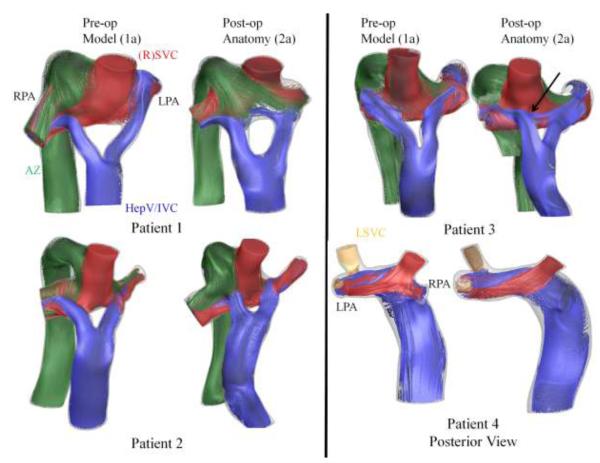
Comparison of pre-operative surgical models (in blue) with post-operative connection design (in red), including a registered overlay of the two, for all four investigated patients.

To demonstrate the geometric agreement between the virtual surgery model and post-operative TCPC reconstructions, Figure 3 provides a qualitative comparison of the virtual geometry (in blue) to the real anatomy (in red). In three cases, the Fontan procedure was performed using commercially available bifurcated aorto-iliac polytetrafluoroethylene (PTFE) grafts (Gore-Tex; Flagstaff, AZ) sized at 18-9-9 mm (patient 1) and 14-7-7 mm (patients 2 and 3)¹⁶. The 4^th patient received a 20 mm extracardiac conduit connection to the right SVC.

There were significant vessel diameter differences measured in all cases (average difference was 1.2 mm) (Table 2). Many of these changes were unrelated to the surgical baffle/intervention given the physical separation involved, instead demonstrating an effect of both imaging (Table 1) and image processing related parameters. The observed size difference in the SVC-azygos “pouch” region for patient 1, for example, is related to the large and differing slice thicknesses used for the image acquisitions. [TABLE 2]

Table 2.

TCPC Vessel Diameter Comparison [all in mm]

Pt		IVC/HepV		Right SVC		Left SVC		AZ*		LPA		RPA
		ave|	min#	ave	min	ave	min	ave	min	ave	min	ave	min
1	Pre	17.5	16.0	17.7	15.7			15.4	12.7	11.8	6.9	13.6	12.7
	Post	16.4	15.7	15.3	14.2			11.7	9.9	8.4	6.1	12.2	11.7
2	Pre	13.1	10.3	12.1	10.0			9.5	8.0	5.5	3.9	9.3	8.7
	Post	11.7	8.4	11.2	10.3			7.5	6.7	5.7	4.4	8.9	6.9
3	Pre	13.2	10.9	13.3	12.1			7.8	3.0	11.5	10.8	9.6	8.7
	Post	11.9	10.8	13.8	12.7			6.6	4.1	10.6	8.9	8.3	7.7
4	Pre	18.3	15.4	8.2	7.3	7.6	6.8			9.5	7.6	7.7	6.0
	Post	17	15.6	7.5	7.0	6.0	5.7			8.9	7.7	9.2	6.5

^*AZ= azygos vein

^|avee= average

^#min= Minimum

Other than the differences in pre/post vessel dimensions, minor variations with respect to the exact angle and positioning of the surgical baffle (IVC/HepV) were observed. The largest discrepancies are apparent in patients 3 (medial placement of right Y branch) and 4 (varied IVC offset).

Hemodynamic Changes from Geometric Variation

To isolate the hemodynamic impact of the observed surgical variations and image reconstruction differences, both the surgical planning and post-operative geometries were simulated under time-averaged, pre-operative boundary conditions (simulations 1a and 2a). The results (Figure 4, Table 3) demonstrated that the effects of geometric mismatch (both surgically-mediated and image-processing related) can be significant. Previous studies have shown strong correlations between minimum PA size and power loss across the TCPC², and the present changes in power loss directly corresponded to variations in the minimum reconstructed PA sizes in each case. As a result, the geometric errors in power loss values ranged between 18-68% with an average of 39%. For HFD, differences ranged between 2-18%, with surgical baffle mismatch (Figure 3) mediating the largest discrepancies (pts. 3, 4). [FIGURE 4, TABLE 3]

Figure 4.

Comparison of pre- and post-operative connections under steady, pre-operative flow conditions. Streamlines are color-coded by vessel of origin (red-RSVC; blue-HepV/IVC; green-AZ; yellow-LSVC).

Table 3.

Geometry-Related Differences: Hemodynamics under Pre-Operative Flow Conditions (Comparison of Simulations 1a and 2a)

Patient	HFD [% LPA] (Surg. Planning Model/ Post-Op Connection)	Hemodynamic Explanation	Power Loss [mW] (Surg. Planning Model/ Post-Op Connection )	Hemodynamic Explanation
1	23 / 14	AZ flow impinging on Rt branch outlet	1.9 / 3.2	Pouch and PA size differences
2	25 / 27		7.7 / 5.1	Different PA size
3	58 / 72	Medial placement of right Y-branch	1.1 / 1.3	Different PA size
4	52 / 34	IVC Offset variation	2.3 / 1.5	Different PA size

Post-Operative Data

The pre- and post-operative arterial oxygen saturation percentages (breathing room air) for 3 of the 4 patients are listed in Table 1. In the 4^th case (pt. 1), the only post-operative saturation data were acquired within 5 days of surgery while the patient was still receiving high flow oxygen via nasal cannula, and the values are therefore not comparable. Oxygen saturations improved in the remaining three cases, including two that were in the mid-90s. Saturations for patient 3 had only improved to 72% (from 61%) at last report, but that was still within 1 month of surgery.

Table 4 shows the phase velocity CMR-derived flows by vessel, plus the cardiac output (measured in the aorta) for each patient. Cardiac output decreased after surgery in 3 of the 4 cases. With respect to TCPC flows, the relative percentage distributions of each vessel were different following surgery; the magnitude of those changes ranged anywhere from 2 to 22%. Notably, the PA changes were all in favor of higher flow percentage toward the lung with PAVM. [TABLE 4]

Table 4.

CMR-derived flow rates

			Percentage Distributions
Patient	Measurement Time	Ao* (L/min)	HepV/IVC	Right SVC	Left SVC	AZ	LPA	RPA
Pt. 1	Pre	3.3	17	34		49	−23	c−77
	Post	2.4	21	52		27	−18	−82
Pt. 2	Pre	2.9	18	54		28	−34	−66
	Post	1.8	30	47		23	−13	−87
Pt. 3	Pre	3.2	18	56		26	−76	−24
	Post	3.7	16	72		12	−85	−15
Pt. 4	Pre	2.6	56	25	19		−62	−38
	Post	1.8	58	20	22		−69	−31

^*Aorta

Hemodynamic Changes from Flow Rate Variation

Figure 5 shows representative, instantaneous streamlines for the CFD-derived post-operative flows (simulation 2b) for each patient. Despite the noted quantitative flow differences, the results for patients 2 and 3 are qualitatively very similar to their corresponding steady flow results (simulation 2a) from Figure 4. For patients 1 and 4, the impact of (decreased) azygos and (increased) IVC flow changes, respectively, are more evident in the 3D hemodynamic differences. [FIGURE 5]

Figure 5.

Representative instantaneous velocity streamlines (color-coded by vessel of origin) from the time-varying post-operative flow simulations on the actual post-operative connections for all four patients.

The hemodynamic results as a function of imposed flow conditions are reported for the surgical planning models and the post-operative anatomies in Tables 5 and 6, respectively. To isolate the effect of varied PA splits from the total change in TCPC flow conditions, Table 5 also provides the results of combining post-operative outflow splits with pre-operative inflow conditions (simulation 1c). The HFD differences ranged between 3-19% (mean of 13%) and 8-21% (mean of 17%) for the virtual models and post-op anatomies, respectively.

Table 5.

Effect of Boundary Condition Variations: Surgical planning models (comparison of simulations 1a,1b,1c)

	HFD [%LPA]			Resistance [mmHg*min/L]
Pt	Pre-op BC	Pre inflow; Post outflow	Post-op BC	Pre-op BC	Pre inflow; Post outflow	Pulsatile Post-op BC
1	23	19	40	0.26	0.28	0.19
2	25	17	28	0.77	0.27	0.2
3	58	58	77	0.18	0.21	0.24
4	52	61	66	0.2	0.18	0.14

Table 6.

Effect of Boundary Condition Variations: Post-operative Anatomy (comparison of simulations 2a and 2b)

Patient	HFD [%LPA] (Pre BC / Post BC)	Hemodynamic Explanation	Connection Resistance [mmHg*min/L] (Pre BC / Pulsatile Post BC)
1	14 / 35	Varied venous flow distributions	0.44 / 0.22
2	27 / 35	Varied venous flow distributions	0.51 / 0.32
3	72 / 91	Varied venous flow distributions	0.22 / 0.35
4	34 / 54	Increased Total LPA Flow	0.14 / 0.18

Connection energetics in tables 5 and 6 are reported as resistance to partially correct for the noted changes in bulk flow rates. Generally minor variations were seen as a function of PA split (Table 5) owing to differences in vessel size. This effect was substantial for pt. 2 because of the relatively small size of the LPA. Neglecting PA size effects and comparing only the 5^th and 6^th columns, the efficiency errors as a function of systemic flow variations ranged from 14-32% with an average of 24%. [TABLES 5, 6]

Efficiency Rankings

To further evaluate the impact of power loss variations with physiologic changes, Table 7 compares the connection resistances and associated relative rankings for the 3 potential options pre-operatively analyzed for patients 2 and 3 (Figure 2). For pt. 2, despite the change in the absolute resistance values, the associated rankings were unchanged. For pt. 3, the order did vary because of the large variation in SVC and azygos flow contributions. The increased SVC flow post-operatively led to much greater dissipation and resistance through collision with the ‘t-junction’ extracardiac model, while decreased azygos flow meant lower resistance for the hepatic-to-azygos connection. [TABLE 7]

Table 7.

Relative Efficiency Rankings (Pre- vs. Post-Operative) for Selected Surgical Options

	Pre- operative Resistance	Pre- operative Rank	Post- operative Resistance	Post- operative Rank
2a	0.76	1	0.12	1
2b	0.77	2	0.19	2
2c	1.21	3	0.28	3
3a	0.17	1	0.41	3
3b	0.18	2	0.24	1
3c	0.34	3	0.33	2

Predictive Accuracy

The explicit comparison of surgical planning predictions to simulated post-operative hemodynamics is shown in Table 8. For HFD, the predictive difference (pre-operative value vs. post-operative result) ranged between 2-33%, with a 90% confidence interval of 14.3 ± 4.3%. For connection resistances, the predictive comparisons (pre-operative inflows with post-operative PA splits vs. post-operative simulation) ranged between 0-40% error with a 90% confidence interval of 19.5 ± 4.8%. [TABLE 8]

Table 8.

Predictive Accuracy

Pt	HFD [%LPA]			Connection Resistance [mmHg*min/L]*
	Surgical Planning Model	Post-op Anatomy	Difference	Surgical Planning Model	Post-op Anatomy	% Error
1	23	35	12	0.28	0.22	22
2	25	35	10	0.27	0.32	16
3	58	91	33	0.21	0.35	40
4	52	54	2	0.18	0.18	0
90% # CInt.			14.3 ±4.3			19.5 ± 4.8

^*Pre-operative values using post-operative outflow splits

^#CInt. = Confidence Interval

Discussion

This study compared the results from pre-operative virtual surgery modeling of the Fontan procedure to the simulated hemodynamic outcomes following the surgical implementation of those models in four patients. While the agreement was not exact, it is important to note that the hemodynamic outcomes with respect to what the patients ultimately needed (i.e., hepatic perfusion of the diseased lung) were achieved in each case, which is not a guarantee in such complex anatomical configurations. The improved/improving arterial oxygen saturation values further support this observation as they suggest the PAVMs are regressing and more blood is being properly routed through the lungs. Ultimately, that is the desired clinical endpoint.

These results suggest that the virtual models mimicked the interventions with sufficient realism to provide relevant insights to the cardiovascular surgeon and help in the decision-making process. The fact that these Y-graft patients were the first for either surgeon in this study provides strong testament that the modeling results were taken into account in their surgical strategy. Furthermore, providing the first assessment of prospective modeling comparisons is a milestone in the development of tools for engineering-based modeling of cardiothoracic surgery because it demonstrates the ability of the modeling to approximate the acute surgical result. Of equal importance, however, was the identification of key variables that dictate the error margins of the approximations. Such information will be critical to both prioritize and further motivate future developments to address these limitations.

HFD

As seen in Table 8, the confidence interval of pre-operative HFD predictions to post-operative results was 14.3 ± 4.3%. This finding is positive for several reasons. HFD is a primary consideration in patients with PAVM diagnoses based on the assumption that achieving desired flow streaming would successfully alleviate the immediate disease state. However, there is a poor clinical understanding with regard to the critical values of HFD that mediate PAVM formation or regression, with the only clearly negative outcome being complete exclusion of hepatic flow from one lung. Interventional target values are therefore broad, ill-defined, and nearly impossible to dictate a priori. Providing a means to achieve a specific outcome, even with up to 19% uncertainty, thus represents a significant refinement of the current approach.

To further improve on these results, Table 3 suggests that surgical/model agreement is a critical mediator of flow streaming predictions. Unfortunately, surgical mismatch is currently an unavoidable factor of the process as consistently exact agreement would require: a) registered, simultaneous visualization of both the patient anatomy and virtual model in the operating room; b) a lack of intra-operative adjustments from the pre-determined plan by the surgeon; and c) simulation of the geometric changes that occur post-operatively (e.g., from chest closure or restoration of normal thoracic pressures). While none of these is impossible for future work to incorporate, they are not currently feasible. Rather than addressing this limitation on the surgical side, however, it would be easier to take preventative measures on the virtual design-side to minimize its impact. Such considerations were subjectively included in these present cases, as in the case of the extracardiac hepatic baffle evaluation (Figure 2), but only on an ad hoc basis. Low sensitivity of desirable hemodynamic values to possible variations in exact implementation (i.e., option robustness) can also be mathematically formalized into a separate evaluation criterion to strengthen the analysis²⁴.

Connection Resistance

Prospective resistance predictions were not as strong as for flow distribution (19.5 ± 4.8%). Yet, even though the clinically relevant thresholds of TCPC power loss are currently unknown, it is assumed that the resistance values found in all cases were acceptably small. It is unlikely that 10-20% differences at such low levels would mediate significant clinical differences given that, from the work of Sundareswaran et al., a 3- or 4-fold increase in resistance would be required to drop cardiac output by ~12%³¹. Furthermore, power loss was only a secondary consideration in the decision making process for these patients (as seen from the pre-operative analyses) and only came into play when two options had similar flow distribution characteristics. In fact, the efficiency differences between the options for which power loss was a discriminator exceeded the 24% mean error margin, so it was still a useful metric in those pre-operative analyses. That said, the secondary importance of connection efficiency is not a permanent fixture and there are likely patients and disease states (e.g., exercise intolerance, high central venous pressure) for which such metrics are of primary concern. Thus, while the present findings from this initial series provide a viable starting point, they are not sufficient for the ultimate promise of such analyses.

Based on the present data, one focal point for making improvements is minimizing the deviation of reconstructed vessel sizes, particularly of the small PAs, which were a primary contributor to predictive errors of efficiency (Table 3). Uncertainties in vessel sizes were related to three primary sources: a) the reconstruction protocol itself (smoothing and surface fitting algorithms tend to shrink the segmented volume); b) the possibility of actual changes occurring in the vessel sizes, as in response to changing flow conditions or surgical manipulation; and c) finite sampling of medical images. Continuous advancements in imaging (particularly the growing use of 3D anatomic sequences) and image processing techniques will help address points (a) and (c); the effects of (b) will need to be studied through future work with larger sample sizes, and may require fluid-structure interaction models to resolve if deemed critical to the result.

Flow boundary condition uncertainty

While surgical agreement and reconstruction errors were each found to impact pre-operative predictions in an isolated fashion (i.e., either HFD or power loss), changes in flow conditions was seen to mediate changes in both metrics of interest and thus deserves particular attention. Decreases in cardiac output post-Fontan have previously been noted by Fogel et al.¹⁰, although no similar report exists with respect to post-operative physiology of interrupted IVC patients. In this limited series, output decreased in 3 of 4 patient cases by as much as 1.1 L/min. Power losses are directly dependent on the total flow rate, so normalizing to express as a resistance better accounted for most of these changes, as evidenced by the similar orders of magnitude in the comparisons of Tables 5, 6, and 8. Dynamic interactions among the various inlets, dictated by their relative flow rates, would have also contributed to the hemodynamic efficiency of the connection. The differences in connection resistances for the surgical planning models of patient 3 (Table 7) demonstrate such dynamic effects. There, the shift to higher SVC and lower azygos flows made the hepatic-to-azygos connection appear more efficient under post-operative flow conditions, while increasing the energy dissipated by the direct collision of hepatic and SVC flows in the extracardiac model. Without this significant physiologic shift, the relative connection rankings would likely have remained more consistent, as with patient 2.

Relative vessel flow rates also impacted HFD. It is known that HFD is generally positively correlated to the pulmonary outflow split³, so this finding came as little surprise. In patient 4, for example, pre-operatively varying the outflow split (Table 5) improved agreement with the result of the post-operative BC simulation. Patients 1 and 2 (both with Y-graft conduits) diverged from this trend, which suggests that the inlet fluid momentum in bifurcated grafts may supersede the outlet conditions under certain conditions. More importantly though, the physiologic factors governing post-operative adaptation of pulmonary splits are not well characterized, and so parametric sensitivity studies should be a critical component of any surgical planning analysis.

Coupling lumped parameter models to 3D fluid solvers has been proposed and evaluated in hypothetical surgical planning studies as a means to mathematically predict physiologic changes and better account for such effects^{1, 22, 32}. This is potentially a very powerful paradigm and certainly represents the future for these techniques. However, there is currently a lack of data in the literature characterizing patient-specific pre- and post-operative physiology for the models to be properly validated. Furthermore, the difficulty in obtaining the data needed to make such models truly patient-specific (e.g., explicit compliance characteristics throughout the various vascular beds) can be challenging. Perhaps the best approach for future protocols would be for these multi-modality approaches to be complemented by clinical experience of serial patient changes (both acute and chronic) to ensure the models have simulated all the relevant conditions. While this development continues, the controlled and hypothesis-driven deviation of the investigated outflow splits as part of our surgical planning analysis is worthwhile approach that, based on the presented findings, should be augmented and complemented with similar variations of the inlet BCs to ensure robust solutions with respect to physiologic changes.

Limitations

While this study has explored factors that limit the similarity of pre-operative simulations to post-operative simulations, there are simplifications inherent to such modeling that may reduce agreement with the in vivo values. Future studies should seek to explicitly quantify such internal uncertainties and sources of error propagation²⁴, in addition to the external error sources and uncertainty ranges elucidated through this work. For example, the use of rigid walls ignores the ability of the vessel walls to store and/or transmit pulsatile pressure wave energy or adapt to changes in bulk flow conditions. However, a recent fluid-structure interaction study showed minimal differences in HFD and time-averaged hemodynamic efficiency in comparing rigid vs. compliant simulations¹⁸. Furthermore, agreement of 4D in vivo velocity measurements with the simulated results^{28, 30} suggests that this simplification yields meaningful hemodynamic insights. The use of time-averaged flow conditions and fixed flow splits for the surgical planning simulations may have negatively impacted the agreement of the comparisons made and will be addressed in future studies.

Finally, the patient follow-up was limited to a single time point and was performed in the early post-operative period, which may not reflect the long-term baseline hemodynamic state. Longitudinal follow-up for these patients will therefore be crucial to understand the long-term hemodynamic and clinical outcomes and how they relate to the pre-operative modeling.

Summary

The results of this study support the hypothesized accuracy of prospective modeling predictions for virtual Fontan surgery; yet, there is clearly room for methodology refinements. Using the information gained from the error assessments conducted, the following steps are proposed for the future development of these planning studies. First, there is an urgent need to improve the characterization of the evolution of systemic venous flows, which had significant influence on both metrics of interest to this analysis. Such improvements can be made through both the continued collection and analysis of relevant serial patient data, and further development and validation of coupled lumped parameter-CFD models. Second, the results communicated to the surgeon should include a) geometric sensitivity (i.e., robustness) of the different surgical options; and b) sensitivity to parametric boundary condition evolution. This information can then be taken into account with past clinical experience and surgical judgment to select the desired treatment strategy. Through careful use in this fashion, the benefits of virtual surgery planning for both the patient and clinician can outweigh its current limitations and provide meaningful clinical insights.