SCALCE: boosting sequence compression algorithms using locally consistent encoding

Abstract

Motivation: The high throughput sequencing (HTS) platforms generate unprecedented amounts of data that introduce challenges for the computational infrastructure. Data management, storage and analysis have become major logistical obstacles for those adopting the new platforms. The requirement for large investment for this purpose almost signalled the end of the Sequence Read Archive hosted at the National Center for Biotechnology Information (NCBI), which holds most of the sequence data generated world wide. Currently, most HTS data are compressed through general purpose algorithms such as gzip. These algorithms are not designed for compressing data generated by the HTS platforms; for example, they do not take advantage of the specific nature of genomic sequence data, that is, limited alphabet size and high similarity among reads. Fast and efficient compression algorithms designed specifically for HTS data should be able to address some of the issues in data management, storage and communication. Such algorithms would also help with analysis provided they offer additional capabilities such as random access to any read and indexing for efficient sequence similarity search. Here we present SCALCE, a ‘boosting’ scheme based on Locally Consistent Parsing technique, which reorganizes the reads in a way that results in a higher compression speed and compression rate, independent of the compression algorithm in use and without using a reference genome.

Results: Our tests indicate that SCALCE can improve the compression rate achieved through gzip by a factor of 4.19—when the goal is to compress the reads alone. In fact, on SCALCE reordered reads, gzip running time can improve by a factor of 15.06 on a standard PC with a single core and 6 GB memory. Interestingly even the running time of SCALCE + gzip improves that of gzip alone by a factor of 2.09. When compared with the recently published BEETL, which aims to sort the (inverted) reads in lexicographic order for improving bzip2, SCALCE + gzip provides up to 2.01 times better compression while improving the running time by a factor of 5.17. SCALCE also provides the option to compress the quality scores as well as the read names, in addition to the reads themselves. This is achieved by compressing the quality scores through order-3 Arithmetic Coding (AC) and the read names through gzip through the reordering SCALCE provides on the reads. This way, in comparison with gzip compression of the unordered FASTQ files (including reads, read names and quality scores), SCALCE (together with gzip and arithmetic encoding) can provide up to 3.34 improvement in the compression rate and 1.26 improvement in running time.

Availability: Our algorithm, SCALCE (Sequence Compression Algorithm using Locally Consistent Encoding), is implemented in C++ with both gzip and bzip2 compression options. It also supports multithreading when gzip option is selected, and the pigz binary is available. It is available at http://scalce.sourceforge.net.

Contact: fhach@cs.sfu.ca or cenk@cs.sfu.ca

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Although the vast majority of high throughput sequencing (HTS) data are compressed through general purpose methods, in particular gzip and its variants, the need for improved performance has recently lead to the development of a number of techniques specifically for HTS data. Available compression techniques for HTS data either exploit (i) the similarity between the reads and a reference genome or (ii) the similarity between the reads themselves. Once such similarities are established, each read is encoded by the use of techniques derived from classical lossless compression algorithms such as Lempel-Ziv-77 (Ziv and Lempel, 1977) (which is the basis of gzip and all other zip formats) or Lempel-Ziv-78 (Ziv and Lempel, 1978). Compression methods that exploit the similarity between individual reads and the reference genome use the reference genome as a ‘dictionary’ and represent individual reads with a pointer to one mapping position in the reference genome, together with additional information about whether the read has some differences with the mapping loci. As a result, these methods (Hsi-Yang Fritz et al., 2011; Kozanitis et al., 2010) require (i) the availability of a reference genome and (ii) mapping of the reads to the reference genome. Unfortunately, genome mapping is a time-wise costly step, especially when compared with the actual execution of compression (i.e. encoding the reads) itself. Furthermore, these methods necessitate the availability of a reference genome both for compression and decompression. Finally, many large-scale sequencing projects such as the Genome 10K Project (Haussler et al., 2009) focus on species without reference genomes. Compression methods that exploit the similarity between the reads themselves simply concatenate the reads to obtain a single sequence: Bhola et al., 2011 apply modification of Lempel-Ziv algorithm, Tembe et al., 2010; Deorowicz and Grabowski, 2011 use Huffman Coding (Huffman, 1952) and Cox et al., 2012 use Burrows Wheeler transformation (Burrows and Wheeler, 1994). In particular, the Lempel-Ziv methods (e.g. gzip and derivatives) iteratively go over the concatenated sequence and encode a prefix of the uncompressed portion by a ‘pointer’ to an identical substring in the compressed portion. This general methodology has three major benefits: (i) Lempel-Ziv–based methods (e.g. gzip and derivatives) have been optimized through many years and are typically fast; in fact, the more ‘compressible’ the input sequence is, the faster they work, both in compression and decompression; (ii) these methods do not need a reference genome and (iii) because these techniques are almost universally available, there is no need to distribute a newly developed compression algorithm.

Interestingly, the availability of a reference genome can improve the compression rate achieved by standard Lempel-Ziv techniques. If the reads are first mapped to a reference genome and then reordered with respect to the genomic coordinates they map to before they are concatenated, they are not only compressed more because of increased locality, but also in less time. This, mapping-first compressing-later approach, combines some of the advantages of the two distinct sets of methods above: (i) it does not necessitate the availability of a reference genome during decompression (compression is typically applied once to a dataset, but decompression can be applied many times), and (ii) it only uses the reordering idea as a front end booster [Burrows Wheeler transform—BWT—is a classical example for a compression booster. It rearranges input symbols to improve the compression achieved by Run Length Encoding and Arithmetic Coding. Further boosting for BWT is also possible: see (Ferragina and Manzini, 2004; Ferragina et al., 2005, 2006)]. Any well-known, well-distributed compression software can be applied to the reordered reads. Unfortunately, this strategy still suffers from the need for a reference genome during compression.

In this article, we introduce a novel HTS genome (or transcriptome, exome, etc.) sequence compression approach that will combine the advantages of the two types of algorithms above. It is based on reorganization of the reads so as to ‘boost’ the locality of reference. The reorganization is achieved by observing sufficiently long ‘core’ substrings that are shared between the reads, and clustering such reads to be compressed together. This reorganization acts as a fast substitute for mapping-based reordering (see above); in fact, the first step of all standard seed and extend-type mapping methods identify blocks of identity between the reads and the references genome.

The core substrings of our boosting method are derived from the Locally Consistent Parsing (LCP) method devised by Sahinalp and colleagues (Sahinalp and Vishkin, 1996; Cormode et al., 2000; Batu et al., 2006). For any user-specified integer c and with any alphabet (in our case, the DNA alphabet), the LCP identifies ‘core’ substrings of length between c and 2c such that (i) any string from the alphabet of length 3c or more includes at least one such core string, (ii) there are no more than three such core strings in any string of length 4c or less and (iii) if two long substrings of a string are identical, then their core substrings must be identical.

LCP is a combinatorial pattern matching technique that aims to identify ‘building blocks’ of strings. It has been devised for pattern matching, and provides faster solutions in comparison with the quadratic running time offered by the classical dynamic programming schemes. As a novel application, we introduce LCP to genome compression, where it aims to act as a front end (i.e. booster) to commonly available data compression programs. For each read, LCP simply identifies the longest core substring (there could be one or more cores in each read). The reads are ‘bucketed’ based on such representative core strings and within the bucket, ordered lexicographically with respect to the position of the representative core. We compress reads in each bucket using Lempel-Ziv variants or any other related method without the need for a reference genome.

As can be seen, LCP mimics the mapping step of the mapping-based strategy described above in an intelligent manner: on any pair of reads with significant (suffix-prefix) overlaps, LCP identifies the same core substring and subsequently buckets the two reads together. For a given read, the recognition of the core strings and bucketing can be done in time linear with the read length. Note that the ‘dictionary’ of core substrings is devised once for a given read length as a pre-processing step. Thus, the LCP-based booster we are proposing is efficient. LCP provides mathematical guarantees that enable highly efficient and reliable bucketing that captures substring similarities. We have applied the LCP-based reordering scheme for (i) short reads of length 51 bp obtained from bacterial genomes and (ii) short reads of length 100 bp from one human genome, and obtained significant improvements in both compression rate and running time over alternative methods.

2 METHODS

2.1 A theoretical exposition to the LCP technique

The simplest form of the LCP technique works only on reads that involve no tandemly repeated blocks (i.e. the reads can not include a substring of the form XX where X is a string of any length ; note that a more general version of LCP that does not require this restriction is described in Sahinalp and Vishkin, 1994, 1996; Batu et al., 2006 so that LCP works on any string of any length). 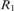Under this restriction, given the alphabet , LCP partitions a given string S into non-overlapping blocks of size at least 2 and at most k such that two identical substrings and 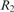of S are partitioned identically—except for a constant number of symbols on the margins. LCP achieves this by simply marking all local maxima (i.e. symbols whose value is greater than its both neighbours) and all local minima, which do not have a neighbour already marked as a local maxima—note that beginning of S and the ending of S are considered to be special symbols lexicographically smaller than any other symbol. LCP puts a block divider after each marked symbol and the implied blocks will be of desirable length and will satisfy the identical partitioning property mentioned above. Then, LCP extends each block residing between two neighbouring block dividers by one symbol to the right and one symbol to the left to obtain core blocks of S. Note that two neighbouring core blocks overlap by two symbols.

2.2 Example

Let 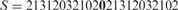; in other words, 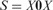, where X = 21312032102. The string S satisfies the above condition; i.e. it contains no identically and tandemly repeated substrings. When the above simple version of LCP is applied to S, it will be partitioned as 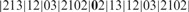. Clearly, with the exception of the leftmost blocks, the two occurrences of X are partitioned identically. Now LCP identifies the core blocks as .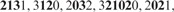

Observe that the (i) two occurrences of string X are partitioned by LCP the same way except in the margins. Further observe that (ii) if a string is identified as a core block in a particular location, it must be identified as a core block elsewhere because of the fact that all symbols that lead LCP to identify that block as a core block are included in the core block. As a result, (iii) all core blocks that entirely reside in one occurrence of X should be identical to those that reside in another occurrence of X. Finally observe that (iv) the number of cores that reside in any substring X is at most 1/2 of its length and at least 1/k of its length.

The above version of LCP can return core blocks with length as small as 4; a length 4 substring is clearly not specific enough for clustering an HTS read; we have to ensure that the minimum core block length c is a substantial fraction of the read length. LCP as described in Sahinalp and Vishkin, 1994, 1996; Batu et al., 2006 enables to partition S into non-overlapping blocks of size at least c and at most 2c – 1 for any user defined c. These blocks can be extended by a constant number of symbols to the right and to the left to obtain the ‘core’ blocks of S. (Please see the Supplementary Data to get a flavour of how this is done.) In the context of compressing HTS reads, if c is picked to be a significantly long fraction of the read size, LCP applied on the HTS reads will guarantee that each read will include at least one and at most three of these core blocks.

Unfortunately, this general version of LCP is too complex to be of practical interest. As a result, we have developed a practical variant of LCP described below to obtain core blocks of each HTS read with minimum length 8 and maximum length 20. Interestingly, we observed that in practice >99% of all HTS reads of length 50 or more include at least one core of length 14 or less. As a result, we are interested in identifying only those core blocks of lengths in the range of 8–14. Still there could be multiple such core blocks in each HTS read; SCALCE will pick the longest one as the representative core block of the read (if there are more than one such block, SCALCE may break the tie in any consistent way). SCALCE will then cluster this read with other reads that have the same representative core block.

2.3 A practical implementation of LCP for reordering reads

The purpose of reordering reads is to group highly related reads, in fact those reads that ideally come from the same region and have large overlaps together so as to boost gzip and other Lempel-Ziv-77–based compression methods. If one concatenates reads from a donor genome in an arbitrary order, highly similar reads will be scattered over the resulting string. Because Lempel-Ziv-77–based techniques compress the input string iteratively, from left to right, replacing the longest possible prefix of the uncompressed portion of the input string with a pointer to its earlier (already compressed) occurrence, as the distance between the two occurrences of this substring to be compressed increases, the binary representation of the pointer also increases. As a result, gzip and other variants only search for occurrences of strings within a relatively small window. Thus reordering reads so as to bring together those with large (suffix–prefix) overlaps is highly beneficial to gzip and other similar compression methods. For this purpose, it is possible to reorder the reads by sorting them based on their mapping loci on the reference genome. Alternatively, it may be possible to find similarities between the reads through pairwise comparisons (Yanovsky, 2011). However each one of these approaches are time-wise costly.

In contrast, our goal here is to obtain a few core blocks for each read so that two highly overlapping reads will have common core blocks. The reads will be reordered based on their common core blocks, which satisfy the following properties: (i) Each HTS read includes at least one core block. (ii) Each HTS read includes at most a small number of core blocks. This would be achieved if any sufficiently ‘long’ prefix of a core block can not be a suffix of another core block (this assures that two subsequent core blocks can not be too close to each other).

We first extend the simple variant of LCP described above so as to handle strings from the alphabet 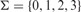(0 = A, 1 = C, 2 = G, 3 = T) that can include tandemly repeated blocks. In this variant, we define a core block as any 4-mer that satisfies one of the following rules:

• (Local Maxima) xyzw where 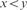and ;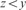

• (Low Periodicity) xyyz where 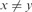and ;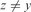

• (Lack of Maxima) xyzw where 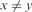and ;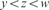

• (Periodic Substrings) yyyx where .

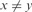We computed all possible 4-mers (there are 256 of them) from the 4 letter alphabet and obtained 116 core blocks that satisfy the rules above. The reader can observe that the minimum distance between any two neighbouring cores will be 2 and the maximum possible distance will be 6 (note that this implementation of LCP is not aimed to satisfy any theoretical guarantee; rather, it is developed to work well in practice). This ensures that any read of length at least 9 includes one such core block.

To capture longer regions of similarity between reads, we need to increase the lengths of core blocks. For that purpose, we first identify the so-called marker symbols in the read processed as follows. Let x, y, z, w, x, v 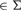, then

• y is a marker for xyz, when 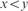and ;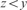

• y is a marker for xyyz, when 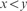and ;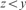

• y is a marker for xyyyz, when 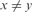and ;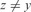

• yy is a marker for xyyyyz, when 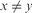and ;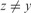

• y is a marker for xwyzv, when 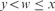and .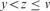

Now on a given read, we first identify all marker symbols. We apply LCP to the sequence obtained by concatenating these marker symbols to obtain the core blocks of the marker symbols. We then map these core blocks of the marker symbols to the original symbols to obtain the core blocks of the original read. Given read R = 0230000300, we identify its marker symbols as follows: 3 is the marker for 230, 00 is the marker for 300003 and 3 is the marker for 030 as per the marker identification rules above. The sequence obtained by concatenating these markers is 3003, which is itself (4-mer) core block according to the LCP description above. The projection of this core block on R is 23000030, which is thus identified as a core block (the only core block) of the read.

For the 4 letter alphabet , we computed all (∼5 million) possible core blocks of length according to the above rules (this is about 1% of all blocks in this length range). These rules assure that the minimum distance between two subsequent core blocks is 4 and thus the maximum number of core blocks per read is at most 11 per each HTS read of length 50. Furthermore, we observed that more than 99.5% of all reads have at least one core block (the other reads have all cores of length 15–20). Although this guarantee is weaker than the theoretical guarantee provided by the most general version of LCP, it serves our purposes.

2.4 A data structure for identifying core substrings of reads

We build a trie data structure representing each possible core substring by a path to efficiently place reads into ‘buckets’. We find ‘all’ core substrings of each read and place the read in the bucket (associated with the core substring) that contains the maximum number of reads (if there are two or more such buckets, we pick one arbitrarily). If one simply uses the trie data structure, finding all core substrings within a read would require 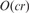time where r is the read length, and c is the length of all core substrings in that read. To improve the running time, we build an automaton implementing the Aho-Corasick dictionary matching algorithm (Aho and Corasick, 1975). This improves the running time to 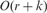, where k is the number of core substring occurrences in each read. Because the size of the alphabet is small (4 symbols), and the number of the core substrings is fixed, we can further improve the running time by pre-processing the automaton such that, for a given state of the automaton we calculate the associated bucket in 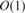time, reducing the total search time to .

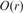2.5 Compressing the quality scores

Note that the HTS platforms generate additional information for each read that is not confined to the 4-letter alphabet . Each read is associated with a secondary string that contains the base calling phred (Ewing and Green, 1998) quality score. Quality score of a base defines the probability that the base call is incorrect, and it is formulated as 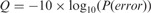(Ewing and Green, 1998). The size of the alphabet for the quality scores is typically 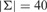for the Illumina platform, thus the compression rate for quality scores is lower than the actual reads. As mentioned in previous studies (Wan et al., 2012), lossy compression can improve the quality scores compression rate. We provide an optional controlled lossy transformation approach based on the following observation. In most cases, for any basepair b, the quality scores of its ‘neighbouring’ basepairs would be either the same or within some small range of b’s score (see Fig. 1). Based on this observation, we provide a lossy transformation scheme to reduce the alphabet size. We calculate the frequency table for the alphabet of quality scores from a reasonable subset of the qualities (1 million quality scores). We first use a simple greedy algorithm to find the local maxima within this table. We then reduce the variability among the quality scores in the vicinity of local maxima up to some error threshold e.

Fig. 1.

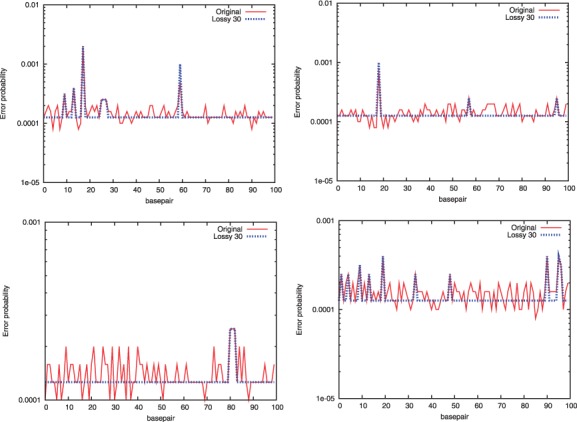
Original (left) and transformed (right) quality scores for two random reads that are chosen from NA18507 individual. The original scores show much variance, where the transformed quality scores are smoothened except for the peaks at local maxima, that help to improve the compression ratio

3 RESULTS

We evaluated the performance of the SCALCE algorithm for boosting gzip on a single core 2.4 GHz Intel Xeon X5690 PC (with network storage and 6 GB of memory).

We used four different datasets in our tests: (i) Pseudomonas aeruginosa RNA-Seq library (51 bp, single lane), (ii) P.aeruginosa genomic sequence library (51 bp, single lane), (iii) whole genome shotgun sequencing (WGS) library generated from the genome of the HapMap individual NA18507 (100 bp reads at 40× genome coverage) and (iv) a single lane from the same human WGS dataset corresponding to ∼1.22× genome coverage (Sequence Read Archive ID: SRR034940). We removed any comments from name section (any string that appears after the first space). Also the third row should contain a single character (+/−) separator character.

The reads from each dataset were reordered through SCALCE and three separate files were obtained for (i) the reads themselves, (ii) the quality scores and (iii) the read names (each maintaining the same order). Note that LCP reordering is useful primarily for compressing the reads themselves through gzip. The quality scores were compressed via the scheme described above. Finally the read names were compressed through gzip as well.

The compression rate and run time achieved by gzip software alone, only on the reads from the P.aeruginosa RNA-Seq library (dataset 1) is compared against those achieved by SCALCE followed by gzip in Table 1. The compression rates achieved by the gzip software alone in comparison with gzip following SCALCE on the combination of reads, quality scores and read names are presented in Table 2. The run times for the two schemes (again on reads, quality scores and read names all together) are presented in Table 3.

Table 1.

Input data statistics and compression rates achieved by gzip only and SCALCE + gzip on reads from the P.aeruginosa RNA-Seq library (dataset 1)

Dataset		gzip			SCALCE + gzip
Number of reads	Size	Size	Rate	Time	Size	Rate	Boosting factor	gzip only time	SCALCE + gzip time
89M	4327	1071	4.04	13 min 18 s	256	16.92	4.19×	53 s	6 min 21 s

File sizes are reported in megabytes.

M, million; B, billion.

Table 2.

Input data statistics and compression rates achieved by gzip only and SCALCE + gzip + AC on complete FASTQ files

Dataset			gzip		SCALCE (lossless)			SCALCE (lossy 30%)
Name	Number of reads	Size	Size	Rate	Size	Rate	Boosting factor	Size	Rate	Boosting factor
P.aeruginosa RNAseq	89M	10 076	3183	3.17	1496	6.74	2.13×	953	10.58	3.34×
P.aeruginosa genomic	81M	9163	3211	2.85	1655	5.54	1.94×	1126	8.14	2.85×
NA18507 WGS	1.4B	300 337	113 132	2.65	76 890	3.91	1.47×	58 031	5.18	1.95×
NA18507 single lane	36M	7708	3058	2.52	2146	3.59	1.42×	1639	4.70	1.86×

File sizes are reported in megabytes.

M, million; B, billion.

Table 3.

Run time for running gzip alone and SCALCE + gzip + AC on complete FASTQ files

Name	gzip	SCALCE + gzip + AC, single thread			SCALCE + gzip + AC, 3 threads
	Time	Reordering	gzip + AC	Total compression	Total compression
P.aeruginosa RNAseq (min)	20	7	6	13	9
P.aeruginosa genomic (min)	20	6	5	11	9
NA18507 WGS	10 h 52 min	3 h	3 h 1 min	6 h 1 min	4 h 28 min
NA18507 single lane	18 min	5 min	5 min	10 min	7 min 32 s

When SCALCE is used with arithmetical coding of order 3 with lossless qualities, it boosts the compression rate of gzip between 1.42- and 2.13-fold (when applied to reads, quality scores and read names), significantly reducing the storage requirements for HTS data. When arithmetical coding of order 3 is used with 30% loss—without reducing the mapping accuracy—improvements in compression rate are between 1.86 and 3.34. In fact, the boosting factor can go up to 4.19 when compressing the reads only. Moreover, the speed of the gzip compression step can be improved by a factor of 15.06. Interestingly, the total run time for SCALCE + gzip is less than the run time of gzip by a factor of 2.09. Furthermore, users can tune the memory available to SCALCE through a parameter to improve the run time when a large main memory is available. In our tests, we limited the memory usage to 6 GB.

Note that our goal here is to devise a fast boosting method, SCALCE, which in combination with gzip gives compression rates much better than gzip alone. It is possible to get better compression rates through mapping-based strategies, but these methods are several orders of magnitude slower than SCALCE + gzip. We tested the effects of the lossy compression schemes for the quality scores, used by SCALCE as well as CRAM tools, to single nucleotide polymorphism (SNP) discovery. For that, we first mapped the NA18507 WGS dataset with the original quality values to the human reference genome (GRCh37) using the BWA aligner (Li and Durbin, 2009), and called SNPs using the GATK software (DePristo et al., 2011). We repeated the same exercise with the reads after 30% lossy transformation of the base pair qualities with SCALCE. Note that the parameters for BWA and GATK we used in these experiments were exactly the same. We observed almost perfect correspondence between two experiments. In fact, 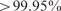of the discovered SNPs were the same (Table 4); not surprisingly, most of the difference was due to SNPs in mapping to common repeats or segmental duplications. We then compared the differences of both SNP callsets with dbSNP Release 132 (Sherry et al., 2001) in Table 4.

Table 4.

Number of SNPs found in the NA18507 genome using original and transformed qualities with 30% noise reduction and qualities reconstructed by CRAM tools

Experiment settings	Number of SNP count	dbSNP v132 (%)	Novel
			Total	In SD + CR (%)
Original qualities	4 296 152	4 092 923 (95.26)	203 229	192 114 (94.53)
Qualities using SCALCE	4 303 140	4 098 875 (95.25)	204 265	192 976 (94.47)
Lost	7931	4596 (57.95)	3335	2963 (88.84)
New	14 919	10 548 (70.70)	4371	3825 (87.51)
Qualities using CRAM tools	4 202 298	4 013 401 (95.50)	188 897	179 875 (95.22)
Lost	101 957	84 607 (82.98)	17 350	15 036 (86.66)
New	8103	5085 (62.75)	3018	2797 (92.67)

Also reported are the number and percentage of novel SNPs in regions of segmental duplication or common repeats (SD + CR).

In addition, we carried out the same experiment with compressing/decompressing of the alignments with CRAM tools. As shown in Table 4, quality transformation of the CRAM tools introduced about 2.5% errors in SNP calling (97.5% accuracy) with respect to the calls made for the original data (set as the gold standard).

One interesting observation is that 70.7% of the new calls after SCALCE processing matched to entries in dbSNP where this ratio was only 62.75% for the new calls after CRAM tools quality transformation. Moreover, 57.95% of the SNPs that SCALCE ‘lost’ are found in dbSNP, and CRAM tools processing caused removal of 18.4 times more potentially real SNPs than SCALCE.

As a final benchmark, we compared the performance of SCALCE with mapping-based reordering before gzip compression. We first mapped one lane of sequence data from the genome of NA18507 (same as above) to human reference genome (GRCh37) using BWA (Li and Durbin, 2009), and sorted the mapped reads using samtools (Li et al., 2009), and reconverted the map-sorted BAM file back to FASTQ using Picard (http://picard.sourceforge.net). We then used the gzip tool to compress the map-sorted file to 3091.5 MB, achieving 2.49-fold compression rate. The pre-processing step for mapping and sorting required 18.2 CPU hours, and FASTQ conversion required 30 min, whereas compression was completed in 28 min. Moreover, the mapping-based sorting did not improve the compression run time even if we do not factor in the pre-processing. In contrast, SCALCE + gzip + AC generated a much smaller file in less amount of time, with no mapping-based pre-processing. We then repeated this experiment on the entire WGS dataset (NA18507). The mapping-based pre-processing took 700 CPU hours for BWA + samtools, 10 CPU hours for Picard, whereas gzip step was completed in 11 CPU hours, resulting in a compression rate of 3.1 × . On the other hand, gzip + AC needed only 3 CPU hours to compress the same dataset (3.67× faster) after the pre-processing by SCALCE, which took 3 CPU hours, and achieved a better compression rate (Tables 2 and 3). The run time of mapping-based pre-processing step can be improved slightly through the use of BAM-file–based compressors such as CRAM tools (Hsi-Yang Fritz et al., 2011), but this would reduce the time only by 10 CPU hours for the Picard step. Thus, in total, SCALCE + gzip is ∼120 times faster than any potential mapping-based scheme (including CRAM tools) on this dataset.

Our tests showed that SCALCE (when considering only reads) outperforms BEETL (Cox et al., 2012) combined with bzip2 by a factor between 1.09 and 2.07, where running time is improved by a factor between 3.60 and 5.17 (see Table 5). SCALCE (on full FASTQ files) also outperforms DSRC (Deorowicz and Grabowski, 2011) compression ratio on complete FASTQ files by a factor between 1.09 and 1.18 (see Table 6).

Table 5.

Comparison of single-threaded SCALCE with BEETL

Name	BEETL time (min)	BEETL size	SCALCE time (min)	SCALCE size
P.aeruginosa RNAseq	29	197	8	95
P.aeruginosa Genomic	31	257	6	137
NA18507 single lane	51	448	10	412

Here, the datasets contained only reads from the FASTQ file, as BEETL supports only FASTA file format.

Table 6.

Comparison of single-threaded SCALCE with DSRC

Name	DSRC time	DSRC size	SCALCE time	SCALCE size
P.aeruginosa RNAseq	12 min	1767	13 min	1496
P.aeruginosa genomic	6 min	1846	11 min	1655
NA18507 WGSa	3 h 16 min	94 707	6 h 1 min	76 890
NA18507 single lane	4 min	2341	10 min	2146

DSRC was tested using the -l option. This option provides better compression ratio but it is slower. ^aDSRC with -l option crashed on WGS dataset. Instead we used a faster but less powerful settings for this dataset.

4 CONCLUSION AND DISCUSSION

The rate of increase in the amount of data produced by the HTS technologies is now faster than the Moore’s Law (Alkan et al., 2011). This causes problems related to both data storage and transfer of data over a network. Traditional compression tools such as gzip and bzip2 are not optimized for efficiently reducing the files to manageable sizes in short amount of time. To address this issue, several compression techniques have been developed with different strengths and limitations. For example, pairwise comparison of sequences can be used to increase similarity within ‘chunks’ of data, thus increasing compression ratio (Yanovsky, 2011), but this approach is also time consuming. Alternatively, reference-based methods can be used such as SlimGene (Kozanitis et al., 2010) and CRAM tools (Hsi-Yang Fritz et al., 2011). Although these algorithms achieve high compression rates, they have three major shortcomings. First, they require pre-mapped (and sorted) reads along with a reference genome, and this mapping stage can take a long time depending on the size of the reference genome. Second, speed and compression ratio are highly dependent on the mapping ratio because the unmapped reads are handled in a more costly manner (or completely discarded), which reduces the efficiency for genomes with high novel sequence insertions and organisms with incomplete reference genomes. Finally, the requirement of a reference sequence makes them unusable for de novo sequencing projects of the genomes of organisms where no such reference is available, for example, the Genome 10K Project (Haussler et al., 2009).

The SCALCE algorithm provides a new and efficient way of reordering reads generated by the HTS platform to improve not only compression rate but also compression run time. Although it is not explored here, SCALCE can also be built into specialized alignment algorithms to improve mapping speed. We note that the names associated with each read do not have any specific information and they can be discarded during compression. The only consideration here is that during decompression, new read names will need to be generated. These names need to be unique identifiers within a sequencing experiment, and the paired-end information must be easy to track. In fact, the Sequence Read Archive developed by the International Nucleotide Sequence Database Collaboration adopts this approach to minimize the stored metadata, together with a lossy transformation of the base pair quality values similar to our approach (Kodama et al., 2011). However, in this article, we demonstrated that lossy compression of quality affects the analysis result, and although the difference is small for SCALCE, this is an optional parameter in our implementation, and we leave the decision to the user. Additional improvements in compression efficiency and speed may help ameliorate the data storage and management problems associated with HTS (Schadt et al., 2010).