Predicting protein residue–residue contacts using deep networks and boosting

Abstract

Motivation: Protein residue–residue contacts continue to play a larger and larger role in protein tertiary structure modeling and evaluation. Yet, while the importance of contact information increases, the performance of sequence-based contact predictors has improved slowly. New approaches and methods are needed to spur further development and progress in the field.

Results: Here we present DNCON, a new sequence-based residue–residue contact predictor using deep networks and boosting techniques. Making use of graphical processing units and CUDA parallel computing technology, we are able to train large boosted ensembles of residue–residue contact predictors achieving state-of-the-art performance.

Availability: The web server of the prediction method (DNCON) is available at http://iris.rnet.missouri.edu/dncon/.

Contact: chengji@missouri.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

The prediction of protein residue–residue contacts is seen by many as an important intermediate step for gaining traction on the challenging task of tertiary structure prediction. This idea has been spurred further recently by encouraging results that demonstrate that predicted contact information can indeed be used to improve tertiary structure prediction and effectively transform some unfolded structures into their folded counterpart (Wu et al., 2011). The addition of a contact guided structure modeling category in the Critical Assessment of Techniques for Protein Structure Prediction (CASP) on a rolling basis has also aided in sparking interesting in residue–residue contact prediction. Beyond the scope of tertiary structure prediction, protein residue–residue contacts have been used in drug design (Kliger et al., 2009), model evaluation (Wang et al., 2011) and model ranking and selection (Miller and Eisenberg, 2008; Tress and Valencia, 2010).

Existing methods for residue–residue contact prediction can be broadly categorized as sequence based or template/structure based. Sequence-based methods attempt to predict contacts from the primary sequence or information that can be derived directly from the sequence. A number of these sequence-based methods use various machine learning methods such as support vector machines (Cheng and Baldi, 2007; Wu and Zhang, 2008), neural networks (Fariselli et al., 2001; Hamilton et al., 2004; Pollastri and Baldi, 2002; Tegge et al., 2009; Walsh et al., 2009; Xue et al., 2009), hidden Markov models (Bjorkholm et al., 2009), Markov logic networks (Lippi and Frasconi, 2009), random forests (Li et al., 2011) and deep architectures (Di Lena et al., 2012) to make residue–residue contact predictions. Other sequence-based approaches have used evolutionary information contained in multiple sequence alignments (MSAs) to identify possible contacts (Gobel et al., 1994; Olmea and Valencia, 1997; Vicatos et al., 2005). Methods using MSAs were among the first sequence-based approaches tried but suffered from low accuracies caused by indirect or transitive correlations. More recent developments by Jones et al. (2012) using large MSAs and sparse covariance matrices have been better able to identify contacting residues from the alignments and resulted in significant improvements in accuracy. Template-/structure-based methods operate by extracting contact information from structural data. For template-based methods, this structural data comes in the form of templates (i.e. homologous proteins with known structure). Once templates have been found and aligned, residue–residue contacts are predicted using the contacts found in the structures (Wu and Zhang, 2008).

Given the relatively high quality of the tertiary structure models generated by template-based techniques, residue–residue contact data is most useful when dealing with hard targets (i.e. those for which a structural template does not exists or hard to identify by sequence alone). For hard targets, the conformational search is much larger and overall model quality is usually much lower. Thus, there is great interest in high quality sequence-based residue–residue contact predictors that do not rely on template data. Such contact predictors would be able to provide additional information when generating models for hard targets. Unfortunately, recent assessments of state-of-the-art sequence-based contact predictors routinely report average accuracies in the 20–30% range, indicating a need for further development and new methods and ideas (Ezkurdia et al., 2009; Izarzugaza et al., 2007; Monastyrskyy et al., 2011).

Here we present a new sequence-based residue–residue contact predictor using deep networks (DNs) and boosting. Our method differs from other implementations of deep architectures owing to its boosted nature, overall network architecture and training procedure. More specifically, for training, we initially use an unsupervised approach to learn patterns in the data and initialize parameters and then fine tune them with back propagation. Furthermore, by using the computational power of graphical processing units (GPUs) and CUDA, we were able to train large boosted ensembles of DN classifiers achieving state-of-the-art performance.

2 METHODS

2.1 Datasets and evaluation metrics

Several datasets were used to train and evaluate our residue–residue contact predictor. The primary dataset, DNCON, was formed by an advanced search of the Protein Data Bank filtering the results by 30% sequence similarity and a resolution of 0–2 Å (Berman et al., 2000). The results from this initial search were then filtered by sequence length and disorder content, retaining sequences that were 30–300 residues in length and contained fewer than 20% disordered residues (i.e. coordinates were missing for fewer than 20% of the residues in the experimentally determined structure). The resulting set of proteins was then merged with the training set from SVMcon and then filtered by three existing datasets D329, SVMCON_TEST and CASP9, which were used as evaluation sets. The filtering process ensured that the pairwise sequence identity between the merged dataset and any sequence in the evaluation sets was ≤25%. The end result of the search and filter process was our primary dataset, DNCON, consisting of 1426 proteins. This dataset was then randomly split into two sets: DNCON_TRAIN consisting of 1230 proteins and DNCON_TEST consisting of 196 proteins. Supplementary Figure S1 illustrates the entire dataset generation and filtering process.

The evaluation datasets used included D329, a set of 329 proteins used to evaluate ProC_S3 (Li et al., 2011); SVMCON_TEST, a set of 48 short to medium length proteins used to evaluate SVMcon (Cheng and Baldi, 2007); CASP9, a set of 111 targets used during the ninth Critical Assessment of Techniques for Protein Structure Prediction (Moult et al., 2011); CASP9_HARD, a subset of 16 targets taken from the CASP9 set that are solely composed of free modeling (FM) or free modeling/template-based modeling (FM/TBM) domains; and DNCON_TEST. Owing to the filtering process used in the creation of our dataset, all evaluation datasets are independent (i.e. <25% sequence identity) to the training set.

In this study, two amino acid residues are said to be in contact if the distance between their C_β atoms (C_α for glycine) in the experimental structure is <8 Å. Short-range contacts are defined as residues in contact whose separation in the sequence is ≥6 and <12. Likewise, medium-range contacts are residues in contact whose separation in sequence is ≥12 but <24 and long-range contacts are defined as having separation in the sequence ≥24 residues. These definitions are in agreement with recent studies and CASP residue–residue contact assessments (Eickholt et al., 2011; Ezkurdia et al., 2009; Grana et al., 2005; Izarzugaza et al., 2007; Li et al., 2011; Monastyrskyy et al., 2011; Tegge et al., 2009).

A common evaluation metric for residue–residue contact predictions is the accuracy of the top L/5 or L/10 predictions where L is the length of the protein in residues. In this context, accuracy (Acc) is defined as the number of correctly predicted residue–residue contacts divided by the total number of contact predictions evaluated. We also considered the coverage (Cov) of residue–residue contact predictions, which is defined as the number of correctly predicted contacts divided by the number of true contacts. As predicting short-, medium- and long-range contacts have varying degrees of difficulty, it is common to separate predicted contacts by sequence separation and then calculate the accuracy and coverage of the top L and L/5 predictions for each range. Note that this evaluation is done on a per target basis and irrespective of the domain architecture. Estimates for the standard error for accuracy and coverage were calculated using the sample mean and sample variance of the per-target accuracies and coverages.

2.2 Restricted Boltzmann machine and deep belief network

The general framework used for classifying residue–residue contacts was a combination of restricted Bolzmann machines (RBMs) trained to form DNs. A RBM is a two-layer network that can be used to model a distribution of binary vectors. In this model, a layer of stochastic binary nodes representing feature detectors are connected via symmetric weights to stochastic binary nodes that take on the values of the vectors to be modeled (Hinton, 2002; Smolensky, 1986). Conceptually, the layer of stochastic nodes corresponding to the feature detectors can be viewed as the ‘hidden’ or ‘latent’ data and the other layer of nodes as the ‘visible’ data. The energy of a particular configuration of this network can be defined by

(1)

where v_i and h_j are the states of the i^th and j^th nodes, b_i is the bias for the i^th visible node, c_j is the bias for the j^th hidden node and w_ji is the weight of the connection between the i^th visible and j^th hidden nodes. A probability can then be assigned to a configuration of visible data by

(2)

where Z is a normalizing constant and the sum is over all possible configurations of h.

Training consists of adjusting the weights of the model such that real data (e.g. training data) has a higher probability than arbitrarily chosen configurations of visible nodes. This can be done using a process called contrastive divergence, which adjusts the weights in a manner that seeks to minimize an approximation to a difference of Kullback–Leibler divergences (Hinton, 2002). The use of contrastive divergence learning as opposed to maximum likelihood learning has to do with a problematic term in the gradient of average log likelihood function, which is exponential in nature and difficult to approximate. With contrastive divergence, the problematic term cancels out. Full details are provided in Hinton’s presentation on training products of experts (2002). In this work, the weights in the n-th epoch of training were updated as follows:

(3)

(4)

(5)

In these equations, the angle brackets represent averages over the batch. The subscripts ‘data’ and ‘recon’ are descriptors that illustrate that the first average is taken over the data and the second average over reconstructions of the data after one round of Gibbs sampling. For < >_data, 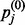is the probability that the j-th hidden unit will be activated when driven by the data and calculated as

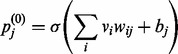(6)

where σ(•) is the sigmoid function. For < >_recon, 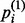is the probability that the i^th visible unit will be activated and is calculated as

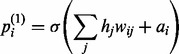(7)

where h_j is a binary value set to 1 with probability 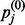. The final value to be computed is 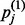_, which is the probability that the j-th hidden unit will be activated when driven by the probabilities of the reconstructed visible nodes and calculated as

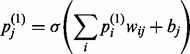(8)

In Equations 3, 4 and 5, ε is the learning rate, η is the weight cost and υ the momentum. These parameters and update equations were used in accordance with recent findings on how to train RBMs in practice (Hinton, 2010). In our study, the learning rate ε was set to 0.01 for w and 0.1 for the biases, and the weight cost η was set to 0.0002. The momentum υ was initially set to 0.5 and after 5 epochs of training increased to 0.9. Training a RBM was done using batches of 100 training examples over 20 epochs. During training, the average free energy of the training data was compared with that of a small holdout set taken from DNCON_TEST to confirm that the RBM was not over-fitting the training data (Hinton, 2010).

RBMs are particularly useful to initialize weights in DNs. This can be done by learning RBMs in a stepwise unsupervised fashion. After training the first RBM, it is applied to the training data and for each training example, the probabilities for activating each hidden node can be calculated and used to train another RBM. This process of training a RBM and then using the hidden activation probabilities as inputs to the next level can be repeated several times to create a multilayer network. For the last level, a one-layer neural network can be added. All the nodes can then be treated as real-value deterministic probabilities and the entire network can be fine tuned using a standard back propagation algorithm to adjust the parameters (Hinton et al., 2006; Hinton and Salakhutdinov, 2006).

To facilitate working with large RBMs and DNs, we implemented the training and classification procedures in terms of matrix operations and used CUDAMat (Mnih, 2009), a python library that provides fast matrix calculations on CUDA-enabled GPUs. CUDA is a parallel computing platform that provides high-level access to the computing cores of certain graphics processing units (http://www.nvidia.com/object/cuda_home.html). Using CUDAMat and GPUs allowed us to train DN classifiers with on the order of 1 million parameters in under an hour.

2.3 Prediction of medium-/long-range contacts

For the prediction of medium- and long-range contacts, we trained multiple ensembles of DNs. The inputs for each DN included sequence-specific values for the residues in two windows centered around the residue–residue contact pair in question, several pairwise potentials, global features and values characterizing the sequence between the contact pair (see Section 2.7 for details). The target was a single binary value that represented the pair being in contact or not. For the size of the windows, we tried lengths of 7, 9, 11, 13, 15, 17 and 19. The overall size of the input feature vector varies from 595 (for windows 7 residues long) to 1339 (for windows 19 residues in length). The variability in the size of the input vector stems from the fact that several features used are residue specific, and consequently, as the number of residues included in the input window grows so does the size of the input vector. The overall architecture of the DN was (595–1339)-500-500-350-1 (see Supplementary Fig. S2). Each layer was trained in a stepwise fashion as a RBM using the previously described process with the exception of the last layer, which was trained as a one-layer neural network. The entire network was fine tuned using back propagation to minimize the cross-entropy error and done over 25 epochs with mini batches of 1000 training examples (see Supplementary Fig. S3).

To create boosted ensembles of classifiers, we trained several DNs in series using a sample of 90 000 medium-/long-range residue–residue pairs from a larger pool. The pool of training examples used came from the training dataset, DNCON_TRAIN, and consisted of all medium- and long-range contacts up to 120 residues in sequence separation and a random sample of approximately twice as many non-contacting pairs. Initially, the residue–residue pairs in the training pool were uniformly distributed and had an equal chance of being included in the training sample. After each round, the training pool was evaluated using the new classifier and the pool was reweighted based on the performance of the classifier. The probability of training data that was misclassified was increased, whereas correctly classified data had its probability of selection decreased. This was done using a variant of AdaBoost (Freund and Schapire, 1997). More specifically, let x_i represent the i-th example in the training pool and y_i ε {0, 1} be the class of the i-th example. Also, let W_t(i) be the probability of selecting the i-th example from the training pool in the t-th round of boosting and call the DN classifier trained in round t to be m_t(•), which outputs a value between 0 and 1. Now, after each round of boosting, W_t(i) is updated via ε_t, α_t and h_t(•) in the following manner.

(9)

(10)

(11)

(12)

After 35 rounds of boosting, the final prediction for an input x_i is given by H(x_i) and is a value between 0 and 1.

(13)

Supplementary Figure S4 shows a boosted ensemble.

Additionally, we found that after several rounds of boosting, the weights of a number of particularly difficult training examples became disproportionately large and dominated the selected training data. Models trained on these sets did not generalize well and prohibited boosting beyond 10 rounds. This phenomenon is not new and has been studied elsewhere (Vezhnevets and Barinova, 2007). One solution was to reinitialize the weights on all the training examples after 7 rounds, which in effect joins bagging with several rounds of boosting. Another solution was to combine reinitializing the weights with a trimming procedure, which removed up to 30% of the hard training cases. This was achieved by removing (i.e. trimming) those training examples that were 5 times more likely to be selected than by chance.

2.4 Consensus predictions for medium-/long-range contacts

In addition to training ensembles for various fixed-length windows, we also averaged the prediction scores for contacts across ensembles. In all, there were 490 classifiers with 35 coming from each possible combination of window size (7, 9, 11, 13, 15, 17 or 19) and sampling scheme (reweighted or reweighted with trimming).

2.5 Prediction of short-range contacts

For the prediction of short-range contacts, we trained one ensemble of DNs. The input for each DN was a window 12 residues in length and the target was all short-range contacts whose residue pairs were contained in the window. In all, 400 features were used for each window and the target contained 21 predictions. The overall architecture of the DN was 400-500-500-250-21 (Supplementary Fig. S5). Each layer was trained as a RBM using the previous described process, and the entire network was fine tuned using back propagation to minimize the cross-entropy error and done over 20 epochs with mini-batches of 1000 training examples. As the 12 residue window slides across the sequence, most short-range residue pairings appear and are predicted multiple times and the final prediction for a residue–residue pair is calculated by averaging the predicted values across all windows.

To create an ensemble of short-range predictors, we trained 30 DNs. When selecting the training set for each model, we randomly sampled 80 000 short-range windows from a pool. For the short-range predictor, the training pool consisted of all possible 12 residue windows contained in the training dataset, DNCON_TRAIN. This resulted in a pool of 198 333 training examples. The initial probability of choosing a training example was uniform and the probability of being selected was updated after each round using a procedure similar to that outlined for the medium-/long-range predictors. The only difference was in how the probabilities were updated. As the output for short-range predictions had multiple values, the probability of an example was increased in a way that was proportional to the number of incorrectly classified targets for the example. Equation 13 indicates how the weights were updated. β is the percentage of the 21 short-range targets that were misclassified for a training example.

(14)

The predicted value for a short-range residue–residue pair was the average of the predictions across the ensemble.

2.6 DNCON

The sum of the aforementioned components is DNCON. It is a sequence-based residue–residue contact predictor capable of predicting short-, medium- and long-range contacts. For medium- and long-range prediction, DNCON uses a consensus from the medium-/long-range boosted ensembles. For short-range predictions, DNCON uses the short-range ensemble trained on fixed windows of 12 residues. The entire boosted network is used when making residue–residue contact predictions.

2.7 Features used and generation

The features we used for training our residue–residue contact predictors are consistent with those used by many other predictors (Cheng and Baldi, 2007; Li et al., 2011; Pollastri and Baldi, 2002; Tegge et al., 2009). These included predicted secondary structure and solvent accessibility, values from the position-specific scoring matrix (PSSM) and several pre-computed statistical potentials. To obtain the PSSM, PSI-BLAST (Altschul et al., 1997) was run for three iterations against a non-redundant version of the nr sequence database filtered at 90% sequence similarity. The secondary structure and solvent accessibility were predicted using SSpro and ACCpro from the SCRATCH suite (Cheng et al., 2005). The Acthely factors are scaled representations of five numerical values that characterize a residue by electrostatic charge, codon diversity, volume, polarity and secondary structure (Atchley et al., 2005). Finally, we mention that all features which took values outside the range from 0 to 1 were rescaled to be from 0 to 1 so as to be compatible with the input layer of the RBM.

For short-range contact prediction, for each residue in the window, we used 3 binary inputs to encode the predicted secondary structure (helix: 100, beta: 010, coil: 001), 2 binary inputs for solvent accessibility at the 25% threshold (exposed: 10, buried: 01), from the PSSM obtained from PSI-BLAST we obtained 1 input for the information score of the residue and 20 inputs for the likelihoods of each amino acid type at that position, and 5 inputs for Acthley factors. Additional global features included 4 binary inputs to encode protein length (<75: 1000, 75–150: 0100, 150–225: 0010, >225: 0001), 20 inputs for the percent representation of each amino acid in the sequence, 3 inputs for the percentage of predicted exposed alpha helix and beta sheet residues, and 1 input for the relative position of the center of the window with respect to the sequence length (i.e. midpoint/protein length). Thus for short-range predictions, there were a total of 400 features (12 × 31 local features + 28 global features).

For medium- and long-range contacts, we used features coming from two windows centered on the residue pair in question as well as pairwise and global features. For each residue in a window, we used the same features as in the short-range residue window (i.e. predicted secondary structure and solvent accessibility, information and likelihoods from the PSSM and Acthley factors). We also encoded these features for a small window of five residues centered at the midpoint between the residue pair to be classified. For global features, we used the same global feature set as described for the short-range contact predictor (i.e. protein length, relative position of contacting pair, percentage of predicted exposed, alpha helix and beta sheet residues) and an additional set of 11 binary features to encode the separation of the residue pair in sequence (1–12, 13–18, 19–26, 27–38, 39–50, 51–62, 63–74, 75–86, 87–98, 99–110, and 111–120). Finally, we used a number of pairwise features that depended on the residue pair, and these included Levitt’s contact potential (Huang et al., 1996), Jernigan’s pairwise potential (Miyazawa and Jernigan, 1999), Braun’s pairwise potential (Zhu and Braun, 1999), the joint entropy of the contact pair calculated from the residue frequency counts in the PSSM, the Person correlation coefficient and cosine calculated on the residue frequency counts for the pair in the PSSM and the four-order of weighted means for secondary structure and solvent accessibility for the sequence segment between the residue pair (Li et al., 2011).

3 RESULTS AND DISCUSSION

3.1 Performance of DNCON

To evaluate our residue–residue contact predictor, we evaluated its performance on a number of datasets and compared it with two state-of-the-art contact predictors, ProC_S3 and SVMcon. These methods were ranked as the best sequence-based residue–residue contact predictors in CASP9 (Monastyrskyy et al., 2011). Table 1 shows accuracy and coverage of the top L/5 and top L predictions for ProC_S3, SVMcon and DNCON. The predictions for SVMcon and ProC_S3 were downloaded from the official CASP website (http://predictioncenter.org/download_area/CASP9/predictions/). The evaluation dataset for this comparison was CASP9_HARD, a set of 16 proteins that were comprised solely of domains classified as FM or FM/TBM by CASP9 assessors. The FM and FM/TBM classification indicates that template-based information was scant or difficult to obtain for these targets. As seen in Table 1, DNCON performed well on these targets, achieving state-of-the-art performance for accuracy and converge of long-range contacts when considering the top L or L/5 contact predictions. Given the comparable performances of the methods, we also examined if the methods were identifying the same contacts or if they were in some sense complementary. We discovered that while there was some overlap between prediction sets (∼18–30%), each method was identifying a number of unique true contacts among those selected (see Supplementary Tables S1–S3 for full details).

Table 1.

Performance of DNCON, ProC_S3 and SVMcon for long-range contact prediction on CASP9_HARD, a set of 16 CASP9 targets that are solely composed of FM and FM/TBM domains

Method	Acc(L)	Acc(L/5)	Cov(L)	Cov(L/5)
DNCON	0.147(0.016)	0.229(0.033)	0.116(0.02)	0.036(0.009)
ProC_S3	0.134(0.029)	0.210(0.036)	0.081(0.015)	0.033(0.010)
SVMcon	0.123(0.014)	0.198(0.042)	0.087(0.017)	0.031(0.009)

Estimates for standard error are provided in parenthesis.

While evaluating residue–residue contacts on hard targets is arguably the best means of evaluation (i.e. it is on these types of targets that contact information may have the largest impact), the drawback is that these datasets are usually composed of a small number of targets. To increase the robustness of our evaluation, we also compared DNCON with SVMcon and ProC_S3 on larger datasets, namely SVMCON_TEST and D329. Table 2 presents the accuracy and coverage of the top L/5 and top L predictions for SVMcon and DNCON on the SVMCON_TEST, the dataset used to evaluate SVMcon. Similarly, Table 3 presents the results for ProC_S3 and DNCON on the D329, a dataset used to evaluate ProC_S3. The predictions for SVMcon on the SVMCON_TEST dataset were obtained by downloading SVMcon and made locally and evaluated with our pipeline. Note that the values for ProC_S3 on the D329 dataset are those reported by Li et al. (2011) in their assessment of their method. Both of these evaluations show that the performance of DNCON is on par with the two state-of-the-art contact predictors (Table 3).

Table 2.

Performance of DNCON and SVMcon for long- and medium-range contact predictions on the SVMCON_TEST dataset

Method	Acc(L)	Acc(L/5)	Cov(L)	Cov(L/5)
DNCON[L]	0.193(0.019)	0.329(0.037)	0.197(0.019)	0.066(0.009)
SVMcon[L]	0.200(0.019)	0.285(0.032)	0.179(0.017)	0.056(0.008)
DNCON[M]	0.230(0.020)	0.427(0.036)	0.548(0.022)	0.200(0.017)
SVMcon[M]	0.257(0.019)	0.418(0.035)	0.518(0.026)	0.192(0.017)

Estimates for standard error are provided in parenthesis. Contact range is denoted within brackets, L for long range and M for medium range.

Table 3.

Performance of DNCON and ProC_S3 for medium and long-range contact prediction on the D329 dataset

Method	Acc(L)	Acc(L/5)	Cov(L)	Cov(L/5)
DNCON[L]	0.191(0.005)	0.326(0.011)	0.149(0.005)	0.052(0.002)
ProC_S3[L]a	0.180	0.297	0.151	0.056
DNCON[M]	0.196(0.006)	0.368(0.011)	0.511(0.009)	0.190(0.005)
ProC_S3[M]a	0.209	0.410	0.520	0.227

^aThese values are reported by Li et al. (2011) using same evaluation metrics. No error estimates provided. Estimates of standard error are provided in parenthesis. Contact range is denoted within brackets, L for long range and M for medium range.

As an additional comparison between DNCON, ProC_S3 and SVMcon, we evaluated each method on all valid CASP9 targets. Again, the predictions for SVMcon and ProC_S3 were downloaded from the official CASP website. Note that this evaluation was done using the entire protein and meant to complement the assessment technique used by CASP assessors, which evaluates predictions on a per domain basis. Tables 4 and 5 show the results of the three methods when evaluated on long- and medium-range contacts. Once again, DNCON performs competitively against SVMcon and ProC_S3.

Table 4.

Performance of DNCON, ProC_S3 and SVMcon for long-range contact prediction on the CASP9 dataset

Method	Acc(L)	Acc(L/5)	Cov(L)	Cov(L/5)
DNCON	0.172(0.016)	0.291(0.033)	0.128(0.02)	0.043(0.009)
ProC_S3	0.168(0.029)	0.282(0.036)	0.103(0.015)	0.041(0.01)
SVMcon	0.141(0.014)	0.233(0.042)	0.096(0.017)	0.034(0.009)

Estimates of standard error are provided in parenthesis.

Table 5.

Performance of DNCON, ProC_S3 and SVMcon for medium-range contact prediction on the CASP9 dataset

Method	Acc(L)	Acc(L/5)	Cov(L)	Cov(L/5)
DNCON	0.189(0.017)	0.356(0.03)	0.513(0.042)	0.191(0.025)
ProC_S3	0.196(0.016)	0.371(0.055)	0.491(0.038)	0.198(0.029)
SVMcon	0.193(0.02)	0.312(0.033)	0.442(0.045)	0.167(0.028)

Estimates of standard error are provided in parenthesis.

The final evaluation set used was DNCON_TEST, an evaluation set of 196 proteins from the dataset that we curated. Table 6 shows the performance DNCON on our evaluation set. We also calculated the sensitivity of DNCON on DNCON_TEST at the 95% specificity rate. For long-range contacts, 38% of the true long-range contacts can be recovered at the 95% specificity rate (i.e. 95% of non contacts are recovered). For medium-range contacts, the sensitivity is 44% at the 95% specificity level.

Table 6.

Performance of DNCON for short-, medium- and long-range contact prediction on the DNCON_TEST dataset

Range	Acc(L)	Acc(L/5)	Cov(L)	Cov(L/5)
Short	0.213	0.509	0.705	0.333
Medium	0.207	0.380	0.508	0.187
Long	0.215	0.341	0.157	0.049

In addition to the evaluation on the entire DNCON_TEST dataset, we also evaluated our method on three subsets of DNCON_TEST. Using the CATH structure classification database (Cuff et al., 2011), we indentified and grouped 140 of the proteins in DNCON_TEST as mainly alpha, α (29), mainly beta, β (30) and alpha beta, αβ (81). These results are summarized in Table 7. Interestingly, our method appears to have more difficulty with mainly alpha proteins than with the mainly beta or alpha beta mix. Difficulty in predicting mainly alpha proteins has been noted elsewhere (Cheng and Baldi, 2007; Di Lena et al., 2012) and is a starting point for future study.

Table 7.

Performance of DNCON on structurally defined subsets of the DNCON_TEST dataset

Range	Type	Acc(L)	Acc(L/5)	Cov(L)	Cov(L/5)
Short	α	0.171	0.440	0.714	0.364
	β	0.285	0.612	0.748	0.318
	αβ	0.201	0.512	0.723	0.350
Medium	α	0.132	0.257	0.570	0.220
	β	0.255	0.448	0.487	0.170
	αβ	0.222	0.420	0.543	0.203
Long	α	0.111	0.156	0.112	0.031
	Β	0.222	0.322	0.147	0.042
	αβ	0.234	0.384	0.169	0.053

Finally, we assessed our contact predictor by evaluating its performance when considering neighborhoods. In this setting, a predicted contact is considered correct if there is a true residue–residue contact with ±δ residues for small values of δ (e.g. for δ = 1, a predicted contact [i,j] would be counted correct if there were a true contact at [i,j], [i±1,j], [i,j±1] or [i±1,j±1]). Table 8 states the accuracy of DNCON on the DNCON_TEST dataset for δ = 1 and δ = 2. These results demonstrate that while the predictions contain some noise, which prohibits residue-level precision, in general, the contact predictions are accurate and contain a strong signal. This strong signal, particularly at the short and medium range, could provide valuable local information, which could be propagated and incorporated into the prediction of longer range contacts. Recent work by Di Lena et al., has demonstrated that propagating neighboring contact predictions can indeed increase performance (2012). Given the flexibility of the DN architecture and its ability to handle a large number of input features, this type of local contact information could easily be included for longer range predictions. This is a line of investigation we are currently pursuing for a future work. As for long-range contact predictions, these too exhibit a strong relatively accurate contact signal, which may prove more useful than the residue-specific accuracies indicate, particularly for the purposes of guiding a search through the protein conformation space. An evaluation of SVMcon and ProC_S3 on DNCON_TEST using the neighborhood criteria found that ProC_S3 and DNCON perform comparably and both outperform SVMcon (data not shown).

Table 8.

Performance of DNCON for short-, medium- and long-range contact prediction on the DNCON_TEST dataset when considering small neighborhoods

Range	Acc(L/5)	Acc(L/2)	Acc(L)
Short (δ = 1)	0.789	0.657	0.532
Medium (δ = 1)	0.648	0.552	0.463
Medium (δ = 2)	0.749	0.678	0.607
Long (δ = 1)	0.550	0.476	0.415
Long (δ = 2)	0.638	0.578	0.552

3.2 Value of boosting and ensembles

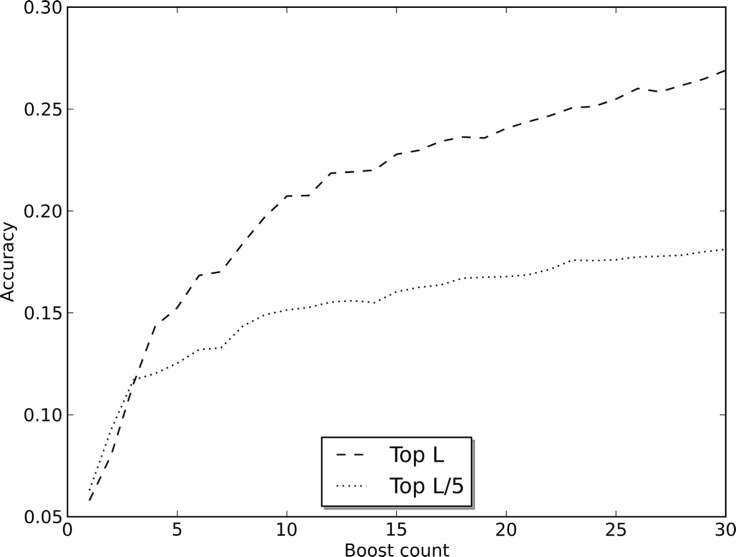
To determine the value of the boosted ensembles and the consensus approach, we studied the performance of the predictions for various configurations of ensembles and across rounds of boosting. Figure 1 characterizes the affect of boosting on the accuracy of the top L and L/5 long-range predictions (see Supplementary Fig. S6 for effect on medium-range predictions). These particular figures are of the ensemble with windows of 13 residues in length and with the reweighted sampling scheme. They show the benefit of boosting and are typical of the affect seen in other ensembles.

Fig. 1.

Accuracy of the top L and L/5 long-range contact predictions for a boosted ensemble (13-win). The graph plots accuracy as a function of the number of rounds of boosting

To determine the effect of the window size on the method’s performance, we evaluated the performance using ensembles comprising DNs with only one window size and reweighting scheme. It is interesting to note that while all of the ensembles perform roughly the same, there is a marked difference in the performance of the individual ensembles and the consensus prediction for top L/5 predictions. Accuracies for the individual ensembles are in the range of 0.24–0.28 for the top L/5 long-range predictions, whereas the accuracy of their consensus is 0.34 (Supplementary Table S4). Similarly, for the top L/5 medium-range predictions, the accuracy jumps from the 0.32 to 0.34 range to 0.38.

4 CONCLUSION

In this work, we have presented DNCON, a new method for protein residue–residue prediction. The approach is based on two concepts, boosted ensembles and DNs, which are novel in the context of residue–residue contact prediction. When compared with the current state-of-the-art, DNCON performs favorably, achieving state-of-the-art performance in the critical area of accuracy on top medium and long range contact predictions. When allowing for less than residue level precision, the performance of DNCON is even more impressive. Given the strong contact signal present for short- and medium-range contacts and the fast flexible architecture of DNs, in the future, we plan on modifying the DNs such that they can incorporate and propagate predicted short- to medium-range contacts when making longer range predictions. We also plan on refining the parameters and network architecture used to increase performance. The method is available as a web service at http://iris.rnet.missouri.edu/dncon/.

Funding: The work was partially supported by a National Library of Medicine Biomedical and Health Informatics Training fellowship (to J.E.) and a NIH NIGMS grant (R01GM093123 to J.C.).

Conflict of Interest: none declared.