Global network alignment using multiscale spectral signatures

Abstract

Motivation: Protein interaction networks provide an important system-level view of biological processes. One of the fundamental problems in biological network analysis is the global alignment of a pair of networks, which puts the proteins of one network into correspondence with the proteins of another network in a manner that conserves their interactions while respecting other evidence of their homology. By providing a mapping between the networks of different species, alignments can be used to inform hypotheses about the functions of unannotated proteins, the existence of unobserved interactions, the evolutionary divergence between the two species and the evolution of complexes and pathways.

Results: We introduce GHOST, a global pairwise network aligner that uses a novel spectral signature to measure topological similarity between subnetworks. It combines a seed-and-extend global alignment phase with a local search procedure and exceeds state-of-the-art performance on several network alignment tasks. We show that the spectral signature used by GHOST is highly discriminative, whereas the alignments it produces are also robust to experimental noise. When compared with other recent approaches, we find that GHOST is able to recover larger and more biologically significant, shared subnetworks between species.

Availability: An efficient and parallelized implementation of GHOST, released under the Apache 2.0 license, is available at http://cbcb.umd.edu/kingsford_group/ghost

Contact: rob@cs.umd.edu

1 INTRODUCTION

We present a novel method for the global pairwise alignment of biological networks. Such alignments are crucial in analyzing the increasing amount of experimental data being generated by high-throughput techniques, such as yeast two-hybrid screening (Fields and Song, 1989), tandem affinity purification mass spectrometry (Gavin et al., 2006) and chip-seq (Johnson et al., 2007) that reveal biological interactions within the cell.

A solution to the global network alignment problem is an injective mapping f from the nodes of one network 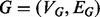into another network 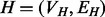such that the structure of G is well preserved. This global mapping allows us to measure the similarity between proteins in G and those in H in terms of shared interaction patterns. By exposing large subnetworks with shared interactions patterns across species, a network alignment allows us to transfer protein function annotations from one organism to another using more information than can be captured by sequence alone. For example, it has been shown that, across species, the protein with the most similar sequence does not always play the same functional role (Sharan et al., 2005), and that topological information can be used to disambiguate sequence-similar proteins and determine functional orthology (Bandyopadhyay et al., 2006). Additionally, by looking at the magnitude of structure conserved between G and H, we can measure the similarity between these networks and infer phylogenetic relationships between the corresponding species (Kuchaiev and Przulj, 2011). We can also hypothesize the existence of unobserved interactions (missing edges), remove noise from error-prone high-throughput experiments and track the evolution of pathways.

Our approach to the global network alignment problem uses a novel measure of topological node similarity that is based on multiscale spectral signatures. These signatures are composed from the spectra of the normalized Laplacian for subgraphs of varying sizes centered around a node. We combine this highly specific yet robust node signature with a seed-and-extend alignment strategy that explicitly enforces the proximity of aligned neighborhoods. The initial alignment is improved by means of a local search procedure. We implement these ideas in our network alignment software, GHOST, which exceeds state-of-the-art accuracy under several different metrics of alignment quality.

There has been significant interest in the network alignment problem, and previous work can naturally be divided into three main categories: approaches to local network alignment, approaches to network querying and approaches to global network alignment. Because we are introducing a system for global network alignment, we restrict our discussion to the relevant work in this area.

Singh et al. (2008) introduced IsoRank, which uses a recursively defined measure of topological similarity between nodes in different networks. They proposed an eigenvector-based formulation to discover a high-scoring matching. Liao et al. (2009) developed IsoRankN, which extends IsoRank with a new algorithm for multiple network alignment based on spectral clustering. Chindelevitch et al. (2010) use a local search heuristic, which they call PISWAP, to iteratively improve an initial alignment that is based solely on sequence data. The Graemlin aligner was originally developed by Flannick et al. (2006) to discover evolutionarily conserved modules across multiple biological networks. Later, it was extended (Flannick et al., 2009) to perform global multiple network alignment. However, this approach relies on a variety of additional information about the networks being aligned, including phylogenetic information. Further, sample alignments are required for the parameter learning phase of Graemlin2.

Recently, multiple attempts have been made to tackle the biological network alignment problem using graph matching. Klau (2009) introduced a non-linear integer program to maximize a structural matching score between two given networks and then showed how the problem can be linearized, yielding an integer linear program, and finally suggested a Lagrangian relaxation approach to the integer linear program. Later, El-Kebir et al. (2011) extended this approach and improved the upper and lower bounds of the relaxation, implementing their approach in the Natalie 2.0 software package. The HopeMap approach of Tian and Samatova (2009) used an algorithm that iteratively merges conserved connected components. Zaslavskiy et al. (2009) explore the use of a number of graph-matching methods, particularly the PATH and graduated assignment methods, which attempt to find a permutation matrix between vertices of the networks being aligned that maximizes a score that is a combination of the structural similarity and conserved interactions of the matched vertices. This optimization is NP hard, and they must rely on a relaxation to discover an approximate solution. Many similar graph-matching approaches have been applied to shape matching in computer graphics and computer vision (Duchenne et al., 2011; Torresani et al., 2008; Noma and Cesar, 2010). All of these matching-based approaches require a large number of constraints to be placed on the set of potential alignments, usually in the form of homology information between the proteins of the networks being aligned, to run in a reasonable amount of time. These constraints vastly reduce the search space and help bring these computationally burdensome methods into the realm of tractability. However, the hard constraints introduced by the homology information can have a negative effect on the ability of these methods to discover truly novel functional homologs between highly divergent species. In a way, these methods focus more on discovering conserved patterns of interactions between proteins that are already posited to be homologous, rather than on performing a truly de novo and unconstrained alignment of biological networks that is merely guided by homology information. GHOST takes a hybrid approach, where the initial alignment can be constrained by some aspect of the scoring function, but the local search procedure allows exploration into regions of the alignment space that do not adhere to the original constraints.

The GRAAL family of programs, like IsoRank, performs unconstrained and global pairwise alignments of biological networks. Kuchaiev et al. (2010) originally introduced GRAAL, which measures the topological similarity of nodes in different networks based on the distance between their graphlet degree signatures and aligns the networks using a seed-and-extend strategy. Milenkoviç et al. (2010) then introduced H-GRAAL, which relies on the same graphlet degree signatures used by GRAAL but performs the alignment of the networks by solving the linear assignment problem via the Hungarian algorithm (Kuhn, 1955). Finally, Kuchaiev and Przulj (2011) introduced MI-GRAAL, which combines these two alignment strategies. It relies on a seed-and-extend alignment procedure but uses the Hungarian algorithm only to compute the assignment between local neighborhoods of the two graphs that maximizes the sum of their linear scoring function. MI-GRAAL also incorporates a number of other topological metrics, in addition to the graphlet degree signatures, to help quantify the topological similarity between nodes.

Our network aligner, GHOST, combines a novel spectral signature to measure topological similarity with a seed-and-extend alignment procedure, and an iterative local search step. In Sections 3.1 and 3.2, we show that GHOST performs much better than current aligners at the network self-alignment task. In Section 3.3, we compare an ensemble of alignments produced by different aligners, as we vary their parameter settings to trade off between the topological and biological quality of the alignments they produce. GHOST consistently outperforms the other aligners in these tests and is able to produce alignments higher overall quality. This improved quality will be useful for more accurate comparative systems biology.

2 METHODS

2.1 Measuring alignment quality

It is challenging to state the global network alignment problem formally and precisely because a ‘good’ alignment balances two, often disparate, goals. A high-quality global alignment between two biological networks should reveal shared topological structure between the networks being aligned while also respecting the strong evidence for homology revealed via sequence analysis.

Neither of these goals, however, should act as hard constraints when aligning two networks, and a high-quality global network alignment should strive to satisfy both the topological and sequence requirements. This naturally leads to two distinct measures for the quality of network alignments; one quantifies topological quality, the degree of shared structure revealed between the two networks, and the other quantifies biological quality, how well the alignment respects the biological and functional similarities of the proteins.

2.2 Topological quality

A topological quality metric should measure the degree to which the structure of G is preserved, under f (the computed injective mapping from VG to VH), when mapped into H. For example, we expect that an alignment of high topological quality will map interacting proteins in G to interacting proteins in H. The most common measure of topological quality is edge correctness (EC), which measures the percentage of edges from G that are aligned to edges in H. Let G[V] be the induced subgraph of G on the vertex set V, 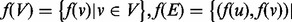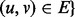and 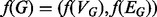. Then, the EC is defined as

(1)

Despite its prevalence, EC fails to differentiate alignments that one might intuitively consider to be of different topological quality (see Fig. 1) because it accounts only for the number of edges from G that are mapped into H and incorporates no notion of the similarity between G and the induced subgraph of f(G).

Fig. 1.

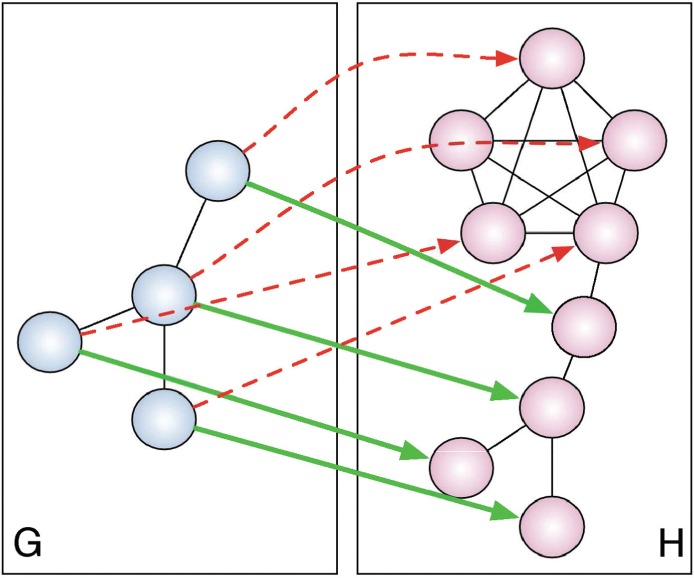
The mapping from G to H given by the solid green arrows can be considered a better alignment than that given by the dashed red arrows, despite the fact that they both have the same EC

We introduce a new measure of topological quality, the induced conserved structure (ICS) score, that uses a more discriminative notion of conserved structure than EC. We define the ICS score between G and H induced by the alignment f as

(2)

Notice that, for the example given in Figure 1, although the edge EC score of both the green and red mappings is 1, the ICS successfully distinguishes the two cases. In particular, the ICS of the green mapping remains 1, whereas the ICS of the red mapping becomes 0.4, agreeing with the intuition that the green mapping conserves more structure than does the red mapping. Also, the ICS score is 1 if and only if G is isomorphic to H[f(V_G)]. Thus, alignments that map subgraphs of G into denser subgraphs of H, where there are potentially many more mappings, will be punished under the ICS score while they will not be punished under the standard EC score. Optimizing EC and ICS directly is, in general, 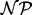hard. This can be shown by reduction from CLIQUE, as when G is a clique, both EC and ICS are 1 if and only if H contains a clique of order .

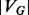2.2.1 Biological Quality

Given an alignment, f: G → H, a measure of biological quality should evaluate the similarity of p and f(p) in terms of biological function. The most common measure of similarity computes the enrichment of shared gene ontology (GO) (Ashburner et al., 2000) annotations between the mapped proteins. The greater the enrichment, the higher the biological quality of the alignment. In most previous work (Kuchaiev and Przulj, 2011; Singh et al., 2008), two GO annotations are considered the same only if they are identical.

This common metric has two main disadvantages. First, many GO terms are assigned largely based on sequence homology to proteins with verified annotations, which strongly biases the results in favor of alignments that ignore topology completely and align proteins based solely on sequence similarity. Additionally, measuring the functional enrichment between proteins by considering only exact overlap between their associated GO annotations ignores the hierarchical structure of annotation similarity encoded in the ontology. Only recently has the literature on network alignment (El-Kebir et al., 2011) started to use methods (Jaeger et al., 2010) that use the hierarchical structure of GO. Most previous work (Kuchaiev et al., 2010; Kuchaiev and Przulj, 2011; Liao et al., 2009; Singh et al., 2008) considers only the exact overlap metric, and it is potentially misleading.

Although the issue that annotations often come from sequence remains a concern, we address the second concern by using an additional metric of protein function similarity that takes into account the relationships between annotations encoded by the GO hierarchy. Pesquita et al. (2009) recently compared a number of methods for computing protein similarities based on GO annotations. They find that one of the best performing methods computes the similarity of GO terms using the Resnik ontological similarity measure and combines annotation similarities using the best-match average strategy to obtain a functional similarity measure on proteins. We adopted an implementation of this measure provided in the csbl.go R-project package (Ovaska et al., 2008). We denote this similarity measure by 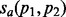, where a is an aspect—biological process (BP), molecular function (MF) and cellular component —of GO. The similarity measure between networks G and H induced by the alignment f under the GO aspect a is given by .

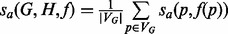2.3 Formal problem statement

Formally, we desire an alignment that maximizes a convex combination of the ICS and biological similarity of the input networks. That is, we wish to find the alignment

where F is the set of all complete injective mappings from G to H and 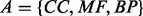is the set of all GO aspects. We choose the ICS as opposed to the EC because it more closely matches the intuition for what constitutes a topologically good alignment. However, as maximizing the ICS directly is NP hard, and we are often missing reliable GO annotations for various proteins, we have developed the method presented later in the text that relies on the spectral signatures (see Section 2.3) and sequence similarity of proteins to determine good seeds for aligning network regions. The alignment is expanded around these seeds by approximating the solution to the quadratic assignment problem (QAP), another NP hard problem. Finally, a local search step attempts to improve the initial alignment by increasing its topological quality. Our results suggest that this heuristic produces results of high quality with regard to the maximizing the objective function described earlier.

2.4 Spectral signature

One of the primary contributions of our work is the introduction of a novel topological signature for nodes in a network. We use these signatures to guide our network alignment and to provide a measure of the similarity, or topological context, of nodes within their respective networks. Useful topological signatures should be precise, robust to topological variation and fast to compute. Spectral graph theory provides tools that allow us to develop a signature having all of these properties.

There is a well-studied and strong relationship between the structure of a graph and the spectrum of its adjacency matrix and other related matrices. For example, isomorphic graphs are necessarily cospectral, though cospectral graphs are not necessarily isomorphic. However, simple comparison of spectra provide a powerful isomorphism filter in practice. In fact, using the eigenvalues and associated eigenvectors of graphs, Babai et al. (1982) developed an algorithm for graph isomorphism that is polynomial in the algebraic multiplicity of the graph.

The spectra of graphs are also robust to topological variations. Wilson and Zhu (2008) show that the distance between the spectra of the normalized Laplacian of graphs correlates well, at least for small perturbations, with the true edit distance between the graphs. Further, such spectra are efficient to compute. It takes O(n³) time to compute the spectrum for dense graphs with n vertices. However, for sparse graphs, like the biological graphs in which we are interested, faster algorithms exist (Pan and Chen, 1999). For any subgraph, the computation of the spectrum is an independent operation and can be parallelized.

Our vertex signature is based on the spectrum of the normalized Laplacian for subgraphs of various radii centered around a vertex. Consider a graph 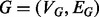and vertex v. We denote by 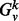, the induced subgraph on all nodes whose unweighted shortest path length from v is ≤k. We denote by 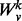, the adjacency matrix of 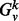. In all experiments performed in this article, we use the unweighted adjacency matrix, though using a weighted adjacency matrix is also possible. Finally, let the matrix 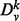be given by

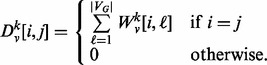(3)

Then, the normalized Laplacian of 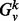is 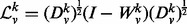, where I is the appropriately sized identity matrix. The eigendecomposition of this normalized Laplacian yields 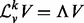, where the sizes of V and 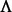are the same as that of 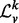, but 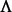is a diagonal matrix. We denote spectrum of 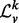by σ(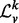), which is simply the entries along the main diagonal of .

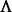Many properties of σ(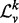) make it an enticing candidate for a vertex signature. As the 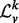is a positive, symmetric, semi-definite matrix with real entries, σ(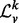) consists entirely of non-negative real numbers. Further, the entries of σ(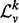) are bounded below by 0 and above by 2. Finally, many topological properties of a graph, such as the number of spanning trees, the Cheeger constant, the distribution of path lengths (Chung, 1997) and the frequency of motifs (Preciado and Jadbabaie, 2010) are known to be related to the spectrum of its Laplacian.

However, for different vertices, the size of their k-hop neighborhoods will vary, and thus the length of their spectra will be different, and so the spectra cannot be directly compared. To overcome this difficulty, we consider the densities of the spectra rather than the spectra themselves. The spectral density simply measures how eigenvalues are distributed over their potential range ([0, 2] in the case of the normalized Laplacian). The intuition behind comparing the spectral densities is that these distributions retain much (but not all) of the information contained in the spectra themselves. Thus, we compare spectral density functions as a proxy for comparing the spectra themselves. This yields a commensurate signature that is independent of the order of the graph, but is nonetheless effective in measuring the structural similarity of graphs (Banerjee, 2012). For each 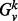, which we will use this spectral density, denoted by 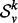, as a signature.

To compare the topological context of vertices at different scales, we simply consider the induced subgraphs for a range of different radii centered about v (i.e. 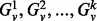). This leads, in turn, to a set of different spectra and, subsequently, different signatures. However, as the radii have the same meaning across different vertices and graphs (it is just the diameter of the neighborhood), the corresponding signatures can be compared directly and independently of the signatures at other radii. This leads to a simple scheme for comparing the topological contexts of two vertices at multiple scales using our signature. Given two graphs, G = (V_G,E_G) and H = (V_H,E_H), with 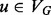and 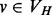, and a sequence of radii 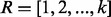(for all experiments performed in this article, we set k = 4), we compute the distance between the signatures of u and v for this sequence of radii as

(4)

where 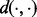can be any desired distance between the two signatures. We use 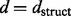, the structural distance as defined by Banerjee (2012). The structural distance is a symmetric information theoretic distance defined on the smoothed spectral densities of two graphs. Specifically, the structural distance between signatures, 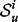and 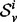, for a particular i, is given by:

(5)

where 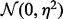is the normal distribution with mean 0 and standard deviation 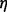[we used a value of 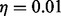as suggested in (Banerjee, 2012)], is the convolution operator and 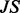is the Jensen–Shannon divergence. In the case that the maximum radius of the subgraph centered around a node u is some 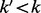, then we define .

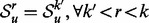In a manner similar to IsoRank (Singh et al., 2008), we can incorporate sequence information into our distance measure between two proteins u and v by using a simple combination of the topological distance—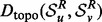 as defined in Equation (4)—and a sequence distance, 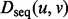, such as the symmetrized BLAST E-value. The total distance measure is a linear combination of the topological and sequence distance, parameterized by some weight 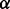and is given by

(6)

If no user-suggested 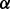is provided, GHOST automatically computes 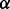by scaling the sequence and topological distances so that the 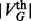smallest sequence and topological distances match.

2.5 Alignment procedure

GHOST aligns networks using a two-phase approach. Much like the strategy used in the sequence alignment tool BLAST (Altschul et al., 1990), GHOST’s initial phase uses a seed-and-extend strategy that seeds regions of an alignment with high scoring pairs of nodes from the different networks and then extends the alignments around the neighborhoods of these two nodes. The neighborhoods are matched by computing an approximate solution to the QAP. This procedure executes in rounds until all nodes from the smaller of the two networks have been aligned with some node from the larger network. GHOST’s second phase uses a local search strategy to explore regions of the solution space around the initial alignment for a potentially better solution.

The algorithm is given formally in Algorithms 1 and 2. First, an alignment is seeded with a high-scoring match 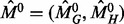. This is a pair of vertices between which the specified 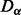[equation (6)] is minimal. Then, we consider all pairwise matches between the 1-hop neighborhoods of these two vertices, 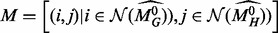, and form a quadratic assignment matrix Q given by:

M[a] is the a^th pair in M and M[a][0] refers to the member of the pair residing in graph G and M[a][1] to the member residing in graph H. 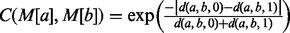measures the pairwise consistency between potential matches M[a] and M[b], where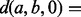 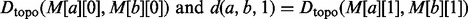. We approximate the solution to the QAP by finding the leading eigenvector of Q and binarizing this vector to select matches that adhere to the matching constraints [further details on this QAP approximation algorithm can be found in Leordeanu and Hebert (2005)]. The solution to the QAP assigns each protein from the smaller of the two neighborhoods to exactly one protein in the larger neighborhood. This mapping is used to align the currently unmapped proteins in these neighborhoods, and the matches are inserted into a priority queue as potential seeds by which to further extend the alignment between these local neighborhoods. However, we only accept mappings that align proteins with a sequence distance less than a certain (user defined) value 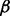. This is because a seed-and-extend approach is implicitly biased in favor of extending topological alignments, and may otherwise match proteins with very little evidence of sequence homology, simply because they reside in the neighborhoods of already aligned proteins. Biologically, it is more plausible that a pair of proteins with very low sequence similarity happens to be adjacent to a pair of currently aligned proteins by chance, or as the result of spurious edges in the measured networks, than it is that they are truly functional homologs.

We continue extending the alignment in this manner, covering larger topological neighborhoods of the original seed nodes, until no further extension of the alignment between the current neighborhoods is possible. Then, the next seed pair, 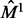, is chosen from among the unaligned nodes, and the same procedure is applied to extend the alignment around this seed. This process continues until all nodes from V_G (assumed, w.l.o.g., to be smaller than V_H) have been aligned.

Once we have computed an initial alignment using the seed-and-extend procedure, we attempt to improve this alignment using a local search. The moves of the local search procedure are similar to those used by PISWAP (Chindelevitch et al., 2010), but the evaluation strategy and application of rules is different. Given an alignment, f, we seek 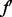similar to f that is superior. Consider a pair of aligned proteins, 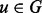and 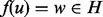, and a third vertex 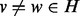. It is possible that we may improve the quality of our alignment by realigning u so that 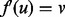if the topological and or biological quality is improved by performing this realignment. When realigning u, there are two cases to consider. Either v is unaligned, in which case we assign 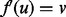, or v s aligned by f, in which case aligning u to v requires realigning 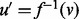. In this case, we consider swapping the aligned protein pairs so that 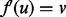and 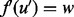. In either case, we will call this realignment a move from (u, w), denoted by 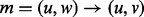. Each move can be given a sco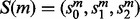re, where

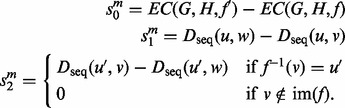For each mapping, (u, w), in the current alignment, the local search procedure scores the potential moves from (u, w), and performs the highest scoring feasible move. The scores are ordered first by 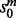, then 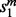and finally 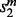. Any remaining ties are broken arbitrarily. We call a move feasible if 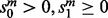and either 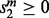or we have decided to allow a non-Pareto-optimal move from (u, w). The purpose of allowing a non-Pareto-optimal move from (u, v) is that it may allow us to escape a local minimum of the alignment space.

There are three parameters that characterize the space of alignments explored by GHOST. First, 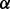determines the relative weight of the sequence and topological distances when performing the seed-and-extend procedure [Equation (6)]. Second, 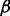acts as a hard constraint on sequence similarity of aligned pairs: no pair, (u, v) of proteins will be aligned if 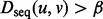. This ensures that, when extending the alignments between local neighborhoods, no pair of proteins with sequences too divergent is aligned simply because the alignment can be extended by aligning them.

During the local search procedure, we allow some number of exceptions to the hard constraint given by 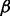. We define a parameter 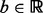that is a budget to be used for accepting non-Pareto-optimal moves during the local search phase of GHOST. The higher this budget, the more likely GHOST will be to accept local moves that increase the topological quality of the alignment at the expense of realigning a pair of proteins with lower sequence similarity than the original pair. We distribute this budget across local search iterations so that we initially allow many such moves, but allow far fewer in later iterations. In particular, during iteration i, we have a budget of 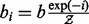, where 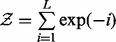is a partition function that normalizes the per-iteration weights. Within iteration i, we consider each mapped pair of the current alignment in turn and draw a number 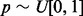. If 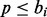, then we will allow a non-Pareto-optimal move when realigning this mapped pair; otherwise, such moves will not be considered. The practical effect of choosing a larger b is to reduce the importance of sequence similarity in the alignment.

2.6 Network data

We performed an alignment of the high-confidence protein interaction networks of Campylobacter jejuni and Escherichia coli. Both of these bacterial species are well-studied model organisms. To draw the most appropriate comparisons to MI-GRAAL, we use the same versions of the interaction networks that were used by Kuchaiev and Przulj (2011). Thus, we used E. coli network composed of interactions from the data of Peregrín-Alvarez et al. (2009), consisting of 1941 proteins among which there are 3989 interactions. We consider the C. jejuni network that consists of the high-confidence interaction from the data of Parrish et al. (2007), containing 2988 interactions among 1111 proteins.

We also explored the ability of GHOST to align the protein interaction networks of distant eukaryotes by performing an alignment of the protein interaction networks of Arabidopsis thaliana and Drosophila melanogaster. We obtained the interactions for these networks from the HitPredict website (Patil et al., 2011). HitPredict places interaction data for each species into three categories: high-confidence small-scale interactions, high-confidence high-throughput interactions (HCHT) and low-confidence high-throughput interactions. The high-confidence small-scale interactions are identified directly in small-scale experiments considering <interactions each. The HCHT interactions are those interactions identified in high-throughput experiments with a likelihood ratio >1, or predicted from protein complex data. The low-confidence high-throughput interactions are those having a likelihood ratio <1. In our experiments, we considered only the high-confidence interactions—the union of those interactions in the high-confidence small-scale interactions and HCHT sets. This resulted in a network for A. thaliana having 2082 proteins and 4145 interactions. The D. melanogaster network consisted of 7615 interactions among 3792 different proteins.

2.7 Comparison with other aligners

To investigate the quality of the solutions produced by the different aligners we consider, we explore how they trade off between topological and biological quality at different points in their parameter spaces. The alignments are compared using the novel measures of the topological and biological quality introduced in Section 2.1. To calculate GO similarities, we rely on the set of GO annotations for each protein retrieved from the European Bioinformatics Institute website in June 2011, and the GO retrieved on November 10, 2011. When producing alignments using MI-GRAAL, we included graphlet degree signatures, clustering coefficients and sequence similarity scores—the topological features that Kuchaiev and Przulj (2011) found to lead to the highest scoring and most stable alignments. MI-GRAAL determines the value of 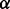—the parameter that trades off between functional and sequence similarity—internally, and so no 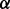value was provided. For IsoRank and Natalie 2.0, we varied 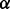between 0 and 1 in increments of 0.1. The rest of Natalie 2.0’s parameters were left at their default values. For GHOST, 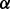was determined automatically using the procedure specified in Section 2.3, 10 iterations of the local improvement procedure were performed, 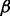was set to 10 and the budget, b, for non-Pareto-optimal moves was varied over .

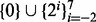3 RESULTS

We evaluated the performance of GHOST in several different scenarios and compared against IsoRank, GRAAL, MI-GRAAL, H-GRAAL and Natalie 2.0. First, we perform two tests that have been used in the past to assess topological alignment quality. These tests, self-alignment and self-alignment with noise, are instructive because the correct node mapping is known when aligning a network to itself. This allows us to measure accuracy in a way that is not possible when comparing networks from different species. The results of these experiments provide important evidence about the robustness and specificity of different topological signatures and the ability of different global alignment approaches to align two networks based solely on topological information. In Sections 3.1 and 3.2, we are interested primarily in the utility of the local topological signatures and the basic alignment procedures. Thus, we do not perform the local search phase of GHOST described earlier. Further, because we cannot use biological sequence information to constrain the space of alignments, we do not consider the performance of the graph matching approach (i.e. Natalie 2.0) on this task.

Subsequently, we consider the alignment between high-confidence protein–protein interaction networks of a pair of bacteria and a pair of eukaryotes. Here, we use the new metrics described in Section 2.1 to measure the topological and biological quality of our alignments. Considering unconstrained alignments using graph-matching approaches either exhausted the memory of our machines (El-Kebir et al., 2011) or failed to finish aligning the networks within 16 h (Zaslavskiy et al., 2009). Thus, when comparing against graph-matching approaches, we use Natalie 2.0 (El-Kebir et al., 2011) to produce a constrained alignment.

3.1 Self-alignment

For networks with many similar sub-regions, even a self-alignment in the absence of noise can be difficult. To demonstrate this difficulty, we consider a self-alignment of the largest connected component of a high-confidence network of the bacterium Mesorhizobium loti. This network was obtained from the interactions reported in the study by Shimoda et al. (2008) and consists of 3006 interactions among 1655 proteins. The alignment produced by GHOST is an automorphism of the graph, with an EC of 100% and a node correctness (the fraction of nodes that were aligned with themselves) of 79%. The alignment produced by IsoRank had an EC of 76% and a node correctness of 53%, whereas the alignment produced by MI-GRAAL had an EC of 38% and node correctness of only 0.3%. Because MI-GRAAL is probabilistic in nature, we performed this alignment multiple times, using a wide variety and combination of the topological features suggested in Kuchaiev and Przulj (2011), to ensure that this failure of self-alignment was not coincidental. None of these subsequent MI-GRAAL alignments differed in topological quality—either node or EC—by more than a fraction of a percent. IsoRank produced an alignment of significantly higher topological quality than the one discovered by MI-GRAAL; this is different from what we see in the rest of the tests described later in the text.

Despite the fact that its node correctness is only 79%, GHOST’s alignment is structurally perfect. Without more information beyond what is provided by the network itself, one cannot hope to obtain a better alignment than the one produced by GHOST.

3.2 Self-alignment under noise

We also re-performed the experiment originally carried out by Milenkoviç et al. (2010), where progressively noisier variants of the Saccharomyces cerevisiae interaction network are aligned to the high-confidence network of Collins et al. (2007). The higher noise networks are created by starting with the highest confidence network, and then adding interactions (constrained to the original, high-confidence protein set) in decreasing order of experimental confidence. As this is again a self-alignment, and sequence information would allow the almost perfect identification of the correspondences between nodes, we consider a purely topological alignment (i.e. 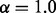and 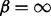). We explore how the fraction of correctly aligned nodes changes as larger quantities of noisy interactions are added to the high-confidence network (Fig. 2).

Fig. 2.

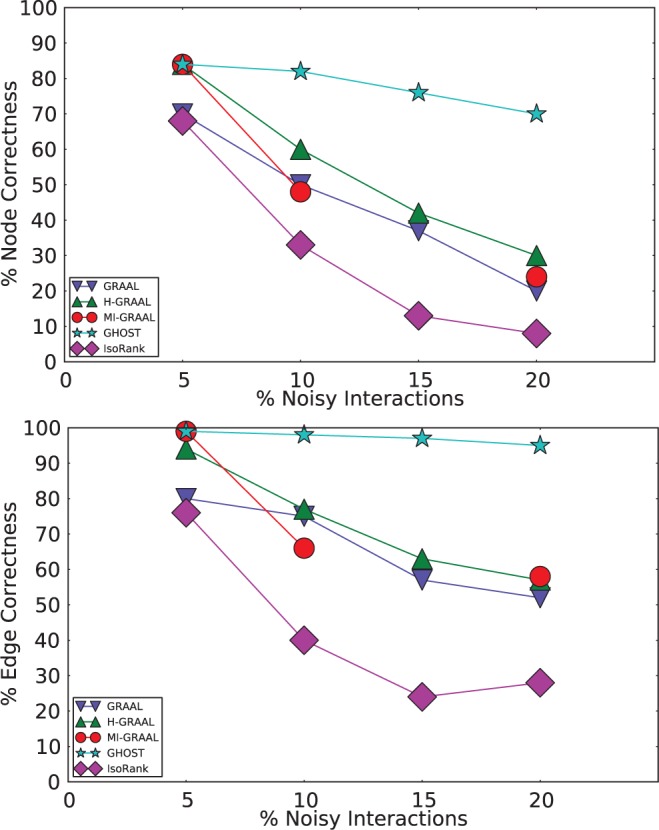
Performance of various aligners on a noisy yeast PPI under the node (top) and edge (bottom) correctness metrics. Note: In the 15% noise case, the performance numbers of MI-GRAAL are not given because it failed to run to completion

In the case with the fewest noisy interactions, most of the programs achieve similar performance. However, as the number of noisy interactions increases, GHOST outperforms all of the other approaches by an increasing margin. By the time 20% of the noisy interactions have been included in the network, the node correctness of GHOST is more than twice that of the next-best-performing aligner, and the EC is >30% higher. There also seems to be a substantial gap between IsoRank and the rest of the alignment procedures in terms of both the node and EC. This is indicative of a trend we observe when aligning real biological networks as well (see later in the text), where the topological quality of the alignments produced by IsoRank, even with a large weight being placed on the topological score, seems to fall behind those produced by the other aligners.

The performance of GHOST in this set of experiments suggests that the spectral signature is robust to the presence of noise in the network, significantly more so than the graphlet degree signatures used in the GRAAL aligners. These results agree with existing evidence, such as that presented by Wilson and Zhu (2008), that the spectral distance between graphs is robust to small topological changes. Both this robustness and the specificity of the spectra seem to carry over to our topological signatures and do not appear to be negatively affected by the use of spectral densities to deal with graphs of different order.

3.3 Alignments between different species

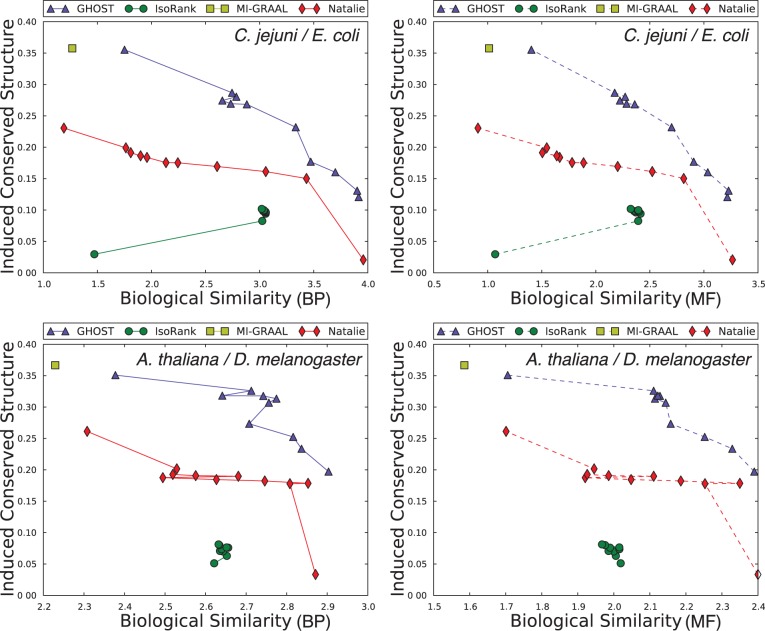
The same general performance trend holds under the C. jejuni/E. coli and A. thaliana/D. melanogaster alignments we considered, as well as under both the BP and MF aspects of the GO (see Fig. 3)—owing to sparseness of annotation, the cellular component aspect was not included in this analysis. GHOST produces alignments with very high biological and topological qualities, and seems capable of trading off between these two goals more effectively than the other aligners. When placing the most weight on the biological quality of the alignment (i.e. b = 0 for GHOST and 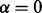for Natalie 2.0), GHOST and Natalie 2.0 produce alignments with substantially higher biological quality than the other aligners. However, GHOST’s alignments exhibit a much higher ICS score than Natalie 2.0’s. As we vary the corresponding parameters and place more weight on topology, GHOST produces alignments with topological quality very close to those obtained by MI-GRAAL, but with significantly higher biological quality. In general, at a similar biological quality under both GO aspects, GHOST is capable of producing alignments with much greater topological quality other aligners.

Fig. 3.

Under both BP and MF GO aspects and both alignments, we observe a consistent trend in the quality of the solutions produced by the different aligners. IsoRank produces alignments of reasonable biological, but poor topological quality, whereas MI-GRAAL exhibits the opposite behavior (i.e. high topological, but poor biological quality). Natalie 2.0 and GHOST consistently produce alignments with competitive trade offs between the competing goals of topological and biological quality, though GHOST’s alignments exhibit consistently higher topological quality

For IsoRank, the precise value of 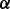seems to matter very little. It produced alignments of reasonable biological quality but very low topological quality. In fact, the highest ICS score achieved by IsoRank was 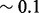, when aligning C. jejuni and E. coli. MI-GRAAL performed very differently from IsoRank, producing alignments of excellent topological quality but generally poor biological quality. Specifically, for both pairs of organisms, the alignments produced by MI-GRAAL exhibited 3–4 times less semantic similarity than those produced by Natalie 2.0 and GHOST.

The alignments obtained by Natalie 2.0 dominate those of IsoRank in terms of topological and biological quality for a large range of 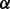. At an approximately equal biological similarity, Natalie 2.0 is capable of obtaining solutions with ICS scores between 50% and 120% higher. When aligning the A. thaliana and D. melanogaster networks, Natalie 2.0 can produce alignments with topological quality 120% greater than that of IsoRank that simultaneously exhibit 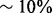greater biological similarity under the GO BP aspect and 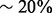greater biological similarity under the GO MF aspect. However, at the same biological quality, GHOST dominates Natalie 2.0, with topological quality improvements ranging from a few percentage to a factor of ≥2.

3.4 Case study: Functional orthology prediction

To assess the fine-scale biological relevance of the alignments produced by GHOST, we have aligned the networks of the well-annotated eukaryotes D. melanogaster and Caenorhabditis elegans. From this alignment, we verify a few known functional orthologs and posit a few more. To consider protein 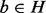and protein 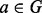as putative functional orthologs, we require that a is aligned to b under f, and that the BLAST e-value between a and b is low. Finally, we consider only those pairs of aligned proteins where b is not in the unique best BLAST hit of a, meaning that this alignment would not necessarily have been determined by sequence alone. Further, the examples we consider later in the text to be known functional orthologs, both share some common biological function in their respective organisms and are verified as isologs in the IsoBase (Park et al., 2011) functional orthology database.

3.4.1 Known functional orthologs

GHOST aligned the nuclear hormone receptor family member nhr-67, a product of gene nhr-67 in C. elegans to the tailless hormone receptor protein, a product of gene tll in D. melanogaster. GO annotations with experimental evidence codes implicate nhr-67 in cell migration, gonad morphogenesis, regulation of growth rate, hermaphrodite genitalia development and transcriptional regulation of an RNA polymerase II promoter (GO:0016477, GO:0035262, GO:0040010, GO:0040035 and GO:0045944). Meanwhile, the tailless hormone receptor protein is also implicated in transcriptional regulation of an RNA polymerase II promoter (GO:0045944) as well as terminal region determination (GO:0007275), gastrulation (GO:0007369), the torso signaling pathway (GO:0008293), cell fate commitment (GO:0054165), regulation of the cell cycle (GO:0051726) and neuroblast division (GO:0055057).

GHOST also mapped the high mobility group protein DSP1, a product of gene Dsp1 from D. melanogaster to the high mobility group protein 1.2, a product of gene hmg-1.2 from C. elegans. These proteins both play a role in the development and morphogenesis of their respective species. For example, experimentally determined GO annotations implicate Dsp1 in segment specification, developmental process and leg disc development (GO:0007379, GO:0032502 and GO:0035218) in D. melanogaster, whereas hmg-1.2 is implicated in epithelium morphogenesis, larval development, gonad development, embryo development, body morphogenesis and regulation of growth rate (GO:0002009, GO:0002119, GO:0009792, GO:0010171 and GO:0040010) in C. elegans.

We also verified the alignment of Guanine nucleotide-binding protein G(i) subunit alpha 65 A, a product of gene G-ialpha65A in D. melanogaster with the Guanine nucleotide-binding protein alpha-16 subunit protein, a product of gene gpa-16 in C. elegans. Both of these proteins are experimentally determined to function in protein binding (GO:0005515). More interestingly, however, G-ialpha65A has been experimentally implicated in asymmetric cell division, cell differentiation, asymmetric neuroblast division and the establishment of spindle orientation (GO:0008356, GO:0030154, GO:0055059 and GO:0055059), whereas gpa-16 has been directly experimentally implicated in embryotic axis specification (GO:0000578), embryo development (GO:0009792) and the establishment of mitotic spindle orientation (GO:0000132). Again, we reiterate that none of these functional ortholog examples uncovered by GHOST represent unique best BLAST-hits of the protein to which they are mapped, and thus they would likely not be uncovered by examining the sequences alone.

3.4.2 Putative novel functional orthologs

In addition to the recapitulation of known functional orthologs, we explore three new pairs of potential functional orthologs. Again, we look for proteins that are mapped to each other under the alignment, where the protein from one network is not the unique best BLAST hit to the mapped protein, suggesting that interaction evidence led to their alignment. Unlike the confirmed functional orthologs earlier in the text, we do not require both the mapped proteins we consider here to be confirmed proteins with experimentally validated function. Rather, the potential functional orthology of these pairs warrants further study.

GHOST mapped the Dredd protein of D. melanogaster to the csp-1 protein of C. elegans. Although not top-ranked sequence matches, these proteins share sequence similarities, and both belong to the peptidase C14A homology family. The csp-1 protein has no experimentally assigned GO terms, though proteolysis (GO:0006580), apoptotic process (GO:0006915), cysteine-type endopeptidase activity (GO:0004197) and cysteine-type peptidase activity (GO:0008234) have been inferred from computational annotation. Dredd, on the other hand, has a host of experimentally determined GO terms, including apoptotic process (GO:0006915) and cysteine-type endopeptidase activity (GO:0004197). These facts both provide evidence that the electronically inferred GO terms of csp-1 may be correct, and also suggest that csp-1 may be implicated in some of the other BP performed with Dredd.

Another intriguing alignment pair produced by GHOST is that of CG9238 in D. melanogaster to H18N23.2 in C. elegans. In fact, although the latter of these proteins is merely ‘predicted’, they both share the same recommended protein name—Protein phosphatase 1 regulatory subunit 3. The D. melanogaster protein is annotated with GO terms for carbohydrate metabolic process (GO:0005975), glycogen metabolic process (GO:0005977) and behavioral response to ethanol (GO:0048149), whereas the C. elegans protein is currently without any GO annotations. The GHOST alignment acts as further evidence for the existence and function of the C. elegans protein H18N23.2.

Finally, our alignment mapped the UGP protein from D. melanogaster to the K08E3.5 protein from C. elegans. In this case, each of these proteins was labeled as the corresponding element (K00963) of the Kyoto Encyclopedia of Genes and Genomes (KEGG) (Kanehisa et al., 2004) module for nucleotide sugar biosynthesis in eukaryotes. Although the D. melanogaster protein has no experimentally assigned GO terms, it has electronically inferred annotations for metabolic process (GO:0008152) and nucleotidyltransferase activity (GO:0016779). In addition to sharing these electronically inferred annotations, the C. elegans protein has experimentally assigned annotations linking it to embryo development ending in birth or egg hatching (GO:0009792), growth (GO:0040007) and positive regulation of growth rate (GO:0040010). Their similar sequence, interaction patterns, inferred annotations and placement in the nucleotide sugar biosynthesis KEGG module suggest that these proteins may act as functional orthologs in their respective organisms.

Although these novel putative functional orthologs warrant further study and experimental support, an exploration of the available evidence suggests that GHOST is positing reasonable and meaningful biological hypotheses by aligning these pairs of proteins. Further, we also demonstrated how GHOST was able to recapitulate previously suggested functional orthologs whose relationships are supported by a substantial amount of evidence. In all of these cases, the alignment of these proteins is not owing to their sequence similarity alone, suggesting that network alignment, in general, and GHOST, in particular, is a useful tool for functional orthology detection.

3.5 Runtime

A tight upper bound on the asymptotic computational complexity of the alignment algorithm used by GHOST remains an open problem. The difficulty of the analysis is primarily owing to the algorithm’s fundamental dependence on the structure of the input networks and the density of aligned neighborhoods. However, solving the spectral relaxation of the QAP is the step of GHOST with the largest potential asymptotic complexity. 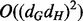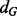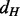This step has worst-case running time where and are the largest degrees in G and H, respectively. This complexity results from the need to find the dominant eigenvector of the largest quadratic assignment matrix, which is quadratic in the size of the matrix (Kuczynski and Wozniakowski, 1992). Despite the potential worst-case complexity, we find that GHOST is fast in practice. First, we note that the computation of the spectral signatures is independent of the alignment being performed. Thus, the signatures need only be extracted once and can be reused for all alignments involving that organism. This also allows for a quicker exploration of the parameter space because alignments can be performed under different parameter settings without recomputing the spectral signatures. Extracting the spectral signatures took 0.5 minutes for E. coli, 14 minutes for C. jejuni, 1 minute for S. cerevisiae, 1 minute for A. thaliana and 218 minutes for D. melanogaster.

The time to perform the actual alignments, given the spectral signatures, ranged between 1 and 6 minutes depending on the networks being compared. All timings were measured using 20 threads on a Java Virtual Machine instance given 16GB of heap space. The testing machine had 8 Opteron 8356 processors and 256GB of memory.

4 DISCUSSION

We have introduced GHOST, a novel framework for the global alignment of biological networks. At the heart of GHOST is a new spectral, multiscale node signature that we combine with a seed-and-extend approach and a local search procedure to perform global network alignment. The spectral signature is highly discriminative and robust to small topological variations. We verify this robustness in Section 3.2 showing that GHOST outstrips the competition in aligning the S. cerevisiae protein interaction network to noisier variants of itself. In these experiments, as well as the self-alignment of the M. loti network, the accuracy of GHOST is significantly higher than that of either IsoRank or MI-GRAAL. These experiments are of particular interest, as the ground truth is known and the ability of different aligners to uncover shared topological structure can be accurately measured.

We find that the alignments produced by GHOST consistently dominate those produced by the other aligners. When producing an alignment of approximately the same biological quality, GHOST yields alignments with substantially higher topological quality than either IsoRank or Natalie 2.0. Furthermore, at a similar level of topological quality, GHOST produces alignments that have far more biological relevance than those produced by MI-GRAAL. Finally, GHOST consistently produces alignments that exhibit a more competitive trade off between topological and biological quality than the other aligners we considered (see Fig. 3).