Mapping Intercellular CO₂ Mole Fraction (C_i) in Rosa rubiginosa Leaves Fed with Abscisic Acid by Using Chlorophyll Fluorescence Imaging

Abstract

Imaging of photochemical yield of photosystem II (PSII) computed from leaf chlorophyll fluorescence images and gas-exchange measurements were performed on Rosa rubiginosa leaflets during abscisic acid (ABA) addition. In air ABA induced a decrease of both the net CO₂ assimilation (A_n) and the stomatal water vapor conductance (g_s). After ABA treatment, imaging in transient nonphotorespiratory conditions (0.1% O₂) revealed a heterogeneous decrease of PSII photochemical yield. This decline was fully reversed by a transient high CO₂ concentration (7400 μmol mol⁻¹) in the leaf atmosphere. It was concluded that ABA primarily affected A_n by decreasing the CO₂ supply at ribulose-1,5-bisphosphate carboxylase/oxygenase. Therefore, the A_n versus intercellular mole fraction (C_i) relationship was assumed not to be affected by ABA, and images of C_i and g_s were constructed from images of PSII photochemical yield under nonphotorespiratory conditions. The distribution of g_s remained unimodal following ABA treatment. A comparison of calculations of C_i from images and gas exchange in ABA-treated leaves showed that the overestimation of C_i estimated from gas exchange was only partly due to heterogeneity. This overestimation was also attributed to the cuticular transpiration, which largely affects the calculation of the leaf conductance to CO₂, when leaf conductance to water is low.

Our understanding of the response of leaf photosynthesis to environmental factors is highly dependent on the interpretation of photosynthetic gas exchange and particularly on the relationship between net CO₂ assimilation and C_i (Farquhar and Sharkey, 1982). C_i estimations from gas exchange, which are formally estimations of the CO₂ mole fraction at the evaporating sites (Parkhurst, 1994), are based on the assumption that photosynthesis and transpiration are relatively uniform over the leaf area. This assumption appears to be adequate for most leaves when stomatal conductance is maximal, as most stomata are open. When stomatal conductance decreases, however, this assumption may not be valid. Upon application of ABA, short-term water stress, or low humidity, the occurrence of a nonuniform distribution or patchy distribution of the stomatal aperture and photosynthesis has been reported (Downton et al., 1988a, 1988b; Terashima et al., 1988; Daley et al., 1989; Raschke et al., 1990; Mott et al., 1993; Mott, 1995).

Upon ABA treatment, photosynthetic capacity measured under nonlimiting CO₂ availability remained unaffected, and since the patterns of distribution of stomatal aperture and photosynthesis were identical, the patchy response has been primarily attributed to a nonuniform distribution of stomatal closure (Terashima et al., 1988). In this context, the commonly reported unresponsiveness of C_i relative to net CO₂ assimilation decline under these conditions, classically described as a nonstomatal inhibition of photosynthesis (Seemann and Sharkey, 1987), has been interpreted as an artifact due to patchy response (Downton et al., 1988a, 1988b; Terashima et al., 1988; Raschke et al., 1990; Mott, 1995).

Potential overestimation of C_i when the distribution of stomatal aperture over the leaf is heterogeneous has been pointed out previously (Laisk et al., 1980). By modeling a bimodal distribution of leaf stomatal conductance, several authors (Downton et al., 1988a, 1988b; Terashima et al., 1988; Van Kraalingen, 1990) have concluded that the occurrence of heterogeneous stomatal distribution fully explains the behavior of C_i under ABA or short-term water stress. Using a modeling approach, Cheeseman (1991) and very recently Buckley et al. (1997) have shown that such large overestimation of C_i could not be fully accounted for by heterogeneous stomatal conductance if a unimodal distribution of the stomatal aperture was assumed. Recently, a corresponding unimodal distribution of photosynthesis under ABA treatment has been reported (Meyer and Genty, 1995; Mott, 1995).

The aim of this study was to assess the significance of C_i under patchy photosynthesis induced by ABA treatment in Rosa rubiginosa leaves. By using an experimental approach that allows the mapping of the photochemical yield of PSII from leaf chlorophyll fluorescence images (Genty and Meyer, 1995), we have demonstrated that ABA primarily affects photosynthesis by decreasing stomatal conductance. Assuming the CO₂ assimilation versus C_i relationship was not affected by ABA, high-resolution images of C_i were constructed from images of the photochemical yield of PSII. Calculations of C_i from gas exchange and images were compared and it was confirmed that C_i estimated from gas exchange is largely overestimated. We have shown that this overestimation is only partly due to stomatal closure heterogeneity, in contrast to previous understanding. This overestimation also results from an overestimation of leaf conductance to CO₂ calculated from conductance to H₂O, which we attribute to cuticular transpiration. Important implications for the interpretation of photosynthetic gas-exchange data are discussed. A preliminary account of some of this work was presented earlier (Meyer and Genty, 1995).

MATERIALS AND METHODS

Plants of Rosa rubiginosa L. were cultivated in pots in a greenhouse under natural sunlight and photoperiod during the summer (1994 and 1995). Daily maximum and minimum air temperatures were 35 and 15°C, respectively. Detached, fully expanded leaves were used, with the petiole kept in distilled water throughout the experiment. Leaves were dark adapted for 1 h before the experiment and the apical leaflet was used for measurement.

Transverse leaflet sections and replicas of epidermis have shown that R. rubiginosa leaves were heterobaric and hypostomatous (Bro et al., 1996). In this early study, the mean leaflet area was 6.3 ± 1.5 (n = 7 leaves) cm², the mean surface of an areole (Terashima, 1992) was 0.221 ± 0.055 mm² (n = 9), and the stomatal density was 112 ± 69 (n = 12) stomata mm⁻².

Gas-Exchange Measurements

An open-flow gas-exchange system and a clamp on the leaf cuvette described in Genty and Meyer (1995) were used for the measurements of CO₂ and water vapor net exchanges. Cuvette foam gaskets were coated with paraffin for minimal water adsorption. Cuvette temperature was kept constant at 25°C. The vapor pressure deficit between the leaflet and air was maintained between 0.8 and 1.2 kPa. Gas-exchange parameters and leaflet temperature were calculated according to the method of von Caemmerer and Farquhar (1981) and Parkinson (1985), respectively, for the leaflet projected area and one transpiring surface (since R. rubiginosa leaflets are hypostomatous). By using a leaf energy-balance method, an average temperature for the area of the leaflet under consideration was provided. g_b was 1.94 mol m⁻² s⁻¹.

Mapping of PSII Photochemical Yield using Chlorophyll Fluorescence Imaging

The method is described in detail in Genty and Meyer (1995). A video charge-coupled-device camera imaged the chlorophyll fluorescence of the upper side of the whole-leaf surface from which gas-exchange measurements were performed. Routine cycles of two images, one of steady-state relative fluorescence yield, Φ, and the other of maximal relative fluorescence yield, Φ_m, were digitized and used to construct in near-real time an image of the photochemical yield of PSII, Φ_PSII by computing pixel by pixel (1 − Φ/Φ_m) (Genty et al., 1989).

Images of Φ_PSII were stored as 512 × 512 pixels frames with an 8-bit resolution. Frequency distribution histograms were computed from native images of Φ_PSII in floating- point mode with 32-bit precision using Labview software (National Instruments, Austin, TX) and dedicated processing routines (Concept VI, Graphtek, Mirmande, France). All images used for quantitative analysis of distribution of gas-analysis parameters correspond to the open area (6.25 cm²) of the gas-exchange chamber, which comprised more than 75 to 90% of the total leaflet area. The single areoles of R. rubiginosa leaflets correspond to about 150 pixels, and 3 to 4 pixels refer to about 1 stoma and 10 epidermal cells.

Mapping of Intercellular CO₂ Mole Fraction, CO₂ Assimilation, Water Vapor Conductance, Transpiration, and Leaf Temperature from Images of the Photochemical Yield of PSII

A, A_n, C_i, g_t, g_s, w_i, T_l, E, and R correspond to global measurements (conventional gas-exchange data): A, gross CO₂ assimilation; A_n, net CO₂ assimilation; C_i, intercellular CO₂ mole fraction; g_t, total water vapor conductance; w_i, intercellular mole fraction of water vapor; T_l, leaf temperature; E, rate of transpiration; and R, respiration in the dark.

A_i, A_ni, C_ii, g_ti, g_si, w_ii, T_ii, E_i, (1 − Φ/Φ_m)_i, and R_i correspond to local measurements (pixel _i) and Ā, Ā_n, C̄_i, ḡ_t, ḡ_s, w̄_i, T̄_l, Ē, 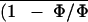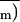, and R̄ correspond to the means of local measurements.

In nonphotorespiratory conditions, (1 − Φ/Φ_m), which is a relative estimate of the quantum yield of gross CO₂ assimilation (Genty et al., 1989), can be used to estimate A_i as:

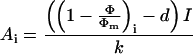1

where I is the incident photon flux density, k and d are the slope, and the Y is the intercept obtained from the linear regression of the relationship between the mean of the photochemical yield of PSII, 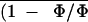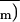, and the quantum yield of gross CO₂ assimilation of the considered experiment (typical regression slope k was 11.4 with d = 0.06).

According to Farquhar et al. (1980), in ribulose-bisphophate saturated and nonphotorespiratory conditions, A_i can be described by a hyperbolic function of C_ii as:

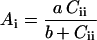2

where a and b were obtained from the best fit of Equation 2 for the gas-exchange data obtained in uniform photosynthesis (before ABA feeding C_ii and A_i equal C_i and A, respectively). We have substituted A_i of Equation 2 by its expression in Equation 1 to resolve for C_ii. These calculations assume no change of the relationship between A and C_i during the course of a considered experiment. The validity of this assumption will be examined in Results and in Discussion.

Making the same assumption, the total conductance to H₂O, g_ti, the transpiration, E_i, and the leaf temperature, T_li, were calculated from (1 − Φ/Φ_m)_i, for each pixel of images of the photochemical yield of PSII by solving numerically for the unknowns g_ti, E_i, T_li and w_ii, the system of Equations 3, 4, 5, and 6:

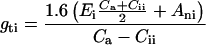3

where A_ni = A_i − R_i, with R_i taken as R and where A_i and C_ii were substituted by their expression in function of (1 − Φ/Φ_m)_i using Equations 1 and 2. C_a is the ambient CO₂ mole fraction in the chamber.

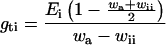4

where w_a is the ambient H₂O mole fraction in the chamber.

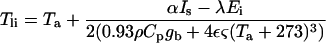5

where T_a is the air temperature (°C) in the chamber, I_s is the total short-wave irradiance on the leaf, α represents the fraction absorbed, λ is the latent heat of vaporization of water, ρ is the air density, C_p is its specific heat capacity, ε is the thermal emissivity of the leaf, and ς is the Stefan-Boltzmann constant. The factor 0.93 is for converting the boundary layer conductance of water vapor (g_b) into heat- transfer conductance for a laminar boundary layer. The factor 2 in the denominator accounts for the two-sided heat conductance of the leaf, since g_b is a one-sided conductance in the first term of the denominator, and thermal absorption and emission by both sides of the leaf in the second term.

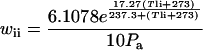6

where P_a is the ambient total pressure (kPa).

Equations 3 and 4 were derived from von Caemmerer and Farquhar (1981). In Equation 3, g_i was directly calculated from the 1.6 ratio of diffusivities of water vapor and CO₂, since stomatal conductance was low in the presence of ABA; so the correction for the “laminar flow”-like transport of water vapor and CO₂ in the boundary layer can be neglected. Equation 5 was derived from the energy-balance method described by Parkinson (1985). In this expression, neither the possible heat-conduction exchange from a local site to another local site nor the small contribution of net energy storage were taken into account. Equation 6 was derived from Buck (1981).

From g_ti, stomatal conductance to water vapor, g_si, was calculated by assuming that g_b was constant over the leaflet. Images of C_ii, A_ni, g_ti, g_si, T_li, and E_i were constructed from a given image of (1 − Φ/Φ_m)_i and the means C̄_i, Ā_n, ḡ_t, ḡ_s, T̄_l, and Ēwere computed from images. All calculations were computed from native images of Φ_PSII in floating-point mode with 64-bit precision using Labview software and dedicated processing routines (Concept VI, Graphtek).

Protocol

Experiments were performed at a photon flux density of 385 to 420 μmol m⁻² s⁻¹ in air. After a steady state was reached, leaf chamber CO₂ mole fraction was varied in steps between ambient air composition and around 100 μmol mol⁻¹ and back to air composition. cis-trans ABA (99% purity, Sigma) was then added to the water supply of the leaf petiole to bring its concentration to 10⁻⁴ m. Sets of images of PSII photochemical yield were recorded just before and during a brief transition to 0.1% O₂, before ABA feeding, for the various external CO₂ mole fraction, and after ABA feeding, when a pseudo-steady state was reached.

A subsaturating photon flux density of 385 to 420 μmol m⁻² s⁻¹ was chosen to remain in ribulose-bisphosphate-saturated condition for Rubisco activity at 340 μmol mol⁻¹ CO₂ during transition in nonphotorespiratory conditions while keeping a large enough quantum yield of CO₂ assimilation for maximal accuracy of (1 − Φ/Φ_m)_i imaging.

RESULTS

Time Course of the Leaf Gas-Exchanges Response to ABA Treatment

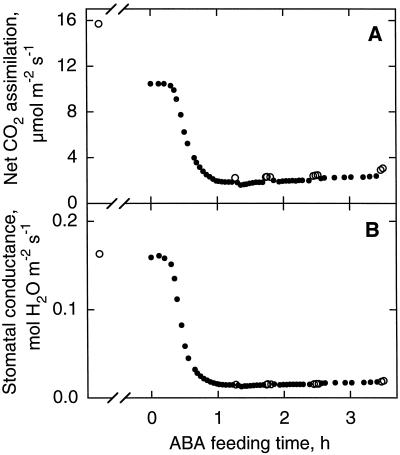
Figure 1 shows the time course of A_n and g_s measured by gas exchange during the ABA feeding of a R. rubiginosa leaflet. The decline of g_s began 10 min after the addition of ABA and preceded the decrease of A_n. A steady state was reached 1 h later. In response to ABA, A_n and g_s decreased by 80 and 90%, respectively, as commonly reported (Cummins et al., 1971; Farquhar and Sharkey, 1982; Raschke and Hedrich, 1985; Mott, 1995). When brief transitions to nonphotorespiratory conditions were performed (open symbols in Fig. 1), A_n increased by about 50 and 25% before and after ABA treatment, respectively, whereas g_t remained unchanged. Thus, stomatal conductance was not significantly affected by transition to an oxygen-depleted atmosphere. After each transition, 5 to 15 min were required for the recovery of steady A_n in air.

Figure 1.

Time course of A_n (A) and g_s (B) during ABA feeding of a leaf of R. rubiginosa. ABA was added to the water supply of the petiole to bring its concentration to 10⁻⁴ m. Leaflet atmosphere was 340 μmol mol⁻¹ CO₂, 21% (•) or 0.1% (○) O₂, and 70% RH. The photon flux density was 410 μmol m⁻² s⁻¹.

Distribution of Photosynthesis in ABA-Fed Leaves

CO₂ and O₂ Dependency

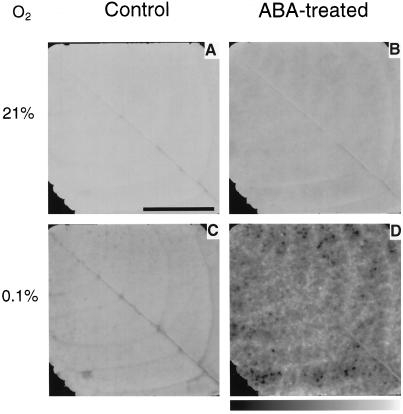
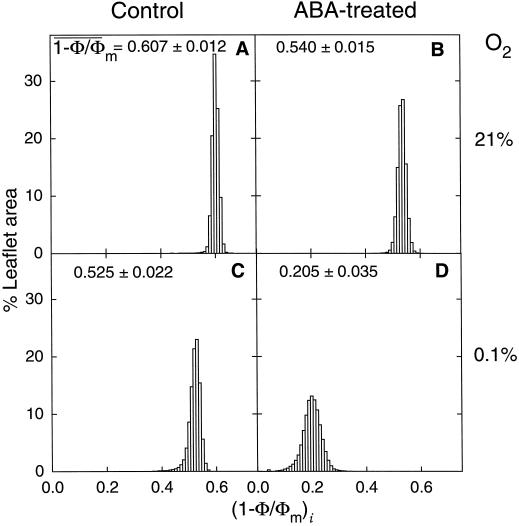
Figure 2 shows images of the photochemical yield of PSII obtained in air (A and B), and during transition to 0.1% O₂ (C and D), before (A and C) and after (B and D) addition of ABA at near-air external CO₂ concentration. Relative pixel intensity was scaled to an 8-bit gray scale, where black and white corresponded to a photochemical yield of 0 and 0.75 (A–C) or 0.4 (D), respectively. Before adding ABA, the distribution of PSII photochemical yield was uniform and the mean photochemical yield was high both in air and during transition in 0.1% O₂ (Figs. 2, A and C, and 3, A and C). In response to the treatment in air, no heterogeneity was observed and photochemical yield was high (Figs. 2B and 3B), whereas a heterogeneous distribution of photochemical yield was revealed in nonphotorespiratory conditions (Fig. 2D). The corresponding distribution of frequencies shows that the mean photochemical yield markedly decreased under nonphotorespiratory conditions and that the distribution function was unimodal (Fig. 3D). This was the case in all experiments, but the shape of the distribution varied from experiment to experiment.

Figure 2.

Images of (1 − Φ/Φ_m)_i taken before (A and C) and during (B and D) treatment of a leaf of R. rubiginosa with 10⁻⁴ M ABA. Leaflet atmosphere was 340 μmol mol⁻¹ CO₂, 21% (A and B) or 0.1% (C and D) O₂, and 70% RH. The photon flux density was 390 μmol m⁻² s⁻¹. The bar indicates 1 cm. Three to four pixels represent about 1 stoma and 10 epidermal cells. Pixel intensity was scaled using an 8-bit gray scale where black and white correspond to a photochemical yield of 0 and 0.75, respectively (A–C), or 0 and 0.4, respectively (D). A_n was 9.1, 2.9, 14.3, and 3.6 μmol m⁻² s⁻¹ for A through D, respectively, and g_s was 142, 23, 153, and 22 mmol m⁻² s⁻¹ for A through D, respectively.

Figure 3.

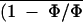
Frequency distributions of (1 − Φ/Φ_m)_i (expressed as a leaflet area percentage) corresponding to the images A through D of Figure 2. with sd are indicated. The class size is 0.01.

Before the addition of ABA, the PSII photochemical yield barely depended on O₂ concentration. After transiently suppressing photorespiration in 0.1% O₂, the mean photochemical yield only decreased by 13.5% (Fig. 2, A and C), although total conductance to water vapor did not decline. This suggests that CO₂ fixation was an electron transport sink almost large enough to compensate for the lack of photorespiration, as predicted by models based on kinetic properties of Rubisco for subsaturating irradiances (Farquhar et al., 1980). In air, O₂-dependent processes other than photorespiration may also have occurred, however, they are not considered in this discussion, since their contribution is likely to be very small in steady-state experiments where C_i never dropped below CO₂ compensation (see Genty and Harbinson, 1996). During the transition to nonphotorespiratory conditions, the PSII photochemical yield especially decreased in mesophyll cells bordering the midrib of the leaflet (Fig. 2C) corresponding to the “tail” of low values of the (1 − Φ/Φ_m)_i distribution (Fig. 3C). In this area (2% of all the mapped leaflet), which was not seen in air, CO₂ availability was presumably lower than in surrounding mesophyll because of a diffusive limitation (Bro et al., 1996).

O₂ dependency of PSII photochemical yield was markedly enhanced after the ABA treatment. The suppression of photorespiration induced a decrease of the mean photochemical yield of 62% (Fig. 3, B and D), which indicates that the allocation of electron transport to the fixation of CO₂ had markedly decreased, as shown by the reduction of net CO₂ assimilation after ABA treatment in an O₂-depleted atmosphere. On the other hand, in air, O₂ reduction by the glycolate pathway and internal reassimilation of evolved CO₂ were able to uniformly drive a large photochemistry over the ABA-treated leaflet. Actually, in air, photorespiration almost masked the heterogeneous decrease in CO₂ fixation, which was revealed by imaging (1 − Φ/Φ_m)_i during the transition in nonphotorespiratory conditions (Figs. 2D and 3D). It is worth noting that a slight decrease of mean photochemical yield occurred in air, in response to ABA (Fig. 3, A and B). This was similar to the one seen after O₂ depletion in the control leaflet (Fig. 3, A and C). However, in contrast to what happens in nonphotorespiratory conditions (Fig. 2C), this slight decrease in photochemical yield occurred randomly distributed over the leaflet area (Fig. 2B) and the distribution of frequencies was narrower and symmetrical (Fig. 3B). This further supports the suggestion that O₂-dependent processes were the major sink for electron transport in ABA-treated leaves, since local internal O₂ concentration is likely to be uniform over the leaflet area.

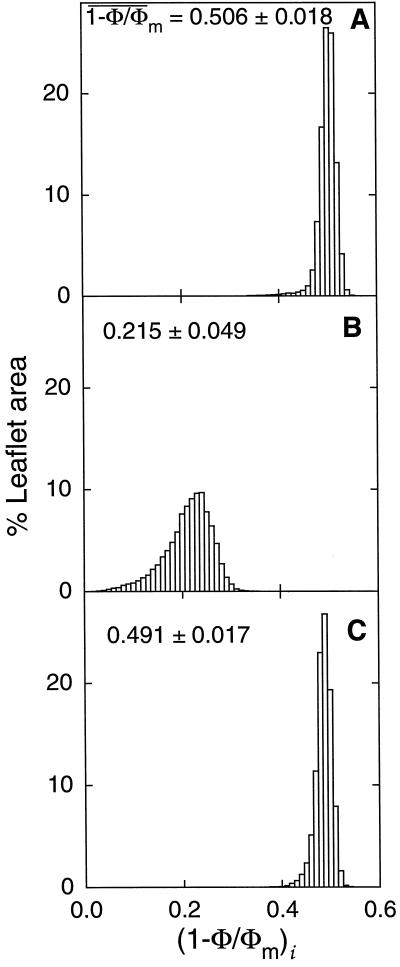
ABA-treated leaves were exposed to a short pulse of high-CO₂ concentration in nonphotorespiratory conditions to test whether a CO₂-supply limitation of photosynthesis could be ruled out. Within 1 min, transient high CO₂ (7400 μmol mol⁻¹ CO₂) fully reversed the heterogeneous decrease of (1 − Φ/Φ_m)_i in response to ABA (Figs. 4 and 5). The fast kinetics of the reversion of the photochemical quantum yield of PSII and therefore of CO₂ assimilation showed that the response of photosynthesis to ABA only involved diffusive phenomena and was unlikely to result from a down-regulation of carboxylation demand, hypothesized as a long-term effect of leaf CO₂ deficiency (Terashima et al., 1988; Ort et al., 1994). This confirmed the intactness and the uniformity of the photosynthetic capacity in ABA-treated leaves. These data provide unambiguous support for the hypothesis that ABA treatment only reduced the diffusion of CO₂ into the leaflet through the closure of stomata, as suggested by previous studies (Downton et al., 1988a; Terashima et al., 1988; Ward and Drake, 1988; Graan and Boyer, 1990; Lauer and Boyer, 1992; Raschke et al., 1990). This also supported the assumption we used in subsequent calculations and discussion of significance of C_i, that no change should occur in the A/C_i relationship during the course of the experiment.

Figure 4.

Images of (1 − Φ/Φ_m)_i taken before (A) and during (B and C) the ABA treatment of a leaflet fraction area of R. rubiginosa at normal (A and B) and high (C) external CO₂ mole fraction for 1 min. Leaflet atmosphere was 330 μmol mol⁻¹ CO₂ (A and B) or about 7400 μmol mol⁻¹ CO₂ (C), 0.1% O₂, and 65% RH. The photon flux density was 420 μmol m⁻² s⁻¹. The bar indicates 4 mm. Pixel intensity was scaled using an 8-bit gray scale where black and white correspond to a photochemical yield of 0 and 0.6, respectively (A and C), or 0 and 0.4, respectively (B). For the whole leaflet area (5.5 cm²), A_n and g_s were 16.1 (A), 4.1 (B) μmol m⁻² s⁻¹, and 165 (A), 27 (B) mmol m⁻² s⁻¹, respectively.

Figure 5.

Frequency distributions of (1 − Φ/Φ_m)_i (expressed as a leaflet area percentage) corresponding to images of Figure 4. 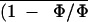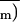and sd are indicated. The class size is 0.01.

Pattern of Heterogeneity

In response to ABA, the decrease in PSII photochemical yield was seen all over the leaflet in nonphotorespiratory conditions (Figs. 2D and 3D). However, the extent of the decrease varied spatially, resulting in a mosaic of patches of about 0.2 mm² (Figs. 2D and 6). In the experiment depicted in Figure 2, patches of similar yield were grouped in such a way that they formed larger areas that drew the net of the major veins that diverged from the midrib; (1 − Φ/Φ_m)_i was the highest in groups of patches close to major veins (Fig. 2D). This pattern varied from experiment to experiment.

Figure 6.

Detail of images of Φ and Φ_m and of the corresponding (1 − Φ/Φ_m)_i taken during the treatment of leaflet of R. rubiginosa with ABA (10⁻⁴ m). Typical surface of an areole was about 0.2 mm². Leaflet atmosphere was 340 μmol mol⁻¹ CO₂, 0.1% O₂, and 70% RH. The photon flux density was 385 μmol m⁻² s⁻¹. The bar indicates 4 mm. Eight to 10 pixels correspond to about 1 stoma and 10 epidermal cells. 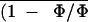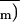was 0.329 ± 0.046 for the leaf area depicted. For the Φ and Φ_m images, the scaling of pixel intensity was done using an 8-bit gray scale where black and white pixels correspond to a relative fluorescence yield of 0 and 0.72, respectively (Φ), or 0 and 1, respectively (Φ_m). For the image of (1 − Φ/Φ_m), black and white pixels correspond to 0 and 0.5, respectively.

Figure 6 shows a detail of images of Φ and Φ_m and the corresponding image of (1 − Φ/Φ_m) for an ABA-treated leaflet during a transition in O₂-depleted atmosphere. Contrast of the image of Φ has been enhanced to better illustrate the local variations of Φ. Images of Φ_m and (1 − Φ/Φ_m) show a similar pattern of heterogeneity. Φ also varied according to similar pattern but to a lesser extent. Thus, the patches in which Φ and Φ_m were low also showed a low (1 − Φ/Φ_m). It is worth noting that in five out of nine experiments, in some patches (no more than 1.5% of all the leaflet area), in nonphotorespiratory conditions, the photochemical yield could be very low (values of about 30% of the mean (1 − Φ/Φ_m)). This was due to a large increase in Φ and Φ_m, which became almost equal (not shown). It mimicked the action of an inhibitor of electron transport-like DCMU (Genty and Meyer, 1995), and was reversible following either a brief addition of high CO₂ or the restoration of normal O₂ concentration. This suggests that ABA could locally inhibit the photochemical efficiency of PSII in some areoles of the leaflet under nonphotorespiratory conditions. This may be the consequence of the severe depletion of sinks that drive electron transport in nonphotorespiratory conditions in these areoles (Genty and Harbinson, 1996). In most experiments after ABA treatment, Φ_m decreased by about 30% and Φ increased by about 10%. In all experiments the percentage of heterogeneity (estimated by the ratio of the sd versus the mean of pixel values over the leaflet area) of Φ and Φ_m distributions was greater than that of (1 − Φ/Φ_m)_i before the ABA treatment (Fig. 6, Φ, Φ_m, (1 − Φ/Φ_m); 7, 9, and 3%, respectively), and lower after the treatment (Fig. 6, Φ, Φ_m, (1 − Φ/Φ_m); 6, 11, and 14%, respectively). Variations of (1 − Φ/Φ_m)_i were not linearly related to variations of Φ_m. This is a consequence of the fact that the quantum yield of PSII is not linearly related to the qN of Φ_m (Genty et al., 1989; Siebke and Weis, 1995).

Using Equations 1 to 6, images of A_n, g_s, C_i, E, and T_l were derived from the image of (1 − Φ/Φ_m)_i obtained for an ABA-treated leaflet in nonphotorespiratory conditions. Figure 7 shows the image of g_si corresponding to the image of (1 − Φ/Φ_m)_i shown in Figure 2D. The frequency distribution remained unimodal (Fig. 8), which was also the case for images of A_ni, C_ii, E_i, and T_li (not shown). The histogram of the frequency distribution of g_s was wider than that of (1 − Φ/Φ_m)_i. The low values of g_si indicated that most of the stomata were almost closed. The percentage of heterogeneity was twice that of (1 − Φ/Φ_m)_i (Fig. 8). The histogram was truncated for zero conductance because of the fact that some spots on the source image of (1 − Φ/Φ_m)_i (only 0.8% of the leaflet area) corresponded to a negative conductance not taken into account in computation of the histogram of g_si. This problem mainly resulted from the assumption we used in Equations 1 through 3 that R_i (local respiration) remained constant over the leaf area and during the time course of an experiment. It is interesting that, although the coefficient of variation was large in images of A_n, g_s, C_i, and E, the coefficient of variation of T_l over the leaf area was always small (i.e. 0.08% for the image of T_l corresponding to the data of Fig. 7, where T_l was 25.6°C). This implies that in our conditions, leaf thermal imaging would have been almost unusable to resolve such a heterogeneous pattern of photosynthesis.

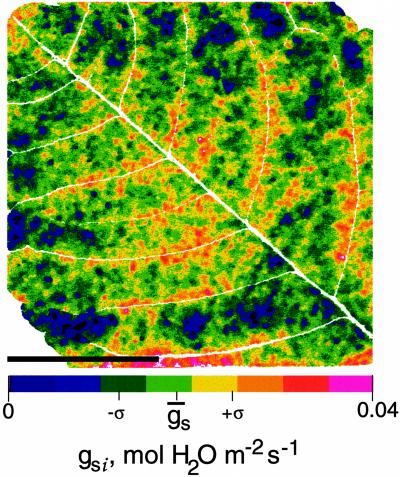
Figure 7.

Image of g_si computed from image of (1 − Φ/Φ_m)_i taken during ABA treatment (Fig. 2D). Image was calculated according to the method detailed in Methods. The bar indicates 1 cm. The 3-bit color scale corresponds to a g_si scale from 0 to 0.04 mol m⁻² s⁻¹. ḡ_s with sd are indicated. Major veins are shown by the white pixels of the image.

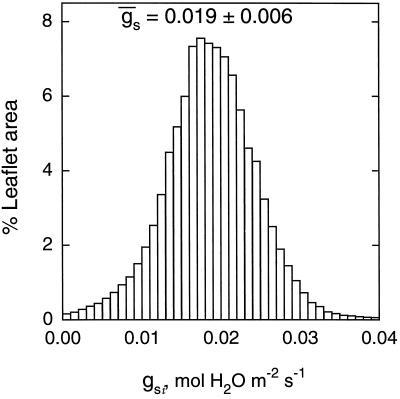
Figure 8.

Frequency distributions of g_si (expressed as a leaflet area percentage) corresponding to Figure 7. ḡ_s with sd are indicated. The class size is 0.001 mol m⁻² s⁻¹. g_s computed from gas exchange was 0.022 mol m⁻² s⁻¹. The image of g_si was computed from an image of (1 − Φ/Φ_m)_i (Fig. 2D) according to Methods: Ā_n, C̄_i, and ḡ_s were 14 ± 0.7, 118 ± 8.6, and 0.105 ± 0.010, respectively, before the ABA treatment and, 3.6 ± 1.1, 25 ± 7.1, and 0.019 ± 0.006, respectively, after the treatment.

Figures 2D, 4B, 6, and 7 show that dark areoles with low (1 − Φ/Φ_m)_i and low g_si could be in contact with brighter areoles with higher (1 − Φ/Φ_m)_i and higher g_si. Only veins separated them. These veins sustained extensions constituted by tightly joined living cells (Wylie, 1952; Terashima, 1992). These vein extensions are an obligate liquid-phase diffusion pathway for CO₂ and consequently may prevent a rapid homogenization of gases in intercellular spaces when stomatal closure is heterogeneous. However, in spite of the compartmentation of gas exchanges, the frequency distributions of heterogeneous (1 − Φ/Φ_m)_i and g_si over the whole leaflet area were unimodal according to Figures 3D and 8, as were the distributions of the corresponding images of Φ and Φ_m (not shown).

The Relationship betwee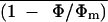n , Net CO₂ Assimilation, and Intercellular CO₂ Mole Fraction

Figure 9 shows 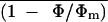and A_n versus C_i relationship in a control leaflet obtained in transient nonphotorespiratory conditions (0.1% O₂) before addition of ABA under varying C_a. After ABA treatment in air, 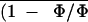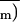determined in transient O₂-depleted air (0.1% O₂) markedly declined (by 70–80%), whereas C_i was relatively less inhibited (circles in Fig. 9). This confirms the well-documented departure from the control A_n (and therefore 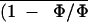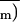) versus C_i relationship after ABA treatment as usually reported in air (Farquhar and Sharkey, 1982; Mott, 1995). Such a departure should not be expected for a limitation of CO₂ supply induced by stomatal closure only, as evidenced in the previous section.

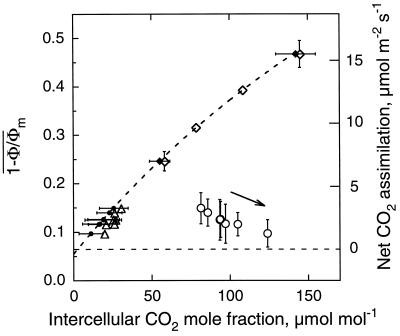
Figure 9.

Relationship between 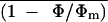and intercellular CO₂ mole fraction in 0.1% O₂ before (⋄, ♦) and after (○, •, Δ) ABA-treatment of a leaf of R. rubiginosa. (⋄, ○) are global C_i conventionally calculated from gas exchange; (♦, •) are C̄_i calculated from the image of C_ii and (Δ) are C_i predicted for gas exchange and calculated from [(ḡ_t/1.6 − Ē/2)C_a − Ā_n]/[ḡ_t/1.6 + Ē/2]. The experiment was the same as Figure 1. Before the treatment, the relationship was obtained by varying the external CO₂ mole fraction. Fit was done according to Equation 2 for data of global C_i (⋄). During the treatment external CO₂ was kept at 340 μmol mol⁻¹. The arrow indicates the temporal trend of the data during the treatment. sds of 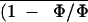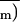and C̄_i are indicated by bars. The corresponding A_n scale, computed from Equation 1 with k = 10.5 and d = 0.055 and with A_n = A − R and R = 0.35 μmol m⁻² s⁻¹, is shown on the right axis.

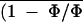
Figure 9 also shows the corresponding C̄_i calculated from the image of C_ii computed from images of (1 − Φ/Φ_m)_i assuming that ABA treatment did not change the A_n and 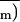versus C_i control relationship. Under the same assumptions, taking into account heterogeneous distribution of stomatal conductance, another estimation of global C_i we called C_i predicted for gas exchange can be derived from images of (1 − Φ/Φ_m)_i as [(ḡ_t/1.6 − Ē/2)C_a − Ā_n]/[ḡ_t/1.6 + Ē/2] (rearrangement of Eq. 3 with Ā_n, ḡ_t, and Ē computed from images of A_ni, g_ti, and E_i, respectively). In Figure 9, the C_i predicted from these calculations are the C_i values that should be obtained using gas-exchange techniques if ABA solely induced heterogeneous stomatal closure. This predicted value corresponds to the C_i described by equation 30b in Farquhar (1989), where C_i was simply modeled as (C_a − 1.6Ā_n/ḡ_t) (see also Meyer and Genty, 1995). The difference between C̄_i and the C_i predicted for gas exchange was rather small and the C_i predicted for gas exchange remained substantially smaller than the global Ci estimated from gas exchange (Fig. 9). Consequently, the ABA induced large departure from control A_n versus conventional C_i relationship could only be partly explained by heterogeneity of stomatal closure.

DISCUSSION

In this study we interpreted the decline of photosynthesis after ABA treatment as having been caused by stomatal closure only. The short time scale of the reversion (within less than 1 min) of low assimilation rate under transient high-CO₂ availability was the strongest indication that stomatal closure was determining the ABA-induced inhibition of photosynthesis. In our experimental conditions the reversion was always almost complete, such that a significant inhibition of metabolic capacity for photosynthesis caused by low-CO₂ supply was unlikely to occur. The weak dependency of photosynthetic electron transport activity on O₂ shown in air, before and after ABA treatment, provides further evidence for the maintenance of a fully competent photosynthetic apparatus. Thus, O₂-dependent processes were able to drive almost as large a photochemical activity as before ABA treatment when maximal A_n occurred. Maintenance of Rubisco activity via O₂ reduction by the glycolate pathway and reassimilation of evolved CO₂ appears as a likely interpretation for such a response. A similar interpretation has been proposed to explain the occurrence of a large photochemical activity in water-stressed leaves (Cornic and Massacci, 1996).

By imaging PSII photochemical yield during a short transition to O₂-depleted air, it was possible to accurately quantify the distribution of A, C_i, and g_s. Thus, in our study, maximal deviation between Ā_n measured by gas exchange and Ā_n estimated by fluorescence imaging was 8%. Such a precision was a prerequisite for an accurate analysis of the significance of C_i.

Continuous frequency distributions of g_s were always seen in contrast to reports of bimodal distributions observed using imaging of qN (Daley et al., 1989). Recently, Mott (1995) using a similar qN imaging also found no evidence for bimodal distribution after ABA treatment. However, in these two earlier studies no experimental basis was provided to characterize the diffusive or metabolic origin of the inhibition of photosynthetic activity induced by ABA treatment. A pure diffusive limitation is a prerequisite for the validity of the assumption used in these imaging studies: the relationship between fluorescence parameters A_n and C_i did not change during the experiment, which allowed the derivation of distributions of A, C_i, and g_s from heterogeneous fluorescence images. In this context, it is important to note that an ABA treatment in O₂-depleted air (Daley et al., 1989) and in air (Mott, 1995; present study) may provide different results (e.g. stomatal closure in O₂-depleted air do not allow a maintenance of Rubisco and photochemical activities). This remark is also valid for many studies where long-term nonphotorespiratory conditions have been used to reveal a heterogeneous photosynthetic activity from fluorescence imaging (e.g. Raschke et al., 1990; Mott et al., 1993; Cardon et al., 1994; Genty and Meyer, 1995; Siebke and Weis, 1995). Equally important is the nonlinearity of the relationship between qN and A, g_t, or C_i both in air and in nonphotorespiratory conditions, which warrants a correct quantification from straight interpretation of qN distribution. Thus, Mott (1995) noted that in air, qN was almost insensitive to C_i at C_i near the CO₂ compensation point. Finally, leaf area probed by gas exchange and imaging may need to be identical for a valid quantification of heterogeneity, which was not the case in previous reports. A selective image of a small fraction of the leaf area may provide a different distribution pattern than an image of a whole leaf or leaflet.

From our comparative analysis of C_i predicted from imaging and global C_i estimated conventionally from gas exchange, it is clear that the large overestimation of C_i observed after ABA treatment can only be partly explained by heterogeneous stomatal closure, in contrast to conclusions of previous studies but in support of the modeling work of Cheeseman (1991) and Buckley et al. (1997). The remaining large difference between global and predicted C_i for gas exchange corresponded to a difference in E and g_t of 58 ± 9 μmol m⁻² s⁻¹ and 3.3 ± 0.8 mmol m⁻² s⁻¹ for the data of Figure 9, respectively. A difference in g_t of 5.6 ± 2.1 mmol m⁻² s⁻¹ was obtained for four experiments (g_s of the control and ABA treated leaflet were 209 and 26 mmol m⁻² s⁻¹, respectively) (Table I). This difference agrees well with the value of cuticular water permeance given for leaves of trees (Kerstiens, 1995). Considering that cuticular conductance to CO₂ is likely to be insignificant (Holmgren et al., 1965), this indicates that the main overestimation of C_i may result from cuticular transpiration, which is not taken into account in the usual calculation of leaf conductance to CO₂ from total conductance to H₂O. As cuticular transpiration occurred on both sides of the hypostomatous R. rubiginosa leaf, we estimated cuticular conductance as 2.8 ± 1.0 mmol m⁻² s⁻¹. Recent data have shown that in Vitis vinifera cuticular conductance to CO₂ was measurable and was approximately 6% of cuticular conductance to H₂O (Boyer et al., 1997). This indicates that the difference between global and predicted g_t for gas exchange may slightly underestimate cuticular conductance to H₂O. Water vapor adsorption by the leaf chamber and the sealing gaskets may also contribute to a residual water vapor net flux we interpreted as cuticular transpiration. However, this problem was minimized by coating the chamber and gaskets with Teflon and paraffin, respectively (maximal error due to water vapor adsorption and release from foam gaskets and walls of the leaf chamber was lower than 9% of the mean Δg_t).

Table I.

Estimated mean difference of g_t, Δg_t, corresponding to the difference between global C_i and C_i predicted for gas exchange

Δgt	gs Control	gs + ABA
	mmol m−2 s−1
5.6 ± 2.1	209 ± 55	26.2 ± 9.5

For each measurement, Δg_t was estimated as Δg_t = (g_t − ḡ_t). g_s at steady state before (g_s control) and after (g_s + ABA) the treatment were also given. Mean values and sd are given for four experiments in nonphotorespiratory (0.1% O₂). Leaf atmosphere contained 340 to 345 μmol mol⁻¹ CO₂ and 66 to 70% RH. The photon flux density was 385 to 420 μmol m⁻² s⁻¹. Maximal error due to water vapor adsorption and release from foam gaskets and walls of the leaf chamber was lower than 9% of the mean Δg_t.

Reduction of stomatal pore size induced by ABA treatment may change the relationship between molecular diffusivity of water vapor and CO₂ and offer an alternative explanation for a break of the relationship between stomatal conductance to water and CO₂. However, this possibility is unlikely, since the ratio of conductance to water over the one to CO₂ has been shown to remain close to the ratio of the free diffusion coefficient for a wide range of width of the stomatal pore (0.01–5 μm) and insensitive to the aperture-dependent change of the diffusion coefficients (Milthorpe and Penman, 1967).

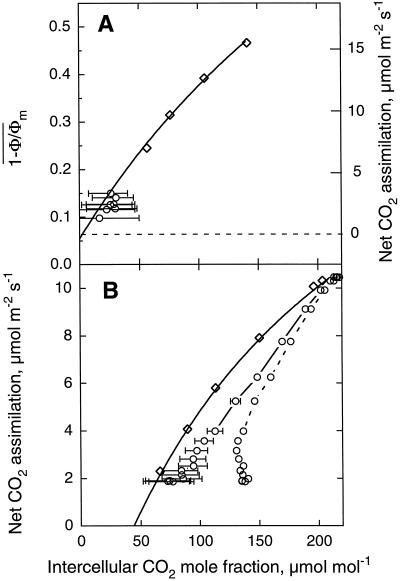
Figure 10 depicts the control relationship between A_n and C_i in nonphotorespiratory (A) and photorespiratory (B) conditions and shows the consequence of not taking into account the cuticular transpiration for the estimation of C_i during ABA treatment for the experiment of Figure 9. The overestimation of C_i resulted mainly from the occurrence of cuticular transpiration when most of the stomata were closed. However, during the early phase of ABA treatment in air when stomatal conductance remained high, heterogeneous stomatal closure was likely to be the only cause of this overestimation (Fig. 10B).

Figure 10.

Corrected relationship of 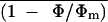or A_n versus intercellular CO₂ mole fraction for cuticular transpiration in nonphotorespiratory (A) and in photorespiratory (B) conditions before (⋄) and after (○) ABA treatment. The experiment was the same as Figure 9. Data were corrected for a cuticular conductance of 3.3 ± 0.8 mmol m⁻² s⁻¹ derived from the difference between conventional C_i and C_i predicted by [(ḡ_t/1.6 − Ē/2)C_a − Ā_n]/[ḡ_t/1.6 + Ē/2] (see Fig. 9). A, Fit was done according to Equation 2 for data of global C_i (⋄). For indication, the corresponding Ā_n scale, computed as in Figure 9, is shown on the right axis. B, Fit was done according to Farquhar et al. (1980) for data of global C_i (⋄). Not corrected data obtained after ABA treatment (○, dotted line) are also shown. Bars indicate the range of C_i predicted for gas exchange for the range of cuticular conductance between the mean values minus sd and the mean values plus sd.

In conclusion, we show that both nonuniform stomatal closure and cuticular transpiration have to be taken into account to accurately predict C_i from gas-exchange measurements when stomatal conductance is low. Our data clearly show that after ABA treatment, heterogeneous decline of Ā_n results only from stomatal closure. In mildly water-stressed leaves where a maintenance of the full integrity of photosynthetic capacity remains questionable (see e.g. contradictory reports of Cornic and Massacci [1996] and Lauer and Boyer [1992]), our approach appears very promising for characterizing the significance of C_i and for separating stomatal from nonstomatal inhibition of photosynthesis.

Abbreviations:

(1 − Φ/Φ_m)_i

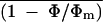, local and mean Φ_PSII

A

A_i, Ā, A_n, A_ni, Ā_n, global (conventional gas-exchange data), local (pixel value), and mean (spatial average) gross and net rate of CO₂ assimilation, respectively

C_a

ambient CO₂ mole fraction inside the cuvette

C_i

C_ii, C̄_i, global, local, and mean intercellular CO₂ mole fraction

E

E_i, Ē, global, local, and mean rate of transpiration

g_b

boundary layer conductance to H₂O

g_s

g_si, ḡ_s, global, local, and mean stomatal conductance to H₂O

g_t

g_ti, ḡ_t, global, local, and mean total conductance to H₂O

Φ

Φ_m, steady-state and maximal fluorescence yields

Φ_PSII

photochemical yield of PSII

qN

nonphotochemical quenching of chlorophyll fluorescence

T_l

T_li, T̄_l, global, local, and mean leaf temperature

w_i

w_ii, w̄_i, global, local, and mean intercellular mole fraction of water vapor