Quantification of Absolute Fat Mass by Magnetic Resonance Imaging: a Validation Study against Chemical Analysis

Abstract

Objective

To develop a magnetic resonance imaging (MRI)-based approach for quantifying absolute fat mass in organs, muscles, and adipose tissues, and to validate its accuracy against reference chemical analysis (CA).

Methods

Chemical-shift imaging can accurately decompose water and fat signals from the acquired MRI data. A proton density fat fraction (PDFF) can be computed from the separated images, and reflects the relative fat content on a voxel-by-voxel basis. The PDFF is mathematically closely related to the fat mass fraction and can be converted to absolute fat mass in grams by multiplying by the voxel volume and the mass density of fat. In this validation study, 97 freshly excised and unique samples from four pigs, comprising of organs, muscles, and adipose and lean tissues were imaged by MRI and then analyzed independently by CA. Linear regression was used to assess correlation, agreement, and measurement differences between MRI and CA.

Results

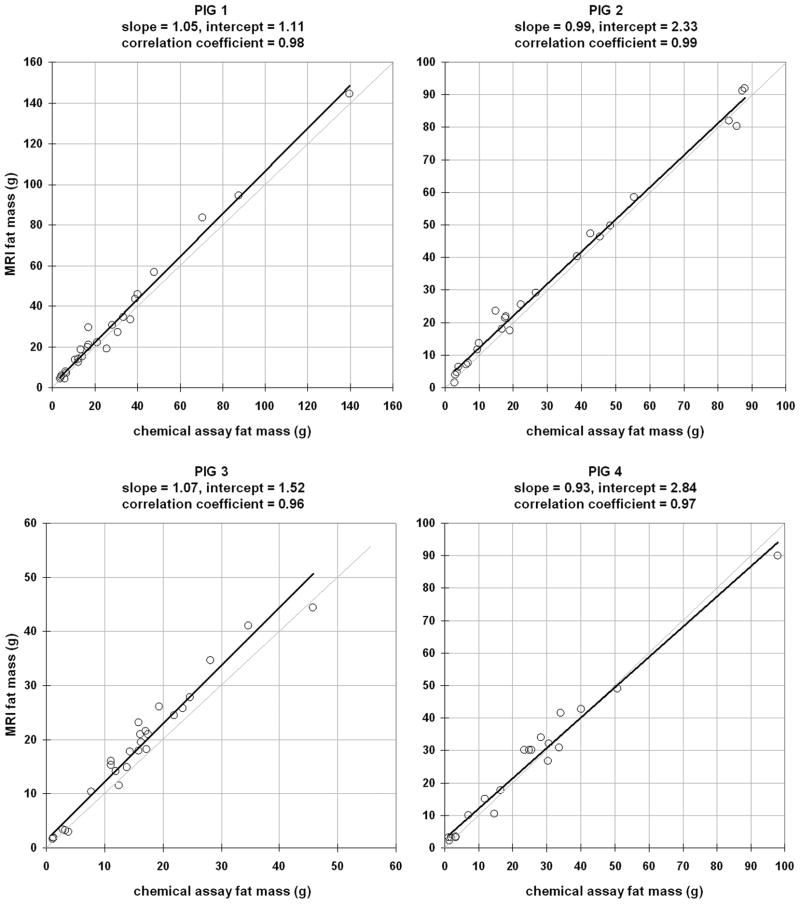
Considering all 97 samples, a strong correlation and agreement was obtained between MRI and CA-derived fat mass (slope = 1.01, intercept = 1.99g, r² = 0.98, p < 0.01). The mean difference d between MRI and CA was 2.17±3.40g. MRI did not exhibit any tendency to under or overestimate CA (p > 0.05). When considering samples from each pig separately, the results were (slope = 1.05, intercept = 1.11g, r² = 0.98, d = 2.66±4.36g), (slope = 0.99, intercept = 2.33g, r² = 0.99, d = 1.88±2.68g), (slope = 1.07, intercept = 1.52g, r² = 0.96, d = 2.73±2.50g), and (slope=0.92, intercept=2.84g, r² = 0.97, d = 1.18±3.90g), respectively.

Conclusion

Chemical-shift MRI and PDFF provides an accurate means of determining absolute fat mass in organs, muscles, and adipose and lean tissues.

Introduction

As the prevalence of obesity continues to rise, accurate tools for quantifying abdominal body and organ fat mass are critically needed. Fat accumulation in organs and skeletal muscles are strong biomarkers of diabetes, the metabolic syndrome, and obesity [1–6]. In addition, the quantity of abdominal subcutaneous and visceral adipose tissue plays critical roles in determining one’s health risks. Rapid fat quantification, particularly in organs and muscles, remains an unsolved problem and unmet need. Magnetic resonance imaging (MRI) is the most promising modality to address such challenge. MRI is non-invasive, utilizes no ionizing radiation, provides 3D visualization of the anatomy, and has immense flexibility in tissue contrast mechanisms.

Many methods have been historically available for body fat assessment [7–9]. Anthropometry, hydrodensitometry, air-displacement plethysmography (ADP), bioelectric impedance (BIA), and dual energy X-ray absorptiometry (DXA) have been widely used. The first four are indirect techniques because they measure body density or resistance, which are then converted into percent body fat using generalized equations [10]. Hydrodensitometry and ADP are limited to estimating total body fat mass, while BIA and DXA are limited to total and regional body fat mass measures. Most importantly, these indirect methods are not able to differentiate between SAT and VAT or quantify organ and muscle fat.

An increased utilization of computed tomography (CT) [11, 12], quantitative magnetic resonance (QMR) [13–15], and particularly MRI for body fat assessment [16–22] has been reported in recent years. DXA, CT, QMR, and MRI are direct techniques because they identify fat based on the tissue’s unique properties and signals in each modality. QMR does not yield images and is limited to measuring total body fat mass. In contrast, CT and MRI can accurately quantify SAT and VAT volume and mass with multi-dimensional images as well as measure relative fat fraction content in organ, muscle, or any arbitrary anatomical region.

Motivated by the fact the chemical analysis (CA) returns an intuitive and direct measure of absolute fat mass, the purpose of this work was to validate an approach based on chemical-shift MRI for computing similar absolute fat mass (e.g. in grams) from available proton density fat fraction (PDFF) data. Since MRI signals fundamentally measures hydrogen proton density, and not typical SI units of volume or mass, we first present a formulation that relates the MRI-derived PDFF to absolute fat mass. Next, the proposed MRI technique was applied to freshly excised samples of adipose tissue, but more importantly to mixed and heterogeneous fat and lean tissue, organ, and muscle samples from four pigs [23, 24]. The samples were independently analyzed for fat mass by gold-standard lipid extraction chemical analysis. We hypothesized that fat mass derived from non-destructive MRI measurements are accurate and in reasonable agreement with values obtained chemical analysis. To our knowledge, this type of comparison of absolute fat mass between MRI and CA in organs has not been previously performed.

Research Methods and Procedures

MRI Principles

This brief section is not intended to educate the reader on MRI principles. The description however, is necessary to familiarize the reader with relevant terminology. The MRI signal S arises primarily from hydrogen protons in free water and fat molecules. While other protons exist in macromolecules, they are not usually detected or observed in conventional MRI. When an object is placed inside a magnetic field, a longitudinal magnetization from the proton ensemble is created. The magnetic field causes the magnetization to undergo precession at the Larmor frequency. In an MRI experiment, radiofrequency (RF) pulses are applied as a pulse sequence to gather data. The RF pulses are tuned to the Larmor frequency to repeatedly excite and tip the longitudinal magnetization into the transverse plane at a specified flip angle. After each RF excitation at a time delay denoted by TE, an echo of the transverse magnetization is acquired by receiver coils. Additionally after each RF excitation, two simultaneous and independent processes occur. First, the perturbed longitudinal magnetization will recover towards its original state prior to RF excitation. The rate of recovery is the T₁ exponential constant. Second, the RF-created transverse magnetization will lose signal coherence at an exponential rate of T₂. T₁ and T₂ values, along with proton density, are intrinsic tissue properties [25, 26].

Chemical Shift MRI

A unique phenomenon in proton MRI of water and fat is chemical shift, which refers to the difference in their Larmor frequencies. Water protons are solely attributed to hydroxyl groups. In contrast, the predominant fat protons are from the methylene groups. Due to chemical shielding, methylene protons have a slightly lower Larmor frequency. In 1984, Dixon described an imaging approach that exploited this chemical shift difference to separate water and fat via image reconstruction [27]. By controlling the TE when data was acquired, the net detected MRI signal can comprise either of water and fat signals in-phase (IP = S_W + S_F) or out-of-phase (OP = S_W − S_F). With this two-point IP/OP approach, separated water and fat images could be obtained by image algebra [28–30].

Over the past 25 years, the chemical-shift MRI has evolved significantly with improvements from many investigators, and recent advances have led to the development of a water-fat 3D imaging technique called IDEAL [31]. IDEAL is a generalized multi-echo approach that is robust to hardware system imperfections such as magnetic field inhomogeneity, and produces separated fat and water images that are optimal in terms of signal-to-noise ratio. A single IDEAL acquisition yields not only reconstructed fat-only and water-only images, but also IP and OP series that are useful for anatomical definition, and most importantly a voxel-wise quantitative fat-signal fraction map [S_F/(S_F + S_W)]. IDEAL fat-signal fraction imaging has been rigorously validated in fatty liver disease [32–34] against other imaging modalities and needle biopsy, and its variants have been used to study brown and white adipose tissues [35] well as fat accumulation in the heart [36] and muscle [37]. Currently, the IDEAL pulse sequence is provided as a research and commercial product from GE Healthcare. Other MRI vendors have similar techniques in development, but are generally referred to as multi-point chemical-shift “Dixon” MRI.

Mass Fat Fraction, Proton Density Fat Fraction, and Fat Mass

In the following discussion, we assume that the principle contributors of MRI signal are proton spins from free water and fat molecules. The fat-signal fraction from IDEAL MRI then fundamentally reflects the underlying ratio of fat to unbound water proton signals in the tissue of interest. Water and fat protons have different relaxation rates, and fat has additional minor spectral components such as methyl and olenfinic groups. Assuming that confounding factors such as T₁ bias, T₂* relaxation (a combination of T₂ and magnetic field inhomogeneity), and the multiple spectral peaks of fat [38–40] have been adequately addressed and compensated for through pulse sequence parameters and the IDEAL reconstruction algorithm, the resultant fat-signal fraction is equal to the PDFF. At first glance, this PDFF is not equivalent to absolute fat mass (volume), or mass (volume) fat fraction. As described thoroughly by Reeder, et al. [41, 42], while the PDFF is a useful quantitative biomarker, gold-standard reference methods such as chemical assay and other body composition modalities traditionally provide estimates of mass fat fraction and absolute fat mass. In the following paragraph, we show that while the proton density and mass fractions are two fundamentally different metrics, they are nonetheless related and that for fat and water moieties, the difference is remarkably small and negligible.

Following the notations of Reeder, et al. for consistency, let us first define the pure un-confounded proton-density signals of water and fat, S_W and S_F, for an arbitrary imaging voxel as

$$\begin{array}{l}{S}_W={\rho }_W·V_W·\left(\frac{{\lambda }_W·N_A}{{MW}_W}\right)=m_W·\left(\frac{{\lambda }_W·N_A}{{MW}_W}\right)\\ S_F={\rho }_F·V_F·\left(\frac{{\lambda }_F·N_A}{{MW}_F}\right)=m_F·\left(\frac{{\lambda }_F·N_A}{{MW}_F}\right)\end{array}$$ [1]

where ρ is the mass density (g/ml), V is the volume of water or fat in the voxel, λ denotes the number of protons per molecule, N_A is Avogadro’s number, and MW represents the molecular weight (g/mol). The numerator of the term in parenthesis has units of the number of protons per mole of substance. Dividing this by the denominator MW, the resultant units of the term in braces is the number of protons per gram of substance. Multiplication by ρ and V gives the unit of S_W and S_F as simply the number of protons. Note that the product of ρ and V is mass m.

Next, let us define in Equation 2a-b the expressions for proton density fat fraction (PDFF) by MRI and mass fat fraction. In the denominators, we have additionally introduced an appropriate parameter with the subscript “o”. This represents the proton contributions from other non-free-water and non-fat moieties, such as macromolecules (proteins, bone mineral, and glycogen) that usually have bound water molecules. Since these elements are typically “invisible” to MRI, partly as a consequence of their high fast T₂ decay rates, partly due to their lower proton density, and remain undetected with imaging parameters in the range of those used in this work, the term S_O can be reasonably set to zero, as shown in Equation [2a]. Thus, the general water-fat chemical-shift MRI signal model, as in IDEAL, comprises of contributions from only free water and fat within a voxel, despite the potential presence of “invisible” components and water bound to macromolecules. Following the notation in reference [42], let us also further define k as the mass proportion of free water.

$${\eta }_{\mathit{PDFF}}=\frac{S_F}{S_W+S_F+S_O}\approx \frac{S_F}{S_W+S_F}$$ [2a]

$$\begin{array}{l}{\eta }_{\mathit{mass}}=\frac{m_F}{m_W+m_F+m_O}=\frac{m_F}{m_F+m_F+m_W\left(\frac{1-k}{k}\right)}=\frac{m_F}{\left(\frac{1}{k}\right)m_W+m_F},\\ \text{where}k=\frac{m_W}{m_W+m_O}\end{array}$$ [2b]

The reader is keen to note that if m_O is zero, then k reduces to unity, and Equation 2b simplifies to m_F/(m_W+ m_F). Substitution of Equation 1 into Equation 2 to replace m yields Equation 3.

$${\eta }_{\mathit{PDFF}}=\frac{S_F}{S_W+S_F}$$ [3a]

$${\eta }_{\mathit{mass}}=\frac{S_F\left(\frac{{MW}_F}{{\lambda }_F}\right)}{\left(\frac{1}{k}\right)\left(\frac{{MW}_W}{{\lambda }_W}\right)S_W+\left(\frac{{MW}_F}{{\lambda }_F}\right)S_F}=\frac{S_F}{\left(\frac{1}{k}\right)·1.02·S_W+S_F}$$ [3b]

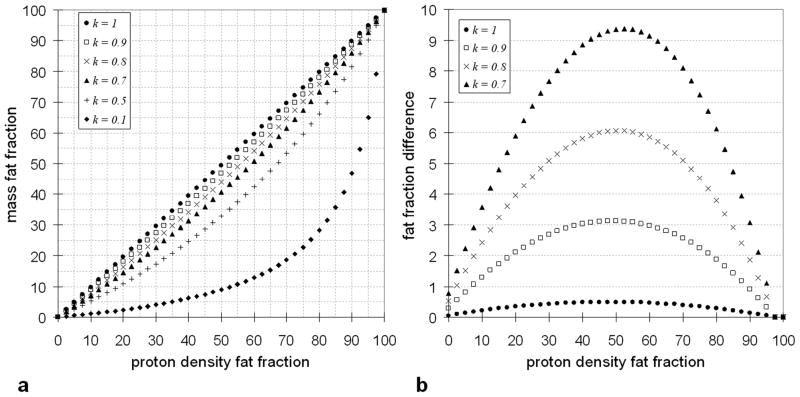
To obtain the 1.02 coefficient on the right-hand-side of Equation 3b in the denominator, we have from past literature [43–49] substituted the following for water: ρ_W = 0.993 g/ml, MW_W = 18.015 g/mol, and λ_W = 2; and the following for the average triglyceride in adipose tissue: ρ_F = 0.92 g/ml, MW_F = 845.52 g/mol, and λ_W = 95.84; and dropped the N_A constant entirely for simplicity. It now becomes clearly evident that the final mathematical expressions for PDFF and mass fat fractions are remarkably similar, with the exception of two coefficient terms in front of S_W, one reflecting the relative ratio of differences in molecular properties between water and fat, and the other denoting the proportion of free and bound water. It should be again noted that the expressions in Equations 1–3 are representative of an individual voxel and thus in a heterogeneous sample, the parameter k can potentially be voxel dependent. Figure 1 plots simulation results for varying values of k using Equation 3 and its effect on fat fraction. Note that the level of disagreement between PDFF and mass fat fraction depends not only k, but also as a function of true fat fraction.

Figure 1.

(a) Plot of simulated proton density fat fraction versus mass fat fraction as described in Equation 3b for different values of k. (b) A plot of the difference in proton density fat fraction and mass fat fraction for k = 0.7 to 1. All axes units are in percent fat fraction. For k = 1, the agreement between proton density and mass fat fraction is very strong, with errors less than 1% across the entire fat fraction range. With k = 0.9, the maximum error in fat fraction estimate is still a manageable 3%, which occurs near the 50% fat fraction mark. With decreasing k, the error becomes much more significant.

Since the value of k is not readily available in the literature for various tissue and organs, difficult to obtain a priori, and can have significant inter-sample variability, we proceeded in this work and in the remaining computations of this work with the assumption that k = 1. Consequently, we can now define absolute fat mass within each imaging voxel as approximated by

$$m_F={\eta }_{\mathit{mass}}·({\rho }_F·v)\approx {\eta }_{\mathit{PDFF}}·({\rho }_F·v)$$ [4]

where v is the volume of the MRI voxel. Equation 4 represents a means of converting PDFF on a voxel-wise basis from MRI to absolute fat mass. Note that with this expression the PDFF itself is in fact linearly proportional to fat mass. The termsρ_F and v in parenthesis are simply scalar constants, and the resultant product yields fat mass.

Animals

All experimental work was approved by the Institutional Animal Care and Use Committee. Four pigs (2 males ages 2 and 2 years old, 2 females ages 11 and 12 years old), with 45.5, 48.7, 78.0, 73.3 kg body weights, respectively, were used in this study. The animals were obtained through the Department of Animal Resources at the University of Southern California. We made no attempts to be selective of the type of pigs used in this study. The decision to use four animals was based on cost and availability from the breeder at the time the experiments were planned. A board-licensed veterinarian euthanized each animal by inducing anesthesia through an intramuscular injection of Telazol (Pfizer, Inc.) and Xylazine (Bayer AG), followed by an intravenous injection of sodium pentobarbital (Pfizer, Inc.).

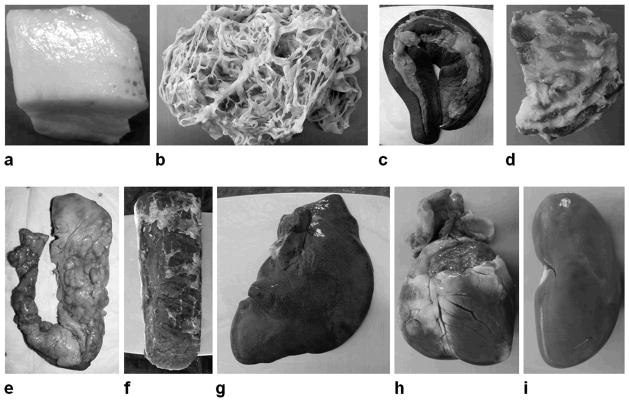
Organs including left and right kidneys, the spleen, the pancreas, and the heart were removed during necropsy. Additionally, samples from different lobes of the liver, the left and right longissimus muscle, subcutaneous adipose tissues from the back and sternum, and omental and peri-renal visceral adipose tissues, were obtained. Finally, random mixture samples containing both lean and fat tissues were excised. Figure 2 illustrates photographs of representative samples. Table 1 lists the scale weights of the 97 unique samples in grams.

Figure 2.

Representative photographs of pig samples from necropsy, including (a) back subcutaneous adipose tissue, (b) omental visceral adipose tissue, (c) spleen, (d) a mixture of fat and lean tissues, (e) pancreas, (f) longissimus muscle, (g) liver, (h) heart, and (i) kidney. Photographs are not to scale.

Table 1.

Scale weights of excised samples. SAT: subcutaneous adipose tissue, VAT: visceral adipose tissue

Samples (weight in grams)	Pig 1	Pig 2	Pig 3	Pig 4
Kidney	202, 364	138, 158	90, 92	82, 86
Liver	158, 212, 226	225, 230, 340	54, 58, 68	62, 86, 96
Heart	408	466	298	212
Spleen	338	294	284	344
Pancreas	22	18	62	88
Longissimus Muscle	530, 648	514, 562	390, 416	400, 466
Peri-renal VAT	18, 20, 22	18, 28, 32	16, 22, 26	36, 36
Omental VAT	20, 28, 28	18, 34	22, 28, 28	38, 44
Back SAT	28, 34, 40	48, 54, 68	22, 26, 34	40, 48
Sternum SAT	26, 34, 50	24, 28, 34	16, 18, 24	12, 20
Mixture of fat and lean	66, 74, 196, 276	188, 212, 224	50, 56, 80, 108, 108	116, 224
Total Number of Samples	26	24	27	20

Magnetic Resonance Imaging

All MRI data acquisition was performed on a 3 Tesla whole-body human scanner (Signa Excite HD 15M4, GE Healthcare, Milwaukee, Wisconsin) within 24 hours after necropsy. Depending on the size of the excised samples, they were either imaged individually or as a group, using either a single-receiver wrist coil, an eight-receiver head coil, or an eight-receiver knee coil to optimize signal-to-noise ratio. No purposeful attempts were made to systematically place the samples in any particular orientation. In other words, placement of samples within the receivers was random and purely a matter of convenience. We utilized an investigational six-echo version of the IDEAL spoiled gradient echo pulse sequence from GE Healthcare. A bandwidth of 250 kHz was used for all data acquisitions. TR and TE timings varied depending on the selected imaging field-of-view, the data sampling matrix, and the size of the specimen. However, TR was always chosen to be the minimum allowed value and in this study varied from 10 to 15 msec. Likewise, the first TE also varied accordingly from 1 to 1.5 msec based on other settings. For a given acquisition, the spacing between adjacent echoes however was always held constant, between 0.7 to 0.8 msec. This corresponded to approximately 120° of phase shift between the water and the methylene proton signals and is a setting that is optimized for signal-to-noise ratio and robustness of the technique to water-fat signal decomposition [31]. Overall, the minimum TR, the first TE, and the echo spacing parameters are automatically determined by the IDEAL pulse sequence with minimal involvement. After data collection, the IDEAL software performed image reconstruction online, providing separated water and fat series, IP and OP series, and quantitative T₂* and PDFF maps. A small RF flip angle of 5° was used to minimize T₁ signal bias on PDFF estimation [38] and a multi-peak spectral model of fat pre-calibrated from human data was used during image reconstruction [39], as previously described and validated in literature. For all samples, spatial resolution was set to 1.1 mm in-plane and 1.0 mm thru-plane (slice thickness) and data acquisition was limited to one pass (e.g. no averaging). The images were then segmented using SliceOmatic software (Tomovision, Inc.) to identify voxels encompassing each sample. Computation of fat mass via Equation 4 was then performed with ρ_F = 0.92 g/ml in Matlab (The Mathworks, Inc.) and summed across all voxels of interest. In this work, we did not make attempts to correct for the nominal 1.02 coefficient or k.

Chemical Analysis

All samples were shipped by overnight courier for chemical analysis (CA) within 72 hours of necropsy. Chemical analysis of all samples was performed independently by the Small Animal Phenotyping Core at the University of Alabama at Birmingham [50]. Briefly, the samples were first weighed and placed in an oven at 60°C for desiccation. The samples were dried until constant weight, upon which loss of water mass was determined. They were then ground to powder, placed in cellulose extraction thimbles, and weighed again. The thimbles were set in a Soxhlet apparatus, where multiple cycles of petroleum ether extraction were performed overnight to remove lipids. Afterwards, the samples were allowed to dry again, and reweighed to determine the loss of fat and the remaining fat-free dry mass. Chemical analysis is the benchmark for animal carcass analysis and was considered the gold-standard reference method in this work. CA-derived fat mass measures for each of the 97 samples were then reported back to the MRI investigators.

Statistics

Linear regression was performed on the MRI-derived and CA-derived fat mass values to assess correlation. Regression line slope, intercept, and correlation coefficient were computed. To test the strength of the agreement between MRI-derived and CA-derived fat masses, we determined whether the regression line slope was statistically different from one and whether the intercept was statistically different from zero with 95% confidence intervals. Bland-Altman plots were also generated to observe any data patterns and best-fit lines were plotted. All results were considered statistically significant with a p-value ≤ 0.05.

Results

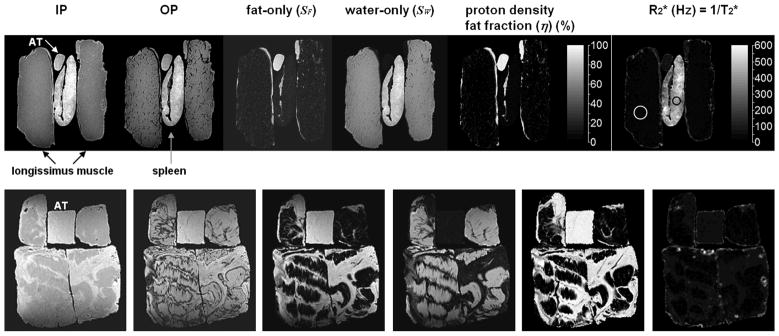
Figure 3 illustrates representative images from IDEAL MRI for the longissimus muscles and spleen, and a collection of mixture samples containing fat and lean tissues. The IDEAL algorithm generates qualitative IP, OP, fat-only, and water-only images as well as quantitative T₂* and PDFF series on a voxel-wise basis that are all perfectly registered. Note in particular the extremely short T₂* values within the spleen, indicative of high iron (hemoglobin in blood) content.

Figure 3.

Representative reconstructed images from IDEAL MRI. In the top row, longissimus muscle (black arrows) and spleen (gray arrow) samples are shown. For reference, a sample of adipose tissue (AT, white arrow) is also included. The IDEAL algorithm generates qualitative anatomical series of IP, OP, fat-only, and water-only images. In addition to these, quantitative fat fraction and T₂* maps are generated by IDEAL. The fat fraction is shown on a black-to-white colorbar in percent. For ease of illustration, the T₂* map is shown in R₂* (= 1/T₂*) format, and the color bar unit is in inverse second (1/second). Note the drastic difference in T₂* values between the muscle and spleen. In the white circle of the muscle, the mean T₂* is a relative long 45.0 msec. In the black circle of the spleen, the mean T₂* is an extremely short 2.44 msec. Similar images are shown for mixed fat and lean tissue samples in the bottom row. Note the significant difference in appearance and quantity of fat speckles and striations between the mixed samples and the longissimus muscles, as seen in the voxel-by-voxel fat fraction maps.

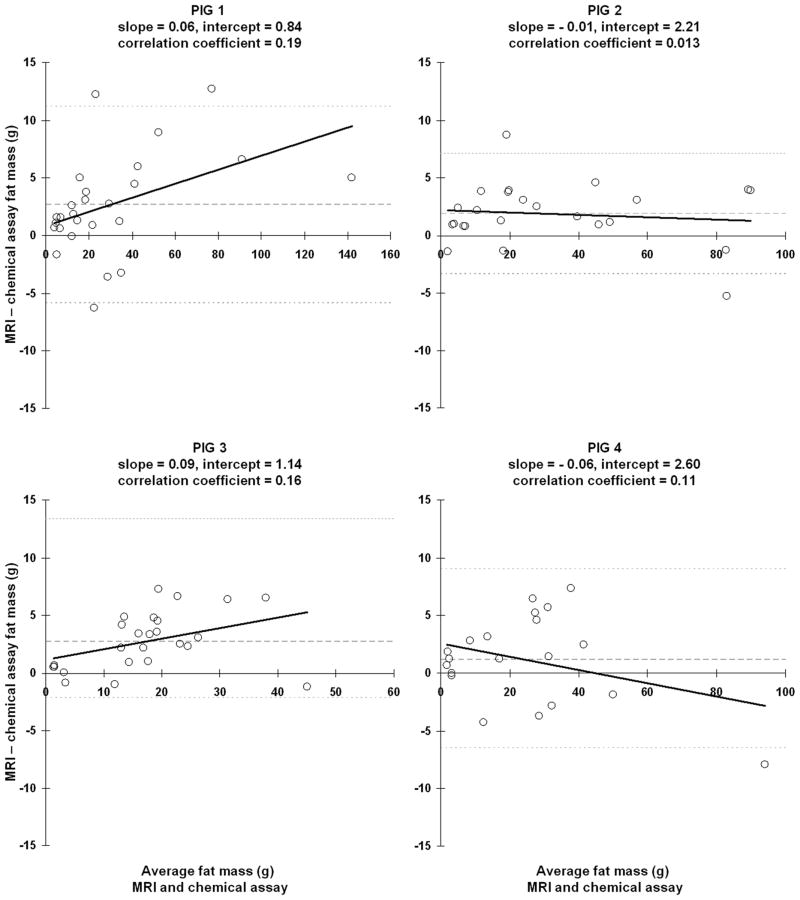
For each of the four pigs, Figure 4 plots the linear correlation between MRI and CA-derived fat mass. Based on the correlation coefficients, there is very strong association in the data from all four animals, with statistical significance of p < 0.01. The slope of the best-fit line suggests the level of numerical agreement between MRI and CA-derived fat mass and the corresponding intercept is indicative of bias in the MRI estimates. The 95% confidence intervals of the regression slope for pig 1 through 4 were [0.99 1.11], [0.94 1.03], [0.98 1.17], [0.85 1.01], respectively. Similarly, the 95% confidence intervals of the regression intercept for pigs 1 through 4 were [−1.19 3.42], [0.63 4.03], [−0.14 3.19], [0.29 5.39], respectively. The 95% confidence intervals of slope contain the value of one for all four pig data sets. However, only the 95% confidence intervals of the intercept of pig #1 and #3 contain the value of zero. Nonetheless, the lower intercept interval limits of pigs #2 and #4 are very close to zero.

Figure 4.

Linear regression plots of fat mass between chemical analysis and MRI for samples from each of the four pigs. In each plot, the light gray diagonal line is identity. The thick black line is the best-fit line through each data set. The slope, intercept, and correlation coefficient of this line is given in each plot’s heading.

Figure 5 illustrates the corresponding Bland-Altman plots. Note that the correlation coefficients of the best-fit lines are very small, indicative of no association. There is also no statistically significant difference between MRI and CA-derived fat mass as the corresponding 95% confidence intervals all include the value zero. The means ± standard deviations (SD) of the difference between the two techniques were 2.66 ± 4.36 g, 1.88 ± 2.68 g, 2.73 ± 2.50 g, and 1.18 ± 3.90 g.

Figure 5.

Bland-Altman scatter plots of samples from each pig. In each plot, light gray dotted lines denote the 95% upper and lower confidence intervals of the mean difference between MRI and chemical assay fat mass. The mean difference is denoted by the dashed gray line. The thick black line represents the best-fit line through the data, and its slope, intercept, and correlation coefficient are given in each plot’s heading. Note that the slope magnitudes are small.

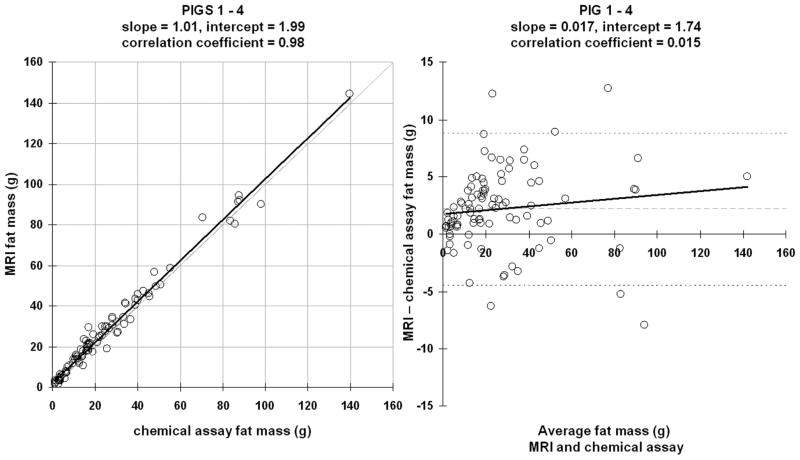
Figure 6 illustrates a linear correlation and a Bland-Altman plot of all samples consolidated across the four pigs. There is excellent agreement between the two fat mass measures as the regression slope is nearly equal to one. The 95% confidence intervals for slope and intercept are [0.98 1.04] and [1.01 2.96], respectively. The difference between MRI and CA was 2.17 ± 3.40 g and was not statistically significant from zero.

Figure 6.

Linear correlation and Bland-Altman plots of all samples consolidated from the four pigs. Figure representations are the same as those in Figures 4 and 5.

Lastly, Table 2 summarizes linear regression parameters categorized by sample type. Strong correlations were obtained in all samples, particularly in the organs, with the exception of the spleen. For the spleen, we speculate that poor correlation was due to the organ’s extremely short T₂* times. It is known that in the presence of fast T₂* decay, estimation of PDFF can be erroneous with a tendency to overestimate, and that additional echoes from an IDEAL acquisition are necessary to improve computational accuracy [51]. From Table 2, it is also evident that there is a wide distribution of regression slopes (e.g. from 0.48 to 1.30). A reason for this observation could be that the MRI-fat mass was derived from a scalar product of the measured PDFF with v and ρ_F = 0.92 g/ml. While v is set from the MRI protocol and is a constant across all samples, ρ_F was an assumption taken from literature. It is possible that ρ_F could slightly vary between different samples and animals.

Table 2.

Linear regression results between MRI and chemical-assay fat mass categorized by sample type across all four pigs

Samples	Slope	Intercept (grams)	Correlation Coefficient
Kidney	1.30	− 1.09	0.89
Liver	1.07	0.90	0.92
Heart	1.03	− 0.22	0.99
Spleen	0.48	18.3	0.49
Pancreas	0.77	− 0.34	0.93
Longissimus Muscle	1.19	− 2.84	0.97
Peri-renal VAT	1.25	− 0.43	0.98
Omental VAT	0.81	4.96	0.94
Back SAT	0.99	2.44	0.86
Sternum SAT	1.00	3.42	0.95
Mixture of fat and lean	0.98	1.93	0.98

Discussion

We have described a quantification model to compute absolute fat mass based on chemical-shift water-fat MRI. Whereas previous MRI studies for body fat composition have been limited to lipid-rich subcutaneous and visceral adipose depots, the proposed chemical-shift MRI technique additionally facilitates fat quantification in organs, muscles, and ectopic depots. In validating the model against reference CA, which provides a direct measure of absolute fat mass, we have first corroborated prior works [41, 42] that the PDFF is indeed highly correlated with mass fat fraction when the influence of MRI-invisible components is negligible. Second, results from this work demonstrated excellent correlation and agreement between MRI and CA-derived fat mass, with no apparent trend for under or overestimation.

It is important to note that in order for the proposed model to work, the PDFF computed from MRI must be minimally influenced by other signal confounding factors, including T₁ and T₂ relaxation, and the multiple spectral peaks of fat. The research version of the IDEAL algorithm currently implemented on GE MRI systems addresses many of these factors automatically, with minimal operator intervention. To describe the implications of each of these factors is beyond the scope of this work. However, a plethora of literature reports have recently investigated the effects of these factors in quantitative fat MRI [38–40, 52] and extensive phantom studies in homogeneous water-fat emulsions have demonstrated the accuracy, stability, and uniformity of the PDFF metric [51–55]. All of the homogeneous adipose tissue samples in this work exhibited highly uniform PDFF, with < 5% standard deviations across the samples. This nominal variability includes any true tissue variations in the underlying adipose tissue. The use of a small flip angle (5°) and a short TR (10 msec) as adopted in this work has been shown to be effective in minimize T₁ bias. A PDFF error of less than 1% is introduced when the true fat fraction is between 0 and 20% and an error of only 2–3% was observed for true fat fractions between 30 and 50% at 1.5 and 3 Tesla field strengths [56]. Furthermore, while the present work was performed on a GE 3 Tesla platform, the concept of a generalized multi-echo chemical-shift approach has been demonstrated by other vendors [57] and a reproducibility study of estimating liver PDFF across two scanner platforms (GE 3 Tesla vs. Siemens 1.5 Tesla) was recently reported with strong agreement and platform independence [58]. In addition, improvements to the IDEAL reconstruction algorithm continue to be developed, increasing the technique’s robustness to undesirable phase errors, such as eddy currents and susceptibility artifacts from air/tissue interface, and accuracy in PDFF measurements [54, 59].

As described in Equation 4, the dimension of the imaging voxel v and the mass density of fat ρ_F are needed to convert PDFF to absolute fat mass. The results presented in this work were all computed with ρ_F = 0.92 g/ml. Conversely, we also performed the following reverse analysis. By plugging into the left-hand-side of Equation 4 the fat mass of each sample as determined by gold-standard reference CA, and into the right-hand-side the measured PDFF and the voxel volume from MRI, we estimated the value of ρ_F in that would give a perfect correlation slope of one. For each of the data sets from the four pigs, we obtained 0.88, 0.93, 0.90, and 0.99 g/ml, respectively. Unsurprisingly, the mean ± SD of these four values is 0.925 ± 0.05 g/ml, in excellent agreement with many past literature reports [43–49]. Furthermore, the proposed model is expected to be valid for a wide range of spatial resolutions and voxel sizes, which has been previously demonstrated in a preliminary study for 1.5, 3, and 4 mm dimensions [24]. In retrospect, one may alternatively consider simply estimating the PDFF and omit the volume and mass density scaling, as the fat fraction metric is directly proportional to fat mass.

One limitation of this study was that ex vivo scans of the pig samples were compared against CA. Based on previous experience, a primary reason we chose to analyze images acquired from freshly excised samples was image registration. While we also performed in vivo MRI scans of the pig in this work prior to euthanasia, it was extremely difficult to affix fiducial markers along the animal’s coarse skin to demarcate anatomical sections of interest. Due largely to involuntary animal motion, the markers were often displaced during transport and transfer from the transport cart to the MRI bed. Upon scanning, it was frequently challenging to perform accurate image segmentation of the MRI data encompassed by the fiducial markers. Additionally during necropsy, it was likewise a daunting task for the veterinarian to excise precisely the anatomical and organs sections outlined by the markers. Thus for these reasons, we opted alternatively for an ex vivo imaging approach in order to minimize any systematic errors between MRI and CA due to variations in the samples. We did however confidently perform image segmentation and fat mass computations of the whole kidneys (n = 8, one pair from each animal) from the in vivo MRI data. We obtained a weaker correlation coefficient of 0.57 in comparison to the ex vivo kidney results in Table 2. The slope and the intercept were 0.87 and 0.31 grams, respectively. The Bland-Altman plot produced a correlation coefficient of 0.04, a slope of 0.16, and an intercept of 0.97 grams. The difference between MRI and CA fat mass was −0.29 ± 1.21 grams. We also attempted to segment the liver from the in vivo data and perform similar fat mass calculations. However, we faced significant image artifacts from respiratory motion due to the lack of automated ventilation equipment that was MRI-compatible. We were unable to manually suspend breathing for an adequate (> 10 sec) period of time in order to obtain a reasonable acquisition encompassing the whole liver. While the liver was recognizable in the resultant images, the computed fat fractions were evidently incorrect due to propagation of subcutaneous and visceral adipose tissue signals into the organ. We believe that many of these motion-related challenges can be easily minimized when translating to in vivo human scans and that human data obtained using this MRI approach will be accurate.

We also recognized that another limitation was that the animals and subsequent ex vivo samples were only scanned by MRI once and thus no metric of reproducibility was assessed in the current work. Likewise, a repeat measurement from CA was also not performed. A test of reproducibility is certainly warranted, and perhaps even a comparison across different MRI platforms and magnetic field strengths of the proposed fat mass approach are directions of future work.

A third limitation of this work was that we did not make an attempt to account for either the MRI-invisible component parameter k or the 1.02 coefficient in the proposed signal model and subsequent computations. Our calculations of absolute fat mass were derived directly from measurements of PDFF. While a correction factor for the 1.02 coefficient can certainly be applied, it must be recognized and cautioned that this is simply a nominal value that was derived from literature reports of average molecular properties and should not be treated as a universal truth. Even if it could be properly accounted for, one must still grapple with the influence of k on the apparent PDFF. It is difficult to assume values of k for different tissues and organs, as very little information regarding the proportion of free water in vivo has been reported in a large array of samples. In the liver, it has been suggested that m_O is 30% of m_w, such that k = 0.77 [60]. Furthermore, in a homogeneous sample, a single global value of k can be reasonably assumed. However, in a heterogeneous sample, k may spatially vary and thus become voxel dependent. Although based on the overall pooled results in Figure 6 of this study it did not appear that a correction factor was necessary, the observed data point scatter in some of the samples about the identity line in Figures 4 and 6 can likely be attributed to the lack of such signal compensation for k in this work. Indeed, as suggested in Figure 1, a k value less than 0.9 can lead to significant fat fraction errors. Other potential reasons for some of the data scatter in the four plots of Figure 1 can also be attributed to errors in IDEAL MRI from rapid T₂* relaxation, such as in the spleen, and the possibility that errors may have also occurred from CA, which were performed by independent investigators from those who analyzed the MRI data.

In conclusion, the ability to accurately estimate absolute fat mass with MRI in lipid-rich adipose tissue as well as in heterogeneous organs and muscles has been demonstrated and validated. The method allows for the computation of absolute fat mass in any arbitrary specimen, as a PDFF map, along with a voxel-wise fat mass map, can be computed and visualized. The further validation and application of the proposed approach in vivo in whole-animals and humans remains an opportunity for future investigation. Based on the author’s current experience, it is suggested that additional whole-animal validation studies be performed in smaller mammals as the pigs used in this study were too large and impractical for full chemical assay as a single specimen. Future work directions can include a rigorous test of reproducibility of the proposed approach in measuring fat mass, a more systematic approach to predict and compensate for the parameter k, comparison studies of the approach on different MRI platforms, and the technique’s ability to non-invasively track longitudinal changes in fat mass during therapeutic intervention. Nonetheless, MRI remains relatively an untapped resource in body composition and obesity research. With rapid and accurate fat quantification methods, MRI represents the most promising “one-stop-shop” modality for non-invasive measurement of localized organ, muscle, and ectopic as well as total body fat distributions.