Models provide specificity: Testing a proposed mechanism of visual working memory capacity development

Abstract

Numerous studies have established that visual working memory has a limited capacity, and that capacity increases during childhood. However, debate continues over the source of capacity limits and its developmental increase. Simmering (2008) adapted a computational model of spatial cognitive development, the Dynamic Field Theory, to explain not only the source of capacity limitations but also the developmental mechanism. According to the model, capacity is limited by the balance between excitation and inhibition that maintains multiple neural representations simultaneously. Moreover, development is implemented according to the Spatial Precision Hypothesis, which proposes that excitatory and inhibitory connections strengthen throughout early childhood. Critically, these changes in connectivity result in increasing precision and stability of neural representations over development. Here we test this developmental mechanism by probing children’s memory in a single-item change detection task. Results confirmed the model’s predictions, providing further support for this account of visual working memory capacity development.

Visual working memory (VWM) provides a critical foundation for our understanding of the visual world around us. Without the ability to represent visual information as we move our eyes around the world, our experience would be a series of disjointed snapshots. Decades of research on VWM have revealed its severely limited capacity, just 3 to 5 simple items in young adults (Cowan, 2010). Capacity is typically estimated using the change detection task, in which a set of items is presented briefly, disappears for a short delay, then reappears with either the same items or one changed item (e.g., Luck & Vogel, 1997). Capacity estimated from change detection performance are often derived with the formula proposed by Pashler (1988; see also Cowan, 2001; Rouder, Morey, Morey, & Cowan, 2011).

Countless studies have demonstrated this limit in adults (see, e.g., Cowan, 2001, for review), and recent work has shown how VWM capacity increases early in development (e.g., Cowan et al., 2005; Riggs, McTaggart, Simpson, & Freeman, 2006; Ross-Sheehy, Oakes, & Luck, 2003). Despite how well-established capacity limits are empirically, there remains an active debate over the source of such limits (see Fukuda, Awh, & Vogel, 2010, for review) and the source of developmental change (see Simmering & Perone, 2011, for review). Studies have shown support for both discrete “slot” models (e.g., Zhang & Luck, 2008) and flexible resource models (e.g., Bays & Husain, 2008) as potential explanations for adults’ decline of performance as the number of items increases in VWM tasks. According to “slot” models, capacity is limited to a small number of items, regardless of those items’ complexity or resolution. Resource models, on the other hand, propose that capacity should be conceptualized as a pool of resources that may be divided among any number of items, with the resolution of memory for the items varying inversely to the number of items. One limitation of these models is that neither has explicitly addressed the developmental source of capacity limitations; most developmental studies have been derived from slot-like theoretical perspectives, but no established computational model has been tested developmentally.

Simmering (2008) sought to address not only the debate between slot and resource models in the adult literature but also the developmental mechanism underlying VWM capacity increases. To this end, Simmering adapted the Dynamic Field Theory (DFT), a model of spatial cognition and development (see e.g., Spencer, Simmering, Schutte, & Schöner, 2007), to capture capacity limits from change detection in a neurally-grounded computational model. The core architecture of the model (described further in Section 2 below) consists of three layers of neurons tuned along a continuous color dimension. Items are represented as localized “peaks” of activation in excitatory layers, which are supported through the local excitatory and lateral inhibitory connections within and between layers. Building on related work in spatial cognitive development, Simmering (2008) demonstrated that the model could capture change detection performance and capacity limits through early childhood into adulthood through an established neuro-developmental mechanism, the Spatial Precision Hypothesis (SPH; first proposed by Schutte, Spencer, & Schöner, 2003).

A primary advantage of using computational models to explain behavior is the ability to generate and test novel predictions. The goal of the current paper is to extend Simmering’s (2008) work in change detection to test the model’s account for developmental changes in VWM. This direction of study serves two purposes. First, it provides a test of predictions derived from the mechanism proposed to underlie developmental changes in VWM capacity. Second, it tests this developmental mechanism more generally, as a similar proposal has been shown to capture numerous other developmental phenomena in spatial cognition (e.g., Ortmann & Schutte, 2010; Perone, Simmering, & Spencer, 2011; Simmering, Schutte, & Spencer, 2008).

In the sections that follow, we outline Simmering’s primary empirical findings and the candidate explanation in the literature. Next, we briefly describe how the model captured improvements in change detection performance through early childhood. Then, we discuss the implications of the DFT and the SPH and use the model to generate novel predictions for a single-item change detection task. We have developed a new task to test how memory representations change during early childhood to adulthood in two experiments. Finally, we conclude by considering new questions raised by our results, how the DFT may address these in the future, and the implications for our understanding of developmental processes in general.

1. Developmental Increases in Capacity

Decades of research have established that working memory capacity is limited, and that capacity increases during early childhood. Across domains (verbal and visual) and task contexts, however, there is wide variability in the specific trajectories of developmental change, including the age at which performance reaches adult-like levels (Simmering & Perone, 2011). In an effort to arrive at more reliable estimates of capacity, research on VWM capacity in adults relies primarily on the change detection paradigm. This task has been applied over a relatively large span of development. Cowan and colleagues (2005) tested children as young as 7 years and found capacity to increase from approximately 3.5 items at this age to 5.7 items for college students. Riggs et al. (2006) expanded on these results by testing 5-, 7-, and 10-year-olds, and found that capacity increased from about 1.5 to 3.8 items during this period of development. Furthermore, Simmering (2008) showed that modifying the change detection task to be more appropriate for younger children allowed children as young as 3 years to successfully complete the task without inflating capacity estimates for older children and adults (see also Simmering, in press). Results of this modified version estimated that capacity increased from 2 to 3 items between 3 and 5 years of age.¹

Both Cowan et al. (2005) and Riggs et al. (2006) discussed whether developmental improvements in children’s performance could be attributed to cognitive processes other than capacity, but provide compelling arguments for why capacity increases are the most likely source of developmental change. However, neither provides a specific proposal for how or why capacity changes during childhood. Other researchers have put forth proposals, based on performance in a variety of working memory tasks, that focused on improvements in the functioning of existing memory systems (e.g., Gathercole, Pickering, Ambridge, & Wearing, 2004), cognitive control (e.g., Marcovitch, Boseovski, Knapp, & Kane, 2010), basic processes of object individuation/identification (e.g., Oakes, Messenger, Ross-Sheehy, & Luck, 2009), or neural connectivity (e.g., myelination; Case, 1995). Although each of these approaches has benefitted our understanding of children’s performance in a given task, none has provided a complete account of the processes underlying performance and developmental change. For example, Case (1995) proposed that myelination allows for more efficient neural processing of information, but did not specify how this results in increased capacity over development: in the context of the change detection task, would improved myelination allow more items to be encoded into memory, more items to be maintained simultaneously, memory representations to persist longer or more accurately, more accurate comparison and decision, or some combination of these changes? As with many theories of cognitive processes, it is unclear precisely how a given proposal translates to the behavior measured in laboratory tasks.

One strategy to eliminate this uncertainty is to encourage theorists to build computational models embodying their proposed cognitive and developmental processes. Models can provide a of level of specificity beyond many verbal theories in that, in order to test them, assumptions regarding how various processes contribute to behavior must be made explicit. This is not to say that all models are necessarily more specific and complete than all verbal theories (see Simmering, Triesch, Deàk, & Spencer, 2010, for discussion); however, formal models often force theorists to a deeper level of explanation than their own verbal theories may incorporate. The DFT model proposed by Simmering (2008) provides an example of such specificity. In Section 2, we describe how the DFT specifies each of the cognitive processes involved in the change detection task—encoding, maintenance, comparison, and decision—and how the SPH implements a developmental change that can capture the pattern of performance through early childhood.

2. Modeling Change Detection Performance over Development

The three-layer architecture of the DFT, shown in Figure 1, was developed to account for performance across a number of spatial memory tasks (Spencer et al., 2007), and was recently extended to capture some characteristics of change detection performance (e.g., Johnson, Spencer, & Schöner, 2009). This type of model architecture, dynamic neural fields, was first developed by Amari (1977) to capture the neural dynamics of visual cortex. In the early 1990s, Schöner and colleagues generalized this style of model to propose a theory of the neural basis of planning eye movements (Kopecz, Engels, & Schöner, 1993), and have since sought to capture a variety of other cognitive behaviors. These models operate at the level of population dynamics, building from work by Georgopoulos and colleagues (Georgopoulos, Kettner, & Schwartz, 1988; Georgopoulos, Taira, & Lukashin, 1993) that linked activation of neurons in motor cortex with movement in pointing tasks. Thus, this style of model is historically grounded in neural principles, although the types of extensions described here have been largely theoretical, and only recently tied to measures of neural activity in humans (e.g, Spencer, Buss, Austin, & Fox, 2011; cf. Edin, Macoveanu, Olesen, Tegnér, & Klingberg, 2007).

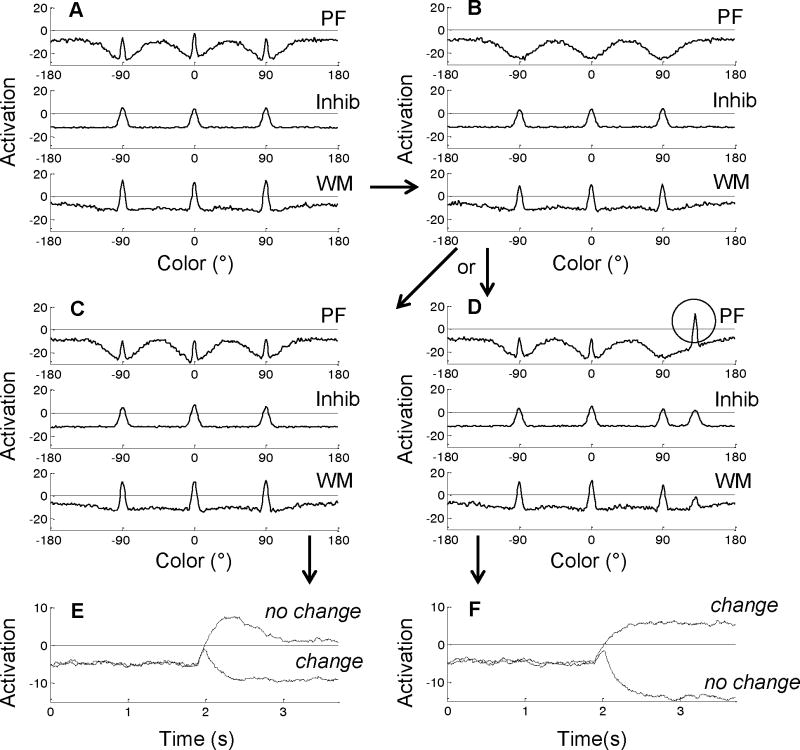
Figure 1.

The Dynamic Field Theory architecture as applied to the change detection task. The model includes a perceptual field (PF), inhibitory layer (Inhib), and working memory layer (WM). Arrows indicate excitatory (green) and inhibitory (red) projections between layers. In each layer, time is shown along the horizontal axis, activation along the vertical axis, and color along the diagonal axis. Responses are generated by two self-excitatory, mutually-inhibitory nodes: one for “change” decisions (CH) receives summed activation from PF; one for “no change” decisions (NC) receives summed activation from WM.

Simmering (2008) built on these previous instantiations to test whether the DFT could provide a source of capacity limits in VWM (see also Johnson, Simmering, Buss, & Spencer, 2011). Figure 1 shows the model performing a change detection trial (shown in more detail in Figure 2). The three layers of the model contribute different cognitive functions to the task. The first excitatory layer, the Perceptual Field (PF), serves as an encoding field: inputs are presented to the model as Gaussian distributions of activation centered at the relevant color values (e.g., red, blue, and green, along a color dimension in Figure 1).² When these inputs are “on” (i.e., projecting activation into PF; not shown in Figure 1) localized peaks of activation form in PF; when the inputs turn “off” (i.e., the visual items disappear from the display, no activation is projected), the neurons in PF quickly return to their resting level. In this way, neurons in PF are tuned to respond only when visual stimuli are present in the array.

Figure 2.

Time slices through the three layers of the model at critical points in two trials: (A) encoding, at the end of memory array presentation; (B) maintenance, at the end of delay; comparison at the time just before a response is generated for (C) no-change test array and (D) change test array. Also shown is activation of the decision nodes following the (E) no-change and (F) change test arrays. Arrows indicate progression through the trial(s). Dashed lines in each panel indicated the activation threshold (i.e., 0).

The second excitatory layer of the DFT, the Working Memory field (WM), also receives weak input from the environment and strong input from PF. Thus, when visual stimuli are presented in the array, the peaks in PF and direct input to WM combine to form localized peaks in WM. Once peaks are established in WM, the items from the array have been encoded into memory. Although both PF and WM are excitatory layers, the excitatory connections within WM are tuned to be stronger than in PF. This allows WM to serve a maintenance function: when inputs are removed, the peaks in WM enter a self-sustaining state and are maintained in the absence of input, unlike activation in PF. Critically, this maintenance depends not only on self-excitation within WM but also on projections from the third layer in the model, the Inhibitory field (Inhib). As the arrows in Figure 1 show, Inhib projects inhibition back into both PF and WM. It is the balance between excitation within PF and WM and the inhibition coming from Inhib that allows the excitatory layers to serve different cognitive functions (i.e., encoding versus maintenance).

As items are maintained in WM during the delay, the shared connectivity with Inhib produces inhibitory troughs in PF at the remembered values (dark blue regions in PF in Figure 1). These troughs support a comparison function between the items held in WM and new items presented to PF (described further below). In the change detection task, this comparison serves as the basis of the required same or different response; in the model, this is implemented through the addition of a simple responses system coupled to the three-layer architecture. This system is comprised of two nodes, one indicating a same response receives projections from WM, and one indicating a different response receives projections from PF. When the test array is presented, this signals to the model that a response is required; we implement this by gating activation to project from PF and WM to the response system and raising the resting level of the nodes to near threshold (i.e, 0). Activation to the response nodes builds in parallel, each with its own self-excitation, and competing through mutual inhibition such that only one can “win” and generate the response for that trial. This response system allows the three-layer architecture to perform the change detection task.

Figure 2 illustrates the model’s performance further with time-slices through all three layers at critical points during the trial. Figure 2A shows the end of the memory array presentation, once the items have been encoded; note that the three peaks in WM area are already inhibiting peaks corresponding to the same colors in PF (via Inhib). Throughout the delay (Figure 2B), the peaks in WM sustain, leading to continued inhibition of the corresponding areas in PF. Functionally, this allows the model to recognize an item as familiar (falling within a trough) or novel (falling outside of a trough) at test. When the test array is presented in the task, if the items are all the same, the new inputs are projected into the troughs in PF and activation does not pierce threshold (Figure 2C). If one item has changed, however, this input falls into a relatively un-inhibited region of PF and forms a new localized peak (see circle in Figure 2D), indicating that a new item has been detected. This serves as the comparison process within the model: if an item is new (a change trial), a peak will form in PF; if all items are old (a no-change trial), no activation will pierce threshold in PF. The result of this comparison process then drives a decision after the test array has appeared. In Figure 2C, the peaks in WM activate the same node (Figure 2E), while in Figure 2D, the peak in PF activates the different node (Figure 2F). The projections to these nodes are tuned such that a single peak in PF (i.e., any new item) will generate a different decision, regardless of the number of items being maintained in WM.

This architecture was shown to predict counter-intuitive effects of item similarity in change detection (Johnson, Spencer, Luck, & Schöner, 2009) and provided a quantitative fit of adults’ performance in a change detection task including array sizes from one to six items (Johnson et al., 2011). The mechanism capturing capacity in this architecture comes not only from the number of peaks that can be maintained simultaneously in WM, but also the comparison and decision processes. The number of peaks is limited by the neural interaction function, that is, the balance between local excitation and lateral inhibition in WM. As more items are encoded in WM, the overall amount of both excitation and inhibition increases. At some point, a critical threshold is reached where the excitation associated with an additional item is not sufficient to overcome the additional inhibition produced, and another peak cannot sustain through the delay. Although the number of peaks that are maintained on any given trial is influenced by details of the stimuli (e.g., “distance” in color space between peaks, timing of presentation; see Johnson et al., 2011, for discussion) and stochastic fluctuations due to noise, the parameters from Simmering have an upper limit of approximately six peaks. Interestingly, even trials on which six peaks are maintained, this does not ensure perfect performance; the processes of comparison and decision generation in the model produce errors that follow adults’ performance (see Simmering, 2008; Johnson et al., 2011, for further discussion).

Having established that the DFT can capture adults’ capacity limits through constraints on neural interactions and the cognitive processes contributing to behavior, Simmering (2008) next turned to the question of developmental change. As discussed above, one advantage of computational models is specificity of processes involved in a given laboratory task. Because the processes operating within the DFT to produce behavior are well-specified, there are a limited number of possible mechanisms to account for developmental increases in capacity. Previous work in spatial cognitive development established the SPH to account for development of children’s spatial recall biases (e.g., Schutte & Spencer, 2009), position discrimination performance (Simmering & Spencer, 2008), interactions between spatial working memory and long-term memory (Schutte et al., 2003), and perception of symmetry axes (Ortmann & Schutte, 2010). According to this hypothesis, neural interactions within and between layers in the model become stronger over development, purportedly through Hebbian learning and/or synaptogenesis (discussed further in Section 6; see also, e.g., Spencer et al., 2007).

In the DFT, the emergent consequence of strengthening local excitation and lateral inhibition is that neural representations (i.e., peaks) increase in strength, precision, and stability over development. Note that these changes in connectivity influence performance in real time (i.e., on a trial-by-trial basis), but the full consequences emerge over repeated instances or trials. Specifically, the precision of peaks refers to how closely they are centered on the presented value, which varies across trials: a given peak may be accurately located on one trial for the “child” model, but across repetitions, the overall precision will be lower than for the “adult” model. This also highlights the importance of stability at different timescales: not only is an individual peak more susceptible to perturbation on an individual trial, but the variation in peak position and strength also varies considerably across trials early in development. Given the successful application to developmental changes in spatial cognition during early childhood (Ortmann & Schutte, 2010; Schutte & Spencer, 2009, 2010; Schutte et al., 2003; Simmering et al., 2008; Simmering & Spencer, 2008) and recent extensions to developmental changes in infant looking behavior (Perone et al., 2011; Perone & Spencer, 2011; Perone, Spencer, & Schöner, 2007), Simmering (2008) tested whether the SPH could also account for developmental increases in capacity.

Quantitative simulations showed that the DFT could produce the same pattern of performance as 3-, 4-, and 5-year-old children and adults through changing a subset of the model’s parameters according to the SPH (Simmering, 2008). In particular, the “child” parameters were tuned such that local excitation (within PF and WM) and lateral inhibition (from Inhib to PF and WM) were weaker, simulating less-established connectivity within and between brain areas. Additionally, direct inputs to PF and WM were weaker and broader to approximate less precise projection from early visual areas. Noise within each layer was also stronger in early development, as would be the case with poorer myelination. These changes within the fields produce peaks that are weaker, broader, and less stable early in development (see Simmering, 2008, for complete details). Direct neural evidence for these types of developmental changes is currently incomplete; only recently has technology allowed for the type of examination needed to ask these questions. General evidence for the developmental trajectory of changes in prefrontal cortex (e.g., synaptic density, Huttenlocher, 1979; myelination, Sampaio & Truwit, 2001) is qualitatively consistent with the changes embodied by the SPH. More recently, an architecture similar to the DFT was used to predict developmental changes in BOLD signals based on increasing excitatory and inhibitory connections (Edin et al., 2007).

To quantitatively fit the behavioral data from children in the change detection task, Simmering (2008) also modified the parameters in the decision system to reflect the types of errors children made. Similar to changes made in the three-layer architecture, the self-excitation and mutual inhibition of the decision nodes were weaker for the “child” parameters. In addition, the projection from WM to the same node was weaker for the child parameters, reflecting children’s tendency to respond “different” more often in the change detection task. Essentially, this made the child model more sensitive to novelty or more input-driven (relative to the “adult” model). The consequences of these changes are illustrated in Figure 3, which shows change detection performance with parameters modified according to the SPH to capture 3-year-olds’ performance. These trials demonstrate some of the ways in which errors arise in the model.

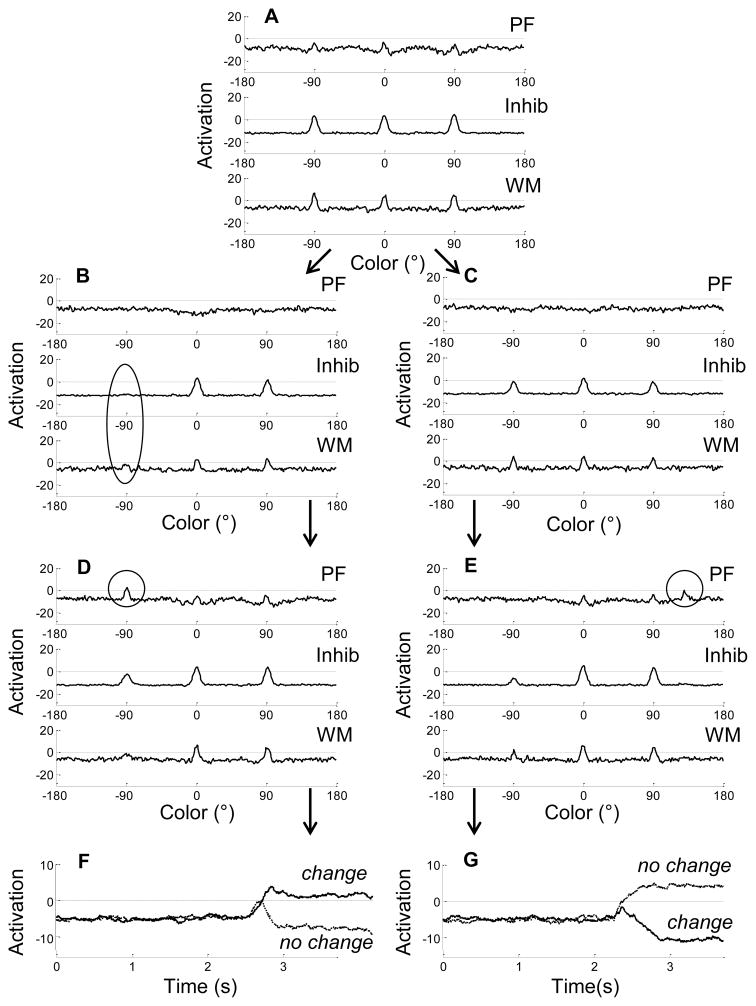
Figure 3.

Time slices through the three layers of the model at critical points in two trials, using parameters tuned to capture 3-year-olds performance: (A) encoding; maintenance during (B) no-change and (C) change trials; comparison for (D) no-change test array and (E) change test array. Also shown is activation of the decision nodes following the (F) no-change and (G) change test arrays. Note that the model made errors on both trials. Arrows indicate progression through the trial(s). Dashed lines in each panel indicated the activation threshold (i.e., 0).

The panels in Figure 3 follow the same general progression as in Figure 2, with an additional delay panel (3C) showing how maintenance of the WM peaks differed across trials. As Figure 3A shows, the first notable difference in performance with the child parameters is the nature of peaks in WM: with the weaker interactions, the child model encodes items much more tenuously. Peaks are weak and unstable. Indeed, by the end of the delay on the no-change trial (Figure 3B), activation of one peak in WM has dropped below threshold, leading to the loss of the corresponding inhibition (see circled region of Inhib and WM). By comparison, this item is held in memory during the delay on the change trial (Figure 3C). Note that the difference between these two sample trials is due to fluctuations in noise, as the input has not yet differentiated the trial type. Thus, the loss of a peak is just as likely to occur on a change trial as on a no-change trial.

The weak peaks in WM formed shallow, broad troughs in PF at the corresponding values on both trials (see Figures 3B–E). When a no-change test array is presented, the inputs reinforce the two peaks that remain in WM (Figure 3D), but the “forgotten” item is identified as new (see circle in PF) which produces an inaccurate different decision (Figure 3F). This is a common source of false alarm errors in the model (see also Johnson et al., 2011). By contrast, on the change trial, the model has maintained all three items in WM (Figure 3C). At comparison (Figure 3E), one item has changed, resulting in no input at −90° and a new input at 120°. Although this new input causes activation in PF to increase, weaker interactions with these parameters are not strong enough to push activation above threshold (see circle in PF). Thus, no activation is projected to the change node, and the model produces an inaccurate same decision (Figure 3G).

Although the sample trials in Figure 3 show the child parameters in the DFT performing inaccurately, the model does still perform accurately on the majority of trials with these parameter settings. Overall, the model makes more errors with the child parameters than with the adult parameters, capturing children’s poorer performance and, by extension, lower capacity estimates (Simmering, 2008). As with the adult simulations described above, errors in the child model come from a combination of sources. First, as shown in Figure 3, the weaker interactions in WM lead the child model to fail to encode and/or maintain items much more often than the adult model, reflecting its lower capacity. Second, even in cases when peaks sustain in WM, the inhibition projected back to PF via Inhib is rather weak, leading to only small troughs at the corresponding values. This, combined with the increased noise in the child parameters, causes the comparison process to be more prone to errors. In some cases, items that have not changed will pierce threshold in PF (due to weak inhibition); in other cases, items that have changed will fail to pierce threshold in PF (due to weak excitation, as in Figure 3). Third, maintenance of peak position in the child model is not as veridical (relative to input) as in the adult model, introducing further noise into the comparison process. Fourth, the weaker interactions within the decision system lead the child model to make more errors, even in cases where the comparison process was correct. Relatively weak inhibition between the decision nodes, coupled with higher noise in the child system, leads to more erroneous responses. Thus, the developmental simulations from Simmering (2008) illustrate that errors occur within all of the processes involved in change detection performance, and suggest that developmental changes in capacity can be captured through strengthening neural interactions within the VWM system.

3. Novel Predictions Derived from the Model

Although the simulations from Simmering (2008) provide a compelling account of developmental changes in VWM capacity in the change detection task, a critical part of theory and model development is to generate new predictions from previous successful accounts. Thus, the goal of the current paper is to build from Simmering’s work to generate new predictions that can be tested to evaluate the DFT and SPH in this domain. As Figure 3 illustrated, scaling parameters according to the SPH leads to differences in how the model is able to perform the encoding, maintenance, comparison, and decision processes involved in the change detection task. Here we chose to explore children’s performance further by developing a new task that will more directly measure the nature of children’s individual memory representations. To this end, we designed a single-item change detection task that tests very small changes in color to assess the stability and precision of children’s memory. Specifically, we predicted that young children’s performance will reveal less precision and stability for colors early in development.

This prediction arises from the processes illustrated in Figures 2 and 3. In particular, weaker interactions in the child parameters have two specific consequences for detecting small changes of a single item. First, the weaker encoding and maintenance of the item means that peaks will less precise, that is, more likely to be centered on a different value than the actual target on each trial (cf. Simmering & Spencer, 2008, for similar developmental changes in a spatial task). A second, related, consequence is lower stability in the color value across trials. Across repeated trials with the same target value, the child parameters will show more variability in the location of the peak than the adult model. Thus, measuring the model’s performance in detecting changes in that color value should show less accuracy and more variability across repeated trials.

We first tested this prediction in the model by using the parameters Simmering (2008) developed to capture performance by 3-year-olds, 5-year-olds, and adults and testing the model in a single-item change detection task with small separations between items.³ Specifically, we presented a target color at 0° followed by a second stimulus that either matched exactly (0°) or changed incrementally across different values for the test stimulus.⁴ We simulated 40 trials at each separation for each parameter setting (i.e., “age”) and tabulated the percent of trials at each separation on which the model responded same versus different.

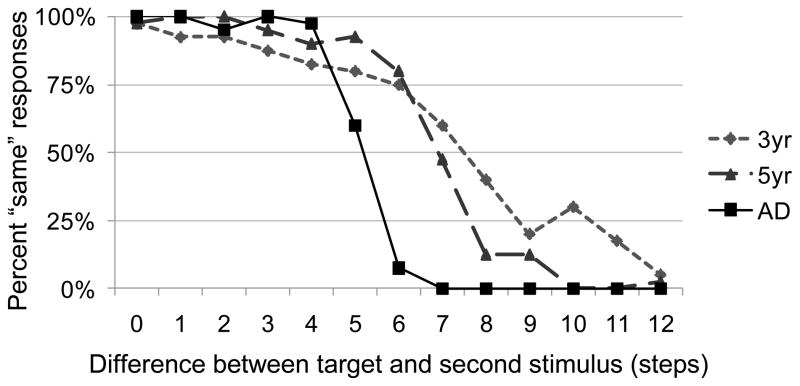
Figure 4 shows our simulation results, demonstrating the developmental effects of changes in the precision and stability of peaks in the model. With the adult parameters (solid line), performance begins with 100% same responses for the matching items and small stimulus separations. As the items become less similar (i.e., increasing steps), the number of same responses drops dramatically. For the child parameters (dashed and dotted dashed lines), however, this is not the case. First, there are fewer same responses when the items are identical or very similar, especially for the 3-year-old parameters, and the number of same responses drops off more gradually. For the adult model, the transition from nearly all same to nearly all different responses happens within only a few steps. For the child model, however, this transition takes much longer, with the 3-year-old parameters only settling near 0% same responses 6 steps further than the adult parameters.

Figure 4.

Model performance with 3-year-old, 5-year-old, and adult parameter settings in the single-item change detection task across incrementally larger changes between items.

To quantify performance of the model with different developmental parameters, we fit a probit function to each of the lines in Figure 4 and estimated the distance (in steps) between items necessary for the model to produce different responses 75% of the time (following Simmering, Spencer, & Schöner, 2006). These estimates were approximately 7.6 steps for the adult parameters, 8.9 steps for the 5-year-old parameters, and 10.3 for the 3-year-old parameters. Moreover, we looked at variability in the estimates across repeated runs of the model as an indication of changes in stability in the model. For the 3-year-old parameters, the standard deviation across 10 runs of the model was 0.76 steps, whereas it was 0.37 steps for the 5-year-old parameters, and 0.23 for the adult parameters. Although these changes in variability are relatively small, it is important to note that this effect in the model only arises through white noise within the layers and response nodes of the model; presumably, participants in our task will have additional sources of variance contributing to performance.

As these estimates suggest, performance should improve through early childhood and into adulthood, both in terms of the ability to discriminate colors in memory, and the reliability of participants’ discrimination across repetitions of the same pairs of stimuli. Here we test the prediction that performance in a single-item change detection task will improve as memory representations become more precise (requiring smaller differences between colors to respond “different”) and more stable (with more consistency in responding over repetitions of the same stimulus separations) over development.

An important question to consider here is whether this model, or any model, is necessary to generate this prediction. After all, predicting developmental improvements in memory tasks is certainly not unique to the DFT and SPH. The model here goes one step further than many theories in predicting generalization from one type of measure (capacity) to a second (precision). A similar generalization has been shown based on Case’s hypothesis (1995; described in Section 1), in that developmental improvements in children’s speed of processing should be evident in tasks that do not measure capacity directly, and that speed of processing should correlate with performance in span tasks. Although our model seems to accomplish the same goal as Case’s theory within visual working memory research, we have the added benefit of connecting to research across a wide variety of domains using similar architectures and developmental mechanisms (e.g., Ortmann & Schutte, 2010; Perone et al., 2011; Simmering et al., 2008). Moreover, implementation of this theory in a formal model allows for exploring hypotheses within the model before testing them experimentally; the advantages of this capability are described our later discussion of how the model can address unexpected findings in our behavioral task (see Section 6).

To test our predictions of improved precision and stability in VWM over development, we developed our color memory task from the position discrimination task used by Simmering and Spencer (2008). In their paper, they used the DFT and SPH to predict how children’s ability to discriminate nearby positions (separated by a short delay) would change between 3 and 6 years. The model predicted not only that discrimination would improve during early childhood, but also how performance depended on the distance of targets from the midline symmetry axis of the task space and the direction in which changes were probed. The task employed a stair-casing procedure in which stimuli were presented first at a large separation; when children correctly responded that the positions were different, the next trial would test a smaller separation, continuing in this fashion until the child responded “same”. This method was repeated across four runs to each of two targets to yield estimates of children’s position discrimination thresholds.

We adapted this task to measure children’s memory for colors by using a similar staircasing procedure to test small changes in color (much smaller than the changes probed in typical change detection tasks), with increasing differences between colors over trials. This task design can also assess the stability of memory representations through the standard deviation across repeated trials within subjects (described further below in Sections 4.1.3 and 4.2). Because similar predictions have been tested and confirmed in spatial working memory (Simmering & Spencer, 2008), results from the current experiment will not only test Simmering’s (2008) account of capacity development, but can also speak to the generality of the developmental mechanism proposed with the SPH.

4. Experiment 1

In our first experiment, we used the method of ascending limits to test participants’ discrimination thresholds. On each trial, participants viewed two colored mittens presented sequentially with a short delay; the “distance” between the mittens in color space (approximated in degrees) increased across trials. We predicted that the difference between colors necessary to elicit reliable “different” responses would decrease over development, reflecting an increase in precision of participants’ memory for colors. Additionally, we tested participants on multiple runs to each of two targets, to assess how variable their responses were across repeated trials. We predicted that cross-run variability would also decrease over development as memory representations become more stable.

4.1. Method

4.1.1. Participants

Participants included 42 four-year-olds (M age = 4.55 yr., SD = 0.21, 26 females, 16 males), 33 five-year-olds (M age = 5.40 yr., SD = 0.20, 13 females, 20 males), 33 six-year-olds (M age = 6.25 yr., SD = 0.21, 22 females, 11 males), and 23 adults (M age = 21.16 yr., SD = 1.55, 18 females, 5 males).⁵ All had normal or corrected-to-normal visual acuity and reported no colorblindness. An additional 9 children participated but were excluded from analyses due to experimenter error (2 six-year-olds), because they chose to end early (6 four-year-olds), or because they did not understand the task (1 six-year-old). We also excluded an additional 16 children (8 four-year-olds, 4 five-year-olds, and 4 six-year-olds) because their responses suggested our stair-casing procedure could not accurately measure their memory for the items (discussed in Section 4.1.3 below). Lastly, 5 additional four-year-olds participated but were excluded from our analyses as outliers; we identified outliers by examining histograms of each age group’s performance (after removing the children listed above). These histograms showed thresholds greater than 56° (i.e., 7 steps) to be outside the normal distribution, leading us to exclude children with one or both thresholds beyond this criterion. Because these exclusions work against our hypotheses (as we excluded young children with high thresholds), we felt excluding these data to be the more conservative approach.

Children were either recruited from the Madison community and tested in the laboratory (27 four-year-olds, 19 five-year-olds, all 6-year-olds) or through area preschools and tested in a designated area within the preschool (15 four-year-olds, 14 five-year-olds). Adults were University of Wisconsin-Madison students and/or staff who were recruited through undergraduate courses or word of mouth and were tested in a laboratory on campus. Informed consent was obtained from adult participants and from parents of child participants before participation began.

4.1.2. Apparatus

All children completed the task on a 15.4″ widescreen Dell Latitude E6500 laptop computer; adult participants were tested on either this laptop (n = 8) or a 21″ LCD monitor on a Dell Optiplex 760 desktop computer (n = 15; note that stimuli were scaled to appear the same size on both displays).⁶ Participants sat approximately 2′ from the display during the task. Stimulus presentation was controlled by Matlab using the Psychophysics Toolbox extension (version 3, Kleiner, Brainard, & Pelli, 2007; see also Brainard, 1997; Pelli, 1997). On each trial, the computer displayed a gray background (RGB = 200, 200, 200) for 500 ms, followed by a left mitten for 1 s, a blank gray screen for a 500 ms delay, a right mitten for 1 s, and finally a gray screen with the prompt “Enter your response (same/different)” that remained visible until a response was entered. At the prompt, participants identified whether the mittens’ colors were “same” or “different”: children responded verbally, often using terms “match” and “no match”, which are more familiar terms in this age range; adults entered their responses on a numeric keypad. Mittens appeared as 2.5″ wide × 3″ tall rectangles with a white background and black outline; the interior colors of the mitten stimuli were determined according to an ascending stair-casing procedure (described in Section 4.1.3 below). Mitten stimuli were centered vertically on the screen and presented on the left half of the screen for trials to Target 1 and the right half of the screen for trials to Target 2. One each trial, the first mitten appeared in the left position and the second appeared on the right position (within the respective half of the monitor).

4.1.3. Procedure

Trials were presented in eight runs alternating between two target colors. The two colors that served as targets were 70° (teal, RGB = 49, 138, 138) and 290° (pink, RGB = 233, 72, 140); these colors were selected to be far from category boundaries based on a separate group of adults’ (n = 12) categorization of the 360° color space used by Johnson and colleagues (2009; see online supplementary materials for images of colors and all corresponding RGB values). We developed a stair-casing procedure (following Abrimov et al., 1984; Simmering & Spencer, 2008) to reduce the total number of trials required by children while providing repeated measures (across runs) of responses to the same stimuli.

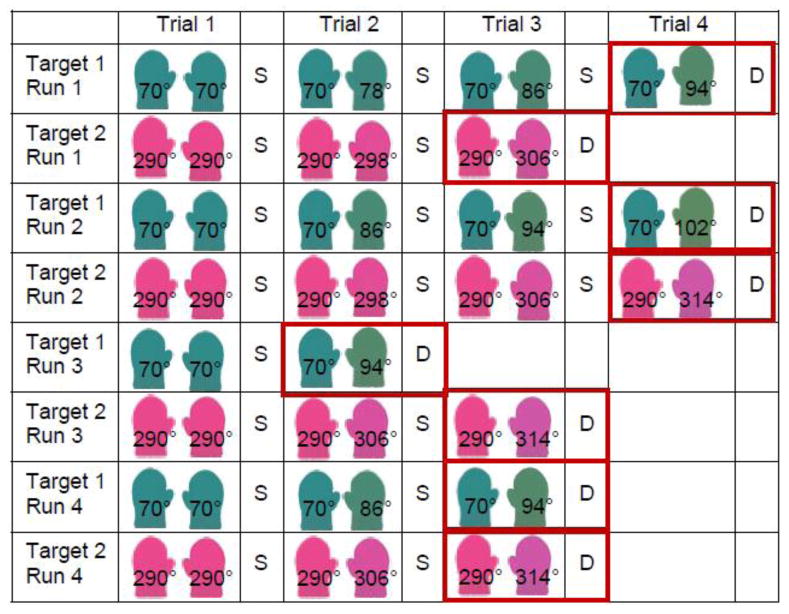
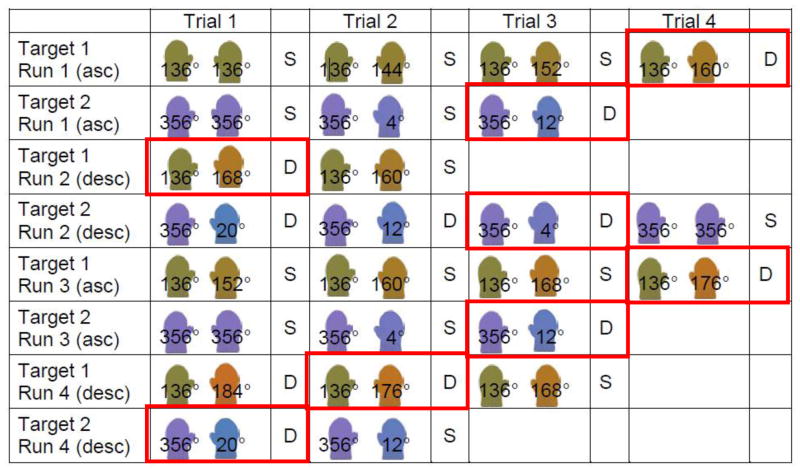
Figure 5 illustrates the stair-casing procedure; note that which color served as Target 1 versus 2 was counter-balanced across participants. Each trial began with the presentation of the Target color as the left mitten. Trial 1 of all runs presented the target color as the right mitten as well (i.e., matching colors; see Figure 5). Here we step through a sample progression of the procedure across runs alternating between the two targets. If the participant responded “same” on Trial 1 of Run 1, Trial 2 presented a one-step different color (i.e., 78° in Figure 5) for the right mitten; we chose a step size of 8° from pilot data. Trials continued in this manner, increasing the separation between the colors by 8° steps on each trial, until the participant responded “different” to terminate the run.

Figure 5.

Example sequence of trials using the ascending stair-casing procedure from Experiment 1 (S=“same”/D=“different” response). Note that degree labels were not present during the task, and the order of target presentation was counter-balanced across participants.

Following the termination of Run 1 to Target 1, Run 1 for Target 2 proceeded in the same manner, beginning with matching mittens and increasing by 8° steps with each “same” response (see Figure 5). After Run 1 for Target 2, the next run returned to Target 1 (Run 2 to this target), again beginning with identical colors for Trial 1 (see Figure 5). For Trial 2 in this run, the right mitten differed from the left by one step less than the color identified as “different” in the previous run (i.e., in Figure 5, Trial 2 of Run 2 for Target 1 presented 86°, or 94° − 8°). Trials and runs continued in this manner, alternating between Targets, until four runs to each target were completed.

As stated above, inspection of the data revealed that this stair-casing procedure was not appropriate to measure thresholds for a subset of the children (the 16 described as excluded in Section 4.1.1). In particular, these were cases in which the child responded “same” for many trials in Run 1, producing a large separation on the final (i.e., “different”) trial. These children then responded “different” on Trial 2 of all subsequent runs to that target, suggesting their true thresholds may be lower than the separations testing in our stair-casing procedure. For example, if Run 1 terminated with a separation of 64°, then Trial 2 of Run 2 (to that target) would test a 56° separation. When the child responded “different”, Run 2 would terminate and Trial 2 of Run 3 would test a 48° separation. When the child responded “different” again, Trial 2 of Run 4 tested a 40° separation. If the child again responded “different” the experiment would terminate without testing smaller separations for that target. It is possible the child in this example situation would have responded “different” at smaller separations, had they been tested on additional runs to that target. We felt that estimates derived from such a pattern could be artificially inflating children’s thresholds, possibly providing false support for our hypothesis; therefore, we chose to exclude them from analysis.⁷ We return to this issue in our design of Experiment 2 (Section 5).

4.2. Results

Performance was analyzed by taking the separation at which the participant responded “different” to end each run⁸ and computing the mean and standard deviation across runs as the participant’s threshold (i.e., difference in color space) and variability (i.e., differences in responses across runs to the same target) scores, respectively. For example, in the series of trials shown in Figure 5, the separations were 24°, 32°, 24°, and 24° for the 70° target, and 16°, 24°, 24°, and 24° for the 290° target; this would produce thresholds of 26° and 22° (means across runs), respectively, and variability scores (standard deviation across runs) of 4° in both cases. Preliminary analyses of gender and testing conditions (preschool versus lab for 4- and 5-year-olds, laptop versus desktop for adults) showed no significant effects. We therefore excluded these factors from further analysis.

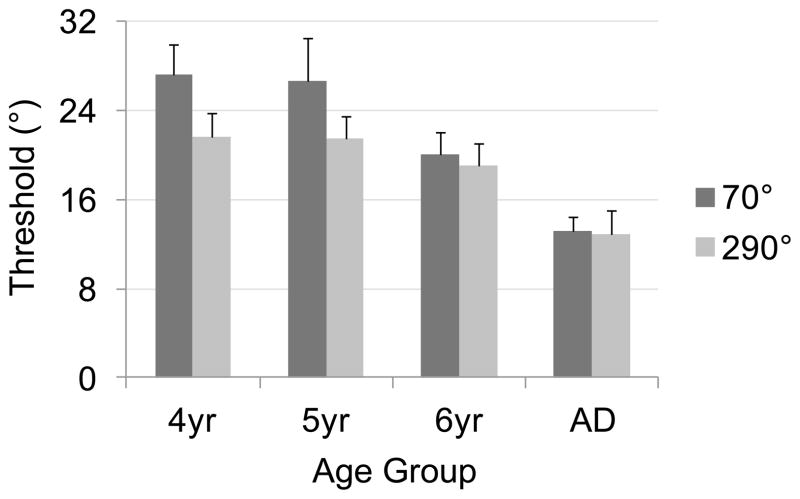
Mean thresholds are shown separately for each target across age groups in Figure 6. As this figure shows, thresholds were generally higher (i.e., worse performance) for children, decreasing over development, as well as higher for the 70° versus 290° target. We analyzed mean thresholds in a two-way ANOVA with Target (70°, 290°) as a within-subjects factor and Age (4, 5, 6, adults) as a between-subjects factor. This analysis revealed significant main effects of Target, F_{1, 127} = 21.11, p < .001, and Age, F_{3, 127} = 21.24, p < .001, as well as a significant Target × Age interaction, F_{3, 127} = 3.46, p < 0.05. As Figure 5 shows, the Target main effect was driven by higher thresholds to the 70° target (M = 22.82°) than the 290° target (M = 19.40°). Follow-up Tukey HSD tests (p < .05) on the Age main effect showed that 4-year-olds (M = 24.41°) did not differ from 5-year-olds (M = 24.08°), but all other differences were significant (6-year-olds M = 19.59°, adults M = 13.00°).

Figure 6.

Mean thresholds across age groups, separated by target, from Experiment 1; note that higher scores indicate poorer performance. Error bars show 95% confidence intervals.

We next explored the source of the Target × Age interaction by conducting separate one-way ANOVAs with Age as a factor for each Target. Both analyses revealed significant improvements over development: for 70°, F_{3, 127} = 17.96, p < .001; for 290°, F_{3, 127} = 10.91, p < .001. Follow-up Tukey HSD tests (p < .05) for the 70° target showed that all age groups differed significantly except 4- and 5-year-olds, mirroring the overall Age main effect. For the 290° target, adults had significantly lower thresholds than all age groups of children, who did not differ significantly from one another. We also conducted separate one-way ANOVAs with Target as a factor for each age group. As Figure 6 suggests, performance only differed across targets for the younger children: 4-year-olds, F_{1, 41} = 13.54, p < .001; 5-year-olds, F_{1, 32} = 8.92, p < .01. In both cases, thresholds were lower for the 290° target than for the 70° target.

Figure 7 presents cross-run variability scores, separated by target and age group. As this figure shows, children showed higher variability, especially for the 70° target, than adults, who had higher variability for the 290° target. We analyzed these scores in a two-way ANOVA with Target (70°, 290°) as a within-subjects factor and Age (4, 5, 6, adults) as a between-subjects factor. This analysis revealed significant main effects of Target, F_{1, 127} = 11.69, p < .001, and Age, F_{3, 127} = 4.31, p < .01. The Target effect was driven by lower cross-run variability to the 290° target (M = 4.51°) than to 70° target (M = 5.87°). Follow-up Tukey HSD tests (p < .05) on the Age main effect showed that 4-year-olds (M = 6.21°) had significantly higher variability across runs than adults (M = 4.01°); no other differences between groups were significant (5-year-olds M = 5.13°; 6-year-olds M = 4.79°).

Figure 7.

Mean cross-run variability scores across age groups, separated by target, from Experiment 1; note that higher scores indicate more variability across runs. Error bars show 95% confidence intervals.

4.3. Discussion

This study tested the proposal put forth by Simmering (2008) that developmental increases in capacity result from strengthening neural interactions. These changes in connectivity improve the stability, strength, and precision of VWM representations over development in the DFT. We tested predictions derived from the model by adapting a single-item change detection task to measure both the precision and stability of VWM representations in 4-, 5-, and 6-year-olds and adults. Results generally supported these predictions. First, as Figure 6 shows, mean thresholds decreased (i.e., precision improved) between 4 and 6 years and again into adulthood. Second, as Figure 7 shows, variability across runs decreased (i.e., stability improved) from childhood to adulthood. These findings support the predictions derived from the DFT and the SPH that precision and stability both increase with development.

One unexpected result we found was the difference in performance and developmental change across targets. The model made no a priori predictions for how performance should compare for different target colors. It is unclear why thresholds did not decrease significantly between 4 and 6 years for the 290° target, and why 4- and 5-year-olds showed significantly better performance to this target than to 70°. Anecdotal reports of children’s performance during the task suggested that 290° may have been a more familiar color; experimenters reported that children were more likely to name “pink”, and that only a few children produced the term “blue” or “teal” (which is how most adults labeled the 70° target color) for the other color. Although this is one possible difference across colors, it does not provide a clear explanation of the improved performance to the pink color. Other studies have shown that labeling colors decreases adults’ ability to discriminate among colors within the category (e.g., Winawer et al., 2007), therefore suggesting we should get the opposite effect in which children performed worse on colors that they labeled.

Another possibility, however, is that the boundary of the “pink” color category was only slightly above 290° for most or all children (perhaps near 310°, as this is where the average thresholds were), leading to reliable discrimination at the category boundary. For the 70° target, on the other hand, categories may have varied more across children and age groups, or the boundary may have been much further from the target color. In this case, children’s production of the “pink” name would be an indication of this as a familiar and stable category representation, whereas they did not have a strong category for the teal color. We tried to reduce the effects of category boundaries by emphasizing the point that small differences in color should be identified as “different”, even they would be labeled with the same name. We illustrated this by demonstrating the task to children using two shades of brown infant socks, followed by flashcards showing different shades of blue. Children typically indicated that they understood this about the task, but we cannot be sure if they applied this criterion reliably across trials. We return to this question in the General Discussion below, where we explore ways in which the model may capture differences across target colors (Section 6).

One final concern with this experiment is the appropriateness of the stair-casing procedure for young children. As described above (Section 4.1.1), 5 children were excluded as outliers due to high thresholds, and another 16 children were excluded because the design may not have accurately measured their memory. The majority of the children who were excluded were 4-year-olds, suggesting that the stair-casing procedure was least suited to their performance. Thus, to ensure that the developmental difference we found for the 70° target was not an artifact of our testing procedure or specific only to that color, we designed a second experiment with a new stair-casing procedure and tested two additional target colors.

5. Experiment 2

In this experiment we hoped to gain a more accurate picture of developmental changes in color memory by modifying our stair-casing procedure to be more appropriate for young children’s performance. An example of this new procedure is shown in Figure 8 (described further in Section 5.1.3). We began as before, with ascending runs in which target colors become more dissimilar with repeated “same” responses. However, when returning to the target for a second run, we presented a descending run, beginning with a larger separation than had been identified as “different” on the previous run to that target and increasing similarity with each “different” response. Our hope was that this method would be more robust to occasional long runs from children, as it allows the following run to descend as far as needed to reach colors they consider to be the same in memory. We also tested two different target colors in this version to determine whether performance to the 70° or 290° target in Experiment 1 was more indicative of developmental change in memory precision.

Figure 8.

Example sequence of trials using the alternating ascending (asc)/descending (desc) stair-casing procedure from Experiment 2 (S=“same”/D=“different” response); for simplicity, we show only four runs per target, although the experiment included six per target. Note that degree labels were not present during the task, and the order of target presentation was counter-balanced across participants.

5.1. Method

5.1.1. Participants

Participants included 25 four-year-olds (M age = 4.49 yr., SD = 0.26, 15 females, 10 males), 24 five-year-olds (M age = 5.54 yr., SD = 0.31, 14 females, 10 males), 25 six-year-olds (M age = 6.46 yr., SD = 0.25, 15 females, 101 males), and 24 adults (M age = 20.35 yr., SD = 3.27, 15 females, 9 males). All had normal or corrected-to-normal visual acuity and reported no colorblindness. An additional 32 participants were excluded from analyses due to experimenter error (1 four-year-old, 2 five-year-olds, 4 adults), choosing to end early (8 four-year-olds, 1 five-year-old), because they did not understand the task (10 four-year-olds, 5 five-year-olds) or due to a vision abnormality (1 four-year-old). We identified 17 additional children (7 four-year-olds, 7 five-year-olds, and 3 six-year-olds) as outliers by plotting performance histograms of each age group. As in Experiment 1, these histograms showed mean thresholds greater than 56° (i.e., 7 steps) to be outside the normal distributions, leading us to exclude children with one or both thresholds beyond this criterion.

Children were recruited from the Madison community and tested in the laboratory on campus. Adults were University of Wisconsin-Madison students and/or staff who were recruited through undergraduate courses or word of mouth and were tested in the laboratory. Informed consent was obtained from adult participants and from parents of child participants before participation began.

5.1.2. Apparatus

The apparatus was identical to that used in Experiment 1. Child participants completed the task on the same laptop computer as in Experiment 1; adult participants were tested the same desktop computer as in Experiment 1.

5.1.3. Procedure

The procedure was similar to Experiment 1 with four modifications. First, participants completed a total of 12 runs rather than 8. Second, runs alternated between two new target colors, 136° (green-brown, RGB = 136, 132, 60) and 356° (purple-blue, RGB = 131, 115, 189). We again chose these colors based on adults’ category ratings from Experiment 1, as well as neither being consistently named by adults (i.e., some called 136° “green”, others “brown”; some called 356° “blue”, others “purple”). Third, we added a “repeat” button to the response pad, allowing the experimenter to repeat an identical trial in cases where the participant indicated s/he was not sure or was not attending to the screen while one or both mittens were presented. Fourth, the stair-casing procedure was modified to begin with ascending runs to each target, then switch to descending on the following run to this target. Figure 8 illustrates this procedure; as in Experiment 1, which color was presented as Target 1 versus 2 was counter-balanced across participants.

The initial ascending run to each target exactly followed the procedure from Experiment 1, terminating when the participant responded “different”. Following the termination of Run 1 for Target 2, the next run returned to Target 1 and began with one step larger than the separation that ended the previous run to that target; in Figure 8, for example, Run 1 terminated at 160° for Target 1, so Run 2 to Target 1 began with 168°. If the participant responded “different” (as most did), the next trial in this run presented a separation one step smaller than the previous trial, and continued in this manner until the participant responded “same”. If the participant responded “same” on the first trial of Run 2, this run continued in an ascending manner. The goal was to provide more sensitivity to participants’ memory and allow recovery from unintended responses on previous runs.

At the termination of a descending run, the subsequent run to that target would begin with a separation one step smaller than the separation that terminated the previous run; in Figure 8, for example, Run 2 to Target 1 terminated at 160°, leading Run 3 to Target 1 to begin with 152°. In some cases, the previous run had terminated when both stimuli were the target color (see Run 2 to Target 2 in Figure 8); in these cases, the ascending run began with this pair rather than stepping in the opposite direction from the Target (see Run 3 to Target 2). Runs continued in this manner, alternating between Targets, until six runs to each target were completed (note that Figure 8 shows only four runs to each target for simplicity). Typically, this resulted in three ascending runs and three descending runs to each Target, although variation in responding occasionally led to more ascending than descending runs.

5.2. Results

Following Experiment 1, we analyzed performance by taking the smallest separation at which the participant responded “different” in each run and computing the mean and standard deviation across runs as the participant’s threshold and variability scores, respectively, separately for ascending and descending runs. In Figure 8, for example, Target 1 would include 160° and 176° for ascending runs, and 168° and 176° for descending runs, leading to averages of 168° and 172°, respectively (note that we show only two runs per direction per target in this figure, though the experiment included three each). These data would yield mean thresholds of 32° for ascending and 36° for descending, with cross-run variance scores (i.e., standard deviation across runs) of 11.31 and 5.66, respectively. Preliminary analyses revealed no significant effect of gender leading us to exclude this factor from further analysis.

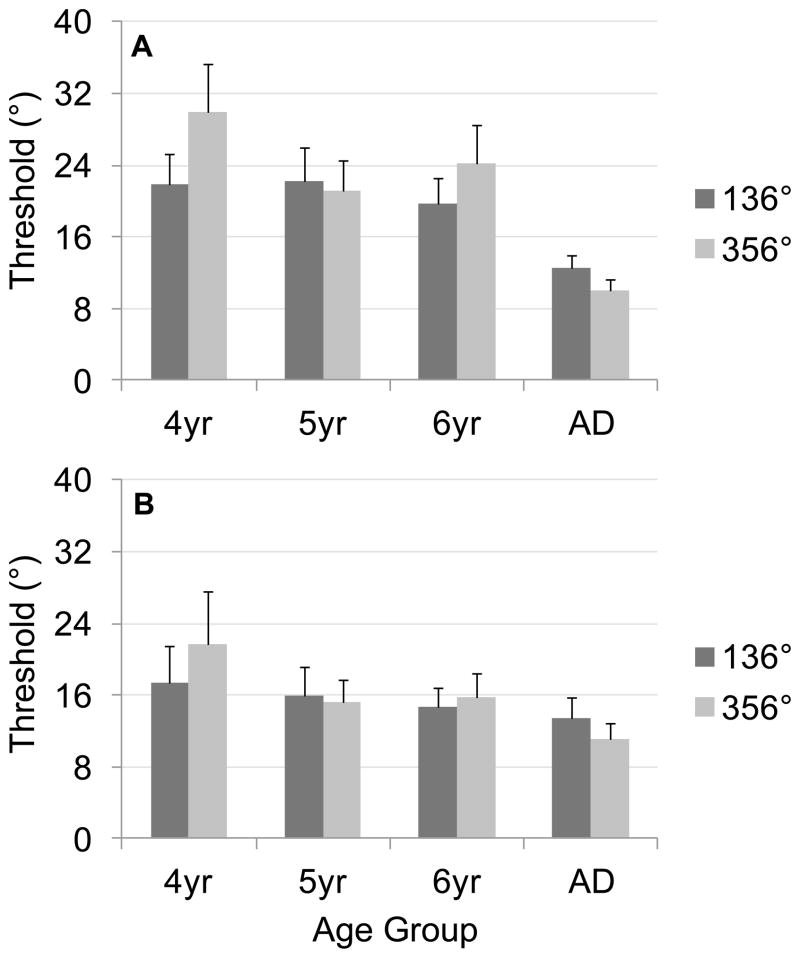
Figure 9 shows mean thresholds separately for each target across age groups, with results from ascending versus descending runs in different panels. As this figure shows, thresholds were higher for ascending runs (Figure 9A) than descending runs (Figure 9B), suggesting our modification of the procedure to include both directions helps avoid over-estimating thresholds as may have been the case in Experiment 1 (using only ascending runs). The overall pattern across targets and development, however, is the same across directions: performance improved over development, with 4-year-olds showing a notable difference across targets and more comparable performance across targets in other age groups.

Figure 9.

Mean thresholds across age groups, separated by target, for (A) ascending runs and (B) descending runs from Experiment 2; note that higher scores indicate poorer performance. Error bars show 95% confidence intervals.

We analyzed mean thresholds in a three-way ANOVA with Target (136°, 356°) and Direction (ascending runs, descending runs) as within-subjects factors and Age (4, 5, 6, adults) as a between-subjects factor. This analysis revealed significant main effects of Direction, F_{1, 96} = 37.17, p < .001, and Age, F_{3, 96} = 13.67, p < .001, as well as significant Direction × Age, F_{3, 96} = 5.84, p < 0.01, Target × Age, F_{3, 96} = 6.61, p < 0.001, and Direction × Target, F_{1, 96} = 3.98, p < 0.05, interactions. As Figure 9 shows, the Direction main effect was driven by overall higher thresholds for ascending runs (M = 20.27°) than descending runs (M = 15.72°). Follow-up Tukey HSD tests (p < .05) on the Age main effect showed that all groups of children had higher thresholds than adults (4-year-olds M = 23.38°; 5-year-olds M = 18.83°; 6-year-olds M = 18.28°; adults M = 11.77°); thresholds were also significantly higher for 4-year-olds than 6-year-olds, supporting our prediction of increased precision during early childhood.

We explored the source of the Direction × Age interaction by conducting separate one-way ANOVAs with Age as a factor for each direction. Both analyses revealed main effects of age: for ascending runs, F_{3, 94} = 16.22, p < .001; for descending runs, F_{3, 94} = 5.38, p < .01. Tukey HSD follow-up tests (p < .05) showed that, for ascending runs, children did not differ (4-year-olds M = 25.90°, 5-year-olds M = 21.64°, 6-year-olds M = 21.95°) but all had significantly higher thresholds than adults (M = 11.26°). For descending runs, only 4-year-olds (M = 19.55°) had significantly higher thresholds than adults (M = 12.31°); 5- (M = 15.57°) and 6-year-olds (M = 15.31°) did not differ from other age groups. We also conducted separate one-way ANOVAs with Direction as a factor for each age group. These revealed significant main effects of direction for each of the age groups of children, but not adults: for 4-year-olds, F_{1, 24} = 10.83, p < .01, for 5-year-olds, F_{1, 23} = 20.08, p < .001, for 6-year-olds, F_{1, 24} = 17.48, p < .001. In all cases, children had higher mean thresholds on ascending runs than on descending runs (see means above).

We next explored the source of the Target × Age interaction by conducting separate one-way ANOVAs with Age as a factor for each Target. Both analyses revealed significant improvements over development: for 136°, F_{3, 94} = 5.24, p < .01; for 356°, F_{3, 94} = 13.90, p < .001. Follow-up Tukey HSD tests (p < .05) for the 136° target showed that 4- (M = 19.98°) and 5-year-olds (M = 19.00°) had had higher thresholds than adults (M = 12.94°); 6-year-olds (M = 17.17°) did not differ from any other age group. For the 356° target, all groups differed significantly except for 5- and 6-year-olds (4-year-olds M = 26.79°, 5-year-olds M = 18.67°, 6-year-olds M = 19.37°, adults M = 10.60°). We also conducted separate one-way ANOVAs with Target as a factor for each age group. These revealed significant main effects of target for 4-year-olds, F_{1, 24} = 6.89, p < .05, and adults, F_{1, 23} = 7.45, p < .05. For 4-year-olds, thresholds were higher to the 356° target than the 136° target; for adults, the pattern was opposite (see means above).

Lastly, we explored the source of the Direction × Target interaction by conducting separate one-way ANOVAs with Direction as a factor for each Target. Both analyses revealed significant differences across Directions: for 136°, F_{1, 97} = 22.58, p < .001; for 356°, F_{1, 97} = 23.65, p < .001. In both cases, thresholds were higher on ascending runs (136° M = 19.14, 356° M = 21.39) than descending runs (136° M = 15.39, 356° M = 16.04). We also conducted separate one-way ANOVAs with Target as a factor for each Direction. Only ascending runs showed a significant difference across targets, F_{1, 97} = 5.22, p < .05, with lower thresholds to 136° than 356° (see means above); the difference on descending runs was not significant (p = .56).

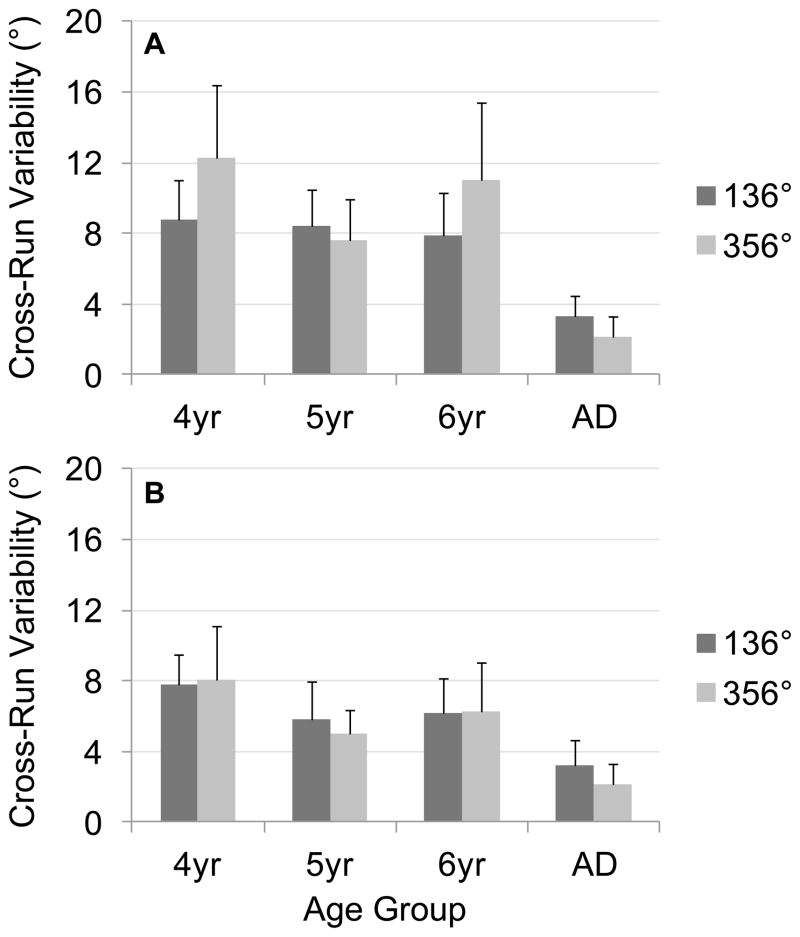
Figure 10 presents cross-run variability scores, separated by target and age group, with results from ascending versus descending runs in different panels. As this figure shows, variability across runs did not differ notably across run directions, and also did not change dramatically over development. Four-year-olds did show a slight difference across targets in parallel to the difference in thresholds shown in Figure 9.

Figure 10.

Mean cross-run variability scores across age groups, separated by target, for (A) ascending runs and (B) descending runs from Experiment 2; note that higher scores indicate more variability across runs. Error bars show 95% confidence intervals.

We analyzed these scores in a three-way ANOVA with Target (136°, 356°) and Direction (ascending run, descending run) as within-subjects factors and Age (4, 5, 6, adults) as a between-subjects factor. This analysis revealed significant main effects of Direction, F_{1, 96} = 11.12, p < .01, and Age, F_{3, 96} = 11.60, p < .001, as well as an Age × Target interaction, F_{3, 96} = 2.72, p < .05. As Figure 10 shows, the Direction main effect was driven by higher variability in ascending runs (M = 7.72°) than descending runs (M = 5.59°). Follow-up Tukey HSD tests (p < .05) on the Age main effect showed that all children (4-year-olds M = 10.14°, 5-year-olds M = 6.91°, and 6-year-olds M = 7.87°), all had significantly higher variability across runs than adults (M = 2.78°); differences between groups of children were not significant.

We explored the source of the Target × Age interaction by conducting separate one-way ANOVAs with Age as a factor for each Target. Both analyses revealed significant improvements over development: for 136°, F_{3, 94} = 7.30, p < .001; for 356°, F_{3, 94} = 8.97, p < .001. Follow-up Tukey HSD tests (p < .05) for the 136° target showed that all groups of children (4-year-olds M = 8.75°, 5-year-olds M = 7.15°, 6-year-olds M = 7.08°) had higher variability than adults (M = 3.27°). For the 356° target, 4-year-olds (M = 11.53°) had significantly higher variability than 5-year-olds (M = 6.67°) and adults (M = 2.29°); additionally, 6-year-olds’ (M = 8.67°) variability was higher than adults’. We also conducted separate one-way ANOVAs with Target as a factor for each age group. These revealed no significant main effects of target (ps > .08).

5.3. Discussion

The goal of this experiment was to overcome some of the limitations of our stair-casing procedure in Experiment 1 while testing two different target colors to see which pattern from Experiment 1 would generalize across other targets. By testing children with a modified stair-casing procedure including both ascending and descending runs, it seemed that we were able to hone in better on children’s true memory for colors. With this modified procedure testing different target colors, we replicated our effects from Experiment 1: thresholds decreased over development, but now for both targets (compared to only 70° in Experiment 1); variability also decreased during childhood for the 356° target, and from childhood to adulthood for the 136° target. Additionally, we found that children’s thresholds were reliably higher when estimated in ascending runs versus descending runs, suggesting that the method including both types of runs is preferable to using only ascending runs.

We found a significant difference across targets for the 4-year-olds as well as for adults. Interestingly, these differences were in opposite directions, with better performance on the 136° target for 4-year-olds versus the 356° target for adults. This suggests that there will be different developmental trajectories for different colors throughout the color space, and that the results from Experiment 1 were not necessarily anomalous. However, this does not give a clear indication of why performance differs so dramatically across targets early in development. We return to this issue in the General Discussion (Section 6) and discuss future studies that could address this question.

6. General Discussion

Across two experiments, we tested the precision and stability of children’s and adults’ memory for colors in a single-item change detection task. The developmental mechanism proposed by Simmering (2008) to capture increasing VWM capacity predicts that memory becomes more precise and stable as capacity increases. Our results supported this prediction, showing significant improvements in both thresholds and cross-run variability over development, although developmental trajectories varied by target color. The strongest support came from changes in thresholds to the 70° and 356° targets between 4 and 6 years of age, and developmental range during which VWM capacity increases from roughly 2 to 3 items. As we argued in Section 2, we believe our model makes important contributions to our predictions, beyond traditional theoretical approaches. In this section, we consider ways in which our approach has benefitted from incorporating computational modeling.

Although our behavioral results provide support for the cognitive and developmental mechanisms embodied within the DFT and SPH, they also raise a critical challenge for the model: why do different target colors show different developmental trajectories? As it stands, the model represents colors within a homogeneous space (i.e., selectively-tuned neural fields), but this is not necessarily the case in the human visual system; indeed, models of color perception have suggested an inhomogeneous perceptual space for color. We attempted to avoid this experimentally by choosing our target colors from 180 colors equally-distributed through the CIELAB 1976 color space to approximate perceptually-uniform color changes between different colors (following Johnson, Spencer, Luck, et al., 2009; see also Lin & Luck, 2009), and by testing different target colors within participants. This revealed unexpected developmental inconsistencies across targets, in that younger children showed large differences in performance for different target colors, while older children and adults showed only small differences.

Could this difference across targets—or even our key developmental finding of improved discrimination—be driven by perceptual differences? Previous research has shown stable color perception over development for colors that varied only in hue (holding brightness and saturation constant; Petzold & Sharpe, 1998, see hue discrimination Test B). Petzold and Sharpe examined developmental change using relatively broad age ranges, comparing preschoolers (3–6 years) to preadolescents (9–11 years) to young adults (22–30 years), but did not look for differences within each of these age groups. The overall similarity of performance between the preschool and adult groups suggests there is not much room for developmental change in perception between 3 and 6 years, but to our knowledge, this question has not been tested directly. Thus, it is possible that perceptual differences caused the effect we see across targets or development here. To rule out this explanation of our developmental effect, we are currently collecting data with a version of our task in which the colors are presented simultaneously.

It is also possible that perception of the target colors was equally sensitive at any given point in development, but that differences in performance across targets arose through memory processes. As discussed above (Section 4.1.3), children’s familiarity with colors and/or color categories may affect their discrimination of colors in different categories. Although the familiarity explanation makes intuitive sense in Experiment 1, with the pink versus teal colors, it does not seem as likely in Experiment 2, where both colors seemed relatively unfamiliar to children and adults. Finding the explanation for the color differences will require further experimentation testing these possibilities through separate assessments of participants’ perception, familiarity, and categorization of target colors. Although further behavioral experiments are beyond the scope of this paper, we can explore some of these questions through model simulation as an initial evaluation of the potential explanations. This is a key advantage of process-based computational models like the DFT over less-specified theories: potential explanations posed to account for our empirical findings can be tested in the model before conducting further experiments. We tested these possibilities in the model in relatively simple ways, by increasing the resting levels of PF and WM.

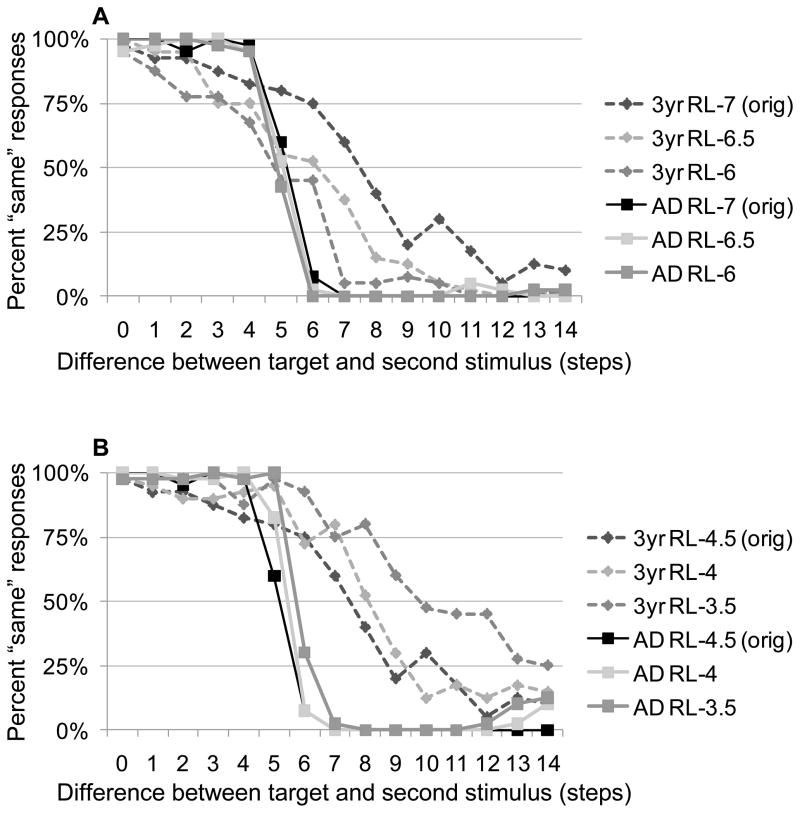
Increasing the resting level of PF would correspond to heightened perceptual processing of the stimuli. For simplicity, we raised the resting level of the entire field and repeated the simulations from our introduction using the 3-year-old and adult parameters; to implement differences across targets, however, the resting level would vary across color space. Our simulation results are shown in Figure 11A: increasing the resting level in PF indeed improved discrimination performance for children by 2–3 steps, from approximately 10.3 steps in the original simulations (resting level of −7) to 8.4 steps (resting level of −6.5) and 7.6 steps (resting level of −6). However, the effect on the adult parameters was negligible, keeping threshold estimates between 7.5 and 7.6 across resting levels. Empirically, this would predict that children who show better perceptual discrimination of colors should also show better memory for those colors, but that the difference would not be evident in adults’ performance. Moreover, these simulations show a reduction in developmental change (i.e., similar performance between children and adults) as the resting level or PF increases. This type of perceptual difference across colors is a potential source for the behavioral differences we found across targets early in development.

Figure 11.

Simulations testing the effects on discrimination performance of increasing the resting level (RL) (A) in PF or (B) WM for 3-year-old (dotted lines) versus adult parameters (solid lines). Performance of the 3-year-old and adult parameters from Figure 4 is included for comparison (labeled “orig”).

Increasing the resting level of WM would correspond to more familiarity with the color. Implementations of long-term memory within the DFT have taken the form of reciprocally-coupled excitatory long-term memory fields (e.g., Simmering et al., 2008), in which repeated exposure to a stimulus effectively boosts the resting level for the corresponding neurons in WM. We approximated this process here by raising the resting level of WM from −4.5 to −4 or −3.5 for both the 3-year-old and adult parameters. The results, shown in Figure 11B, suggest the opposite effect of our intuition for children’s performance: rather than familiarity improving discrimination with the 3-year-old parameters, the increased resting level led to a decrease in performance, requiring larger separations to reliably respond “different” (from 10.3 to 10.8 to 16.3 steps as the resting level increased). For the adult parameters, however, we again see very little change (from 7.6 to 7.8 to 8.1 steps). These simulations suggest an interesting prediction—that children, but not adults, should show worse discrimination performance on more familiar colors—that would need to be tested empirically, but may relate to the category/labeling effect shown by Winawer et al. (2007).

As the simulations presented here and in the introduction illustrate, computational models can provide the specificity needed to generate novel, testable predictions and to test potential explanations for empirical outcomes before conducting further behavioral experiments. The type of process-based model we use here is especially well-suited to these goals, as it performs a task on a trial-by-trial basis and incorporates multiple cognitive processes to generate the same type of behavior measured in laboratory tasks. The current empirical results provide a first step in this direction, but much work remains to provide a more complete test of the explanations embodied in the DFT and SPH. Although these results are consistent with the predictions derived from the model, they do not provide direct evidence for the link between precision and capacity: the change in these processes could be coincidental, driven by different developmental mechanisms. To test the link between precision and capacity further will require experiments comparing performance across tasks within the same groups of participants. If performance is correlated between the two tasks over development, this will provide stronger evidence for a common underlying mechanism.

Even if future studies provide evidence for this link, the SPH may not account for the full developmental trajectory of changes in VWM capacity. Empirical evidence has shown developmental improvements in a host of cognitive processes supporting working memory tasks, including speed of processing, executive functioning, resistance to interference, maintenance over delays, and more (see, e.g, Towse & Hitch, 2007, for discussion). How can a simple mechanism like the SPH address this variety of changes? Although the DFT has not been designed to address these questions specifically, it can be tested in different tasks to examine how broadly the SPH may generalize. For example, Perone and colleagues (2011) used the SPH in a related architecture to capture infants’ looking behavior in a task designed to measure VWM capacity during the first year. Their simulations showed that the “young” infant model could perform similarly to the “old” infant model by removing the delays between items, suggesting that one consequence of strengthening neural interactions is improved maintenance of items over delay. Similarly, Schutte and Spencer (2009) found that their “young” parameters (capturing 3-year-olds’ performance in spatial recall) showed greater spatial “drift” over memory delays, as well as increased variability across repeated trials to the same target, when compared to their “old” parameters (capturing 5-year-olds’ performance). Thus, implementing a theoretical explanation like the SPH in a real-time process model allows exploration of multiple consequences that may arise from a single underlying change.

Beyond the implementation of the SPH described here and used by Perone et al. (2011) and Schutte and Spencer (2009), developmental changes in other dynamic neural field architectures have been used to capture behavioral development in other tasks. Buss and Spencer (2008) developed a multi-layered architecture of neural fields to perform the dimensional change card sort task, in which young children (typically 3-year-olds) have difficulty shifting rules used to sort cards. In their model, Buss and Spencer approximated executive control through the process of boosting the resting levels in fields used to represent the different dimensions of the cards (e.g., shape versus color) used to generate the sorting rules. Through simple, quantitative changes in the magnitude of the boosts over development, they have successfully captured performance across variety of conditions of this task.

Samuelson, Schutte, and Horst (2007) have also applied a dynamic neural field architecture to word learning tasks, and showed that changes in the strength of inputs corresponding to object characteristics (e.g., shape versus material) captured developmental changes in children’s novel noun generalization in both yes/no and forced-choice tasks. As these examples demonstrate, the SPH is only one potential developmental change that can be implemented in a model like the DFT. This brings us to the final question we address in this paper: what can our current behavioral and simulation results tell us about the nature of developmental change?

We contend that one of the most important implications of our current results is that we cannot answer questions about developmental mechanisms until we specify the ways in which cognitive processes operate in service of the behaviors we measure in the lab. This paper highlights how this can be achieved using computational models, and shows how providing rich structure of the real-time processes of cognition and behavior can simplify the “work” that must be done by developmental change. Across a variety of behaviors and domains, neural field models have captured complex patterns of developmental change through relatively simple changes in connectivity in the model. The complexity of developmental change builds on the complexity of real-time behavior, and understanding the former requires a richer understanding of the latter. Computational models provide a powerful tool for understanding processes at both of these levels. The full explanatory scope of these relatively simple developmental mechanisms remains to be seen as models are applied to additional domains and tasks.