Actomyosin kinetics of pure fast and slow rat myosin isoforms studied by in vitro motility assay approach

Abstract

An in vitro motility assay approach was used to investigate the mechanisms of the functional differences between myosin isoforms, by studying the effect of MgATP and MgADP on actin sliding velocity (V_f) of pure slow and fast rat skeletal myosin at different temperatures. The value of V_f depended on [MgATP] according to Michaelis–Menten kinetics, with an apparent constant (K_m) of 54.2, 64.4 and 200 μm for the fast isoform and 18.6, 36.5 and 45.5 μm for the slow isoform at 20, 25 and 35°C, respectively. The presence of 2 mm MgADP decreased V_f and yielded an inhibition constant (K_i) of 377, 463 and 533 μm for the fast isoform at 20, 25 and 35°C, respectively, and 120 and 355 μm for the slow isoform at 25 and 35°C, respectively. The analysis of K_m and K_i suggested that slow and fast isoforms differ in the kinetics limiting V_f. Moreover, the higher sensitivity of the fast myosin isoform to a drop in [MgATP] is consistent with the higher fatigability of fast fibres than slow fibres. From the Michaelis–Menten relation in the absence of MgADP, we calculated the rate of actomyosin dissociation by MgATP (k_+ATP) and the rate of MgADP release (k_–ADP). We found values of k_+ATP of 4.8 × 10⁶, 6.5 × 10⁶ and 6.6 × 10⁶ M⁻¹ s⁻¹ for the fast isoform and 3.3 × 10⁶, 2.9 × 10⁶ and 6.7 × 10⁶ M⁻¹ s⁻¹ for the slow isoform and values of k_–ADP of 263, 420 and 1320 s⁻¹ for the fast isoform and 62, 107 and 306 s⁻¹ for the slow isoform at 20, 25 and 35°C, respectively. The results suggest that k_–ADP could be the major determinant of functional differences between the fast and slow myosin isoforms at physiological temperatures.

It is generally believed that the mechanical properties of skeletal muscle fibres, including unloaded shortening velocity (V₀), are to a large extent determined by the myosin isoforms expressed in the fibres (Schiaffino & Reggiani, 1996). In a series of recent studies (Weiss et al. 2001; Capitanio et al. 2006; Nyitrai et al. 2006; Iorga et al. 2007), the mechanochemical properties of pure myosin isoforms isolated from skeletal muscle fibres were studied in order to define the kinetic and molecular basis of myosin diversity, but the issue remains important and somewhat unresolved.

Muscle contraction results from a cyclical interaction of myosin cross-bridges with actin, coupled with the hydrolysis of MgATP to MgADP and inorganic phosphate (P_i). The events in the cycle are essentially the same for all muscle myosins; during the actomyosin interaction, myosin propels an actin filament for a distance δ (or step size) in a time t_on, i.e. the time it remains attached to actin. The sliding velocity of the actin filament and the shortening velocity of the muscle fibre are therefore equal to δ/t_on (i.e. distance travelled/time required). The difference between slow and fast myosin isoforms could be due to a different step size or to a different duration of the attached state, or to both. To address this question, actomyosin kinetics of single fibres (Cooke & Pate, 1985; Lu et al. 1993; Zhao & Kawai, 1994; Wang & Kawai, 1996; Galler et al. 2005) and pure myosin isoforms in solution were studied (Siemankowski et al. 1985; Weiss et al. 2001; Nyitrai et al. 2006; Iorga et al. 2007). Many of these studies successfully measured the rates of the two major transitions known to determine the duration of actomyosin interaction in sarcomeric isoforms, namely the rate of MgADP release from actomyosin (k_–ADP) and the rate of actomyosin dissociation by MgATP (k_+ATP), and suggested that k_–ADP had a major role in defining V₀.

This conclusion was also supported by a recent study in which the elementary event of force generation and shortening produced by a single motor domain of pure fast and slow skeletal myosin isoforms was studied (Capitanio et al. 2006). For the first time, two phases in the attached state of skeletal myosin were observed. Several lines of evidence supported the hypothesis that the duration of the first phase, which was very different for the slow and fast isoforms, was related to k_–ADP. Interestingly, the second phase, which was very similar for both isoforms, was found likely to be related to k_+ATP.

Thus, both kinetic analysis in solution and single-molecule analysis suggest that k_–ADP is the rate constant of the cross-bridge cycle that mostly defines the unloaded shortening velocity (V₀) of skeletal muscle myosin and may account for the main difference between the fast and slow myosin isoforms. Nevertheless, it was recently suggested that the relative contributions of k_–ADP and k_+ATP in defining shortening velocity could be different for the slow and fast isoforms at different temperatures (Nyitrai et al. 2006). The work of Nyitrai et al. (2006) has demonstrated that, at a low temperature (12°C), k_+ATP plays a significant role in limiting the velocity of fast isoforms, and the hypothesis that, at physiological temperatures, k_–ADP might limit V₀ for both the isoforms was only suggested by extrapolation of the experimental data. The suggestion that k_–ADP and k_+ATP can have different relative roles in limiting V₀ for the slow and fast isoforms is also supported by the study by Iorga et al. (2007).

In the present study, we have used an in vitro motility assay (IVMA) approach to investigate the effect of MgATP and MgADP concentrations on actin sliding velocity (V_f) of pure slow and fast skeletal myosin isoforms at different temperatures in order to investigate the kinetics mechanism underlying the functional differences between slow and fast myosin isoforms. The IVMA is a simplified model of muscle contraction that enables analysis of the molecular events that couple MgATP hydrolysis to mechanical work and enables this analysis to be performed on pure myosin isoforms over a wide range of temperatures (Homsher et al. 1992; Yamashita et al. 1994; Rossi et al. 2005). It has been suggested that MgADP binding/release can occur in two steps, because an isomerization step can precede MgADP release (Sleep & Hutton, 1980; Nyitrai & Geeves, 2004; Nyitrai et al. 2006; Albet-Torres et al. 2009; Mansson, 2010). While the analysis of actomyosin kinetics in solution might miss the isomerization step, the determination of k_–ADP by IVMA is free from such uncertainty.

Our results suggest that, in the experimental conditions of IVMA, at physiological temperature and low ionic strength, k_–ADP is the major determinant of the difference between slow and fast skeletal myosins in the actin sliding velocity.

Methods

Ethical approval

The experimental protocol was approved by the local Animal Ethics Committee, and all the experimental procedures conformed to the UK Animals (Scientific Procedures) Act, 1986.

Muscle sampling and protein preparation

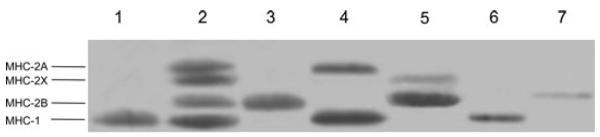
Gastrocnemius and soleus muscles were dissected from 3- (n = 5) and 6-month-old Wistar rats (n = 6), respectively. Rats were anaesthetized with ether and then decapitated. Muscle samples were characterized for myosin heavy chain (MHC) isoform composition by 8% SDS-PAGE, as described by Pellegrino et al. (2003). The gels were silver stained, so that a minor MHC band can be detected when its density is 1% of the major band (Bottinelli et al. 1994). Whole gastrocnemius muscles contained 80% of MHC-2B and 20% of MHC-2X (Fig. 1); however, the superficial portion of the muscles, which was used as a source of myosin, showed a pure MHC-2B content (Fig. 1). Soleus muscles contained 80% of MHC-1 and 20% of MHC-2A (Fig. 1). Muscles were placed in cold skinning solution and divided into several fibre bundles that were stored at –20°C in skinning solution with 50% glycerol for up to 2 weeks.

Figure 1. Examples of myosin heavy chain (MHC) electrophoretic separation in muscle samples and single fibres.

The distribution of MHC isoforms in soleus (line 4), gastrocnemius (line 5), the superficial portion of gastrocnemius (line 3) and a mixed sample composed of soleus and diaphragm muscles (line 2). Examples of the MHC composition of single fibres are shown in line 1 (pure type 1 fibre), line 6 (pure type 1 fibre) and line 7 (pure type 2B fibre). Gels were silver stained.

On each day of the experiment, fibre bundles were removed from the freezer and used for myosin extraction. Pure type 2B myosin isoform was prepared from the bulk superficial portion of gastrocnemius muscles according a procedure previously described in detail (Canepari et al. 2000). Pure myosin isoform 1 was prepared from single fibres containing only MHC-1 isoform. Briefly, single fibres (at least 8 mm long) were manually dissected from muscle samples, chemically skinned for 1 h in skinning solution containing 1% Triton X-100, and cut into two segments. The shorter segment (about 2 mm long) was dissolved in standard buffer (Laemmli et al. 1970) and used for MHC isoform identification on an 8% SDS-PAGE gel using a procedure previously described (Pellegrino et al. 2003). The longer segment (at least 6 mm long) was used for myosin extraction. In order to obtain sufficient pure type 1 myosin to perform IVMA experiments with different MgATP concentrations at different temperatures, at least 100 pure fibres containing the MHC-1 isoform were pooled before myosin extraction (Canepari et al. 2000). Extracted myosin was used to prepare heavy meromyosin (HMM) by proteolytic digestion with α-chymotrypsin according to a modification of the method of Margossian & Lowey (1982) previously described in detail (Canepari et al. 2000).

In vitro motility assay

The IVMA was performed according to Canepari et al. (1999, 2000) in the temperature range 20–35°C. A water–glycol ethylene solution from a thermostat (Thermo Haake DC10 Newington, NH, USA) was circulated through a coiled pipe created on the microscope stage and in a jacket of Perspex surrounding the microscope objective in order to maintain the desired temperature in the flow cell. The flow cell temperature was continuously monitored in all experiments by a thermometer probe (Delta Ohm HD8601P Thermometer) placed outside but very closely in contact with the flow cell.

The composition of the experimental buffer (AB) was as follows: Mops, 25 mM (pH 7.4 at 25°C); KCl, 25 mM; MgCl₂, 4 mM; EGTA, 1 mM; DTT, 1 mM; glucose oxidase, 200 μg ml⁻¹;catalase, 36 μg ml⁻¹;glucose, 5 mg ml⁻¹;and ATP, 2 mM. The concentration of HMM solution for all the experiments was 0.3 mg ml⁻¹. The sliding velocity of the actin filaments (V_f) was measured at 20, 25 and 35°C in the absence and in the presence of 2 mM MgADP, varying MgATP concentrations in the range 0.01–2.00 mM. The [MgCl₂] and [KCl] were changed to maintain the basic conditions above and the ionic strength. To ensure that at very low MgATP concentrations V_f was not affected by MgATP consumption, some experiments at low MgATP concentrations were performed in the presence of a MgATP regenerating system (creatine phosphate, 2 mM; and creatine phosphokinase, 100 units ml⁻¹) in the AB buffer. No differences were found in V_f values. Moreover, no differences were observed between V_f values determined at the beginning and at the end of experiments lasting several minutes, indicating that no change in MgATP concentration occurred.

The compositions of solutions were determined using a computer program based on that developed by Fabiato & Fabiato (1979).

At each temperature and [MgATP], for each myosin sample, the velocities of at least 50 filaments were measured using purpose-designed software, and their distribution was characterized according to parametric statistics (Canepari et al. 1999, 2000).

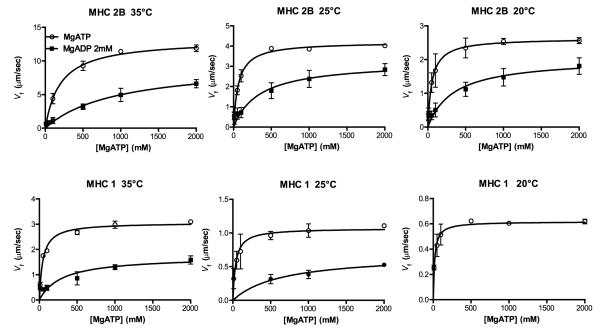
The relations between V_f and [MgATP] in the presence and in the absence of 2 mM MgADP (Fig. 2) represent the average of at least three data sets obtained with three different myosin samples. In turn, each data point of each sample was obtained from the average V_f of at least 50 filaments. Consequently, each data point in the curves reported in Fig. 2 is representative of ~150 filaments.

Figure 2. Michaelis–Menten relations between actin sliding velocity (V_f) and MgATP.

The V_f is shown at different MgATP concentrations in the absence (open circles) and presence of 2 mM MgADP (filled circles) for pure type 2B (MHC-2B) and type 1 myosin isoforms (MHC-1) at 20, 25 and 35°C. The values of V_f recorded at 20°C for slow myosin in the presence of 2 mM MgADP are not reported (see Methods). Each data point in the figure represents the mean ± SEM of at least three curves obtained with different muscle samples in the same experimental conditions (see Methods). Each data point of each relation was obtained from the average V_f of at least 50 filaments.

The values of V_f recorded at 20°C for slow myosin in the presence of 2 mM MgADP were very low and close to the sensitivity threshold of our system; therefore, these data are not reported.

Equations

The data points of the relations between V_f and [ATP] were fitted with the following Michaelis–Menten relation:

$$V_{\mathrm{f}}=V_{\max }\left[\mathrm{M}\mathsf{g}\mathrm{ATP}\right]∕K_{\mathrm{m}}+\left[\mathrm{M}\mathsf{g}\mathrm{ATP}\right]$$ (1)

This enabled the calculation of K_m, i.e. the concentration of MgATP at which the velocity was half-maximum, and V_max, the velocity at infinite [MgATP].

Assuming that the inhibition of V_f by MgADP follows the behaviour of a competitive enzyme inhibitor, we could calculate the inhibition constant (K_i) from the following equation:

$$K_{\mathrm{mt}}=K_{\mathrm{m}}(1+[\mathrm{M}\mathsf{g}\mathrm{ADP}]∕K_{\mathrm{i}})$$ (2)

where K_mt is K_m in the presence of 2 mM MgADP.

According to a detachment-limited model of actin sliding velocity (Huxley, 1990), V_f is proportional to the myosin step size (d) divided by the duration of actin binding (t_on), i.e. V_f = d/t_on. The t_on is the sum of the time required for MgADP release (1/k_–ADP) from myosin plus the time required for MgATP to bind and induce dissociation from actin (1/k_+ATP), as follows:

$$V_{\mathrm{f}}=d∕t_{\mathrm{on}}=d∕(1∕k_{-\mathrm{ADP}}+1∕k_{+\mathrm{ADP}})$$

The MgATP-induced dissociation of the cross-bridge is a function of MgATP concentration. The [MgATP] dependence of t_on depends upon whether MgATP binding or MgADP release defines the overall time of detachment. If we assume that MgADP release is the rate-limiting factor and that [MgADP] ≈ 0, then k_+ATP is a linear function of [MgATP], that is k_+ATP = k′_+ATP [MgATP], where k′_+ATP is the apparent second-order rate constant of MgATP binding to the cross-bridge. Then:

$$V_{\mathrm{f}}=d∕t_{\mathrm{on}}=d∕(1∕k_{-\mathrm{ADP}}+1∕k_{+\mathrm{ATP}}^{\prime }[\mathrm{M}\mathsf{g}\mathrm{ATP}\left]\right)$$

that is:

$$\begin{array}{cc}\hfill V_{\mathrm{f}}∕d& =1∕(k_{-\mathrm{ADP}}+1∕k_{+\mathrm{ATP}}^{\prime }[\mathrm{M}\mathsf{g}\mathrm{ATP}\left]\right)\hfill \\ \hfill & =k_{-\mathrm{ADP}}{k}_{+\mathrm{ATP}}^{\prime }\left[\mathrm{M}\mathsf{g}\mathrm{ATP}\right]∕(k_{-\mathrm{DP}}+k_{+\mathrm{ATP}}^{\prime }[\mathrm{M}\mathsf{g}\mathrm{ATP}\left]\right).\hfill \end{array}$$

Dividing by k′_+ATP, we obtain the following expression:

$$V_{\mathrm{f}}∕d=k_{-\mathrm{ADP}}\left[\mathrm{M}\mathsf{g}\mathrm{ATP}\right]∕(k_{-\mathrm{ADP}}∕k_{+\mathrm{ATP}}^{\prime }+[\mathrm{M}\mathsf{g}\mathrm{ATP}\left]\right)$$ (3)

Thus, the plot of V_f versus [MgATP] will provide values of V_max = k_–ADP × d and K_m = k_–ADP/k′_+ATP; hence, V_max/K_m = k′_+ATP × d. From these relations, the values of k_–ADP and k′_+ATP can be determined (see Table 2).

Table 2.

Kinetic parameters calculated from the Michaelis–Menten relations

Myosin isoform	20°C	25°C	35°C	Ratio 35°C/25°C
MHC-2B
k–ADP (s–1)	263	420	1319	3.14
k′+ATP (106 M–1 s–1)	4.8	6.5	6.6	1.01
MHC-1
k–ADP (s–1)	62	107	306	2.86
k′+ATP (106 M–1 s–1)	3.3	2.9	6.7	2.3

The rate of MgADP release (k_–ADP) and the rate of actomyosin dissociation induced by MgATP (k′_+ATP) were calculated from V_max (V_max = k_–ADP × d, where d = 10 nm) and from the ratio V_max/K_m(V_max/K_m = k′_+ATP × d, where d = 10 nm), respectively (see Methods). Data were obtained on pure myosin 2B (MHC-2B) and pure myosin 1 (MHC-1) at 20, 25 and 35°C.

Data analysis

The relation between V_f and [MgATP] was analysed with a non-linear regression fitted with a Michaelis–Menten equation by a computer program (Prism 5.0; Graphpad Software Inc., La Jolla, CA, USA), which provided the values of K_m and V_max expressed as means±SEM. The statistical significance of the differences was assessed by two-way ANOVA for repeated measures followed by the Student–Neuman–Keuls post hoc test. A probability of less than 5% (P < 0.05) was considered to be significant.

The temperature dependence of the actin filament sliding velocity was analysed with Arrhenius plots. From the slopes of the linear regression lines, the kinetic energy that must be provided to start the reaction or activation energy (E_a) and the temperature coefficient (Q₁₀) were calculated as described by Rossi et al. (2005).

Results

Effect of the concentration of nucleotides on actin sliding velocity

Actin sliding velocity was studied on pure slow (type 1) and pure fast (type 2B) myosin isoforms at MgATP concentrations of 0.01, 0.02, 0.1, 0.5, 1.0 and 2.0 mM (Fig. 2). Experiments were performed at 20, 25 and 35°C, in the absence and in the presence of 2 mM MgADP (Fig. 2). As expected, V_f was higher for the fast than for the slow isoform and increased with temperature (Fig. 2). The V_f increased with MgATP concentration, both in the presence and in the absence of MgADP. Velocities were lower in the presence of 2 mM MgADP at all MgATP concentrations (Fig. 2). Assuming that the relation between V_f and MgATP concentration followed the behaviour of a simple enzymatic reaction with MgATP as a substrate, we fitted the data with a Michaelis–Menten relation [eqn (1)] and calculated the following parameters: (a) the Michaelis constant (K_m), which is the [MgATP] at which velocity is half-maximum; (b) V_max, which is the maximal velocity at infinite MgATP concentration; and (c) the ratio V_max/K_m, which characterizes myosin enzyme kinetics at subsaturating MgATP concentrations.

The values of K_m were lower for the slow than for the fast isoform at all temperatures, indicating that the velocity saturates at a lower MgATP concentration in the slow than in the fast isoform (Table 1). The K_m increased with temperature in both isoforms. In the temperature range 25–35°C, the increase was much more evident for the fast (3.1-fold change) than for the slow isoform (1.25-fold change), indicating that MgATP binding to the slow isoform was little affected by temperature. The opposite was observed in the range 20–25°C, i.e. K_m of the fast isoform had a lower temperature sensitivity (1.42-fold change) than that of the slow isoform (3.8-fold change).

Table 1.

Biochemical parameters calculated from the Michaelis–Menten relations

	20°C		25°C		35°C
Myosin isoform	Mean	SEM	Mean	SEM	Mean	SEM	Ratio 35°C/25°C
MHC-2B
Km(μM)	54.16*‡	8.94	64.43*‡	4.87	199.80‡	21.52	3.10
Kmt (μM)	342	100	343	112	949.60	268	2.77
Ki (μM)	376.58	–	462.58	–	532.90	–	1.15
Vmax (μm s–1)	2.63†‡	0.08	4.20†‡	0.07	13.19†‡	0.33	3.14
Vmax/Km (106 nm M–1 s–1)	48	–	65	–	66	–	1.01
Vmaxinh (μm s–1)	2.04	1.69	3.23†‡	0.31	9.69†‡	1.22	2.99
MHC-1
Km (μM)	18.62*‡	3.79	36.51‡	7.15	45.52‡	5.06	1.25
Kmt (μM)	–	–	647	253	302	112	0.47
Ki (μM)	–	–	119.60	–	354.80	–	2.97
Vmax (μm s–1)	0.62†‡	0.02	1.07†‡	0.03	3.06†‡	0.06	2.86
Vmax/Km (106 nm M–1 s–1)	33	–	29	–	67	–	2.3
Vmaxinh (μm s–1)	–	–	0.62†‡	0.12	1.725†‡	0.17	2.78

Values of K_m ([MgATP] at which the velocity was half-maximum) and V_max (velocity at infinite [MgATP]) were obtained from the relations between V_f and [MgATP]. Values of K_mt (K_m in the presence of 2mM MgADP); Ki (inhibition constant) and V_maxinh (V_max in the presence of 2mM MgADP) were obtained from the same relation in the presence of 2 mM MgADP. Data were obtained on pure myosin 2B (MHC-2B) and pure myosin 1 (MHC-1) at 20, 25 and 35°C. Data at 20°C in the presence of 2 mM MgADP are not reported (see Methods). Values are expressed as means ± SEM.

^*Significantly different from 35°C for the samemyosin (P < 0.05);

^†significantly different from values of the same parameter at all other temperatures for the same myosin (P < 0.05); and

^‡significantly different from the corresponding value for the other isoforms (P < 0.05).

Values of V_max were three- to fourfold higher for the fast than for the slow isoform at all temperatures (Table 1), consistent with V_f values. In the range 25–35°C, Q₁₀ values for V_max were 2.86 and 3.14 and activation energies were 77.73 and 76.58 kJ mol⁻¹ for the slow and fast isoform, respectively, indicating similar temperature sensitivity of the two isoforms, consistent with what was previously observed (Rossi et al. 2005).

Following the addition of 2 mM MgADP, the substrate concentration dependence of V_f was shifted towards higher MgATP concentrations. Fitting the data with the Michaelis–Menten equation, we could determine K_mt (K_m in the presence of 2 mM MgADP). Values of K_mt were, at all temperatures and for both isoforms, higher that the corresponding values of K_m (Table 1). Assuming that the inhibition of V_f by MgADP followed the behaviour of a competitive enzyme inhibitor, we could also calculate the inhibition constant [eqn (2)]. The values of K_i were lower for the slow than for the fast isoform at all temperatures (Table 1). The temperature dependence of K_i was greater for the slow (2.97-fold change between 25 and 35°C) than for the fast isoform (1.15-fold change in the same temperature range; Table 1). The analysis of the V_f dependence on [MgATP] for the slow isoform in the presence of MgADP at 20°C was not performed because V_f dropped to a very low value that prevented reliable measurements.

From the Michaelis–Menten equation in the presence of 2 mM MgADP, we could also calculate V_maxinh (V_max in presence of 2 mM MgADP). Values of V_maxinh were, at all temperatures and for both isoforms, lower than the corresponding V_max values, and Q₁₀ values for V_maxinh were similar as those for V_max, suggesting that MgADP does not affect temperature sensitivity of velocity (Table 1).

Rate of actomyosin dissociation by MgATP (k′_+ATP) and rate of MgADP release from actomyosin complex (k_–ADP)

The values of k_–ADP and k′_+ATP were calculated from V_max = k_–ADP × d and V_max/K_m = k′_+ATP × d [eqn (3)], assuming a step size d = 10 nm (Table 2). The value of d = 10 nm is at the upper end of the 5–10 nm range of measured step size (Hooft et al. 2007). It was considered to be identical for the slow and fast isoforms and therefore not responsible for the differences in shortening velocities among the isoforms (Palmiter et al. 1999; Capitanio et al. 2006).

While the values of k_–ADP were much lower for the slow than for the fast isoform at all temperatures, the values of k′_+ATP were similar for both isoforms (Table 2). Moreover, k_–ADP showed temperature dependence comparable to the temperature dependence of V_max for both isoforms. In contrast, k′_+ATP showed a temperature dependence that was different for the slow and the fast isoform and varied with the temperature range. The k′_+ATP of the fast isoform varied much more than that of the slow isoform in the range 20–5°C, but did not vary with temperature in the range 25–35°C. In contrast, the k′_+ATP of the slow isoform varied much more than that of the fast isoform in the range 25–35°C, but did not vary with temperature in the range 20–25°C.

Discussion

The in vitro motility assay approach was used to study the effect of MgATP and MgADP concentrations on the actin sliding velocity of pure slow and fast skeletal myosin isoforms at different temperatures. In IVMA, as the viscous force imposed on moving actin filaments is negligible, the filament velocity (V_f) is expected to be limited only by cross-bridge kinetics and, therefore, to be a good index of actomyosin kinetics in unloaded conditions. Moreover, a very significant correlation was found between V₀ and V_f of actin on myosin extracted from the same fibres (Canepari et al. 1999; Pellegrino et al. 2003). The IVMA approach enables reliable study of the following factors: (a) the cross-bridge kinetics over a wide range of temperatures (20–35°C), because isolated myosin is stable up to physiological temperatures (Homsher et al. 1992; Yamashita et al. 1994; Rossi et al. 2005); and (b) the mechanical and the kinetic properties of pure myosin isoforms in the same experimental conditions that reproduce the actomyosin cycle as a whole.

Binding of MgATP to myosin

The value of V_f for slow and fast myosin depended on [MgATP] and increased with increasing temperature. The values of Q₁₀ and E_a were consistent with those expected on the basis of previous studies on isolated myosin in similar temperature ranges (Homsher et al. 2003; Rossi et al. 2005), muscle fibres (Pate et al. 1994) and muscles (Ranatunga, 1984; Kawai et al. 2000).

The relation between V_f and MgATP followed classic michaelian behaviour. Values of K_m (Table 1) for the fast skeletal isoforms were in good agreement with those for the shortening velocity of rabbit skeletal fibres in similar temperature ranges (Cooke & Pate, 1985; Pate et al. 1992) and with those for rabbit, rat and chicken pectoralis fast myosin in similar assay systems (Homsher et al. 1992; Yamashita et al. 1994; Regnier et al. 1998; Baker et al. 2002; Debold et al. 2008). The small differences among these studies may be explained by the differences in the skeletal muscle types (usually a mixture of fast isoforms), myosin preparation (myosin or the proteolitic fractions HMM or S1) and/or assay conditions (temperature, pH, ionic strength and the presence of MgATP back-up system). The values of K_m related to pure type 1 skeletal myosin are reported here, for the first time, and are very similar to those found for rat α-cardiac myosin in the IVMA system (Yamashita et al. 1994). The much lower values of K_m indicate that the V_f of the slow isoform is less sensitive to the decrease of substrate concentration than V_f of the fast isoform (Pate et al. 1992; Yamashita et al. 1994). As both decrease in force and a decrease in velocity of shortening occur in fatigue, the latter observation is consistent with the lower fatigability of slow compared with fast fibres. Moreover, as K_m = k_–ADP/k_+ATP [see eqn (3)], K_m can be considered to define the [MgATP] above which k_–ADP plays a larger role than k_+ATP in defining V_f. Therefore, the higher K_m of fast compared with slow myosin suggests that k_+ATP plays a more relevant role in defining V_f in fast than in slow myosin at subsaturating [MgATP].

Interestingly, the slow and fast isoforms showed a different temperature sensitivity, which also varied with the temperature range considered. In the range 25–35°C, the sensitivity to the decrease of substrate concentration did not change much on increasing temperature for the slow isoform (1.25-fold change), but increased significantly for the fast isoform (3.1-fold change). As K_m = k_–ADP/k_+ATP, the larger effect of temperature on k_+ATP of slow than fast myosin and the similar effect on k_–ADP of both isoforms (Table 2) can account for the latter phenomenon. Vice versa, in the range 20–25°C, the temperature sensitivity of K_m was high for the slow (3.8-fold change) and low for the fast isoform (1.42 fold change), consistent with the lack of sensitivity of k_+ATP in the slow isoform and the increase in sensitivity of k_+ATP of the fast isoform.

Binding of MgADP to myosin

In the presence of 2 mM MgADP, the substrate dependence of the velocity shifted towards higher [MgATP] for both isoforms. The value of K_mt was much higher than K_m for both isoforms at all temperatures, suggesting a competition between MgADP and MgATP for the myosin binding site.

To better define the impact of MgADP on velocity, assuming a competitive inhibition of V_f by MgADP, the inhibition constant (K_i) was calculated [eqn (2)]. The values of K_i (Table 1) are consistent with the values for rat skeletal and cardiac myosin in a similar assay system (Yamashita et al. 1992), but somewhat higher than those obtained for the shortening velocity of rabbit fibres (Cooke & Pate, 1985) and for the actin filament velocity of rabbit HMM and of rabbit and chicken myosin (Baker et al. 2002; Homsher et al. 2003; Greenberg et al. 2009). The differences in the values of K_i among these studies may be attributed to the differences in muscle types, myosin preparations, ionic strengths, MgADP concentrations and the temperature of the assay conditions.

The inhibition constant can be considered proportional to k_–ADP/k′_+ATP (Homsher et al. 2003). Thus, an elevated K_i for the fast isoform may be a result of a faster dissociation rate of MgADP, because k_–ADP can be considered a diffusion-limited process and therefore similar for all myosin isoforms (Nyitrai et al. 2006). Higher k_–ADP could account for the higher V_f of the fast isoform compared with the slow isoform, which is consistent with a major role of k_–ADP in defining shortening velocity (Weiss et al. 2001). The temperature dependence of K_i was different for the two isoforms. The values of K_i increased about threefold for the slow isoform and about 1.15-fold in for the fast isoform between 25 and 35°C. These results seem to be in accordance with the results of Nytrai and colleagues that showed, in the range between 12 and 25°C, that K_AD (K_AD = k_–ADP/k′_+ATP) was almost temperature independent in rat fast S1 and increased with increasing temperature in rat slow S1 (Nyitrai et al. 2006; Bloemink et al. 2007; Iorga et al. 2007). On the basis of these results, a significant role of k_–ADP in limiting the velocity of fast myosin isoform seems unlikely.

If we assume, however, that MgADP competes with MgATP for the nucleotide site on the myosin molecule in a competitive way (Siemankowski & White, 1984) then we would expect that high [MgATP] could remove the MgADP competition and produce the same V_max values. Surprisingly, values of V_maxinh (V_max in the presence of 2 mM MgADP calculated from the Michaelis–Menten equation) were, at all temperatures and for both isoforms, lower than the corresponding values of V_max (Table 1); therefore, the reliability of K_i and the suggestion regarding the role of k_–ADP in the fast isoform might be questionable.

Cross-bridge kinetics

According to a detachment-limited model of actin sliding velocity, k′_+ATP and k_–ADP could be calculated [eqn (3)]. The values of k′_+ATP were similar for the slow and fast isoforms (Table 2). The values of k′_+ATP were similar to those obtained for fast isoforms in IVMA (Baker et al. 2002; Homsher et al. 2003; Jackson & Baker, 2009) and to those obtained for fast and slow isoforms in optical trap experiments (Capitanio et al. 2006). The values were also similar to those obtained from biochemical measurements in solution (Nyitrai et al. 2006). However, while k′_+ATP determined in solution increased 2.5-fold between 12 and 25°C for both slow and fast isoforms (Nyitrai et al. 2006), in the present study the sensitivity of k′_+ATP to temperature was different for the slow and the fast isoform and varied with the temperature range. In the range 25–35°C, k′_+ATP of the slow isoform, but not of the fast isoform, increased with temperature, whereas in the range 20–25°C, k′_+ATP of the fast isoform, but not of the slow isoform, increased with temperature (Table 2). The discrepancy could be due to the known variation in temperature sensitivity with the temperature ranges analysed (Ranatunga, 1998; Rossi et al. 2005) and to the different experimental conditions (i.e. ionic strength, 50 versus 100 mM).

Importantly, k′_+ATP values were much higher than k_–ADP values (Table 2). Therefore, the present results suggest that in the temperature range 20–35°C k′_+ATP is unlikely to define V_f of slow and fast isoforms and its temperature sensitivity.

At all temperatures, the values for k_–ADP were greater (fourfold) in the fast than in the slow isoform and increased with V_f between 20 and 35°C in both isoforms. The values of k_–ADP are higher than those found for fast chicken myosin (291 s⁻¹ at 25°C and 100 mM ionic strength; Hooft et al. 2007; Jackson & Baker, 2009), but similar to those determined by optical trap experiments for fast and slow isoforms in similar experimental conditions (42.8 and 1156 s⁻¹ for the slow and the fast isoform, respectively; Capitanio et al. 2006). The data are also consistent with those obtained in solution (Nyitrai et al. 2006; Bloemink et al. 2007; Iorga et al. 2007) for the slow isoform. The data are not consistent with those obtained for fast isoform, which showed that k_–ADP was faster than k′_+ATP and temperature independent. At variance with what observed by Baker and co-workers (Baker et al. 2002; Hooft et al. 2007; Jackson & Baker, 2009), in our experimental conditions the values of k_–ADP determined at low [MgATP] were not different from those determined at high [MgATP].

Discrepancies with Nyitrai et al. (2006) regarding the role of k_–ADP can have several explanations. The different temperature range studied could account for the different temperature sensitivity of k_–ADP. Moreover, the lower ionic strength in the present study could contribute to the lower values of k_–ADP compared with k′_+ATP for fast isoforms. In fact, k_–ADP decreases twofold for slow myosin, but does not change for fast myosin with decreasing ionic strength from 200 to 30 mM, whereas over the same ionic strength range k′_+ATP increases twofold more for slow than for fast isoform (Nyitrai et al. 2006). Finally, in IVMA an ‘MgADP state’, which could be inaccessible in solution, can be sensed. It has been suggested, in fact, that MgADP binding/release can occur in two steps, because an isomerization step can precede MgADP release (Sleep & Hutton, 1980; Nyitrai & Geeves, 2004; Nyitrai et al. 2006; Albet-Torres et al. 2009; Mansson, 2010). The MgADP state, which precedes isomerization, is inaccessible by simply adding MgADP to actomyosin in rigor, as in solution studies (Nyitrai et al. 2006), whereas it occurs normally in IVMA, because the whole actomyosin cycle takes place.

In conclusion, the data presented here indicate that the rate of MgADP release from the actomyosin complex could define V_f in IVMA and therefore the difference between the fast and the slow myosin isoform. However, this conclusion applies to the conditions of IVMA (20–35°C) and low ionic strength (50 mM). We cannot exclude the possibility of a different relative role of k_–ADP and k_+ATP with different ionic strengths and at lower temperatures (Nyitrai et al. 2006; Iorga et al. 2007). Future experiments comparing the load dependence of the different isoforms could be useful to confirm and extend the present findings.