Prediction of New Clinical Vertebral Fractures in Elderly Men using Finite Element Analysis of CT Scans

Abstract

Vertebral strength, as estimated by finite element analysis of computed tomography (CT) scans, has not yet been compared against areal bone mineral density (BMD) by dual energy x-ray absorptiometry (DXA) for prospectively assessing the risk of new clinical vertebral fractures. To do so, we conducted a case-cohort analysis of 306 men aged 65 yrs and older, which included 63 men who developed new clinically-identified vertebral fractures and 243 men who did not, all observed over an average of 6.5 years. Non-linear finite element analysis was performed on the baseline CT scans, blinded to fracture status, to estimate L1 vertebral compressive strength and a load-to-strength ratio. Volumetric BMD by quantitative CT and areal BMD by DXA were also evaluated. We found that, for the risk of new clinical vertebral fracture, the age-adjusted hazard ratio per standard deviation change for areal BMD (3.2; 95% CI: 2.0–5.2) was significantly lower (p<0.005) than for strength (7.2; 3.6–14.1), numerically lower than for volumetric BMD (5.7; 3.1–10.3), and similar for the load-to-strength ratio (3.0; 2.1–4.3). After also adjusting for race, BMI, clinical center, and areal BMD, all these hazard ratios remained highly statistically significant, particularly those for strength (8.5; 3.6–20.1) and volumetric BMD (9.4; 4.1–21.6). The area-under-the-curve for areal BMD (AUC=0.76) was significantly lower than for strength (AUC=0.83, p=0.02), volumetric BMD (AUC=0.82, p=0.05), and the load-to-strength ratio (AUC=0.82, p=0.05). We conclude that, compared to areal BMD by DXA, vertebral compressive strength and volumetric BMD consistently improved vertebral fracture risk assessment in this cohort of elderly men.

INTRODUCTION

Vertebral fractures, the most common clinical manifestation of osteoporosis, can cause significant pain and portend future vertebral and hip fractures ⁽¹⁾. The most widely used clinical predictor of vertebral fracture is areal bone mineral density (BMD) as measured at the hip or spine by dual-energy absorptiometry (DXA) ⁽²⁾. However, areal BMD cannot distinguish between the cortical and trabecular bone or variable depth in the anterior-posterior direction, and for the spine is further confounded by osteophytes, facet arthritic changes, and aortic calcification. As a result of these limitations and because most of those who suffer osteoporotic fractures are not in fact osteoporotic as classified by areal BMD ^(3,4), there remains a need to develop clinically-feasible approaches that can improve fracture risk assessment for the spine.

One possible approach for improving fracture risk assessment for the spine combines quantitative computed tomography (CT) with finite element analysis and bone biomechanics to provide estimates of vertebral strength and a load-to-strength ratio. For the spine, this “biomechanical CT” (BCT) technique has been validated in cadaver experiments by multiple research groups ^(5,6), has provided unique insight into therapeutic treatment effects ^(7,8), and has surpassed DXA in differentiating individuals with versus without prevalent vertebral fracture ^(9,10). However, BCT remains untested against DXA for prospectively assessing the risk of new vertebral fractures. Addressing this limitation, we compared BCT-derived vertebral strength and the load-to-strength ratio, as well as volumetric BMD from quantitative CT, versus DXA-derived areal BMD for assessing the risk of new clinical vertebral fractures in elderly men. This study is novel since it is the first to report on such a comparison for the prediction of new vertebral fractures.

MATERIALS AND METHODS

Study Population

All participants in this study were from the multi-center MrOS observational study, which enrolled 5,994 volunteer community-dwelling participants from March 2000 through April 2002 at six sites throughout the U.S. and is described in detail elsewhere ^(11,12). All participants gave written informed consent. Eligible participants were at least 65 years of age, could walk without assistance from another person, and had not had bilateral hip replacement surgery. Proportions of Black, Asian, and Hispanic men enrolled at each study site were generally representative of those reflected in the local population of older men by US Census data ^(11,12). Because of resource constraints, CT scans at baseline were obtained for only 3,663 participants, with an effort to scan as many non-white men as possible. The demographics of the men in this “CT cohort” and the full cohort were comparable, except for a slightly greater proportion of non-white men in the CT cohort ⁽¹³⁾.

Study Design

We used a case-cohort design, our study cohort consisting of the approximately 3600 men from the overall MrOS “CT cohort” who also had a DXA exam at baseline. Our cases consisted of all men from this study cohort who had an incident (new) radiographically-confirmed “clinical” vertebral fracture, that is to say, a new vertebral fracture that presented clinically during the course of the observation period. These cases were compared to a randomly selected subset from our study cohort (any cases in that subset were removed). Age, weight, height, BMI, and areal BMD properties for our study sample were similar to those for the full MrOS CT cohort (Table 1). BCT analysis was performed on the baseline CT scans in a blinded fashion to provide measures of vertebral compressive strength; we also measured a load-to-strength ratio ^(14,15), as well as volumetric BMD by quantitative CT and areal BMD by DXA. The outcomes were then compared for their ability to predict the new clinical vertebral fractures.

Table 1.

Baseline means (SD in parentheses) for the full MrOS cohort who had CT at baseline, and for the sub-cohort included in this BCT study. Data are shown for the pooled dataset and also by fracture status (No-FX: no-fracture group; FX: fracture group). Percent differences (FX vs. No-FX) for the BCT sub-cohort are also shown when significant (p<0.05 at least; absolute difference is shown for age).

Measurement (units)	Full MrOS CT Cohort			BCT Sub-Cohort
	Pooled n=3489	No-FX n=3411	FX n=78	Pooled n=306	No-FX n=243	FX n=63	Difference %
Age (Years)	73.5 (5.8)	73.5 (5.8)	75.6 (5.9)	74.3 (6.2)	73.7 (6.1)	76.3 (6.3)	+2.6 *
Weight (kg)	83.0 (13.3)	83.0 (13.4)	80.9 (11.6)	83.8 (13.5)	84.4 (13.9)	81.4 (11.9)	n.s.
Height (cm)	174 (7)	174 (7)	174 (7)	174 (7)	175 (7)	174 (6)	n.s.
Body Mass Index (kg/m2)	27.4 (3.8)	27.4 (3.8)	26.8 (3.4)	27.5 (3.8)	27.6 (3.9)	27.0 (3.5)	n.s.
LS aBMD (g/cm2)	1.07 (0.19)	1.07 (0.19)	0.91 (0.15)	1.04 (0.19)	1.08 (0.19)	0.91 (0.14)	−15.7 **
FN aBMD (g/cm2)	0.78 (0.13)	0.79 (0.13)	0.72 (0.13)	0.76 (0.12)	0.78 (0.12)	0.71 (0.14)	−9.0 **
Integral vBMD (mg/cm3)	n.m.	n.m.	n.m.	189 (47)	199 (44)	151 (36)	−24.1 **
Vertebral Strength (N)	n.m.	n.m.	n.m.	6360 (2410)	6880 (2300)	4320 (1620)	−37.2 **
Load-to-Strength Ratio	n.m.	n.m.	n.m.	0.41 (0.18)	0.36 (0.12)	0.58 (0.26)	+61.1 **
Strength-to-Density Ratio (Ncm3/mg)	n.m.	n.m.	n.m.	32.7 (6.1)	34.0 (5.7)	27.9 (5.5)	−17.9 **

LS — Total Lumbar Spine; FN — femoral neck; aBMD — areal BMD from DXA; vBMD — volumetric BMD from quantitative CT; Load-to-Strength ratio is the ratio of estimated in vivo loading (N) to vertebral strength (N); Strength-to-Density ratio is the ratio of vertebral strength to Integral vBMD (the volumetric BMD of all bone in the finite element model. n.m. — data not measured in this analysis. Difference: n.s. — not significant;

^*p<0.005;

^**p<0.0001.

To assess new clinical vertebral fractures, every four months after baseline, MrOS participants completed a mailed questionnaire regarding recent falls and fractures. All thoracic and lumbar spine fractures that were reported by participants were then adjudicated centrally. To adjudicate, the radiological image (x-ray or MRI) used to diagnose the fracture by the participants’ physician in the community was obtained and sent to the Coordinating Center. The study radiologist confirmed the presence of a new vertebral fracture using these community acquired images, comparing them to lateral thoracic and lumbar x-rays that were obtained for all MrOS participants at baseline. A new clinical vertebral fracture was then defined as a change in Semi-Quantitative “SQ” grade ⁽¹⁶⁾ of at least one between the baseline film and follow-up image. The average (± SD) follow-up time for new fractures was 6.5 ± 2.2 years.

Scanning Procedures

Baseline CT and DXA scans were used for all analyses. The quantitative CT scans were obtained using a standardized protocol in which the lumbar region was scanned from 5 mm above the L1 superior endplate to 5 mm below the L2 inferior endplate. The scans were acquired using the settings: 120 kVp, 150 mA, 1-mm slice thickness (pitch of 1), 48 cm (or equivalent) field of view, 512×512 matrix in spiral reconstruction mode using a standard kernel. Although different types of CT machines were used at each site, the same type of calibration phantom (Image Analysis Inc., Columbia, KY) with known hydroxyapatite concentrations (0, 75 and 150 mg/cm³) was included in every scan. Areal BMD (in g/cm²) at the hip and spine was measured using the same model of fan-beam DXA scanner (QDR 4500W, Hologic Inc.). Centralized quality control procedures, certification of DXA operators, and standardized procedures for scanning were used to ensure reproducibility of DXA measurements.

BCT Analysis

BCT analysis of the anonymized CT scans was performed at UC Berkeley blinded to the fracture status of participants. Using custom software developed at UC Berkeley, each vertebral image was first calibrated using the external phantom (Image Analysis, Kentucky) visible in each image, segmented from the surrounding tissue using a constant threshold value, resampled to 1 × 1 × 1 mm³ voxels, rotated into a standard coordinate system, cropped to remove the posterior elements, then converted into a 1 × 1 × 1 mm³ voxel-type mesh of 8-node cube-shaped finite elements. To measure overall (“integral”) volumetric BMD for each vertebra, the volumetric BMD of each resampled voxel was averaged over all voxels in each finite element model.

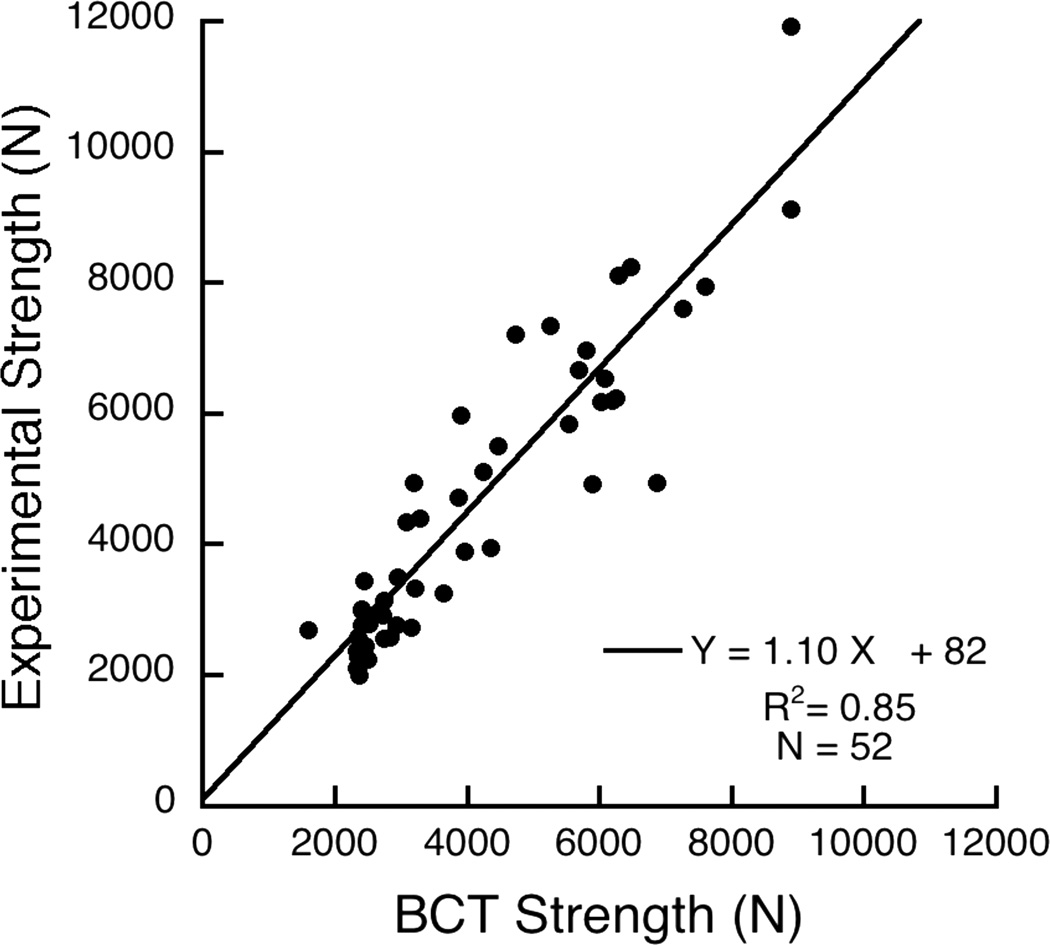
Following methods for finite element analysis similar to those described elsewhere ⁽¹⁷⁾, the volumetric BMD of each element was used to assign element-specific material properties to each finite element and the resulting “voxel-type” of finite element models were then virtually loaded to failure. All models were virtually loaded in uniform compression via a thin layer of polymethylmethacrylate (E = 2500 MPa) placed over the endplates, and all bone material was modeled as elastic-perfectly-plastic using a Mises failure criterion, based on cadaver data for human vertebral trabecular bone ⁽¹⁸⁾. Anisotropic elastic and isotropic strength properties that were implemented are described elsewhere ⁽¹⁷⁾ and were further adjusted to account for side-artifact errors ⁽¹⁹⁾ using the inverse-linear pooled density relations from Bevill et al. ⁽²⁰⁾. Non-linear finite element analysis (ABAQUS v6.6, Simulia) was used to compute a value of compressive strength, defined as the total reaction force generated at an imposed overall deformation equivalent to 1.9% strain. Results from cadaver biomechanical testing of 52 elderly vertebral bodies (Appendix) confirmed that this overall implementation provided highly correlated (R²=0.85) estimates of vertebral compressive strength compared to the experimentally measured values, with statistical Y=X accuracy (Figure A1).

Figure A1.

Validation of the BCT-derived compressive strength estimates against experimental measurements from biomechanical testing. Data are for 52 isolated individual vertebral body specimens (T7–L4) taken from 52 cadavers. Least squares regression analysis indicated that the slope was not significantly different than zero (95% confidence intervals of 0.97–1.23) and the intercept was not different than zero (p=0.78).

In addition to the vertebral compressive strength, we measured a number of secondary outcomes. To account for an estimate of the in vivo loading on a patient-specific basis, a load-to-strength ratio was calculated using patient-specific weight and height data. For this calculation, we used a static equilibrium model ⁽¹⁵⁾ to simulate 90° forward flexion while lifting a 10 kg mass in outstretched arms ⁽¹⁴⁾. Volumetric BMD (in mg/cm³) of all the bone in the finite element model, i.e. the entire vertebral body not including the posterior elements, was measured from the quantitative CT scans using the density information described above. To help assess any predictive effects of compressive strength over and above those associated with volumetric BMD, a strength-to-density ratio was computed from these two variables.

All BCT analyses were performed for the L1 vertebral level when acceptable CT scans were available for that level, or L2 otherwise. Originally, 374 CT scans were selected from the MrOS CT cohort for BCT analysis. Of these scans, 11 were not transferred to Berkeley, 39 were eliminated from further analysis due to missing slices in the CT scan, 15 scans were eliminated due to poor image quality, and 3 were eliminated due to an unusual vertebral body shape that prevented analysis. Hence, we obtained BCT data for 306 men. For 20 of these men, L2 was analyzed instead of L1 since L1 showed imaging artifacts.

Statistical Analysis

All statistical analyses were performed at the San Francisco Coordinating Center, after completion of all BCT analyses. Pearson correlation coefficients were calculated for the biomechanical parameters among themselves and versus lumbar spine areal BMD, age, weight, and BMI to determine associations with established predictors of fracture. Modeling of the time to incident spine fracture was performed using Cox proportional hazards regression with the Prentice weighting method and robust variance estimate necessitated by the case-cohort design ⁽²¹⁾. Hazard ratios for fracture were expressed per 1 SD change in the parameter, and also by quartiles with respect to the lowest risk quartile as the referent group. Covariates were then added to the model sequentially (age, race, BMI, study geographic site, then total lumbar spine areal BMD from the spine DXA) to assess their effect on the hazard ratio. To test the equivalence of hazard ratios (vs. that for areal BMD), two similar Cox models were fit to the same data simultaneously using a repeated measures approach. To assess prediction of fracture, receiver-operator-characteristic (ROC) analysis was used on the unadjusted variables and values of area-under-the-curve (AUC) for the various predictors were compared to the AUC for areal BMD using logistic regression. Because the most clinically relevant portion of the ROC curve for fracture risk prediction is the high-specificity region, we calculated values of sensitivity at 90% and 95% specificity. All statistical analyses were performed using SAS (version 9.1) except for the receiver-operator-characteristic analysis, which used STATA (version 11, SJ9-1 st0154).

RESULTS

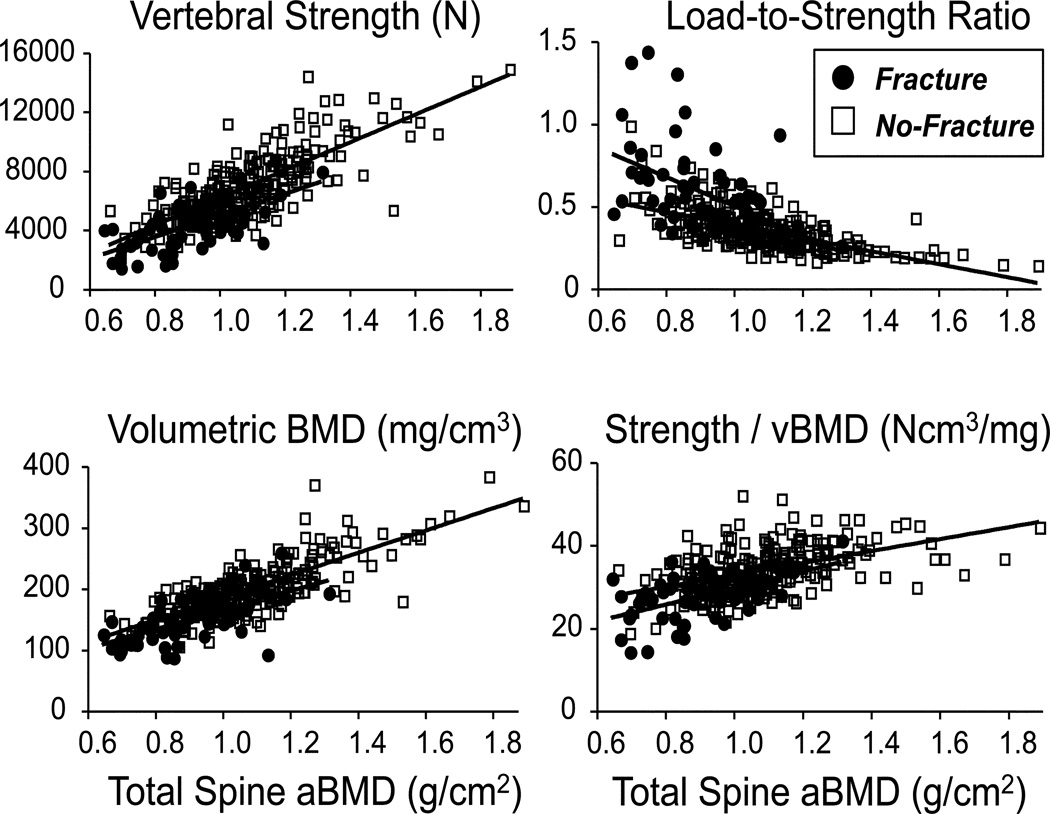
On average, compared to the men who did not fracture (n=243), the men who fractured (n=63) had lower values of all BMD measures, even lower values of strength, and proportionally higher (worse) values of the load-to-strength ratio (Table 1). Total lumbar spine areal BMD (−15.7%), femoral neck areal BMD (−9.0%), volumetric BMD (−24.1%), vertebral strength (−37.2%), and strength-to-density ratio (−17.9%) were all lower for those who fractured and the load-to-strength ratio was higher (+61.1%), compared to men without a fracture. Correlation analysis with age for the pooled data indicated that all properties were lower as age increased except for total lumbar spine areal BMD (not significant) and the load-to-strength ratio (which was higher, Table 2). As expected, both total lumbar spine areal BMD (r=0.79) and volumetric BMD (r=0.92) were positively correlated with vertebral strength (Table 2). Scatter plots revealed a trend for fracture cases to occur at very low values of strength and volumetric BMD, and high values of the load-to-strength ratio (Figure 1).

Table 2.

Pearson correlation coefficients between the various outcomes; univariate analysis; fracture and no-fracture groups are pooled.

	Age (Years)	Weight (kg)	Height (cm)	BMI (kg/m2)	LS aBMD (g/cm2)	FN aBMD (g/cm2)	vBMD (mg/cm3)	Strength (N)	Load-to- Strength Ratio	Strength-Den Ratio (Ncm3/mg)
Age	1.00	−0.32	−0.22	−0.25	−0.08	−0.16	−0.22	−0.25	0.20	−0.26
Weight	−0.32	1.00	0.50	0.87	0.23	0.39	0.21	0.29	0.03	0.31
Height	−0.22	0.50	1.00	0.02	0.15	0.17	0.00	0.11	0.06	0.24
Body Mass Index	−0.25	0.87	0.02	1.00	0.18	0.37	0.25	0.27	0.00	0.22
LS aBMD	−0.08	0.23	0.15	0.18	1.00	0.63	0.80	0.79	−0.60	0.56
FN aBMD	−0.16	0.39	0.17	0.37	0.63	1.00	0.58	0.56	−0.43	0.41
Integral vBMD	−0.22	0.21	0.00	0.25	0.80	0.58	1.00	0.92	−0.76	0.57
Vert. Strength	−0.25	0.29	0.11	0.27	0.79	0.56	0.92	1.00	−0.79	0.83
Load-Str Ratio	0.20	0.03	0.06	0.00	−0.60	−0.43	−0.76	−0.79	1.00	−0.74
Str-Den Ratio	−0.26	0.31	0.24	0.22	0.56	0.41	0.57	0.83	−0.74	1.00

See Table 1 for legends and units.

p ≤ 0.05 at least, except for italicized cases for which p > 0.05

Figure 1.

Vertebral strength, load-to-strength ratio, volumetric BMD, and the ratio of vertebral strength to volumetric BMD, all plotted against total lumbar spine areal BMD (by DXA). Fracture cases are shown in solid red (n=63), no-fracture cases are shown in open black (n=243). Total lumbar spine areal BMD values of 0.82 and 0.98 g/cm² correspond to T-scores of −2.5 and −1.0, respectively, using young male reference values.

On average, hazard ratios were generally higher for strength and volumetric BMD than for areal BMD (Table 3). Specifically, the age-adjusted hazard ratio per SD decrease for lumbar spine areal BMD (3.2; 95% CI: 2.0–5.2) was significantly lower (p<0.005) than for vertebral strength (7.2; 3.6–14.1), numerically lower than for volumetric BMD (5.7; CI: 3.1–10.3) and similar for the load-to-strength ratio (3.0; CI: 2.1–4.3). All hazard ratios were relatively insensitive to adjustment for age, race and BMI, but the hazard ratios for strength (9.6; 4.6–19.8) and volumetric BMD (9.9; 5.0–19.7) both increased appreciably after adjusting for clinical site. All hazard ratios for BCT-derived variables remained statistically significant and were only moderately attenuated when lumbar spine areal BMD was included in the statistical model (Table 3). When the hazard ratios were broken down by quartiles, the gradient of risk for the highest-risk quartile was consistently higher for each biomechanical outcome and volumetric BMD than for areal BMD (Table 4).

Table 3.

Relative Hazard per unit change in SD (95% confidence intervals in parentheses) for each of the main explanatory variables of new clinical vertebral fractures, with and without additional variables in the model.

Main Variable	Additional Variables in the Model
	None	Age	Age Race BMI	Age Race BMI Site	Age Race BMI Site LS aBMD
LS aBMD	3.5 (2.2–5.4)	3.2 (2.0–5.2)	3.3 (2.1–5.2)	3.4 (2.1–5.4)	—
FN aBMD	2.1 (1.4–3.2)	1.8 (1.2–2.9)	2.1 (1.3–3.6)	2.1 (1.2–3.5)	0.9 (0.4–1.8)
Integral vBMD	6.1 (3.4–11.1) *	5.7 (3.1–10.3)	5.8 (3.2–10.8)	9.9 (5.0–19.7) ***	9.4 (4.1–21.6)
Strength	7.6 (3.9–14.9) **	7.2 (3.6–14.1) **	7.3 (3.7–14.5) **	9.6 (4.6–19.8) ***	8.5 (3.6–20.1)
Load-to-Strength Ratio †	3.1 (2.2–4.4)	3.0 (2.1–4.3)	3.0 (2.1–4.5)	3.6 (2.5–5.1)	2.9 (1.9–4.4)
Strength-to-Density Ratio	3.4 (2.3–5.1)	3.3 (2.2–4.9)	3.3 (2.2–5.0)	3.4 (2.2–5.0)	2.2 (1.4–3.6)

Site — imaging geographic region. See Table 1 for legends and units.

^†Relative Hazard denotes an increase is risk per decrease in one standard deviation for all variables except for the load-to-strength ratio, for which it indicates an increase is risk per increase in one standard deviation.

^*p≤0.05,

^**p≤0.01,

^***p≤0.001 is for comparison vs. LS aBMD (same column) for the models in which LS aBMD was not included in the model (the last column).

Table 4.

Relative Hazard for each quartile, normalized with respect to the lowest-risk quartile, all adjusted for age (95% confidence intervals in parentheses).

Predictor	Relative Hazard for each Quartile†
	Q1	Q2	Q3	Q4
LS aBMD	14.3 (4.1–49.7)	7.5 (2.1–27.0)	3.2 (0.8–12.4)	1.0
Integral vBMD	26.9 (6.2–116)	10.9 (2.4–48.8)	3.9 (0.8–19.5)	1.0
Vertebral Strength	27.3 (6.2–120)	8.9 (1.9–40.8)	3.5 (0.7–17.5)	1.0
Load-to-Strength Ratio	1.0	2.1 (0.5–8.6)	6.4 (1.8–23.1)	19.6 (5.7–67.7)
Strength-to-Density Ratio	42.3 (5.5–326)	22.6 (2.9–177)	9.6 (1.2–77.6)	1.0

See Table 1 for legends and units.

^†Q1 is taken as the lowest quartile, having the lowest absolute values of the predictor variable; Q4 has the highest values. For the calculation of relative hazards, the quartile with the lowest risk is the referent, and has its relative hazard set to unity; this referent quartile is Q4 for all predictors except for the load-to-strength ratio, for which it is Q1.

These trends for the hazard ratios were accompanied by improvements in fracture prediction, as characterized by the receiver-operator-characteristic analysis. Compared to the AUC value for total spine areal BMD (AUC=0.76; Table 5), AUC values were higher for each of vertebral strength (AUC=0.83, p=0.02), volumetric BMD (0.82, p=0.05), and the load-to-strength ratio (AUC=0.820, p=0.05). At clinically relevant levels of high specificity, the sensitivity for vertebral strength was higher than for total spine areal BMD (0.52 vs. 0.43 at 90% specificity; and 0.37 vs. 0.30 at 95% specificity) and similar trends were seen for the load-to-strength ratio. Sensitivity for volumetric BMD was less consistent. At 95% specificity, the sensitivity for volumetric BMD was higher than for areal BMD (0.38 vs. 0.30), but at 90% specificity the sensitivity values were similar (0.44 vs. 0.43).

Table 5.

Area-under-the-curve (AUC) values from ROC analysis (unadjusted variables), and the associated sensitivity values for two clinically relevant values of high specificity (90% and 95%).

Variable	AUC	p-value*	Sensitivity (%)
			90% Specificity	95% Specificity
LS aBMD	0.76		43	30
FN aBMD	0.65		30	21
Integral vBMD	0.83	0.05	44	38
Vertebral Strength	0.83	0.02	52	37
Load-to-Strength Ratio	0.82	0.05	52	37
Strength-to-Density Ratio	0.77	0.74	30	24

See Table 1 for legends.

^*p-value is for comparing the AUC value against that for LS aBMD; not performed for FN aBMD.

DISCUSSION

Our main goal in this observational multi-center study was to assess BCT-derived vertebral strength compared to areal BMD for assessing the risk of new clinical vertebral fractures in older men. By all metrics employed for this comparison, fracture risk assessment was significantly improved by vertebral strength. Although BCT-derived estimates of vertebral strength or the load-to-strength ratio in cross-sectional studies have been shown to better discriminate those with from those without prevalent spine fractures ^(9,10), this study is the first to demonstrate improved vertebral fracture risk assessment in a prospective manner, that is to say, for prediction of new spine fractures. Although not our main focus in this analysis, our results also demonstrated improved assessment using volumetric BMD. While average values for the load-to-strength ratio were much higher (worse) for fracture than non-fracture men, it appears that of the biomechanical variables investigated in this analysis, strength was the most robust predictor.

These results provide new insight into the etiology of spine fractures. The high correlation between strength and volumetric BMD indicates that much of the association of strength with fracture risk in this study can be ascribed to inter-individual variations in volumetric BMD. This is an insightful etiologic finding for the spine since it indicates that average volumetric density dominated the improvement of the strength-based fracture risk assessment over areal BMD, as opposed to, for example, more subtle factors such as 3D vertebral shape or intra-specimen variations in BMD. This is not to say that geometry and spatial variation in density is not important for vertebral strength. We focused on measurement of L1 vertebral strength in this study, but the fractures were recorded anywhere in the thoracic and lumbar spine. If geometric information implicitly embedded in the measure of L1 strength does not adequately reflect the geometry of the vertebral level at which actual fracture occurs, it is possible that that geometric information could actually confound the prediction. However, since we found that vertebral strength performed at least as well as volumetric BMD at prediction of vertebral fracture, the geometry information within the L1 vertebral strength metric did not confound the fracture prediction. Our finding that strength tended to perform more robustly than the load-to-strength ratio was somewhat surprising, particularly since we found comparable performance of strength and the load-to-strength ratio in our prior study of vertebral fractures in women ^(10,14). This finding suggests that the role of loading on vertebral fracture risk may differ between men and women, and further studies are required to address this open issue.

Despite the new insight provided by these results, it remains to be seen how the improvements found here translate into clinical improvements in terms of identifying patients at highest risk of fracture. While beyond the scope of this first BCT study of the spine on this cohort, recent types of reclassification analysis might be well suited for such purposes ^(22,23). This is because the traditional AUC analysis used in our study is rather broad for applications such as osteoporosis for which clinical classifications relevant to treatment decisions are made only over a narrow range of (high) specificity. In the meanwhile, the data shown in Figure 1 suggest some possibilities. For example, for the 20 men who fractured and who also had a strength value of less than about 3500 N, 10 of them had a T-score below −2.5 (“osteoporotic”) and 10 of them had a BMD T-score between −1.0 and −2.5 (“osteopenic”). While we are not advocating here that this specific strength value be used as a clinial cut point, these data nevertheless suggest that men with the very lowest values of L1 vertebral strength may have a high risk of vertebral fracture even if classified as osteopenic based on traditional areal BMD criteria. Consistent with this trend for individuals, on average, the hazard ratio analysis indicated that strength and volumetric BMD were predictors independent of areal BMD, and when the hazard ratios were broken down by quartile (Table 4), relative hazards in the highest-risk quartiles were much higher for volumetric BMD and the biomechanical outcomes than for areal BMD.

This study design had a number of novel features compared to other studies ^(9,10) that used BCT to assess vertebral fracture risk. Most uniquely, our study was prospective in nature, predicting new fractures in a fully blinded manner. We maximized statistical power for the given sample size by focusing on “clinical” spine fractures, i.e. those that presented clinically and that were confirmed radiographically. However, it is not clear how our results would apply to radiographically-defined deformities, although it appears that inclusion of mild deformities would likely dilute the predictive ability, both of DXA and BCT ⁽¹⁰⁾. Our study design is somewhat limited in that the small sample size — due to both the relatively small number of fractures and the use of a randomly sampled subset of the cohort — produces wide confidence intervals, diminishing our ability to detect significance differences, e.g. between the age-adjusted hazard ratios for volumetric BMD vs. areal BMD. These study-design issues can be addressed in the future for the MrOS cohort when more clinical and all deformity fractures become available for analysis.

In generalizing our results, we note that our cohort included only men, all of whom were older than 65 and most of whom were Caucasian, and that our study is the only one currently available for BCT assessment of vertebral fracture in men. Additional studies are therefore required to confirm these results for other cohorts of men. For women, there are no prospective BCT spine studies available yet. Given the high statistical significance of the results observed here, particularly the high hazard ratio after including areal BMD in the hazards model, and given results from multiple BCT studies that consistently show an advantage of either BCT or volumetric BMD parameters over areal BMD for assessment of prevalent vertebral fractures in women ^(9,10), it is reasonable to hypothesize that BCT would also predict new clinical vertebral fractures in women, although this remains to be demonstrated. Regarding race, although the MrOS population does include some non-Caucasian men, there were few fractures in non-white men in our sample and whether the current results are applicable in non-Caucasian populations also requires confirmation in other studies. However, compared to areal BMD, BCT-derived vertebral strength did improve assessment of prevalent fractures in Japanese women ⁽²⁴⁾.

From a technical perspective, the finite element models, although detailed, do provide only estimates of actual vertebral strength. While our estimates of compressive strength were well validated by biomechanical testing of cadaver vertebrae (Figure A1), and while our technique is in good general agreement with finite element predictions made from much higher resolution micro-CT-based finite element models ⁽²⁵⁾, the evolving clinical BCT technology does allow room for improvement. For example, model predictions might be improved by using alternative strategies for constitutive modeling of the bone ⁽⁶⁾, or by including such additional biomechanical features as bending type loads ^(6,26), patient-specific descriptions of kyphosis and musculature, or inclusion of a disc instead of polymethylmethacrylate^(27,28), or even patient-specific modeling of the disc ⁽²⁹⁾. Further, evaluation of such other measures as the volumetric BMD of the trabecular or cortical compartments ^(10,30) and the strengths associated with these compartments ⁽⁷⁾ was beyond the scope of this initial study, but such measures may improve prediction⁽¹⁰⁾, as might combining strength and other measures in a multivariate statistical-based risk model. Due to limited spatial resolution, any DXA- or (clinical) CT-based assessment provides no information on such micro-scale effects as microstructure ^(31,32), mineral characteristics ⁽³³⁾, microdamage ⁽³⁴⁾, resorption cavities ^(35,36), or collagen cross-linking ^(37,38).

Since the BCT technology is still evolving, we caution that absolute values reported here for vertebral strength, and even for volumetric BMD, may be different if different software is used due to different assumptions made in the finite element analysis and different region-of-interest volumes sampled in the volumetric BMD measurement. The software used in this analysis was developed at UC Berkeley for the purposes of this specific research study and was not optimized for robust clinical use. As a result, we did not analyze about 15% of the original scans due to various types of imaging artifacts and technical problems. While this loss rate partly represents the inevitable challenges of early adoption of CT scanning and cross-calibration in a large multi-center study such as MrOS, it also signals a challenge if using BCT in a heterogeneous clinical setting.

In summary, we found that vertebral strength, other BCT outcomes, and volumetric BMD were strongly associated with the risk of new clinical vertebral fractures in elderly men, alone and after accounting for age, BMI, and areal BMD. A large part of the predictive ability of vertebral strength was associated with variations in volumetric BMD. Overall, compared to areal BMD by DXA, vertebral compressive strength and volumetric BMD consistently improved vertebral fracture risk assessment in this multi-site study of elderly men.

Appendix

A cadaver study was performed to validate the BCT-derived estimates of vertebral compressive strength against experimentally measured values from biomechanical testing. We analyzed 52 cadaver vertebral bodies (T7–L4), each bone from a separate cadaver (age 67.1±11.8 years, range 20–87; 25F, 27M). All vertebral bodies were separated from surrounding tissue, had their posterior elements removed, and were then scanned with quantitative CT while submerged in a bath of water (Philips Mx8000 IDT 16 CT scanner, 120kV, 200mA, “bone” kernel at 1 mm slice thickness; Philips Medical Systems NA, Bothell, WA). After imaging, the vertebral bodies were molded to endplates using a 1–3 mm layer of polymethylmethacrylate (PMMA) and compressed at a displacement rate of 0.15 mm/sec to beyond the ultimate point (Instron Model 5583, Instron Corporation, Canton, MA) following a protocol similar to that described elsewhere ⁽³⁹⁾. The ultimate strength was taken as the first obvious local maximum force observed from the force-deformation curve. Finite element models were created from each scan, according to the methods used in our clinical study. Results indicated a strong correlation between experiment and model, with statistical Y=X type of agreement (Figure A1).