Simultaneous, accurate measurement of the 3D position and orientation of single molecules

Abstract

Recently, single molecule-based superresolution fluorescence microscopy has surpassed the diffraction limit to improve resolution to the order of 20 nm or better. These methods typically use image fitting that assumes an isotropic emission pattern from the single emitters as well as control of the emitter concentration. However, anisotropic single-molecule emission patterns arise from the transition dipole when it is rotationally immobile, depending highly on the molecule’s 3D orientation and z position. Failure to account for this fact can lead to significant lateral (x, y) mislocalizations (up to ∼50–200 nm). This systematic error can cause distortions in the reconstructed images, which can translate into degraded resolution. Using parameters uniquely inherent in the double-lobed nature of the Double-Helix Point Spread Function, we account for such mislocalizations and simultaneously measure 3D molecular orientation and 3D position. Mislocalizations during an axial scan of a single molecule manifest themselves as an apparent lateral shift in its position, which causes the standard deviation (SD) of its lateral position to appear larger than the SD expected from photon shot noise. By correcting each localization based on an estimated orientation, we are able to improve SDs in lateral localization from ∼2× worse than photon-limited precision (48 vs. 25 nm) to within 5 nm of photon-limited precision. Furthermore, by averaging many estimations of orientation over different depths, we are able to improve from a lateral SD of 116 (∼4× worse than the photon-limited precision; 28 nm) to 34 nm (within 6 nm of the photon limit).

The recent emergence of superresolution far-field optical microscopy techniques has provided a means for attaining resolution beyond the diffraction limit (∼250 nm) in noninvasive fluorescence imaging of biological structures (1, 2). Some of these techniques [including (f)PALM (3, 4), STORM (5), and PAINT (6)] rely on precise localization of sparse subsets of single-molecule (SM) emitters to surpass the diffraction limit by up to an order of magnitude (precisions of tens of nanometers). Collectively, these SM-based superresolution techniques can be grouped under the name SM Active Control Microscopy (SMACM), because they all rely on using various experimental strategies (photoactivation, switching, blinking additives, etc.) to maintain a very low concentration of emitters in each imaging frame, enabling the localization of SMs without overlap. Typically, the SM fitting uses estimators that assume isotropic emission, i.e., that the center of the photon distribution of an SM image corresponds directly to the true position of the molecule. Examples of these estimators include centroid finding, least-squares fitting to a 2D Gaussian function, and maximum likelihood methods that assume isotropic emitters.

However, immobile fluorescing SMs produce an inherently anisotropic emission pattern that depends on the orientation of the SM emission dipole moment relative to the optical axis (7, 8). The work by Enderlein et al. (9) has shown that fitting such an SM image to a 2D Gaussian can result in position errors of tens of nanometers for molecules located in the microscope’s focal plane. Even more strikingly, the work by Engelhardt et al. (10) noted that, with modest defocusing (z = ±300 nm), the position error associated with fitting to a centroid can exceed 100 nm for certain SM dipole orientations. If labels are sufficiently rotationally mobile such that they explore much of the orientation space within a single acquisition, this effect is averaged away, and accuracy can be recovered. However, in some cases, labels of biological structures can exhibit well-defined orientations (11). Furthermore, fluorophores can be purposely anchored to convey orientation information about biological macromolecules, such as work in various SM studies on motor protein translocation (12–14). Although this position error has important implications for 2D SMACM techniques, the implications for 3D SMACM techniques are even more significant. Namely, techniques such as astigmatism (15), multiplane (16), iPALM (17), and Double-Helix Point Spread Function (DH-PSF) (18) imaging depend explicitly on precise 3D localization of SMs over an extended depth of field of up to ∼2 μm. Failure to account for this dipole orientation effect can clearly lead to large position inaccuracies that severely limit the superresolving capabilities of these techniques. Of these 3D methods, the DH-PSF is uniquely suited to address orientation effects, because its double-lobed shape results from the superposition of various waves in the microscope’s pupil plane that converge and interfere in the image plane; the intensities of these waves are strongly affected by the dipole radiation pattern of SMs.

There are many established methods for determining dipole orientation of single fluorophores. Approaches have been developed that rely on excitation and/or emission with multiple polarizations (19, 20), introduction of defocus and pattern matching (21), direct imaging of pupil functions (22), and use of annular illumination to create characteristic field distributions (23) to name a few. The alternating measurement of 2D position and orientation has also been addressed (24). Two groups considered simultaneous 2D localization and orientation fitting for molecules located in the focal plane (25) or molecules at a known defocus (26). However, neither explicitly addresses the correction of systematic errors on the order of 50–100 nm, and these methods require fine sampling and accurate fitting of detailed patterns in SM images. This paper shows simultaneous measurement of precise and accurate 3D localization and molecular orientation. We account for and correct large localization errors using an adaptation of the established DH-PSF method.

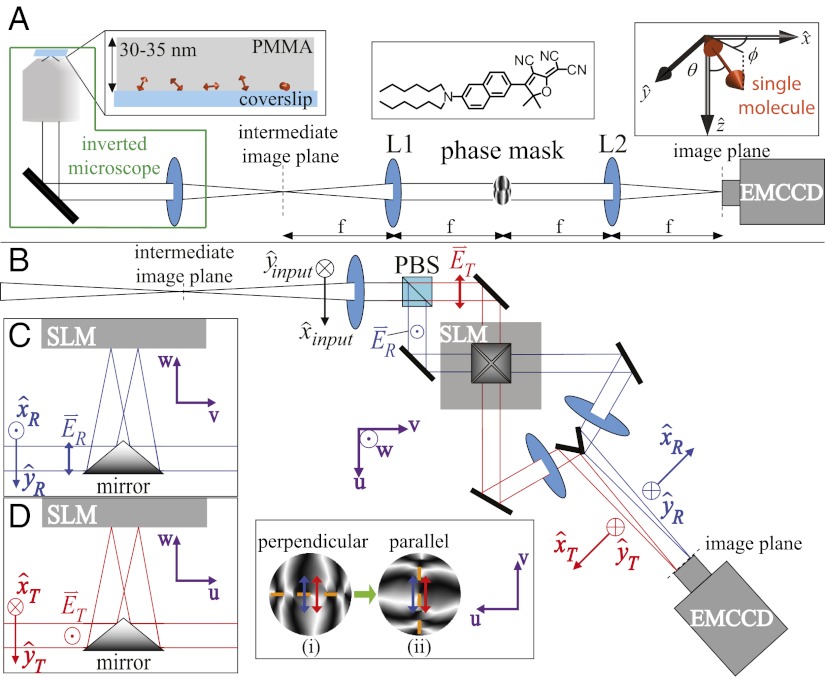
The basics of the DH-PSF microscope have been described in detail elsewhere (18). Briefly, the DH-PSF causes a single fluorescent emitter to appear on the detector as two closely spaced lobes. Here, we use an estimator based on fitting the two lobes with two Gaussian functions. Precise x and y localization can be extracted from the midpoint (x, y) position between the two lobes, whereas precise z localization is determined by the angle of the axis connecting the two lobes. As an emitter is moved in z, the DH-PSF revolves, effectively tracing out a double helix along the optical axis and thus, encoding the z position in the angle of revolution calibrated separately by z translation of a fluorescent bead. In the experimental implementation (Fig. 1A), the DH-PSF response is generated by convolution with the standard SM image using an appropriate phase mask at the Fourier plane of a 4f imaging system built directly after the intermediate image plane of a standard microscope. Typically, the phase mask is loaded onto a phase-only reflective liquid crystal spatial light modulator (SLM) (27–29). This type of SLM can only modulate vertically polarized light, and therefore, the emission must be polarized before being detected. Previously, a dual-polarization DH-PSF microscope was described, in which two orthogonal polarizations were split by a polarizing beam splitter, the horizontally polarized channel was rotated with a λ/2 wave plate, and each polarization channel was then reflected separately off the SLM at necessarily disparate angles of incidence (30). This scheme is not ideal for our application, because the different angles of incidence on the SLM cause each channel to incur dissimilar aberrations. For the measurement in this paper, it was necessary to detect the two polarization channels with maximal channel symmetry provided by the setup shown in Fig. 1B. The two polarization channels are forced to have the same angle of incidence on the SLM by making use of a square pyramidal mirror to deflect the beams out of the plane into the w direction (marked in Fig. 1 B–D) and onto the SLM mounted from above with its face to the mirror (Fig. 1 C and D). Polarized images are measured with two orthogonal orientations of the phase mask (Fig. 1B Inset) for reasons described below.

Fig. 1.

DH-PSF imaging system. (A) Inverted microscope and 4f optical system schematic, where L1 and L2 are focal length-matched achromatic lenses. Our sample for the experiments described consisted of DCDHF-N-6 molecules (Center Inset) embedded in a thin layer of PMMA (Left Inset). Orientation angles (θ, ϕ) are defined in Right Inset and have ranges (0°, 90°) and (−180°, 180°), respectively. (B) The high efficiency dual-polarization detection DH-PSF setup used for these experiments (inverted microscope omitted for simplicity). The collected fluorescence is split by a polarizing beam splitter (PBS) into reflected (R; blue) and transmitted (T; red) channels. Input Cartesian unit vectors 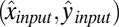define molecular orientation (θ, ϕ) and are propagated differently through the various reflections in the two polarization channels [ 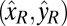and 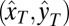]. 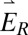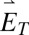The two electric field polarization axes and are projected identically onto the phase mask (Inset). Inset shows how each polarization axis (blue and red arrows) is oriented relative to the mask’s axis of phase discontinuities (dashed orange) when the mask is upright (i; polarization perpendicular to discontinuities) and rotated (ii; polarization parallel to discontinuities). (C and D) Two side-on views of the SLM portion of the setup showing the square pyramidal mirror.

It is well-known that splitting emission into orthogonal polarization channels alone yields some information about an emitter’s azimuthal (ϕ) (Fig. 1A Insets) orientation based on the computed linear dichroism,

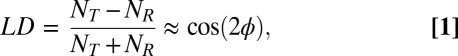in which N_T and N_R are the numbers of photons detected above background in the transmitted and reflected polarization channels, respectively, and the last equality is exact only if the partially depolarizing effect of high numerical aperture (N.A.) optics is ignored. Here, transmitted and reflected are defined relative to the polarizing beam splitter (Fig. 1B). Clearly, LD is related to the projection of an SM dipole onto the detection polarizations, which in turn, is related to ϕ, but there exist degeneracies if LD is the only recorded measurement (12). To break degeneracies and measure polar orientation (θ) (Fig. 1A Insets), another parameter must be measured. Interestingly, the DH-PSF uniquely offers such a parameter. Namely, the relative intensity of the two lobes of the DH-PSF is actually a function of (z, θ, ϕ) of an SM emitter. Whereas an isotropic point source yields lobes of equal intensity for all z when convolved with the DH-PSF, our simulations (vide infra) show that images of SM dipoles can exhibit large lobe asymmetries (LA) for certain orientations at various values of defocus (Fig. 2A). Qualitatively, this asymmetry is introduced because the asymmetric pupil functions of SM dipoles (22) are multiplied by the DH-PSF phase mask, causing various spatial frequencies of the ordinary DH-PSF to be attenuated as a function of orientation and defocus. We quantify the lobe asymmetry as

in which A_L1 and A_L2 are the amplitudes (as determined by a nonlinear least squares fit to a double Gaussian function) of lobes 1 and 2 of the DH-PSF, respectively. By measuring (z, LD, LA) from DH-PSF images of an emitter, we are, thus, able to determine the molecule’s orientation as described below.

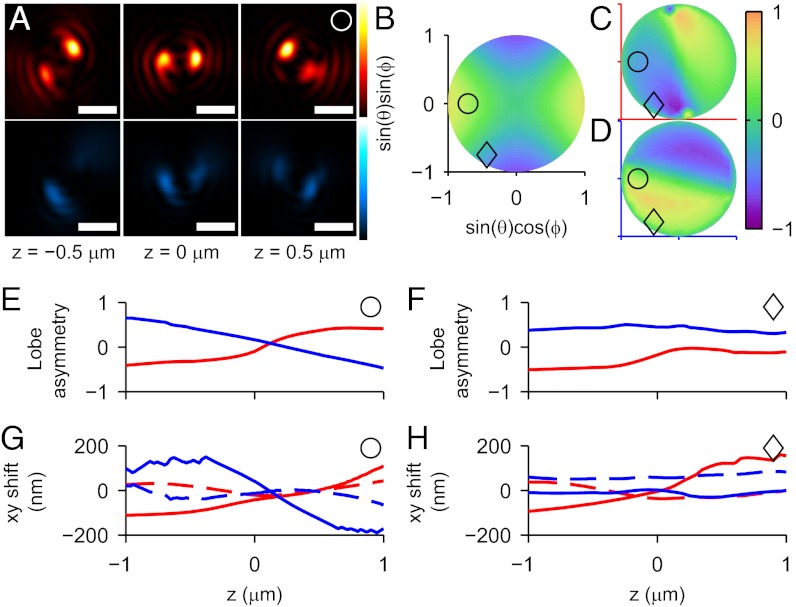
Fig. 2.

Simulated behavior of the DH-PSF response to dipole orientation. (A) Example DH-PSF images of a molecule with orientation (θ = 45°, ϕ = 180°) at several z positions. Upper (red) shows images that appear in the parallel polarization channel, whereas Lower (blue) shows images from the perpendicular polarization channel (definitions in the text). (Scale bar: 1 μm.) (B) A z cross-section (z = −500 nm) of LD as a function of (θ, ϕ), where (θ, ϕ) are projected into rectangular coordinates according to the relations marked on the axes. The center of the plot corresponds to a dipole aligned with the optical axis (θ = 0°), whereas the perimeter of the plot corresponds to molecules with θ = 90°; ϕ is the azimuthal angle from the positive x axis that increases in a counterclockwise direction. The points marked with ○ and ◇ correspond to the orientations (θ = 45°, ϕ = 180°) and (θ = 60°, ϕ = −120°), respectively. (C and D) Corresponding plots showing the functional behavior of LA vs. orientation for constant z = −500 nm in the parallel (C; red axes) and perpendicular (D; blue axes) channels, respectively. (E) LA vs. z in the parallel (red) and perpendicular (blue) channels for a fixed example dipole orientation (○). (F) The same plot for a different orientation (◇). (G) Δx (solid line) and Δy (dashed line) vs. z in the two channels for the ○ orientation. (H) The same plot for the ◇ orientation.

Simulations

We simulated the DH-PSF response to dipole orientation based on full vectorial diffraction calculations (21), in which dipole emitters are embedded in a polymer at a fixed distance below the air–polymer interface (SI Text and Fig. S1). The polarized electric field distributions from this calculation were propagated to the intermediate image plane and convolved with the DH-PSF as in the experimental setup, and the final images (Fig. 2A) were fit with a double Gaussian estimator (SI Text and Fig. S2). This procedure was repeated for various (z, θ, ϕ) to sample the functions LD(z, θ, ϕ) and LA(z, θ, ϕ) at resolution (δz = 50 nm, δθ ∼ 6.5°, δϕ ∼ 6.5°). Fig. 2 B–D shows a z cross-section of this functional behavior, linearly interpolating between samples, whereas Fig. 2 E and F gives two examples of how LA varies with z for fixed (θ, ϕ). Notably, LA has a distinct functional form in each of the parallel and perpendicular polarization channels (where parallel and perpendicular refer to the relative orientation between the axis of polarization and the axis of phase discontinuities in the DH-PSF phase mask) (Fig. 1B Inset) because of the fact that the asymmetry of the phase mask itself breaks the degeneracy of the two channels. From the estimator fit, we also mapped the apparent lateral shifts (Δx, Δy) associated with the DH-PSF as a function of (z, θ, ϕ). Fig. 2 G and H shows that this shift can, indeed, be on the order of ∼200 nm, similar to the behavior of the standard PSF (10). In general, more highly inclined molecules (θ closer to 0°) tend to exhibit both larger LA and larger (Δx, Δy).

These simulations provided a library that was used to fit orientation and correct the associated position error of a real measurement using the following algorithm. First, polarized DH-PSF images were fit with a double Gaussian estimator, yielding the observables (x_apparent, y_apparent, z, LA, LD). The apparent lateral position (x_apparent, y_apparent) is the true lateral position of the molecule (x_true, y_true) plus the apparent lateral shift (Δx, Δy) caused by the dipole emission effect. Second, (z, LA, LD) were fed to the simulated look-up table to give an estimate of the orientation (θ, ϕ). Third, (z, θ, ϕ) were referenced by the simulation to give a predicted (Δx, Δy) that was then subtracted from (x_apparent, y_apparent) to recover the true lateral position of the molecule: (x_true, y_true). In principle, SM dipole emission also causes errors in the double Gaussian-based estimate of z; however, our simulations show that this error is small compared with our precision in z. Here, we neglect this effect, but in principle, it can be corrected by extending the scheme above.

Experimental Validation

To show our ability to fit orientation and correct apparent shifts, we recorded SM images using the setup in Fig. 1B. Samples consisted of dicyanomethylenedihydrofuran-N-6 (DCDHF-N-6) (31) molecules spun in a layer of poly(methyl methacrylate) (PMMA) (Fig. 1A Insets) that provided a rigid enough environment such that angular flexibility of the dipole orientation was minimized. For a given field of view, the objective was scanned over z in 50-nm steps over a 2-μm total depth range (DR) centered about the focal plane. Images were recorded at every z step, and therefore, for each SM, many different sets of observables (x_apparent, y_apparent, z, LA, LD) were recorded. From each single measurement of this set, we estimated orientation and 3D position according to the prescription detailed above, and ultimately, we subtracted lateral shifts (Δx, Δy) from the apparent positions. Because we do not expect the orientation or lateral position of an SM to change on our imaging timescale for PMMA at room temperature, each independent measurement should produce the same (x_true, y_true, θ, ϕ) within some precision. In other words, our method is validated if the determined (x_true, y_true, θ, ϕ) of an SM are each constant functions of z.

Simulations show that the DH-PSF dipole response is dependent on 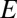-field polarization, as a consequence of the asymmetry of the phase mask. Because of the geometry of our setup, however, the polarization axis of each polarization channel is identical in the SLM plane (propagation of 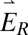and 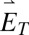in Fig. 1 B–D). This property of our optical system has the effect of rendering both experimental polarization channels with either parallel-type behavior or perpendicular-type behavior, depending on the orientation of the mask (Fig. 1B Inset). Thus, to capture the full behavior of the DH-PSF response to dipole emission patterns, we measured each SM with the mask oriented upright (perpendicular) and rotated by 90° (parallel). It is important to note that the two simultaneously recorded images (in the T and R channels) are not identical and do not purvey degenerate information, despite both exhibiting parallel-/perpendicular-type behavior, because the molecular coordinates are projected differently onto the mask in the T and R channels. Hence, we used nondegenerate information provided from four different images (two acquisitions of two polarization channels) of each SM to produce a single estimate of (x_true, y_true, θ, ϕ). We collected ∼3,000–8,500 (Table S1) total photons per set of four images, a number on the same order as typical SMACM measurements, but the high stability of the SMs allowed this collection to be done for many z positions.

As an independent verification of these orientation estimates, we also measured orientation directly through defocused images of SMs using the standard PSF (21). The defocused images were acquired by toggling off the DH-PSF phase mask (thereby invoking a clear aperture) and defocusing the microscope objective by 1.00 ± 0.15 μm away from the sample. By comparing these images with simulations using template matching (SI Text and Fig. S3), we extracted a separate estimate of (θ, ϕ). Interestingly, we found it necessary to correct primary astigmatism and coma using the SLM and include spherical aberration in our simulations to match experimental images to simulated ones (SI Text). DH-PSF orientation estimation, however, did not require accounting for these aberrations explicitly to produce the results described below [although some amount is included implicitly in the calibrated DH-PSF response of (x, y) vs. z] (SI Text). Because the DH-PSF mask itself works by imparting a sizeable distortion on the wave front, the associated images seem to be more robust to minor disturbances of the wave front caused by aberrations (32).

Results and Discussion

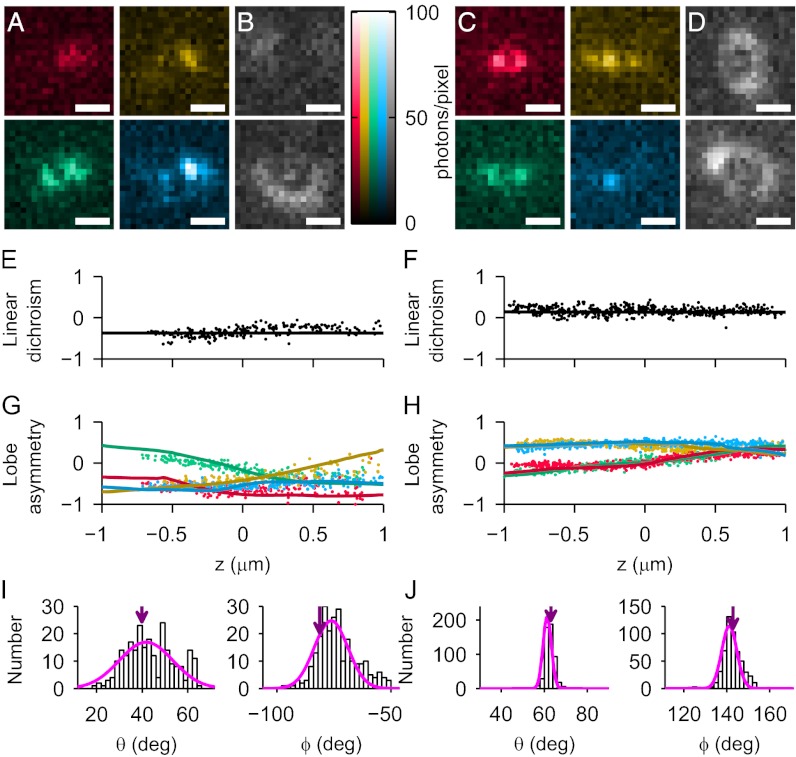
Using our DH-PSF–based method, we estimated the orientations of six SMs (two example molecules are shown in Fig. 3, and more examples are shown in Fig. S4). To distinguish the four images, we assigned colors to each mask orientation/polarization channel combination: mask parallel/transmitted polarization is the red channel, mask perpendicular/transmitted polarization is the gold channel, mask parallel/reflected polarization is the green channel, and mask perpendicular/reflected polarization is the blue channel. Fig. 3 A and C shows representative images of the DH-PSF for each example molecule in the four channels at a single z position, whereas Fig. 3 B and D shows the corresponding clear-aperture defocused images. For both example molecules, we show each measurement of LD (Fig. 3 E and F) and LA (Fig. 3 G and H) as a scatter point plotted vs. z. For each quartet of LA measurements and associated LD measurements, there is a corresponding estimation of (θ, ϕ). The mean orientation of the Gaussian fit of these distributions of (θ, ϕ) yields the solid overlays in Fig. 3 E–H. The full distributions of DH-PSF–extracted (θ, ϕ) are shown in Fig. 3 I and J. The sequential build up of these histograms as the objective was scanned for molecule 1 is shown in Movie S1. Also displayed for each molecule in Fig. 3 I and J is the orientation estimated from our independent defocused measurement (Fig. 3 I and J, purple arrows). We show excellent agreement between the defocus-determined orientation and the DH-PSF–based measurements: (θ_DH-PSF = 42° ± 12°, ϕ_DH-PSF = −76° ± 7°) and (θ_defocus = 40° ± 2°, ϕ_defocus = −81° ± 4°) for molecule 1; (θ_DH-PSF = 61° ± 2°, ϕ_DH-PSF = 141° ± 4°) and (θ_defocus = 63° ± 3°, ϕ_defocus = 143° ± 5°) for molecule 2. The SDs of each distribution (2°–12°) are comparable with the SDs of other methods (12).

Fig. 3.

Orientation fitting results for example molecule 1 (A, B, E, G, and I) and example molecule 2 (C, D, F, H, and J). (Scale bars: 1 μm.) (A) Four example DH-PSF images (which constitute one measurement of orientation) of molecule 1 at z ∼ −250 nm as it appears in each of four mask orientation/polarization channel combinations: red, gold, green, and blue (definitions in the text). Note that only one lobe is easily visible in the red and gold channels. (B) The transmitted (Upper) and reflected (Lower) polarization defocused standard PSF images used for independent orientation measurement. (C) The equivalent of A for example molecule 2 at z ∼ 0 nm. (D) The equivalent of B for example molecule 2. (E and F) Each measurement of LD (scatter points) and the predicted LD based on the mean fit orientation (solid line) for each molecule. (G and H) Each measurement of LA in each channel (color code is the same as in A) and the overlaid predicted LA for the mean fit orientation. (I and J) Histograms of θ and ϕ extracted from DH-PSF based measurements. Magenta line is Gaussian fit. Purple arrow denotes orientation extracted from defocused imaging.

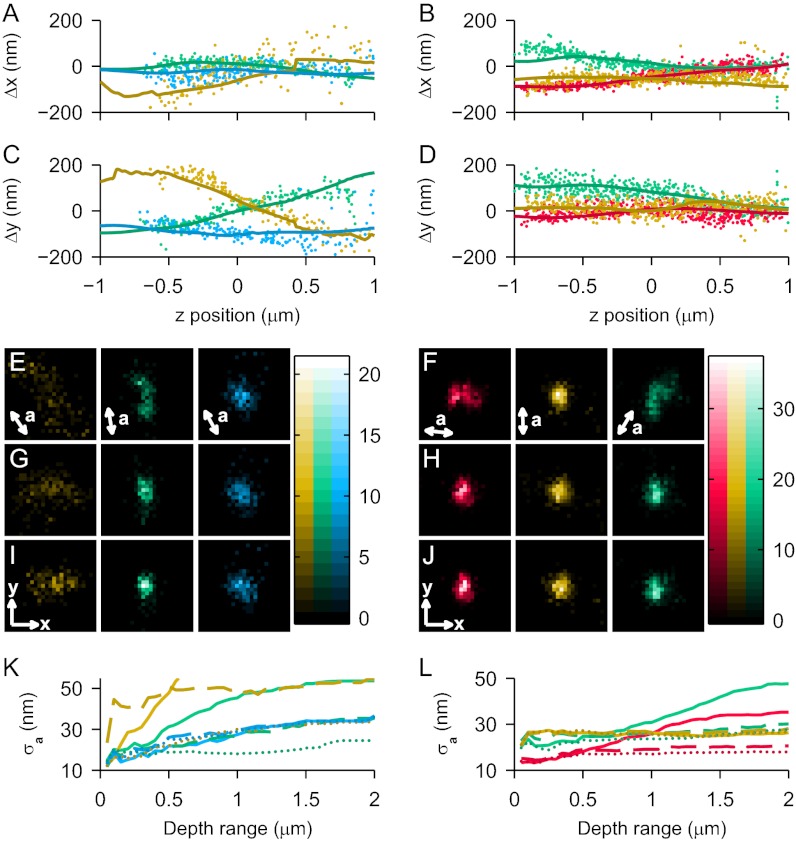
Apparent shift corrections for these example molecules are shown in various ways in Fig. 4. First, (Δx, Δy) are plotted as functions of z and overlaid again with those predictions for the mean orientation fit (Fig. 4 A–D). By binning the (x, y) positions of both SMs recorded across our entire 2-μm DR, we produced the 2D histograms shown in Fig. 4 E and F. For an isotropic emitter, for which (x_apparent, y_apparent) does not depend on z, the 2D distribution should be circularly symmetric, with width approximately proportional to 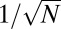, where N is the number of photons collected in that channel. Because of the dipole effect, the uncorrected distributions have irregular, elongated shapes in some cases (e.g., the green channel of molecule 1 and the green and red channels of molecule 2). By subtracting the apparent shifts (Δx, Δy) predicted from each individual fit of orientation, we recovered the corrected distributions shown in Fig. 4 G and H. Importantly, cases that were elongated and irregularly shaped when uncorrected became more concentrated and symmetric when corrected. Uncorrected cases that were relatively concentrated and symmetric to begin with did not undergo much change upon correction (e.g., the gold channel of molecule 2). The gold channel of molecule 1 shows a case where a large (>200 nm) shift is followed closely by simulation and removed on correction, but fewer photons detected in this channel make for a more diffuse corrected histogram than in other cases.

Fig. 4.

Measured and predicted (Δx, Δy) caused by dipole orientation effects for example molecule 1 (A, C, E, G, I, and K) and molecule 2 (B, D, F, H, J, and L). Color code is the same as in Fig. 3. (A–D) Measured (scatter points) Δx and Δy vs. z for each example molecule, with overlay (solid line) of simulated shift based on the mean extracted orientation. For each molecule, one mask orientation/polarization combination did not produce meaningful localizations because of low signal and/or high LA (omitted channels). (E and F) 2D histogram of uncorrected (x_apparent, y_apparent) localizations over the 2-μm DR. In each panel, a is the predominant direction of lateral shift for that mask orientation/polarization channel. Bin size, 15 nm. (G and H) Corresponding 2D histograms of the corrected localizations as produced by subtracting each predicted (Δx, Δy) based on each individual estimation of (θ, ϕ). (I and J) The corrected 2D histograms produced by subtracting the predicted (Δx, Δy) based on the average estimation of (θ, ϕ). Displayed (x, y) axes are 100 nm in length. (K and L) Additional quantification of the improvement in lateral localization showing σ_a, the SD along the direction a in each channel, as a function of DR about the focal plane. We compare σ_a calculated for the uncorrected case (solid line), the individual measurement-based correction (dashed line), and the average-based correction (dotted line).

Large values of LA can also affect the precision of position measurements, because the midpoint between one very bright and one very dim lobe is difficult to localize. Commonly in our experiment, a combination of few detected photons and large LA made spatial localizations in one of four mask orientation/polarization channels highly erratic (omitted cases in each example molecule). However, we still obtained meaningful estimates of LD and LA from such cases that were highly valuable in the extraction of (θ, ϕ). These orientation estimates, in turn, resulted in shift corrections that improved the localizations in channels that did have meaningful (x, y, z) fits. There is, thus, a tradeoff between the benefit of being able to fit orientation and correct dipole-induced shifts and the cost of splitting photons into multiple channels.

For additional improvement in correction, Fig. 4 I and J shows the results of using the average values of all measurements of (θ, ϕ) to correct each localization. In general, this method improved the localizations slightly more than the individual measurement-based method, because it makes use of a less noisy correction vector. The individual measurement-based method is more practical, however, because it requires far fewer measurements and therefore, is easier to adapt for use in a SMACM measurement. Taken together, these observations suggest that an individual set of four images is sufficient to correct the bulk of the dipole-induced shift for a molecule but that this correction can be improved somewhat if it is possible to measure the same molecule several times at multiple z positions.

As a final quantification, we also calculated the SD of (x, y) localizations along the lateral direction a for each channel and molecule over various ranges in z (Fig. 4 K and L). The axis a for each case is depicted in the lower left of each panel in Fig. 3 E and F, and it was determined by treating the 2D distribution as an ellipse and finding its major axis. Thus, a large σ_a implies a systematic apparent shift along the direction a. A corrected distribution should remove the systematic shift and therefore, should reduce σ_a to the SD expected from photon-limited precision. Data for a given DR about the focal plane were calculated by including all localizations for which |z| was less than that DR/2. As expected, in each case for which the deviation along a was relatively large, the corrected values were markedly improved, especially at large DR. Table S2 summaries the σ_a values calculated at the full 2-μm DR and compares them with the σ expected from photon-limited precision. For example, in the green channel of molecule 1, the uncorrected σ_a (54 nm) was three times larger than the statistical localization precision (18 nm). The individual measurement-based correction improved σ_a to 35 nm, whereas the average-based method improved it further to 24 nm. In the gold channel of molecule 1, the large (>200 nm) shift produced an uncorrected σ_a of 116 nm (vs. 28-nm precision along that direction). Individual correction reduced this number by more than a factor of two (55 nm), whereas the average correction brought σ_a to within 6 nm of the precision (34 nm) along that direction. This channel is still relatively diffuse along the x direction on correction, however, because of limited photon detection (the DH-PSF in general gives unequal σ_x and σ_y, because it is not circularly symmetric) (27). In the green channel of molecule 2, σ_a (48 nm) was nearly two times as large as the precision (25 nm). This SD was corrected to within 5 nm of the precision in both the individual correction (30 nm) and the average correction (28 nm). Similarly, the red channel of molecule 2 gave uncorrected, individually corrected, and average corrected σ_a values of 35, 21, and 18 nm compared with a precision of 17 nm.

In some cases (e.g., the red channel of molecule 2), we found that the corrected value was actually slightly worse at small DR but still much better at sufficiently high DR. This effect suggests that an efficient algorithm that corrects orientation effects in a SMACM experiment will only apply corrections in cases in which it is beneficial (e.g., at large |z|, molecules with inclined orientations, and polarization channels with a high enough signal-to-background ratio). Overall, these results show that the DH-PSF has the powerful ability to correct large lateral position errors caused by the SM dipole effect over an extended 2-μm DR.

Conclusion and Outlook

With this direct experimental demonstration, we show that the DH-PSF can be used to simultaneously extract precise 3D localization, estimate dipole orientation, and dramatically reduce (x, y) systematic errors caused by the orientation effect over an extended z range. Although our method requires two camera exposures for every set of measurements, our SLM can alternate phase mask orientations programmatically at speeds of at least 30 Hz (limited by the liquid crystal composition of our SLM). Different phase modulators can be toggled faster. Additionally, an optical setup containing separate phase masks for each polarization channel may be able to provide orientation from just a single acquisition using a slightly modified analysis.

This proof of principle shows that our method works best for correcting shifts of intermediately inclined molecules (∼θ ∈ [35°, 75°]). Our method has more difficulty fitting the orientations of less-inclined molecules (θ > 75°); because |LA| is closer to zero for all z, there exist near-degeneracies in some of these cases (Fig. S4). However, this limitation is not likely to prohibit the correction of significant dipole-induced mislocalizations in SMACM experiments, because those same noninclined molecules produce negligible (Δx, Δy) (Fig. S5). We did not encounter many very highly inclined molecules (θ < 35°) in our measurement, because both pumping and collection efficiencies are diminished for these cases (33). A standard SMACM experiment also would have difficulty detecting these molecules for the same reasons.

The theoretical limit of the DH-PSF's ability to extract position and orientation can be quantified using a Fisher information calculation; in particular, because the double-lobed shape of the DH-PSF is conserved over various dipole orientations and axial positions, the orientation precision of the DH-PSF is uniform over a large range of (z, θ, ϕ) (SI Text and Fig. S6). Thus, because the DH-PSF has been established as a highly precise method for 3D SMACM (28, 29), our orientation extraction/shift correction method to improve accuracy by removing systematic error is a good candidate to be incorporated into such experiments. As pointed out above, if labels are rotationally mobile, the dipole shift can be averaged out during an acquisition. At the other extreme, if labels are fixed in orientation during an acquisition, our method can be applied. The intermediate regime of rotational flexibility will be the subject of future work. Importantly, the fact that DH-PSF LA deviates from zero when SMs are fixed in their orientation and sufficiently inclined suggests that the DH-PSF can be used as a diagnostic tool in determining when labels are sufficiently rotationally mobile.

Although we found that we did not need to explicitly account for aberrations in the DH-PSF to yield good results for the examples given here, it may be necessary to address aberrations in the future to broaden the scope of our method and improve its performance. Finally, the DH-PSF–based orientation-sensing method may also be improved by using more sophisticated estimators and phase retrieval (34), particularly when high LA or aberrations make the DH-PSF deviate from its typical double Gaussian shape. With the correction of localization errors from the SM dipole orientation effect, far-field superresolution microscopy is one step closer to attaining molecular spatial resolution (∼1 nm) (35) to reveal the nanoscale machinery at work within living cells.

Materials and Methods

Sample Preparation.

Nanomolar concentrations of DCDHF-N-6 (31) were spun in a thin layer of 1% (by mass) PMMA of thickness 30–35 nm as measured by ellipsometry. Fluorescent beads (FluoSpheres, 100-nm diameter, 580/605; Invitrogen) were adhered directly to the air–polymer interface by spinning a dilute solution on top of the polymer layer and allowing it to dry. The beads served as both internal calibration markers for the DH-PSF response and fiducial markers for drift and sample tilt corrections (SI Text). They could not be spun directly into the polymer matrix because of instability in organic solvents.

Imaging.

Samples were mounted on an inverted Olympus IX71 fluorescence microscope, and the optical setup described in Fig. 1B was constructed outside the left-side port with the use of a phase-only spatial light modulator (Boulder Nonlinear Systems XY Phase Series). Fluorophores were excited with an Ar-ion laser emitting at 514 nm. The wide-field excitation beam was tilted at a slight angle to compensate for the dynamic range of brightness presented by the beads vs. the SMs. The laser was roughly circularly polarized (∼1.4:1) at the sample. Molecules were irradiated at relatively low intensity (∼0.1 kW/cm²) to ensure a full cycle of measurements before photobleaching. Fluorescence was collected through a 100× 1.4 N.A. oil-immersion objective (Olympus UPlanSApo 100×/1.40) and filtered using a Chroma Z514RDC dichroic and a 590/60 band pass. Images were recorded on an Andor iXon+ DU897-E EMCCD camera operating at an EM gain setting of 300.

For DH-PSF imaging, the sample was scanned over a z range of 2 μm at 50-nm spacing using an objective z positioner (C-Focus operating in open-loop mode; Mad City Labs). The DH-PSF mask was first loaded on the SLM with perpendicular orientation. Frames were recorded with 0.5-s exposures at 5 frames per z step. The loaded mask was then rotated 90° clockwise, and the sample was scanned again. After two full scans, the sample was refocused and then defocused by 1.00 ± 0.15 μm; therefore, the objective was moved away from the air–polymer interface. The coma/astigmatism correction mask (SI Text) for the transmitted channel was then loaded onto the SLM, and 10–30 1-s exposures were recorded. Then, the coma/astigmatism correction mask for the reflected channel was loaded, and another such series of images was recorded. This full process of scanning two times and then taking defocused snapshots was repeated until a field of view was sufficiently photobleached.

Analysis.

Tiff image stacks were exported by the Andor Solis software and analyzed with custom MATLAB routines. Each analyzed molecule was picked by hand based on the presence of a single-step bleaching event (indicating an SM), sufficient local sparsity to avoid overlapping signals, and sufficient signal-to-noise ratio. A constant background offset was subtracted from each SM region, which was calculated from a user-defined local background region. The resulting image was fit to a double Gaussian (i.e., the sum of two Gaussians) through nonlinear least squares regression using the MATLAB function lsqnonlin (SI Text). Simultaneously recorded gold and blue channel images (mask perpendicular) of an SM were paired with green and red channel images (mask parallel) of the same molecule based on z proximity. From each set of four images, the observables (x_apparent, y_apparent, z, LA, LD) were calculated. (x_apparent, y_apparent) were given by the midpoint position between the two lobes as determined by the double Gaussian fit along with a composite calibration correction to account for the nonideality of the DH-PSF response because of optical aberrations, sample tilt, stage drift, and the difference between the surrounding medium of the SMs vs. the medium of the fluorescent beads (SI Text and Fig. S7); z was given by the measured angle of the line connecting the centers of the two lobes relative to the horizontal, which was referenced to the calibrated response of the bead DH-PSF to the stepping of the stage by known amounts. LA was computed from the estimated amplitudes of the two Gaussians. LD was calculated from the total integrated photons above background in the region of the SM. If the automatic double Gaussian fit failed, the image was fit to two Gaussians by hand-selecting the regions of the two peaks. In this way, bounds or estimates of LA and LD could still be extracted and fed to the orientation look-up program even if (x, y, z) localizations were not reliable in that channel. To estimate (θ, ϕ) for each measurement of (z, LD, LA), the MATLAB function lsqnonlin was used to converge on the best (θ, ϕ) that minimized the difference between the measured LA and LD vs. predictions of the theoretical response of the DH-PSF (SI Text).