Folding of the four-helix bundle FF domain from a compact on-pathway intermediate state is governed predominantly by water motion

Abstract

Friction plays a critical role in protein folding. Frictional forces originating from random solvent and protein fluctuations both retard motion along the folding pathway and activate protein molecules to cross free energy barriers. Studies of friction thus may provide insights into the driving forces underlying protein conformational dynamics. However, the molecular origin of friction in protein folding remains poorly understood because, with the exception of the native conformer, there generally is little detailed structural information on the other states participating in the folding process. Here, we study the folding of the four-helix bundle FF domain that proceeds via a transiently formed, sparsely populated compact on-pathway folding intermediate whose structure was elucidated previously. Because the intermediate is stabilized by both native and nonnative interactions, friction in the folding transition between intermediate and folded states is expected to arise from intrachain reorganization in the protein. However, the viscosity dependencies of rates of folding from or unfolding to the intermediate, as established by relaxation dispersion NMR spectroscopy, clearly indicate that contributions from internal friction are small relative to those from solvent, so solvent frictional forces drive the folding process. Our results emphasize the importance of solvent dynamics in mediating the interconversion between protein configurations, even those that are highly compact, and in equilibrium folding/unfolding fluctuations in general.

Protein folding has been modeled successfully as a diffusive conformational search occurring on a rugged low-dimensional free energy landscape (1). Kramers’ theory and its extensions (2, 3) predict the rate of diffusive barrier crossing in the inertial (weak friction) and diffusive (strong friction) limits as well as in the crossover between the two regimes (4). Simulations and experiments have confirmed that protein conformational barrier crossing events in aqueous solution occur in the diffusive limit (5–7). In this strong friction regime, the rate constant for folding (k_f) is given by

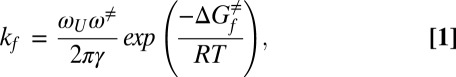where ω_U and ω^≠ reflect the curvatures of the potential energy surface at the position of the unfolded state and the barrier top, respectively, ΔG_f^≠ is the activation free energy for folding (3), and γ is the frictional coefficient that explicitly takes into account the frictional forces that influence the reaction rate (3, 6, 8).

Early experimental investigations have established that the frictional force slowing protein conformational exchange has both solvent dependent and independent contributions (9). The solvent-dependent part derives from the friction experienced by a spherical particle of radius ‘r’ moving in a solvent of viscosity η that can be related to γ via the Stokes equation, γ = 6πηr. Contributions to friction that are solvent independent, termed internal friction, are denoted by σ (in viscosity units) and have been modeled in polymer theory as originating from resistance of a polymer chain to local reconfiguration and from intrachain torsional energy barriers (10). Solvent and internal friction terms can be collectively incorporated into the Kramers equation as

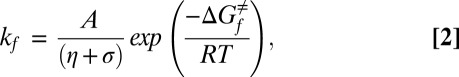where A is a constant that contains the dynamical terms ω_U and ω^≠ (9). This equation has been observed to robustly model the viscosity dependence of protein conformational changes over a large range of solvent viscosities (9, 11), especially in cases in which exchange occurs between compact conformations.

Frictional forces arise from the random motion of solvent and protein molecules (6). These random fluctuations dampen motion along the folding pathway but also provide the energy necessary for protein molecules to cross the folding activation energy barrier. These twin effects of random forces in solution are related by the fluctuation-dissipation theorem (12). Studies of frictional forces in solution thus may provide fundamental insights into reaction dynamics by identifying the relative importance of water and protein fluctuations in driving folding and other conformational exchange processes.

Previous experimental measurements on the viscosity dependence of folding rate constants have identified solvent friction to be important in folding reactions starting from the unfolded ensemble (7, 13) whereas internal friction from the protein chain is expected to dominate in the interconversion between compact protein conformations (8, 11, 14), although this is not always the case (15, 16). Additional studies have reported the importance of internal friction for small proteins folding “downhill” near the speed limit (14, 17). However, the number of proteins analyzed to date is so small that it is difficult to establish general principles as to when internal friction likely plays an important role in folding. A further issue is that many of the studies have been limited by a lack of structural information on the states involved in the folding process, the consequences of which are twofold. First, perturbations in structure caused by the viscogen cannot be assessed. Second, the frictional forces observed in the exchange process cannot be interpreted or rationalized from a molecular standpoint. Moreover, several of these reports have invoked the isostability approximation (8), wherein denaturants are added to counteract the stabilizing effects of viscogens. Because additives may influence the structures of conformers residing along the folding pathway, the changes in rate constants as a function of viscogen may not solely be the result of increased friction.

NMR spectroscopy is an important tool for understanding conformational dynamics (18, 19). The pioneering solution NMR studies of the isomerization of cyclohexane and its derivatives by Jonas and coworkers (20) are among the most convincing experimental validations of Kramers’ theory in both the inertial and diffusive regimes. More recently, Carr-Purcell-Meiboom-Gill (CPMG) relaxation dispersion NMR spectroscopy has emerged as a powerful and robust tool to characterize millisecond timescale dynamics of proteins in solution (18, 19) and to determine the structures of transiently and sparsely populated protein excited states with millisecond lifetimes (21–24). Using CPMG methodology (18) and chemical shift-based structure prediction algorithms (25, 26), the structure of an on-pathway “invisible” intermediate in the folding of both the wild-type (wt) (22) and L24A (27) four-helix bundle FF domains was determined recently.

Here, we use CPMG relaxation dispersion NMR to evaluate the viscosity dependence of the rates of interconversion between native (N) and sparsely populated intermediate (I) states of wt and L24A FF modules. We show that the viscogens used in our study do not alter the relative energies of the native, intermediate and transition states, nor the structures of N and I. The FF folding intermediates for both wt and L24A FF domains (see later) are compact and stabilized by long-range nonnative contacts, such as those between helices 1 and 3, that must be broken en route to the native state (22, 27). Given the collapsed topology of the intermediate and the extent of intrachain reconfiguration that must occur during folding, we hypothesized that solvent-independent internal friction would play an important role in folding. Contrary to our expectations, however, the internal friction contributions to the folding of wt and L24A FF domains are small, σ ∼0.2 and 0.4 cP, respectively. The viscosity of water is ∼1 cP, implying that the bulk of the frictional force in the I–N interconversion originates from solvent motion.

Results and Discussion

Characterizing the wt FF Domain I–N Interconversion as a Function of Viscosity.

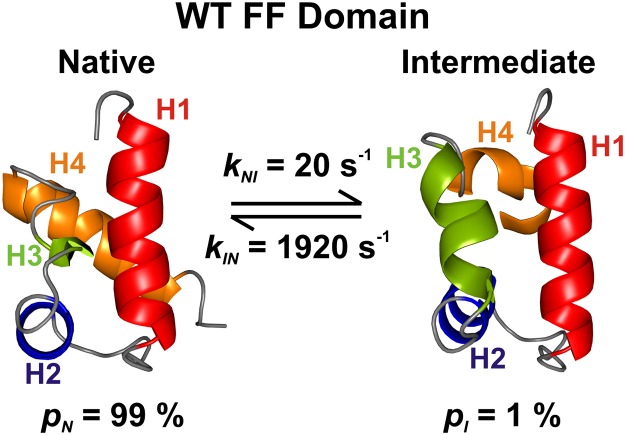
Previous relaxation dispersion NMR studies of the wt FF domain have established a two-site exchange process involving interconversion between a highly populated native state, N (fractional population p_N = 99% under the conditions here), and a sparsely and transiently formed intermediate, I, that cannot be directly detected in spectra. On the basis of extracted backbone ¹H, ¹⁵N, and ¹³C chemical shifts, as well as one-bond ¹H-¹⁵N residual dipolar couplings, an atomic resolution model of state I has been constructed (Fig. 1) (22). Helices H1 and H2, as well as the intervening H1–H2 loop, are native-like in the wt FF intermediate state, whereas H3 is nonnative and significantly longer than the native state 3₁₀-helix H3. By contrast, H4 is not well structured in I. It is apparent that nonnative interactions at the H1–H3 and H2–H3 helix interfaces of I have to be broken while forming the native state.

Fig. 1.

Structures of the native [N; Protein Data Bank (PDB) ID code 1UZC] (49) and intermediate states (I; PDB ID: 2KZG) (22) of the wt FF domain, along with the fractional populations of N and I, and the rate constants for interconversion, 25 °C, as determined in the present study. Helix boundaries are defined according to TALOS+ (37), as described previously (22). MOLMOL (50) predicts slightly different helix boundaries.

We used glycerol as a viscogen to probe the viscosity dependencies of the I N interconversion rates of the wt FF domain. Samples of ¹⁵N/¹H-labeled wt FF in the absence and presence of up to 25% (vol/vol) glycerol were prepared as detailed in SI Materials and Methods. The viscosity of each sample was determined using acetate molecules as in situ probes. The relative diffusion coefficient of acetate in each sample was measured using pulsed-field gradient NMR techniques (28) and the viscosity calculated from the Stokes-Einstein equation (D = kT/6πηr), assuming that the viscosity of the NMR buffer (Materials and Methods) devoid of protein is given by the concentration-weighted average of H₂O and D₂O viscosities (29). The viscosity values obtained from acetate diffusion deviate by less than 10% from bulk viscosity measurements reported in the literature (30). Different metrics of viscosity, such as the translational diffusion coefficient of the small molecule acetate and the translational and rotational diffusion coefficients of the wt FF domain, all scale inversely with viscosity, as expected from the Stokes-Einstein equation (Fig. S1A).

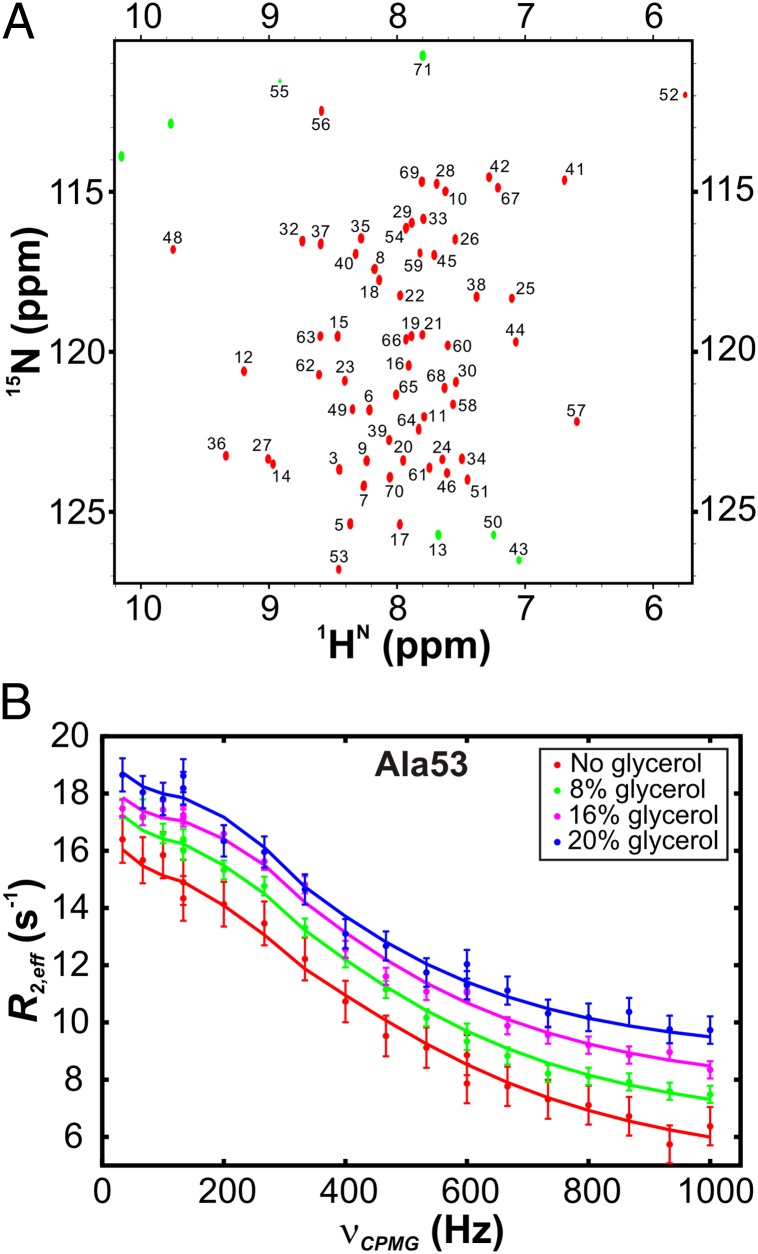
Fig. 2A shows a ¹H,¹⁵N heteronuclear single quantum coherence (HSQC) spectrum of the native state of the ¹⁵N-labeled wt FF domain at pH 5.7 and 25 °C in the absence of glycerol. Resonances belonging to the intermediate state are not directly visible in the ¹H,¹⁵N HSQC dataset, but the millisecond exchange between the intermediate and native states increases the effective transverse spin relaxation rates (R_2,eff) of resonances derived from residues of the native conformation that are observed, leading to peak broadening. R_2,eff values of probe nuclei may be modulated by applying a train of equally spaced 180° refocusing pulses at varying frequencies ν_CPMG (ν_CPMG = 1/(4δ), where 2δ is the spacing between two successive 180° pulses) over a constant time interval (31, 32). Residue-specific ¹⁵N relaxation dispersion curves (Fig. 2B, circles) profiling the variation of R_2,eff of backbone amide ¹⁵N nuclei with ν_CPMG are sensitive to millisecond timescale dynamics and may be fit to models of chemical exchange to extract exchange parameters (see later).

Fig. 2.

NMR spectroscopic methods for analyzing wt FF domain folding from the intermediate state. (A) ¹H,¹⁵N HSQC spectrum of the wt FF domain, with assignments of residues as indicated (46). Aliased cross-peaks in the dataset are shown as green contours. (B) ¹⁵N relaxation dispersion curves acquired at 18.8 T for Ala53 at four different viscogen concentrations, 25 °C. Solid lines are global best fits to a two-state exchange model between N and I at each viscogen concentration.

¹⁵N CPMG relaxation dispersion profiles were acquired at static magnetic field strengths of 11.7 and 18.8 T for six samples with varying glycerol concentrations. For each sample, the curves for 7–12 residues at two magnetic fields were fit globally to a two-site exchange model by numerically propagating the Bloch-McConnell equations (33), resulting in reduced χ² values ranging from 0.5 to 1.1 (Table S1 and Materials and Methods). Populations of the intermediate and native states, the rates of interconversion between the two states, and the absolute values of the chemical shift differences between N and I (|Δϖ_IN|, ppm or (|Δω_IN|, rad/s) were extracted from the fits as a function of viscosity.

At 25 °C, p_N = 99%, p_I = 1 – p_N = 1%, and rate constants of 1,920 s⁻¹ (k_IN) and 20 s⁻¹ (k_NI) are fitted for the sample with no added viscogen (Fig. 1), which is well within the experimental window of the dispersion methodology (34). Robust measures of exchange parameters are obtained, as discussed in detail in SI Text. Correlations between p_I and k_ex observed in slow exchange, and between p_I and |Δϖ_IN| in fast exchange (34), are not an issue with analysis of the present data on the FF domain because residues covering a wide range of exchange timescales, from slow (k_ex/|Δω_IN| < 1) to fast (k_ex/|Δω_IN| > 1), are available to be used in data fitting (Fig. S2 and SI Text) so that robust exchange parameters are obtained (34). Distributions of k_ex values as a function of viscosity are clearly separated from one another and vary in the manner expected (Eq. 2, Fig. S3). In addition, errors in the exchange parameters have been obtained using both a covariance matrix method (35) and a bootstrap analysis (36) (Table S1–S3) and are in excellent agreement.

Glycerol Does Not Alter the Structures or the Relative Energies of N and I.

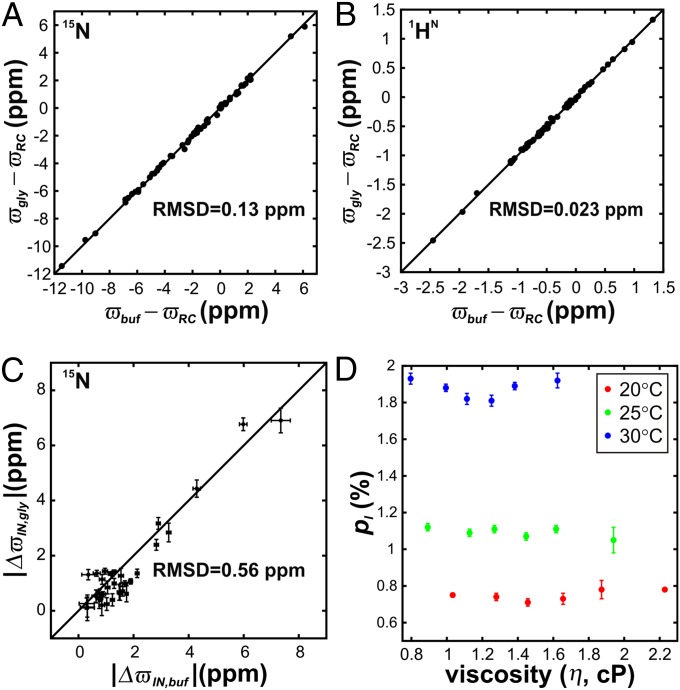
Fig. 3 A and B shows correlation plots of backbone amide nitrogen (¹⁵N) and proton (¹H^N) chemical shifts in the absence and presence of the highest values of added glycerol [25% (vol/vol)]. Because both ¹⁵N and ¹H^N nuclei are sensitive probes of protein secondary and tertiary structure (37), the small RMSD values of 0.13 and 0.023 ppm, respectively, in the correlation graphs provide direct evidence that the native structure of the wt FF domain is not perturbed by addition of glycerol. As an illustration, comparable chemical shift changes are expected for ¹H^N nuclei if the temperature of the sample is increased by as little as 5 °C (38). Structural changes in the intermediate induced by glycerol were probed using ¹⁵N chemical shift differences between N and I obtained from fitting relaxation dispersion data. The good correlation between |Δϖ_IN| values in the absence (|Δϖ_IN,buf|) and presence (|Δϖ_IN,gly|) of glycerol and the absence of prominent outliers confirms that glycerol does not modify the intermediate structure as well (Fig. 3C).

Fig. 3.

Glycerol does not perturb the structure or energetics of the N and I states of the wt FF domain. A comparison of backbone (A) ¹⁵N and (B) ¹H^N chemical shifts (parts per million) of the native wt FF domain measured in the absence, ϖ_buf (x axis), and presence, ϖ_gly (y axis), of 25% (vol/vol) glycerol. Residue-specific random coil chemical shifts have been subtracted from the observed ϖ_buf and ϖ_gly values in both panels. (C) ¹⁵N |Δϖ_IN = ϖ_N − ϖ_I| values fitted from relaxation dispersion profiles measured without (x axis, |Δϖ_IN,buf|) and with 25% (vol/vol) glycerol (y axis, |Δϖ_IN,gly|). RMSD values of data points from y = x (solid line) are indicated in all three panels. (D) Intermediate-state populations, p_I (fractional values), as a function of sample viscosity at 20 °C, 25 °C, and 30 °C.

Having established that glycerol does not alter the intermediate and folded state structures, we next examined the relative populations of the two states as a function of viscosity. Dispersion profiles from all the samples fit robustly to two-state exchange models (Table S1) and Fig. 3D plots the extracted p_I values as a function of glycerol over the three temperatures examined. Notably, p_I does not vary with increasing glycerol concentration, with a maximum deviation of p_I from the mean of only 0.03%. Taken together, our results establish that glycerol does not perturb the I N exchange of the wt FF domain at either an energetic or a structural level.

Small Internal Friction for the wt FF Domain I N Reaction.

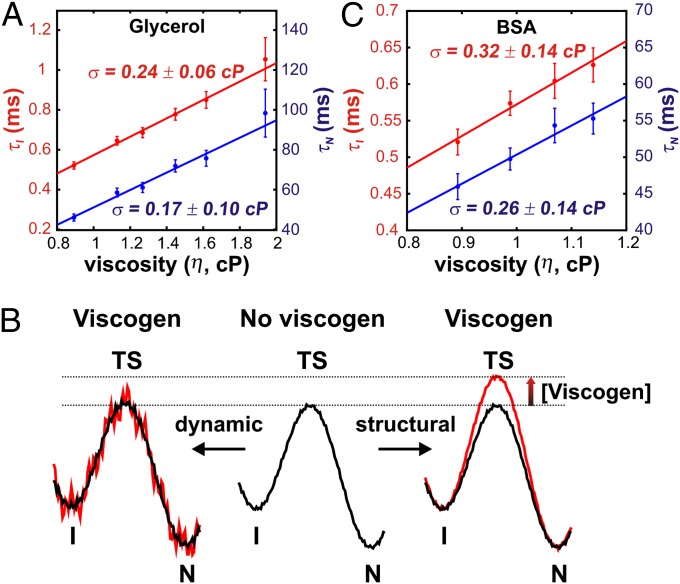
The viscosity dependencies of the intermediate (τ_I = 1/k_IN) and native (τ_N = 1/k_NI) state lifetimes are shown in Fig. 4A. Each curve was fit to a linear equation of the form (8),

to extract the value of σ that derives from internal friction. Here, we have assumed that C_i (i.e., the exponential term of Eq. 2) is viscosity independent so that the effect of added viscogen is to increase the ruggedness of the folding landscape through changes in η, allowing the separation of η and σ (see below) and the interpretation of the extracted σ values in terms of contributions from internal friction. The σ for wt FF domain folding at 25 °C is 0.20 ± 0.12 cP (average of σ values from independent fits of τ_I, τ_N), which is small compared with the viscosity of water (0.9 cP). Values of σ do not change substantially with temperature over the range examined, 20–30 °C (σ_{20 °C} = −0.12 ± 0.10 cP, σ_{30 °C} = 0.13 ± 0.13 cP). In addition, the values of σ obtained from fitting the intermediate and native state lifetimes indicated in Fig. 4A are within error, as expected from microscopic reversibility.

Fig. 4.

Small internal friction in the folding of the wt FF domain. (A) Viscosity-dependent intermediate- (τ_I) and native-state (τ_N) lifetimes as a function of added glycerol. The solid line is a fit of the data to Eq. 3. Values of σ obtained from the fit are denoted on the graph. (B) Schematic illustrating two possible effects of viscogen on the folding potential energy landscape of the wt FF domain (Center) that may account for the results in (A). In the model on the right, the transition state (TS) is destabilized by viscogen (red curve), with little effect on the landscape ruggedness. Shown on the left is an “instantaneous” snapshot of a landscape in which the effect of viscogen is to increase ruggedness (red). Note that each point on the energy curve will change with time because of the stochastic nature of the frictional forces so that averaged over time, the landscape is less rugged as depicted in black. For both models, the relative energy differences between I and N remain unchanged, as observed experimentally. These models may be distinguished as described in the text. (C) Increase in τ_I and τ_N with viscosity, controlled by addition of variable amounts of BSA. σ values obtained from fits of the data to Eq. 3 (solid lines) are indicated within the panel.

The small magnitude of σ shows that FF folding from the intermediate is driven primarily by water dynamics. Interpreted in the terminology of the “slaving model” (39), the steep viscosity dependence of folding rates and the small internal friction imply that FF folding is slaved to water motion. This result is surprising because the intermediate state is compact and stabilized by nonnative contacts so that considerable intrachain remodeling must occur during folding (22).

Effect of Viscogen on the I,N Lifetimes Is Dynamic and Not Structural.

The intermediate- and native-state wt FF domain lifetimes vary linearly with viscosity (Fig. 4A). This may be interpreted within the framework of Kramers’ theory (Eqs. 1–3) in terms of an increase in the friction of the folding energy landscape with solvent viscosity, as we have done above. Nevertheless, it is possible to observe an identical viscosity dependence of folding rates if the added viscogen destabilizes the transition state by a small amount without affecting the roughness of the landscape (i.e., assuming rates of the form k = Aexp(−ΔG^≠/RT), where A does not depend on viscosity). Assuming a linear relation for the free energy of activation ΔG^≠(η) of the form 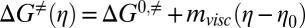, where ΔG^0,≠ and ΔG^≠ are the folding activation energies in the absence and presence of viscogen, η is the solution viscosity, and η₀ is the viscosity of water, it can be shown that an m_visc value of ∼0.5 kcal⋅mol⁻¹⋅cP⁻¹ can explain the viscosity dependencies of k_IN and k_NI.

The dynamic model in which glycerol increases friction along the folding pathway and the static (structural) model wherein glycerol interacts with the transition state (Fig. 4B) cannot be distinguished using only the data we have obtained with glycerol. Mathematically, the two models differ in that added viscogen leads to a change in either the prefactor (dynamic) or exponential (structural) terms in Eq. 2. The interpretation of the extracted σ values is thus quite different depending on which of the two models is relevant. To investigate the relative applicability of the two models in explaining our results we repeated the viscosity dependence measurements with a structurally different viscogen, BSA. If different values of σ are measured from glycerol and BSA, then it is likely that one or both viscogens affect the transition state, lending support to the structural model (Fig. 4B, Right). By contrast, similar σ values provide strong evidence that the effect of viscogen is to slow down rates by increasing the ruggedness of the energy landscape (by increasing solvent friction, η; Fig. 4B, Left) because it is highly unlikely that two very different classes of viscogen would influence the transition state in the same manner. If the latter scenario is true (Fig. 4B, Left), then the values of σ extracted report on the internal friction contribution to the FF domain folding.

Samples of FF domain were prepared with varying concentrations of BSA, with viscosity estimated from the diffusion coefficient of acetate molecules as outlined previously. BSA decreases the rotational diffusion coefficient of the wt FF domain more than it affects the translational diffusion of acetate (Fig. S1B) (40). However, because acetate is similar in size to solvent water whereas the FF module is not, the diffusion of acetate was used as an appropriate metric for calculating changes in solvent viscosity with added protein viscogen (8, 40). ¹H,¹⁵N HSQC spectra of the wt FF domain acquired in the absence and presence of 200 mg/mL BSA are virtually superimposable (Fig. S4A), confirming that BSA does not bind to or structurally alter the FF domain native state. ¹⁵N relaxation dispersion profiles were acquired with varying amounts of BSA and fit to two-state exchange models, as described earlier for glycerol (Materials and Methods). The populations of the intermediate state in samples without and with BSA are identical within measurement error (largest deviation of p_I from the average is 0.02%; Fig. S4B) and the ¹⁵N chemical shift differences between the folded and intermediate states are highly correlated in the absence and presence of BSA (RMSD = 0.2 ppm; Fig. S4C). Thus, BSA does not perturb the intermediate state structurally or change the relative energetics between I and N.

Fig. 4C plots the lifetimes of the native and intermediate states as a function of viscosity. Both curves were fit to Eq. 3 to extract σ. An average value of 0.29 ± 0.14 cP was obtained, very similar to the small average σ calculated using glycerol as a viscogen (0.20 ± 0.12 cP), providing confidence in a model whereby added viscogen increases the ruggedness of the energy landscape. Values of σ thus faithfully report on contributions from internal friction to the I,N interconversion.

Small Internal Friction in the I N Folding Reaction of the L24A FF Domain.

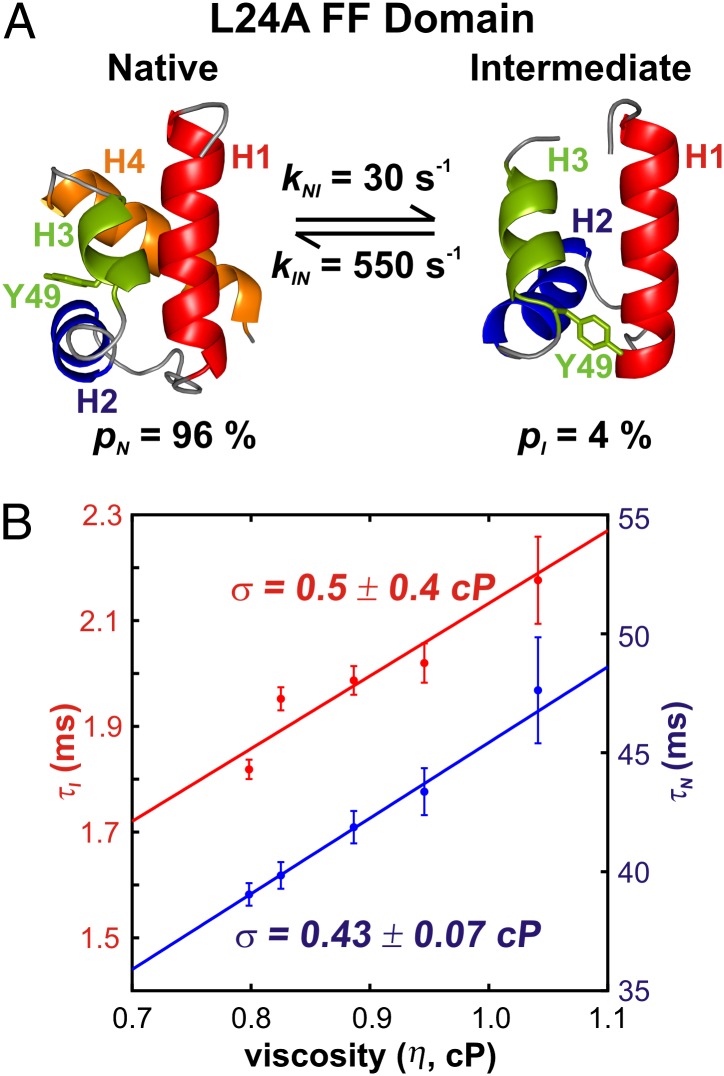
Having established that folding of the wt FF domain from the intermediate state is driven predominantly by solvent fluctuations, we set out to determine whether the L24A FF module, which folds approximately fourfold slower than the wt FF domain under the conditions reported here, has a higher internal friction along its folding pathway. The intermediate states for both wt and L24A FF domain folding share several features, including native-like secondary structures of H1 and H2, nonnative docking of the longer helix H3 onto H1, and a poorly structured H4 (22, 27). In addition, mutation of L24 to the smaller Ala residue leads to a nonnative contact between Y49 and A24 in the intermediate state, with the Y49 ring flipped toward the core of the protein (Fig. 5A). The Y49 ring must vacate the core during folding, contacting the surface-exposed I44 residue in the native state. The additional restructuring that must occur during the I-to-N transition for the L24A mutant led us to hypothesize that internal friction would contribute substantially to L24A FF folding, at least to a higher extent than for the wt FF domain.

Fig. 5.

Small internal friction in the folding of the L24A FF domain. (A) Structures of the native (27) and intermediate states (PDB ID: 2L9V) (27) of the four-helix bundle L24A FF domain, the fractional populations of N and I, and k_IN, k_NI rate constants, 30 °C, as measured in the present study. Helix boundaries are depicted according to TALOS+ (37), as described previously (27), whereas MOLMOL (50) predicts slightly different boundaries. Y49, which moves out of the protein core during folding, is shown explicitly. (B) Variation in intermediate- and native-state lifetimes as a function of viscosity in BSA-containing samples. Internal friction values obtained from fits to Eq. 3 (solid lines) are indicated.

In a preliminary relaxation dispersion study of the L24A FF domain, it was found that p_I increased from 2% at 25 °C to 4% at 30 °C, leading to significantly larger dispersion profiles and more accurate quantification of exchange parameters at 30 °C. We therefore have conducted studies for the mutant at the higher temperature. The small-molecule viscogens glycerol, ethylene glycol, sucrose, glucose, and trehalose all change the intermediate-state population as determined by fitting ¹⁵N relaxation dispersion curves to two-state models of exchange at the highest viscogen concentrations. However, BSA does not alter the folded and intermediate states structurally or energetically (Fig. S5) and therefore was used as a viscogen. The viscosity dependencies of L24A FF native- and intermediate-state lifetimes are depicted in Fig. 5B, and σ, determined by fitting the viscosity dependence of τ_N to Eq. 3, is 0.43 ± 0.07 cP. This σ value is marginally larger than the corresponding value for the wt FF domain; however, it is still substantially smaller than solvent viscosity so that the I-to-N transition for the L24A FF domain also is governed by solvent fluctuations.

The analysis described in the preceding paragraph for the L24A FF domain and the corresponding interpretation of the rate vs. viscosity dependence of the folding of the wt FF module both have made use of Eq. 3. As described in the introduction, this relation has been shown to be valid for viscosities ranging over several orders of magnitude and, in particular, for systems that exchange between compact conformations (9, 11). In general, however, it is not straightforward to separate the effects of internal and solvent friction on exchange rate constants (41). Many heuristic (9, 42) and theoretical models (41, 43) have been proposed to explain the deviation of viscosity-dependent rate constants from predictions made by Kramers’ theory. Differences in the quality of fits to these models become discernible only when the data span a large range of viscosities (8); unfortunately, that is not possible in our NMR experiments. For example, NMR experiments in general, including the dispersion methodology used here, are limited by the tumbling time of the protein, which increases in proportion to solvent viscosity. Moreover, the relaxation dispersion experiments are sensitive to exchange processes occurring within a fairly narrow k_ex window, extending roughly between 200 s⁻¹ < k_ex < 2,000 s⁻¹ and are further limited in the present set of studies because exchange rates decrease as viscosity increases. Hence, our measurements with glycerol are carried out over a 2.2-fold variation in viscosity, which is typical for protein-folding studies probing reaction friction (16). We find that both k_IN and k_NI scale inversely with viscosity, with the rates well fit using Kramers’ theory in the high friction regime (Eq. 1) that contains only a friction term arising from solvent (Fig. S6A). Thus, our conclusions concerning the importance of water in the FF domain I-to-N interconversion are valid irrespective of the particular model used to interpret the viscosity dependencies of k_IN and k_NI. Although we prefer using Eq. 3, which provides a straightforward separation of η and σ, we also have fit our data to a power law model, τ_i = τ_i,oη^α, where τ_i is the lifetime of state i. The near-unity values of α obtained, ranging from 0.83–0.87 (Fig. S6B), provide further confirmation that water viscosity provides most of the friction during the folding of the FF domain.

On the Importance of Water in the I–N Transition.

At least two models can be proposed for rationalizing the dominant role of solvent friction in the folding of the FF domain. Both are based, at least in part, on the fact that nonnative contacts formed in the intermediate state (22, 27) must be broken during folding to the native conformation. In the case of model 1, partial chain unfolding that ensues upon breakage of these nonnative interactions results in the formation of an expanded transition state that is less compact than either I or N. Partial unfolding would require motion of the polypeptide chain through solvent, leading to the observed viscosity dependence of k_IN, k_NI. Small Φ values (<0.3) have been reported for residues at the beginning of helix H1, in the H3–H4 loop and in helix H4 of the FF domain in 2-M urea (44), supporting a model based on a partially unfolded transition state.

A second plausible model involves breaking or establishing interactions with water during the I N transition, such as would be the case in α-helix formation in which intramolecular backbone amide hydrogen bonds replace amide hydrogen bonds with water. Movement of water in or out of the protein during folding will manifest as a viscosity-dependent reaction rate. Shortening of helix H3 and formation of helix H4 are both critical for FF folding, and this rearrangement likely is mediated by solvent. Water expulsion from a collapsed intermediate state during the final folding step was observed previously in simulations for an SH3 domain and provides precedence for this model (45). Note that neither of the aforementioned models requires the direct interaction of viscogen with protein, and indeed our NMR data establish that such interactions are not present (see above).

Concluding Remarks

We have used CPMG-based relaxation dispersion NMR experiments to dissect the contributions of solvent and internal friction to the folding kinetics of the four-helix bundle FF domain. The viscosity dependencies of the rates of interconversion between states I and N were measured in the absence of denaturants under conditions in which the added viscogen does not perturb the structures of the folded and intermediate states and the relative energies of the folded, intermediate, and transition states. Surprisingly, σ values for both wt and L24A FF domains are small compared with the viscosity of water, indicating that I–N exchange is driven primarily by random water motion. This result emphasizes the importance of solvent in mediating protein folding and conformational exchange at equilibrium, even in cases involving the interconversion between compact states.

Materials and Methods

Sample Preparation for NMR Spectroscopy.

¹⁵N-labeled wt and L24A FF domains were overexpressed and purified as described previously (44). The buffer for all NMR samples was 50 mM sodium acetate, containing 100 mM NaCl, 1 mM EDTA, and 1 mM sodium azide, pH 5.7, 90% H₂O/10% ²H₂O. Further details may be found in SI Materials and Methods.

NMR Experiments.

¹⁵N relaxation dispersion data were acquired on Varian Inova spectrometers operating at magnetic field strengths of 11.7 T [ν(¹H) = 500 MHz] and 18.8 T [ν(¹H) = 800 MHz] and equipped with standard triple-resonance gradient probes. A transverse relaxation optimized spectroscopy–based constant-time CPMG pulse sequence was used for all measurements (32). Sample temperature was calibrated with a thermocouple inserted into an NMR tube. Dispersion experiments were recorded with constant time delays of 30 ms, and data were collected at 16 different CPMG field strengths, ν_CPMG, varying between 33.33 and 1,000 Hz, with two repeat values for error analysis (46). Two-dimensional datasets were acquired in an interleaved manner by recording data for all ν_CPMG values at a particular t₁ time before proceeding to the next increment.

Data Analysis.

NMR data were processed using NMRPipe (47), whereas NMRDraw (47) and Sparky (48) were used to visualize the processed NMR spectra. Peak intensities in relaxation dispersion datasets were extracted using FuDA and fit to a two-state exchange model using an in-house–written software package CATIA (http://pound.med.utoronto.ca/software.html), as described previously (46). Errors in p_I, k_IN, k_NI, and |Δϖ_IN| were estimated from the data-fitting routine using the covariance matrix method (35) or from a bootstrap analysis (36) and are reported throughout the manuscript as ±1 SD about the mean value. Exchange parameters (p_I, k_ex) at each concentration of viscogen were extracted by simultaneously fitting all dispersion profiles for which R_2,eff(ν_CPMG = 33.3 Hz) − R_2,eff(ν_CPMG = 1,000 Hz) > 2 s⁻¹ (average “size” of dispersions was 7 s⁻¹ and 17 s⁻¹ for wt and L24A FF domains, respectively). Typically ∼10 (wt FF) or ∼30 (L24A FF) dispersion curves recorded at 11.7 and 18.8 T were included in each analysis. Extracted values of (p_I, k_ex) were then fixed and all of the other profiles fit to obtain site-specific values of |Δϖ_IN|. Values of (p_I, k_ex) are somewhat different from those previously reported (22, 27) because protein samples used in the present study were fully protonated, whereas in previous studies, highly deuterated samples were used.

Details on the acquisition and analysis of NMR diffusion experiments may be found in SI Text.