A classification of spin frustration in molecular magnets from a physical study of large odd-numbered-metal, odd electron rings

Abstract

The term “frustration” in the context of magnetism was originally used by P. W. Anderson and quickly adopted for application to the description of spin glasses and later to very special lattice types, such as the kagomé. The original use of the term was to describe systems with competing antiferromagnetic interactions and is important in current condensed matter physics in areas such as the description of emergent magnetic monopoles in spin ice. Within molecular magnetism, at least two very different definitions of frustration are used. Here we report the synthesis and characterization of unusual nine-metal rings, using magnetic measurements and inelastic neutron scattering, supported by density functional theory calculations. These compounds show different electronic/magnetic structures caused by frustration, and the findings lead us to propose a classification for frustration within molecular magnets that encompasses and clarifies all previous definitions.

One of the motivations underpinning molecular magnetism is the idea that chemistry can provide model systems that allow detailed analysis of behavior in homogeneous materials, and hence, theory can be tested without any need to allow for sample inhomogeneity. A classic example is the demonstration of quantum tunneling of magnetization in molecules such as [Mn₁₂O₈(O₂CMe)₁₆(H₂O)₄] (1) or [Fe₈O₂(OH)₁₂(tacn)₆]Br₈ (2) (tacn = 1,4,7-triazacyclononane). One area where molecular magnetism might contribute is in spin frustration (3), which is important in condensed matter physics in areas such as spin ice (4) and spin liquids (5). Potential model systems would be odd-numbered metal rings where the metal array forms equilateral triangles, or regular pentagons, heptagons, and larger 2D rings. Alternatively 3D solids made from regular odd-numbered rings should also be frustrated, e.g., regular tetrahedra and octahedra contain triangular faces and regular icosahedra contain pentagonal faces.

Studies of spin frustration in molecular systems are largely restricted to that of triangular trimetallic species (6, 7). There are a few reports of five-metal rings but no detailed magnetic studies of such compounds (8), with the exception of a {Cu₅} cage (9). The only significant examples of larger frustrated molecules are studies of the {M₃₀} Keplerates (10) and a recent report of a heptametallic {VO}₇ ring (11), where the studies are limited to low temperature magnetization. There is also a report of an {Fe₉} complex that can, very approximately, be described as a nine-metal ring (12).

A further difficulty is that precisely what is meant by frustration varies in this area. The strictest definition used in molecular magnetism, from Kahn (13), states that frustration must result in a spin degenerate ground state, typically a degenerate pair of S = 1/2 states. Surprisingly, this definition excludes all possible models built from integer spins, as in such cases (for example a regular pentagon of s = 1 spins), the ground total spin state is unique and has S = 0. This definition thus seems prohibitively strict. At the other extreme, the term frustration has been used to describe cases where there are competing antiferromagnetic interactions, even where those interactions result in a unique spin ground state that can be described using a classical picture, with spins represented as arrows pointing alternately up and down. This definition seems, if anything, too permissive.

We have reported studies of a {Cr₈Ni} ring that we described as a magnetic Möbius strip, because the magnetic studies suggest a spin ground state that could not be described using classical spins (14). Using the strictest definition of frustration (13), this compound cannot be frustrated because the {Cr₈Ni} ring contains an even number of electrons and has a singly degenerate spin ground state; however, the magnetic behavior cannot be described using a picture of classical spins. The molecule has also been described as a valence bond solid (15). Here we report our attempts to make the homometallic odd-metal, odd-electron ring that, if regular, would be frustrated by the strictest definition of Kahn (13), and describe two new molecules and their physical characterization.

Results

Our route to a homometallic {Cr₉} ring is based on the reaction that gives a {Cr₇} “horseshoe” (an open ring). The reaction involves hydrated chromium trifluoride dissolved in pivalic acid in the presence of di-isopropylamine. With a ratio of Cr:NHⁱPr₂ of 1.2:1, we isolated {[ⁱPr₂NH₂]₃[Cr₇F₁₂(O₂C^tBu)₁₂]}₂ (1) in 20% yield, where we have two {Cr₇} horseshoes linked through their open ends by hydrogen bonding to di-iso-propylammonium cations (16). If we reduce the amine to chromium ratio, we reasoned it may be possible to cyclize the horseshoe. This is what we find for a Cr:NHⁱPr₂ ratio of 8:1. A green precipitate is isolated initially, which contains at least three compounds. The first compound eluted by chromatography was crystallized and contains the known homometallic [CrF(O₂C^tBu)₂]₈ (2) ring (17). The second band was crystallized and contains [ⁱPr₂NH₂][Cr₉F₁₀(O₂C^tBu)₁₈] (3), and the third band contains [ⁱPr₂NH₂][Cr₉F₁₁(O₂C^tBu)₁₇] (4). The relative yields of the three compounds in our initial studies were 20, 16, and 10%, respectively. By variations on the reaction conditions, we could eliminate formation of compound 3 and raise the yield of 4 to 40% (SI Text).

To understand the reaction, we followed the formation of cyclic compounds by cryospray and electrospray mass spectroscopy. This has previously been used to probe the reaction mechanism by which giant polyoxopalladate wheels form (18). Here we mixed the reagents chromium trifluoride and ⁱPr₂NH in an 8:1 ratio in pivalic acid and followed the reaction. The result (Figs. S1 and S2) shows that after 1.5 h, significant amounts of 4 have formed. After 3 h, we observe formation of 3 and growth of peaks due to [(ⁱPr₂NH₂)2]⁺, which is a species not observed in the solid state. At 4 h, the amount of 3 formed has peaked, and the quantity gradually declines. By 24 h, the solution contains 4 and [(ⁱPr₂NH₂)2]⁺, and we see evidence of a compound related to [(ⁱPr₂NH₂)[CrF(O₂C^tBu)₂]₉]⁺. After 1 d, the amount of 4 begins to decrease, and mass spectral peaks for [(ⁱPr₂NH₂)2]⁺ and [(ⁱPr₂NH₂)[CrF(O₂C^tBu)₂]₉]⁺ grow in intensity. Attempts to separate and to crystallize the compounds after 3 d lead exclusively to isolation of 2, which suggests the other species present in solution at this point decompose to 2 during chromatography.

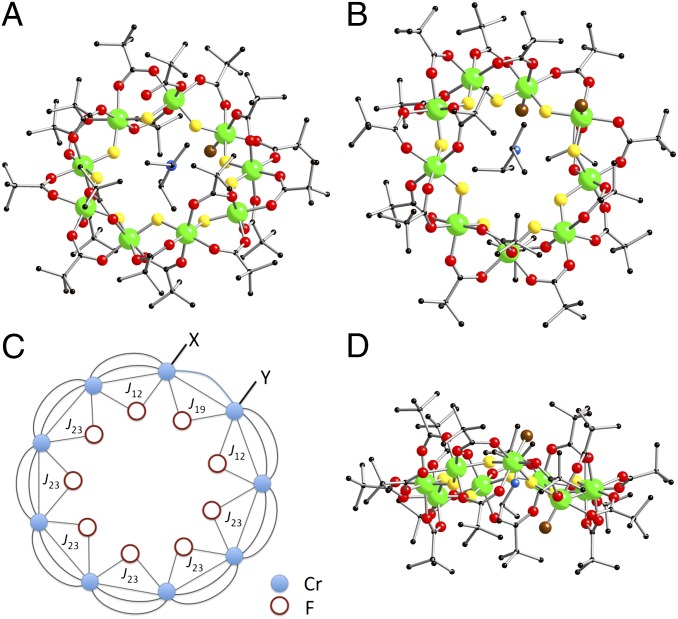
The structures of 3 and 4 are closely related (Fig. 1). The nine-metal rings have eight edges bridged by one fluoride and two pivalate ligands, in a manner similar to all eight edges in 2. Only a single fluoride and a single pivalate bridge the ninth edge, and therefore, both chromium sites in this edge have a terminal group attached to them. In 3, one terminal group (Y in Fig. 1C) is a fluoride and the second (X in Fig. 1C) is a pivalate; in 4, both terminal ligands are fluorides. We will discuss bond lengths and angles below when discussing possible structural explanations for magnetic behavior.

Fig. 1.

The structures of (A) 3 and (B) 4 in the crystal, viewed close to perpendicular to the plane of the nine Cr centers. (C) A schematic representation of the structure, with the magnetic exchange interactions used in Hamiltonian (Eq. 1) included. (D) A view of 4 looking into the unique edge, showing the arrangement of terminal ligands. Colors: Cr, green; O, red; N, blue; C, black; bridging F, yellow; terminal F, brown.

The X-ray structures indicate the problem of repeating connectivity with an odd-membered ring compared with an even-membered ring. In 2, one-half of the carboxylate ligands lie in the plane defined by the eight chromium centers, with the other half of the carboxylates alternately above and below this plane. In 3 and 4, on eight edges of the ring, there is a carboxylate in the plane and a carboxylate either above or below the plane. On the unique edge, we have one terminal ligand above the plane and the second below (Fig. 1D): this clearly prevents the terminal ligands from being displaced by a single carboxylate.

Magnetic Measurements.

We have studied compounds 3 and 4 to determine whether they show frustration as would be expected for a regular nine-spin ring. For an odd-electron, odd-metal antiferromagnetically coupled system, the strictest definition of frustration would require a degenerate pair of S = 1/2 spin states as the ground state. The point where frustration is said to be broken is reached, in the strictest sense, when the ground state spin degeneracy is lost because of inequivalent exchange couplings around the ring. If the inequivalence in exchange constants around the ring becomes sufficiently large, the ground state will change from S = 1/2 to S = 3/2, i.e., a state that can be derived from considering a finite chain with alternate up and down spins.

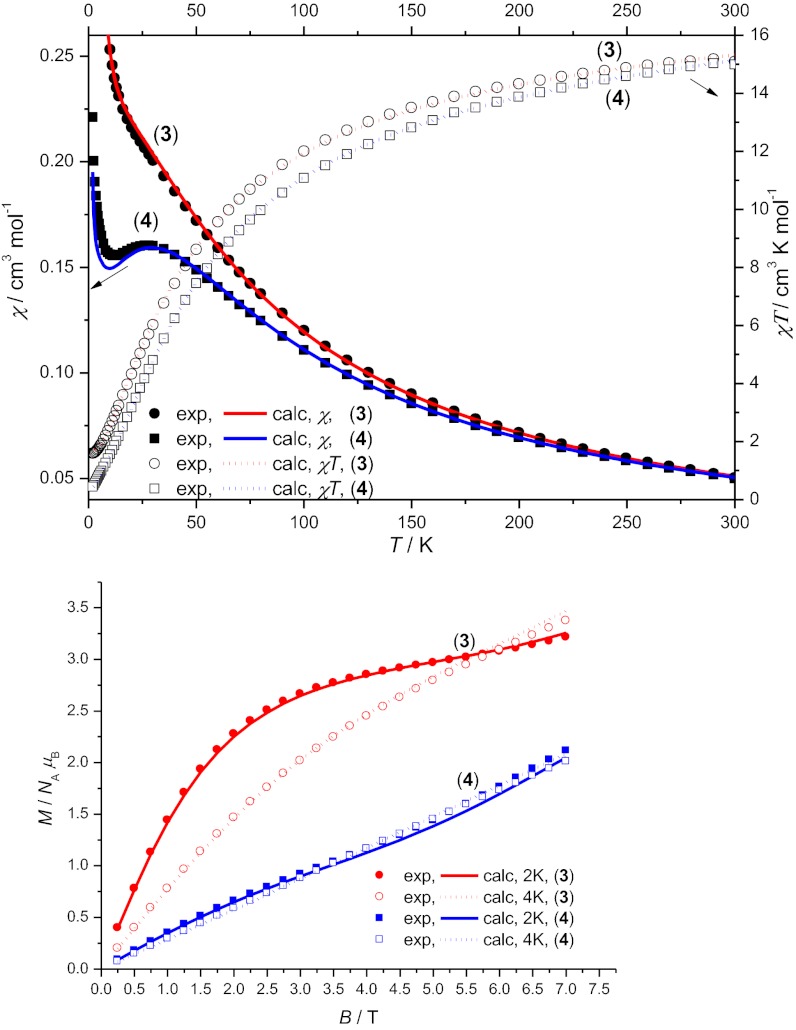
Direct current (DC) magnetic susceptibility measurements were performed on powdered microcrystalline samples of 3 and 4 in an applied magnetic field of 0.5 T and in the temperature range 300–1.8 K (Fig. 2). The high temperature χ_MT value of 15.1 cm³⋅K⋅mol⁻¹ and of 15.0 cm³⋅K⋅mol⁻¹, for 3 and 4, respectively, are lower than the value calculated (16.5 cm³⋅K⋅mol⁻¹) for nine noninteracting Cr^III (3d³) ions, assuming g = 1.98. This suggests relatively strong intramolecular antiferromagnetic interactions in 3 and 4. The χ_MT product of 3 and 4 decreases continuously with temperature to reach the value of 1.6 and 0.4 cm³⋅K⋅mol⁻¹, for 3 and 4, respectively, at 2 K. The behavior of the low temperature molecular magnetization, M, versus magnetic field, B, also varies (Fig. 2B). For 3, M rises rapidly with increasing field, and at 2 K, it approaches saturation at a value of 3 μ_B by 5 T; this behavior suggests an S = 3/2 ground state for 3. For 4, M increases more slowly with increasing field and shows no evidence for saturation to the highest field measured (7 T). The behavior of M for 4 suggests the likelihood of a ground spin-state of total spin, S, less than 3/2, which implies compound 4 shows signs of frustration.

Fig. 2.

The magnetic behavior of compounds 3 and 4. (Upper) Magnetic susceptibility (χ) versus temperature (T) and χT versus T for 3 and 4. (Lower) Magnetization (M) against field measurements for 3 and 4 at 2 and 4 K. In both cases, the simulations are based on Eq. 2 using parameters given in Table 1.

Inelastic Neutron Scattering.

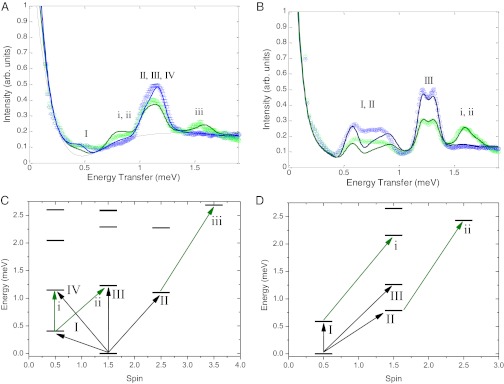
The inelastic neutron scattering (INS) spectra obtained for 3 and 4 differ considerably (Fig. 3). The Q integrated energy spectra of 3 (Fig. 3A) show the main cold band centered at 1.14 meV (containing overlapping transitions II, III, and IV), with a further cold transition centered at 0.5 meV (transition I). At 6.0 K, warm bands emerge at 0.8 (transitions i and ii) and 1.5 meV (transition iii). A high-resolution (9.0 Å) INS energy spectrum of 3 (Fig. S3) within this low energy region shows a cold peak at 0.08 meV that can be assigned, by analogy to Cr₇ horseshoes, which have an S = 3/2 ground state (16), as an intramultiplet transition within the potential S = 3/2 ground state quartet. The same measurement on 4 shows no band in the same energy range, suggesting a different ground spin state. The measurements on 4 at 1.6 K show two sets of cold bands, a group of transitions centered between 0.60 and 0.85 meV (transitions I and II), and a pair of transitions with a Gaussian line shape at 1.2 and 1.3 meV (transition III). At 6.0 K, an unsymmetric warm band emerges at 1.6 meV (transitions i and ii).

Fig. 3.

INS studies and energy levels for 3 and 4. (A and B) INS energy spectra for 3 and 4, respectively, measured with a 5.0-Å incident neutron setting at 1.5 (blue open circles) and 6.0 K (green open circles). The solid lines represent spin Hamiltonian simulations as described within the text. The labels correspond to the transitions marked in C and D. (C and D) Low energy spin multiplets as a function of their total spin for the isotropic exchange Hamiltonian for 3 and 4, respectively.

Fitting Magnetic and INS Data.

The magnetic susceptibility of 3 and 4 was numerically fitted to the isotropic spin-Hamiltonian (Eq. 1), using the self-written software ITO-MAGFIT (19) that makes use of irreducible tensor operator algebra (20) to block-diagonalize the spin-Hamiltonian and uses the Levenberg–Marquardt algorithm (21):

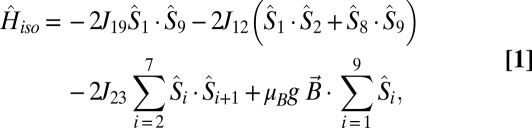where J_ij is an isotropic exchange parameter, 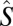is a spin operator, μ_B is the Bohr magneton, g = 1.98 was used as the g value for Cr^III (16, 17), and 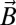is the applied magnetic field vector. The spin-Hamiltonian (Eq. 1) includes the nearest neighbor exchange with three differing exchange-coupling constants (Fig. 1B): one exchange constant (J₂₃) is the coupling between the chromium ions that are not in the unique edge; the second (J₁₉) is the coupling on the unique edge bridged by one pivalate and one fluoride; and the third (J₁₂) is the coupling between the chromium ions in the unique edge and their nearest neighbor. Studies on the Cr₇ horseshoe (1) found that the exchange constant to the terminal Cr ions differed from that of the body of the Cr chain—justifying the use of three exchange interactions (16).

The best fit parameters of the magnetic susceptibility alone give an energy level picture that matches the INS well, but with small deviations. To eliminate these deviations observed between experimental and calculated INS spectra, we modified the program ITO-MAGFIT to fit simultaneously the observed INS transition energies and the susceptibility data of 3 and 4 in the temperature range 300–1.8 K (Fig. 2). This gives the best fit parameters given in Table 1.

Table 1.

Parameters used to fit magnetic and INS data and calculated by DFT

	3		4
	Best fit parameters	DFT calculation	Best fit parameters	DFT calculation
J12/meV	−0.409 (1)	−0.621 (10)	−0.71163 (4)	−0.91 (10)
J19/meV	−0.0037 (5)	−0.197 (10)	−0.2715 (1)	−0.346 (10)
J23/meV	−0.726*	−0.914 (10)	−0.726*	−0.930 (10)
DCr/meV	−0.029	Not applicable	−0.038	Not applicable
Spin ground state	3/2	1/2	1/2	1/2

Numbers in parentheses are estimated error on last digit.

*Fixed based on previous studies (e.g., ref. 17).

The INS results clearly indicate nondegeneracy in total spin transitions as a result of the effect of single-ion anisotropy, D_Cr. For the simulation of the low-temperature magnetization vs. field data (Fig. 2B) and INS spectra of 3 and 4 (Fig. 3), single-ion anisotropy terms were added in spin-Hamiltonian (Eq. 1), as mainly evidenced by the splitting of the observed INS bands. Thus, the anisotropic spin-Hamiltonian (Eq. 2) used is of the following form:

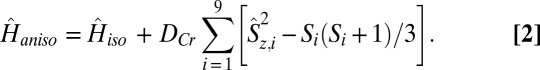The values of D_Cr were determined directly from the INS spectra and are given in Table 1. For 3, the low energy transition in the 9.0-Å spectra (Fig. S3) is the Δm_s = ±1 transition within the S = 3/2 ground state, which allows calculation of D_Cr = −0.029 meV. For 4, transition III is from the S = 1/2 ground state to an S = 3/2 excited state, and the appearance as a doublet (Fig. 3B) is due to zero-field splitting, which gives a D_Cr value of −0.038 meV.

The most significant difference between the two compounds is that for 3 the ground state is S = 3/2, whereas for 4 it is a single S = 1/2 state. Clearly the change in ground state is caused by the very small value of J₁₉ in 3. The energy gap to the first S = 1/2 doublet for 4 (transition I) is 0.62 meV, which is a measure of how far 4 deviates from a frustrated system by the Kahn definition (13). The behavior of 3 can essentially be modeled as a classical spin chain, whereas the physics of 4 cannot be explained with classical spins.

INS measurements at higher energy transfers show four additional cold transitions in compound 4. Fig. S4 shows cold excitations IV–VII with energies 2.13, 2.79, 3.28, and 3.75 meV. These excitations all come from the S = 1/2 ground state going up to sets of S = 3/2 excited states and are simulated using the parameters in Table 1.

Density Functional Theory Calculations.

To understand the different exchange interactions found in 3 and 4, density functional theory (DFT) calculations were performed on the X-ray structures of 3 and 4 but with pivalate replaced by acetate; the results are given in Table 1. These computed J values give a reasonable fit of the experimental magnetic susceptibility, but do not fit with the INS data. For both complexes, the order J₂₃ > J₁₂ > J₁₉ is reproduced by theory. It is also found that J₁₉ is larger in 4 than in 3, but with the absolute value of J₁₉ predicted to be significantly larger in 3 by DFT than what was observed. The result is that DFT predicts that both 3 and 4 should have an S = 1/2 ground state. In 3, the DFT calculation has the S = 3/2 first excited state lying nearby at 0.36 meV, with a much larger gap (4.19 meV) to the first excited state in 4. This discrepancy in predicting the correct ground state for 3 is caused by the overestimation of J₁₉ in 3 (Table 1).

The coupling J₁₉ involves one bridging fluoride and only one bridging acetate; to test whether this is the reason for the smaller exchange interaction, we performed calculations on model complexes (Fig. S5). Removal of one acetate bridge from a dimetallic {Cr(μ-F)(μ-O₂CMe)₂Cr} fragment leads to a reduction of the exchange interaction by approximately 0.7 meV, which is consistent with the difference between J₁₉ and J₂₃ in 3 and 4 (Table 1). The experimental J₁₂ of complex 4 is also found to be larger than for 3, and this is reproduced in the DFT values, with the explanation due to the terminal substitution (fluoride compared with carboxylate; see Structural Analysis below).

Discussion

Structural Analysis.

The structural parameters of compounds 3 and 4 are very similar. There are two types of Cr–F bonds: the Cr–F terminal bonds are the shorter in both compounds, with the terminal Cr–F bond = 1.834(6) Å in 3 and the two terminal Cr–F bonds in 4 averaging 1.818(8) Å. The Cr–F bonds involving bridging fluorides are all longer, averaging 1.928(8) Å in 3 and 1.927(7) Å in 4. There is no significant difference in the bridging Cr–F bonds within the unique edge and the other eight edges. The Cr–O bonds average 1.950(8) Å in 3, with the single terminal Cr–O bond the longest in the structure at 1.989(8) Å, and the next longest bond being the Cr–O bond [1.983(8) Å]. In 4, the Cr–O bonds average 1.951(10) Å. The bond angles are also very similar, as expected for Cr^III. All trans-angles in both structures fall in the range 172.6–179.8(4)°, whereas all bar one cis-angles fall in the range 83.0–96.3(4)°. There is one cis-O–Cr–F angle in 3 of 79.7(3)°. A final factor to consider is the angle at the bridging fluoride. In 3, the Cr–F–Cr angle in the unique edge is 131.0(3)° compared with angles in the other eight edges that lie in the range 120.1(3)–124.2(3)°. In 4, the unique Cr–F–Cr angle is 130.9(4)°, with the other eight Cr–F–Cr angles lying in the range 121.1(4)–123.5(4)°.

Examining the ranges of bond lengths at Cr in the two structures shows some subtle differences. In 4, the average difference between the shortest and longest Cr–X bond at each Cr is 0.050 Å, whereas in 3, the same average difference is 0.074 Å. This implies a greater distortion from octahedral geometry in 3 than 4 and may be an explanation for the slightly greater value for |D_Cr| in 4.

Therefore, the difference in each of the exchange interactions J₁₉ and J₁₂ between the two compounds is not caused by bond length or angle variations. The best explanation we can give is related to the variation in the coordination geometry at the Cr sites in the unique edge. In 4, both Cr sites have terminal F ligands and very similar coordination geometries, e.g., the shortest bonds are to the terminal fluorides for each site. In 3, the two Cr sites are significantly different, with one having a short bond to a terminal fluoride and the other a long bond to a terminal pivalate ligand. The DFT calculations offer a possible explanation; the Cr site in 4 with a terminal fluoride has a significantly smaller spin density compared with the site having a terminal carboxylate in 3 (2.905 vs. 2.971). The larger the spin density found on the Cr sites, the less spin delocalization onto bridging ligands and hence weaker antiferromagnetic interactions result (22). We have reported previously that the magnetic exchange interactions between Cr sites are dependent on the terminal ligands attached to the Cr ions (16).

Frustration.

Compounds 3 and 4 clearly show different physics, but curiously they would be classified identically by the current commonly used terminology. By the strict Kahn definition, neither 3 nor 4 is frustrated, and by the looser definition based on the presence of unsatisfied antiferromagnetic interactions, both are frustrated. Because the difference in the physics is not described by the current terminology, we propose that a new nomenclature is required for frustrated molecular systems. The idea is inspired by the classification of mixed-valent systems introduced by Robin and Day (23). We propose to have type I, type II, and type III frustration.

Type I systems obey the strict definition given by Kahn. Physically, they must have an odd number of electrons and result in a degenerate, spin-active ground state, i.e., multiple S = 1/2 levels. The spin number of the ground states will be lower than can be reached by regarding the quantum spins of the system classically. Structurally this will require a very regular geometry and the presence of odd-numbered circuits—either triangles, pentagons (as in the Keplerates), or larger rings.

Type II frustration is where the single ground state has a spin value lower than can be achieved by treating the molecule as having classical spins. Compound 4 shows type II frustration, in that the spin ground state is S = 1/2, which is lower than can be achieved by coupling nine classical s = 3/2 centers. The degenerate ground state required for type I frustration is not evident in type II systems. Structurally, a type II system is likely to contain odd-numbered circuits of spin centers, but with some structural distortion. Thus, in 4 we have eight edges of one type and a ninth of another. Conversely, in the related type II {Cr₈Ni} ring, we have a nonagon that has one vertex different from the other eight (14). The heptametallic {VO}₇ ring reported by Hoshino and colleagues also shows type II frustration (11).

Type III frustration is found in cases where the ground state could be derived from a classical treatment of the spin, but where there are competing antiferromagnetic exchange interactions. Compound 3 is a good illustration because J₂₃ >> J₁₉ leads to the spins on the Cr sites within the unique edge aligning parallel, leading to an S = 3/2 ground state.

The difference between type II and type III frustration is dependent on the relative magnitudes of the competing exchange interactions present. To understand this in the {Cr₉} rings, the behavior of a ring of nine s = 3/2 was calculated using numerically exact methods involving quantum transfer matrices and exact diagonalization (24), setting J₂₃ = J₁₂ to reduce the complexity of the phase diagram. The calculation shows that the spin ground state is S = 3/2 if the ratio 0 < J₁₉/J₂₃ < 0.154, which we would describe as type III frustration. For ratios of 0.154 < J₁₉/J₂₃ < 1, we have type II frustration and a single S = 1/2 ground state. For compound 4, the ratio of J₁₉/J₂₃ is at least 0.3, which is consistent with the theoretical analysis. Type I frustration would only be found if J₁₉ = J₂₃, and this illustrates why type I frustration is so rare.

Introducing a new classification can seem unnecessary; however, the different uses of the term frustration in the molecular magnetism community is also frustrating. Using type I, type II, and type III descriptions should clarify the position. In a recent tutorial review (3), Schnack discussed frustration in terms of bipartite descriptions of a system and suggested that a frustrated system is one that cannot be described as bipartite. This covers types I and II systems; our new classification also allows for the use in describing competing antiferromagnetic interactions. Thus, we are spreading frustration!

Materials and Methods

Synthesis.

All reagents and solvents were purchased from commercial sources and used without further purification. Complexes were prepared in Erlenmeyer Teflon flasks.

Pivalic acid (25 g, 245 mmol), di-isopropylamine (0.35 g, 3.5 mmol), and chromium(III) fluoride tetrahydrate (5.0 g, 27.6 mmol) were stirred together at 150 °C for 46 h. The flask was cooled to room temperature, MeCN (100 mL) was added, and the solution was stirred for 3 h to produce a solid precipitate. This was collected by filtration and washed with MeCN, and the solid was extracted with acetone (550 mL) while stirring overnight. The resulting solution was filtered and then evaporated to dryness under reduced pressure. The residue contained a mixture of compounds 2, 3, and 4; separation was achieved with column chromatography on silica gel.

With toluene as an eluent, compound 2 elutes first as an intense green band (1.45 g found after evaporation). The eluent was changed to 40:1 toluene:ethyl acetate, and 3 was eluted as the next band. Evaporation of the solution under reduced pressure gives 3 as a green powder with a yield of 1.25 g (16%). Calculated elemental analysis (%) of 3 as C₉₆H₁₇₈Cr₉F₁₀N₁O₃₆ are Cr 18.14, C 44.68, H 6.95, and N 0.54 compared with experimental values, which gave (%) Cr 18.40, C 44.46, H 7.09, and N 0.50. Positive ion electrospray mass spectrometry (+ES-MS) using THF as carrier solvent gave m/z values of +2603 assigned as the molecular ion plus one sodium, [M + Na]⁺, +2682 assigned [M + ⁱPr₂NH₂]⁺.

Thereafter, a mixture of 20:1 toluene:ethyl acetate was used to elute 4. After evaporation to dryness, 4 remained as a green powder with a yield of 0.8 g (10%). Calculated elemental analysis (%) of 4 as C₉₁H₁₆₉Cr₉F₁₁N₁O₃₄ are Cr 18.73, C 43.75, H 6.82, and N 0.56 compared with experimental values, which gave (%) Cr 18.62, C 43.16, H 6.96, and N 0.59. Positive ion electrospray mass spectrometry (+ES-MS) using THF as carrier solvent gave m/z values of +2520 assigned as the molecular ion plus one sodium, [M + Na]⁺, +2600 assigned [M + ⁱPr₂NH₂]⁺.

Structural Studies.

Single crystals of 3 and 4 were grown from Et₂O/MeCN solutions. X-ray data were collected using an Enraf Nonius CCD single crystal X-ray diffractometer using Mo-K_α radiation (λ = 0.71073 Å). All data were collected at 100 K. Structures were solved and refined by full-matrix least-squares techniques on F² using the SHELX-97 program (25). The absorption corrections were done by Multiscan methods. Hydrogen atoms were included in the refinement process as per the riding model.

Crystal Data.

Crystallographic data collected for 3, C_96.5H₁₈₁Cr₉F₁₀NO_37.5 of relative molecular mass M = 2613.4, showed a monoclinic space group, P2₁/n, with unit cell parameters a = 19.4799(4), b = 27.4301(6), c = 27.2085(7) Å, β = 90.4480(10)^o, and cell volume V = 14538.0(6) ų, with four molecules per unit cell (Z = 4), and density ρ = 1.194 g·cm⁻³. 26,498 data points were collected of which 13,514 were considered unique with R_int = 0.0677 and μ = 0.721 mm⁻¹. There were 1,386 parameters and 2,448 restraints were applied to produce a residual R₁ = 0.0883 for I ≥ 2σ(I) and a weighted residual wR₂ = 0.2278 for all data. The equivalent numerical crystallographic data for 4 were: C₉₉H₁₈₅Cr₉F₁₁N₃O₃₅, M = 2654.5, orthorhombic space group P2₁2₁2₁, a = 19.6327(4), b = 21.5606(4), c = 32.6247(8) Å, V = 13809.8(5) ų, Z = 4, ρ = 1.277 g·cm⁻³, total data 27,741, unique data 14,505 (R_int = 0.1004), μ = 0.76 mm⁻¹, 1,417 parameters, 3,244 restraints, R₁ = 0.0858 for I ≥ 2σ(I) and wR₂ = 0.2247 for all data.

CCDC 893834 and 893835 contain the supplementary crystallographic data for this paper. These data can be obtained free of charge from The Cambridge Crystallographic Data Centre via www.ccdc.cam.ac.uk/data_request/cif.

Physical Measurements.

Magnetic susceptibility measurements were performed in the temperature range of 300–1.8 K, using a Quantum Design MPMS-XL SQUID magnetometer equipped with a 7-T magnet. Magnetization measurements were performed at 2 and 4 K using the same equipment. Diamagnetic corrections were estimated using Pascal's constants, and magnetic measurements were corrected for sample holder contributions.

INS was performed on the IN5b time-of-flight inelastic spectrometer (26) at the Institute Laue-Langevin, Grenoble, France. IRIS is a time-of-flight inverted-geometry crystal analyser spectrometer at ISIS, the centre for research in the physical and life sciences at the Science and Technology Facilities Council, Rutherford Appleton Laboratory, United Kingdom, on polycrystalline nondeuterated samples of 3 or 4 loaded into a hollow aluminum cylinder for measurement.

Modeling Experimental Data.

Simultaneous fitting of the susceptibility and INS data of 3 and 4 was based on a sparse matrix technique described elsewhere (27), using the Davidson algorithm (28). Susceptibility data measured in an applied magnetic field of 0.5 T and in the temperature range 300–1.8 K were included in the fit. In addition, a number of INS transitions were included by assigning the observed INS bands and including the energy difference of the relative eigenstates, at zero-field, as an observation. Assignment of the bands was made on the basis of the preliminary energy spectrum obtained by fitting only the susceptibility data to spin-Hamiltonian (Eq. 1). In cases where the relevant states were split at zero-field, the barycenter of the state was taken into account to create an effective isotropic model. Further detail is given in SI Text.

DFT Calculations.

The DFT calculations were performed using Noodleman’s broken symmetry (BS) approach (29) to compute J values, using Gaussian 09 software (30) with the hybrid B3LYP functional (31–33). We used a triple zeta valence (34) basis set on Cr and split valence polarization for the rest of the elements (35). Calculations were performed on models of 3 and 4 where the pivalates were replaced by acetates, as in previous work (36, 37). The magnetic exchange interactions were extracted using the pairwise interaction model (38) based on the energies of five spin configurations, given in SI Text, which were calculated for both 3 and 4. Errors on the computed interactions were estimated and are included in Table 1 (39).