Shear-induced phase transition of nanocrystalline hexagonal boron nitride to wurtzitic structure at room temperature and lower pressure

Abstract

Disordered structures of boron nitride (BN), graphite, boron carbide (BC), and boron carbon nitride (BCN) systems are considered important precursor materials for synthesis of superhard phases in these systems. However, phase transformation of such materials can be achieved only at extreme pressure–temperature conditions, which is irrelevant to industrial applications. Here, the phase transition from disordered nanocrystalline hexagonal (h)BN to superhard wurtzitic (w)BN was found at room temperature under a pressure of 6.7 GPa after applying large plastic shear in a rotational diamond anvil cell (RDAC) monitored by in situ synchrotron X-ray diffraction (XRD) measurements. However, under hydrostatic compression to 52.8 GPa, the same hBN sample did not transform to wBN but probably underwent a reversible transformation to a high-pressure disordered phase with closed-packed buckled layers. The current phase-transition pressure is the lowest among all reported direct-phase transitions from hBN to wBN at room temperature. Usually, large plastic straining leads to disordering and amorphization; here, in contrast, highly disordered hBN transformed to crystalline wBN. The mechanisms of strain-induced phase transformation and the reasons for such a low transformation pressure are discussed. Our results demonstrate a potential of low pressure–room temperature synthesis of superhard materials under plastic shear from disordered or amorphous precursors. They also open a pathway of phase transformation of nanocrystalline materials and materials with disordered and amorphous structures under extensive shear.

Synthesis of superhard materials in the boron carbon nitride (BCN) system under high pressure and temperature is one of the modern directions in high-pressure material science with significant technological potential. In particular, superhard wurtzitic boron nitride (wBN) and, especially, cubic boron nitride (cBN) are of great interest because of their unique properties: high hardness, high thermal conductivity, chemical inertia to ferrous materials, high dynamic strength, and high wear resistance, etc. (1). They can be obtained, in particular, by the direct solid–solid phase transitions initiated from the graphite-like boron nitride (BN) phases [i.e., hexagonal (h)BN and rhombohedral (r)BN] under extreme conditions. Specifically, hBN-to-wBN phase transition has been extensively studied in both dynamic and static high-pressure experiments. An important parameter that determines transformation pressure and mechanism is the concentration of the turbostratic stacking faults or degree of disordering. It was found that a highly ordered hBN transforms to wBN when compressed to high pressures [8.1–13 GPa (2–5)] at either room or high temperatures. The lowest pressure at which highly ordered hBN-to-wBN transformation starts at room temperature is, thus far, 8.1 GPa; it starts to become irreversible above 10 GPa; transformation does not complete up to 25 GPa (4, 6). In ref. 3, highly ordered hBN started to transform at 10 GPa under nonhydrostatic compression; after pressurizing to 12 GPa, wBN was quenchable. With an increase in degree of disorder, transformation pressure drastically increases (7, 8). In particular, wBN was not observed at room temperature with a degree of disorder higher than 0.1, even above 30 GPa (7).

For highly ordered hBN, transformation to wBN occurs by a martensitic mechanism (7, 9). A highly disordered hBN transforms to wBN or cBN by a reconstructive (diffusion) mechanism, which requires high temperature. There has not been any report about the formation of wBN or cBN from a disordered hBN under high pressure at room temperature.

Recently, special interest has been demonstrated in transformation of completely disordered (turbostratic) phases in the BCN system, in which a lack of order for directions other than the <001> direction (7, 10) is observed, in particular, in hBN (11–13), BC₄ (14), and BCN (15). The idea is that because martensitic phase transformation for turbostratic phases is impossible, reconstructive transformation will lead to stable cubic rather than metastable wurtzitic phases. Also, increase in degree of disorder, while suppressing martensitic transformations, promotes reconstructive transformations. Of course, high temperatures along with high pressures are required for reconstructive transformations.

The superposition of large plastic shear on high pressure drastically changes the microstructure, mechanism, thermodynamics, and kinetics of phase transitions (8, 16–19). The rotational diamond anvil cell (RDAC), a modified design of traditional diamond anvil cell (DAC) with the capability to rotate one anvil against the other one about the loading axis at constant force, is an ideal tool to generate large plastic shear at high pressure (19). Technical developments for RDAC, namely the gasket technique to produce quasihomogeneous pressure distribution in the sample chamber (8, 20) and the detection technique to measure X-ray diffraction (XRD) and ruby fluorescence at a fixed point in a sample (21), make it possible to explore the pressure and shear effect on the phase transformations of a material. Previous studies with an RDAC revealed that plastic shear can significantly reduce phase-transformation pressure, substitute a reversible phase transformation with an irreversible one, lead to new phases, and cause fast strain-induced kinetics (18). The three-scale theory developed in ref. 18 explains that plastic-shear deformation generates defects (such as dislocation pileups and various boundaries) with high stress and pressure concentration at their tips, which allows nucleation under much lower external pressure.

In application of plastic shear to highly ordered hBN, however, pressure for initiation of transformation to wBN was surprisingly close to that under hydrostatic conditions (9.6–10.3 GPa) (8, 20, 22, 23). Using in situ synchrotron energy-dispersive XRD techniques, it was found that in addition to the promoting effect of plastic shear, plastic strain significantly increases the degree of disorder, which should increase phase transformation pressure (8). It happens that both opposite effects practically eliminate each other.

The goal of the current study is to perform an exploratory study of phase transformation in nanocrystalline highly disordered hBN under high pressure and shear at room temperature and compare results with hydrostatic compression up to 52.8 GPa. The main objective is to find which transformation (if any) will occur under large plastic strain, how much the transformation pressure can be reduced by large shear rather than high temperature, and whether this direction is worth further investigation from the applied point of view. Under hydrostatic compression up to 52.8 GPa, no phase transformation to wBN or cBN was observed. Surprisingly, strain-induced transformation to wBN in RDAC occurred at pressures as low as 6.7 GPa. Our results demonstrate a potential for low pressure–room temperature synthesis of superhard materials under plastic shear from highly disordered and amorphous precursors. The possible transformation mechanisms are discussed.

Results and Discussion

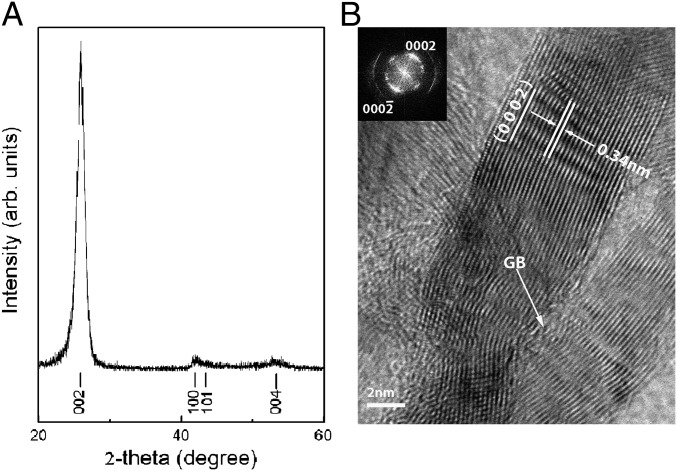
The XRD pattern of the sample at ambient conditions is shown in Fig. 1A. The pattern shows the appearance of a broad diffraction maximum (d = 3.440 Å) with two weak and diffused humps. The peaks can be indexed into hBN with lattice parameters as a = 2.50 ± 0.02 Å and c = 6.88 ± 0.03 Å. Although this material is claimed to be fully turbostratic in refs. 10–12, it is synthesized using the same technology described in ref. 10 and possesses the large d-spacing of the (002) planes of 3.440 Å like in turbostratic hBN in ref. 10 [compared with the reported 3.33–3.35 Å in highly ordered hBN (24, 25), it is highly but not completely disordered (turbostratic)]. Indeed, the (002) peak is relatively narrow, and peaks with three indexes [such as (101)] are present. Fig. 1B shows a selected high-resolution transmission electron microscopy (HRTEM) image of the initial sample. The bulk crystal consists of mostly nanograins of hexagonal structure, with distinct grain boundaries. The approximate size of the grains is 9 nm.

Fig. 1.

(A) XRD pattern at ambient condition. Peaks are indexed with hexagonal lattice. (B) HRTEM image of starting sample.

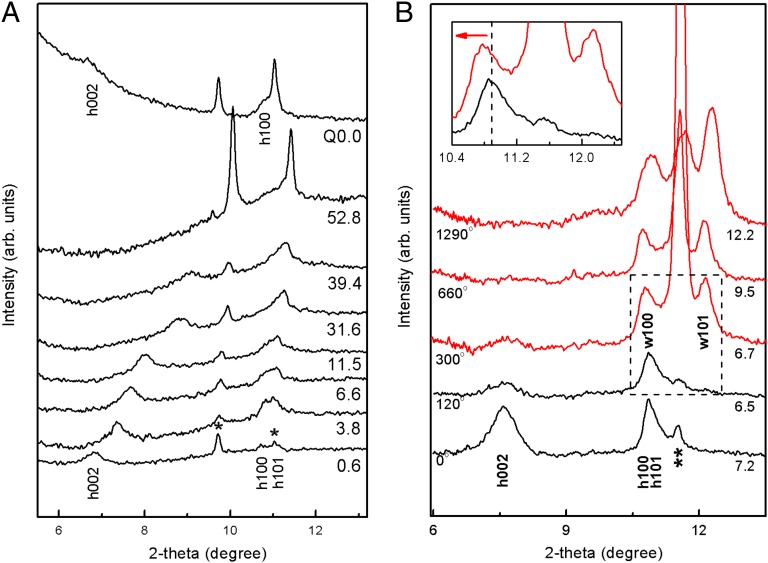
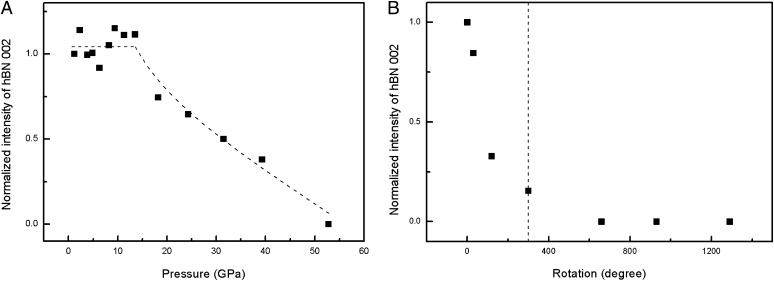
In Fig. 2A, selected diffraction patterns obtained from run I for compression to 52.8 GPa within hydrostatic medium are shown. Diffraction peaks can be indexed as from the sample and the rhenium gasket. With compression, the hBN (002) peak significantly reduces its intensity but obviously survives to 39.4 GPa (Fig. 3A). Although at 52.8 GPa, the hBN (002) peak cannot be detected, the quenched pattern still indicates an hBN structure. Thus, no phase transition to wBN or cBN can be identified under the hydrostatic and subsequent quasihydrostatic compression to 52.8 GPa. This confirms that martensitic phase transformation is impossible for a disordered structure and reconstructive transformation requires thermal activation and high atomic mobility that are unavailable at room temperature. In addition, nanograins suppress martensitic phase transformation as well. In general, nanocrystalline material can possess different transformation paths, metastable phases, and transformation pressures under hydrostatic conditions (26, 27). Nano-sized grains can either suppress (26–28) or promote (26, 27, 29) phase transformations. At the same time, some features of X-ray patterns are similar to those in other turbostratic structures, such as BCN solid solution (15) and BC₄ (14). In particular, here, the (002) peak reduces its intensity with pressure and completely disappears in the pressure range of 18.2–52.8 GPa (Fig. 3A) but returns after unloading (Fig. 2A). A similar behavior was observed for the (001) peak for BCN solid solution (15) and BC₄ (14). It was interpreted as a buckling of the layers followed by a sluggish reversible transformation to a high-pressure disordered phase with closed-packed buckled layers; however, covalent bonding between the layers did not occur. In ref. 30, to some extent, similar buckling was observed during cold compression of graphite, which preceded formation of a new superhard high-pressure phase that was also reversible at unloading. Thus, it is reasonable to assume that disordered nanocrystalline hBN also undergoes buckling and reversible phase transformation to diamond-like disordered phase under quasihydrostatic cold compression. Still, the transformation from this phase to wBN or cBN requires a reconstruction of the crystal lattice, which is impossible at room temperature and the achieved pressure.

Fig. 2.

(A) Selected high-pressure XRD patterns from run I for hydrostatic and quasihydrostatic cold compression of hBN in DAC. Numbers under the patterns are pressures in gigapascals, and Q represents quenched. The asterisk marks the diffraction peaks from the rhenium gasket. (B) Selected high-pressure XRD patterns from run II for compression and shear of hBN in RDAC. The lowest pattern was obtained at the center of the sample chamber, and other patterns were obtained 75 μm away from the center of the sample chamber. Angles of anvil rotation (in degrees) and pressures (in gigapascals) are noted below the patterns. The double asterisk marks the diffraction peak from the gasket [α-Fe (110) peak]. (Inset) Magnified view of the pattern enclosed in the dashed frame. The dashed line and arrow are visual guides.

Fig. 3.

(A) Pressure-dependent relative intensity of the hBN (002) peak. Normalization was done against the intensity of the (002) peak at 1.2 GPa. The dashed line serves as a visual guide. (B) Normalized intensity of the hBN (002) peak versus rotation angle of an anvil. Normalization was done against the integrated intensity of the hBN (002) peak of the pattern at 7.2 GPa without rotating. The dashed line indicates the rotation angle at which phase transition started.

Fig. 2B shows the selected patterns obtained under compression and shear in RDAC from run II. Upon compression to 7.2 GPa, the (002) and (100) peaks commonly shift to higher 2-θ angles. The (002) peak shifts by a larger extent than the (100) peak because of the weak Van der Waals force between the layers compared with the intralayer covalent bonding. The hBN-to-wBN phase transition was observed at 6.7 GPa when the anvil was rotated by 300°. At this condition, a new peak appears and the previous hBN (100) peak shifts toward a lower 2-θ angle (Fig. 2B, Inset). The new peak was identified as the wBN (101), and the shifting of hBN (100) peak was considered to signify the emergence of wBN (100). We attribute the shifted hBN (100) to the emergence of wBN (100) for two reasons: (i) wBN (100) has a larger but comparable d-spacing with hBN (100); and (ii) the hBN (100) was broad and diffused initially. Thus, the wBN (100) peak is unable to split completely from the parent hBN (100) peak. The deviation of the wBN peak d-spacing in this experiment from what was reported in previous studies is attributed to the irregular cell parameters of the starting material. By further rotating the anvil by 990°, the pressure was increased to 12.2 GPa, and no further phase change could be identified. Because we did not see any remaining hBN peaks, it is very probable that this transformation was complete, similar to strain-induced transformation in hBN in ref. 8. The probability is determined by the complete disappearance of the hBN (100) peak, which cannot be clearly resolved from the wBN (100). It is noteworthy to point out that the phase transition pressure of 6.7 GPa is the lowest pressure threshold for the initiation of irreversible transformation of hBN to wBN at room temperature without a catalyst reported by far (Table S1). Such a low pressure makes it potentially attractive for practical applications. Moreover, even assuming that wBN can eventually be obtained from highly disordered and nanocrystalline hBN under cold hydrostatic compression, we observed a reduction in transformation pressure by at least an order of magnitude. This extremely strong effect demonstrates the significant impact of large plastic shear on thermodynamic and kinetics of transformation in disordered and nanocrystalline hBN that can also be applied to other material systems, such as BCN and BCNO.

Usually, large plastic shear may transform crystalline structures to highly disordered and amorphous phases (17, 31, 32). In the current work, an exactly opposite effect of transformation of highly disordered hBN into crystalline wBN was revealed.

We consider a mechanism with two effects of large plastic shear on phase transformation in nanocrystalline hBN. As in ref. 18, where a model of nucleation at dislocation pileup generated by prescribed plastic shear was used to explain its strong effect on phase transformation, plastic shear leads to generation of defects and to an increase in concentration of pressure and deviatoric (nonhydrostatic) stresses at the tip of defects with growing shear (for example, because of increase in number of dislocations in dislocation pileup). The local pressure may even be an order of magnitude higher than the applied pressure. Beyond the pressure elevation, high deviatoric stresses produce additional thermodynamic driving force for lattice reconstruction toward high-pressure phases and the possibility of additional atomic transformation paths. Because the disordered nanocrystalline sample used in our experiments had a much larger yield strength than highly ordered bulk hBN, the plastic shear effect can be more pronounced.

The other effect of shear on a phase transformation is applied through the atomic rearrangements during plastic deformation. In a nanocrystalline material, additional deformation mechanisms related to shear in large angle grain boundaries have been observed (33). It was modeled (33) as plastic deformation in amorphous material through localized shear zones (34, 35), with shear stress equal to half of theoretical strength in shear. Thus, large shear in highly disordered grain boundaries leads to atomic rearrangements that play the part similar to thermal activation at high temperature and to a transformation to wBN. Because strength of wBN is significantly higher than hBN, shear zones localize in the weaker places (18, 33), i.e., they shift into new hBN–wBN boundaries.

During rotation of an anvil at pressures around 6.7 GPa, reduction in the intensity of the (002) peak (similar to that during increase in pressure) precedes the phase transformation into wBN (Fig. 3B). Because the local pressure near defects may be even an order of magnitude higher than the applied pressure, it leads to the layer buckling and transformation to wBN observed at such pressure. This does not conflict with the presence of (002) peak before transformation to wBN in Figs. 2B and 3B, because the buckling starts at the localized positions (stress concentrators) and stress and plastic strain fields are extremely heterogeneous along the sample width (36, 37). Because patterns averaged over the width are measured in experiments, the remaining (002) peak may be from the nonbuckled regions.

If the hBN were to transform to wBN martensitically, it would have occurred under high hydrostatic pressure (driving force), where thermal fluctuations are not necessary. Thus, we believe that the transformation of the disordered nanocrystalline hBN to wBN is through a reconstruction mechanism.

The fact that wBN rather than cBN is formed is also nontrivial. Under hydrostatic conditions, highly disordered and turbostratic hBN also transforms to wBN at lower pressure and temperature and to cBN at higher pressure and temperature (12, 14). In ref. 12, the formation of wBN from disordered and turbostratic hBN was explained by a thermally induced ordering of hBN followed by a martensitic transformation. It is hard to imagine that the plastic strain that usually increases the degree of disordering in hBN (8) will reduce it; actually, we expect that plastic strain may lead to turbostratic hBN. Also, even initially highly ordered hBN did not transform below 9.6 GPa (8). In addition, because a reduction of intensity and subsequent disappearance of the (002) peak was observed and is interpreted as the new high-pressure phase, thermal- or strain-induced ordering of hBN seems improbable. We believe that reconstruction of crystal lattice is more pronounced for transformation to cBN than to wBN. That is why at smaller thermodynamic driving forces and thermal- or strain-induced activation, the closest wBN phase appears. For the larger driving force and thermal- or strain-induced activation, transformation can reach the more stable cBN.

For strain-induced transformations, we see two opposite ways to obtain cBN instead of wBN. One of them is to increase pressure, to increase the global driving force for phase transformation. However, in this case, transformation will require smaller plastic strain and, consequently, smaller local nonhydrostatic stresses, thus reducing strain-induced activation. If we reduce external pressure and increase the plastic shear to cause phase transformation, local deviatoric stresses will be higher and will strongly promote the strain-induced activation. Under very large plastic shear, hBN may transform to the amorphous phase, similar to the case with pressure–shear treatment during the ball milling (38). Because the main mechanism of plastic deformation of amorphous phases is related to a series of irreversible rearrangements in small shear transformation zones (34, 35), it plays a similar role for atomic rearrangements toward a stable state as what thermal fluctuations do. Also, the amorphous phase possesses numerous stochastic configurations, which give numerous chances for transformation to the stable cBN under plastic shear to occur. The second way is also more interesting for practical applications, because it requires smaller external pressure.

Conclusions

In summary, an experimental study of highly disordered and nanocrystalline hBN under high pressure and large plastic shear was performed in RDAC using in situ synchrotron XRD. The phase transition from disordered nanocrystalline hBN to superhard wBN was detected at room temperature under large plastic shear. This phase transition was not observed under hydrostatic compression of the same sample up to 52.8 GPa. Under shear, it was initiated and probably completed under pressures as low as 6.7 GPa. It is probable that in both experiments, hBN first transformed to a high-pressure disordered phase with closed-packed buckled layers. Whereas under hydrostatic compression, this transition was reversible, under shear, it was followed by irreversible reconstructive transition to wBN. Traditionally, large plastic shear is used to obtain highly disordered and amorphous structures. Here, the opposite effect of transformation of highly disordered hBN into crystalline wBN was revealed, which leads to direct phase transitions from hBN to wBN at low pressure and room temperature. The mechanisms of strain-induced phase transformation and the reasons for transformation at such low pressure are discussed. One of them is related to the dislocation mechanism of plastic flow in grains, in which the nucleation occurs at the strong pressure and deviatoric stress concentrator at the tip of the strain-induced defects. For smaller grain size, additional plastic flow occurs in disordered grain boundaries through atomic rearrangements in localized shear zones, which plays a part similar to the thermal activation at high temperature and leads to transformation to wBN. Our results demonstrate a practical potential of strain-induced synthesis of superhard materials at low pressure and room temperature from nanocrystalline, highly disordered, turbostratic, and amorphous precursors in BN, BCN, and BCNO systems. It, thus, opens the door for the study of the effect and mechanisms of plastic strain-induced phase transformations in turbostratic and amorphous structures.

Materials and Methods

The pyrolytic hBN samples produced by a chemical vapor deposition (CVD) method described in ref. 10 with nano-sized grains and high concentrations of turbostratic stacking faults were used. The two runs of high-pressure in situ synchrotron angle-dispersive XRD (ADXRD) experiments were performed using both traditional DAC with pressure media (run I) and RDAC without pressure media (run II). The ADXRD experiments were carried out at the X17C beamline of the National Synchrotron Light Source (Brookhaven National Laboratory), with a monochromatic beam of 0.4066-Ǻ wavelength. The high-resolution lattice imaging was performed using a JEOL 2100 TEM operated at 200 kV and point-to-point resolution of 0.14 nm. The ambient XRD pattern was obtained on a Philips X’pert PW3098/20 diffractometer with Cu Kα radiation. A detailed description of the methods is available in SI Materials and Methods.