Bottom-up construction of in vitro switchable memories

Abstract

Reaction networks displaying bistability provide a chemical mechanism for long-term memory storage in cells, as exemplified by many epigenetic switches. These biological systems are not only bistable but switchable, in the sense that they can be flipped from one state to the other by application of specific molecular stimuli. We have reproduced such functions through the rational assembly of dynamic reaction networks based on basic DNA biochemistry. Rather than rewiring genetic systems as synthetic biology does in vivo, our strategy consists of building simplified dynamic analogs in vitro, in an artificial, well-controlled milieu. We report successively a bistable system, a two-input switchable memory element, and a single-input push-push memory circuit. These results suggest that it is possible to build complex time-responsive molecular circuits by following a modular approach to the design of dynamic in vitro behaviors. Our approach thus provides an unmatched opportunity to study topology/function relationships within dynamic reaction networks.

Cellular information processing relies on dynamic networks of biochemical reactions (1). For example, genes and their products regulate each other in intricate assemblies that embrace numbers of components and interactions. The function of these assemblies (i.e., the computation that they perform at the molecular level) is encoded both in the structure and in the physical characteristics of the web of chemical interactions that links their components. These in vivo networks are often difficult to identify in their entirety. Indeed, a complete description requires (i) a detailed analysis of the macroscopic dynamic behavior, (ii) a molecular understanding of the structure of the underlying biological network sustaining the function, and (iii) a chemical (thermodynamic and kinetic) knowledge of the reactions at hand. For technical reasons, this information can be very hard to obtain, even in the simplest biological cases (2–5).

Rather than attempting a systematic analysis of natural reaction networks, synthetic biology harnesses cells as a receptacle (i.e., the hardware) to implement artificially designed networks (6, 7). These networks are typically engineered through the recycling of original biological parts, their modification, and their reassembly in nonnatural architectures, which endow cells with additional functions (8, 9). This strategy aims at understanding the cell regulatory processes through a bottom-up approach, which is expected to reveal the underlying design rules (10). In this way, small-scale circuits encoding elementary functions, such as cascades (11), counters (12), bistability (7, 13–15), or oscillations (6, 14), have successfully been engineered.

The richness of the cell’s inner biochemistry provides a platform that theoretically allows the engineering of an infinite number of increasingly complex synthetic networks (16). It also poses formidable challenges to a rational designer. In practice, only small synthetic networks (compared with their natural models) have been reported (17). One reason is that synthetic biologists face a shortage of known interoperable units (17, 18). Also, harnessing the cell’s machinery is a complex task; nonlinear effects (10, 19, 20) and unintended interactions between the synthetic circuit and the host housekeeping functions (21) are frequent and difficult to pinpoint. Moreover, the lack of quantitative knowledge of in vivo processes strongly constrains the predictive power of the in silico models used in the design process (16, 18).

Engineering analogs of gene networks out of the cell, in purposely created and better controlled in vitro environments, provides an attractive alternative (22–25). Going cell-free offers better control of the system parameters, minimizes unintended couplings, and allows easier quantitative analysis (26). Like in vivo gene networks, in vitro analogs are constructed from elementary units; however, this time, one is freed from the constraints of the cellular machinery. Various and possibly simpler chemistries can be used, toxicity and host interference disappear, and stochastic effects can be handled. Still, in analogy to synthetic biology, it is possible to build basic functions, such as oscillators (23, 27), bistable systems (22, 28), or logic gates (29, 30), through a rational bottom-up strategy. The expectation is that it will be possible to assemble these elementary modules in a wealth of large-scale circuits (31, 32), potentially with life-like behaviors (33).

This paper focuses on in vitro reaction circuits encoding memory functions. In the context of biological circuits, memory refers to the ability to integrate a transient molecular stimulus into a sustained molecular response (34). In most cases, this information is digitized into a small number of alternative states, which correspond to the multiple steady states of a dynamic chemical system. In the cell, various mechanisms exist to keep memory of an event. Slowly changing protein levels can result in memory-like behaviors transmitted over a few cell generations (35). Phage-like genetic recombination can be used reversibly to switch one bit of information on the DNA of engineered cells (36), creating passive data storage that can be passed down through generations. Epigenetic switches use bistability to carry a robust, heritable memory (37–39). Other bistable switches naturally occur in gene networks and play important roles in fundamental cell functions (3, 4), cell cycle (2, 40), cell commitment (5, 41), and signal transduction pathways (42).

Such biological memories based on multistability also require interfacing with upstream and downstream molecular processes. In particular, this includes the ability, given the correct stimuli, to toggle reversibly and sensitively between the reciprocally exclusive stable states (4, 5). From a chemical point of view, the memory function therefore incorporates a form of antagonism. On the one hand, robust information storage imposes stability against molecular perturbations or noise; however, on the other hand, the function also requires a sensitive mechanism to integrate environmental information and, if appropriate, update its state. The synthetic bistable switches constructed so far in vivo have not yet solved this dilemma. The host cells are typically forced on one state by exposition to strong inducer drugs for the whole switching time (7, 13, 43). Alternatively, nonmolecular stimuli, such as temperature or light, are used. For example, Lou et al. (15) have recently reported a synthetic switchable “push-push” bistable circuit in which UV stimulation was used to switch the system back and forth between its two stable states. However, such systems that use nonmolecular inputs cannot be cascaded (i.e., integrated into larger circuits). Additionally, in this case, extreme phototoxicity has a negative impact on the host cells.

Because the alternative states of a bistable system are all equally stable over time, thermodynamics imposes that multistability is fundamentally an energy-consuming, out-of-equilibrium process (44). Switching to the new state requires the complete disappearance or degradation of the constituents of the previous state. This poses a severe constraint for the design of in vitro analogs of biological memory circuits. Nevertheless, a couple of batch bistable systems (22, 28) have been reported, thanks to the use of an enzymatic sink to maintain the dynamics of the system. However, no attempt was made to switch these bistable networks after they first reached one of their steady states.

Herein, we use enzyme-catalyzed, DNA-based reactions (23) to construct various in vitro memory circuits in a rational manner. We present a DNA toolbox composed of three modules encoding elementary reactions: activation, autocatalysis, and inhibition. These modules can be arbitrarily connected in circuits encoding desired behaviors (SI Appendix, section I). We use these modules sequentially to construct three dynamic reaction circuits implementing memory functions of increasing complexity.

We start with a foundational bistable switch circuit, which always reaches one of only two possible steady states, depending on the initial conditions. This bistable switch is very robust to perturbation, and making it switchable requires a specific strategy. We use the modularity of the reactions to upgrade the bistable circuit to a two-input in vitro switchable memory circuit. This system comprises six modules and is able to flip between two stable states on administration of a small amount of the correct exogenous input. Next, we construct and experimentally characterize a push-push memory circuit that accepts a single external input. Depending on its present state, the same input flips it in one direction or the other. This push-push memory circuit culminates at eight modules, showing the ability of the DNA toolbox to serve as a tool to construct scaled-up in vitro reaction circuits rationally. All the experimental observations are rationalized by a quantitative mathematical analysis.

DNA Toolbox: Three Basic Modules

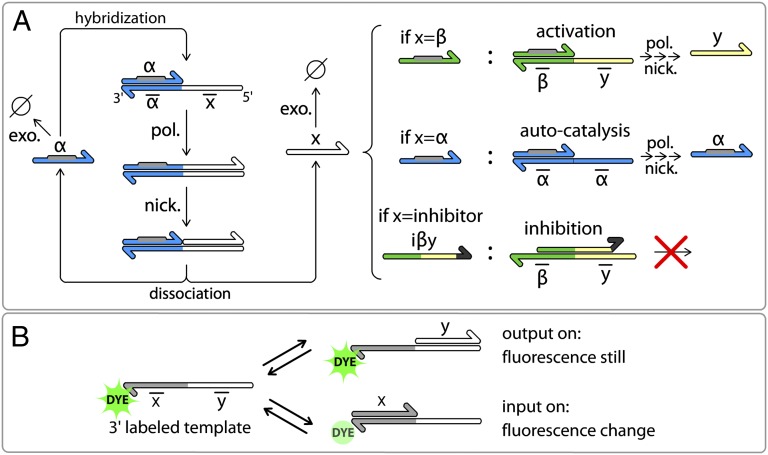
Our constructions are based on a stripped-down in vitro genetic machinery based on three enzymatic reactions (23) (Fig. 1A). Short DNA signal molecules hybridize with stable DNA template molecules in a set of basic reactions that structures the topology of the reaction circuits. Templates are 22- or 26-base-long, single-stranded deoxyoligonucleotides composed of a 3′ input site and a 5′ output site. Signal molecules come in two types: 11-base-long inputs activate templates; conversely, 15-base-long inhibitors block them. Reactions take place at a temperature (42 °C) at which both inputs and inhibitors are dynamically hybridizing and separating. Note that the short length of the inputs (11 bases) limits the number of available sequences, but the construction of relatively large circuits is still possible (SI Appendix, section II.4).

Fig. 1.

DNA toolbox uses DNA templates to shape reaction networks performed by a set of three enzymes. (A) Templates (bottom strands) have an input site (3′) and an output site (5′) and receive signal molecules (upper strands). When an input (α) hybridizes to a template, it is elongated by a DNA polymerase (pol.). Inputs bear the recognition site (gray) of a nicking enzyme (nick.) that cuts the elongated upper strand between input and output. Input α and output x then dissociate and are free to start another reaction or to be degraded by a single-strand specific exonuclease (exo.). Following this scheme, three types of modules can be obtained depending on the output sites of the template. (B) Nucleobase quenching on the dye-labeled templates allows sequence-specific monitoring of the reactions.

Templates encode basic reactions following the pattern input → input + output. When an input correctly hybridizes on the input site of a template, it is elongated by a DNA polymerase, leading to the double-stranded form of the template. Next, a nicking endonuclease nicks the new strand, such that input and output are released from the template. When free in solution, these short oligonucleotides can be degraded by ttRecJ, a single-strand specific 5′→3′ exonuclease (45, 46). Templates are protected from degradation by a few phosphorothioate backbone modifications located at their 5′ end (SI Appendix, section II.2). If not degraded, the input can start another round of reaction, whereas the output can, for instance, play the role of input for a separate reaction encoded by another template. Templates are thus fully composable, and can be classified into the following three modules depending on their input and output:

• Activation module if input ≠ output (α → α + β)

• Autocatalytic module if input = output (α → α + α)

• Inhibition module if output = inhibitor (α → α + inh)

Inhibitors are longer than inputs; hence, they are more stable when fully hybridized. A given inhibitor targets a template and strongly binds to it, overlapping on the input and output sites of the template. An inhibitor denoted as iα will target the autocatalytic module αtoα, and an inhibitor denoted as iαβ will target the activation module αtoβ. Inhibitors do not have the recognition site for the nicking enzyme; hence, they cannot be cut (SI Appendix, sections II.1 and II.3). They also possess two mismatched bases in 3′, which prevents the polymerase from extending them. Therefore, they are able to block the production of output by their target modules.

To observe the dynamics of these reactions, we use N-quenching (47), a versatile fluorescent technique for the monitoring of oligonucleotide hybridization. To follow a given input, the input site of the corresponding template is labeled in its 3′ end with a single fluorophore. Hybridization of the corresponding input produces a change in the fluorescence level, whereas hybridization of the template’s output does not (Fig. 1B). Therefore, templates themselves serve as specific reporters of the presence of their inputs. This monitoring technique eliminates the need for additional probes to monitor the system, which could, in turn, affect the function of the network through the load effect (48).

Using this toolbox, it is possible to build time-responsive DNA reaction circuits of various topologies and to follow in real time the behavior of some specific sequences within these dynamic systems. We demonstrate next the design and assembly of a bistable switch function.

Bistable Switch: Designing the Reaction Circuit

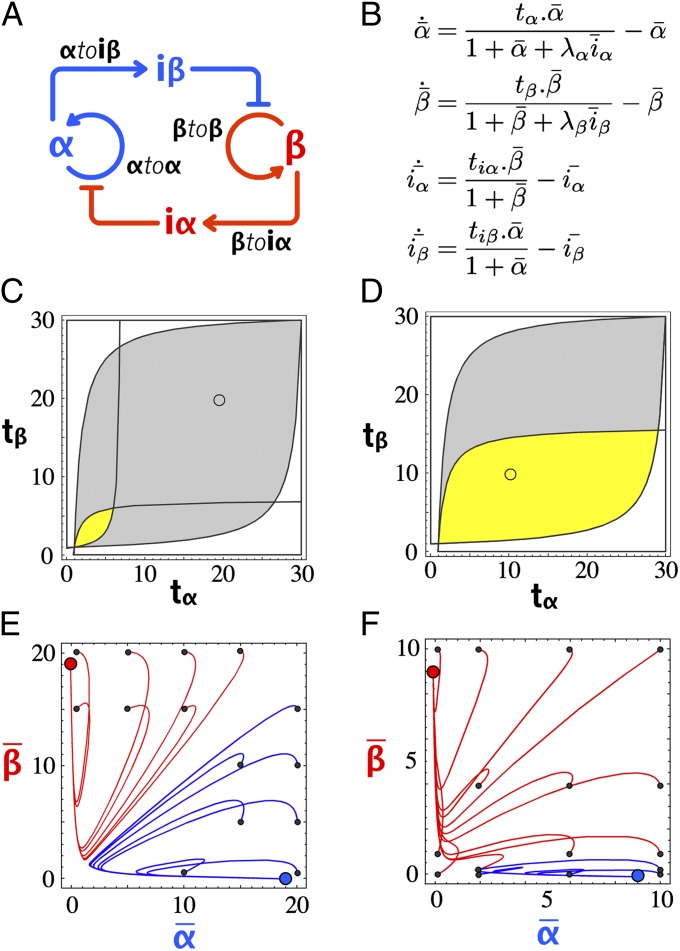
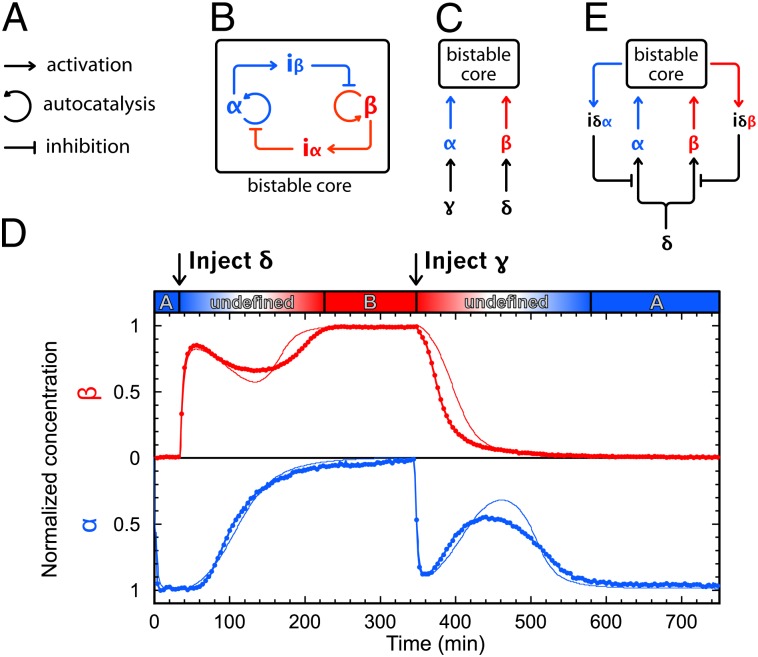
Bistability can be obtained from a variety of elementary motifs (49, 50), all including at least one positive feedback loop, but only a couple of basic designs do not require cooperative binding (51) (SI Appendix, section III.2). We chose here a symmetrical design (7) in which two autocatalytic modules negatively regulate one another. When one autocatalytic module is active, it dynamically represses the activity of the other (Fig. 2A). Given this topology, we decided on two signal strands (α and β), and designed two templates (αtoα and βtoβ, respectively) responsible for their autocatalytic production. Between αtoα and βtoβ are two inhibition modules that encode the cross-inhibition function. Inhibition module αtoiβ takes α as input and produces iβ. It therefore inhibits the production of β when α is present. Inhibition module βtoiα does the opposite job. By combining the four templates αtoα, βtoβ, αtoiβ, and βtoiα in appropriate ratios and conditions, we expect a system featuring bistability (i.e., where either α or β, but not both, can exist at the steady state).

Fig. 2.

Bistable circuit design. (A) Circuit encoding bistability. (B) Nondimensionalized equations of the simplified model: t_x is the scaled template concentration, and λ_x is the ratio of activator over inhibitor binding constant. Periods indicate multiplications. (C) Phase diagram of the bistable circuit in the {t_α, t_β} plane, with yellow indicating the bistable domain for {λ_α, λ_β} = {20, 20} and gray indicating the bistable domain for {λ_α, λ_β} = {100, 100}. (D) Same as in C, with yellow indicating the bistable domain for {λ_α, λ_β} = {100, 50} and gray indicating the bistable domain for {λ_α, λ_β} = {100, 100}. (E) Plot of the calculated trajectories of the bistable circuit for different initial {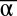, 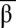} (small black dots). The bistable circuit is evolving to a stable state A (blue dot) or B (red dot). {λ_α, λ_β} = {100, 100} and {t_α, t_β} = {20, 20}, corresponding to the small circle in the gray area of C. (F) Same for {λ_α, λ_β} = {100, 50} and {t_α, t_β} = {10, 10}, corresponding to the small circle in the yellow area of D).

We started with the building of a simple model to check the consistency of the design with a bistable function when implemented within the toolbox. In this coarse-grained model, four equations express the life cycle (production and degradation) of the two inputs and two inhibitors (α, β, iα, and iβ) (details about the model construction are provided in SI Appendix, section III.1). To find out the control parameters of this bistable circuit design, we put the model in a nondimensional form (Fig. 2B), where productions of inputs and inhibitors are described by Michaelis–Menten equations with maximum rates (t_α, t_β, t_iα, t_iβ) controlled by the concentration of the template encoding the corresponding reaction. Sequestering of templates by the inhibitors tends to decrease the production rate following a competitive mechanism (enzyme saturation, which would lead to cross-coupling terms, is not considered in this simple model). Parameters λ define the relative strength of an inhibitor against the input it is competing with. Degradation is represented by a first-order term, with the same degradation rate for all four species.

When looking for stable equilibria in the {t_α, t_β} plane, the model suggests that the emergence of bistability is favored by high λ_α and λ_β (i.e., inhibitors stronger than inputs) (Fig. 2C). Experimentally, λ_α and λ_β can be adjusted by increasing the binding constants of iα and iβ (e.g., making these inhibitors longer). In the case of a nonideal system (e.g., nonsymmetrical λ_α and λ_β), the bistability domain in the {t_α, t_β} plane shrinks (Fig. 2D). To be bistable, the circuit needs to be adjusted by, for instance, changing the concentration of αtoα and βtoβ. Fig. 2 E–F shows the basins of attraction of the two states A and B for an ideal bistable circuit and a nonideal bistable circuit: For each combination of initial {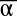, 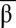}, the bistable circuit tends to one of the two states {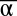, 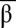} = {0, 1} or {1, 0}. One notes that even in the cases in which the system is bistable, the basins of attraction of the two states can be very asymmetrical.

Experimental Building of the Bistable Circuit

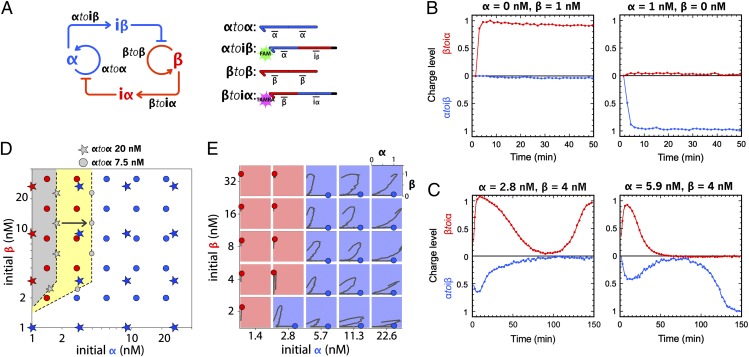
Given these theoretical considerations, we selected the sequences of α and β so that their predicted binding constants were close to each other at the working temperature. We then designed inhibitors so that their predicted binding constants were approximately two orders of magnitude higher than the ones of α and β [i.e., high enough to produce a large bistability domain but small enough to maintain a dynamic binding equilibrium with their target templates (this ensures the responsiveness of the circuit)]. Templates αtoiβ and βtoiα are labeled at their 3′ end with two different fluorophores (Fam and Tamra, respectively), which allows specific and simultaneous monitoring of both α and β (Fig. 3A). More details about the design rules are presented in SI Appendix, section II.1.

Fig. 3.

Experimental building of the bistable circuit. (A) Topology and templates of the bistable circuit. Templates αtoiβ and βtoiα are labeled with Fam and Tamra, respectively, allowing multiplex monitoring of the hybridization status of these two templates. (B) Time plots of the “charge level” of the bistable switch taking either state B (Left) or state A (Right). The charge level is the normalized fluorescence at 0 in the absence of the corresponding template’s input and 1 at the steady state of input. (C) Time plots of the charge level of the adjusted bistable switch for two different initial [α] and [β] combinations. (D) Bistable circuit picks its state (A or B) according to the initial combination of α and β concentrations. With each template (20 nM), the basin of attraction of state B (gray domain) is small compared with that of state A. Decreasing the concentration of αtoα to 7.5 nM results in an expansion of the basin of attraction of state B (yellow domain). Colored stars and dots are experimental points for, respectively, the bistable with 20 nM each template and the adjusted bistable with 7.5 nM αtoα for 20 nM βtoβ. Domain boundaries are drawn to facilitate the plot reading. (E) Experimental trajectories of the adjusted bistable for different combinations of initial α and β. For each trajectory, the x axis corresponds to the charge level of template αtoiβ and the y axis corresponds to the charge level of template βtoiα. After some transients, the bistable stabilizes in either state A (blue dot) or B (red dot).

To assemble the experiment, we combined the four templates and the three enzymes in a consistent buffer containing dNTPs and incubated them isothermally in a closed tube. We first checked for the presence of two stable states, which should be selected depending on the initial conditions. Indeed, we found that if the system is initiated with α only, it evolves to a stable state characterized by a strong shift in Fam fluorescence but no perturbation in Tamra fluorescence (called state A; Fig. 3B). Initial conditions containing only β produced the opposite fluorescent pattern (called state B). This suggests that the system possesses only two stable states. Note that working in a closed configuration imposes a limited lifetime for the system. Once all the dNTPs are consumed, it will simply die out toward its unique thermodynamic equilibrium.

To assess the bistable behavior of the circuit quantitatively (i.e., the convergence toward one of these states at the exclusion of any other trajectory), we initiated the reactions with various mixtures of α and β. We observed that after some transients, the system always stabilized on either stable state A or stable state B (Fig. 3C). These experiments also led to a matrix representing the basin of attraction of each stable state, which were initially quite asymmetrical (Fig. 3D). Even if templates were present in the same concentration and sequences had similar thermodynamic constants (but were still different: dissociation rate of α is more than twice that of β as seen in SI Appendix, Table S3), side A tended to win as soon as α was initially present in significant quantities, irrespective of the initial concentration of β. However, as suggested by the simple model, we could adjust this by tuning the concentrations of templates αtoα and βtoβ (Fig. 3D). Fig. 3E shows the trajectories of an adjusted system for different initial input combinations. Although the behavior is still not ideal, both states possess a reasonable basin of attraction.

To assess unambiguously and quantitatively the identity of the two states, aliquots were withdrawn from the solution after the system, initiated with {α, β} = {10 nM, 0.1 nM} or {0.1 nM, 10 nM}, had reached one or the other stable state. We analyzed the α and β content of these aliquots and found a concentration of 55 nM α for state A and 40 nM β for state B (SI Appendix, section IV). This similitude between the steady levels of α and β further validates that both sides of the bistable circuit are well balanced, thanks to the tuning of the concentrations of αtoα and βtoβ. At the same time, we measured about 1,000-fold less of the output of the losing state. The simple model predicts that the losing side should evolve asymptotically toward 0, but leak reactions not considered therein probably maintain a small basal level. Combining these results with the fluorescence measurement, we conclude that after having taken a stable state depending on the initial α/β ratio, the bistable system continuously and unambiguously delivers information about its current status.

The simple model predicts that the bistable circuit is robust to perturbations in the concentrations of α and β as long as they do not exceed the concentration of input currently at the steady state (SI Appendix, section III.3). Experimentally, we found that the bistable circuit is much more robust than this prediction. For example, when in the stable state A, an injection of a concentration of β (100 nM) twice as large as the steady concentration of α is not enough to flip the bistable circuit to the opposite state (Fig. 4A). This discrepancy could be attributed to the fact that the simple model rests on immediate equilibria for all the hybridization reactions. Because the inhibitor strands are stable enough to have slow dissociation constants, this assumption is probably not realistic. We therefore built a detailed mathematical model that takes into account the full set of reactions taking place in the system (SI Appendix, section III.4). Indeed, this newly developed model predicts a higher resilience of the bistable circuit (Fig. 4B). When the perturbation is introduced as a single Gaussian spike, a ∼20-fold concentration of the opposite input is predicted to be necessary to switch the system to its opposite state (SI Appendix, section III.5). Because this did not appear to be a very practical solution to flip the system back and forth, we turned to an alternative switching strategy.

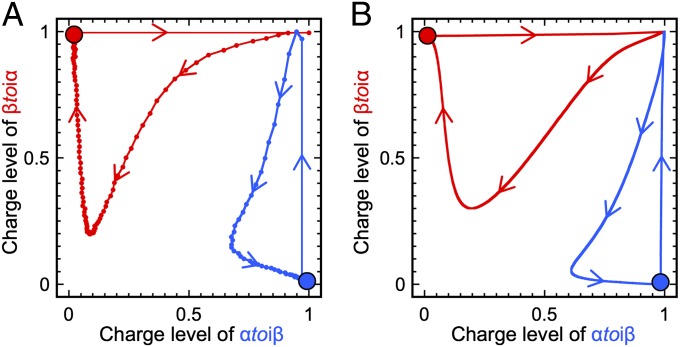
Fig. 4.

Perturbation of the bistable at the steady state. The red dot (charge level {αtoiβ, βtoiα} = {0, 1}) corresponds to stable state B. The blue dot (charge level {αtoiβ, βtoiα} = {1, 0}) corresponds to stable state A. Experimental (A) and calculated (B) (using the detailed model) trajectories of the bistable perturbed by 100 nM opposite input.

Two-Input Switchable Memory

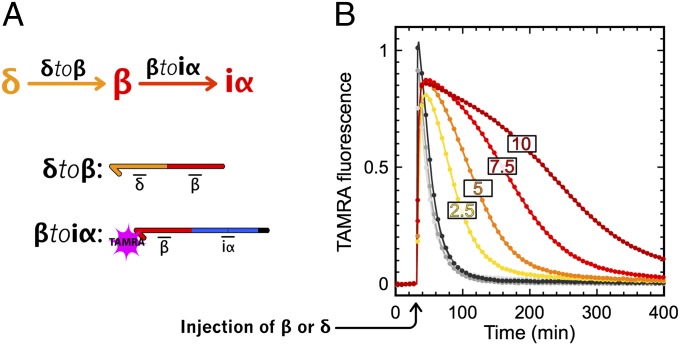
To obtain an updatable memory circuit, we decorated the bistable circuit with two activation modules that connect this bistable core to two different and specific external signals. Activation modules γtoα and δtoβ take γ and δ as inputs, respectively, to produce a long-lasting pulse of α or β, which should stimulate the bistable core to flip between states (SI Appendix, section III.6).

Experimentally, the width of the pulse of α or β produced by an activation module can be adjusted by changing the concentration of the corresponding template (Fig. 5). These activation modules therefore provide a handle with which to push the bistable core toward one state or the other. Correct tuning of the concentration of the activation modules is important. If the concentration is too low, the stimulus will fail to push the bistable core beyond the separatrix, to the basin of attraction of the opposite state (Fig. 6B). Conversely, if it the concentration is too high, the system will lose responsiveness (the activation module will stay active for too long). For a concentration of 5 nM both activation modules, we found that injection of a small amount [30 nM (i.e., even less than α and β at the steady state)] of γ or δ is enough to flip the memory between its two states.

Fig. 5.

Production of β by activation module δtoβ. (A) Circuit and templates of the system. (B) Experimental time plot of TAMRA fluorescence (baseline removed) produced by the hybridization of β on βtoiα. Gray curves correspond to the injection of 30–150 nM β. Yellow to red correspond to the injection of 30 nM δ in the presence of 2.5, 5, 7.5, or 10 nM δtoβ.

Fig. 6.

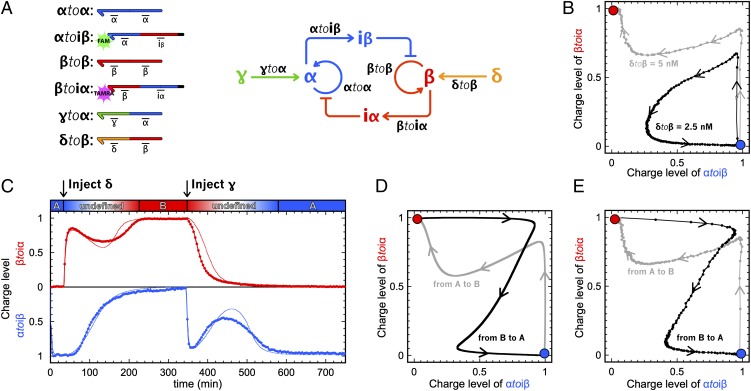
Switchable memory circuit. (A) Circuit and templates of the bistable switchable memory. (B) Trajectories of two attempts to flip the bistable memory from A to B, with δtoβ = 2.5 nM (black, failure) and δtoβ = 5 nM (gray, success). (C) Experimental (thick line) and fitted model (thin line) time plot of the charge levels of αtoiβ and βtoiα. The memory circuit is started in state A, is flipped from A to B, and is then flipped from B to A. Predicted (D) and experimental (E) trajectories of the memory switching reversibly from A to B (gray) and from B to A (black).

The complete switchable memory circuit contains six templates (Fig. 6A), has two stable states characterized by the exclusive presence of α or β, and can be controlled by the two external inputs γ and δ. Fig. 6C displays the fluorescence curves of the memory initiated in state A and then switched back and forth once (failed attempts at further switching are discussed in SI Appendix, section VI). When flipping between states, one observes a characteristic biphasic evolution of the charge levels of αtoiβ and βtoiα. Injection of the external input (e.g., δ) provides the bistable core with a long-lasting pulse of the currently OFF internal input (e.g., β). This pulse charges the inhibition module (e.g., βtoiα, increase in the red curve) and initiates the inhibition of the ON state. The concentration of α then starts decreasing (slow evolution of the blue curve toward 0) and in turn, this releases the inhibition of the OFF state. When the external stimulation comes to its end (reversal in the evolution of the red curve), the system has already reached the basin of attraction of B and β ultimately eliminates α (second increase of the red curve and final decrease in the blue curve). The memory has flipped between states. These curves were used to optimize the parameters of the detailed mathematical model [i.e., all other predictions use this same set of parameters (SI Appendix, section III.4)]. They are also plotted as calculated (Fig. 6D) and experimental (Fig. 6E) trajectories in two dimensions, showing the good agreement between the model and the experiments. The trajectories (from A to B and from B to A) appear to be crossing only because they are a 2D projection of a higher dimensional system (52) (SI Appendix, Fig. S12).

The bistable core takes around 200 min to flip between states. This duration is comparable to the period of the oscillator previously reported (23). Also, switching requires a concentration of external input (30 nM) that is of the same scale as the produced α or β at the steady state (∼50 nM). This suggests that the switchable memory circuit could be connected with other circuits made with the DNA toolbox in the quest for more complex reaction networks.

Push-Push Memory

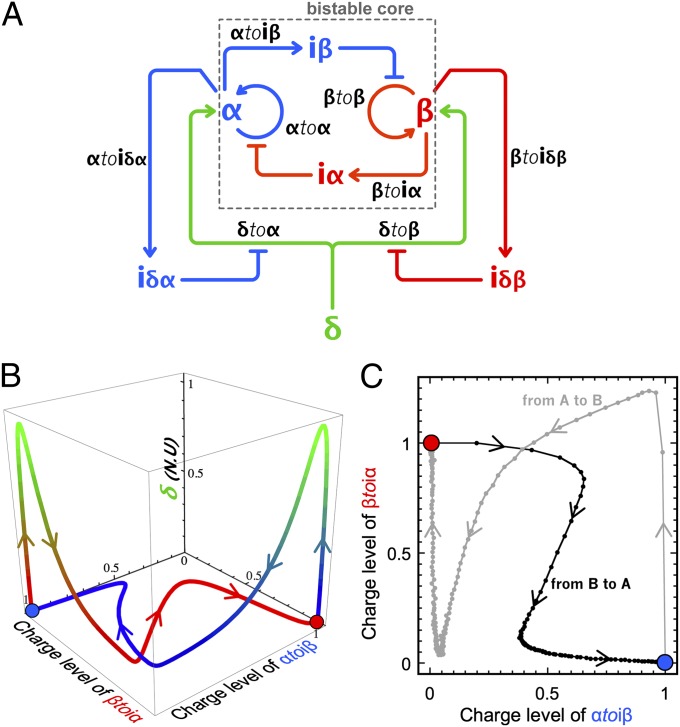
The push-push memory is another type of updatable memory element, in which a bistable system is switched back and forth by a unique stimulus (hence, the name push-push, in reference to a push-button mechanical switch). A chemical implementation of this function can be obtained by further enriching the previous memory circuit (Fig. 7A). The two activation modules (δtoα and δtoβ) now respond to the same external input δ. To carry out the push-push functionality, two additional inhibition modules (αtoiδα and βtoiδβ) feed the current state of the bistable core back to the activation modules. When the bistable is in state A, they ensure that the corresponding activation module (δtoα) is inhibited, and vice versa. In the presence of the four templates, δtoα, δtoβ, αtoiδα, and βtoiδβ, injection of δ will only trigger the production of the input of the OFF state of the bistable core, whereas the input of the currently ON state will not be produced. This strategy was theoretically validated by a model (SI Appendix, section III.7).

Fig. 7.

(A) Circuit of the push-push memory: A single external input δ controls the bistable core. (B) Calculated 3D trajectories in the space {charge level of αtoiβ, charge level of βtoiα, total concentration of δ in normalized units (N.U.)} for the push-push memory switching from A to B (blue) and B to A (red). Normalized values of δ (injected as a Gaussian spike) from 0 to 1 are associated with a color gradient ranging from blue/red to green. (C) Experimental trajectories of the push-push memory circuit show two independent experiments: one in which the system is initially set on the state A and then flipped to B upon injection of 30 nM δ and another in which the same system is set in state B and then flipped to A upon injection of the same input. The charge level of βtoiα higher than 1 indicates that the amount of β transiently produced by activation module δtoβ during switching exceeds the concentration of β at the stable state B.

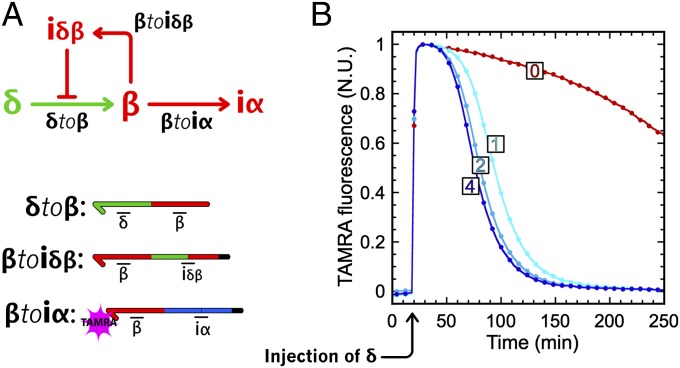
The detailed model suggested that the full circuit would work with the same bistable core and same concentration of activation modules as the memory circuit, in the presence of a few nanomolar amounts of αtoiδα and βtoiδβ (Fig. 7B). Before assembling the full circuit, we experimentally checked the subparts encoding the push-push functionality. Fig. 8 shows that, indeed, a concentration of βtoiδβ as low as 1 nM efficiently regulates the pulse of β produced by δtoβ.

Fig. 8.

Push-push negative feedback. (A) Circuit and templates. On injection of δ, production of β is activated. Then, β hybridizes to βtoiα (resulting in an increase of TAMRA fluorescence) and to βtoiδβ, which, in turn, produces the inhibitor of δtoβ, stopping the production of β. (B) Experimental time plot of the TAMRA fluorescence in normalized units (N.U.; 1 at the highest and 0 at the lowest) for different concentrations (0, 1, 2, and 4 nM) of inhibition module βtoiδβ.

When experimentally assembling the eight templates of the push-push memory circuit, we had to adjust the concentrations of δtoβ and βtoiδβ to strengthen the response of the B side to the exogenous input δ. Note that in the bistable core, state B is less attractive than state A (Fig. 3C), which may explain why switching to B requires stronger amplification of the external stimulus δ. We therefore kept the concentrations of activation module δtoα and inhibition module αtoiδα proposed by the model (5 nM and 4 nM, respectively) and adjusted the concentration of δtoβ to 10 nM. This explains the large amount of β produced on injection of δ (exceeding the concentration of β at the steady state). After fine-tuning of the concentration of βtoiδβ (we settled on a concentration of 1 nM; SI Appendix, section V), the push-push circuit could be flipped from state A to B, and from state B to A, by a 30-nM injection of its unique external input, δ (Fig. 7C). The corresponding fluorescence time plots are shown in SI Appendix, Fig. S11.

Discussion

Bistability is a fundamental feature of dynamic systems. Bistable switches have been identified or postulated in a number of important biological circuits (2–5, 37–42). More generally, bistability seems to be at the basis of the dynamic behaviors of many nonlinear artificial chemical systems, such as oscillators (53, 54).

Molecular bistability can theoretically be obtained from a great variety of reaction network topologies (49, 50, 55), and the mechanistic requirements for this function have been explored in detail (51, 56, 57). The presence of a positive feedback loop is a necessary but not sufficient signature (2, 4, 7, 51). An isolated single autocatalysis provides bistability only if sufficient nonlinearities are included in the loop. In vivo, mechanisms such as ultrasensitivity or cooperative binding—proteins that acquire new regulatory functions through the formation of multimers—typically provide these sources of nonlinearity.

Bistable systems without cooperative nonlinearity can be obtained at the cost of a slightly increased topological complexity of the network (51). The in vitro toolbox that we use here does not provide a mechanism to introduce cooperative effects; however, it allows easy assembly of relatively large networks. Hence, we decided on a robust and symmetrical design that contains two autocatalytic loops responsible for the self-amplification of two cross-repressing species (another design compatible with the chemistry at hand is discussed in SI Appendix, section III.2). The advantages of the present design are twofold: (i) Both stable states correspond to a high concentration of one of two species (and not to the presence or absence of a single species), making the reading and interfacing easier, and (ii) the symmetry facilitates the identification of the control parameters for the network behavior. In particular, even for sequences that are not symmetrical, one can theoretically tune the concentrations of templates to obtain and balance the bistable domain. In practice, this proved to be a useful feature for the construction of the more complex target behaviors.

The requirement to switch from one state to the other poses another design challenge. In the ideal case of a system that adapts immediately to a perturbation, as in the simple model presented in Fig. 2, flipping from A to B is obtained as soon as the concentration of β is pushed above that of α. This reactivity should not be expected in systems constructed out of complex biochemical transformations, which is typical of biological systems. Such slow loops will increase the hysteresis found in the bistable behavior (58). However, although cellular bistable switches are self-contained and can be exposed to input stimuli over long periods of time (7), this is not the case in our in vitro batch design. By construction, inputs α and β are degradable species, and an injection of α or β will only produce a spike of limited length (Fig. 5). Therefore, we had to look for an alternative switching strategy. We introduced an additional dimension in the sequence space to provide a switching pathway with a much lower concentration threshold (Fig. 5). The complete system provides a stable memory, which is able to resist very strong transient fluctuations of its chemical signature but which also specifically responds to short and dilute spikes of external inputs. Steady-state concentrations of outputs α and β (∼50 nM) are of the same scale as the external input required to flip the memory (∼30 nM), which suggests that the memory circuit is itself modular. It could be used as such in a plug-and-play manner for the building of more complex reaction circuits.

The step-by-step assembly of large-scale systems, such as the push-push memory circuit presented here, rests heavily on the modularity of the molecular toolbox that we use. By modularity, we refer here to the fact that a priori, any activating or inhibiting relation between two signal molecules (input or inhibitor) can be implemented. One only needs to design the corresponding templates. However, in practice, this modularity may be limited by a number of design issues: Load effect (48) arises when a downstream module sequesters the product of an upstream module, enzyme saturation can lead to unintended coupling between unconnected modules because of the competition for enzymatic resources (19), and spurious interactions between noncomplementary sequences may also lead to some extent of cross-talk (59). These effects become more prevalent when the size of the system increases (31). However, their consequences can be circumvented through the emphasis on the robustness of the design, which, in turn, is identified using toy mathematical models (SI Appendix, section III.1). A complete set of reactions (SI Appendix, section III.4) can then be combined to provide a better quantitative understanding of the consequences of nonmodular interactions, which generally lie beyond our intuition. In the end, building and understanding the dynamics of these complex networks strongly rest on the good agreement between the experimental result and the mathematical approach. Although this process can be time-consuming, one may envision that design rules similar to those of engineering disciplines will emerge in the future to mitigate or incorporate these complex effects directly. It is also interesting to note that such design rules may have a direct impact on our understanding of in vivo regulatory processes. For example, in vitro models suggest that competition for enzymatic resources may be an important contribution to the dynamics of cellular circuits (10, 19).

In this paper, reaction circuits were assembled in a closed environment. This stands in contrast to most chemical or biological bistable networks reported to date, which perform in open systems (7, 13–15, 54). This closeness imposes specific challenges, for example, the presence of precisely controlled internal source and sink energetic pathways. It also implies that each experiment has a limited lifetime and that true steady states cannot be obtained, because various reaction parameters are modified over time. For instance, the dNTP concentration decreases, and enzymes can lose activity. Worse, even though the templates are protected from the exonuclease, they get slowly degraded (SI Appendix, section II.2). These factors may pile up to modify the circuit behavior and explain the loss of function that we have observed after long experimental times (SI Appendix, section VI). Still, we were able to obtain satisfying pseudosteady states and to perform at least one complete cycle of the two-input memory circuit through its alternative states. For the push-push memory circuit, the longer time required for switching may explain why repetitive operations were not successful. Note that an eventual breakdown is unavoidable considering our closed experimental setup. We anticipate that if the reactions were performed in an open system (e.g., in a reactor with a constant flow of fresh precursors), they could be run for an infinite amount of time and switched continuously.

Conclusion

Biological behaviors are built from and controlled by assemblies of biochemical reactions connected in complex networks. Despite the enormous molecular complexity of living systems, we may expect that correct characterization of the individual components will lead to a rational understanding of the biological organization and dynamics. A critical test for this approach is the man-made rational design of molecular systems reproducing nontrivial biological behaviors. The in vivo version of this idea, synthetic biology, is based on the assumption that biological systems are built from modular, interchangeable subelements: Cells provide a platform in which exogenous genetic programs can be run. Successes along this systematic line are interpreted as proof of a correct understanding of the molecular basis of complex, life-like behaviors. However, many studies in this direction have resulted in a significant deviation from this idealized view of a cell as a universal platform. In many cases, interference with the housekeeping functions cannot be neglected; modularity is not provided for free but must be carefully enforced. Our results here suggest that the in vitro approach, which reproduces some of the essential features of biological networks (including universality) but avoids some of their limitations, mitigates these concerns, and hence may provide a faster learning curve regarding the potential of reaction networks. Here, the push-push memory circuit of the eight “genes” already compares favorably with the largest realizations of in vivo synthetic biology. Moreover, because it is fully modular, it could theoretically be connected to other circuits. For instance, two push-push circuits in series would give a two-bit binary counter, and one push-push downstream of an oscillator would perform frequency division, oscillating at half the driving frequency.

Materials and Methods

Oligonucleotides.

DNA oligonucleotides were purchased from either Integrated DNA Technologies or biomers.net, with HPLC purification. All templates have three phosphorothioate backbone modifications at their 5′ end to protect them from degradation by the exonuclease. Templates αtoiβ and βtoiα are modified at their 3′ end with FAM and TAMRA NHS ester modification, respectively. All the other templates are phosphorylated at their 3′ end to prevent any polymerization. Template sequences and concentrations are provided in SI Appendix, section II.3.

Reaction Assembly.

Reactions were assembled in a buffer containing 10 mM KCl, 10 mM (NH₄)₂SO₄, 50 mM NaCl, 2 mM MgSO₄, 45 mM Tris⋅HCl, 5 mM MgCl₂, 6 mM DTT, 2 μM Netropsin (Sigma–Aldrich), 100 μg/mL BSA (New England Biolabs), 0.1% Synperonic F108 (Sigma–Aldrich), and dNTPs (200 μM each). Exonuclease ttRecJ was a kind gift from R. Masui (Osaka University, Japan) and used at a concentration of 50 nM throughout this study. Unless otherwise specified, Bst DNA polymerase, large fragment (New England Biolabs) was used at a concentration of 25.6 U/mL. For the Nt.BstNBI nicking endonuclease (New England Biolabs), we noticed a large fluctuation in the activity from batch to batch, and consequently used the enzyme at a concentration ranging from 32 to 400 U/mL. Experimental adjustment of Nt.BstNBI concentration was done by comparing the activity of a new batch with the activity of the previous batch, using the assay presented in SI Appendix, Fig. S3.

Reactions were run at 42 °C (except if specified otherwise) in a Bio-Rad iQ5 or CFX96 real-time thermocycler in a 20-μL volume. Experiments for which the bistable circuit was flipped from one state to the other required administration of an external input (γ or δ) that was diluted in TE buffer and injected in a volume of 0.6 μL while the run was paused for a minimal period.

Fluorescence Curve Acquisition and Normalization.

Fluorescence cross-talk between FAM and TAMRA was removed by the Bio-Rad built-in thermocycler software. For the experiments requiring an injection of external input, instantaneous signal artifacts at the time of injection (e.g., due to a slight displacement of the tube or the production of bubbles during mixing) were corrected to keep the curve continuity. “Charge levels” were normalized from fluorescence data: to the high plateau (ON state of the autocatalytic module; if unavailable, a reference tube with the same reacting mix set in the ON state was used) and low plateau (OFF state of the autocatalytic module; if unavailable, the reaction was run until depletion of dNTPs, thus revealing the OFF state of the autocatalytic module).

Simulations.

The simple model of the bistable reaction circuit was analytically analyzed using Mathematica (Wolfram) (SI Appendix, section III.1). Detailed models of the bistable circuit, switchable memory, and push-push memory were made with a set of measured and predicted (DINAMelt) parameters, refined by fitting on the experimental curves of the switching memory, using Mathematica (SI Appendix, section III.4). The set of refined parameters was used for all other model predictions.