Abstract
Recent development of constant pH molecular dynamics (CpHMD) methods has offered promise for adding pH-stat in molecular dynamics simulations. However, until now the working pH molecular dynamics (pHMD) implementations are dependent in part or whole on implicit-solvent models. Here we show that proper treatment of long-range electrostatics and maintaining charge neutrality of the system are critical for extending the continuous pHMD framework to the all-atom representation. The former is achieved here by adding forces to titration coordinates due to long-range electrostatics based on the generalized reaction field method, while the latter is made possible by a charge-leveling technique that couples proton titration with simultaneous ionization or neutralization of a co-ion in solution. We test the new method using the pH-replica-exchange CpHMD simulations of a series of aliphatic dicarboxylic acids with varying carbon chain length. The average absolute deviation from the experimental pKa values is merely 0.18 units. The results show that accounting for the forces due to extended electrostatics removes the large random noise in propagating titration coordinates, while maintaining charge neutrality of the system improves the accuracy in the calculated electrostatic interaction between ionizable sites. Thus, we believe that the way is paved for realizing pH-controlled all-atom molecular dynamics in the near future.
INTRODUCTION
Solution pH is an important environmental factor in biological and chemical processes. It affects the stability and function of proteins and nucleic acids by shifting the protonation/deprotonation equilibria of titratable (ionizable) groups. To enable molecular simulations of such proton-coupled phenomena, significant progress has been made in recent years in the development of the so-called constant pH molecular dynamics (CpHMD) technique, which allows the protonation states to fluctuate in response to changes in local chemical environment and solution pH. These methods fall into two main categories based on whether the protonation states are represented by discrete or continuous coordinates. In the discrete approach, Monte-Carlo steps are periodically performed to sample protonation states during molecular dynamics.1, 2, 3, 4, 5 In the continuous approach, an additional titration degree of freedom is added for every titratable site and the titration degrees of freedom are propagated alongside conformational dynamics.6, 7, 8
Among these methods, the continuous pH molecular dynamics (pHMD) method7, 8 based on λ dynamics,9 which will be referred to as CpHMD hereafter, has been successfully applied to pKa predictions10 and pH-dependent protein folding11 and conformational dynamics.12, 13 The first version of the CpHMD technique makes use of the generalized Born (GB) implicit-solvent model for propagating both conformational and titration coordinates and the temperature-based replica-exchange protocol for accelerated sampling in the coupled conformational and protonation-state space.14 Recently, the method was extended to conformational sampling in explicit solvent while propagating the titration coordinates via GB calculations, in an attempt to circumvent the conformational bias of implicit-solvent models while retaining the ability to quickly evaluate solvation free energies.15 This hybrid-solvent scheme, combined with a pH-based replica-exchange protocol,15 has been shown to offer more realistic pH-dependent conformational sampling and more accurate pKa prediction for proteins15 as well as surfactant micelles.16
Most recently, two groups have reported on the development of CpHMD techniques based solely on explicit-solvent models and testing on small model systems.17, 18 In these implementations the GB-based single-site CpHMD method7 was extended to explicit-solvent simulations by replacing the calculation of solvation forces due to the GB model with deriving forces on real and λ particles from interactions involving explicit water molecules. A noted key ingredient is the alternative functional form (other than sin2θ) for the λ variable. However, two major issues have not been addressed. The long-range electrostatics was calculated using truncation with force shift18 or Ewald summation without accounting for the additional forces on λ particles.17 Potential artifacts due to the fluctuation in overall net charge were also neglected.
In this work we show that leveling the net charge of the system and properly treating long-range electrostatics are two critical factors in developing all-atom constant pH molecular dynamics techniques. While it has been a standard practice to neutralize the simulation system in explicit-solvent simulations under periodic conditions with particle mesh Ewald (PME) treatment of extended electrostatics,19 it has not been attempted in constant pH simulations.20 This is because in such simulations the net charge of the solute may fluctuate as a result of exchanging proton(s) with solvent. Residual net charge is not a concern for methods that use GB implicit-solvent model for computing forces on λ particles (titration coordinates).14, 15 However, it needs to be compensated in fully explicit-solvent simulations. Here we present a technique which couples proton titration with simultaneous ionization or neutralization of a co-ion in solution. This approach allows the net charge of the system to remain constant during protonation or deprotonation of the solute. For treatment of long-range electrostatics we apply the generalized reaction field (GRF) method.21 Incorporation of the GRF method in the CpHMD framework is straightforward because electrostatic force is calculated from strictly pairwise interactions, unlike the smooth Ewald methods where the force is calculated in part from convolution over the charge interpolation grid.22 Although Ewald-based methods have been traditionally believed to be more accurate, evidence of artifacts due to imposed periodicity emerged.23 Subsequently, numerous papers have been published comparing the two methods. GRF has been shown to give results comparable to the more computationally expensive Ewald methods in simulations of highly charged proteins,24 RNA,25 small peptide folding,26 small peptides over long timescales,27 and the calculation of protein-folding kinetics from MD simulations.28 Additionally, in a recent pHMD study based on the discrete approach and a mixed-solvent scheme, the GRF method gave more accurate pKa values than the particle mesh Ewald method.29
We implemented the new method in the existing pHMD module of the CHARMM program and tested it by running titration simulations and obtaining pKa’s for a series of aliphatic dicarboxylic acids, HO2C–(CH2)n–CO2H, where n varies from 3 to 7. This series of molecules has attractive qualities as a test case. There are two interacting titratable sites, so the accurate calculation of the two macroscopic pKa values resulting from stepwise protonation/deprotonation is non-trivial and offers a stringent test for computational methods. Understanding the pKa difference between the two is a classical problem dated back to the 1930s when Kirkwood developed analytical theories to describe the electrostatic influence of substituents on the dissociation constants of organic acids.30, 31 It has continued to fascinate and challenge the theoretical and computational communities until now.1, 4, 32, 33 Another reason for choosing the dicarboxylic acids is the small molecular size. Adequate sampling of all relevant conformations should not be an issue. Furthermore, since the experimental data are extrapolated to zero ionic strength,34 potential complexity in calculating the deprotonation energies due to salt screening is absent. Finally, we note that while CpHMD methods are rooted on the λ-dynamics technique9 for free energy calculations, classical35 or quantum mechanics/molecular mechanics free energy simulations36 can also be applied to obtain pKa’s. A major strength of the CpHMD methods is that the protonation states, or more precisely, the fraction of the unprotonated form, of all titratable sites are simultaneously determined in a “regular” molecular dynamics at a specified pH condition. The pKa value of each group can be then calculated in the same fashion as in experiment, i.e., by fitting the fraction of the unprotonated form for multiple pH conditions to the Henderson-Hasselbalch equation. In an upcoming work, we will demonstrate the capability of the fully explicit-solvent CpHMD method in determination of pKa values for proteins.
The rest of the paper is organized as follows. We first present the new method and discuss the implementation. We then test the all-atom CpHMD simulation with the pH-based replica-exchange sampling protocol on the series of dicarboxylic acids. We calculate the pKa values of the dicarboxylic acids and compare the results with experimental data as well as with two other methods, the GB-based CpHMD and the explicit-solvent CpHMD without co-ions. The new CpHMD method gives the closest agreement with experiment. The average absolute error of the calculated pKa values is about 0.18 units. We also examine the pH-dependent conformational dynamics and changes in solvent distributions around the dicarboxylic acid. These results suggest that a fully atomistic “pH-stat” will soon become available for molecular dynamics simulations.
METHODS
Formalism of continuous constant pH molecular dynamics
Based on the λ-dynamics technique,9 continuous constant pH molecular dynamics utilizes an extended Hamiltonian to simultaneously propagate spatial (real) and titration (virtual) coordinates. Thus, the total Hamiltonian of the system can be written as
| (1) |
where a = 1, Natom is the atomic index for spatial coordinates, and i = 1, Ntitr is the index for the continuous variables θi, which is related to the titration coordinate λi by λi = sin2(θi). Boundaries are naturally imposed on the titration coordinates through the sine function, where λi = 0 corresponds to the protonated state and λi = 1 corresponds to the deprotonated state. For groups with two competing titration sites such as histidine or those containing a carboxyl group, a second continuous variable is included to facilitate the interconversion between the two tautomers. This is indicated in Eq. 1 by bold θ.
In Eq. 1 the first term is the kinetic energy of the real system (atoms), Uint is the internal potential energy, which is independent of titration, and U* is a biasing potential, which contains three terms. Ubarr is a harmonic potential to suppress the intermediate values of λ, Umod is a potential of mean force (PMF) function for titrating the model compound, and UpH is the free energy imposed on the protonation equilibrium due to the change in solution pH.
| (2) |
where UpH is given by
| (3) |
and p is the experimental pKa of a model compound, also known as the reference pKa. In GB simulations, due to the pairwise form of the solvation energy, Umod for a single titratable site can be described by a quadratic function,
| (4) |
where A and B are the fitting parameters. For groups with two competing titratable sites, Umod is second order in both λ and x, where the latter represents the tautomeric degree of freedom.8 Finally, we consider Uhybr, which is a hybrid energy term that couples the dynamics of conformational and titration degrees of freedom. In GB simulations, it is a sum of van der Waals, Coulombic, and the GB electrostatic solvation energies:
| (5) |
Titratable co-ions for charge leveling
During proton titration the net charge of the solute fluctuates. This does not present a problem in GB-based CpHMD method. We also demonstrated that the potential artifacts are negligible in the hybrid-solvent scheme where GB model is applied to propagating the titration coordinates.15 However, a varying net charge is a major issue that needs to be addressed for developing an accurate CpHMD method based on the explicit-solvent model. If neglected, overestimation of electrostatic coupling between ionizable sites may occur, as will be shown in Sec. 4. Here we describe a charge-leveling scheme, which couples proton titration with charging or neutralization of a titratable dummy ion. Specifically, the deprotonation of each acidic site is coupled to the neutralization of a dummy anion and the deprotonation of each basic site is coupled to the ionization of a dummy cation. The dummy ion absorbs the change in charge during titration, thus mimicking the effect of gaining or releasing a proton to solution. Except for being titratable, these dummy ions are treated on the same footing as regular ions and randomly distributed in the simulation box at the beginning of a simulation. Chloride and sodium ions are used in the current implementation for no specific reason other than the availability of the force field parameters and the fact that they present the simplest chemical species that can be used as a charge reservoir. Since there is one dummy ion for each titratable site, we will refer to it as co-ion in the remainder of the paper. Thus, the net reaction under consideration is
| (6) |
for each acidic site, and
| (7) |
for each basic site. Here represents the dummy hydrogen atom attached to the titratable site (as CpHMD does not model bond breaking or formation). represents the corresponding co-ion. Since on each side of the reactions only one of the species carries a charge, formation of an artificial contact pair is avoided.
In the CpHMD simulation, we aim to calculate the deprotonation free energy of a titration site in a specific environment (e.g., protein) by making use of a reference free energy, i.e., the free energy for deprotonating a reference (or model) compound in solution. The difference between the two can be obtained by considering classical interactions only, because the quantum mechanical energy of breaking or forming the bond with a proton for a titratable moiety in solution () and that embedded in the solute molecule (ΔGquant) are approximately identical.
| (8) |
With the incorporation of a titratable co-ion, the above free energy difference includes the contribution from the difference between neutralizing the co-ion in the solute environment and in solution. However, since the co-ion remains in solution, the free energy of neutralization will not be significantly affected by the presence of the titrating solute. Therefore,
| (9) |
Finally, the above free energy difference is related to the pKa shift in reference to the model compound pKa value by
| (10) |
The pKa can be obtained by running CpHMD titration at several pH conditions, calculating the fraction of the time spent in each protonation state, and fitting the unprotonated fraction to an appropriate titration model (see Sec. 3).
Generalized reaction field for long-range electrostatics
Now we come back to the hybrid-energy term in the Hamiltonian (Eq. 1). In the explicit-solvent simulations, Uhybr({ra}, {θi}) describes the van der Waals and Coulomb energies for solute-solute and solute-solvent interactions. In our previous work with the hybrid-solvent scheme, we mentioned large fluctuation in titration coordinates when using interactions with explicit solvent under periodic boundary conditions to calculate forces on λ particles.15 Detailed analysis revealed that this is a result of neglecting the effects due to long-range electrostatics (data not shown). In the present implementation, we employ the generalized reaction field method21 to account for the missing forces resulting from extended electrostatics. Thus, the hybrid energy becomes
| (11) |
where the GRF term is given by21, 24
| (12) |
Here rab is the distance between two atoms, qa and qb are the respective partial charges, ε0 is the vacuum permittivity, εin is the dielectric constant (typically set to one) within Rc, the cut-off radius. CRF, which governs the magnitude of the reaction field, carries the dependence on ionic strength and is given by
| (13) |
where εout is the dielectric constant (typically the value for water) of the surrounding medium outside of the cutoff sphere, and κ is the inverse Debye screening length, κ2 = 2NAIe2/ε0εoutkBT, where I is the ionic strength.
COMPUTATIONAL DETAILS
Simulation protocol
All simulations were carried out using an in-house version of the CHARMM program (version c35b3).37 The explicit-solvent CpHMD method was implemented in the pHMD module. The pH-based replica-exchange protocol15 was added to the REPDSTR module.15
The CHARMM22 force field38 was used. The parameters for the dicarboxylic acids were adapted from glu residue and the methylene unit of alkanes. For the explicit-solvent simulations we utilized the modified CHARMM TIP3P water model,39 an updated van der Waals radius for the sodium ion,40 and a modified sodium-chloride van der Waals interaction distance to reduce sodium chloride contact-ion pair formation.41
In all simulations, the SHAKE algorithm was applied to the bonds and angles involving hydrogen atoms to allow a 2 fs time step. The titration degrees of freedom were propagated using the Langevin algorithm with a collision frequency of 5 ps−1. The simulation temperature was 300 K. The mass of the fictitious θ particles was set to 10 amu consistent with previous work.7, 8 To accelerate sampling convergence the pH-based replica-exchange protocol was applied.15 In this protocol, the pH condition ranges from 3 to 7 with an interval of 0.5 units. Exchanges between adjacent replicas were attempted every 500 molecular dynamics steps (or 1 ps). Simulation of each replica lasted 5000 exchange steps or 5 ns.
For the GB-based simulations, the GBSW (generalized-Born model with simple switching) model42 was used with the atomic input radii of Nina et al.43 and a surface tension coefficient of 5 cal mol−1 Å−2. In the GB-based simulations, conformational dynamics was propagated via the Langevin algorithm with a collision frequency of 5 ps−1. Non-bonded interactions were truncated at a cut-off radius of 20 Å using a switching function. The ionic strength was set to zero.
For the explicit-solvent simulations, a cubic water box with 30 Å edges was used. Any water molecule within 2.4 Å of the solute was deleted. Two titratable chloride ions were added as co-ions to maintain a total net charge of −2. Two sodium ions were added as counterions to achieve charge neutrality in the simulation system. In the simulation of the model compound, only one co-ion and one counterion were present. The initial locations of these ions were set randomly. The coordinates of the water molecules and ions were subjected to energy minimization with the solute restrained prior to starting the CpHMD simulation. Simulations were carried out with periodic boundary conditions at ambient temperature and pressure using the Hoover thermostat44 and Langevin piston pressure-coupling algorithm45 as in the previous hybrid-solvent CpHMD simulations.15 The non-bonded interactions were truncated at 14 Å, beyond which the electrostatic effects were treated by the GRF method. In the GRF term, εin was set to 1.0 and εout was set to 80.0. The ionic strength in CRF was set to zero consistent with experimental data.
Model compound
For no particular reason other than convenience, we used azelaic acid, which has the longest carbon chain, as the model compound. Only one carboxylic site was allowed to titrate and the other site was kept protonated. The model pKa, which is the microscopic value pK1a/pK1b, was set to 4.85, based on the experimental macroscopic pK1 of 4.5534 and the relationship in Eq. 18. Because of the fast exchange of the two carboxylate oxygens, the single-site titratable model was used.7 To determine the potential of mean force for model titration, thermodynamic integration ΔG = ∫⟨dU/dθ⟩θ was applied, where the average force, ⟨dU/dθ⟩, was obtained at θ values of 0.2, 0.4, 0.6, 0.7854, 1.0, 1.2, and 1.4 from 500 ps simulations in explicit solvent or 100 ps simulations with the GB model. Convergence was verified by examining the cumulative values of the average forces. The average force was then fit to the following equation:
| (14) |
to obtain the A and B parameters (see Sec. 4). The same procedure was used to derive the PMF for the co-ion in explicit solvent.
Data analysis
Calculation of macroscopic pKa values for dicarboxylic acids
The deprotonation/protonation of a dicarboxylic acid involves four microscopic equilibria. Since the two carboxylic sites are chemically equivalent, k1a = k1b and k2a = k2b. Thus, the titration of dicarboxylic acids can be described by two macroscopic equilibria,
| (15) |
where K1 and K2 are the macroscopic constants. By expressing K1 and K2 in terms of the population of the four microstates (Figure 1), one arrives at the following relationships:46
| (16) |
| (17) |
Thus, the macro- and microscopic pKa values are linked to each other by a simple additive shift:
| (18) |
| (19) |
To facilitate comparison with experiment, we will calculate and discuss the macroscopic pKa’s in the remainder of the article. Following Ullmann,46 we can write down the fraction of deprotonated as well as singly- and doubly protonated states as
| (20) |
| (21) |
| (22) |
where Z is the partition function,
| (23) |
Consequently, the average number of bound protons becomes4, 46
| (24) |
Consistent with experiment, the two macroscopic pKa’s are determined by fitting ⟨P⟩ obtained from the simulation to the equation above.
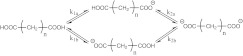
Figure 1.
Microscopic titration of dicarboxylic acids. k1a, k1b, k2a, and k2b are the equilibrium constants.
Cross-correlation analysis
The correlation between the two protonation events in a dicarboxylic acid can be quantified using the cross-correlation function of the λ values. The normalized cross-correlation function between two time series of properties x and y, shifted by an offset Δr, is defined by
| (25) |
where and are the population means and σ is the standard deviation. Rxy ranges from −1 (completely anti-correlated) to +1 (completely correlated). N is the total number of data points.
RESULTS AND DISCUSSION
Potential of mean force for model compound titration
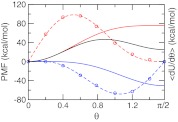
We found that the PMF for titrating the model compound and the co-ion in explicit solvent can be accurately described by a quadratic function as in GB simulations. Figure 2 shows a perfect fitting of the average force along the θ coordinate to Eq. 14 for the first deprotonation reaction of azelaic acid and the chloride co-ion. Table 1 summarizes the resulting parameters as well as the corresponding free energies in comparison to those from the GB-based simulation. It can be seen that the deprotonation free energy with the GB model is about 10 kcal/mol (or 20%) smaller than with the explicit-solvent model, indicating that the charged form is less favored by the GB model, consistent with our observation that solvation energies in GB simulations are underestimated.47
Figure 2.
Potential of mean force (PMF) for titrating the model compound and co-ion in explicit solvent. Solid curves are the PMFs for the deprotonation reaction of the model azelaic acid (blue), neutralization reaction of the chloride co-ion (red), and the sum of the two (black). The average force at each θ value is shown as circle and the fitting function is shown as dashed curve. Integration of the fitting function gives the PMF.
Table 1.
Parameters in the model PMF and the corresponding free energy in the explicit-solvent and GB-based CpHMD simulations.1
| Solvent | Parameters | ΔG (kcal/mol) | |
|---|---|---|---|
| A | B | ||
| Explicit | −56.16 | 0.05 | −50.54 |
| GB | −62.39 | 0.18 | −39.93 |
Model PMF corresponds to the blue curve in Figure 2.
Efficiency of replica exchange and sampling convergence
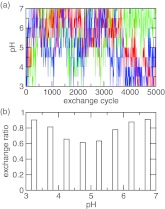
With the model PMF in place, we simulated the titration of azelaic acid allowing both carboxyl sites to protonate or deprotonate. The simulation continued for 5000 replica-exchange steps (or 5 ns) with pH conditions ranging from 3 to 7 with an interval of 0.5 unit. The flow of replicas in the control parameter space, which in this case is the pH, is critical for the efficiency of a replica-exchange simulation as it is directly linked to the mean first passage time for crossing the energy barriers in the state space.48 We picked three replicas and examined the pH conditions they were subjected to during the simulation. Figure 3a shows that all three replicas had a full walk-through in the pH ladder. The acceptance probability for the pH exchange is above 50% for all neighboring pairs of pH conditions (Figure 3b). It is also worthwhile to notice that the exchange ratio is smaller in the middle of the pH range. This is where doubly, singly protonated, and fully unprotonated states coexist (see Sec. 4C1).
Figure 3.
Efficiency of replica exchange in the simulation of azelaic acid. (a) The pH condition visited by the replica after each exchange cycle. Three randomly chosen replicas are shown in blue, red, and green. (b) The exchange probability between adjacent pH replicas.
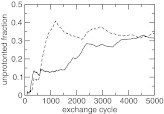
To examine the convergence of the protonation-state sampling, we plotted the unprotonated fraction of the two carboxylic groups as a function of replica-exchange steps (Figure 4). At the beginning the two S values deviate from each other significantly. However, as the simulation proceeds, they move closer and become nearly identical at the end of 5000 exchange steps (or 5 ns). This is required because the two carboxylic groups have identical microscopic pKa values due to the equivalent chemical environment in solution.
Figure 4.
Convergence of the CpHMD simulation of azelaic acid in explicit solvent with charge leveling. The unprotonated fraction for the two carboxylic groups at pH 4.5 as a function of the replica-exchange steps.
Titration simulation of azelaic acid
Macroscopic pKa values of azelaic acid
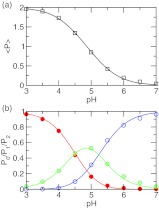
We first calculated the fractions of the population having two, one, and zero protons at each pH (Figure 5b). At pH 3 the azelaic acid is doubly protonated, while at pH 7 it is fully deprotonated. In the intermediate pH range between 4 and 6, these two states coexist with the singly protonated state, indicating that the two carboxylic groups are simultaneously titrating. From these fractions, the total average protonation, ⟨P⟩, can be calculated using Eq. 24. Figure 5a shows that fitting of ⟨P⟩ at each pH to Eq. 24 is nearly perfect (correlation coefficient, >0.999). The resulting macroscopic pKa’s are 4.4 and 5.3, with a difference of 0.8 unit between them (Table 2). These numbers are within 0.15 unit from the respective experimental values of 4.55, 5.41, and 0.86. Note that while the agreement for pK1 is expected because the first ionization is described by the model PMF, it is very encouraging to see that the predicted pKa difference is only 0.06 lower than experiment, suggesting that the new method is able to quantitatively capture the electrostatic influence on the protonation of the two carboxylic groups. For comparison we also calculated the pKa’s using GB- and explicit-solvent simulations without charge leveling. While the pKa difference in the GB simulation is 0.98, 0.18 unit larger than experiment, the simulation without charge leveling overestimates the pKa difference by 2 units.
Figure 5.
Simulated titration of azelaic acid. (a) The average number of bound protons at each pH. Best fit to the data using Eq. 24 is shown as solid curve. The resulting pKa’s are 4.4 and 5.3. (b) Fraction of the population having two (P2, red), one (P1, green), and zero (P0, blue) bound protons at each pH. Best fits to Eqs. 20, 21, 22 are shown as solid curves. The two pKa’s obtained in all three fittings are within 0.2 units from those obtained in (a).
Table 2.
Experimental and calculated pKa’s of a series of dicarboxylic acids.
| Acid | Expt.1 | E+CL2 | GB3 | E−CL4 | |
|---|---|---|---|---|---|
| n5 | pK1 | ||||
| Azelaic | 7 | 4.55 | 4.4 | 4.20 | 4.2 |
| Suberic | 6 | 4.52 | 4.6 | 4.19 | 4.3 |
| Pimelic | 5 | 4.48 | 4.5 | 4.17 | 4.2 |
| Adipic | 4 | 4.42 | 4.7 | 4.04 | 4.1 |
| Glutaric | 3 | 4.34 | 4.0 | 3.57 | 3.7 |
| AAE | 0.18 | 0.43 | 0.38 | ||
| pK2 | |||||
| Azelaic | 7 | 5.41 | 5.3 | 5.18 | 7.1 |
| Suberic | 6 | 5.40 | 5.2 | 5.25 | 7.1 |
| Pimelic | 5 | 5.42 | 5.3 | 5.25 | 7.0 |
| Adipic | 4 | 5.41 | 5.4 | 5.42 | 7.1 |
| Glutaric | 3 | 5.42 | 5.0 | 5.05 | 6.6 |
| AAE | 0.18 | 0.19 | 1.55 | ||
| ΔpKa6 | |||||
| Azelaic | 7 | 0.86 | 0.8 | 0.98 | 2.9 |
| Suberic | 6 | 0.88 | 0.6 | 1.06 | 2.8 |
| Pimelic | 5 | 0.94 | 0.8 | 1.08 | 2.8 |
| Adipic | 4 | 0.99 | 0.7 | 1.38 | 2.9 |
| Glutaric | 3 | 1.08 | 1.0 | 1.48 | 2.9 |
| AAE | 0.19 | 0.24 | 1.9 | ||
Experimental data are taken from Ref. 34.
E+CL refers to the simulations based on explicit solvent with charge leveling.
GB refers to the simulations based on the GB implicit-solvent model.
E−CL refers to the simulations based on explicit solvent without charge leveling.
n refers to the number of methylene groups in the dicarboxylic acid HO2C–(CH2)n–CO2H.
In all simulations, the microscopic pK1a of azelaic acid (4.85) was used as the model pKa (see Sec. 3).
pH-dependence of the conformational states, solvent and counterion distributions
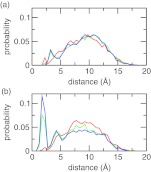
Examination of the conformational states at different pH conditions reveals that azelaic acid prefers states with larger end-to-end distance when it is doubly deprotonated (at pH 7) as compared to the doubly protonated form (at pH 3). At pH 7 the distribution of the distance between the two carboxyl carbons has greater intensity at 9 and 10 Å but reduced intensity at distances below 8.5 Å (Figure 6a). This is expected since there is electrostatic repulsion between the charged carboxylate groups at pH 7.
Figure 6.
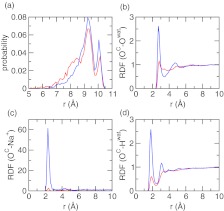
pH-dependent conformation, solvent, and counterion distribution around azelaic acid. (a) Probability distribution of the distance between the two carboxylate carbons at pH 3 and 7. (b) Radial distribution function (RDF) between the carboxylate oxygen and water oxygen. (c) RDF between the carboxylate oxygen and sodium counterion. (d) RDF between the carboxylate oxygen and water hydrogen. Data obtained at pH 3 and 7 are colored red and blue, respectively.
To investigate the response of solvent and counterions to different pH conditions, we calculated the radial distribution function (RDF) involving the carboxylate oxygens of azelaic acid. At pH 7 there is a dramatic increase in the intensity of the first peak in the RDF between the carboxylate-oxygen and water-oxygen at 3 Å (Figure 6b), and in the RDF between carboxylate-oxygen and water-hydrogen at 2 Å (Figure 6c). This is due to the formation of hydrogen bond between the carboxylate group and water, whereby water acts as a hydrogen-bond donor, to solvate the charged azelaic acid. At pH 7 a strong peak appears in the RDF between the carboxylate-oxygen and sodium ion near 2.5 Å, suggesting that the counterion is attracted to the carboxylate group upon deprotonation (Figure 6d), consistent with the observation of ionization-induced condensation of counterions around the titratable site made in the CpHMD simulation of micelles.16
Distribution of charge-leveling co-ions around solute
A major assumption we made with the charge-leveling co-ions is that they remain in solution such that only the titration free energy of the solute is of concern (see Eq. 9). To verify that it is the case, we calculated the minimum distance between the chloride co-ions and azelaic acid (Figure 7a). The probability distribution is relatively flat, indicating the absence of accumulation of co-ions around the titration sites. The probability elevates around 10 Å, which is a distance where the effect of electrostatic interactions on pKavalues becomes negligible.8 Furthermore, the distribution remains virtually the same at pH conditions of 3, 5, and 7, where the azelaic acid is neutral (pH 3) or ionized (charge of −1 at pH 5 and −2 at pH 7), suggesting that the co-ions do not respond to the change in the ionization states. For comparison, we also examined the minimum distance between the sodium counterions and azelaic acid. As shown in Figure 7b, there is a significant population of counterions in the vicinity of azelaic acid as it becomes ionized at pH 5 and 7. This is expected because of the electrostatic attraction.
Figure 7.
Probability distribution of the minimum distance from the azelaic acid to (a) any co-ion and (b) any counterion. Three pH conditions are shown with the azelaic acid being doubly protonated (pH 3, red), singly protonated (pH 5, green), or fully deprotonated (pH 7, blue).
Titration simulations of a series of dicarboxylic acids
Accuracy of the calculated pKa values
Table 2 summarizes the calculated and experimental pKa values for dicarboxylic acids with 3–7 intervening methylene groups. For comparison, the values obtained with the GB-based method and the method without charge leveling (E-CL) are also listed. Examining the first macroscopic pKa’s, we notice that the change in the experimental pKa value as n decreases from 7 to 3 is very small (0.2 units), suggesting that the strength of electrostatic interaction does not significantly change. This can be attributed to the relatively large separation distance between the two carboxylic groups. Nevertheless, the trend is decreasing, which is captured by all three methods. We also notice that the error slightly increases with the decreasing number of intervening methylene groups (n) and becomes the largest for glutaric acid in all three methods. With the method E+CL, the absolute error increases from 0.15 for azelaic acid, to 0.34 for glutaric acid. With the GB method, the error is all negative and the absolute value increases from 0.35 for azelaic acid, to 0.77 for glutaric acid. Thus, the method E+CL performs slightly better. Interestingly, with the method E−CL, the error is also negative and the absolute value increases from 0.35 for azelaic acid, to 0.64 for glutaric acid, which is comparable to the GB method. We attribute the most pronounced error for glutaric acid (n = 3) in all three methods to the neglect of quantum effects. As the number of intervening methylene units decreases, the electronic-structure environment of the carboxylic groups starts to deviate from those in the model compound (n = 7). The classical treatment (Eq. 8) is no longer very accurate. Similar observation was made in an early work by Potter, Gilson, and McCammon.32 Interestingly, the quantum effects tend to stabilize the doubly charged form, thereby reducing the magnitude of the electrostatic coupling due to charge-charge repulsion.
Calculation of the second pKa of dicarboxylic acids provides a stringent test for the accuracy of modeling the electrostatic interaction between the two ionizable sites. Both E+CL and GB methods show only slight underestimation with the largest absolute errors of 0.42 and 0.37, respectively. By contrast, the method E−CL results in large overestimation with errors of 1.2–1.7 units, indicating that the electrostatic repulsion between the two charged carboxylic groups is grossly overestimated due to the uncompensated charges. This comparison provides strong evidence for the necessity of maintaining charge neutrality in the simulation system.
The next quantity to be compared is the difference between the first and second pKa values, ΔpKa. The trend follows as before. Both the E+CL and GB methods give very accurate predictions with the average absolute errors of 0.19 and 0.24, respectively. By contrast, the average absolute error is 1.9 for the E–CL method. It is worth noting that the difference is slightly underestimated in all simulations with the E+CL method, while it is slightly overestimated in all the GB simulations. There are two sources for the difference between the two pKa’s. The first source arises from the so-called statistical factor due to the fact that the first deprotonation reaction involves one of the two protons, while the second reaction involves only one proton (Eq. 15).30 It follows that K1 = 4K2 in the absence of interactions between the two titratable sites.30 Thus, the statistical factor results in 0.6 units for ΔpKa. The second source for ΔpKa, which is more difficult to accurately account for, is electrostatic in nature. Deprotonation of the first carboxylic group imposes an electrostatic penalty for the deprotonation of the second group, and causes ΔpKa to be greater than 0.6 units. Thus, it is also reasonable to expect that the instantaneous protonation states of the two equivalent carboxylic groups should be anti-correlated with one another. The ionization of one carboxylic group should favor the protonation of the other at an intermediate pH that allows both groups to be protonated. We will discuss this topic next.
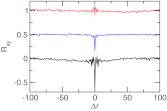
Coupling between titration events
The difference between the two pKa values for dicarboxylic acids is due to the anticorrelation between the two protonation events, since deprotonation of the first carboxylic group imposes an electrostatic penalty for the deprotonation of the second group. To understand the extent of the coupling between the two protonation events, we calculated the normalized cross-correlation function based on the λ values of two titrating sites in glutaric acid (Eq. 25). Glutaric acid is a good example because it has the strongest coupling among the series of dicarboxylic acids and ΔpKa was calculated with good accuracy using the E+CL method. For comparison we also calculated the cross correlation using the data from the GB and the explicit-solvent simulation without co-ion. The cross-correlation at zero delay time correlates with the accuracy of the calculated pKa difference (Figure 8). There is a strong anti-correlation between the titration events in the simulation without charge leveling, which severely overestimates ΔpKa. The degree of anti-correlation is reduced and the accuracy of the calculated ΔpKa is improved with the GB model. In the simulation with the E+CL method the cross-correlation is virtually nonexistent while ΔpKa is the most accurate. Thus, our data indicate that overestimation of the electrostatic repulsion between the ionized carboxylate groups in the GB and the explicit-solvent simulation without co-ions exaggerates the coupling between the two titration events leading to an overestimation in the pKa difference.
Figure 8.
Correlated titration of the two carboxylic groups in glutaric acid. Rxy is the normalized cross-correlation function based on the λ values of two titrating sites at pH 4. Δr is the offset in the exchange cycles. Results based on the GB simulation, explicit-solvent simulation with and without charge leveling are shown in blue, red, and black, respectively. For clarity the baseline for the first two sets of data is shifted.
CONCLUSION
We have developed an all-atom CpHMD technique that makes use of the generalized reaction field for treatment of long-range electrostatics and a charge-leveling scheme that maintains the solute net charge constant by coupling titration to the ionization or neutralization of co-ions serving as a charge reservoir. We tested the new method on a series of aliphatic dicarboxylic acids with the number of intervening methylene units ranging from 3 to 7. We compared the calculated macroscopic pKa values with those resulting from the GB-based simulation as well as the simulation without charge-leveling. The all-atom method with charge leveling delivers the most accurate pKa values with the average absolute error being only 0.18 units for both macroscopic pKa values. This performance is slightly better than the GB-based method, which gives the average absolute errors of 0.43 and 0.19 units for the respective first and second pKa values. In contrast, the simulation without charge leveling overestimates the second pKa value by an average of 1.55 units. Analysis reveals that the electrostatic repulsion between the two ionized carboxyl groups is too large, leading to exaggerated coupling between the two titration events and consequently an overestimation of the second pKa. Our results demonstrate that proper treatment of long-range electrostatics and maintaining charge neutrality of the system are both critical. While the former removes large random noise in propagating titration coordinates, the latter corrects for systematic deviations from experiment, suggesting that the way is paved for realizing pH-controlled molecular dynamics in the near future. Nevertheless, further testing and improvement are needed. One major issue is related to potential artifacts of co-ions. Although in the current simulations, clustering of co-ions and interactions with the solute and counterions are not observed, such artifacts may arise as the number of titratable sites and hence co-ions becomes very large. Another issue is related to sampling convergence. The additional ions may further slow down convergence for explicit-solvent simulations. Work is underway to explore these topics using protein systems.
ACKNOWLEDGMENTS
J.K.S. is indebted to Dr. Charles L. Brooks III for support during the development of the GB-based CpHMD method which laid a foundation for this work. We acknowledge National Science Foundation (MCB-1054547) and National Institutes of Health (RO1GM098818) for financial support.
References
- Baptista A. M., Teixeira V. H., and Soares C. M., J. Chem. Phys. 117, 4184 (2002). 10.1063/1.1497164 [DOI] [Google Scholar]
- Bürgi R., Kollman P. A., and van Gunsteren W. F., Proteins 47, 469 (2002). 10.1002/prot.10046 [DOI] [PubMed] [Google Scholar]
- Mongan J., Case D. A., and McCammon J. A., J. Comput. Chem. 25, 2038 (2004). 10.1002/jcc.20139 [DOI] [PubMed] [Google Scholar]
- Dlugosz M. and Antosiewicz J. M., Chem. Phys. 302, 161 (2004). 10.1016/j.chemphys.2004.03.031 [DOI] [Google Scholar]
- Meng Y. and Roitberg A. E., J. Chem. Theory Comput. 6, 1401 (2010). 10.1021/ct900676b [DOI] [PMC free article] [PubMed] [Google Scholar]
- Börjesson U. and Hünenberger P. H., J. Chem. Phys. 114, 9706 (2001). 10.1063/1.1370959 [DOI] [Google Scholar]
- Lee M. S., F. R.SalsburyJr., and C. L.BrooksIII, Proteins 56, 738 (2004). 10.1002/prot.20128 [DOI] [PubMed] [Google Scholar]
- Khandogin J. and C. L.BrooksIII, Biophys. J. 89, 141 (2005). 10.1529/biophysj.105.061341 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kong X. and C. L.BrooksIII, J. Chem. Phys. 105, 2414 (1996). 10.1063/1.472109 [DOI] [Google Scholar]
- Wallace J. A., Wang Y., Shi C., Pastoor K. J., Nguyen B.-L., Xia K., and Shen J. K., Proteins 79, 3364 (2011). 10.1002/prot.23080 [DOI] [PubMed] [Google Scholar]
- Khandogin J., Chen J., and C. L.BrooksIII, Proc. Natl. Acad. Sci. U.S.A. 103, 18546 (2006). 10.1073/pnas.0605216103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khandogin J. and C. L.BrooksIII, Proc. Natl. Acad. Sci. U.S.A. 104, 16880 (2007). 10.1073/pnas.0703832104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khandogin J., Raleigh D. P., and C. L.BrooksIII, J. Am. Chem. Soc. 129, 3056 (2007). 10.1021/ja0688880 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khandogin J. and C. L.BrooksIII, Biochemistry 45, 9363 (2006). 10.1021/bi060706r [DOI] [PubMed] [Google Scholar]
- Wallace J. A. and Shen J. K., J. Chem. Theory Comput. 7, 2617 (2011). 10.1021/ct200146j [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morrow B. H., Wang Y., Wallace J. A., Koenig P. H., and Shen J. K., J. Phys. Chem. B 115, 14980 (2011). 10.1021/jp2062404 [DOI] [PubMed] [Google Scholar]
- Donnini S., Tegeler F., Groenhof G., and Grubmüller H., J. Chem. Theory Comput. 7, 1962 (2011). 10.1021/ct200061r [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goh G. B., Knight J. L., and C. L.BrooksIII, J. Chem. Theory Comput. 8, 36 (2012). 10.1021/ct2006314 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dixit S. B. and Chipot C., J. Phys. Chem. A 105, 9795 (2001). 10.1021/jp011878v [DOI] [Google Scholar]
- Wallace J. A. and Shen J. K., Methods Enzymol. 466, 455 (2009). 10.1016/S0076-6879(09)66019-5 [DOI] [PubMed] [Google Scholar]
- Tironi I. G., Sperb R., Smith P. E., and van Gunsteren W. F., J. Chem. Phys. 102, 5451 (1995). 10.1063/1.469273 [DOI] [Google Scholar]
- Essmann U., Perera L., Berkowitz M. L., Darden T., Hsing L., and Pedersen L. G., J. Chem. Phys. 103, 8577 (1995). 10.1063/1.470117 [DOI] [Google Scholar]
- Hünenberger P. H. and McCammon J. A., Biophys. Chem. 78, 69 (1999). 10.1016/S0301-4622(99)00007-1 [DOI] [PubMed] [Google Scholar]
- Gargallo R., Hünenberger P. H., Avilés F. X., and Oliva B., Protein Sci. 12, 2161 (2003). 10.1110/ps.03137003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nina M. and Simonson T., J. Phys. Chem. B 106, 3696 (2002). 10.1021/jp013855m [DOI] [Google Scholar]
- Baumketner A. and Shea J.-E., J. Phys. Chem. B 109, 21322 (2005). 10.1021/jp051325a [DOI] [PubMed] [Google Scholar]
- Monticelli L., Simões C., Belvisi L., and Colombo G., J. Phys. Condens. Matter 18, S329 (2006). 10.1088/0953-8984/18/14/S15 [DOI] [Google Scholar]
- Robertson A., Luttman E., and Pande V. S., J. Comput. Chem. 29, 694 (2008). 10.1002/jcc.20828 [DOI] [PubMed] [Google Scholar]
- Machuqueiro M. and Baptista A. M., Proteins 72, 289 (2008). 10.1002/prot.21923 [DOI] [PubMed] [Google Scholar]
- Kirkwood J. G. and Westheimer F. H., J. Chem. Phys. 6, 506 (1938). 10.1063/1.1750302 [DOI] [Google Scholar]
- Westheimer F. H. and Kirkwood J. G., J. Chem. Phys. 6, 513 (1938). 10.1063/1.1750303 [DOI] [Google Scholar]
- Potter M. J., Gilson M. K., and McCammon J. A., J. Am. Chem. Soc. 116, 10298 (1994). 10.1021/ja00101a059 [DOI] [Google Scholar]
- Price D. J., Roberts J. D., and Jorgensen W. L., J. Am. Chem. Soc. 120, 9672 (1998). 10.1021/ja9812397 [DOI] [Google Scholar]
- Gane R. and Ingold C. K., J. Chem. Soc. 1931, 2153. 10.1039/jr9310002153 [DOI] [Google Scholar]
- Simonson T., Carlsson J., and Case D. A., J. Am. Chem. Soc. 126, 4167 (2004). 10.1021/ja039788m [DOI] [PubMed] [Google Scholar]
- Kamerlin S. C. L., Haranczyk M., and Warshel A., J. Phys. Chem. B 113, 1253 (2009). 10.1021/jp8071712 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brooks B. R., C. L.BrooksIII, A. D.MackerellJr., Nilsson L., Petrella R. J., Roux B., Won Y., Archontis G., Bartles C., Boresch S., Caflisch A., Caves L., Cui Q., Dinner A. R., Feig M., Fischer S., Gao J., Hodoscek M., Im W., Lazaridis K. K. T., Ma J., Ovchinnikov V., Paci E., Pastor R. W., Post C. B., Pu J. Z., Schaefer M., Tidor B., Venable R. M., Woodcock H. L., Wu X., Yang W., York D. M., and Karplus M., J. Comput. Chem. 30, 1545 (2009). 10.1002/jcc.21287 [DOI] [PMC free article] [PubMed] [Google Scholar]
- A. D.MackerellJr., Feig M., and C. L.BrooksIII, J. Comput. Chem. 25, 1400 (2004). 10.1002/jcc.20065 [DOI] [PubMed] [Google Scholar]
- Jorgensen W. L., Chandrasekhar J., Madura J. D., Impey R. W., and Klein M. L., J. Chem. Phys. 79, 926 (1983). 10.1063/1.445869 [DOI] [Google Scholar]
- Noskov S. Y. and Roux B., J. Mol. Biol. 377, 804 (2008). 10.1016/j.jmb.2008.01.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo Y. and Roux B., J. Phys. Chem. Lett. 1, 183 (2010). 10.1021/jz900079w [DOI] [Google Scholar]
- Im W., Lee M. S., and C. L.BrooksIII, J. Comput. Chem. 24, 1691 (2003). 10.1002/jcc.10321 [DOI] [PubMed] [Google Scholar]
- Nina M., Beglov D., and Roux B., J. Phys. Chem. B 101, 5239 (1997). 10.1021/jp970736r [DOI] [Google Scholar]
- Hoover W. G., Phys. Rev. A 31, 1695 (1985). 10.1103/PhysRevA.31.1695 [DOI] [PubMed] [Google Scholar]
- Feller S. E., Zhang Y., Pastor R. W., and Brooks B. R., J. Chem. Phys. 103, 4613 (1995). 10.1063/1.470648 [DOI] [Google Scholar]
- Ullmann G. M., J. Phys. Chem. B 107, 1263 (2003). 10.1021/jp026454v [DOI] [Google Scholar]
- Wang Y., Wallace J. A., Koenig P. H., and Shen J. K., J. Comput. Chem. 32, 2348 (2011). 10.1002/jcc.21813 [DOI] [PubMed] [Google Scholar]
- Nadler W. and Hansmann U. H. E., Phys. Rev. E 75, 026109 (2007). 10.1103/PhysRevE.75.026109 [DOI] [PubMed] [Google Scholar]