Abstract
Feedback loops are ubiquitous features of biological networks and can produce significant phenotypic heterogeneity, including a bimodal distribution of gene expression across an isogenic cell population. In this work, a combination of experiments and computational modeling was used to explore the roles of multiple feedback loops in the bimodal, switch-like response of the Saccharomyces cerevisiae galactose regulatory network. Here, we show that bistability underlies the observed bimodality, as opposed to stochastic effects, and that two unique positive feedback loops established by Gal1p and Gal3p, which both regulate network activity by molecular sequestration of Gal80p, induce this bimodality. Indeed, systematically scanning through different single and multiple feedback loop knockouts, we demonstrate that there is always a concentration regime that preserves the system’s bimodality, except for the double deletion of GAL1 and the GAL3 feedback loop, which exhibits a graded response for all conditions tested. The constitutive production rates of Gal1p and Gal3p operate as bifurcation parameters because variations in these rates can also abolish the system’s bimodal response. Our model indicates that this second loss of bistability ensues from the inactivation of the remaining feedback loop by the overexpressed regulatory component. More broadly, we show that the sequestration binding affinity is a critical parameter that can tune the range of conditions for bistability in a circuit with positive feedback established by molecular sequestration. In this system, two positive feedback loops can significantly enhance the region of bistability and the dynamic response time.
Keywords: gene-regulatory network, phenotypic variation, ultrasensitivity
Cells are continuously faced with the challenge of sensing signals in their environment and eliciting intracellular programs accordingly. Although changes in some environmental cues engender graded and proportional responses, others induce decisive action whereby a cell exhibits a binary (on or off) phenotypic change. In the latter case, amplification of phenotypic heterogeneity may arise because single cells in a population make individual decisions based on their perception of the environmental stimulus, stochastic fluctuations in their molecular components, and memory of past conditions. This thresholded cellular response can manifest as a bimodal distribution in network activity across an isogenic cell population.
Feedback regulation, which links the output of a circuit back to its input, expands the set of possible biological properties, including robustness to uncertainty (1), and can produce single-cell phenotypic heterogeneity in a uniform environment. Many features of individual positive and negative feedback loops have been elucidated, including enhancement of response time and reduction of gene expression noise by negative autoregulation, as well as signal amplification and bistability using positive autoregulation (2–5). However, quantitative characterization of how multiple feedback pathways interact to regulate and fine-tune cellular decision-making presents many unresolved challenges.
The galactose gene-regulatory network of Saccharomyces cerevisiae (GAL) contains numerous feedback pathways. Isogenic single cells respond heterogeneously to a range of galactose concentrations, which manifests as a bimodal distribution of GAL gene expression across the cell population (6). In contrast to a graded response, in which the mean of a unimodal distribution is continuously adjusted as the input is modulated, variations in the concentration of galactose within a range shift the fraction of the cell population distributed between distinct metabolic states. Here, we focused on how the multiple feedback loops in the system shape this bimodal cellular decision-making strategy in response to galactose.
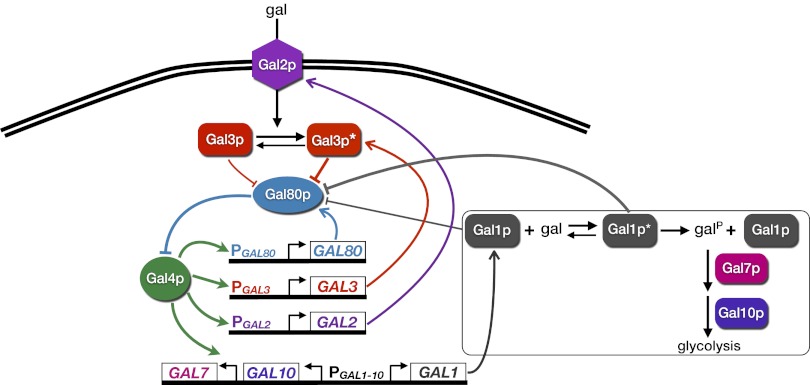
The GAL circuit consists of regulatory machinery (Gal2p, Gal3p, Gal80p, and Gal4p) that dictates network activity and a set of enzymes required for metabolizing galactose (Gal1p, Gal7p, and Gal10p). In the absence of galactose, GAL genes are repressed due to the sequestration of the potent transcriptional activator Gal4p by the repressor Gal80p (7) (Fig. 1). In the presence of galactose, the membrane-bound permease transporter Gal2p significantly increases the rate of galactose uptake from the extracellular environment (8). Galactose and ATP-dependent activation of the signal transducer Gal3p lead to repression of Gal80p by sequestration, thus liberating Gal4p (9). The galactokinase Gal1p catalyzes the first step in galactose metabolism by phosphorylating galactose to form galactose 1-phosphate and has been shown to possess weak coinducing functionality (10).
Fig. 1.
The galactose gene-regulatory network in S. cerevisiae. The permease Gal2p facilitates intracellular galactose transport. By binding to galactose, the signal transducer Gal3p becomes highly activated to sequester the transcriptional repressor Gal80p. In the absence of galactose, Gal3p can also inhibit Gal80p, presumably with lower affinity, leading to GAL gene induction (10). Repression of Gal80p liberates the transcriptional activator Gal4p to up-regulate a set of target enzymatic and regulatory genes. A series of enzymatic reactions (interactions inside the box) transforms galactose into glucose-6-phosphate for glycolysis through the activities of the galactokinase Gal1p, transferase Gal7p, and epimerase Gal10p. The regulatory proteins Gal2p, Gal3p, and Gal80p form positive, positive, and negative feedback loops, respectively. Gal1p, a paralog of Gal3p, has been shown to possess bifunctional activities by sequestering Gal80p in the presence and absence of galactose with different affinities, leading to GAL gene activation (10, 51). GAL1 and GAL10 share a bidirectional promoter (PGAL1-10).
Galactose-dependent regulation of Gal2p, Gal3p, and Gal80p forms feedback loops because these proteins modulate network activity and are themselves transcriptionally regulated by Gal4p (11). Gal2p and Gal3p form positive feedback loops because up-regulation of their expression levels leads to an increase in pathway activity, whereas Gal80p reduces pathway activity and thus forms a negative feedback loop.
In addition to Gal2p, Gal3p, and Gal80p, there is evidence to suggest that Gal1p has a regulatory role beyond its vital enzymatic function for growth on galactose (10, 12, 13). Gal1p is a close homolog of Gal3p and has been shown to interact with Gal80p with a weaker affinity than Gal3p (14, 15). Furthermore, a GAL3 deletion strain was shown to induce GAL gene expression at a significantly slower rate compared with WT, whereas cells with combined GAL1 and GAL3 deletions fail to activate their GAL pathway (16). A recent study demonstrated that cells initially grown in galactose and then transferred to glucose exhibit a faster induction response to a second galactose exposure than cells grown only in glucose, and that Gal1p was critical for this decrease in response time (17). Finally, galactose induction was shown to consist of two stages, the first of which is dominated by rapid association of Gal3p to Gal80p and a delayed second stage consisting of dominance of the Gal1p–Gal80p complex (18).
In this paper, we use a combination of experimental measurements and computational modeling to demonstrate that the observed bimodality in the galactose metabolic pathway arises from an underlying bistability in the system and that this bimodal response relies on the synergistic interplay of the GAL1 and GAL3 feedback loops. These central mediators have unique mechanistic roles in the GAL system because they both regulate circuit activity by competitive molecular sequestration of Gal80p. Although the bimodal response can be transformed into a graded response in the absence of the individual GAL1 and GAL3 feedback loops, this only occurs in a specific parameter regime in which the constitutive production rates of Gal1p and Gal3p are greater than a threshold. A mathematical model recapitulates the experimental results and provides crucial insights about the roles of the autoregulatory loops on bistability. More broadly, a simple mathematical model is used to identify generalizable properties of positive feedback loops created by molecular sequestration that implement robust switch-like responses.
Results
History-Dependent Response Indicates That Bimodality Arises from Underlying Bistability and Gal1p Significantly Enhances Sensitivity to Galactose.
The presence of bimodality does not necessarily imply bistability because a bimodal distribution can arise from stochastic effects (19–21). Hysteresis is a characteristic feature of bistability, in which the system jumps from one branch of stable steady states to a different branch of steady states as a parameter is continuously increased but jumps from the second branch of steady states back to the first branch at a different value of the parameter as it is continuously decreased. This behavior stems from a difference in the local stability of multiple stable equilibria. To determine if bimodality in the GAL system was linked to bistability, we checked for a history-dependent response, which is an indicator of local equilibrium point stability. The bistable stochastic counterpart of a deterministic bistable system may not exhibit hysteresis due to an insufficient time-scale separation, and a deterministic system can be bistable without displaying hysteresis (22, 23). Here, we tested for a stochastic system that exhibits hysteresis, which would be consistent with an underlying bistability in a deterministic model of the system. Distinguishing whether bimodality arises from stochastic interactions or a deterministic bistability provides critical information about the operation of the system, including the types of molecular interactions that might be underlying this response, and suggests a mathematical modeling framework for studying this phenotype.
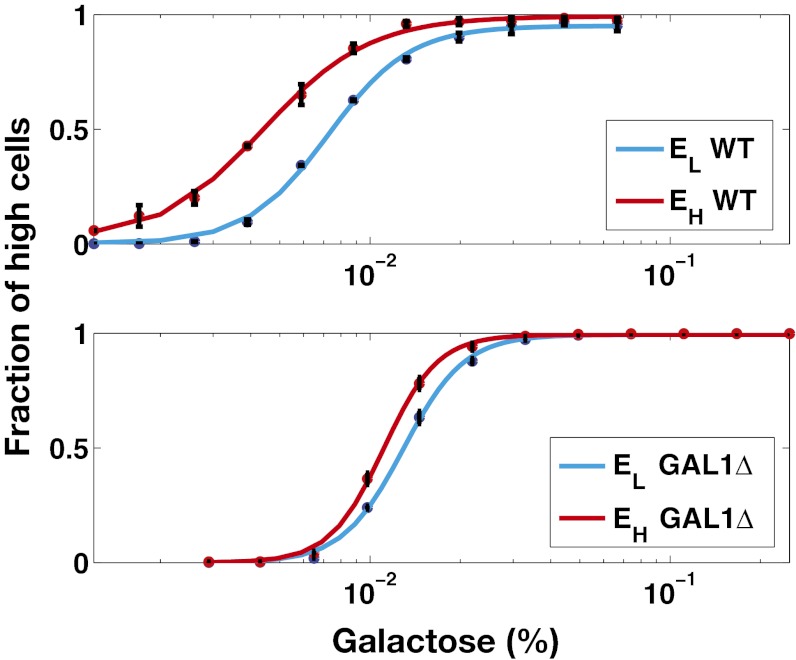
We investigated the GAL system’s history-dependent response by comparing the stability of its high and low metabolic states as a function of galactose. To measure relative expression state stability, we used flow cytometry to quantify the fluorescence distributions of a genome-integrated GAL10 promoter fusion to Venus (YFP) in WT single cells as an indicator of network activity (PGAL10Venus) (24). The cells were grown first in the presence (EH) and absence (EL) of an environment of 2% galactose in 2% (wt/vol) raffinose media. Cells from the two environments were then shifted to a second set of environments containing a wide range of galactose concentrations.
A history-dependent response existed if cell populations grown in the two environments (EL and EH) had a different fraction of cells distributed between the high and low expression states in a range of galactose concentrations after ∼10 cell divisions after the shift (30 h). A 30-h induction period was selected to allow a sufficient number of cell divisions for dilution of the fluorescent reporter from EH cells (SI Text, section S1). Within a range of galactose concentrations, cells from EL and EH were distributed differently between the high and low metabolic states (Fig. 2), revealing a history-dependent response and corroborating the existence of bistability.
Fig. 2.
History-response experiment indicates that GAL bimodal response arises from underlying bistability. In this experiment, isogenic cells were grown in two environments, EH (2% galactose and 2% raffinose) and EL (2% raffinose) until steady state. Cells were then transferred from the two initial environments to a new set of environments containing a range of galactose concentrations. A history-dependent response was present if cells from EH and EL were distributed differently between the high and low states for a range of galactose concentrations after 30 h of induction. (Upper) Experimental data show history-response region for WT cells. (Lower) Cells that do not metabolize galactose (GAL1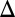 ) also displayed a history-dependent response. Each data point is the mean of the fraction of cells in the high expression state, and the error bars represent 1 SD (n = 3). Lines represent fitted Hill functions.
) also displayed a history-dependent response. Each data point is the mean of the fraction of cells in the high expression state, and the error bars represent 1 SD (n = 3). Lines represent fitted Hill functions.
To exclude the possibility that the difference in the thresholds of the dose–responses was due to variable consumption of galactose, the history-response experiment was performed using a GAL1 deletion strain that is incapable of metabolizing galactose (GAL1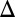 ) (25). The GAL1
) (25). The GAL1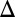 strain was used because cells with gene deletions for the transferase GAL7 and epimerase GAL10 are unable to grow in the presence of galactose due to the toxic accumulation of phosphorylated galactose (26).
strain was used because cells with gene deletions for the transferase GAL7 and epimerase GAL10 are unable to grow in the presence of galactose due to the toxic accumulation of phosphorylated galactose (26).
Investigation of history dependence in the GAL1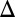 strain revealed that its dose–response threshold was approximately twofold higher than WT, demonstrating that Gal1p significantly contributes to galactose sensitivity. The GAL1
strain revealed that its dose–response threshold was approximately twofold higher than WT, demonstrating that Gal1p significantly contributes to galactose sensitivity. The GAL1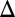 cells also exhibited a history-dependent difference in the galactose threshold. However, the area separating the activation response curves for GAL1
cells also exhibited a history-dependent difference in the galactose threshold. However, the area separating the activation response curves for GAL1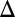 was smaller than WT, indicating a diminished history-dependent response. Taken together, these data corroborate bistability as the source of bimodality in the response of the GAL network to galactose and strongly suggest that Gal1p plays an important regulatory role in addition to its metabolic function.
was smaller than WT, indicating a diminished history-dependent response. Taken together, these data corroborate bistability as the source of bimodality in the response of the GAL network to galactose and strongly suggest that Gal1p plays an important regulatory role in addition to its metabolic function.
Combined Deletion of the GAL1 and GAL3 Feedback Loops Produces a Graded Response, Demonstrating the Unique Role of Gal1p and Gal3p in Generating Bistability.
To explore Gal1p as a regulatory component of the system further and to evaluate its role relative to the other autoregulatory loops, we constructed a series of feedback loop deletions involving different components of the system. To do so, we deleted the coding region of a given gene and integrated a single copy of this gene regulated by an inducible TET promoter or a constitutive promoter. The rate of production from the TET promoter could be adjusted by doxycycline (dox)-dependent activation of rtTA, a reverse mutant of the transcription factor TetR (27). In this fashion, the expression of the gene involved in the feedback loop can be decoupled from the activity of the galactose pathway because the regulation of the constitutive or inducible promoter is external to the GAL regulatory circuit.
To compare the operation of the WT system and the different feedback mutants on equal footing, we selected the strength of constitutive expression of each gene by mapping it to the corresponding WT expression levels using real-time quantitative PCR (qPCR) (Table 1). We also explored a range of TET promoter expression levels by scanning different dox concentrations to investigate the relationship between constitutive expression of each regulatory component and the steady-state dose–response. The fluorescence distributions were classified as unimodal or bimodal using a Gaussian mixture model (GMM) threshold (Materials and Methods).
Table 1.
Summary of real-time qPCR measurements comparing constitutive expression in the feedback deletion strains and WT mRNA levels of GAL1, GAL2, GAL3, and GAL80
| Promoter gene | Range of WT expression |
| PTET GAL1 | 0 (4%) and 100 (20%) ng/mL dox |
| PTET GAL2 | 100 (37%) ng/mL dox |
| PTET GAL3 | 0 (50%) and 20 (100%) ng/mL dox |
| PTET GAL80 | 0 (40%) and 25 (100%) ng/mL dox |
| PADHI GAL2 | 58% |
| PSTE5 GAL80 | 21% |
Expression levels were compared with WT fully induced with galactose (0.5% galactose). Each value is the mean of at least three independent qPCR measurements (Fig. S3).
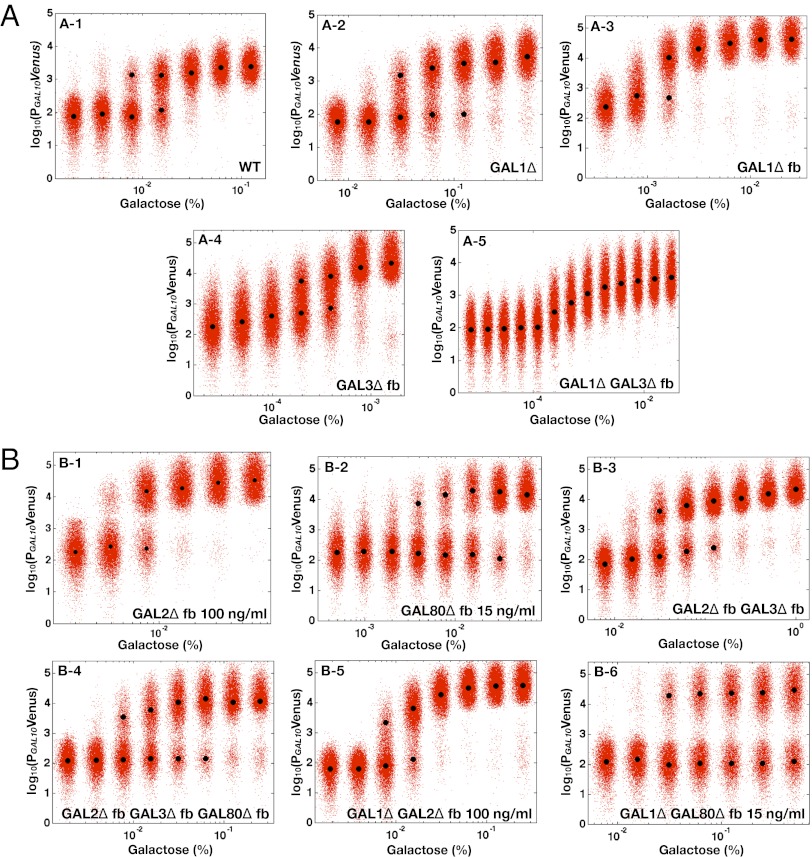
Eliminating the GAL2 or GAL80 feedback loop did not abolish the GAL system’s bimodal response (Fig. 3 B1 and B2). Instead, bimodality persisted for a range of expression levels for Gal2p and Gal80p (Fig. S1 A and B). Compared with WT, cells with a deleted GAL80 feedback loop (GAL80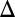 fb) displayed bimodality for a larger number of galactose concentrations. Contrary to a previous study (28), we observed that the GAL3 feedback loop was not necessary for bimodality for WT expression levels of Gal3p (Fig. 3 A4 and Fig. S2). However, in the GAL3
fb) displayed bimodality for a larger number of galactose concentrations. Contrary to a previous study (28), we observed that the GAL3 feedback loop was not necessary for bimodality for WT expression levels of Gal3p (Fig. 3 A4 and Fig. S2). However, in the GAL3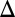 fb cells, the bimodal response could be transformed into a graded response by driving the rate of constitutive Gal3p production beyond a critical threshold (SI Text, section S2). We found that the discrepancy with the previous study (28) can be explained by constitutive Gal3p expression above this threshold.
fb cells, the bimodal response could be transformed into a graded response by driving the rate of constitutive Gal3p production beyond a critical threshold (SI Text, section S2). We found that the discrepancy with the previous study (28) can be explained by constitutive Gal3p expression above this threshold.
Fig. 3.
Double deletion of GAL1 and the GAL3 feedback loop abolishes bimodality. Representative steady-state flow cytometry data of PGAL10 Venus in WT and a set of single and multiple feedback loop deletions induced with a range of galactose concentrations. Each black circle indicates the mean of the distribution determined by a GMM algorithm (Materials and Methods). Small random deviations were added to each galactose concentration to highlight the spread of the fluorescence distributions. (A) Either GAL1 or the GAL3 feedback loop is required for bimodality. The WT, GAL1 deletion (GAL1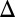 ), GAL1 feedback deletion (GAL1
), GAL1 feedback deletion (GAL1 fb), and GAL3 feedback deletion (GAL3
fb), and GAL3 feedback deletion (GAL3 fb) strains displayed bimodality for at least one galactose concentration. GAL1
fb) strains displayed bimodality for at least one galactose concentration. GAL1 fb and GAL3
fb and GAL3 fb were not induced with dox. Eliminating the GAL3 feedback loop in the absence of GAL1 (GAL1
fb were not induced with dox. Eliminating the GAL3 feedback loop in the absence of GAL1 (GAL1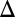 GAL3
GAL3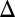 fb) produced a graded response for the full range of galactose. (B) Bimodality was preserved for a series of feedback loop disruptions. The single GAL2 (GAL2
fb) produced a graded response for the full range of galactose. (B) Bimodality was preserved for a series of feedback loop disruptions. The single GAL2 (GAL2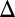 fb) and GAL80 (GAL80
fb) and GAL80 (GAL80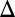 fb) loop deletions were induced with 100 and 15 ng/mL dox, respectively. Bimodality persisted for a dual feedback loop disruption of GAL2 and GAL3 (GAL1
fb) loop deletions were induced with 100 and 15 ng/mL dox, respectively. Bimodality persisted for a dual feedback loop disruption of GAL2 and GAL3 (GAL1 fb GAL3
fb GAL3 fb) and a triple feedback deletion of GAL2, GAL3, and GAL80 (GAL2
fb) and a triple feedback deletion of GAL2, GAL3, and GAL80 (GAL2 fb GAL3
fb GAL3 fb GAL80
fb GAL80 fb). For these two strains, GAL2, GAL3, and GAL80 were expressed from ADH1, TET, and STE5 promoters, respectively, in the absence of dox. Deleting the GAL2 (GAL1
fb). For these two strains, GAL2, GAL3, and GAL80 were expressed from ADH1, TET, and STE5 promoters, respectively, in the absence of dox. Deleting the GAL2 (GAL1 GAL2
GAL2 fb) and GAL80 (GAL1
fb) and GAL80 (GAL1 GAL80
GAL80 fb) feedback loops individually in a strain lacking GAL1 preserved bimodality. GAL1
fb) feedback loops individually in a strain lacking GAL1 preserved bimodality. GAL1 GAL2
GAL2 fb and GAL1
fb and GAL1 GAL80
GAL80 fb were induced with 100 and 15 ng/mL dox, respectively.
fb were induced with 100 and 15 ng/mL dox, respectively.
Because the GAL2, GAL3, and GAL80 feedback loops were not individually necessary for bimodality, we hypothesized that they play compensatory roles or that bimodality relies on yet another uncharacterized feedback loop. To address the possibility that the feedback loops had overlapping or compensatory functions, we constructed combinations of feedback loop deletions of GAL2, GAL3, and GAL80 by constitutively expressing them from the ADH1, TET, and STE5 promoters, respectively. Remarkably, bimodality was preserved in the absence of both the GAL2 and GAL3 feedback loops (GAL2 fb and GAL3
fb and GAL3 fb) and also in a triple feedback loop deletion strain of GAL2, GAL3, and GAL80 (Fig. 3 B3 and B4).
fb) and also in a triple feedback loop deletion strain of GAL2, GAL3, and GAL80 (Fig. 3 B3 and B4).
Therefore, combinations of GAL2, GAL3, and GAL80 feedback loops did not functionally overlap to create bimodality. Because Gal1p regulates both the sensitivity and memory of the GAL network to galactose (Fig. 2B), we explored the possibility that Gal1p could be an important component of the system’s bimodality.
In contrast to Gal3p and Gal80p transcriptional regulation, Gal1p is tightly repressed in the absence and strongly induced in the presence of galactose. As a consequence, matching the open and closed loop production rates using the TET promoter was challenging. Similar to Gal3p, Gal1p has been shown to activate GAL genes independent of galactose, and a sufficiently strong constitutive Gal1p production rate could shift the operating point of the network (10). We first explored the lowest regime of Gal1p expression using a GAL1 gene deletion (GAL1 ), and bimodality was detected in this strain for several galactose concentrations (Fig. 3A2). The GAL1 feedback loop deletion, PTET GAL1 (GAL1
), and bimodality was detected in this strain for several galactose concentrations (Fig. 3A2). The GAL1 feedback loop deletion, PTET GAL1 (GAL1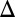 fb) was also bimodal in the absence of dox for at least one galactose concentration (Fig. 3A3) but was graded in the presence of 10, 25, 50, and 100 ng/mL dox (Fig. S4).
fb) was also bimodal in the absence of dox for at least one galactose concentration (Fig. 3A3) but was graded in the presence of 10, 25, 50, and 100 ng/mL dox (Fig. S4).
We examined the combined effect of removing the GAL2, GAL3, or GAL80 in a strain lacking GAL1. As shown in Fig. 3 B5 and B6, the combined deletion of GAL1 and the GAL2 feedback loop (GAL1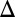 GAL2
GAL2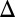 fb) and dual deletion of GAL1 and the GAL80 feedback loop (GAL1
fb) and dual deletion of GAL1 and the GAL80 feedback loop (GAL1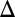 GAL80
GAL80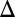 fb) displayed bimodality for at least two galactose concentrations.
fb) displayed bimodality for at least two galactose concentrations.
In stark contrast, the simultaneous deletion of GAL1 and the GAL3 feedback loop (GAL1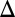 GAL3
GAL3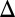 fb) produced a graded response for the entire range of galactose (Fig. 3A5). Remarkably, this graded response persisted irrespective of the constitutive Gal3p production rate in contrast to the single GAL3 feedback KO that displayed bimodality for some range of constitutive Gal3p levels (Fig. S5A). These data provide further evidence that GAL1 is an active regulatory component of the circuit and that the interplay between the GAL1 and GAL3 feedback loops is crucial for bimodality.
fb) produced a graded response for the entire range of galactose (Fig. 3A5). Remarkably, this graded response persisted irrespective of the constitutive Gal3p production rate in contrast to the single GAL3 feedback KO that displayed bimodality for some range of constitutive Gal3p levels (Fig. S5A). These data provide further evidence that GAL1 is an active regulatory component of the circuit and that the interplay between the GAL1 and GAL3 feedback loops is crucial for bimodality.
In addition to eliminating bimodality, our results revealed that removing GAL1 and the GAL3 feedback loop abolished ultrasensitivity in the dose–response to galactose, indicating a coupling between the mechanisms for ultrasensitivity and bistability in the GAL network. We found that the Hill coefficient for PGAL10 Venus in WT was ∼3, whereas this same reporter exhibited a Hill coefficient of ∼1.3 in the absence of GAL1 and the GAL3 feedback loop (GAL1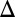 GAL3
GAL3 fb) (Fig. S5B). This link between ultrasensitivity and bimodality may arise due to the necessity of ultrasensitivity for bistability (29).
fb) (Fig. S5B). This link between ultrasensitivity and bimodality may arise due to the necessity of ultrasensitivity for bistability (29).
Cooperative Gal4p Interactions at the Promoter Level Do Not Generate Bimodal Response.
Bimodality was not observed using the GAL3 and GAL80 promoters as reporters of GAL network activity in WT for any concentration of galactose (Fig. S1E). In contrast to the GAL10 promoter, these promoters each contain a single GAL4 binding site. Multiple GAL4 binding sites may augment the dynamic range of the reporter to provide a sufficient separation of the high and low expression states, or cooperativity of Gal4 proteins at the promoter level may be an important parameter of the bimodal response. To test whether multiple GAL4 binding sites are necessary for bimodality, a synthetic GAL promoter containing a single Gal4p binding site from the GAL7 promoter driving the expression of a fluorescent reporter was constructed (Materials and Methods). This reporter had minimal cooperativity, yet bimodality was detected for two galactose concentrations at steady state (Fig. S6). These data demonstrate that bimodality is not an exclusive property of promoters with multiple GAL4 binding sites but is instead a property of the upstream regulatory network.
Deterministic Model of GAL Network Recapitulates Experimental Results and Provides Insight into the Roles of Feedback Loops.
To probe the roles of the feedback loops further, we constructed an ordinary differential equation (ODE) model of the system (SI Text, section S4) that takes into account the concentrations of Gal1p (G1), Gal3p (G3), Gal4p (G4), and Gal80p (G80). Because Gal1p and Gal3p can function as coinducers of GAL gene expression independent of galactose, presumably with lower affinities than the galactose-bound forms, these different forms were not differentiated in the model (10).
Based on these assumptions (a full description is provided in SI Text, section S4), the set of differential equations for G1, G3, G4, and G80 that models the interactions shown in Fig. 1 is given by
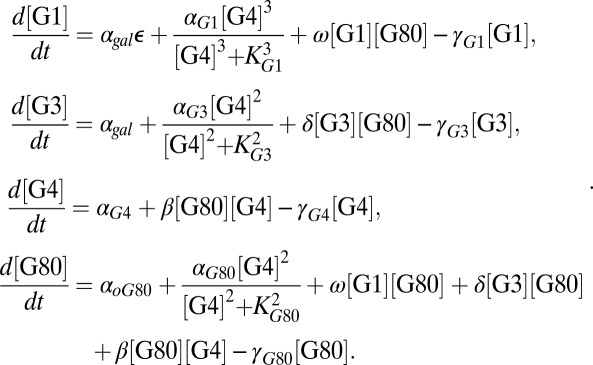 |
Here, 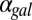 represents galactose at a constant input rate. Parameters were approximated from experimental measurements and values from the literature (SI Text, section S5 and Table S1). Using these estimates, the Hill coefficients for the feedback functions involving GAL1, GAL3, and GAL80 were set to 3, 2, and 2, respectively, but our conclusions were not sensitive to variations in these values. Models of the individual GAL1, GAL3, and GAL80 and combined GAL1 and GAL3 feedback KOs (GAL1
represents galactose at a constant input rate. Parameters were approximated from experimental measurements and values from the literature (SI Text, section S5 and Table S1). Using these estimates, the Hill coefficients for the feedback functions involving GAL1, GAL3, and GAL80 were set to 3, 2, and 2, respectively, but our conclusions were not sensitive to variations in these values. Models of the individual GAL1, GAL3, and GAL80 and combined GAL1 and GAL3 feedback KOs (GAL1 fb, GAL3
fb, GAL3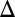 fb, GAL80
fb, GAL80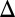 fb, and GAL1
fb, and GAL1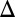 GAL3
GAL3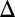 fb, respectively) were constructed by modifying appropriate terms in the WT model (SI Text, section S6).
fb, respectively) were constructed by modifying appropriate terms in the WT model (SI Text, section S6).
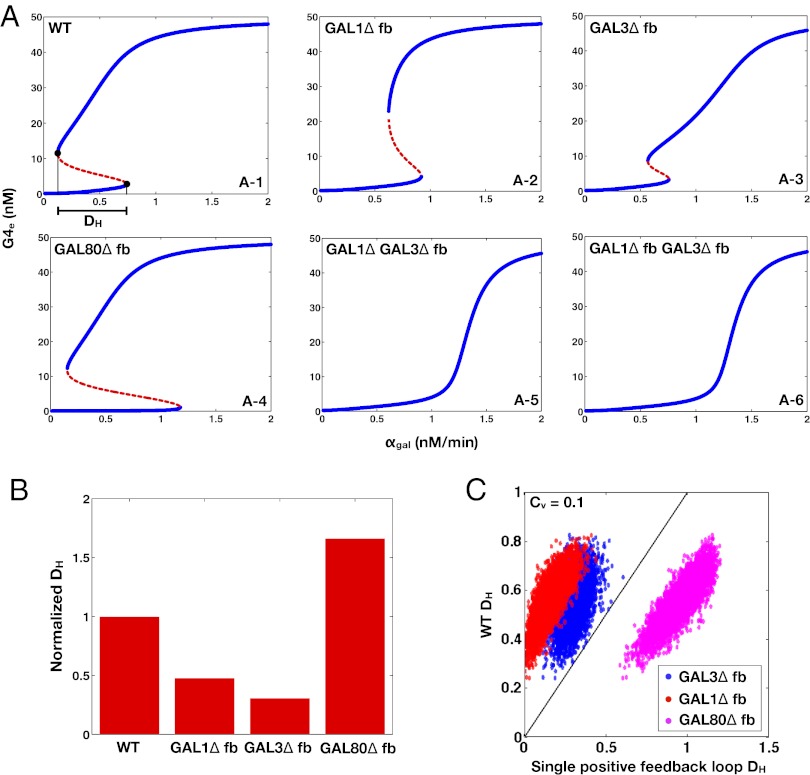
Bifurcation Analysis of GAL Model Confirms That Only the Combined GAL1 and GAL3 Feedback Deletion Eliminates Bistability.
At equilibrium, the concentration of Gal4p can be written as an 11th-order polynomial as described in SI Text, section S4. Similarly, the individual feedback deletion models for GAL1, GAL3, and GAL80 and for combined GAL1 and GAL3 were simplified to eighth-, ninth-, ninth-, and sixth-order polynomials, respectively (SI Text, section S6). The roots of these polynomials include the equilibrium concentrations of Gal4p, which represent the activity of the GAL network. All the models had the potential for bistability for some region of parameter space because the degrees of the polynomials were larger than a quadratic. Indeed, models with individual feedback deletions were still capable of bistability as a function of 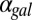 (Fig. 4 A1–A4). By contrast, removing both the GAL1 and GAL3 feedback loops abolished bistability for the entire range of
(Fig. 4 A1–A4). By contrast, removing both the GAL1 and GAL3 feedback loops abolished bistability for the entire range of 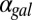 , consistent with experimental data (Fig. 4 A5 and A6).
, consistent with experimental data (Fig. 4 A5 and A6).
Fig. 4.
Bifurcation analysis of the GAL model qualitatively matches experimental results and reveals that the GAL1 and GAL3 feedback loops combine synergistically to expand the parameter region for bistability. The bifurcation parameter 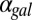 represents galactose, and the equilibrium value of Gal4p (G4e) represents the activity level of the GAL network. (A) Bifurcation plots of WT and the feedback deletions of GAL1 (GAL1
represents galactose, and the equilibrium value of Gal4p (G4e) represents the activity level of the GAL network. (A) Bifurcation plots of WT and the feedback deletions of GAL1 (GAL1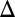 fb), GAL3 (GAL3
fb), GAL3 (GAL3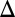 fb), GAL80 (GAL80
fb), GAL80 (GAL80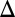 fb), and combined GAL1 and GAL3 (GAL1
fb), and combined GAL1 and GAL3 (GAL1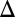 GAL3
GAL3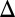 fb and GAL1
fb and GAL1 fb GAL3
fb GAL3 fb). Blue and red represent stable and unstable equilibrium points, respectively. Reflecting the experimental results in Fig. 3, WT, GAL3
fb). Blue and red represent stable and unstable equilibrium points, respectively. Reflecting the experimental results in Fig. 3, WT, GAL3 fb, GAL1
fb, GAL1 fb, and GAL80
fb, and GAL80 fb exhibit bistability, whereas GAL1
fb exhibit bistability, whereas GAL1 GAL3
GAL3 fb and GAL1
fb and GAL1 fb GAL3
fb GAL3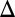 fb are monostable for the full range of
fb are monostable for the full range of 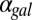 . A representative distance between the bifurcation points, DH, is highlighted by a solid black line. (B) Quantification of the range of bistability for the WT and single feedback KOs shown in A. Normalized DH is equal to the range of
. A representative distance between the bifurcation points, DH, is highlighted by a solid black line. (B) Quantification of the range of bistability for the WT and single feedback KOs shown in A. Normalized DH is equal to the range of 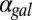 that produces bistability relative to WT. (C) Comparison of DH in the WT, GAL1
that produces bistability relative to WT. (C) Comparison of DH in the WT, GAL1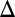 fb (blue), GAL3
fb (blue), GAL3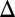 fb (red), and GAL80
fb (red), and GAL80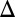 fb (magenta) models for 5,000 representative randomly generated parameters sets sampled from a normal distribution with Cv = 0.1. Data points above the
fb (magenta) models for 5,000 representative randomly generated parameters sets sampled from a normal distribution with Cv = 0.1. Data points above the 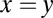 line (black) correspond to parameter sets, where DH is larger in WT compared with the single feedback loop KOs.
line (black) correspond to parameter sets, where DH is larger in WT compared with the single feedback loop KOs.
GAL1 and GAL3 Feedback Loops Combine Synergistically to Augment Bistability.
Using the model, we explored the effects of the GAL1 and GAL3 feedback loops on the range of 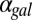 for which the system exhibits bistability. We defined the hysteresis strength,
for which the system exhibits bistability. We defined the hysteresis strength, 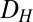 , as the difference between the bifurcation points of
, as the difference between the bifurcation points of 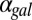 , as shown in Fig. 4A1 (Materials and Methods).
, as shown in Fig. 4A1 (Materials and Methods). 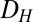 represents the range of conditions in which the system exhibits bistability; thus, the robustness of bistability to parameter variations increases with DH. The GAL1 and GAL3 feedback deletion models had approximately 48% and 31%
represents the range of conditions in which the system exhibits bistability; thus, the robustness of bistability to parameter variations increases with DH. The GAL1 and GAL3 feedback deletion models had approximately 48% and 31% 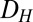 , respectively, compared with WT (Fig. 4B). By contrast, removing the GAL80 feedback significantly increased
, respectively, compared with WT (Fig. 4B). By contrast, removing the GAL80 feedback significantly increased 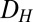 to 166% compared with its WT value, indicating that this negative autoregulatory loop undermines bistability.
to 166% compared with its WT value, indicating that this negative autoregulatory loop undermines bistability.
The generality of these results and the dependence on parameters were explored by comparing the DH of the WT and feedback deletions using randomly generated parameter sets. A total of 10,000 parameter sets were obtained by sampling a normal distribution with a mean equal to the values of parameter set I and a coefficient of variation equal to 0.1. All parameters were varied, except for the constitutive production rates of Gal1p (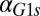 ), Gal3p (
), Gal3p (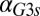 ), and Gal80p (
), and Gal80p (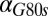 ). This computation confirmed that GAL80
). This computation confirmed that GAL80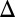 fb had a larger DH compared with WT and that the WT exhibited a larger DH than either the GAL1
fb had a larger DH compared with WT and that the WT exhibited a larger DH than either the GAL1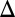 fb or GAL3
fb or GAL3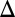 fb model for all parameter sets (Fig. 4C). These findings are consistent with the experimental characterization of the history-dependent response of the GAL1
fb model for all parameter sets (Fig. 4C). These findings are consistent with the experimental characterization of the history-dependent response of the GAL1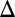 strain (Fig. 2B) and the data showing that the range of galactose concentrations that produced bimodality was expanded in the absence of the GAL80 feedback loop (Fig. 3B2).
strain (Fig. 2B) and the data showing that the range of galactose concentrations that produced bimodality was expanded in the absence of the GAL80 feedback loop (Fig. 3B2).
In summary, collaboration between the GAL1 and GAL3 autoregulatory loops expands the region of bistability across a broad region of parameter space, suggesting that this synergy between dual positive feedback loops may be a consequence of the unique regulatory roles of Gal1p and Gal3p in the GAL circuit. In addition, we found that GAL1 fb GAL3
fb GAL3 fb and GAL1
fb and GAL1 fb GAL3
fb GAL3 fb were monostable for all 10,000 parameter sets, indicating that one of these autoregulatory loops is necessary for generating bistability across a broad region of parameter space.
fb were monostable for all 10,000 parameter sets, indicating that one of these autoregulatory loops is necessary for generating bistability across a broad region of parameter space.
Recently, a two-stage galactose induction model has been proposed whereby the Gal3p–Gal80p complex (C83) dominates initially and the Gal1p–Gal80 complex (C81) dominates at a later stage (18). To check the consequences of including this feature in our model, we scanned a wide range of parameters using the Latin hypercube sampling method (30) (SI Text, section S5) and identified sets of parameters that qualitatively matched all our data in addition to the dynamic ordering response of C83 and C81 (Fig. S7 B and C). This newly identified parameter set exhibited the same roles for the GAL1 and GAL3 feedback loops in enhancing DH across a broad region of parameter space, further illustrating the generality of our results (Fig. S7D).
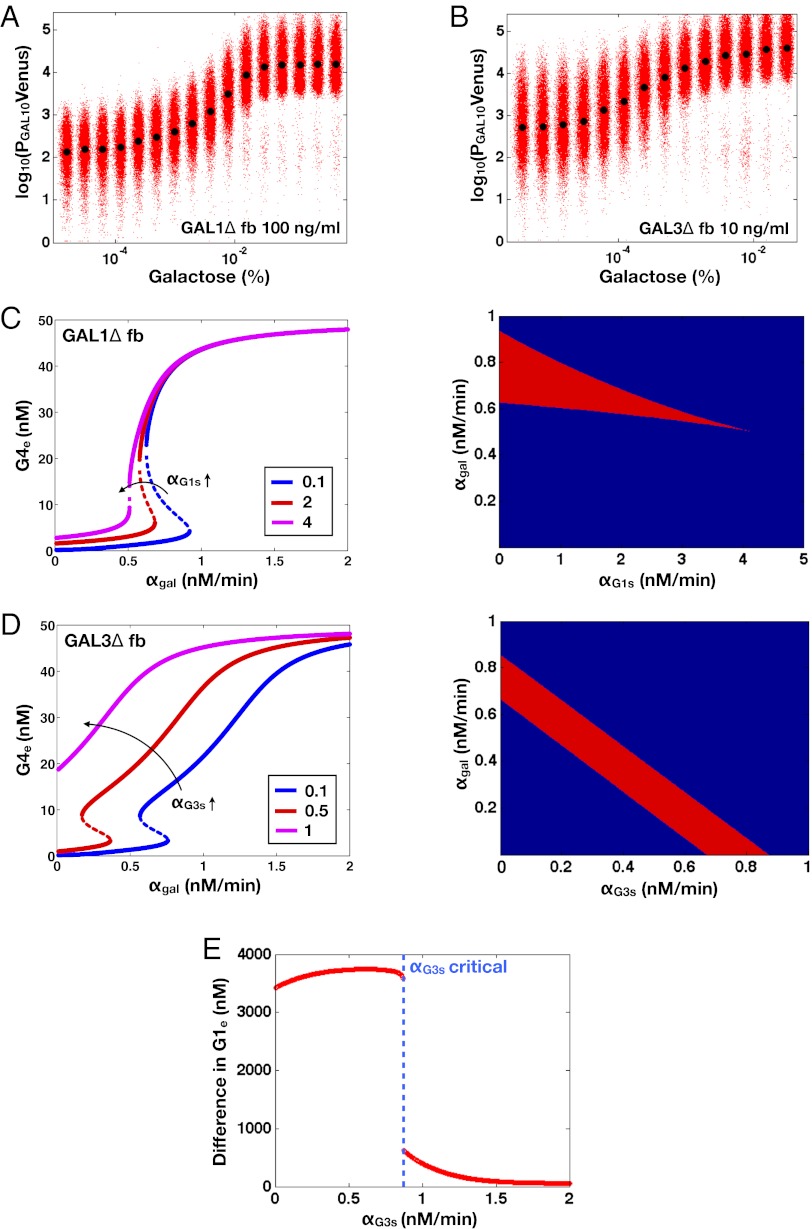
Constitutive Production of Gal1p and Gal3p Can Abolish Bimodality in the Absence of the Individual GAL1 and GAL3 Feedback Loops.
We next tested whether the model could predict and explain the disappearance of bimodality due to high unregulated levels of Gal1p and Gal3p in the absence of their individual feedback loops (Fig. 5 and Figs. S2 and S4). The individual GAL1 and GAL3 feedback loop deletion models predicted the loss of bistability as the rate of constitutive production, 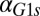 or
or 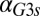 , was increased (Fig. 5 C and D). An increase in
, was increased (Fig. 5 C and D). An increase in 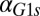 in the GAL1
in the GAL1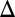 fb model caused the bistable region to contract and vanish at a critical value (
fb model caused the bistable region to contract and vanish at a critical value (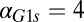 ) (Fig. 5C). In the GAL3
) (Fig. 5C). In the GAL3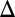 fb model, increasing
fb model, increasing 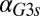 caused the bistable region to shift to smaller values of
caused the bistable region to shift to smaller values of 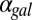 (Fig. 5D) and eventually move out the positive orthant to negative values of
(Fig. 5D) and eventually move out the positive orthant to negative values of 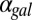 at a critical
at a critical 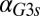 (
(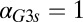 ), thus producing monostability for all physically realistic values of
), thus producing monostability for all physically realistic values of 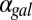 .
.
Fig. 5.
Model predicts that constitutive production of Gal1p or Gal3p above a threshold can abolish bistability in the absence of the individual GAL1 or GAL3 feedback loop (matching experimental data in SI Text, section S2 and Figs. S2 and S4). (A) Critical constitutive level of Gal1p in the absence of the GAL1 feedback loop produced a graded response. Flow cytometry measurements of PGAL10 Venus in a GAL1 feedback deletion strain (GAL1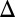 fb). In this strain, GAL1 was expressed from a TET promoter and induced with 100 ng/mL dox, corresponding to ∼20% of fully induced WT levels (Fig. S3A1). (B) Critical level of Gal3p in the absence of the GAL3 feedback loop produced a graded response. Flow cytometry measurements of the GAL3 feedback deletion strain (GAL3
fb). In this strain, GAL1 was expressed from a TET promoter and induced with 100 ng/mL dox, corresponding to ∼20% of fully induced WT levels (Fig. S3A1). (B) Critical level of Gal3p in the absence of the GAL3 feedback loop produced a graded response. Flow cytometry measurements of the GAL3 feedback deletion strain (GAL3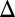 fb). GAL3 was expressed from a TET promoter and induced with 10 ng/mL dox, corresponding to ∼63% of fully induced WT levels (Fig. S3A3). (C) In the GAL1
fb). GAL3 was expressed from a TET promoter and induced with 10 ng/mL dox, corresponding to ∼63% of fully induced WT levels (Fig. S3A3). (C) In the GAL1 fb model, increasing the constitutive production rate of Gal1p (
fb model, increasing the constitutive production rate of Gal1p (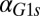 ) decreases the region of bistability and causes bistability to vanish at a critical value (
) decreases the region of bistability and causes bistability to vanish at a critical value (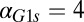 nM/⋅min). Regions of bistability (red) and monostability (blue) for different values of
nM/⋅min). Regions of bistability (red) and monostability (blue) for different values of 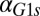 and
and 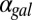 in GAL1
in GAL1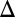 fb show that the bistability parameter region contracts and eventually vanishes with increasing
fb show that the bistability parameter region contracts and eventually vanishes with increasing 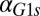 . (D) In the GAL3
. (D) In the GAL3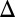 fb model, increasing the constitutive production rate of Gal3p (
fb model, increasing the constitutive production rate of Gal3p (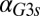 ) eliminates bistability by shifting the bistable region to smaller
) eliminates bistability by shifting the bistable region to smaller 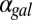 values. A critical threshold of
values. A critical threshold of 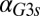 (
(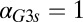 nM/⋅min) causes the bistable region to move out of the positive orthant, producing monostability for all physically realistic
nM/⋅min) causes the bistable region to move out of the positive orthant, producing monostability for all physically realistic 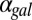 values. Regions of bistability (red) and monostability (blue) for different values of
values. Regions of bistability (red) and monostability (blue) for different values of 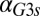 and
and 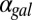 are shown. (E) GAL1 feedback nonlinearity disappears with increasing
are shown. (E) GAL1 feedback nonlinearity disappears with increasing 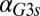 in the GAL3
in the GAL3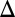 fb model. The maximum difference in Gal1p steady-state concentration (G1e) was computed across the full range of
fb model. The maximum difference in Gal1p steady-state concentration (G1e) was computed across the full range of 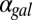 for a series of
for a series of 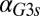 values and represents the activity of the GAL1 feedback loop. Above the critical
values and represents the activity of the GAL1 feedback loop. Above the critical 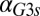 threshold (dashed blue line), G1e does not change in response to
threshold (dashed blue line), G1e does not change in response to 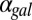 , indicating that the GAL1 autoregulatory loop is not active in this parameter regime.
, indicating that the GAL1 autoregulatory loop is not active in this parameter regime.
Because Gal1p and Gal3p played an important role in generating bistability, we suspected that the disappearance of bistable behavior for 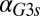 or
or 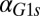 exceeding critical values could be the result of an indirect neutralization of the remaining loop. For example, it could be case that overexpression of Gal3p in a GAL3 feedback deletion had the effect of neutralizing the GAL1 feedback loop. The computational model afforded us the possibility of testing this hypothesis. For a given value of
exceeding critical values could be the result of an indirect neutralization of the remaining loop. For example, it could be case that overexpression of Gal3p in a GAL3 feedback deletion had the effect of neutralizing the GAL1 feedback loop. The computational model afforded us the possibility of testing this hypothesis. For a given value of 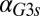 , we defined the GAL1 feedback activity as the maximum change in steady-state Gal1p concentration across the full range of galactose (
, we defined the GAL1 feedback activity as the maximum change in steady-state Gal1p concentration across the full range of galactose (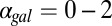 nM⋅min). As shown in Fig. 5E, the GAL1 feedback was highly active for a range of
nM⋅min). As shown in Fig. 5E, the GAL1 feedback was highly active for a range of 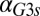 values but abruptly approached 0 at a critical threshold of
values but abruptly approached 0 at a critical threshold of 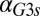 (dashed blue line). Therefore, increasing the constitutive production rate of Gal3p was indeed equivalent to removing the GAL1 feedback because a sufficiently large
(dashed blue line). Therefore, increasing the constitutive production rate of Gal3p was indeed equivalent to removing the GAL1 feedback because a sufficiently large 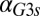 mapped the GAL1 feedback nonlinearity to a saturated (inactive) regime.
mapped the GAL1 feedback nonlinearity to a saturated (inactive) regime.
The insight generated by the model about the link between the constitutive production rates of Gal1p or Gal3p and the loss of bistability suggested that the graded response observed in GAL3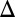 fb (Fig. 5B) should be the result of overexpressing the Gal3 protein. To test this possibility, we compared the GAL3 mRNA expressed from the TET promoter with that of WT induced with 0.005% and 0.05% galactose using qPCR. These data showed that the GAL3 mRNA level in GAL3
fb (Fig. 5B) should be the result of overexpressing the Gal3 protein. To test this possibility, we compared the GAL3 mRNA expressed from the TET promoter with that of WT induced with 0.005% and 0.05% galactose using qPCR. These data showed that the GAL3 mRNA level in GAL3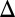 fb induced with 10 ng/mL dox was overexpressed by 43% relative to WT induced with 0.05% galactose, which was significantly higher than GAL3 mRNA levels for the bimodal range of WT and GAL3
fb induced with 10 ng/mL dox was overexpressed by 43% relative to WT induced with 0.05% galactose, which was significantly higher than GAL3 mRNA levels for the bimodal range of WT and GAL3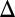 fb (Fig. S3A3). These results argue that to study the functional contribution of feedback loops to a phenotype, the strength of constitutive expression needs to be carefully tuned to recapitulate the physiological operating point(s) of the WT circuit.
fb (Fig. S3A3). These results argue that to study the functional contribution of feedback loops to a phenotype, the strength of constitutive expression needs to be carefully tuned to recapitulate the physiological operating point(s) of the WT circuit.
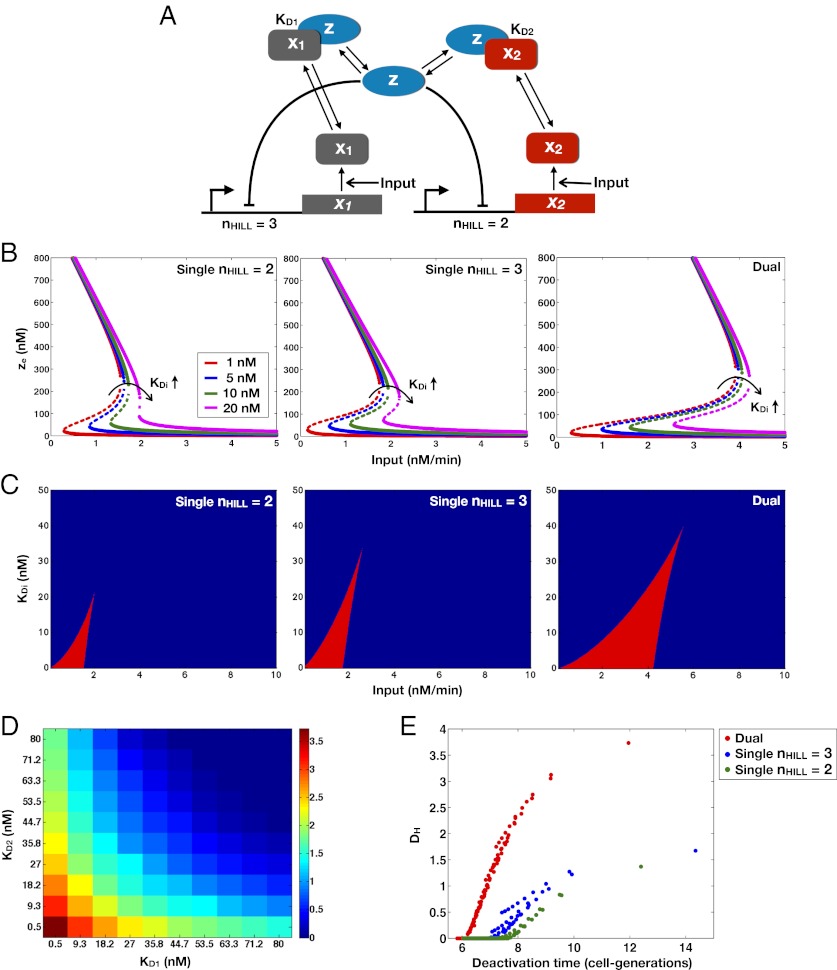
Properties of Positive Feedback Loops Established by Molecular Sequestration.
Sequestration binding affinity of an activator and repressor can tune the range of conditions for bistability.
To generalize our results further, we explored the principles by which the interactions of the positive feedback loops mediated by Gal1p and Gal3p generate bistability. Characterizing the set of essential molecular interactions that combine to generate bistability in the GAL system may be useful for analyzing other natural switch-like biological networks and for constructing robust and tunable bistable synthetic circuits. Gal1p and Gal3p competitively sequester a common protein, Gal80p. Competitive binding interactions and molecular sequestration can produce ultrasensitivity, which is a crucial building block for a bistable system (31–34). Therefore, we suspected that the competitive sequestration of Gal80p by Gal1p and Gal3p may constitute a critical feature of the system.
To probe the functionalities provided by positive feedback loops linked to molecular sequestration, we examined a simple model of a single positive feedback loop that is implemented by an activator x that can form an inactive complex with a transcriptional repressor z. In this circuit, z transcriptionally represses the production of x, and a positive feedback loop is thus established by inhibition of the transcriptional repressor using molecular sequestration (Fig. S8A). We first examined the parameter dependence of this system in the absence of transcriptional cooperativity and found that this circuit could exhibit bistability depending on the value of the binding affinity of the activator and repressor (Fig. S8B). Therefore, modifying this parameter is an alternative mechanism to induce bistability in the circuit without increasing the cooperativity.
Building on these results, we next investigated the roles of double positive feedback loops connected by molecular sequestration. We considered a three-state ODE model consisting of a transcriptional repressor z that directly regulates two activators, 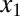 and
and 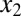 , with Hill coefficients of 3 and 2, respectively.
, with Hill coefficients of 3 and 2, respectively. 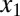 and
and 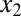 can form inactive heterodimers with z; hence,
can form inactive heterodimers with z; hence, 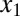 and
and 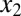 compete to bind z (Fig. 6A). In this model, the mechanisms of sequestration and positive feedback are triggered by an input (u) that represents a basal production rate of
compete to bind z (Fig. 6A). In this model, the mechanisms of sequestration and positive feedback are triggered by an input (u) that represents a basal production rate of 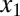 and
and 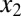 . The system of equations that model the interactions in Fig. 6A (a full description is provided in SI Text, section S7) is
. The system of equations that model the interactions in Fig. 6A (a full description is provided in SI Text, section S7) is
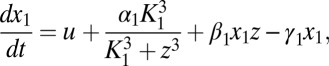 |
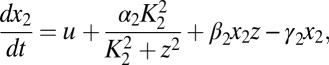 |
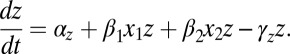 |
Fig. 6.
Molecular consequences of positive feedback loops established by molecular sequestration. Sequestration binding affinities (KD1 and KD2) can tune the parameter region for bistability, and the addition of a second positive feedback loop can reduce the deactivation response time and augment the range of conditions for bistability. (A) Circuit diagram for dual positive feedback loops mediated by the activators, 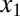 and
and 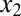 , coupled by molecular sequestration to a transcriptional repressor, z. Transcriptional feedback regulation of
, coupled by molecular sequestration to a transcriptional repressor, z. Transcriptional feedback regulation of 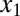 and
and 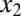 is modeled by Hill functions with Hill coefficients of 3 (nHill = 3) and 2 (nHill = 2), respectively. The single positive feedback loop models were obtained by removing the appropriate repression arrow from z to the promoter of
is modeled by Hill functions with Hill coefficients of 3 (nHill = 3) and 2 (nHill = 2), respectively. The single positive feedback loop models were obtained by removing the appropriate repression arrow from z to the promoter of 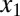 or
or 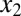 or, equivalently, by replacing the Hill functions with a constant production rate,
or, equivalently, by replacing the Hill functions with a constant production rate, 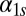 or
or 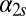 . (B) Bifurcation diagrams relating the input to the steady-state concentration of z (
. (B) Bifurcation diagrams relating the input to the steady-state concentration of z (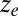 ) reveal that symmetrically (KD1 = KD2) weakening the binding affinities shrinks the region of bistability. (C) Parameter regions of bistability (red) and monostability (blue) for different values of the input and symmetrically varying KD1, KD2 in the single and double feedback loop models. (D) Range of bistability (DH) for a range of KD1 and KD2 values in the double feedback loop system. (E) Relationship between DH and the deactivation response time measured in cell-generations (SI Text, section S7). For a constant nonzero DH, the dual feedback loop circuit exhibited a faster deactivation response time compared with the either of the single positive feedback loop models.
) reveal that symmetrically (KD1 = KD2) weakening the binding affinities shrinks the region of bistability. (C) Parameter regions of bistability (red) and monostability (blue) for different values of the input and symmetrically varying KD1, KD2 in the single and double feedback loop models. (D) Range of bistability (DH) for a range of KD1 and KD2 values in the double feedback loop system. (E) Relationship between DH and the deactivation response time measured in cell-generations (SI Text, section S7). For a constant nonzero DH, the dual feedback loop circuit exhibited a faster deactivation response time compared with the either of the single positive feedback loop models.
In the double positive feedback case, bistability could be induced in this system by adjusting the binding affinities KD1 and KD2 (which modify 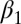 and
and 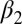 ) as bifurcation parameters without changing the cooperativity of the transcriptional regulation (Fig. 6 B and C). Setting KD2 = KD2, we found that the range of the input that produced bistability was inversely related to the magnitude of the binding affinities (Fig. 6B). In addition, the range of the input that generated bistability was increased in a system with two positive feedback loops compared with a single positive feedback loop for the set of symmetrically varying KD1 and KD2 values (Fig. 6C).
) as bifurcation parameters without changing the cooperativity of the transcriptional regulation (Fig. 6 B and C). Setting KD2 = KD2, we found that the range of the input that produced bistability was inversely related to the magnitude of the binding affinities (Fig. 6B). In addition, the range of the input that generated bistability was increased in a system with two positive feedback loops compared with a single positive feedback loop for the set of symmetrically varying KD1 and KD2 values (Fig. 6C).
To explore asymmetry in the binding affinities, DH was computed for a series of linearly spaced KD1 and KD2 values within the range of 0.5–80 nM (Fig. 6D). The largest range of bistability was obtained for the strongest binding affinities, and DH decreased monotonically with increasing KD1 or KD2. In addition, fixing one KD and varying the other (Fig. 6D, left column and bottom row) did not decrease DH as significantly as symmetrically changing the two binding affinities together (Fig. 6D, diagonal). These results suggest that asymmetry in the binding affinity strengths, whereby one activator interacts strongly and the other activator binds weakly to the same repressor, can preserve bistability over a wide range of values for the weaker KD, thus reducing the system’s sensitivity to variations in this parameter.
Double-positive feedback loops can produce a larger range of bistability and a faster dynamic response than a single feedback loop.
We suspected that modulating the binding affinities to induce bistability may concurrently alter other circuit functions, such as the dynamic response time to a change in the input. To explore these relationships, we measured the response times of the circuits to switch from the low → high state (activation response time) and from the high → low state (deactivation response time). To do so, a step function increase or decrease in the input was applied and the delay for the circuit to adapt to this transition was quantified (SI Text, section S7). The time required for an output species that was transcriptionally repressed by z (representing a fluorescent reporter) to increase or decay to half of its maximum value was quantified in cell-generations.
In the double feedback loop system, the activation response time decreased with the strength of the binding affinities, whereas the deactivation response time had the opposing relationship and increased with the strength of the binding affinities (Fig. S8 C and D). For a constant nonzero DH, the dual feedback loop system could switch faster to the high state than either of the single feedback loop models (Fig. S8E). Because both the DH and the deactivation response time are inversely related to KD1 and KD2, a tradeoff exists between increasing the range of conditions for bistability and decreasing the deactivation response time (Fig. 6E). A comparison of DH and the response times for the single and double feedback loop systems revealed that dual feedback loops can produce a larger DH over a narrower range of deactivation response times compared with the single feedback loop systems with Hill coefficients of 2 or 3. Taken together, the dual feedback loop system can produce a larger range of bistability and exhibit a faster response time to abrupt changes in the environment compared with a single feedback loop system.
Discussion
A bimodal distribution of gene expression across a population of isogenic cells, which generates two distinct cellular states, can produce significant cell-to-cell heterogeneity. This bimodality can also lead to a switch-like response that filters out noise below a threshold and produces a large fold change in the system’s output if the input crosses this threshold (35). In this work, we used the GAL gene-regulatory circuit as a model system to dissect and analyze the origins of bimodality in a natural biological network. We demonstrated that bistability underlies this bimodality and used a combination of experiments and computational modeling to identify two key features that produce bistability: (i) a threshold established by two positive feedback loops mediated by Gal1p and Gal3p and (ii) an ultrasensitive stage produced by competitive molecular sequestration of Gal80p by Gal1p and Gal3p.
To unravel the molecular interactions critical for bistability in the GAL system, we performed a comprehensive exploration of multiple feedback loops. Our investigations revealed that the GAL bimodal response is remarkably robust to feedback loop perturbations. Indeed, individual elimination of the GAL1, GAL2, GAL3, and GAL80 feedback loops was insufficient to abolish bimodality. Furthermore, bimodality persisted for multiple deletions of these loops and, surprisingly, only disappeared in a double deletion of GAL1 and the GAL3 feedback loop. We therefore identified Gal1p and Gal3p as central mediators of two synergistic positive feedback loops that generate bistability in the GAL gene-regulatory network. Multiple positive feedback loops can facilitate the bistable behavior of a circuit by expanding the range of conditions for bistability, which improves the robustness of bistability to parameter variations (35).
A previous study attributed bimodality in the GAL pathway to the activity of the GAL3 feedback loop (28). Here, we demonstrate that cells with a deleted GAL3 feedback loop are still capable of bimodality in their response to galactose for low levels of constitutive Gal3p expression. However, we found experimentally that bimodality vanishes when Gal3p is expressed at high and unregulated levels. Our computational model explains this behavior by the loss of remaining GAL1 feedback due to constitutive expression of Gal3p beyond a threshold. Interestingly, in this regime, the genetic wiring of the GAL1 feedback loop is present but the feedback loop was rendered inactive indirectly by constitutive Gal3p expression above a threshold.
These results underscore the challenges inherent in the interpretation of feedback deletion experiments in which the specific range of constitutive expression of the deleted link might become an important determinant of the system’s properties and can mask the true functional roles of the feedback pathway. These findings also argue that the complete interpretation of feedback KOs requires thorough investigation of active mechanisms and nonlinearities that are operational in a given circuit, beyond static snapshots of the circuit’s topology as determined by genetics (36).
Stoichiometric binding interactions, for example, molecular sequestration of a repressor by an activator or inhibition of an enzyme by a small molecule, can produce ultrasensitivity in biological circuits (31–34, 37). Our computational model indicates that competitive molecular sequestration of Gal80p by Gal1p and Gal3p produces an ultrasensitive change in the concentration of free Gal4p in response to small variations in extracellular galactose and that this ultrasensitivity does not rely on cooperative binding of Gal4p to GAL promoters and/or oligomerization. These results suggest that the stoichiometric inhibition of Gal80p by Gal1p and Gal3p is a crucial source of ultrasensitivity in the GAL network that sets the stage for a robust bistable response to galactose because ultrasensitivity is required for bistability (34, 38).
Beyond the GAL system, we believe these results to be applicable to many bistable systems. We used a simple computational model to explore the general mechanisms by which positive feedback loops linked to competitive sequestration can produce ultrasensitivity and bistability. Using this model, we found that the positive feedback and sequestration topology can be used to build a bistable system in the absence of transcriptional cooperativity by adjusting the binding affinity parameter between the activator and inhibitor. If bistability confers a fitness advantage, this parameter could be adjusted through mutation of the protein–protein binding interface and may be more evolvable than modifying the cooperativity of transcriptional regulation through oligomerization or multiple transcription factor binding sites. In addition, we identified a tradeoff between the range of bistability and the deactivation response time of this circuit. In response to an abrupt change in the stimulus, we found that a system with double positive feedback loops can switch faster to the low state compared with the single feedback loop system for a fixed range of bistability, highlighting an additional property of multiple positive feedback loops.
Positive feedback loops established by molecular sequestration may represent a general class of systems for implementing robust switch-like cellular responses. For example, the conserved regulatory network that controls cell differentiation in Drosophila consists of molecular mechanisms similar to those of the GAL circuit, including molecular sequestration and multiple feedback loops that implement a switch-like developmental program (39, 40). Activation of this cell-differentiation circuit relies on molecular titration of a repressor, Extramacrochaetae by the activators Daughterless (Da) and Achaete-Scute complex (As-c). Da and As-c transcriptionally autoregulate, and thus form two positive feedback loops (41).
S. cerevisiae cells growing on galactose could benefit from bistability on a single-cell and population level. A bistable circuit can produce a decisive response to a slow variation in the stimulus (37). This decoupling ensures that the abrupt change in the system’s output is not dependent on the rate of change of the stimulus and is instead an intrinsic property of the circuit’s dynamic system. In addition, bimodality due to underlying bistability can produce stable lineages of cells with a memory of previous environmental conditions. As a consequence of hysteresis, cells with a history of the stimulus will respond differently to a second exposure due to a shift in the threshold of deactivation. This epigenetic memory of previous environments can fine-tune the switching threshold and provide an additional source of cell-to-cell heterogeneity in the perception of the stimulus.
There are also several potential advantages of bimodality at a population level. For example, significant single-cell phenotypic variation, generated by bimodality, can serve as a bet-hedging strategy for microbial populations in uncertain environments (42, 43). Because S. cerevisiae grows poorly even in the presence of high concentrations of galactose and risks accumulation of the toxic intermediate galactose-1-phosphate, the bimodal response may serve as a population strategy to weigh the energetic costs and benefits of activating the GAL regulon (26). Another intriguing possibility is whether bimodality establishes a division of labor in which the high population metabolizes galactose and produces a byproduct that is used by the low population (44).
Feedback loops are ubiquitous in biological systems, and dissecting their precise quantitative roles is a crucial step for unraveling the organizational principles of cellular decision making. Although a single transcriptional positive feedback loop can generate bistability with cooperativity and precise parameter tuning, this study suggests that a single noncooperative positive feedback loop with sequestration can generate bistability and that this bistability parameter region can be significantly augmented by the addition of a second positive feedback loop. These insights will be essential for pinpointing the operational principles of switch-like cellular responses, in addition to suggesting rules for designing robust synthetic circuits.
Materials and Methods
Strains.
All plasmids used in this study were derived from a set of yeast single integration vectors constructed in the laboratory of Wendell Lim (University of California, San Francisco). These vectors contain markers and targeting sequences for the LEU2, HIS3, TRP1, and URA3 loci. These vectors were linearized for transformation by digestion with PmeI and transformed using standard techniques. Promoters were cloned between the PspOMI and XhoI restriction sites, and coding sequences were inserted between the XhoI and BamHI sites. These plasmids contained an ADH1 terminator downstream of the BamHI site. All strains were haploid, with the exception of MA0182 and WT diploid (28). In the haploid backgrounds, rtTA-M2 was expressed from a medium-strength variant of the TEF promoter, TEFm4 (27, 45). Gene deletions were verified using PCR. A functional test for constitutive PGAL10 Venus expression in the absence of galactose was also used to verify successful deletion of GAL80. Strains are listed in Table S2. The sequences for the GAL3, GAL10, and GAL80 promoters were 1,017, 646, and 283 bp upstream of the start codons, respectively. The TET promoter consisted of a region of the CYC1 promoter and two TetR operator binding sites (46). The synthetic single GAL4 binding site promoter, PCYC1-G4BS, consisted of a binding site from the GAL7 promoter (CGGACAACTGTTGACCG) upstream of the CYC1 core promoter.
Growth Conditions and Flow Cytometry.
Cells were grown in appropriate dropout media supplemented with 2% filter-sterilized raffinose at 30 °C. In 2% raffinose media supplemented with no or small amounts of galactose, cell divisions occurred approximately every 3 h during the exponential growth phase. Steady-state measurements were performed after a 20-h induction period. Cells were induced for 30 h for hysteresis experiments (a discussion is provided in SI Text, section S1). OD600 (cell density) was maintained below 0.1 to prevent significant changes in the galactose concentration for the duration of the experiment. Flow cytometry measurements were made using a MACSQuant VYB (Miltenyi Biotec) or LSRII analyzer (BD Biosciences). For both instruments, a blue (488 nm) laser was used to excite YFP. Emission was detected on the MACSQuant or LSRII using 525/50-nm and 530/30-nm filters, respectively. At least 10,000 cells were collected for each measurement.
Analysis of Flow Cytometry Distributions.
Bimodality classification.
Flow cytometry distributions were analyzed using a GMM algorithm (MATLAB; MathWorks) (47). The GMM algorithm assumes that the data are a mixture distribution, where the probability density function is a linear combination with coefficients that sum to 1 (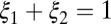 ):
):
The parameters for the GMM algorithm include the means, 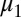 and
and 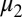 ; SDs,
; SDs, 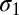 and
and 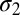 ; and mode weights,
; and mode weights, 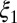 and
and 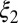 . A distribution was categorized as bimodal if the following conditions were true:
. A distribution was categorized as bimodal if the following conditions were true:
Activation responses.
Activation responses for bimodal transitions were analyzed using the fraction of high expressing cells (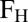 ). The threshold was set to the minimum separating the two local maxima.
). The threshold was set to the minimum separating the two local maxima. 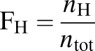 , where
, where 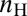 and
and 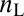 are the number of high and low expressing cells, respectively (
are the number of high and low expressing cells, respectively (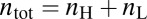 ). The activation level for a graded response was quantified using the normalized mean fluorescence level (MY):
). The activation level for a graded response was quantified using the normalized mean fluorescence level (MY):
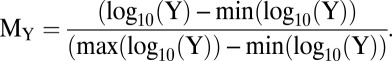 |
Real-Time qPCR.
Total RNA was isolated using a YeaStar RNA Kit (Zymo Research Corp.). Oligonucleotides for real-time qPCR were designed using Integrated DNA Technologies PrimeTime qPCR assay. Five hundred nanograms of total RNA was reverse-transcribed using the iScript cDNA synthesis kit (Bio-Rad). The reaction mix contained 5 μL of SsoFast Probes SuperMix (Bio-Rad), 0.5 μL of primer probe corresponding to 250 nM primers and 125 nM probe (20× stock), and 0.5 μL of cDNA. Three technical replicates for each sample were analyzed using the CFX96 real-time PCR machine (Bio-Rad). Relative expression levels were determined by the 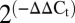 method (48). Each sample was normalized by the cycle threshold geometric mean for the reference genes ACT1 and UBC6 (49).
method (48). Each sample was normalized by the cycle threshold geometric mean for the reference genes ACT1 and UBC6 (49).
Computational Modeling.
Code for mathematical modeling was written in MATLAB and Mathematica (Wolfram Research).
We identified turning, fold, and saddle-node bifurcation points that can create bistability by computing the values of 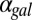 that caused a real eigenvalue of the Jacobian matrix to change from negative to positive, producing a singular Jacobian matrix at the point where the real part of the eigenvalue equaled 0. The bifurcation parameter (
that caused a real eigenvalue of the Jacobian matrix to change from negative to positive, producing a singular Jacobian matrix at the point where the real part of the eigenvalue equaled 0. The bifurcation parameter (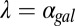 ) appeared linearly in the polynomial equations for the equilibrium concentrations of Gal4p. To satisfy the conditions of a singular Jacobian matrix and equilibrium, there were two equations in two unknowns using the Gal4p polynomial (
) appeared linearly in the polynomial equations for the equilibrium concentrations of Gal4p. To satisfy the conditions of a singular Jacobian matrix and equilibrium, there were two equations in two unknowns using the Gal4p polynomial (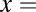 Gal4p):
Gal4p):
We solved the system of equations using the Sylvester resultant (50). This resultant provides conditions for the coefficients of two polynomials of a single variable to have a root in common. Sylvester matrices A and B contained the coefficients of f, 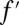 and g,
and g, 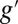 , respectively. The dimensions of A and B were
, respectively. The dimensions of A and B were 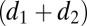 ×
× 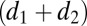 , where d1 and d2 are the degrees of highest polynomial of either f or g and, correspondingly,
, where d1 and d2 are the degrees of highest polynomial of either f or g and, correspondingly, 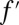 or
or 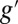 , respectively. The bifurcation points were computed by solving the generalized eigenvalue problem
, respectively. The bifurcation points were computed by solving the generalized eigenvalue problem 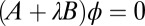 .
.
Supplementary Material
Acknowledgments
We thank Louis Romero for mathematical modeling insights and Rochelle Diamond and Josh Verceles for assistance with flow cytometry. We are grateful to the laboratory of Christina Smolke and to Murat Acar for providing yeast strains used in this study. This research project was supported by the Institute for Collaborative Biotechnologies through Grant W911NF-09-0001 from the US Army Research Office.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
See Author Summary on page 19527 (volume 109, number 48).
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1211902109/-/DCSupplemental.
References
- 1.Astrom K, Murray R. Feedback Systems: An Introduction for Scientists and Engineers. Princeton: Princeton Univ Press; 2008. [Google Scholar]
- 2.Rosenfeld N, Elowitz MB, Alon U. Negative autoregulation speeds the response times of transcription networks. J Mol Biol. 2002;323(5):785–793. doi: 10.1016/s0022-2836(02)00994-4. [DOI] [PubMed] [Google Scholar]
- 3.Becskei A, Serrano L. Engineering stability in gene networks by autoregulation. Nature. 2000;405(6786):590–593. doi: 10.1038/35014651. [DOI] [PubMed] [Google Scholar]
- 4.Isaacs FJ, Hasty J, Cantor CR, Collins JJ. Prediction and measurement of an autoregulatory genetic module. Proc Natl Acad Sci USA. 2003;100(13):7714–7719. doi: 10.1073/pnas.1332628100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Brandman O, Meyer T. Feedback loops shape cellular signals in space and time. Science. 2008;322(5900):390–395. doi: 10.1126/science.1160617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Biggar SR, Crabtree GR. Cell signaling can direct either binary or graded transcriptional responses. EMBO J. 2001;20(12):3167–3176. doi: 10.1093/emboj/20.12.3167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Torchia TE, Hamilton RW, Cano CL, Hopper JE. Disruption of regulatory gene GAL80 in Saccharomyces cerevisiae: Effects on carbon-controlled regulation of the galactose/melibiose pathway genes. Mol Cell Biol. 1984;4(8):1521–1527. doi: 10.1128/mcb.4.8.1521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Tschopp JF, Emr SD, Field C, Schekman R. GAL2 codes for a membrane-bound subunit of the galactose permease in Saccharomyces cerevisiae. J Bacteriol. 1986;166(1):313–318. doi: 10.1128/jb.166.1.313-318.1986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Torchia TE, Hopper JE. Genetic and molecular analysis of the GAL3 gene in the expression of the galactose/melibiose regulon of Saccharomyces cerevisiae. Genetics. 1986;113(2):229–246. doi: 10.1093/genetics/113.2.229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bhat PJ, Hopper JE. Overproduction of the GAL1 or GAL3 protein causes galactose-independent activation of the GAL4 protein: Evidence for a new model of induction for the yeast GAL/MEL regulon. Mol Cell Biol. 1992;12(6):2701–2707. doi: 10.1128/mcb.12.6.2701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bajwa W, Torchia TE, Hopper JE. Yeast regulatory gene GAL3: Carbon regulation; UASGal elements in common with GAL1, GAL2, GAL7, GAL10, GAL80, and MEL1; encoded protein strikingly similar to yeast and Escherichia coli galactokinases. Mol Cell Biol. 1988;8(8):3439–3447. doi: 10.1128/mcb.8.8.3439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hawkins KM, Smolke CD. The regulatory roles of the galactose permease and kinase in the induction response of the GAL network in Saccharomyces cerevisiae. J Biol Chem. 2006;281(19):13485–13492. doi: 10.1074/jbc.M512317200. [DOI] [PubMed] [Google Scholar]
- 13.Sellick CA, Jowitt TA, Reece RJ. The effect of ligand binding on the galactokinase activity of yeast Gal1p and its ability to activate transcription. J Biol Chem. 2009;284(1):229–236. doi: 10.1074/jbc.M807878200. [DOI] [PubMed] [Google Scholar]
- 14.Thoden JB, Sellick CA, Timson DJ, Reece RJ, Holden HM. Molecular structure of Saccharomyces cerevisiae Gal1p, a bifunctional galactokinase and transcriptional inducer. J Biol Chem. 2005;280(44):36905–36911. doi: 10.1074/jbc.M508446200. [DOI] [PubMed] [Google Scholar]
- 15.Hittinger CT, Carroll SB. Gene duplication and the adaptive evolution of a classic genetic switch. Nature. 2007;449(7163):677–681. doi: 10.1038/nature06151. [DOI] [PubMed] [Google Scholar]
- 16.Johnston M. A model fungal gene regulatory mechanism: The GAL genes of Saccharomyces cerevisiae. Microbiol Rev. 1987;51(4):458–476. doi: 10.1128/mr.51.4.458-476.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zacharioudakis I, Gligoris T, Tzamarias D. A yeast catabolic enzyme controls transcriptional memory. Curr Biol. 2007;17(23):2041–2046. doi: 10.1016/j.cub.2007.10.044. [DOI] [PubMed] [Google Scholar]
- 18.Abramczyk D, Holden S, Page CJ, Reece RJ. Interplay of a ligand sensor and an enzyme in controlling expression of the Saccharomyces cerevisiae GAL genes. Eukaryot Cell. 2012;11(3):334–342. doi: 10.1128/EC.05294-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Artyomov MN, Das J, Kardar M, Chakraborty AK. Purely stochastic binary decisions in cell signaling models without underlying deterministic bistabilities. Proc Natl Acad Sci USA. 2007;104(48):18958–18963. doi: 10.1073/pnas.0706110104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Samoilov M, Plyasunov S, Arkin AP. Stochastic amplification and signaling in enzymatic futile cycles through noise-induced bistability with oscillations. Proc Natl Acad Sci USA. 2005;102(7):2310–2315. doi: 10.1073/pnas.0406841102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kepler TB, Elston TC. Stochasticity in transcriptional regulation: Origins, consequences, and mathematical representations. Biophys J. 2001;81(6):3116–3136. doi: 10.1016/S0006-3495(01)75949-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lestas I, Paulsson J, Ross N, Vinnicombe G. Noise in gene regulatory networks. IEEE Trans Automat Contr. 2008;53(Special Issue):189–200. [Google Scholar]
- 23.Guidi G, Goldbeter A. Bistability without hysteresis in chemical reaction systems: A theoretical analysis of irreversible transitions between multiple steady states. J Phys Chem. 1997;101(49):9367–9376. [Google Scholar]
- 24.Nagai T, et al. A variant of yellow fluorescent protein with fast and efficient maturation for cell-biological applications. Nat Biotechnol. 2002;20(1):87–90. doi: 10.1038/nbt0102-87. [DOI] [PubMed] [Google Scholar]
- 25.Douglas HC, Hawthorne DC. Enzymatic expression and genetic linkage of genes controlling galactose utilization in Saccharomyces. Genetics. 1964;49:837–844. doi: 10.1093/genetics/49.5.837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Riley MI, Dickson RC. Genetic and biochemical characterization of the galactose gene cluster in Kluyveromyces lactis. J Bacteriol. 1984;158(2):705–712. doi: 10.1128/jb.158.2.705-712.1984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Urlinger S, et al. Exploring the sequence space for tetracycline-dependent transcriptional activators: Novel mutations yield expanded range and sensitivity. Proc Natl Acad Sci USA. 2000;97(14):7963–7968. doi: 10.1073/pnas.130192197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Acar M, Becskei A, van Oudenaarden A. Enhancement of cellular memory by reducing stochastic transitions. Nature. 2005;435(7039):228–232. doi: 10.1038/nature03524. [DOI] [PubMed] [Google Scholar]
- 29.Angeli D, Ferrell JE, Jr, Sontag ED. Detection of multistability, bifurcations, and hysteresis in a large class of biological positive-feedback systems. Proc Natl Acad Sci USA. 2004;101(7):1822–1827. doi: 10.1073/pnas.0308265100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Iman R, Davenport J, Zeigler D. Latin Hypercube Sampling Program Users Guide. Albuquerque, NM: Sandia Labs; 1980. [Google Scholar]
- 31.Ferrell JE., Jr Tripping the switch fantastic: How a protein kinase cascade can convert graded inputs into switch-like outputs. Trends Biochem Sci. 1996;21(12):460–466. doi: 10.1016/s0968-0004(96)20026-x. [DOI] [PubMed] [Google Scholar]
- 32.Buchler NE, Louis M. Molecular titration and ultrasensitivity in regulatory networks. J Mol Biol. 2008;384(5):1106–1119. doi: 10.1016/j.jmb.2008.09.079. [DOI] [PubMed] [Google Scholar]
- 33.Buchler NE, Cross FR. Protein sequestration generates a flexible ultrasensitive response in a genetic network. Mol Syst Biol. 2009;5:272. doi: 10.1038/msb.2009.30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kim SY, Ferrell JE., Jr Substrate competition as a source of ultrasensitivity in the inactivation of Wee1. Cell. 2007;128(6):1133–1145. doi: 10.1016/j.cell.2007.01.039. [DOI] [PubMed] [Google Scholar]
- 35.Ferrell JE., Jr Feedback regulation of opposing enzymes generates robust, all-or-none bistable responses. Curr Biol. 2008;18(6):R244–R245. doi: 10.1016/j.cub.2008.02.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Dunlop MJ, Cox RS, 3rd, Levine JH, Murray RM, Elowitz MB. Regulatory activity revealed by dynamic correlations in gene expression noise. Nat Genet. 2008;40(12):1493–1498. doi: 10.1038/ng.281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Thron CD. A model for a bistable biochemical trigger of mitosis. Biophys Chem. 1996;57(2-3):239–251. doi: 10.1016/0301-4622(95)00075-5. [DOI] [PubMed] [Google Scholar]
- 38.Ferrell JE., Jr Self-perpetuating states in signal transduction: Positive feedback, double-negative feedback and bistability. Curr Opin Cell Biol. 2002;14(2):140–148. doi: 10.1016/s0955-0674(02)00314-9. [DOI] [PubMed] [Google Scholar]
- 39.Cabrera CV, Alonso MC, Huikeshoven H. Regulation of scute function by extramacrochaete in vitro and in vivo. Development. 1994;120(12):3595–3603. doi: 10.1242/dev.120.12.3595. [DOI] [PubMed] [Google Scholar]
- 40.Bhattacharya A, Baker NE. A network of broadly expressed HLH genes regulates tissue-specific cell fates. Cell. 2011;147(4):881–892. doi: 10.1016/j.cell.2011.08.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Van Doren M, Ellis HM, Posakony JW. The Drosophila extramacrochaetae protein antagonizes sequence-specific DNA binding by daughterless/achaete-scute protein complexes. Development. 1991;113(1):245–255. doi: 10.1242/dev.113.1.245. [DOI] [PubMed] [Google Scholar]
- 42.Veening JW, et al. Bet-hedging and epigenetic inheritance in bacterial cell development. Proc Natl Acad Sci USA. 2008;105(11):4393–4398. doi: 10.1073/pnas.0700463105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Veening JW, Smits WK, Kuipers OP. Bistability, epigenetics, and bet-hedging in bacteria. Annu Rev Microbiol. 2008;62:193–210. doi: 10.1146/annurev.micro.62.081307.163002. [DOI] [PubMed] [Google Scholar]
- 44.Pfeiffer T, Bonhoeffer S. Evolution of cross-feeding in microbial populations. Am Nat. 2004;163(6):E126–E135. doi: 10.1086/383593. [DOI] [PubMed] [Google Scholar]
- 45.Nevoigt E, et al. Engineering of promoter replacement cassettes for fine-tuning of gene expression in Saccharomyces cerevisiae. Appl Environ Microbiol. 2006;72(8):5266–5273. doi: 10.1128/AEM.00530-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Lutz R, Bujard H. Independent and tight regulation of transcriptional units in Escherichia coli via the LacR/O, the TetR/O and AraC/I1-I2 regulatory elements. Nucleic Acids Res. 1997;25(6):1203–1210. doi: 10.1093/nar/25.6.1203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Bishop C. Pattern Recognition and Machine Learning. New York: Springer; 2006. [Google Scholar]
- 48.Livak KJ, Schmittgen TD. Analysis of relative gene expression data using real-time quantitative PCR and the 2(-Delta Delta C(T)) Method. Methods. 2001;25(4):402–408. doi: 10.1006/meth.2001.1262. [DOI] [PubMed] [Google Scholar]
- 49.Teste MA, Duquenne M, François JM, Parrou JL. Validation of reference genes for quantitative expression analysis by real-time RT-PCR in Saccharomyces cerevisiae. BMC Mol Biol. 2009;10:99. doi: 10.1186/1471-2199-10-99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Dickenstein A, Emiris I. Solving Polynomial Equations: Foundations, Algorithms, and Applications (Algorithms and Computation in Mathematics) Berlin: Springer; 2005. [Google Scholar]
- 51.Timson DJ, Ross HC, Reece RJ. Gal3p and Gal1p interact with the transcriptional repressor Gal80p to form a complex of 1:1 stoichiometry. Biochem J. 2002;363(Pt 3):515–520. doi: 10.1042/0264-6021:3630515. [DOI] [PMC free article] [PubMed] [Google Scholar]