Molecular response in one-photon absorption via natural thermal light vs. pulsed laser excitation

Abstract

Photoinduced biological processes occur via one-photon absorption in natural light, which is weak, continuous wave, and incoherent, but are often studied in the laboratory using pulsed coherent light. Here, we compare the response of a molecule to these two very different sources within a quantized radiation field picture. The latter is shown to induce coherent time evolution in the molecule, whereas the former does not. As a result, the coherent time dependence observed in the laboratory experiments will not be relevant to the natural biological process. Emphasis is placed on resolving confusions regarding this issue that are shown to arise from aspects of quantum measurement and from a lack of appreciation of the proper description of the absorbed photon.

The nature of the molecular response to weak electromagnetic fields, where the probability of absorbing a photon is small, is a subject of considerable importance in light-induced biological processes. Examples include light-harvesting complexes (1–3) and vision (4–8), both of which operate in the domain of weak photon flux.

Recent experimental studies have generated considerable excitement (9–11) due to the observation of long-lived coherent [electronic and vibrational (12)] quantum time evolution subsequent to pulsed laser excitation of various biomolecules (13–19). Similar enthusiasm (20) has been generated by the coherent vibrational dynamics observed in retinal isomerization induced by pulsed laser light (4, 8). These references, as well as many others, either explicitly or implicitly assume that the observed coherent time evolution is of considerable biological significance.

Of particular relevance, then, is whether the observed coherent time evolution does, indeed, play a biological role. Is the molecular response in laboratory laser experiments that use pulsed coherent laser light (6, 13, 15, 16) relevant when the system is irradiated with natural light, i.e., radiation arising from a thermal source that is essentially CW and highly incoherent (7, 21, 22)? This issue (albeit not biologically motivated) was treated some time ago using a semiclassical approach to the light–matter interaction within first-order perturbation theory (21), leading to the conclusion that the responses are very different: Isolated molecules subject to pulsed coherent laser light display subsequent coherent time evolution, whereas those subject to incoherent light from a thermal CW source do not. In addition, that study showed that pulsed incoherent light, which by definition is partially coherent, induces time evolution on the time scale of the pulse, i.e., the molecule responds to the time envelope of the light pulse. However, for sunlight, for example, the time scale of the envelope is hours, whereas a stationary nonevolving state is reached almost immediately.

These results have profound implications for biological processes induced by weak fields (photosynthesis, vision), where the probability of single-photon absorption is small due to the low photon flux. They have, however, been largely ignored, and have recently been confused by arguments based on a qualitative picture of photons and of photon–molecule interactions.

For example, a current qualitative description (23) suggests that the absorption of a single photon triggers the same coherent molecular response, regardless of the character of the light source. There the view is that a single photon, incident on a molecule, whether arising from a pulsed coherent laser source or from a natural incoherent CW blackbody source (such as the sun), “kicks” the molecule and undergoes coherent time evolution. Further, there are related concerns within the community associated with times of arrival of the photons, the role of different bases that can be used to describe the incident light, etc. Clearly, clarifying these issues is necessary to understand coherent quantum processes in biology, and benefits from a proper quantized picture of the photon and its interaction with molecules used in this paper.

This paper addresses these issues in two parts. In the first part we formulate the problem of one-photon absorption using quantized radiation fields (extensive introductions to the approach used below in One-Photon Absorption are provided in refs. 24–26). This quantized radiation field approach provides a focus on the role of the photon, explicitly displays issues related to light–matter entanglement, permits consideration of an expanded collection of photon sources, and allows us to obtain results without requiring details of light–molecule time evolution. This treatment clearly shows that one-photon absorption from a pulsed coherent source induces coherent molecular dynamics whereas one-photon absorption from a natural incoherent CW thermal source does not. In the second part, we use these results to provide qualitative insight into the nature of the photon and its role in comparing pulsed coherent laser excitation to excitation with natural light. Specifically, we emphasize that the description of the photon necessarily carries with it information about the source of the radiation, and that problems that have arisen in qualitatively understanding this process and its role in biology result from (i) a simplified view of the particulate nature of the incident light and of light–matter interactions, and (ii) an incomplete understanding of issues in quantum measurement theory.

Three initial clarifying remarks are in order:

• i) The literature, in discussing the role of “quantum coherence” in biological processes, uses the term in two different ways. The first, relevant here (4, 5, 8, 13–16), refers to coherent time evolution of a system that is, by definition, associated with coherent superpositions of nondegenerate eigenstates of the Hamiltonian. That is, off-diagonal elements of the system density matrix in the energy representation 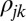evolve with phases of the form 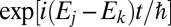, where the 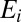’s are energy eigenvalues of the system. The second, unrelated to the issue addressed here, refers to the character of the stationary energy eigenstates that span numerous subcomponents within the overall system [e.g., various molecular sites within a photosynthetic complex (27)].

• ii) We emphasize that considerations below apply to an isolated system. Open systems coupled to an environment are discussed elsewhere using a semiclassical approach to light–matter interactions (7, 22) with similar qualitative conclusions. In addition, open quantum system and related scenarios introduce yet a third definition of the word “coherences.” Specifically, open quantum systems permit the existence of off-diagonal system density matrix elements 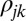which do not evolve in time, or which appear in steady-state scenarios. These are “stationary coherences” (see, e.g., refs. 22, 28 or the time-independent 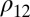in equation 14 of ref. 29), which are distinctly different from the time-evolving coherences which are the focus of this paper.

• iii) Changes in the populations of energy eigenstates of the system, without the involvement of time-dependent off-diagonal 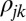, are also mentioned below in Natural Incoherent Thermal Sources, where they are termed “incoherent dynamics.”

One-Photon Absorption

Consider the interaction of radiation with an isolated material system that is initially in a stationary state 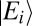. For notational convenience this state is assumed energetically nondegenerate. Higher eigenstates of energy 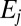are denoted 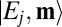, where 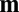denotes any additional quantum numbers needed to describe the state. States of the radiation field are described below in terms of number states 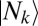. Here, is the number of photons in the 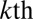mode, of frequency 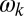, and 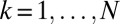is a plane-wave mode index.

Coherent Sources.

Consider now absorption from an arbitrary radiation field. A general field of this kind, linearly polarized along the 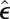direction, can be parametrized as a sum of superpositions of products of number states :

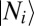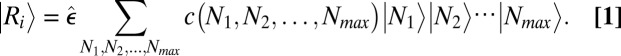For computational simplicity we also use the notation

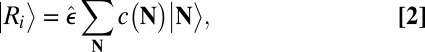where .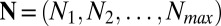

For example, output from a standard multimode laser source can be well represented as a product 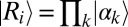of coherent states 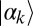, where (24, 30)

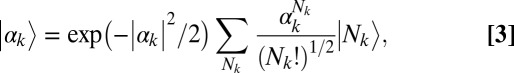i.e.,

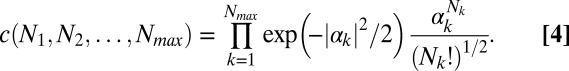The larger the parameter 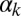, the closer the radiation is to classical light.

Consider then the interaction of the radiation field with an isolated material system that is initially in a stationary state 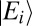. The initial radiation–matter state is then given by

Assuming the dipole approximation and using first-order perturbation theory, the final state, after absorbing one photon from the field, becomes a radiation–matter wave packet, in the excited state, of the form

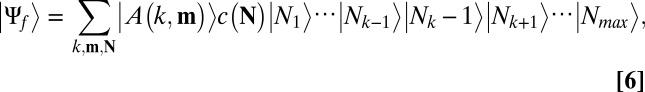where

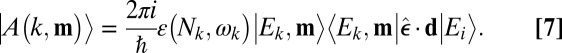Here, 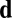is the electric dipole operator and 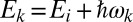is the energy imparted to the material system as a result of the absorption of one photon of frequency 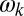. The field amplitude 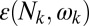introduced above is defined as

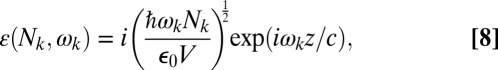where z denotes the axis of propagation of the light beam, 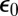is the permittivity of the vacuum, and V is the cavity volume. Note that the resultant state (Eq. 6) is an entangled superposition of the states of the molecule and the radiation field (31).

The density matrix 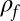associated with 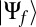is given by

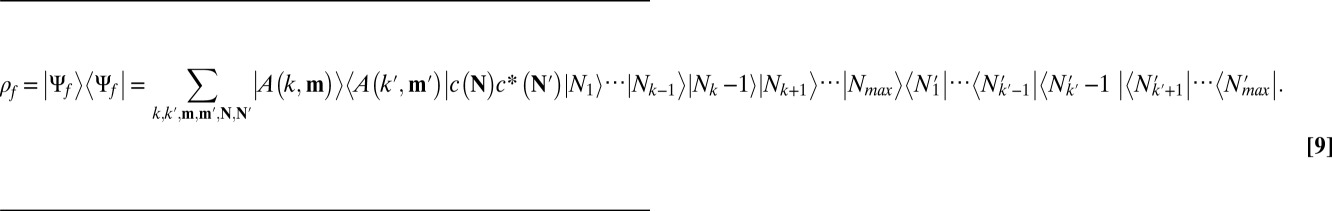Our interest lies in the state of the system, as opposed to the state of the system + radiation field. In accord with standard quantum mechanics (32), one extracts this information from 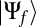by constructing the density matrix 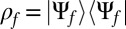and tracing over the radiation field to give the density matrix of the molecule, denoted 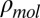. Doing so gives

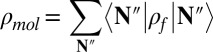where denotes the complex conjugate of the term that precedes it, and

Consider now a coherent pulse of light. If denotes the time at which the pulse is over, then, given Eq. 10, the molecule will evolve after 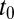as

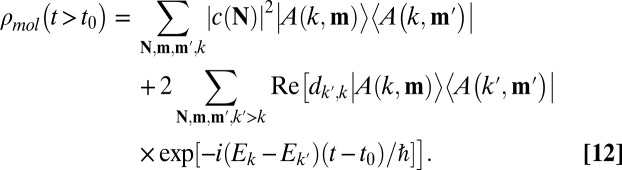For example, for coherent states the real, positive 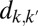can be composed from Eq. 4.

It is clear from Eq. 12 that one-photon absorption from the coherent pulse of light excites many material states, producing a coherent molecular superposition state that evolves coherently in time with frequencies 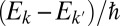. The energy of this superposition state, which is composed of many 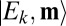eigenstates, is not sharply defined. The fact that the system evolves coherently in time after pulsed coherent light absorption is intimately tied to this energy uncertainty. This, in turn, arises from the fact that 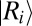is itself a superposition of nonenergetically degenerate states of the radiation field.

Natural Incoherent Thermal Sources.

Consider now absorption of a photon that is emitted by an incoherent thermal source, such as sunlight. This source consists of a statistical mixture of number states described by a radiation field density matrix (24):

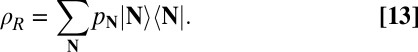Here, 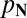is the probability of finding the number state 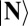in the radiation emitted from the thermal source. If the source is at temperature T, this is given by

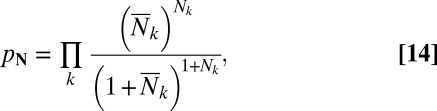with 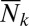being the mean number of photons at temperature T: .

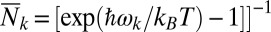This radiation field is a statistical mixture of number states. As a consequence, irradiation with this source will yield an uncorrelated mixture of states resulting from excitation with the state 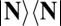. Excitation with the single state 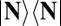can be obtained from the above treatment by setting

in Eq. 9. In this case, in Eq. 11 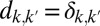and Eq. 10 becomes

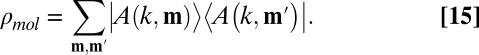Hence, the result of one-photon excitation with radiation emitted by a thermal incoherent CW source (Eq. 13) would be given by an incoherent weighted sum over Eq. 15.

The system, after one-photon excitation, is then in a mixture of stationary states, and 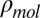does not subsequently evolve coherently in time. Rather, as the natural light continues to stay on for long times compared with molecular time scales, the subsequent time evolution is entirely incoherent, with the populations of the energy eigenstates evolving incoherently in accord with Einstein’s rate laws (33).

Discussion and Summary

The results of the above analysis are clear, but a discussion is warranted. Absorption of one photon from a coherent pulse creates a superposition of energy eigenstates, and hence a state that evolves coherently in time. By contrast, absorption from a thermal incoherent CW source such as the sun is seen to create a stationary mixture. The qualitative results of this quantized-radiation field analysis of one-photon absorption is in agreement with that obtained (21) in a treatment using semiclassical light–matter interactions. What is clearer here, however, is the specific focus on the absorption of a single photon. This analysis can now be used to comment on the associated physics and on current concerns that have arisen regarding one-photon absorption.

Recent qualitative considerations have led to incorrect conclusions, such as that the coherence of the molecule, postexcitation, is independent of the nature of the radiation source (23). Related incorrect pictures have also arisen, suggesting, for example, that each incident photon in weak CW light gives the molecule a kick, which induces dynamics in the molecule. These views, not supported by the above analysis, arise from a simplistic particle picture of the photon (34), and are dispelled when one appreciates the role of measurement in quantum-mechanical particle/wave duality. That is, as is typically the case, whether a system behaves like a wave or a particle depends upon the nature of the measurement (35). For example, in the case of pulsed light absorption described above, no measurement is made that would reveal particle-like properties of the photon. Hence, using language associated with a particle picture is not correct for this physical scenario.

Analogously, for the pulse case, if one were to undertake an experiment in which measurements of the energy of the molecule subsequent to absorption of light from a pulse were made, then stationary states at fixed energy would emerge. Such a measurement is not made, and hence the energy of the system is uncertain, which is intimately related to the fact that the molecule undergoes coherent time evolution. By contrast, a thermal source, by its very nature, comprises independent fixed energy photons and, as such, creates stationary molecular states upon irradiation. That is, conservation of energy ensures that an initial energy eigenstate, absorbing a single photon of known energy, reaches a stationary excited state with known energy, and no subsequent coherent time evolution.

Similarly, adopting a classical picture of the photon as a particle incident on the molecule, possessing only information about its energy and polarization, and possessing no characteristics associated with the source of the radiation, is incorrect. Specifically, as is evident from the analysis above, the effect that the photon has on the molecule depends intimately on the nature of the light source. Multimode coherent pulses induce coherent dynamics whereas CW sources (and likewise natural thermal sources) do not.

The classical picture of the photon as a particle incident on the molecule, repeatedly initiating dynamics, also assumes a known photon arrival time. This too is incorrect and inconsistent with the quantum analysis insofar as no specific arrival time can be presumed unless the experiment itself is designed to measure such times.

Finally, suggestions have been made that a thermal source may be regarded as a collection of random femtosecond pulses. One suggestion is that each molecule feels the effect of individual femtosecond pulses and undergoes coherent time-dependent evolution (1). This perspective is also unjustified. Specifically, there is no justification for imposing a specific physical picture associated with femtosecond pulses on the natural process if the natural scenario makes no such measurement. That is, the electric field from a thermal light source can be expanded in a variety of different bases. However, (i) at best the expansion should be done in a basis related to the physics, i.e., a source of spontaneous emission that is phase interrupted (24), and (ii) regardless of the basis used, it is the overall effect of the light that is important, and this overall effect is to populate energy eigenstates of the molecule.

One final note is in order. As is well known, even thermal sources will create very short time initial coherences associated with the initial time that the molecule feels the turn-on of the light. Short time coherent dynamics is then manifest. However, under natural circumstances (such as moonlight or sunlight) such initial time evolution (on the order of tens of femtoseconds) is totally irrelevant of the time scales associated with natural light (7). That is, after this short time, the system is in a mixture of stationary states.

It is worthwhile, nonetheless, to appreciate the character of such initial dynamical coherences. Consider, for example, natural thermal light incident on pyrazine. Here, the well-known excitation is from the S₀ electronic ground state to an S₂ excited state (36–38). This S₂ state is, in turn, coupled to an S₁ state, which will be occupied as the CW light drives the system into stationary states. Hence, on the short time scale there is coherent S₂ to S₁ internal conversion, because (i) the S₂ state is the bright state that is created upon excitation, and (ii) the exact energy eigenstates to which the system is driven by the CW light contain density on both the S₂ and S₁ electronic states. Hence, there is initial coherent transient dynamics. However, this coherent dynamics does not continue after the short transient time. Rather, in accord with the analysis above, because the light is thermal, no coherent molecular dynamics will occur after the brief initial transient. Rather, the population of the stationary states will change incoherently without the establishment of coherence between energy levels, and the ratio of the population of S₂ to S₁ will be unchanged as time progresses.

In summary, one-photon molecular excitation with pulsed coherent laser light and with natural incoherent light yield qualitatively different responses. Further, the above approach makes clear the extent to which quantum mechanics allows a physical picture of one-photon absorption in an isolated molecule. An analogous picture arises in open systems (7, 22). Any additional imposed qualitative picture may well be inconsistent with quantum mechanics.