HYST: A Hybrid Set-Based Test for Genome-wide Association Studies, with Application to Protein-Protein Interaction-Based Association Analysis

Abstract

The extended Simes’ test (known as GATES) and scaled chi-square test were proposed to combine a set of dependent genome-wide association signals at multiple single-nucleotide polymorphisms (SNPs) for assessing the overall significance of association at the gene or pathway levels. The two tests use different strategies to combine association p values and can outperform each other when the number of and linkage disequilibrium between SNPs vary. In this paper, we introduce a hybrid set-based test (HYST) combining the two tests for genome-wide association studies (GWASs). We describe how HYST can be used to evaluate statistical significance for association at the protein-protein interaction (PPI) level in order to increase power for detecting disease-susceptibility genes of moderate effect size. Computer simulations demonstrated that HYST had a reasonable type 1 error rate and was generally more powerful than its parents and other alternative tests to detect a PPI pair where both genes are associated with the disease of interest. We applied the method to three complex disease GWAS data sets in the public domain; the method detected a number of highly connected significant PPI pairs involving multiple confirmed disease-susceptibility genes not found in the SNP- and gene-based association analyses. These results indicate that HYST can be effectively used to examine a collection of predefined SNP sets based on prior biological knowledge for revealing additional disease-predisposing genes of modest effects in GWASs.

Introduction

Genome-wide association studies (GWASs) have identified numerous risk loci associated with common diseases. Although thousands of disease-susceptibility loci have been reported,¹ they only explain a small proportion of the genetic component of their respective diseases.^2,3 Yang et al.^4,5 estimated that common genetic variants could account for a large proportion of this missing heritability, but a large number of these variants have an effect size that is too small to pass the standard genome-wide significance level (typically p < 5 × 10⁻⁸). Numerous meta-analyses of GWAS of human diseases have thus been carried out to improve the statistical power to detect variants of small or modest effects by increasing sample sizes.^6,7 Meanwhile, a number of set-based approaches that combine association p values of multiple single-nucleotide polymorphisms (SNPs) have been proposed to assess the overall statistical significance of association at the gene and pathway levels, in order to alleviate the multiple-testing burden and enrich potential association signal in the individual SNP-based tests.

Among all the set-based tests available, the Fisher’s combination test⁸ and threshold truncated products of p value method⁹ are the simplest but produce inflated type 1 errors when the SNPs are in linkage disequilibrium (LD). Permutation can solve this problem but is time consuming for real GWAS data sets. Liu et al.¹⁰ proposed a faster method (known as VEGAS [versatile gene-based association study]) to estimate the set-based p values by using Monte-Carlo simulation, in which a large number of multivariate normal random vectors with zero mean and a variance matrix of pairwise LD values were simulated. But the approach is still computationally intensive for large data sets. Therefore, Li et al.¹¹ extended the Simes’ test, known as GATES (gene-based association test using extended Simes procedure), to rapidly evaluate the overall statistical significance at the gene level, and the method does not rely on any time-consuming permutation and simulation procedures to account for LD. At the same time, Moskvina et al.¹² implemented the scaled chi-square test to quickly assess the overall significance of multiple-dependent tests in GWAS given the pairwise LD information. Nevertheless, neither of these two quick tests is optimal under all scenarios as one can be inferior or superior to the other (in terms of statistical power), depending on the number of SNPs in a set and their underlying LD patterns.¹¹

Physical interactions among proteins are central to life and form the basis of cellular functions.¹³ The development of techniques such as protein arrays and computational prediction methods¹⁴ have led to an explosion of reported protein-protein interactions (PPIs) in the public domain. Because proteins often work or interact in a modular fashion, mutations in physically interacting proteins may lead to the same or similar diseases.^15,16 Several studies have demonstrated that genes associated with the same complex diseases, compared to genes associated with different diseases, tend to share a common PPI pair.^17–20 This observation has motivated researchers to use PPI information to prioritize candidate genes in GWAS. For example, Jia et al.²¹ established a dense module searching method, known as dmGWAS, to search for PPI subnetworks enriched with low p value genes in the GWAS data sets, and Akula et al.²² developed a tool, known as NIMMI (network interface miner for multigenic interactions), to combine gene weights with the GWAS association signals to identify disease-prioritized PPI subnetworks. However, all these methods suffer from the fact that LD among multiple proteins (genes) is not taken into account and therefore computationally intensive permutations are needed to estimate statistical significance of association.

In this paper, we introduce a novel set-based statistical test called HYST (hybrid set-based test) combining the extended Sime’s test (i.e., GATES)¹² and the scaled chi-square test to examine the overall association significance in a set of SNPs. We describe how the test can be used to evaluate statistical significance for association at the PPI level without the use of permutation. To avoid ambiguity in defining subnetworks, we only focus on PPI pairs. The aim is to identify whether both genes involved in a PPI pair are potentially disease susceptible. We investigate the empirical point-wise type 1 error and statistical power by simulations, and the genome-wide type 1 error rate with an in-house GWAS data set and the HapMap LD data. We also apply the method to three public GWAS data sets for complex diseases, that is, Crohn Disease (CD [MIM 266600]), Rheumatoid arthritis (RA [MIM 180300]), and type 2 diabetes (T2D [MIM 125853]), to examine the improvements in statistical power over the SNP- and gene-based methods for GWAS in detecting disease-susceptibility genes of moderate effect.

Material and Methods

Construction of the HYST

Figure 1 illustrates how statistical significance for a set of SNPs can be calculated by using HYST. We assume that a test of association between the disease and each of the typed SNPs within a set was carried out and that the resulting p values and pairwise LD coefficients r² for all SNPs are available. First, the SNPs in the set are partitioned into n different blocks (step 1 in Figure 1). For instance, SNPs within a gene can be partitioned into different LD blocks that display weak LD, and SNPs within a biological pathway or network can be partitioned into genes or even LD blocks in multiple genes. Second, for each ith block (i = 1… n), GATES is used to calculate the block-based p value (P_i) for association and to mark the key SNP (S_i) from which P_i was derived (step 2 in Figure 1).¹² Finally, the scaled chi-square test is employed to combine the n block-based p values, $P_1,P_2,\cdots ,P_n$, into a single test statistic, accounting for LD between the n key SNPs (step 3 in Figure 1):

$$X=-2\sum _{i=1}^n\ln P_i$$ (Equation 1)

where the distribution of X can be approximated by $c{\chi }_f^2$²³ with the scale

$$c=1+\frac{\sum _{i=1}^{n-1}\sum _{j=i+1}^n\mathrm{cov}\left(-2\ln P_i,-2\ln P_j\right)}{2n}$$ (Equation 2)

and the degree of freedom (df)

$$f=\frac{2n}{c}$$ (Equation 3)

Figure 1.

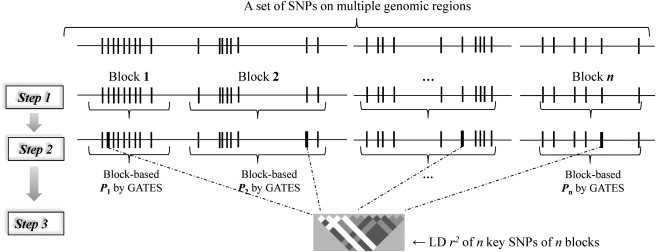
Diagram Illustrating How Statistical Significance for a Set of SNPs Is Calculated in HYST

Vertical bars denote SNPs. When two blocks are on different chromosomes or far away on the same chromosome, the blocks can be assumed to be independent, that is, LD r² between the two key SNPs of the two blocks equals zero. Step 1: define n blocks of SNPs according to LD and/or gene information; step 2: compute a block-based p value in each block by GATES and mark the SNPs from which the block-based p value is derived (the broad-brush in the plot); step 3: combine the n block-based p values by using scaled chi-square test, correcting for LD among the n key SNPs.

According to Li et al.,¹¹

$$P_i=C_i{P}_{S_i},$$ (Equation 4)

where C_i and $P_{S_i}$ are, respectively, the adjustment coefficient based on the effective number of independent tests and the p value of the key SNP, S_i, in the ith block. Because C_i is nearly unchanged given the LD structure of the block, in Equation 2,

$$\mathrm{cov}\left(-2\ln P_i,-2\ln P_j\right)=\mathrm{cov}\left(-2\ln C_i\ast P_{S_i},-2\ln C_j\ast P_{S_j}\right)=\mathrm{cov}\left(-2\ln P_{S_i},-2\ln P_{S_j}\right).$$ (Equation 5)

According to Brown²³ and Moskvina et al.,¹² the quantity $\mathrm{cov}\left(-2\ln P_{S_i},-2\ln P_{S_j}\right)$ in Equation 5 can be approximated by using the positive genotype correlation coefficient between two key SNPs (S_i and S_j) of blocks i and j, $r^{\text{'}}$ :

$$\text{cov}\left(2\ln P_{S_i},2\ln P_{S_j}\right)\approx r^{\text{'}}\left(3\text{.}25+\text{0}\text{.}75r^{\text{'}}\right),$$ (Equation 6)

Moreover, HYST can be modified to incorporate prior weights of the blocks as follows:

$$X=-2\sum _{i=1}^n{w}_i\ln P_i,$$ (Equation 7)

where w_i is the weight of the ith block. The distribution of X is again approximated by $c{\chi }_f^2$,^24,25 but with

$$c=\frac{2\sum _{i=1}^n{w}_i^2+\sum _{i=1}^{n-1}\sum _{j=i+1}^n{w}_i{w}_j\mathrm{cov}\left(-2\ln P_i,-2\ln P_j\right)}{2\sum _{i=1}^n{w}_i}$$ (Equation 8)

and

$$f=\frac{2\sum _{i=1}^n{w}_i}{c}$$ (Equation 9)

HYST for PPI-Based Association Analysis

To avoid ambiguity in defining PPI subnetworks, we focus only on PPI pairs in the present paper. Consider that within a PPI pair, genes 1 and 2 have m₁ and m₂ SNPs, respectively, and each SNP has an association p value; we can partition these m₁ and m₂ SNPs into n₁ and n₂ LD blocks (which display weak LD), respectively. For each ith block (i = 1… n₁ + n₂), GATES is used to calculate the block-based p value (P_i) and to mark the key SNP (S_i) from which P_i was derived. The scaled chi-square test is then used to combine the n₁ + n₂ block-based p values into a single test statistic, accounting for LD between the n₁ + n₂ key SNPs:

$$X=-2\sum _{i=1}^{n_1}\ln P_i-2\sum _{i=1}^{n_2}\ln P_i$$ (Equation 10)

When genes 1 and 2 are on different chromosomes or far away on the same chromosome, the blocks between these two genes can be assumed to be independent.

The alternative hypothesis of HYST for the PPI-based analysis is that at least one gene involved in a PPI pair is associated with the disease. As a gene-based association test can be straightforwardly used to detect whether a gene is significant itself, the aim of a PPI-based association analysis would be to identify PPI pairs in which both genes are potentially disease susceptible. Let P_A and P_B denote the p values of the two genes involved in a PPI pair calculated by GATES. So we use Cochran’s Q²⁶ (i.e., $Q={\left\{{\varphi }^{-1}\left(1-P_A\right)-{\varphi }^{-1}\left(1-P_B\right)\right\}}^2$, where Φ⁻¹ denotes the inverse normal distribution function) and/or Higgins’s I^2,27 (i.e., I² = (Q – 1)/Q if Q ≥ 1, 0 otherwise) to exclude significant PPI pairs in which only one gene is associated with the disease. Note that the two tests were originally used for detecting heterogeneity in conventional meta-analyses.

We implemented HYST for PPI-based association analysis in a graphical user interface (GUI) software tool named KGG (Knowledge-Based Mining System for Genome-wide Genetic Studies) (Figure S1, available online; see also Web Resources). In a test of running speed, KGG generated the association p values of as many as 127,231 PPI pairs for the in-house GWAS data set (described below) within 8 min by using 1 GB memory on a 3.10GHz Intel processor when the SNP-based p values and LD information between SNPs were provided as input.

Simulations on a PPI-Pair Scale

We performed simulation studies to compare the empirical type 1 errors and power of HYST with those of the following PPI-based association tests:

• •GATES:¹¹ All SNP-based p values (by allelic association test) within the two genes involved in a PPI pair were directly combined by GATES to produce a single test of significance at the PPI level without going through the block-based analysis.
• •Scaled chi-square test:^12,23 Similar to GATES, we used the scaled chi-square test (accounting for LD between SNPs) to combine all SNP-based p values of the two genes.
• •Fisher’s combination test:⁸ For each of the two genes involved in a PPI pair, GATES was first used to combine the p values of all SNPs within the gene to give a gene-based association p value. Let P_A and P_B denote the two gene-based p values. A PPI-based test statistic was constructed by using the Fisher’s combination test as $X=-2\ln P_A-2\ln P_B$, where X follows a chi-square distribution with 4 df under the null hypothesis when PA and PB are independent.
• •Stouffer’s Z transform method: A PPI-based test statistic was constructed (in the same way as we did for the Fisher’s combination test) as $Z=\left(Z_A+Z_B\right)/\sqrt{2}$, where $Z_i={\Phi }^{-1}\left(1-P_i\right)$ and Φ⁻¹ denotes the inverse normal distribution function. Note that Akula et al.²² proposed to use the weighted version of this test for the PPI-network-based association test.
• •VEGAS:¹⁰ The p values of all SNPs within the two genes involved in a PPI pair were directly combined to produce a set-based p value by VEGAS. The test employed a simulation procedure to account for LD between SNPs. We ran VEGAS to sum p values of all SNPs in the set, which would be more powerful to detect the association signals in a set of SNPs with more than one independent disease-susceptibility locus than that uses the p value of only the top SNP.¹¹
• •PlinkSet: Phenotypes and genotypes were inputted into PLINK²⁸ for the SNP set-based test. All SNPs were considered to be within a set. The parameter settings used in the analysis include a LD pruning r² cutoff of 0.5, SNP-based p value selection cutoff of 0.05 and at most 5 SNPs were selected in the set for testing. The allelic association test was used to generate the SNP-based association p values, and 1,000 permutations were used to generate the empirical set-based p values.
• •Logistic kernel machine test:²⁹ Simulated phenotypes and genotypes were inputted into the R package of SKAT for a SNP-set association analysis, which was built on a kernel machine framework to jointly evaluate the effect of multiple SNPs at a time. In this comparison, we used the linear kernel, which assumes a linear relationship between the logit of the probability of being a case and the SNPs’ genotypes.

We selected, from an in-house GWAS data set (described below), a region on chromosome 2 covering the SLC3A1 [MIM 104614] and CAMKMT [MIM 609559] genes, both involved in the same PPI pair. In this region, SLC3A1 and CAMKMT had 10 and 53 typed SNPs (with a minor allele frequency [MAF] > 0.05), respectively, and multiple SNPs between these two genes were in strong LD (Figure S2). We extracted the LD pattern and the allele frequencies of these 63 SNPs from the in-house data set and used a program based on the HapSim algorithm³⁰ to generate a population of two million individuals. To assess the type 1 error rate, these individuals were randomly assigned in equal numbers to case and control groups. To evaluate the statistical power, we arbitrarily assigned a disease-susceptibility SNP to each gene in which the minor allele was assumed to increase the risk ratio multiplicatively by a factor of 1.15. In this paper we present the results of two different alternative hypotheses (or scenarios):

• Alternative Hypotheses A. the seventh SNP (with a risk allele frequency [RAF] of 0.092) of SLC3A1 and the 22^nd SNP (with a RAF of 0.079) of CAMKMT were taken as the disease-susceptibility loci; and

• Alternative Hypotheses B. the fourth SNP (with a RAF of 0.283) of SLC3A1 and the 47^th SNP (with a RAF of 0.094) of CAMKMT were taken as the disease-susceptibility loci.

The disease status of an individual is generated according to the conditional probability of being affected given the genotypes of their disease-susceptibility SNPs. The baseline risk corresponding to the absence of any risk-increasing (minor) alleles was calculated from the allele frequencies, risk ratios of the disease susceptibility SNPs and the disease prevalence in the population (which was set at 0.1); 200 random samples, each with 2,000 cases and 2,000 controls, were drawn, without replacement, from the population and subjected to different tests for PPI-based association. The type 1 error (and power) rate at nominal error (power) rate α is estimated by the fraction of samples (out of the 200) resulting in a p value ≤ α. This Monte-Carlo simulation procedure was repeated 500 times to produce 500 empirical type 1 errors and powers.

In addition, a permutation procedure was performed to assess the validity of the approximate p values of HYST. Given a simulated data set of 2,000 cases and 2,000 controls generated under each alternative hypothesis (A and B), HYST was first used to calculate the approximate p value (P_app). The case/control labels of subjects in the simulated data set were then randomly shuffled and HYST was reapplied to this permuted data set to compute a permuted set-based p value. We used an adaptive permutation procedure similar to that implemented in PLINK, in which we stop permuting case/control labels when the empirical set-based p values are clearly going to be nonsignificant. We performed at most 1 million permutations for each simulated data set. The empirical p value (P_emp) was estimated by the fraction of the permuted data sets resulting in a permuted p value ≤ P_app. We randomly chose 200 simulated data sets under each alternative hypothesis to run this time-consuming permutation procedure for this assessment.

Simulations on a Genome-wide Scale

We also evaluated the type 1 error rate of HYST on a genome-wide scale. Individuals in our in-house GWAS data set were randomly assigned in equal numbers to case and control groups. SNP-based association analysis was then carried out under a genotypic model in PLINK.²⁸ Two LD data sets (i.e., the actual LD information for the subjects and the LD information for the HapMap CHB [Han Chinese in Beijing, China] population) were used in order to compare the performance of using different LD information sources in the computation. We used HYST to combine SNP-based p values to obtain PPI-based p values. The type 1 error rate of HYST at nominal error rate α was estimated by the proportion of PPI pairs resulting in a p value ≤ α. In addition, we used a quantile-quantile (Q-Q) plot to compare the overall distribution of the PPI-based p values against the null distribution, that is, standard uniform distribution.

Application to Real GWAS Data Sets

We applied HYST (implemented in KGG) to three public GWAS data sets (CD, RA, and T2D) in which only summary statistics are available (described below) to compute the PPI-based p values. GATES was used to compute the gene- and PPI-based p values for comparison. A summary of the SNPs, genes, and PPI pairs involved in these GWAS data sets is provided in Table S1. The LD information for the HapMap CEU panel was used to account for LD between SNPs in the gene- and PPI-based association analyses.

Data Sets

PPI Data Set

We downloaded the PPI data set (3.2 million PPI pairs with confidence score > 0.7) from a bioinformatics database named STRING³¹ in which all interactions included are supported by at least one piece of experimental or computational evidence demonstrating physical interaction between the two human proteins. We mapped each protein involved onto the corresponding protein-coding gene by using the Gene Cross-References from the International Protein Index (IPI) database. Because a gene can have multiple protein isoforms, 203,393 unique gene pairs covering 60% of (10,383) coding genes were identified in the current data set. Around 1% of (2,000) and 2% of (4,000) PPI pairs, respectively, involved genes within 100 kbp and 1 mbp on the same chromosome.

HapMap LD Data Set

We downloaded the latest version (Release 27) of pairwise LD data (r²) for the CHB and CEU populations from HapMap. This release merged SNPs of phases I, II, and III. In total, there are 2,554,939 and 2,776,528 SNPs found in the CHB and CEU LD data sets, respectively. These LD data sets were used to account for the dependency of SNPs throughout the analysis in this paper.

Public GWAS Data Sets

We downloaded the published GWAS results of CD,³² RA,³³ and T2D³⁴ in Caucasians online (See Web Resources). The SNP-based p values in the CD and T2D studies were adjusted via genomic inflation factors (λ_CD = 1.159; λ_T2D = 1.081),³⁵ but no adjustment was made in the RA study (λ_RA = 1.003). The SNPs were then mapped to their respective genes based on their coordinates in the RefGene (hg18) data set from the UCSC database.

In-House GWAS Data Set

A total of 2,514 Chinese subjects were typed with the Illumina Human610-Quad BeadChip in the local research projects³⁶ in Hong Kong with institutional review board approval. After standard quality-control procedures, we had the genotype data at 473,931 SNPs, of which 215,451 were mapped to 16,908 genes, each with 5,000 base-pair extension at both sides, according to their coordinates in the RefGene (hg18) data set from the UCSC database.

Results

In the previous section, we describe in detail how HYST is derived. In this section, using simulations we first look at the empirical type 1 errors and powers of HYST (or specifically HYST when applied to PPI-based association analysis) as well as other alternative tests for PPI-based association analysis (i.e., GATES, the scaled chi-square test, the Fisher’s combination test, the Stouffer’s Z transform method, VEGAS, the PlinkSet, and the logistic kernel machine test). Then, we apply HYST to three public real GWAS data sets (CD, RA and T2D) in order to see how many extra disease-susceptibility genes the method can find in addition to those using SNP- and gene-based methods.

Type 1 Errors and Powers of HYST for PPI-Based Association Analysis: PPI-Pair Scale

Given a nominal error rate (α) of 0.05, the medians of empirical type 1 error rate of HYST, HYST with arbitrary weights, GATES, VEGAS, PlinkSet, and logistic kernel machine test were 0.045, 0.050, 0.050, 0.060, 0.045, and 0.045, respectively (Figure 2A), indicating that the six tests are valid tests for PPI-based association analysis. However, the scaled chi-square test is slightly conservative, with a median of empirical type 1 errors of 0.030. Moreover, the two tests not accounting for LD between genes (i.e., the Fisher’s combination test and Stouffer’s Z transform method) were liberal in the simulations (the medians of empirical type 1 error rate were 0.066 and 0.076, respectively, at α = 0.05), and so were excluded in our comparison of powers for PPI-based association analysis. Note that here the Fisher’s combination test is equivalent to HYST without correction of LD between genes.

Figure 2.

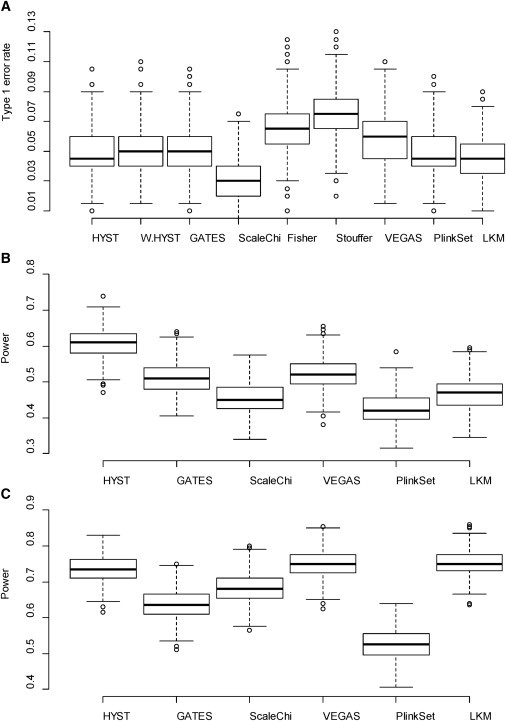
Box-Plots of Empirical Type 1 Errors and Statistical Powers of Various PPI-Based Association Tests

(A–C) Empirical type 1 error (A); power under the alternative hypothesis A (B); and power under the alternative hypothesis of B (C), for the various PPI-based association tests. Detailed descriptions of the two alternative hypotheses are available in the Material and Methods section. Note that Fisher’s and Stouffer’s methods were excluded in the power comparison because of inflated type 1 error rates. Fisher: the Fisher’s combination test combining two gene-based p values calculated by GATES; Stouffer: Stouffer’s Z transform method combining two gene-based p values calculated by GATES. The following abbreviations are used: W.HYST, HYST with arbitrary weights (1:5 for SLC3A1:CAMKMT); ScaleChi, scaled chi-square test; LKM: the Logistic Kernel Machine Test.

We also observed that the approximate p values of HYST were very close to the empirical p values obtained from permutations (Figure S3) under the two different alternative hypotheses A and B mentioned in Material and Methods. So we compared the power of HYST with those of other PPI-based association tests under the two alternative hypotheses. HYST had greater power than all other methods under the alternative hypothesis A (Figure 2B). Compared to its parental tests, GATES and the scaled chi-square test, HYST had over 10% more power to detect a PPI pair for association (according to the medians of the empirical powers). Under the alternative hypothesis B, HYST had similar power to VEGAS and logistic kernel machine test and was more powerful than the PlinkSet test, GATES, and the scaled chi-square test (Figure 2C).

Type 1 Errors of HYST for PPI-Based Association Analysis: Genome-wide Scale

We randomly assigned the disease status of 2,514 subjects in a GWAS data set to examine the type 1 error rate of the PPI-based association analysis by HYST on a genome-wide scale. Table 1 shows the empirical type 1 error rates of HYST at various nominal error rates, α, when the actual LD information for the subjects is used and when the LD information for the HapMap CHB population is used instead. The empirical type 1 errors were close to the family-wise nominal error rates, α, no matter whether the actual LD or HapMap LD data were used in the analysis. Figure 3 shows the distribution of p values against the null distribution under a randomly selected scenario that uses the LD data from the subjects (Figure 3A) and from the ancestry-matched HapMap panel (Figure 3B). The results indicated the validity of HYST in GWAS. Moreover, the similarity of results obtained through the use of different LD sources implies that HYST can use ancestry-matched LD information from public databases, such as HapMap and the 1000 Genomes Project, to carry out a robust genome-wide PPI-based association scan when only summary statistics from GWAS are available.

Table 1.

Empirical Type 1 Error Rates of HYST for PPI-Based Association Analysis at Various Nominal Error Rates, α

	α = 0.05	α = 0.01	α = 0.001
When actual LD was used	0.0454	0.0100	0.00087
When HapMap CHB LD was used	0.0471	0.0103	0.00091

Figure 3.

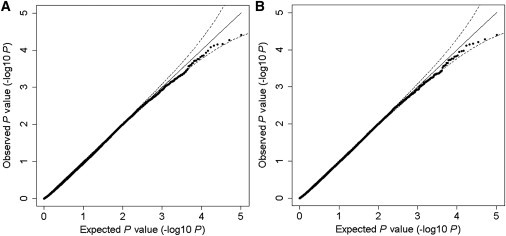
Quantile-Quantile Plots of the PPI-Based p Values Calculated by HYST in a GWAS Simulated under the Null Hypothesis

(A and B) The LD information was calculated from the actual genotypes of the subjects (A); and the ancestry-matched HapMap population (CHB) LD data (B) were used. Higgins’s I² ≤ 0.5 was used to remove PPI pairs where two genes are significantly different in effect. The straight line represents the distribution of p values under the null hypothesis and the dotted lines represent estimated 95% confidence bands.

Application to Real GWAS Data Sets

Crohn Disease

In PPI-based association test by HYST for the CD data set, 13 PPI pairs with I² < 0.5 involving 13 genes were found significant (Figure 4A and Table S2). Among the genes involved in the significant PPI pairs, six (IL23R [MIM 607562], ATG16L1 [MIM 610767], NKX2-3 [MIM 606727], NOD2 [MIM 605956], CYLD [MIM 605018], and PTPN2 [MIM 176887]) were genome-wide significant in the SNP-based analysis (i.e., the gene has at least one SNP reaching genome-wide significance at p < 5 × 10⁻⁸) and have been confirmed to be susceptibility genes for CD (Table S5). Gene-based analysis did not discover additional CD-susceptibility loci (with gene-based p < 0.05/25,782 ∼1.94 × 10⁻⁶) in this data set. However, of the seven genes involved in these significant PPI pairs but nonsignificant in either the SNP-based, the gene-based test, or both tests, five (IL18RAP [MIM 604509], JAK2 [MIM 147796], TNFSF15 [MIM 604052], CCL2 [MIM 158105], and STAT3 [MIM 102582]) were confirmed CD-susceptibility genes (with at least 1 SNP having a minimum p value < 5 × 10⁻⁸ in the GWAS catalog¹ as of February 14, 2012), and their associations were supported by multiple independent studies (Table S5).The p values of the most significant SNPs in these five genes were all above 2.0 × 10⁻⁶, and IL18RAP even has a SNP-based and gene-based p value as large as 7.6 × 10⁻⁵ and 6.3 × 10⁻⁴, respectively, in this data set (Table S5). Besides, GATES only detected eight significant PPI pairs among the 13 significant PPI pairs detected by HYST and no extra significant PPI pairs (Figure S4A). These show that the use of PPI information via HYST adds power for uncovering disease-susceptibility genes of moderate or small effects in GWAS, compared to the SNP-based and gene-based association analyses.

Figure 4.

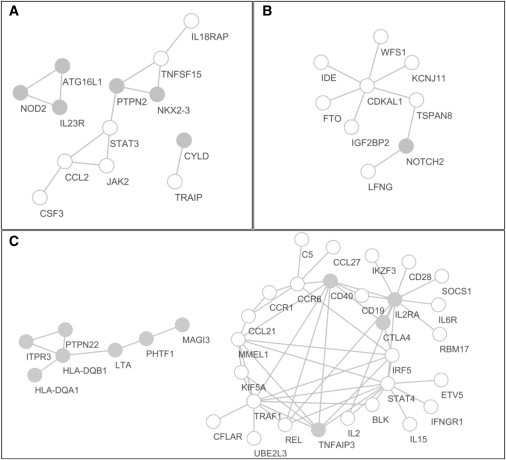
Network Views of Significant PPI Pairs in the Applications of HYST to Three GWAS Data Sets

(A–C) The PPI-based association analyses were shown in the GWAS data sets of (A) CD, (B) T2D, and (C) RA. Higgins’s I² ≤ 0.5 was used to remove PPI pairs where two genes are significantly different in effect. Each node and edge represents a gene (protein) and a PPI, respectively. Genes significant in either the SNP-based, the gene-based analysis, or both tests are colored in gray.

Interestingly, three of the genes involved in the significant PPI pairs but not significant in the SNP- and gene-based analyses (i.e., JAK2, STAT3, and CCL2) automatically formed a fully connected triangle (Figure 4A). The proteins encoded by the JAK2 and STAT3 genes are members of the STAT-JAK pathway that controls the signal transduction between cell surface receptors and the nucleus and is long known to be implicated in CD.³⁷ CCL2 is one of the several Cys-Cys cytokine genes involved in immunoregulatory and inflammatory processes and is implicated in the pathogenesis of diseases characterized by monocytic infiltrates, such as psoriasis,³⁸ and in the susceptibility to colitis.³⁹

Type 2 Diabetes

HYST for PPI-based association analysis found eight significant PPI pairs with I² < 0.5 involving nine genes in the T2D study (Figure 4B and Table S3). None of these nine genes was genome-wide significant in the SNP-based analysis and only one (NOTCH2 [MIM 600275]) was genome-wide significant (with gene-based p value < 0.05/21,502 ∼2.33 × 10⁻⁶) in the gene-based analysis (Table S6). However, of the eight genes in the significant PPI pairs but nonsignificant in either the SNP-based test, the gene-based test, or both tests, seven (IGF2BP2 [MIM 608289], WFS1 [MIM 606201], CDKAL1 [MIM 611259], IDE [MIM 146680], KCNJ11 [MIM 600937], TSPAN8 [MIM 600769], and FTO [MIM 610966]) were confirmed T2D-susceptibility loci (with at least one SNP having a p value < 5 × 10⁻⁸ in the GWAS catalog¹ as of February 14, 2012), and their associations were well supported by other studies (Table S6). The p values of the most significant SNPs in these seven genes were all larger than 5.4 × 10⁻⁷ and WFS1 has a SNP-based and gene-based p value as large as 8.226 × 10⁻³and 2.478 × 10⁻², respectively, in this data set (Table S6), which are far below genome-wide significance at the SNP and gene levels, respectively. Also, GATES did not detect any significant PPI pairs in this data set (Figure S4B).

Rheumatoid Arthritis

For the RA study, HYST for PPI-based association analysis identified 56 significant PPI pairs (with I² < 0.5) involving 35 genes (Figure 4C and Table S4). Of these 35 genes, nine (MAGI3 [no MIM number], PHTF1 [MIM 604950], PTPN22 [MIM 600716], CTLA4 [MIM 123890], LTA [MIM 153440], HLA-DQA1 [MIM 146880], HLA-DQB1 [MIM 604305], ITPR3 [MIM 147267], and CD40 [MIM 109535]) were genome-wide significant in the SNP-based analysis and two more (TNFAIP3 [MIM 191163] and IL2RA [MIM 147730]) were genome-wide significant in the gene-based analysis (with gene-based p value < 0.05/29,738 ∼1.68 × 10⁻⁶) (Table S7). Of the 24 genes in the significant PPI pairs but nonsignificant in either the SNP-based test, the gene-based test, or both tests, eight (REL [MIM 164910], CCR6 [MIM 601835], IRF5 [MIM 607218], BLK [MIM 191305], CCL21 [MIM 602737], TRAF1 [MIM 601711], C5 [MIM 120900], and KIF5A [MIM 602821]) were known RA-susceptibility genes (with at least one SNP having a p value < 5 × 10⁻⁸ in the GWAS catalog¹ as of February 14, 2012) (Table S7). The p values of the most significant SNPs in these eight genes were all over 1.3 × 10⁻⁷ and KIF5A even has a minimum SNP-based and gene-based p value as large as 1.0 × 10⁻⁴ and 1.7 × 10⁻³, respectively, in this data set (Table S7). Besides, GATES only detected 13 significant PPI pairs among the 56 significant PPI pairs detected by HYST and no additional significant PPI pairs (Figure S4C).

Discussion

We introduce HYST, a newborn independent statistical test from a hybrid of GATES¹² and the scaled chi-square test,^12,23 to assess the overall significance of association in a set of SNPs. It inherits a number of attractive properties from its parental tests. First, it does not resort to any time-consuming permutation or simulation procedure and is able to quickly produce valid set-based p values for a set of correlated SNPs. Second, it is versatile and does not require the raw genotype or phenotype data as inputs but needs only the SNP-based p values and ancestry-matched LD information. These properties make it suitable for post-GWAS analyses (i.e., meta-analyses of GWAS,⁴⁰ genotype imputation,⁴¹ DNA-pooling, or even next-generation sequencing studies of common variants⁴²). Moreover, it can incorporate the degree of importance of genes as prior weights in the computation.

In the present paper, we describe how HYST can be used to evaluate significance of association at the PPI level, with the aim of detecting novel disease-susceptibility genes of moderate effect size. Computer simulations demonstrated that HYST for PPI-based association analysis has reasonable type 1 errors and is generally more powerful than other tests for PPI-based association. Also, our application to three real disease data sets available in the public domains revealed a number of significant PPI pairs in which multiple confirmed disease-susceptibility genes were involved but most of these genes could not be identified by using the conventional SNP- and gene-based tests. The results show that HYST is potentially powerful for detecting significant associations between a set of SNPs and the disease in GWAS. Coexpression of genes and pair relations in pathways, for example, KEGG pathways, are also potentially useful ways to define gene pairs or gene sets for HYST. However, it is not straightforward to define the cut-off value in correlation for the presence of coexpression or the boundaries of gene pathways. Thus, although the HYST methodology can incorporate these additional sources of information, the actual implementation and evaluation will involve substantial further work. Here, we have demonstrated the use of PPI information alone already results in a test with added power to detect modest effects.

The hybrid creates a more powerful set-based statistical test. According to Li et al.,¹¹ the methods of combining individual p values in a set can be divided into two categories: best-SNP picking and all-SNP aggregating. Best-SNP picking tests, as the name implied, uses only one SNP-based p value after the multiple testing adjustment to produce the set-based p value and GATES is the representative of such tests. All-SNP aggregating tests accumulate the effects all SNPs into a statistic, and the scaled chi-square test is one member of these tests. Under alternative hypothesis, the best-SNP picking tests are more powerful when there are a few disease-susceptibility loci in a large SNP set because they are less sensitive to the dilution of SNPs with no effect in the set. On the other hand, in the all-SNP aggregating tests, the presence of multiple SNPs with no effect in the set will considerably dilute the combined association signal, but the presence of multiple disease-susceptible SNPs can markedly strengthen the combined association signal (see Table 2 of Li et al.¹¹). HYST attempts to have the best of both categories: GATES is first used to combine SNP p values in each predefined block in which there are many neutral SNPs but very few disease-susceptibility loci, and the scaled chi-square test is then used to combine multiple block-based p values, each contain some signals of disease-susceptibility loci. In the hybrid, the critical point is the LD of key SNPs of GATES is subtly used to account for the dependency of block-wise p values in the scaled chi-square test. In a sense, this is a seamless combination of two separate tests. Consequently, we observed that HYST always achieved more power to detect a PPI in which both genes contain a disease-susceptibility locus than its parental tests in the simulation experiments. In the three real GWAS data sets, this powerful test detected sizeable disease-susceptibility genes that cannot be detected by the PPI-based association test that uses GATES. On the other hand, in principle, HYST can also be applied for gene-based association analysis when SNPs of a gene are partitioned into multiple blocks. Also in the three data sets, the numbers of significant genes by HYST and GATES are 24 and 26 (24 overlapped), 3 and 2 (2 overlapped), and 317 and 318 (312 overlapped) for CD, T2D and RA, respectively (unpublished data), which implies both methods have similar power for gene-based association analysis in reality. Accordingly, because GATES is always implemented by KGG for gene-based association only, KGG users do not need to adjust their GATES results with the new HYST method and can continue to use GATES for gene-based association without loss of power. In addition, if they want to combine evidences of association over multiple risk SNPs in a much larger SNP set (defined by PPI and/or pathway), the HYST method is now available on KGG for this purpose.

In the PPI-based analyses, we are interested in the combined effect of both genes in a PPI pair on the disease instead of the significance of only one gene, which can be assessed by the gene-based association analyses. Because HYST itself cannot discriminate whether only one or both genes in a PPI pair are potentially disease-susceptible, we adopted the heterogeneity test from the conventional meta-analyses to exclude the significant PPI pairs whose significance is overwhelmingly dominated by that of only one gene. This idea could actually be extended to pathway- or network-based association analyses in GWAS. When the significance of a pathway is dominated by an extremely significant gene and all other genes in the same pathway are far from being significant, that specific pathway, as an analysis unit, is very unlikely to be related to the diseases in question although the significant gene itself should be very interesting. In that case, the heterogeneity test is useful because it helps to eliminate such pathways. However, one should not expect that, unlike the situation of a PPI pair, every gene in a pathway or network is disease-susceptible and has a significant or promising association p value. Thus, how the heterogeneity test should be properly used in pathway- and network-based analyses is still unclear at the moment.

When two genes of a PPI pair are physically close and some of their SNPs have LD across these genes, HYST is able to correct for the LD between the genes to avoid inflation of the type 1 error and to produce a valid association p value. A significant PPI-based p value passing the heterogeneity test indicates both of the genes are statistically associated with (but not necessarily causal to) the disease. For example, in the RA data set, we found the HLA-DQB1 and HLA-DQA1 (∼23 kb away) have a significant PPI-based P, 3.792 × 10⁻²⁰³ (Table S4), and the p values of both genes are also extremely significant (Table S7). There are at least three possible scenarios underlying this significant PPI: (1) both of the genes in LD are very likely to contribute to the risk of RA given the fact that they are functionally linked; (2) there is only one RA-susceptibility-contributing gene, and the other gene is merely in high LD with the former; (3) neither gene predisposes to this disease, and both are in high LD with another nearby RA-susceptibility-contributing gene. All of the three possibilities are consistent with the alternative hypothesis of HYST (and almost all set-based association tests mentioned in the paper). However, identification of the genuine causal genes requires other follow-up analysis and data, such as the SNP conditional analysis with raw genotypes⁴³ and functional validation by molecular experiments at cells or tissues.

This set-based association analysis using PPI information is different from that using the pathway data.⁴⁴ First, in terms of resources, the PPI data set covered 60% of the protein-coding genes in the human genome, whereas the popular pathway databases such as KEGG⁴⁵ only covered 30%. Second, in terms of hypothesis testing, the PPI-based analysis, similar to SNP- and gene-based analyses, requires less prior knowledge of the biological processes (lipid and glucose homeostasis, detoxification, etc.), whereas pathway-based analyses are limited by the current knowledge of metabolic or signaling pathways and these, to some extent, may limit their power for identifying novel disease-susceptibility genes not yet known to be involved in any of these pathways. Nevertheless, pathway-based analyses have their power for detecting causal pathways in which the genes may have no PPIs. Apparently, in a PPI network, risk genes with few interaction partners (i.e., involved in few edges, small connection degrees) will be analyzed and detected with less chance than those with high connection degrees. Besides, the PPI-based association test cannot detect regulatory SNPs in intergenic regions and noncoding genes, which are not trivial according to existing GWAS results in the GWAS catalog.¹ So, we recommend researchers to run PPI-, pathway-, gene- and SNP-based analyses to exhaustively explore all kinds of association signals, particularly in the discovery stage of GWAS.

From a systems biology perspective, genes work in a complicated network. The SNP- and gene-based approaches in GWAS treat each SNP or gene as autonomous and ignore the fact that genes do not function alone but through physical communication. This “not seeing the forest for the trees”⁴⁶ attitude, has received much criticism in biotechnology.⁴⁷ Our applications of the method to public GWAS data sets of complex diseases, that is, CD, RA and T2D, found a number of PPI pairs significantly associated with the corresponding disease. Although many of the genes could not reach a genome-wide significance level by both SNP- and gene-based association tests in their original GWAS, quite a number of them have been proven to increase the risk of the corresponding disease. Therefore, we hope that researchers will further explore association analyses at other biological levels besides SNP and gene to increase the chance of finding novel genes of modest effect that contribute to disease susceptibility in GWAS and sequencing studies.

Web Resources

The URLs for data presented herein are as follows:

• CD GWAS results, http://www.broad.mit.edu/∼jcbarret/ibd-meta/

• HapMap LD Information, http://hapmap.ncbi.nlm.nih.gov/downloads/ld_data/latest/

• International Protein Index Database, ftp://ftp.ebi.ac.uk/pub/databases/IPI/current/ipi.genes.HUMAN.xrefs.gz

• KGG, http://bioinfo.hku.hk/kggweb/

• Online Mendelian Inheritance in Man (OMIM), http://www.omim.org/

• PLINK, http://pngu.mgh.harvard.edu/∼purcell/plink/

• R package of SKAT, http://www.hsph.harvard.edu/research/skat/

• RA GWAS results, http://www.broadinstitute.org/ftp/pub/rheumatoid_arthritis/Stahl_etal_2010NG/

• RefGene (hg18) in the UCSC database, http://hgdownload.cse.ucsc.edu/goldenPath/hg18/database/refGene.txt

• STRING version 9.0, http://string-db.org

• A Meta-Analysis of Genome-Wide Association Results in Type 2 Diabetes, http://www.broadinstitute.org/∼debakker/meta_t2d.html