Phase Transitions in Coarse-Grained Lipid Bilayers Containing Cholesterol by Molecular Dynamics Simulations

Abstract

Coarse-grained simulations of model membranes containing mixtures of phospholipid and cholesterol molecules at different concentrations and temperatures have been performed. A random mixing without tendencies for segregation or formation of domains was observed on spatial scales corresponding to a few thousand lipids and timescales up to several microseconds. The gel-to-liquid crystalline phase transition is successively weakened with increasing amounts of cholesterol without disappearing completely even at a concentration of cholesterol as high as 60%. The phase transition temperature increases slightly depending on the cholesterol concentration. The gel phase system undergoes a transition with increasing amounts of cholesterol from a solid-ordered phase into a liquid-ordered one. In the solid phase, the amplitude of the oscillations in the radial distribution function decays algebraically with a prefactor that goes to zero at the solid-liquid transition.

Introduction

Biological membranes usually consist of a mixture of different lipids and proteins. In eukaryotic cells, one of the most abundant lipids is cholesterol together with the major constituent, the phospholipids. Cholesterol stiffens the fluid membranes and softens the gel-to-liquid crystalline phase transition. The behavior of simple model systems consisting of just two components, a phospholipid and cholesterol, has been extensively studied as a function of composition and temperature. Some of the focus in contemporary experimental research, however, is shifting toward still more complex multicomponent systems that constitute the basis for proposed raft structures (1). Nevertheless, the two-component system is, as of this writing, far from understood and constitutes an important challenge to the simulation community.

Pure phospholipid bilayers undergo a phase transition from a gel phase at low temperatures to a disordered high temperature phase. The gel phase is characterized by having the lipid positions ordered on a two-dimensional lattice in the membrane plane as well as having ordered chains. This phase may therefore be called solid-ordered (S_o). At high temperatures, the lipid positions in the plane resemble a two-dimensional liquid and the chains are disordered. Therefore, the liquid-crystalline phase (high temperature or fluid phase) may be called liquid-disordered (L_d). Cholesterol molecules induce conformational ordering of the disordered fluid-phase lipid chains. Furthermore, they also perturb the lateral packing order of low-temperature gel-phase bilayers. Thus, cholesterol changes both the high-temperature fluid phase and the gel phase into a new phase, that is, the liquid-ordered (L_o) one, which has a liquid structure in the membrane plane and ordered fatty acid chains. This phase was suggested by Ipsen et al. in 1987 (2,3). Experimental studies support this scenario (4,5).

Different phase diagrams have been suggested for these mixtures. At low concentrations of cholesterol, the main gel-to-liquid crystalline-phase transition is only slightly perturbed by the presence of cholesterol. This means that at low temperatures, one has a gel phase (S_o) that is characterized by positional order (the lipids are pinned to regular positions of a triangular lattice), ordered lipid chains, small area per lipid, and a small lateral diffusion constant. When the temperature is increased, the system undergoes a sudden transition during which the positional order, order of the lipid chains, area per lipid, and translational mobility suddenly change into values characteristic of the liquid-disordered (L_d, L_α, or liquid crystalline) phase. At high concentrations of cholesterol and a low enough temperature, the liquid-ordered (L_o) phase emerges with liquidlike positional order and ordered hydrocarbon chains. In addition, two-phase regions may emerge in the phase diagram at intermediate concentrations of cholesterol. See, for example, the phase diagrams in the review by Veatch and Keller (6). The experimental phase diagrams, which are based on calorimetry and NMR spectra (7), suggest the formation of domains that are either rich or poor in cholesterol for both ternary and binary systems (4). Fluorescence microscopy provides evidence of the existence of liquid-liquid (micrometer-to-submicrometer size) domains in three-component systems (8,9); however, no domains are observed in two-component (DPPC (1,2-dipalmitoyl-sn-glycero-3-phosphocholine)/cholesterol) systems.

Thus, it is not entirely clear where in the phase diagram such domain formation occurs and what the sizes of such domains are. Two possible schematic phase diagrams are shown in Fig. 1. The one on the right, which contains two-phase regions above as well as below the main phase transition, is essentially the one first suggested in Ipsen et al. (2). The one on the left is more minimalistic and differs just by the absence of two-phase regions. Similar phase diagrams were suggested in Veatch and Keller (6), lacking the high-temperature two-phase region but not the-low temperature one. A similar phase diagram is also suggested in Huang et al. (10). Almeida (11) has recently formulated a model that lacks phase separation above the main phase transition, but has a two-phase region below it. These issues have been the subject of considerable discussion in the literature. One idea that is important in this context relates to the formation of condensed complexes between cholesterol and phospholipids. These may not necessarily be long-lived and are very specific (12–14). Several more or less different phase diagrams have been proposed, based on the study of different systems using different experimental techniques in the last 20 years. After a study of this literature, Marsh (15) concludes that some of these phase diagrams “may not be quite as solidly based as generally assumed”. The situation might be a bit clearer for ternary systems, but even in that case, the evidence for phase separation is not as extensive as generally assumed (16).

Figure 1.

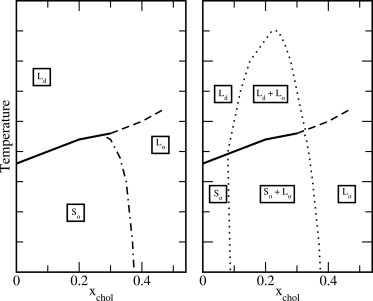
Two possible schematic phase diagrams for a cholesterol/phospholipid system. (Solid, nearly horizontal lines) First-order transition between gel and fluid. (Dashed lines) Not firmly established where, if, and how it ends. (Left-hand phase diagram) Supported by our simulations, no two-phase region exists, but there is a continuous conversion between the L_d and L_o phases. (Dot-dashed line) Second-order phase transition between the S_o and L_o phases. (Right-hand diagram) The two-phase region.

Molecular dynamics simulations of atomistic lipid bilayers (17–19) at high temperatures show that cholesterol successively orders the conformational degrees of freedom in the L_d phase. See also the review in Berkowitz (20). The simulations show a gradual change in the properties of the system, i.e., no signs of sudden changes in chain order or area density, which would indicate a proper first-order phase transition with the concentration of cholesterol. However, this could be due to the existence of a critical point that ends the two-phase region at a temperature below that of these simulations (DPPC, 323 K). A phase transition could also be of a higher order and be difficult to observe in simulations, due to the finite system size as well as difficulties in monitoring higher derivatives accurately. Nevertheless, atomistic simulations do not support a two-phase region above the gel-liquid crystalline phase transition, as indicated in the left-hand phase diagram in Fig. 6 of Veatch and Keller (6); instead, they are in line with the right-hand phase diagram in that same Fig. 6, indicating that larger amounts of cholesterol gradually order the L_d phase without any proper phase transition. It is clear that the ordering of the conformational degrees of freedom may be gradual, and by no means needs to be a sudden process. At low temperatures, there is some evidence in the literature for a two-phase region between the S_o and L_o phases. However, recent x-ray scattering experiments (21) indicate that such a two-phase region, although present for an unsaturated lipid like DOPC (1,2-dioleyl-sn-glycero-phosphocholine), is absent for DPPC.

Figure 6.

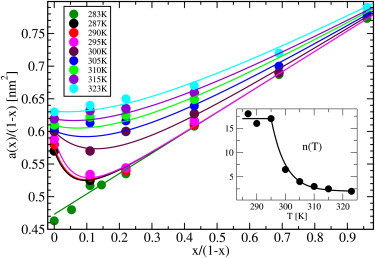
A plot of a(x)/(1 − x) vs. x/(1 − x) from CG simulations at different temperatures with fits to Eq. 8. (Lower-right inset) Variation of the parameter n(T) with temperature (dots), together with a fit containing a constant and an exponentially decaying region.

From the experimental point of view, the results are clearer, when studying the phase transition versus the temperature at fixed concentrations of cholesterol. Calorimetry as well as NMR order parameters indicate a rather sharp transition for pure phospholipids that successively widens and softens with increasing amounts of cholesterol (10). At a high enough concentration of cholesterol, it is doubtful whether there is a phase transition anymore. The main phase transition for the phospholipids takes place slowly; therefore, it has not been possible to study this in atomistic computer simulations. Coarse-grained models like the MARTINI model (22), however, offer good possibilities to cover long enough timescales to pursue this. Even three-component systems have been studied (23) using this model. The main purpose of our own article is to extensively study the two-component system with this model and provide a full characterization of the different phases.

The ordering of the chains in the different phases may then be characterized by the order parameter

$$S_{chain}=\frac{1}{2}\left(3\langle {\text{cos}}^2\theta \rangle -1\right),$$ (1)

with θ being the angle between the director and the vector defining the orientation of the main part of the lipid chains. As the coarse-grained MARTINI model for the lipids only has a small tilt in the gel phase (24), the director may be replaced by the normal of the membrane. As the vector defining the lipid-chain orientation, we take the vector joining two next nearest-neighbor beads. In experiments, the chain order is usually measured using deuterium NMR giving an order parameter defined in the same way, but with the angle θ being the angle between the director and the carbon deuterium (hydrogen) bond. To a good approximation, the order parameters are related as S_chain = −2S_CD. This makes a comparison with NMR-order parameters possible. Alternatively, one can compare with experimental fluorescence data, where the fluorescent probe aligns with the hydrocarbon chains, and yields the S_chain order parameter (25).

The fraction of trans bonds or the area per lipid are alternative measures for the bilayer order. The area could be defined as area per lipid (a(x) = A(x)/N_l with N_l = N_pl + N_chol), or area per phospholipid (A(x)/N_pl), or, preferably, as partial specific area (26),

$$a_{pl}\left(x\right)=\frac{\partial A\left(x\right)}{\partial N_{pl}},$$ (2)

where x is the cholesterol mole fraction, A(x) is the total area of the system, N_pl is the number of phospholipids per monolayer, and N_chol is the number of cholesterols per monolayer. All these quantities are well defined from the simulations. The partial specific areas of the components are most easily obtained from the slope and intercept of the tangent of the curve showing the area per phospholipid versus x/(1 − x):

$$\frac{A\left(x\right)}{N_{pl}}=\frac{a\left(x\right)}{1-x}=a_{pl}\left(x\right)+\frac{x}{1-x}{a}_{chol}\left(x\right).$$ (3)

Alternatively, the partial specific areas may be obtained in a similar manner from

$$a\left(x\right)=a_{pl}\left(x\right)+x\left(a_{chol}\left(x\right)-a_{pl}\left(x\right)\right).$$ (4)

All these order parameters measure the conformational order and may be approximately related to one another.

To describe the order in the membrane plane, lipid/lipid radial distribution functions (RDFs) are used. In the liquid phase, The RDF has a single peak at the nearest-neighbor distance, followed by a fast decay to 1. In the solid-ordered phase, a large number of peaks are seen. The peak height versus the distance may in that case be fitted by a power law with exponent −1 for all concentrations of cholesterol. The amplitude, on the other hand, is a function of the concentration of cholesterol and decreases successively to vanish at ∼50% cholesterol. Thus, we take that amplitude divided by the amplitude in the cholesterol-free system as an order parameter for the solid/liquid phase transition. The behavior of this order parameter is rather typical for a second-order phase transition. It goes continuously to zero. When the cholesterol concentration reaches 50% in the gel phase, the RDF changes behavior qualitatively and is characterized by a single peak as in the fluid phase. This indicates the transition from the solid (S_o) to the liquid (L_o) phase.

No observations were made of any two-phase regions, either at low or at high temperatures. One possible explanation for this could be that the simulations are too short for the systems to segregate into regions with different composition. Based on the lipid lateral translational diffusion constant, which is 1 × 10⁻¹³ m²/s (24) in the gel phase, we estimate that a single lipid typically moves a distance of 2 nm during a 10-μs simulation. This is <3 interlipid distances and an order-of-magnitude smaller than the systems size. Therefore, simulation times are probably not long enough for the gel-phase systems to segregate even if there were to be a driving force for this. In the high-temperature fluid phase, which has a two orders-of-magnitude larger lateral diffusion coefficient, the time is sufficient for segregation. We did, in fact, observe the inverse process, that of mixing, when starting from nonuniform systems. Another issue is that the minimum size of coexisting two-phase regions is not known and our lateral system sizes (10–20 nm) might be too small.

Methods

Force fields

The simulations were performed with the coarse-grained (CG) Martini model (22,27), using Vers. 2.0 of the force field. For comparison, a few detailed united-atom (UA) simulations were performed using the Berger force field (28). The MARTINI force field is based on a parameterization against the solvation free energies in water and oil. The coarse-graining consists of mapping four united atoms (including nonpolar hydrogens) into one bead, although a two-to-one or three-to-one mapping is used in ring structures. Four types of beads (namely, polar, nonpolar, apolar, and charged) are defined for lipids, while a special set is used for ring structures such as the ones found in cholesterol. All nonbonded particles (beads) interact through a Lennard-Jones potential with a cutoff at 1.2 nm and a shift starting at 0.9 nm. Charged particles interact through a screened Coulomb potential (ε_r = 15) with a linear term added that gives the force as well as the potential equal to zero at the cutoff. For the bonded interactions, harmonic potentials in the bond lengths and in the cosine of the bond angles are used. A coarse-grained DPPC molecule consists of 12 beads (50 united atoms) while cholesterol consists of eight beads (29 united atoms). The charged beads represent the headgroup dipole in DPPC, while a single polar bead represents the OH-headgroup of cholesterol.

Initial structures

Initial structures of a coarse-grained pure DPPC and a DPPC/cholesterol bilayer containing 30% cholesterol were downloaded from the MARTINI home page (http://md.chem.rug.nl/cgmartini/). Systems with other concentrations, ranging from 5% to 60%, were generated by removing randomly chosen cholesterol molecules or replacing randomly chosen phospholipids with cholesterols. The small systems were replicated to obtain systems with up to ∼2000 lipids. UA initial coordinates with 1024 lipids at various concentrations of cholesterol were taken from Hofsäss et al. (18).

Computational details

All simulations were performed using Vers. 4.0.5 of the GROMACS package (29) on computer clusters at Swedish High Performance Computing Centers. The systems were subject to periodic boundary conditions in all directions. Separate Berendsen thermostats (30) with time constants 0.5 ps⁻¹ were applied to water, lipid, and cholesterol molecules in the CG simulations while Nosé-Hoover thermostats (31,32) were used for the UA model. The CG systems were simulated over the temperature range 283–323 K. The pressure was fixed to 1 atm in all spatial directions using Berendsen barostats (30) with a time constant of 5 ps⁻¹ for the CG systems and Parrinello-Rahman barostats (33,34) for the UA systems. The integration of the equations of motion was performed using a leap-frog algorithm with time step 25–40 fs in the CG simulations. The UA simulations required a 10-times-smaller time step, 4 fs. In the UA simulations, the bond lengths in the lipids were fixed using the LINCS algorithm (35) while the analytic SETTLE algorithm (36) was used for the bonds in the simple-point-charge water (37). Simulations were performed at slightly different hydration, all well above 10 CG waters per phospholipid corresponding to 40 simple-point-charge waters. Simulations were performed at fixed temperatures but also as simulated annealing. The fixed-temperature CG simulations were typically performed for 400 ns, of which the first 200 ns were considered as an equilibration and discarded in the analysis. Close to the phase transition, up to 10-times longer simulations were required. The CG simulated-annealing simulations were performed using a linear sweep speed of 1 K μs⁻¹. The simulations were performed separately in heating and cooling modes.

Results and Discussion

The gel-to-liquid crystalline transition with temperature

We began by monitoring the phase transition versus the temperature at different fixed concentrations of cholesterol. In Fig. 2, the variation of the conformational order parameter, area per lipid, and enthalpy are shown versus the temperature. All these quantities indicate a sharp transition between an ordered gel phase and a disordered fluid phase. The order parameter, S_chain (Eq. 1), reflects the ordering of the hydrocarbon chains and is shown (averaged over the two lipid chains) versus the temperature in Fig. 2 A. The change of the order parameter between the phases is large and sharp at low concentrations of cholesterol and shows a substantial hysteresis (±15 K). By increasing the amount of cholesterol, the transition broadens, the hysteresis decreases, and the change in order parameter at the transition is reduced. Similar trends of a decreasing change in the order parameter at higher concentrations of cholesterol have been observed in experiments for DPPC/cholesterol (10,38) and PPEt-PC (1-palmitoyl-2-petroselinoyl-3-phosphocholine)/cholesterol systems (5,39). The area per lipid (Fig. 2) shows a similar change at the phase transition. Similar to the order parameter, the area indicates a slight upwards shift of the phase transition temperature with increasing concentration of cholesterol. This means that cholesterol stabilizes the ordered gel phase up to slightly higher temperatures, which perhaps would be expected. In Fig. 2 E, the area fluctuations are shown versus the temperature. They are significant in a small (5–10 K) region close to the phase transition. Conversion of the area fluctuations into an area compressibility modulus, K_A, is performed through the equation

$$K_A\equiv A{\left(\frac{\partial \gamma }{\partial A}\right)}_{T,V}=\frac{A{k}_{\text{B}}T}{{\sigma }_A^2}=\frac{a{k}_{\text{B}}T}{N_l{\sigma }_a^2}.$$ (5)

K_A varies more than three orders of magnitude with a pronounced minimum at the transition. It is clear that the transition also softens (that is, fluctuations decrease with increasing amounts of cholesterol). The enthalpy behaves in a similar way, giving rise to a pronounced peak in the derivative (heat capacity) as well as increased fluctuations close to the transition temperature. The heat capacity, C_p, was calculated from the enthalpy fluctuations, σ_H, by the equation

$$C_P\equiv {\left(\frac{\partial H}{\partial T}\right)}_p=\frac{{\sigma }_H^2}{k_{\text{B}}{T}^2},$$ (6)

and are shown versus the temperature in Fig. 2 C. Similar but less accurate and noisier results may be obtained by calculating the heat capacity as a numerical derivative. With increasing concentration of cholesterol, the changes in the order parameter, enthalpy, and the area across the transition are successively reduced. This is shown in Fig. 3, where the error bars are estimates of the statistical errors from fluctuations. The changes drop linearly in a similar fashion. One might expect that the phase transition line would end at ∼55% cholesterol. Simulations going as high as to 60% indicate a persistent weak transition. Because we would now be nearly reaching concentrations at which experiments indicate that cholesterol and phospholipids may no longer be miscible, we did not pursue the study further in search for a possible end of the phase transition line.

Figure 2.

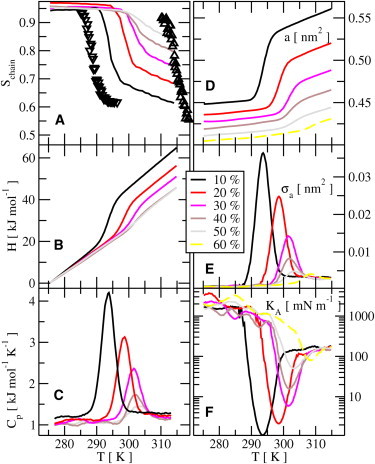
Simulated annealing results. (A) Order parameter versus temperature for different concentrations of cholesterol. (B) Enthalpy versus temperature for different concentrations of cholesterol. (C) Heat capacity C_p, calculated from Eq. 6 versus temperature. (D) Area per lipid versus temperature. (E) Area fluctuations per lipid versus temperature. (F) Area compressibility modulus (calculated from Eq. 5) versus temperature. For all quantities, there is a hysteresis of ±15 K when passing through the transitions. (A, up- and downtriangles) Order parameters during the cooling and heating through the phase transition for the cholesterol-free system. Otherwise, all quantities are monitored during the downwards (freezing) transition.

Figure 3.

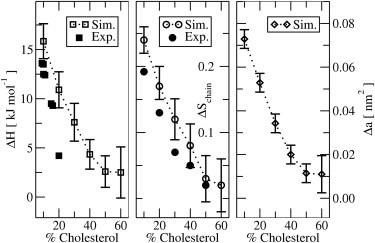
The change in enthalpy, order parameter, and area per lipid at the phase transition versus mole % cholesterol. The experimental ΔH values shown are taken from McMullen et al. (40) and McMullen and McElhaney (41) while the experimental ΔS_chain values shown originate from fluorescence data (25).

These results may be compared to measured heat capacities. See, e.g., Huang et al. (10), McMullen et al. (40), and McMullen and McElhaney (41). The integral under the heat capacity peak gives the phase transition enthalpy. We note from Fig. 3 that there is a reasonable agreement with the experiments for this quantity and for the change in order parameter. The width of the peaks, however, does differ. For multilamellar DPPC vesicles, the experimental peak is ∼2 orders-of-magnitude narrower (10,42). For unilamellar vesicles, the peak width is more similar to those of our simulations (42). With cholesterol, the experimental peaks broaden (10,40,41) and are similar in width to those from our simulations. One should, however, keep in mind that these systems are quite small; therefore, one would expect finite size broadening of the phase transition. Accordingly, these simulations cannot shed light on the detailed nature of the phase transition. Larger simulations and finite size scaling would be necessary for this. Alternatively, other methods (for example, mean-field models (43), which are not as limited in system size as our simulations) may be able to shed some light on this issue.

The solid-ordered to liquid-ordered transition with varying concentration of cholesterol

Both above and below the main transition, the area per lipid and the order parameters change smoothly with varying fractions of cholesterol. The area per lipid (phospholipid + cholesterol) is shown in Fig. 4 for the CG model at different temperatures and for the UA model at 323 K. We observe the best agreement in area per lipid between the UA systems simulated at 323 K and the CG systems simulated at 305 K. This reflects the lower melting temperature of the CG model. The UA curve is more curved, indicating that the mixture is slightly less ideal in the UA case. Below the main transition (283 K), the mixture is ideal (except at some of the lowest concentrations) with the area 0.473 nm² for the phospholipid and 0.312 nm² for cholesterol. The conformational order parameter of the lipid chains is shown versus the concentration of cholesterol for a few temperatures in Fig. 4. In the gel phase (283 K), the lipids stay ordered for all concentrations of cholesterol. The order parameter decreases slightly upon increasing the amount of cholesterol from 0% to 50%. In the fluid phase (315 K for the CG model and 323 K for the UA model), an almost linear increase of the order parameter from 0.4 to 0.8 is observed. The numerical values agree quite well with those of −2S_CD for DMPC (1,2-dimyristoyl-sn-glycero-3-phosphocholine) just above the phase transition (306 K). The results agree qualitatively with experimental (NMR) order parameters (10) for DPPC/cholesterol, and wide-angle x-ray scattering (44,45) averaged orientational order parameters (S_x-ray). We also calculated S_chain for the UA model simulations of DPPC/cholesterol systems in order to compare with experiments and CG model simulations. The resulting order parameters were slightly low at high concentrations of cholesterol.

Figure 4.

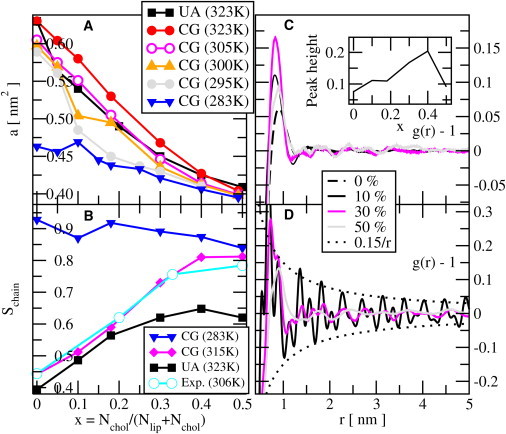
(A) Area per lipid versus mole fraction cholesterol (x) from CG simulations at different temperatures and from UA simulations at 323 K. (B) Calculated order parameter, S_chain, from simulations as a function of concentration of cholesterol for a few temperatures. Minus two-times the experimental order parameter S_CD is also shown for DMPC just above the main transition temperature. The experimental data were taken from the Supplementary Information for the review in Leftin and Brown (47) (also available at http://cbcarizona.edu/brown/group/database). (C) RDFs based on the molecular center of mass for different concentrations of cholesterol at 323 K using the CG model. (Inset) Height of the single peak versus concentration of cholesterol. (D) RDFs for molecular center of mass for different cholesterol mole fractions at 283 K.

The liquid-solid transition as monitored by the RDF

The positional ordering of the lipids in the membrane plane during the liquid/solid transition is best monitored by an RDF. This may be calculated for different atoms in the headgroup region (46). We calculated the RDF using the center of mass of the entire lipid or the phosphorous and nitrogen atom of the headgroup and obtained similar results. However, fitting of the gel-phase peaks to a triangular lattice worked best when the center of mass of the entire lipid was used. In the fluid phase (323 K), we noted as indicated in Fig. 4 that it is hard to distinguish more than one single broad peak (at ∼0.85 nm) for any concentration of cholesterol. Thus, the system is liquidlike in two dimensions from the point of view of the RDF. This single peak is lowest in the cholesterol-free system and increases in height with the concentration of cholesterol. The height is largest at 40% cholesterol and decreases at higher concentrations.

In the low-temperature phase (283 K), Fig. 4, we noted that the peaks of the RDF although damped extend as far out as 10 nm. There is a long-range order; however, because the gel phase does not form a perfect triangular structure, the order decays with distance at all concentrations of cholesterol. The decay of the height of the peaks (and depths of the minima) can be fitted quite well to a power law

$$g_{max}\left(r\right)=1+\frac{g_0}{r^n},$$ (7)

with r being the peak position and the exponent n being close to 1 at all concentrations. This is shown in Fig. 5. One may construct a translational order parameter from g₀(x) divided by g₀(0). The inset to Fig. 5 shows this liquid-solid (i.e., translational) order parameter versus the concentration of cholesterol. We noted that this order parameter drops almost linearly with cholesterol mole fraction and approaches zero just above 50%. This qualitative change of the RDFs indicates a (second-order) transition from a solid with successively weakened long-range order into a liquid. We have data (not shown) for the UA model indicating a similar behavior.

Figure 5.

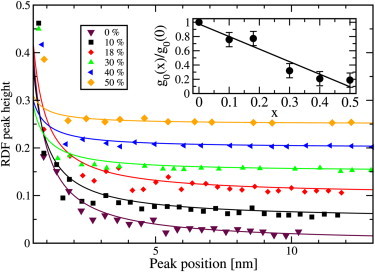
The peak heights of the RDFs of the gel-phase lipids as a function of r and concentration of cholesterol. The six data sets have been shifted successively by 0.05 in the vertical direction to avoid overlap. (Lines) Fits to curves of the form g₀/r. (Right inset) Parameter g₀ as a function of cholesterol mole fraction, x.

Partial specific areas

In Fig. 6 the area per phospholipid is plotted versus x/(1 − x) to make an analysis using Eq. 3. The simulation data have also been fitted to the simple model suggested in Edholm and Nagle (26),

$$\frac{a\left(x\right)}{1-x}=a_{pl}^0-\Delta a\left(1-e^{-nx}\right)+\frac{x}{1-x}{a}_{chol}^0.$$ (8)

Although this model contains four temperature-dependent parameters, all of them have precise physical meanings and a fairly limited range of variation. Further, all, except one, are determined from the properties of the cholesterol-free system and the behavior of the ideal mixture at high concentrations of cholesterol. Based on the data in Fig. 6 and additional simulations at intermediate temperatures (for clarity, not shown in Fig. 6), we conclude the following. The value $a_{pl}^0$, the area per phospholipid in the pure system, is easily calculated from the phospholipid system and found to be in fair agreement with the experiments. For the gel phase, we find the constant value 0.473 nm². For the high-temperature phase, the simulations indicate an area of 0.632 nm² at 323 K and a thermal area expansion coefficient,

$$A^{-1}\left(\partial A/\partial T\right)=0.003{\text{K}}^{-1}.$$

Thus, we should have

$$\Delta a\left(T\right)=0.158+0.002\left(T-323\right)$$

and finally obtain $a_{chol}^0$ = 0.312 nm² from the slope of the area per lipid versus mole fraction cholesterol at high concentrations and low temperatures. Thus, one parameter, n(T), remains to be determined from the actual shape of the curves. This parameter indicates the number of phospholipid molecules that are ordered (and reduce their area by Δa) due to the insertion of a single cholesterol molecule into the bilayer. We noted that the gel phase (at 283 K) is an ideal mixture (with some minor exception at small values of x) with the area per phospholipid 0.473 nm² and that per cholesterol 0.312 nm². Just above the main transition (287–295 K), an excellent fit to the simulation data is obtained using n = 17 ± 2. At temperatures above 295 K, we need to reduce the parameter $a_{chol}^0$ with temperature from 0.312 down to 0.27 nm² at 323 K. The value n(T) decreases exponentially with a temperature constant of 5 K to reach the constant value 2 at 323 K. With these values of the parameters, Eq. 8 results in the continuous curves shown in Fig. 6. The partial specific areas can then be calculated from the model as

$$\begin{array}{l}{a}_{chol}\left(x,T\right)=a_{chol}^0-n\left(T\right)\Delta a\left(T\right){\left(1-x\right)}^2{e}^{-n\left(T\right)x}\text{and}\\ a_{pl}\left(x,T\right)=a_{pl}^0\left(T\right)-\Delta a\left(T\right)\left[1-\left(1-n\left(T\right)x\left(1-x\right)\right)e^{-n\left(T\right)x}\right].\end{array}$$ (9)

Data for a_chol(x,T) are shown in Fig. 7 using parameters from Table 1.

Figure 7.

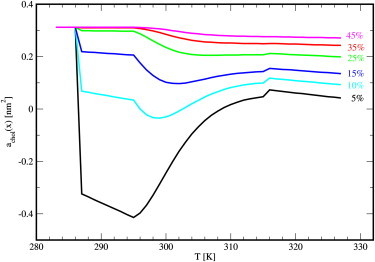
The partial specific area of cholesterol versus temperature for different concentrations of cholesterol calculated from the model given by Eq. 8 using parameters from Table 1.

Table 1.

Fitted parameters of Eq. 8

T[K]	$a_{pl}^0$[nm2]	$a_{chol}^0$[nm2]	Δa[nm2]	n
283	0.473	0.312	—	—
287	0.570	0.312	0.097	18.3
290	0.575	0.312	0.104	15.7
295	0.584	0.312	0.114	16.8
300	0.600	0.310	0.127	6.5
303	0.600	0.310	0.127	4.5
305	0.601	0.300	0.126	4.0
310	0.609	0.290	0.136	3.0
315	0.618	0.280	0.145	2.5
320	0.628	0.275	0.150	2.3
323	0.631	0.270	0.158	2.0

Conclusions

No signs of phase segregation, i.e., coexisting regions with different composition, were observed in the simulations. A more detailed analysis (not shown) indicates that the types of molecules in nearest-neighbor pairs do not deviate from what would be expected in a random mixture. In the fluid phase, we are able to show that a nonuniform mixture of cholesterol and phospholipids will mix in simulation times that are less then a few hundred nanoseconds. It is not possible to definitely show whether the situation is the same (or not) in the gel phase, because the slower dynamics for these systems would require two orders-of-magnitude longer simulations. The simulations show that the gel-to-liquid crystalline-phase transition with temperature weakens with increasing amounts of cholesterol, but that a transition persists at least up to 60% cholesterol.

Our simulations, as well as those of experiments, have difficulties in showing whether the phase-transition line ends (with vanishing latent heat and change in order parameter) before reaching concentrations of cholesterol at which it could be questioned whether cholesterol and phospholipids still uniformly mix. The phase-transition temperature increases slightly with varying concentrations of cholesterol. When the amount of cholesterol is increased in the gel phase, the area per lipid behaves as for an ideal mixture. The orientational order parameter remains almost constant or decreases slightly. The system undergoes a transition from a solidlike structure in the membrane plane into a liquidlike one at ∼50% cholesterol. Below this concentration, the solid becomes less ordered with increasing cholesterol concentration. The amplitude of the peaks in the RDF decays algebraically as g₀/r, where g₀ drops continuously and reaches zero close to 50%.

Thus, g₀ could be taken as an order parameter for the solid-liquid phase transition. The partial specific area of cholesterol drops abruptly just above the phase transition. The effect is pronounced at low concentrations of cholesterol, while the mixture is more ideal for large amounts of cholesterol. Here, the partial specific area of cholesterol becomes almost constant and is close to 0.25–0.3 nm². Our simulations support the left-hand-side phase diagram in Fig. 1, without two-phase regions. Two-phase regions that are larger than 10–20 nm, however, would require larger simulations to be seen. In the gel phase, phase segregation would also require longer timescales than those accessible in the present simulations. Our work is, therefore, by no means conclusive at this point.