Colocalization of Multiple DNA Loci: A Physical Mechanism

Abstract

A variety of important cellular processes require, for functional purposes, the colocalization of multiple DNA loci at specific time points. In most cases, the physical mechanisms responsible for bringing them in close proximity are still elusive. Here we show that the interaction of DNA loci with a concentration of diffusing molecular factors can induce spontaneously their colocalization, through a mechanism based on a thermodynamic phase transition. We consider up to four DNA loci and different valencies for diffusing molecular factors. In particular, our analysis illustrates that a variety of nontrivial stable spatial configurations is allowed in the system, depending on the details of the molecular factor/DNA binding-sites interaction. Finally, we discuss as a case study an application of our model to the pairing of X chromosome at X inactivation, one of the best-known examples of DNA colocalization. We also speculate on the possible links between X colocalization and inactivation.

Introduction

DNA spatial organization in eukaryotic cells has a prominent role in genome regulation (1–6). Such an organization involves complex interactions between distant DNA loci that come together with precise spatial/temporal patterns. The physical mechanisms regulating the organization of chromatin conformations remain largely unknown. In some cases, active transport mechanisms (for example, actin/myosin-dependent) are known to drive spatial colocalization. However, in many other cases, such cross-talks are independent of active motors, and based on a kind of Brownian passive-shuttling (1,3,4,7). Many examples of DNA interactions mediated by molecular factors are known, but the fundamental questions on how these interactions are self-organized, how colocalization timing is reliably controlled by the cell, etc., remain open.

As a case study, we consider X chromosomes colocalization at X-chromosome inactivation (XCI), one of the best-characterized examples of interchromosomal interactions. During XCI in female mammalian cells one of the two X chromosomes present in the cell, randomly chosen, is silenced, to equalize X genes products with respect to males. This process is regulated by a region on the X called the X-inactivation center (Xic) (8–10). The Xic from the two X chromosomes must come in close proximity at the onset of XCI, in a step crucial to the process (11,12). Xic pairing has been shown to involve some few-kb-long DNA segments: the so-called Xpr region (X pairing region) (13) and a sequence between Tsix/Xite genes (11,12), containing clusters of binding sites for Ctcf and Yy1 zinc-fingers (14–16), and other proteins such as Oct4 and Sox2 (17). Starting from experimental observations, it has been proposed that a protein-RNA bridge is somehow self-assembled at Xic regions and mediates the Xic-Xic interaction (14,18,19).

We discuss here, via a schematic physics model, a general molecular mechanism that could be responsible for the self-organization of chromatin in space (18,19). It describes the scenario where pairing of distal DNA sites results from their interactions with a concentration of DNA-binding, diffusing molecular factors. In our model, recognition and colocalization of a couple of DNA loci occur in a switchlike manner when the concentration/affinity of the binding molecules rises above precise threshold values, as a thermodynamic phase transition takes place in the system. While its thermodynamic roots guarantee the robustness of the mechanism, the model can rationalize a number of experimental observations and explain how a cell can reliably control Brownian-motion-based colocalization processes serving vital functional purposes (18,19).

In this article, for the first time to our knowledge, we use this model to estimate the probability of colocalization of multiple DNA loci in a cell (i.e., two, three, and four distinct sites) as a function of the concentration and affinity of molecular factors that bind to them, and depict a comprehensive scenario of their stable patterns. A complex picture emerges, with different thermodynamic phases in the system, each characterized by a specific spatial arrangement of DNA. As a speculation, we discuss a possible application of our models to X chromosome pairing at XCI in cells with three and four copies of X chromosomes, aiming to discriminate different model variants. We derive the probability distribution of the allowed spatial arrangements of the X chromosomes as predicted by our models, and by use of a recently proposed model for “counting&choice” at XCI (20), we compare such predictions against available data (21) to investigate the still-undiscovered link between “counting&choice” and X-pairing at XCI.

Models

Our model is based on minimal ingredients: it includes diffusing DNA segments and molecular factors that can form molecular bridges between specific DNA binding loci. We represent DNA segments as self-avoiding random-walk polymers of n beads (see examples later in Fig. 4, c and d), with n₀ of them acting as binding sites (BSs) for a set of diffusing molecular factors (MFs). To depict a comprehensive scenario, we study two versions of the model that produce different results and, in particular, we analyze colocalization in systems with two, three, or four identical polymer segments.

Figure 4.

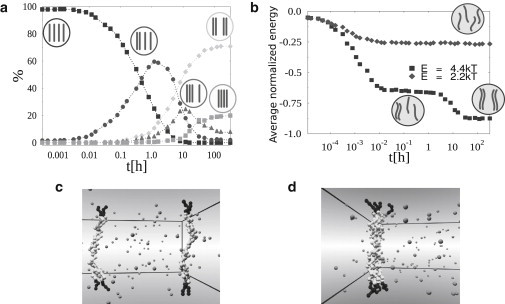
Dynamics of colocalization of four polymers in Model A. (a) Dynamics of the probability distribution of the different states is shown as function of time, t. Here molecule concentration, c, and binding affinity, E (c = 1.0% E = 4.4 kT), are chosen to have an equilibrium state where the state with two-polymer couples is the most likely (upper region in the phase diagram of Fig. 3b). Polymers are initially set in a random configuration, with no couples. After t ∼ 1 h, a first couple is formed. Later on, in the majority of cases, a second couple is assembled. (b) Average normalized energy of the system, ɛ, plotted as a function of time. (Squares) Same value of c and E used for the plot in panel a, with the first plateau corresponding to the formation of the first polymer couple, and the second, lower plateau to the formation of the second couple. (Diamonds) Dynamics when a below-threshold value of the energy is chosen: the system approaches the phase where no stable couples are formed and ɛ(t) reaches a comparatively higher plateau. Panels c and d show pictorial representations of two typical system configurations from Monte Carlo simulations in Model A in the region where two couples are formed (c), and in Model B where the four polymers come together (d); see text.

Model A

In the first version of the model, we impose a constraint on the number of bonds that can be formed between molecules and polymer sites. We impose that the binding valency of a molecule is equal to two, thus each molecule can bridge a maximum of two polymers. Note also that each polymer site cannot be bound by more than one molecule.

Model B

In the second version, we relax such constraints and allow polymer binding sites and molecules to form multiple bonds. Because the precise value of the valency of molecules does not change our general results, unless it is below three, we discuss below the case where it is set to four.

Lattice

To deal with such a many-body system including diffusing polymers and molecules, we used a lattice version of the model. Lattice models are well established in polymer physics (22) as they allow us to circumvent the problem of huge computational efforts by permitting comparatively faster simulations with respect to off-lattice systems (23). In our simulations we consider a cubic lattice with sizes L_x = 2L, L_y = 2L, and L_z = L. Lengths are given in units of d₀, the characteristic size of a polymer bead (see below). Periodic boundary conditions are imposed to reduce boundary effects. Each particle, i.e., a polymer bead as well as a molecule, occupies a single lattice site. Different particles are not allowed to seat at the same time on the same lattice site.

For sake of simplicity, the polymers are treated like directed chains along the z axis, with their tips bound to move on the top and the bottom surface of the lattice. They consist of n = L beads that randomly diffuse under a nonbreaking constraint: two proximal beads on a polymer must be on next or nearest-next lattice sites. While the use of directed polymers allows faster simulations, it does not affect the colocalization mechanism we describe because it relies on general thermodynamic bases (see below). If nondirected polymers were used, the colocalization scenario we discuss would be valid as well, but without a perfect alignment of polymers as in our case. On the other hand, other strategies could be used to attain a perfect pairing of the sequences, e.g., by having a gradient of binding sites on the polymer chains.

In our models, a molecule and a polymer-binding bead can form a bond of energy E only when they are on nearest-neighbor lattice sites. Molecules are present in the lattice with a volume concentration, c. We try to set all the system parameters (c,E,n₀) by using the available biological data, as we explain below.

System parameters

We explored a range of values of binding energies, molecule concentrations, and polymer binding site number, in the biological range where they are expected to be. In particular, we use as a guide the information available on X chromosome pairing where CTCF, a well-characterized chromatin organizer protein, is involved (14). The precise value of in vivo DNA-molecule binding energies can be very hard to measure, yet experiments provide a typical energy range of E ∼ 0–20 kT, where k is the Boltzmann constant and T the room temperature (see (24–31)). This is the energy range we consider here.

The volume concentration of molecules, c, can be roughly estimated from real transcription factor concentrations. Because in our model the number of molecules per unit volume is c/d³₀, where the value d₀ is the linear lattice spacing constant, the molar concentration can be written as

$$\rho =\frac{c}{\left(d_0^3{\mathcal{N}}_A\right)},$$

where $\mathcal{N}$_A is the Avogadro number. The value d₀ must be the typical size of a BS, which we consider to be ∼30 bp (the order of magnitude of a CTCF BS in Tsix/Xite region). This gives a d₀ ∼ 10 nm. By using such a value of d₀, typical concentrations of regulatory proteins such as ρ ∼ 10⁻³–10⁻¹ μmol/liter (i.e., ∼10³–10⁵ molecules per nucleus) would correspond to volume concentrations in our model c ∼ 10⁻³–10⁻²%.

Finally, in our simulations we set n = L = 32 and each polymer is endowed with n₀ = 24 binding sites, of the order of magnitude of CTCF known sites in the Tsix/Xite region (15). The robustness of our results to changes in system size derives from the scaling properties of polymer physics (22), and stems from the thermodynamic origin of our colocalization mechanism (22,32). However, we checked different combinations of L,n₀ in the 16–256 range and we verified that our results remain unaltered.

Monte Carlo simulations

We run Monte Carlo (MC) simulations to study the equilibrium properties of our system. We use a standard Metropolis-Kawasaki algorithm (23): during each MC step the algorithm tries to move, on average, all the particles of the system (one at a time), with a transition probability proportional to $e^{-\Delta \mathcal{H}/kT}$, Δ$\mathcal{H}$ being the energy change caused by the move. Specifically, the Arrhenius factor is r₀$e^{-\Delta \mathcal{H}/kT}$, where r₀ is the bare reaction rate. A single MC step corresponds to a time τ₀ = r₀⁻¹ (23). By imposing that polymer diffusion constant is equal to typical values found experimentally, we derive τ₀ = 10⁻¹ s, which is of the order of magnitude of typical biochemical reaction rates (33).

To monitor the spatial configuration of the polymers in our model system, we measure three quantities:

• 1.
  The normalized mean-squared distance between two polymers, as

  $$d^2\left(t\right)=\sum _{z=1}^{n_0}\frac{\langle r^2\left(z,t\right)\rangle }{d_{rand}^2},$$

  where r²(z,t) is the squared distance between the beads at the same height, z, on two distinct polymers and d²_rand is the random square distance between two beads. The symbol 〈…〉 indicates the average over independent runs.
• 2.The pairing probability p(t) of two or more polymer sites (here we define two polymer segments as “paired” whose relative distance is <10% of the linear size L).
• 3.
  The normalized energy of the system,

  $$\mathcal{E}\left(t\right)=\frac{1}{n_0{N}_X}\sum _{i=1}^{n_0{N}_X}\langle {\mathit{ϵ}}_i\left(t\right)\rangle ,$$

  where N_X is the total number of polymers. The sum runs over all the n₀N_X polymer binding sites in the system, and ϵ_i(t) = −1,0 whether the i^th binding site is bound or not to a molecule. Note that ɛ = −1 if all the possible polymer-molecule bonds are saturated.

We measure these quantities at equilibrium and as function of the MC time t. Note that MC algorithms produce artificial dynamics. Yet, in the prevailing interpretation (23), in a system dominated by diffusive motion, the MC Metropolis dynamics is supposed to describe well the general long time evolution of the system. In each simulation, polymer chains and molecules initially occupy random positions in the lattice. To reach the thermodynamic equilibrium state, up to 10⁹ MC steps are carried out. Averages are made over up to 1500 independent runs.

Results

Our investigation has focused on the description of the stable conformations of the polymers that spontaneously emerge in our model systems.

Model A

In this section, we discuss the results obtained with the first version of the model, i.e., when each polymer binding site can bind at most one molecular factor and each molecule can bind at most two binding sites.

A two-polymers system

We start our analysis by considering a system with only two polymers and we investigate how their equilibrium conformational state changes as function of the concentration, c, and binding energy, E, of their binding molecules.

Equilibrium polymer configurations

We find that at low concentrations and binding energies, the conformation of the system corresponds to freely diffusing and independent polymers. Conversely, a colocalization transition occurs if c and E rise above specific thresholds: the two polymers come together and become closely bound to each other. This is outlined by the behavior of the equilibrium value of the polymer pairing probability, p. In Fig. 1 a, p is plotted as function of the binding energy E for a given value of the concentration, c. The value p(E) has a strongly nonlinear behavior: it suddenly increases from 0 to 1 when a threshold value in the energy, $\tilde{E}$ (here defined as the inflection point of p(E)), is crossed. It signals that the two polymers move from a regime where they are independent to a different regime where they are stably kept together by molecular bridges. The value p(E) has a Fermi function behavior, well fitted by

$$p\left(E\right)\simeq {\left[1+exp\left(-\frac{E-\tilde{E}}{\Delta E}\right)\right]}^{-1},$$

where ΔE gives the width of the range where p(E) has values intermediate between zero and one. We find that p(E) behaves similarly at different values of the molecule concentration, c, but the threshold is a function of c: $\tilde{E}=\tilde{E}\left(c\right)$ (see below). Note that an analogous behavior is found if p is plotted as function of c for a fixed value of E, as shown in Fig. 1 b.

Figure 1.

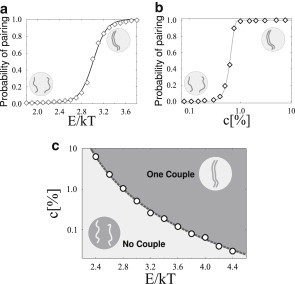
Colocalization in a system with two polymers. The equilibrium colocalization probability, p, of the polymers is shown (a) as function of the bridging molecule binding energy, E (at a fixed value of molecule concentration c = 1.0%) in Model A (Model B gives similar results). p(E) has a sigmoidal behavior highlighting that stable colocalization is only possible if E rises above a threshold value (defined, conventionally, by the inflection point of the curve). (b) p is plotted as function of the concentration, c, of bridging molecules for a fixed value of E (here E = 2.8 kT), showing a similar threshold behavior. In our models, polymer colocalization results from a thermodynamic phase transition occurring in the system. (c) Phase diagram in the (c,E) plane. (Circles) Values of (c,E) at which the phase transition takes place. For (c,E), below the indicator (dashed line), the two polymers diffuse independently, while above threshold they stably colocalize at equilibrium, kept together by the bridging molecules.

In fact, $\tilde{E}\left(c\right)$, in the thermodynamic limit, marks the transition between two phases: when $\tilde{E}$ is exceeded, the paired state becomes thermodynamically stable, because the energy gain deriving from the formation of molecular bridges compensates the entropy loss related to the polymer colocalization. The transition line $\tilde{E}\left(c\right)$ is marked by the dashed curve in the phase diagram of Fig. 1 c. In the region we explored, the transition line can be reasonably well fitted by a power law:

$$c\left(E\right)={\left(E-E_0\right)}^{-\varphi }.$$

Here E₀ represents the minimum value of the binding energy necessary to have the phase transition; we find E₀ = 1.8 kT and ϕ = 3.6. Below the transition line no stable polymer colocalization is possible (p ∼ 0); above it, instead, the polymers are bound to colocalize at equilibrium (p ∼ 100%). The phase diagram illustrates that the transition occurs in a wide range of (c,E) values, showing the robustness and generality of such a thermodynamic mechanism. It also highlights the two main routes that can be followed to induce colocalization: by increasing the polymer-molecule affinity, E (e.g., by changing the chromatin state), or the production of binding molecules (increasing c). Importantly, the energy and concentration values of the transition fall well within the biological expected range (see above).

The dynamics of colocalization

We measured the mean-squared distance of the polymers, d²(t), as function of time to analyze the dynamics of the system. Fig. 2 shows d²(t) for two different values of (c,E), one in the independent polymer phase, the other in the colocalized phase. As expected, for (c,E) below the threshold, d²(t) approaches the value predicted for two randomly placed polymers. Conversely, with higher values of (c,E), d² at long times approaches zero, signaling that polymer colocalization has been attained. An exponential fit well describes the data:

$$d^2\left(t\right)\sim d^2(\infty )+\left[d^2\left(0\right)-d^2(\infty )\right]\text{exp}\left(\frac{-t}{\tau }\right).$$

Here d²(∞) is the equilibrium value of d²(t), and τ is a measure of the characteristic time needed to reach equilibrium. The value τ turns out to be compatible with typical biological timescales: in the (c,E) range we explored (see Fig. 2), we find τ ∼ 1–10 h (33).

Figure 2.

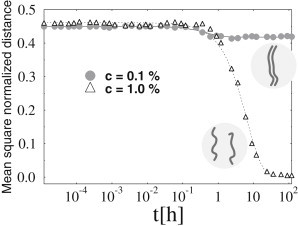
Dynamics of colocalization in a two-polymer system. The normalized polymer mean-squared distance, d²(t), is plotted as function of time t at a fixed binding energy E = 3.4 kT, for the two shown values of the molecule concentration, c, above and below threshold. The polymers are initially positioned at a given distance. At the lower concentration (c = 0.1%, circles), the polymers do not colocalize and attain the average distance of two randomly located polymers. When the concentration is raised to c = 1.0% (triangles), the colocalization transition occurs (see Fig. 1) and the polymers pair off at equilibrium, as shown by d²(t), which eventually collapses to zero. The cases shown concern Model A, but similar behaviors are found with Model B.

The value τ is found to increase with E as well as with c; this suggests that, whereas (c,E) must be above threshold to induce colocalization, upper bounds exist for these two quantities to reach the colocalized equilibrium configuration in a time short enough to be biologically relevant.

A four-polymer system

Next we analyze colocalization in a system with four polymers. A more complex scenario arises because different stable conformations become possible.

Equilibrium polymer configurations

The variety of stable polymer conformations and colocalization states are illustrated in Fig. 3 a, where the probability of each possible state at equilibrium is plotted as a function of the binding energy, E (at a fixed value of the concentration, c). We find that, as seen before, at low energies polymers float independently as all other conformations have a roughly zero probability, but at high E the configuration with two-polymer couples (independent from each other) becomes the most likely. These two regimes are separated by a cross-over region where, on average, only a single, yet unstable polymer couple is formed in the majority of cases. In the high E region, other conformations are also possible (see Fig. 3 a). Their probability slightly increases with an increasing number of binding sites n₀, yet it drops down to zero in the thermodynamic limit (32). For such a reason, and for the sake of simplicity, we do not illustrate further those configurations.

Figure 3.

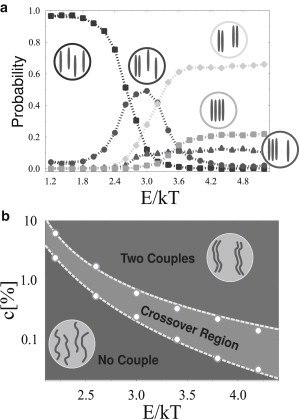
Colocalization of a system of four polymers in Model A. (a) Probability of the different polymer equilibrium configurations as a function of the molecule binding affinity, E, at a fixed molecular concentration (c = 1.0%). Drastic changes in the probability of the different states are observed by increasing E. At low energies no colocalization is found, with the polymers floating independently. As E increases, a region exists where a single unstable couple is formed on average, but strong fluctuations are present. Finally, above a threshold value, a phase transition is crossed and the most likely state corresponds to the formation of two independent, stable couples. As illustrated, other states, having a smaller probability, also exist. (b) System-simplified phase diagram in the (c,E) plane. (Circles) Cross-over region (which disappears in the thermodynamic limit) where only one unstable couple is formed. Upper and the lower regions correspond, respectively, to the state where two couples and four independent polymers are the most probable configurations.

The system phase diagram summarizing the stable conformations in the (c,E) plane is reported in Fig. 3 b. The area within the two dashed lines is the cross-over region, and the circles mark the corresponding transition points (the lower and upper boundaries are defined as the inflection points of the curves in Fig. 3 a corresponding to the probability to have independent polymers and two polymer couples). The cross-over region appears to shrink in the thermodynamic limit.

The dynamics of colocalization

The dynamics in the low E and c phase behaves in a way similar to that described in the previous section. Thus, for brevity, here we focus on the system dynamics in the phase where two-polymer couples emerge at equilibrium, i.e., in the upper region of the phase diagram shown in Fig. 3 b. In Fig. 4 a the probability of each configuration is plotted as function of time. The system starts from a configuration where polymers are randomly positioned. After a time t ∼ 1 h, a first polymer couple is formed, in the relative majority of the samples. At this point, the most likely event to occur is the formation of a second, independent couple, which, after ∼10 h become the most probable conformation (Fig. 4 c shows a typical equilibrium state in this configuration).

However, in a small percentage of cases, three or four (see Fig. 4 d) polymers come together. The corresponding plot of ɛ(t), i.e., the normalized energy of the system, as function of time (Fig. 4 b, square markers) clearly shows the different stages of the average dynamics. The first plateau marks the building of the first, stable polymer couple. This is achieved comparatively quickly (order of minutes), as in this first part of the dynamics all the polymers move independently and six possible couples can be formed. After a longer time (t ∼ 1–10 h, comparable to the time of pairing in a two-polymer system, see Fig. 2), the other two polymers have also paired off, as the second, lower plateau of ɛ(t) signals. Conversely, ɛ(t) has only one plateau when the system is in the unpaired phase (Fig. 4 b, diamond markers): in this case, the number of polymer-molecule bonds reaches an equilibrium value that is not sufficient to form thermodynamically stable polymer couples.

A three-polymer system

Equilibrium polymer configurations

Finally, we briefly discuss a system with three polymers. Note that, in this case, the equilibrium state of the system drastically changes at certain values of the concentration/affinity of the molecules, switching between a configuration with uncoupled, independent polymers and a regime where all the three polymers are colocalized. Rarely we find one stable couple with a third free polymer (∼5%, see Fig. 5, a and b). As in the four-polymer system, such a configuration is expected to vanish in the thermodynamic limit and for simplicity is not reported in the phase diagram of Fig. 5 b. As in the previous case, a cross-over region exists with a single, unstable polymer couple (Fig. 5 a, circles; and Fig. 5 b).

Figure 5.

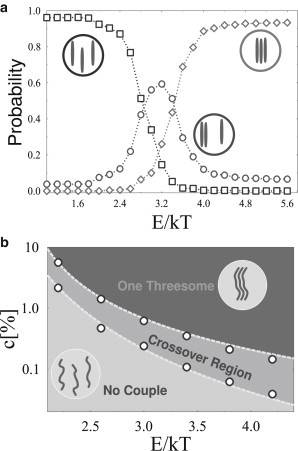
Colocalization of a system of three polymers in Model A. (a) Probability of the different polymer states at equilibrium as a function of the polymer-molecule binding energy, E (c = 0.5%). Polymers are independent at low E, while all of them colocalize above a threshold (after a cross-over region; see text and Fig. 3). (b) System phase diagram in the (c,E) plane; (circles) indication of boundary of the cross-over region between the two main phases.

Model B

In this section, for comparison, we briefly illustrate the corresponding results obtained with the second version of the model where multiple bonds among molecules and polymer binding sites are allowed.

Two polymers

The overall properties of a two polymer system do not differ appreciably in the two versions of the model, and the system dynamics is very similar to the one described above. In both model versions two different equilibrium states are found. The nature of the phase transition is the same, but in Model B it is found at comparatively lower values of molecule concentration/affinity (see also Scialdone and Nicodemi (19)).

Three and four polymers

Important differences are found in a system with more than two polymers. Two major thermodynamics phases are still observed: below threshold the polymers diffuse independently at equilibrium while, above thresholds, they become colocalized altogether. While the dynamics in the unpaired phase remains unchanged, in the paired one the polymers are observed to gradually come together and remain bound (data not shown). Fig. 6 schematically summarizes and compares the results of the two versions of the model.

Figure 6.

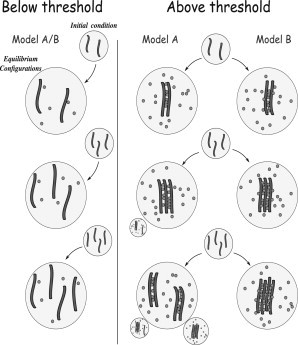
Summary of the stable states in Model A and B. Here the different equilibrium configurations of the polymers in the two variants of the model are pictorially illustrated. (Left panel) System configurations found in the low E and c phase, where polymers float independently. (Right panel) Summary of the configurations emerging in the high E and c phase, for Model A (left) and B (right column). In a two-polymer system, the same dynamics/equilibrium behavior is found in Models A and B, while in a system with many polymers, different configurations can be found in the two models. The equilibrium configurations having small probability (vanishing in the thermodynamic limit) are represented at a smaller scale.

X chromosome colocalization at XCI

The above sections have illustrated the variety of stable conformations in which our simple system can be found. The following and final part of our article is very speculative: we now explore the possible scenarios linking our results above to the colocalization of X chromosomes observed at X inactivation (XCI) (11–13). We also discuss the possible connections between X colocalization and X inactivation in cells with different copy numbers of the X by comparing model predictions against available data (21). These arguments could help in restricting the number of models consistent with the contemporary data on XCI.

X chromosomes have been shown to colocalize in XX diploid cells during the early stages of X inactivation (11–13). The colocalization regions lie within the so-called X-inactivation center (Xic), which controls the inactivation process (11–13). Xic pairing is known to be strictly related to the “counting&choice” step of XCI, whereby the cell has to count the number of X chromosomes and to choose the X to be silenced (11–13). Recent investigations appear to indicate that X colocalization is required for “counting&choice” and occurs before that (34). And here we work starting from such evidences. We assume that colocalization is produced by the thermodynamic mechanisms described above. Then we use our predictions on the possible X-pairing configurations, along with the so-called symmetry-breaking (SB) model of “counting&choice” (20,35,36), to obtain a probability distribution for the number of inactive X chromosomes in cells with multiple X copies. This is the quantity that can be compared with the data available as of this writing. Other interesting models of “counting&choice” (37,38) could also be employed along with the scenario on colocalization discussed here; nevertheless, for definiteness, we only consider the SB one.

X inactivation in XX and XY diploid cells

In the following, we focus on the version of the SB model investigated in Scialdone et al. (20). It poses that XCI is regulated by two molecular aggregates, an Activating Factor (AF) and a Blocking Factor (BF) that, in diploid XX cells, bind in a mutually exclusive way the two X chromosomes, such that one is marked for inactivation, while the other remains active. In XY males, the only X is assumed to be bound by a BF (e.g., because its affinity for the Xics is higher than the one of the AF; see Scialdone et al. (20)), and so it remains active. Monte Carlo computer simulations show that the situations discussed above correspond to the most likely events, having a very high probability. In a small fraction of cases, though, deviations can be observed: for instance, the molecular aggregates can fail to bind the X, determining an aberrant number of inactive X. The probability of these events can be calculated by Monte Carlo simulations and we now discuss their effects in the estimation of the inactivation probability for the X.

Let us consider first the case of XX diploid cells. In these cells, as the X chromosomes colocalize, in the vast majority of cases one inactive and one active X are found, say, with a probability w. However, there is also a probability p that the inactivation process is not initiated, and neither X is inactivated; if we assume, for sake of simplicity, that in the SB model an X gets inactivated only when bound by an AF, this corresponds to the case when the AF does not bind any X. By Monte Carlo simulations, we find that w ∼ 95% and p ∼ 5% (for values of E ∼ 5 kT; see also Nicodemi and Prisco (36)). These probabilities are consistent with the data reported, e.g., in Monkhorst et al. (21), where the percentage of wild-type cells that fails to trigger X inactivation is ∼6–7%. Experiments also show that in a very small fraction of cells both X chromosomes are inactivated (∼2% (21)). This can be explained, for instance, by assuming that by a fluctuation two AFs have formed and bound the X chromosomes. Yet, for the sake of simplicity, in the discussion below, we neglect those rare events (see below for further discussion on this point).

Cells with multiple copies of the X chromosomes

While several experiments have been carried out to count the number of inactive X chromosomes in cells having multiple X copies (see, e.g., Monkhorst et al. (21,37)), so far no experimental study has addressed the question of how X colocalization occurs in these cells and which distinct groups of paired X chromosomes form. Our calculations above (for definiteness, consider Model A) indicate that the physical contacts between different groups of colocalized X chromosomes are very rare and the groups behave independently. Thus, we can assume that, in each group of colocalized X chromosomes, the above SB mechanism will be activated independently. Under these hypotheses, the number of inactive X in a cell results from two main stochastic processes: the colocalization event, which determines the number of independent groups of X chromosomes; and the SB process, that is responsible for the inactivation of the X chromosomes in each independent group.

The colocalization models we discussed in this article (Model A and B) can be used to estimate the probability of the different configurations of the X in a cell with three or four copies of X chromosomes. We can then combine the results of our model for colocalization and the probabilities of inactivation derived from the SB model, to calculate the probability distribution of inactive X. In general, in the SB model, the inactivation probability depends on the relative abundance of the molecular components of the AF and the BF (20), that, in turn, is likely to depend on the number of X copies as well as on the cell's ploidy (Xu et al. (14), Scialdone et al. (20), Monkhorst et al. (37), Jonkers et al. (39), and see also below).

As a first approximation, in the following we assume that the inactivation probabilities estimated above for diploid XX cells can be also employed for tetraploid XXXX cells, because the autosome/X ratio is the same, and for simplicity that they are approximately correct also for tetraploid XXXY cells. Namely, we assume that, in these cells, in any group of two or more paired X chromosomes, only a single X can get inactivated with a probability w ∼ 95%, because it is bound to an AF (see above). Starting from these assumptions, we calculate the probability distribution of the number of inactive X chromosomes, $\mathcal{P}$(X_i), for tetraploid XXXX and XXXY cells, where experimental data are available for a direct comparison (21). In the last paragraph of this section, we discuss our approximations and the case of cell types with different ploidies.

Tetraploid XXXX cells

In a system with four interacting polymers, described by Model A, we saw that each phase is characterized by one polymer configuration that has the highest occurrence probability (see Fig. 3): four independent X chromosomes, or a single X couple, or two independent couples. Below, to simplify the discussion, we neglect the configurations with marginal probabilities in each regime. Thus, for example, in Model A at high concentration/affinity of the molecular binders, we assume that only the configuration with two independent X couples is found. The closer the thermodynamic limit, the more accurate is such an approximation.

As discussed above, and coherently with the requirements needed to explain XCI in males (20), we assume that an unpaired X is bound in the majority of cases by a BF (with a 95% probability, see above) and remains active. The inactivation process in a couple of paired X chromosomes proceeds as described in the previous section in diploid XX cells. With these simplifying hypotheses and the assumptions that groups of unpaired X chromosomes are independent, $\mathcal{P}$(X_i) can be finally calculated: the three top panels of Fig. 7 show the predictions of our model in the three pairing states along with the experimental data reported for tetraploid XXXX cells (21). The results in Fig. 7 illustrate that, under our hypotheses, the configuration with two independent couples (top-left panel in Fig. 7) is the one that better explains the complex experimental distribution.

Figure 7.

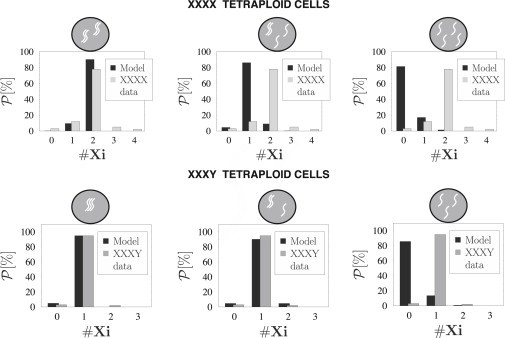
Probability distribution of inactive X chromosomes in XXXX and XXXY tetraploid cells. (Top panel) Probability distribution of the number of inactive X chromosomes, $\mathcal{P}$, in tetraploid XXXX cells. (Shaded bars) Experimental data (21). (Solid bars) Predictions in the different colocalization states (top of each panel). Colocalized state, corresponding to the configuration where two independent X couples are formed (top-left panel), best describes the data. (Bottom panel) Probability distribution of the number of inactive X chromosomes in tetraploid XXXY cells. (Shaded bars) Experimental data (21). (Solid bars) Predictions. Good agreement is found in the configurations where at least two X chromosomes are paired (bottom-left and central panels).

Model B can be also considered to describe the colocalization of the X chromosomes in XXXX cells. In Model B, only a state with all the X chromosomes bound together is found beyond the state with four independent X chromosomes. Under the very same assumptions we made before, the probability distribution of the number of inactive X, $\mathcal{P}$, can be calculated. In this case, the predicted $\mathcal{P}$ does not match the experimental results (data not shown) because, for example, with four X colocalized, in the vast majority of cases three active X and one inactive X would be found, in contrast to experimental results. Thus, under our schematic hypotheses, Model A can better explain the data.

A different set of assumptions can be considered to estimate $\mathcal{P}$ (e.g., by taking into account some rare events like the formation of multiple AF/BF). Yet, $\mathcal{P}$ remains qualitatively unaffected as long as the assembly of a single AF and BF in each group of paired X is assumed to be the most likely event (i.e., having a probability ≳90%).

In summary, the best agreement with data, is found when X colocalization is described by Model A in its high-affinity/binder concentration phase.

Tetraploid XXXY cells

Fig. 5 illustrates the three possible spatial configurations in a system with three X chromosomes as predicted by Model A: three independent X chromosomes, a single X couple, or all the three X chromosomes grouped together. In Model B, instead, the three X chromosomes either remain separated, or come together to form a single group. The bottom panels in Fig. 7 show $\mathcal{P}$(X_i) in each of these configurations. In particular, it is seen that the experimental shape of $\mathcal{P}$ in tetraploid XXXY cells (gray bars) is well fitted when at least a couple of paired X chromosomes are present in the system (bottom-left and central panel), whereas the configuration with the three independent X chromosomes produces wrong predictions (bottom-right panel).

In summary, the best agreement with data is found when X colocalization is described by either Model A or B in its high-affinity/binder concentration phase.

Cells with other ploidy

As mentioned before, the SB model predicts that the inactivation probability depends on the relative concentration of the AF/BF molecular components (20), and recent data suggest that autosomes as well as the X chromosomes themselves code for these molecular components (14,39). The estimation of these effects on purely theoretical grounds is hard because key experimental information is still missing. Yet, it has been shown that the number of inactive X chromosomes in a cell depends on the ratio between the number of X chromosomes and the ploidy of the cell (X:A ratio) (37): on this basis, the hypotheses we made above, i.e., that the same inactivation probability can be used in diploid XX cells (X:A = 1), tetraploid XXXX cells (X:A = 1), and tetraploid XXXY cells (X:A = 0.75), could be a roughly correct first approximation.

In cells with different X:A ratios, the change in the relative concentration of AF/BF components can make the system get stuck in transient, nonequilibrium states where more than a single AF/BF are assembled in a group of paired X chromosomes, and this can greatly affect the shape of $\mathcal{P}$. For example, the experimental observation that, in most of the cases, two X are inactivated in diploid XXX cells (see Starmer and Magnuson (38) and references therein) can be rationalized by assuming that in the group of three paired X chromosomes, two AF are assembled, as a result of the increased concentration of AF components encoded by the X themselves. Similarly, a possible reason for the failure of X inactivation initiation in tetraploid XXYY cells (21), is the overabundance of BF components produced by the autosomes, which may hinder the AF assembly. While qualitative predictions (e.g., the position of the peak of $\mathcal{P}$) can be easily made for these cells, quantitative descriptions of $\mathcal{P}$ would be too speculative at this stage without any additional experimental information.

Conclusions

In summary, we investigated statistical physics models to explore different scenarios about DNA colocalization, with a particular focus on systems including multiple copies of interacting DNA loci. We considered the general framework where DNA colocalization results from the bridging of diffusing molecular factors. In that context, we showed that stable colocalization of DNA loci is possible only when the concentration/affinity of the molecular factors arises over a precise threshold (18,19), via thermodynamic phase transitions. The specific spatial conformation attained depends on the properties of the DNA-molecule interaction and, for example, a key role is played by the binding valency. When multiple MF-BS bonds are allowed (Model B), the general scenario is that in the colocalized configuration, all the DNA loci come together and form a single group. A quite different, and more complex picture emerges when the constraint of single valency is introduced (Model A): in a system with three DNA loci, in the colocalized phase they group all together, whereas in a system with four DNA loci, two independent couples of loci are typically formed. The Brownian phase and the colocalization phase are separated by a cross-over region, characterized by the formation of a single unstable DNA couple.

The presence of such cross-over regions is typical of phase transitions in finite systems, and their width decreases as the size of the system is increased, until they disappear in the thermodynamic limit (32). Our model predicts that in such a region the formation of transient, unstable polymer couples should be observed. We show that in our minimal model the transition between the different phases is predicted to occur in biologically relevant ranges of concentration/affinity of the molecular binders. These provide only an estimate of real concentrations/affinities, because in real biological situations a number of complications arise (40).

Because Model A and B provide different predictions on colocalization, they can be discriminated against real data in different situations. Here we considered X chromosome pairing at XCI as a case study because some indirect information about pairing in cells with multiple copies of the X have been reported. Starting from the above models of pairing we obtained the distributions of colocalized X and, under some additional assumptions, the probability distributions of the number of inactive X chromosomes in a tetraploid XXXX and XXXY cells. By comparing our in silico data with experimental data, we found that the scenario best describing the data from XXXX cells corresponds to the colocalization phase of Model A, i.e., when two independent couples of X chromosomes are formed. Data from XXXY cells are, instead, compatible with the colocalization phase of either Model A or B.

Precautions must be taken when considering the result of such comparisons, though, as many complications arise in reality. For example, our results refer to an ideal population of perfectly synchronized cells, whereas experimental samples do contain cells at different stages of differentiation and XCI. The probability distribution $\mathcal{P}$ measured in real cells could be also biased by the death of cells with a wrong number of inactive X and by cell divisions that occur at a rate depending on the number of inactive X (21). Nevertheless, the analysis of our models provides a first quantitative scenario on DNA colocalization, to our knowledge; and our further speculations, under a number of simplifying hypotheses, may shed some light on the relation between X colocalization and “counting&choice” at XCI.