Abstract
The NaK channel is a cation-selective protein with similar permeability for K+ and Na+ ions. Crystallographic structures are available for the wild-type and mutated NaK channels with different numbers of cation-binding sites. We have performed a comparison between the potentials of mean force governing the translocation of K+ ions and mixtures of one Na+ and three K+ ions in a mutated NaK channel with only three cation-binding sites (NaK-CNG). Since NaK-CNG is not selective for K+ over Na+, analysis of its multi-ion potential energy surfaces can provide clues about how selectivity originates. Comparison of the potentials of mean force of NaK-CNG and K+-selective channels yields observations that strongly suggest that the number of contiguous ion binding sites in a single-file mechanism is the key determinant of the channel’s selectivity properties, as already proposed by experimental studies. We conclude that the presence of four binding sites in K+-selective channels is essential for highly selective and efficient permeation of K+ ions, and that a key difference between K+-selective and nonselective channels is the absence/presence of a binding site for Na+ ions at the boundary between S2 and S3 in the context of multi-ion permeation events.
Introduction
How potassium channels select K+ ions instead of Na+ ions has been a matter of intense debate since the discovery of independent K+ and Na+ conduction pathways across cell membranes more than 50 years ago. A first glimpse of how K+ selectivity is realized at the atomic level was initially provided in 1998 by the crystallographic structure of the KcsA K+-channel (1). More recently, the first atomic structures of a Na+-selective channel (2) and of a Na+/K+ nonselective channel (NaK) (3) have also been solved, offering a more complete view at the atomic level of some of the proteins responsible for selective conduction in cells. The NaK channel, similar to cyclic-nucleotide-gated (CNG) channels, conducts Na+, K+, Rb+, and Ca2+ ions (4). Here, we have simulated ion conduction through a mutated NaK channel (5), NaK-CNG, which differs from K+-selective channels in the number of cation-binding sites. To reveal key differences in selectivity, the potentials of mean force governing the translocation are compared with analogous simulations in a K+-selective channel (6).
The amino acid sequence associated with the region of K+ channels responsible for selective conduction, the selectivity filter (SF), is highly conserved among different K+ channels. It is located at the extracellular side of the protein pore, and it contains a sequence motif (TVGYG) characteristic of K+ channels. The crystal structure of the NaK channel shows that the overall structure is very similar to the pore domain of K+ channels. The major differences between the NaK channel and K+ channels are in the ion-binding regions (Fig. 1). Five binding sites for K+ ions, S0–S4 (numbered from the extracellular side), are defined in the SF of potassium channels. A K+ ion is coordinated by eight oxygen atoms from the protein in sites S1–S4. In contrast, only four protein oxygen atoms interact with the ion in S0, with the remaining oxygen atoms of the ion-coordination shell donated by water molecules. The SF of NaK, T63VGDG, has only two ion-binding sites, which are built using the backbone carbonyl oxygen atoms of residues Thr63 and Val64 along with the side-chain hydroxyl of Thr63 (3). These two binding sites in the NaK channel are structurally similar to the S3 and S4 binding sites in the SF of K+ channels. Instead of binding sites S1 and S0 of K+ channels, the crystallographic structure of wild-type NaK presents a water-filled vestibule. An impressive number of x-ray structures for NaK mutants in complex with different cations have been solved at high resolution and characterized electrophysiologically. The mutated NaK channel, NaK-CNG, used in this study has the NaK sequence T63VGDGNF changed to T63VGDTPP, and like the wild-type NaK channel, it is still nonselective. The determination of a high-resolution crystal structure revealed a dramatic main-chain conformational change in the position of the acidic residue Asp66 and the preceding Gly65 residue. The SF of NaK-CNG is characterized by three contiguous ion-binding sites where the water-filled vestibule in wild-type NaK is replaced with an additional ion-binding site in the mutant, utilizing eight backbone carbonyl oxygen atoms from Val64 and Gly65 and equivalent to S2 in the SF of K+ channels.
Figure 1.
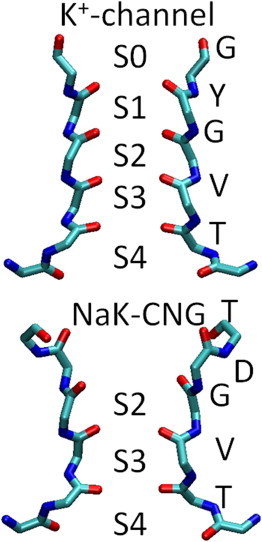
SF of K+-selective channels and of NaK mutated channel with three-cation binding sites (NaK-CNG). Filter residues are shown in licorice representation for just two opposite subunits.
Molecular dynamics (MD) simulations were crucial for understanding how K+ ions and water translocate through the SFs of potassium channels. Numerical approaches as diverse as free-energy perturbation (7), umbrella sampling (8,9), Brownian dynamics simulations (10), hybrid MD-Brownian dynamics simulations (11), classical MD simulations (12–14), and MD simulations with external electric fields (15,16) all render the same description of K+ permeation. In a conductive potassium channel, the SF switches between two different loading states with ions in S4–S2 and S3–S1, respectively. These two states have similar energies, and they are separated by low energy barriers (2–4 kcal/mol). An incoming ion will prompt a concerted motion of the ions already inside the SF, which will be followed by ejection of the ion at the opposite side of the pore. Hodgkin and Keynes introduced the idea of the knock-on mechanism in their classical studies of K+/Na+ conduction (17).
To understand how selectivity for K+ ions emerges, it is necessary to explain how the presence of Na+ ions perturbs the knock-on conduction mechanism. Some leading evidence of the effects of a Na+ ion on the multi-ion conduction mechanism of K+-selective channels was provided by Thompson et al. (18). A combination of numerical simulations and experimental analyses determined that a Na+ ion approaching the SF from the intracellular side can bind to the upper boundary of site S4. However, this Na+ ion encounters energy barriers higher than a K+ ion when it moves deeper inside the pore. Recently, the potential of mean force of a Na+ ion permeating the channel in the context of a K+-occupied SF was described (6). Analysis of the free-energy profiles illustrated that K+ and Na+ ions in a mixture encounter much higher energy barriers than do K+ ions alone when translocating though the pore of the KirBac1.1 channel (6). Similar results were obtained by Egwolf and Roux for the KcsA channel (19). Briefly, when a Na+ ion approaches the intracellular side of a SF loaded with three K+ ions, it can easily access a position between S4 and S3. However, an energy barrier of ∼7 kcal/mol prevents Na+ from any further displacements toward binding site S2. In a similar way, when a Na+ ion approaches a SF loaded with three K+ ions from the extracellular side, it can easily reach a position between S0 and S1, but further progress of the Na+ ion toward S2 is hampered by an energy barrier of >10 kcal/mol.
Two observations are crucial to understanding the disqualification of a Na+ ion from a K+-occupied SF. First, Na+ and K+ ions tend to bind at different positions along the SF of K+ channels. K+ ions bind at the centers of sites S0–S4, where an ion is coordinated by eight oxygen atoms disposed in an antiprism geometry. This cage of oxygen atoms mimics the first hydration shell of K+ ions (20). In contrast, Na+ ions have a preference for binding at the boundaries of sites. At these positions, a Na+ ion is coordinated by four oxygen atoms from the protein and two oxygen atoms from surrounding water molecules. These oxygen atoms form an octahedron with the Na+ ion at its center, a configuration that resembles the first hydration shell of Na+ (20). Second, when a mixture of three K+ ions and one Na+ ion permeates the pore, the energy minima for the Na+ ion are usually located at the boundaries between two binding sites, with a significant exception in S2. Here, the minimal energy configuration of the permeating Na+ ion corresponds to a situation where the ion is at the center of the binding site rather than at its boundaries. In this case, Na+ is not coordinated by oxygen atoms in an octahedral configuration, and from the point of view of the permeating Na+ ion, a pore mainly occupied by K+ ions does not present a sequence of identical binding sites. Therefore, when only K+ ions are considered, a set of equally spaced binding sites exists and permeation proceeds through a knock-on mechanism characterized by low energy barriers. In contrast, in a situation with three K+ ions and one Na+ ion, the chain of consecutive binding sites is interrupted and high energy barriers are encountered by Na+.
The connection between selectivity and a particular number of consecutive binding sites for cations was experimentally established in an elegant study by Jiang and co-workers (5). X-ray structures were described for a set of mutated NaK channels that differ only in their number of binding sites. Selectivity for K+ over Na+ emerged only when four binding sites were present in the structure. In contrast, pores with just two or three binding sites were not selective. These experimental structures of nonselective channels are a good starting point to continue dissecting and analyzing selectivity mechanisms by numerical simulations. Previously, we analyzed the conduction of K+ ions in the NaK-CNG mutated channel, which presents three binding sites analogous to sites S2–S4 of K+-selective channels (21). According to our numerical simulations, K+ ions permeate NaK-CNG and K+ channels in a similar way. If selectivity emerges as a result of disrupting the sequence of binding sites in the presence of K+/Na+ mixtures, as suggested by free-energy maps of ion conduction in K+ channels (6), the NaK-CNG channel should not exhibit this property. In other words, in contrast to what is observed in K+ channels, binding sites S2−S4 of NaK-CNG should offer a low energy path for conduction of K+ ions, Na+ ions, and mixtures of K+ and Na+ ions. To follow this line of inquiry, free-energy profiles have been calculated for mixtures of three K+ ions and one Na+ ion in the pore of the mutated NaK channel, NaK-CNG.
Materials and Methods
The atomic coordinates of the NaK-CNG channel were defined according to the Protein Data Bank entry 3K03 (5). Residues 22–113 were included in the model together with the crystallographic water molecules and the K+ ions in the SF. The channel was centered in the xy plane with the permeation pathway aligned to the z axis, and it was embedded in a preequilibrated bilayer of 569 dioleoylphosphatidylcholine molecules. The upper layer of the lipid membrane was aligned to the center of mass along the z axis of Phe74 residues. Lipid molecules that were <1.2 Å from protein atoms were removed. The system was solvated with >15,000 water molecules. Potassium and chloride ions were added to neutralize the system to a final concentration of 150 mM. To equilibrate the atoms around the channel, 2000 steps of energy minimization and 400 ps of MD simulation were performed, with restraints applied to the backbone atoms of the protein, the oxygen atoms of the crystallographic water molecules, and the ions in the filter. Restraints were initially set to 10 kcal mol−1 Å−2 and gradually reduced to zero. Unrestrained MD simulation followed. The starting atomic systems used for the free-energy calculations were taken after 1 ns of unrestrained MD.
MD trajectories were simulated with version 2.8 of NAMD (22), using the CHARMM27 force field with CMAP corrections (23), and the TIP3 model was used to simulate water molecules (24). Parameters for K+ and Na+ ions inside the channel were defined according to Roux and Bernèche (25). All the simulations were performed in the NPT ensemble. The pressure was maintained at 1 atm using a Nosé-Hoover Langevin piston control (26), with a period of 100 fs and damping-time constant of 50 fs. Temperature was maintained at 300 K by coupling to a Langevin thermostat, with a damping coefficient of 5 ps−1. Electrostatic interactions were treated by the particle mesh Ewald algorithm (27), with grid spacing <1 Å. A smoothed cutoff (10–12 Å) was used for the van der Waals interactions. Equations of motion were integrated with a time step of 2 fs. The SETTLE algorithm was used to restrain hydrogen atoms (28). The cumulative simulation time in this study was >450 ns.
The free-energy maps for the mixtures of three K+ ions and one Na+ ion were calculated using the umbrella sampling technique (29,30). Free-energy maps were calculated with the Na+ ion occupying any of the four positions in the chain of the permeating ions. In what follows, ions are numbered from 1 to 4 starting at the extracellular side. Harmonic potentials restrained the positions along the z axis of ions 1 and 4 (force constant 10 kcal mol−1 Å−2), as well as the center of mass of ions 2 and 3 (force constant 20 kcal mol−1 Å−2). Our initial guess was that the center of the harmonic potential acting on ion 4, the innermost ion, moved from 7 Å below the position of the carbonyl oxygen atoms of residue Thr63 to 1 Å above them, in steps of 1 Å. The center of the harmonic potential acting on the center of mass of ions 3 and 2 moved from 6 Å to 13 Å above the center of the harmonic potential acting on ion 4, in steps of 0.5 Å. Finally, the center of the harmonic potential acting on ion 1, the outermost ion, moved from 6 Å to 13 Å above the center of the harmonic potential involving ions 3 and 2, in steps of 1 Å. This initial set of umbrella-sampling simulation covers all the possible configurations of ions in the filter, with two adjacent ions never less than one binding site, and never more than three binding sites, from each other (3 Å is the average distance between the centers of two consecutive binding sites). For each free-energy map, ∼600 windows were simulated. Umbrella-sampling simulations with harmonic potential restraints centered outside the predefined ranges were added when the preliminary analysis revealed the presence of energy minima that extended beyond the region of the configurational space sampled. The starting structures for the umbrella-sampling simulations were generated by systematically translating the ions to their selected positions, moving the surrounding water molecules accordingly, and mutating one of the ions involved in the permeation process to Na+. Each umbrella-sampling simulation consisted of 5000 steps of energy minimization with restraints applied to the backbone atoms of the filter, followed by an MD trajectory with harmonic restraints applied only to ions 1–4. The first 20 ps of the trajectories were considered the equilibration periods and were thus discarded; the remaining time was used to calculate the 4-dimensional free-energy maps according to the weighted histogram analysis method (31). In the extracellular solution, the displacement of ions perpendicular to the permeation axis is unbounded; this could affect the quality of the estimated energy difference between bulk solution and binding sites inside the filter, but it does not affect the quality of the free-energy maps inside the filter, where the analysis is focused.
The difference in the free energy of the minima from different energy maps were calculated using the free-energy perturbation (FEP) technique under the dual-topology paradigm (32). The structures of the terminal states for the FEP simulations corresponded to the last snapshot of the umbrella-sampling simulations with the center of the harmonic restraints closer to the energy minima under analysis. Soft-core potentials were used with a shifting coefficient of 2.0 Å for the van der Waals radii. The alchemical transformation was realized by changing the coupling parameter λ, which is a general-extent parameter introduced to transform the system between the reference, i.e., the state with λ = 0, and the perturbed state, i.e., the state with λ = 1. The FEP calculations were carried out using 20 intermediate states with window lengths of 300 ps, which represents a total simulation time of 6 ns for each unidirectional simulation. The first 100 ps of each window was discarded as the equilibration period. Six independent runs were performed for each transformation, three in each direction. Energy differences were calculated as the average value in these six independent runs, with the standard deviation giving an estimate of the error.
Results and Discussion
Using the same convention employed to define binding sites S0–S4 in potassium channels, ions occupying the SF of NaK-CNG are numbered from the extracellular to the intracellular side. Accordingly, the energy map for the ion configuration K+/K+/K+/Na+ describes the entrance of a Na+ ion (designated Na4) from the intracellular side of the pore, when the SF is loaded with two K+ ions (designated K3 and K2) and a fourth K+ ion (K1) is in the extracellular side. The same convention is adopted for the rest of the ion configurations analyzed. When Na4 is in the intracellular cavity of the channel, K+ ions occupy sites S4, S2, and S1 in the most stable energy configuration (Fig. 2 A, I). In the NaK-CNG channel analyzed here, S1 differs from the conventional S1 binding site defined in potassium channels. The carbonyl oxygen atoms that delimit the upper boundary of site S1 in NaK-CNG are distant from the channel axis. As a consequence, a perfect antiprism cage of oxygen atoms cannot be formed in S1 (Fig. 1), and the density of water molecules reaches a value close to the bulk density already at the upper boundary of this site (whereas in K+-selective channels this happens at the upper boundary of site S0). Nevertheless, K+ ions still bind at this site, and the same nomenclature used in potassium channels will be used here for convenience. If ion Na4 moves from the intracellular cavity toward the pore, a second energy minimum is found with the Na+ aligned with the plane defined by the side-chain oxygen atoms of Thr63 residues, and K+ ions in S3, S1, and above the plane defined by the carbonyl oxygen atoms of Asp66 (Fig. 2 A, II). The energy minima characterized by the presence of Na4 in the intracellular cavity and at the lower boundary of binding site S4, respectively, are separated by energy barriers of ∼6 kcal/mol. A third energy minimum exists with Na4 at the boundary of sites S4 and S3, K3 in S2, K2 close to the carbonyl oxygen atoms of Asp66, and K1 in the extracellular solution (Fig. 2 A, III). The energy barriers between energy minima II and III are <6 kcal/mol.
Figure 2.
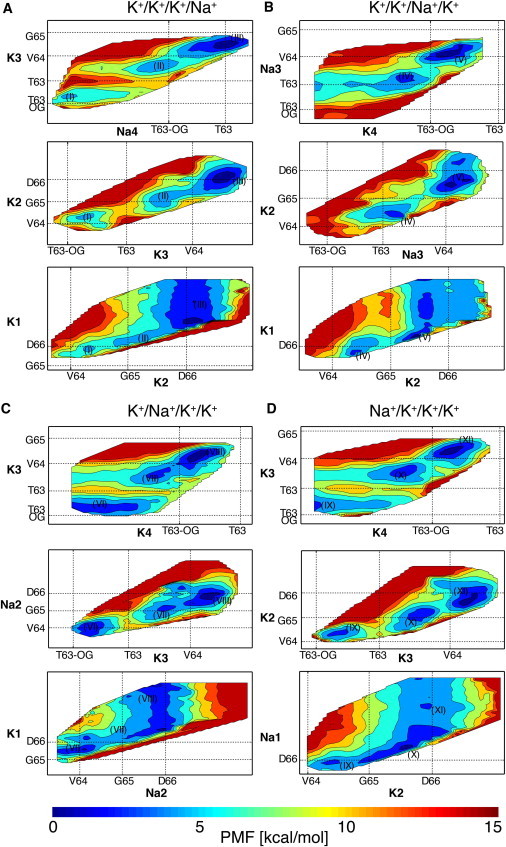
Free-energy map for the configuration of ions K+/K+/K+/Na+ (A), K+/K+/Na+/K+ (B), K+/Na+/K+/Na+ (C), and Na+/K+/K+/Na+ (D). Two-dimensional projections of the calculated 4-dimensional energy map are shown. Contour lines are drawn every 2 kcal/mol. Labels along the x/y axes refer to the average positions along the permeation pathway of the carbonyl oxygen atoms of residues Thr63 (T63), Val64 (V64), Gly65 (G65), Asp66 (D66), and of the side-chain oxygen atoms of residues Thr63 (T63-OG). These oxygen atoms delimit the K+-binding sites S1–S4. Roman numerals are used to identify the different energy minima in the 2-dimensional projections.
Displacement of a Na+ ion away from the S4-S3 boundary and moving toward the inside of the pore was studied by calculating the energy map using the K+/K+/Na+/K+ ion configuration (Fig. 2 B). The first energy minimum displays K4 in the intracellular cavity, Na3 at the S4-S3 boundary, K2 in S2, and K1 close to the carbonyl oxygen atoms of Asp66 (Fig. 2 B, IV). Occupancy of binding sites S1–S4 is identical in configurations IV and III, with the exception that a K+ ion has moved from the extracellular side of the pore (ion K1 in configuration III) to the intracellular cavity (ion K4 in configuration IV). The free-energy perturbation technique was used to calculate the energy difference between configurations III and IV. For this calculation, the K+ ion at the extracellular side of the channel in configuration III was alchemically transformed into a water molecule, and at the same time, a water molecule in the cavity was alchemically transformed into a K+ ion. The estimated energy difference in six independent runs was close to zero (0.61 ± 0.29 kcal/mol). A second energy minimum is found in the energy map corresponding to a configuration of ions K+/K+/Na+/K+, with K4 in S4, Na3 between S3 and S2, K2 in S1, and K1 outside the pore at the extracellular side (Fig. 2 B, V). The energy of configuration V is ∼2 kcal/mol lower than the energy of configuration IV. The energy barrier between IV and V is ∼4 kcal/mol in the outward direction, and ∼6 kcal/mol in the inward direction.
Ions inside the pore are in analogous sites in configuration V of the free-energy map corresponding to the K+/K+/Na+/K+ set (Fig. 2 B) and in configuration VI of the free-energy map of the K+/Na+/K+/K+ set (Fig. 2 C). What differentiates configuration V from configuration VI is that the K+ ion is at the extracellular side of the pore in the former and at the intracellular side in the latter. In configuration VI, ion Na2 is aligned with the side-chain oxygen atoms of Val64 residues. Other two energy minima are observed with 1), Na2 at the boundary of S2 and S1 sites, and K+ ions in the intracellular cavity, S3, and above Asp66 (Fig. 3, VII), and 2), Na2 close to the carbonyl oxygen atoms of Asp66, and K+ ions in S4, S2, and the extracellular solution (Fig. 2 C, VIII). The energy barriers between the three minima VI–VIII are <6 kcal/mol. From the region around Asp66, a Na+ ion can easily travel toward the extracellular solution once an incoming ion at the extracellular side of the pore assists the concerted ionic movement, as shown in the energy map corresponding to ion configuration Na+/K+/K+/K+ (Fig. 2 D). The free-energy perturbation technique was used to calculate the energy difference between configurations I and XI. In these configurations, K+ ions occupy the same position, whereas the position of the Na+ ion differs (intracellular in I and extracellular in XI). The estimated energy difference in six independent runs was close to zero (0.45 ± 0.30 kcal/mol).
Figure 3.
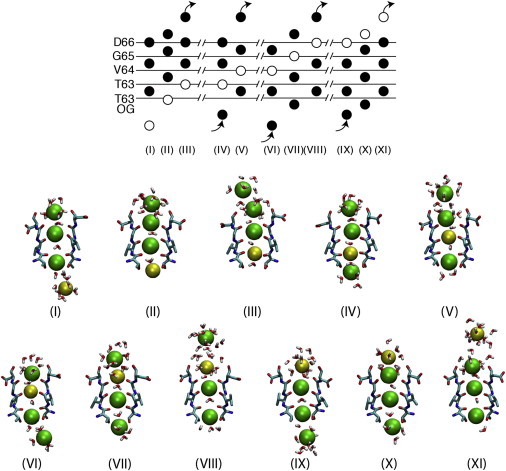
Representative minimum energy configurations from the permeation pathways of three K+ and one Na+. Roman numerals indicate the energy minima from Fig. 2. (Upper) Schematic representation of a complete permeation event of a Na+ ion (white circle) in the context of three K+ ions (black circles). (Lower) Structures of the filters in the various energy minima are shown. Two opposite subunits of the filter (residues 63–66) are shown in licorice representation, together with the permeating ions (green, K+; yellow, Na+) and the water molecules that are <4 Å from these ions. The snapshots were taken from the umbrella-sampling simulations.
A complete permeation event of a Na+ ion moving from the intracellular to the extracellular side of the pore, or vice versa, is schematically depicted in Fig. 3. K+ and Na+ ions are shown as black and white circles, respectively, in the scheme of Fig. 3. Snapshots of the filter extracted from the umbrella-sampling trajectories, and closer to the energy minima I–XI, are also shown below the scheme. On the timescale of the simulations presented here, the structure of the SF does not change with the ion occupancy state (Fig. 4). The highest energy barriers encountered by the ions along this permeation pathway are of the order of 6 kcal/mol. In the mutated NaK-CNG channel, analogous energy barriers for the permeation of four K+ ions have been estimated (21). In all the energy minima described along the permeation pathway, the Na+ ion lies in the planes defined by the protein oxygen atoms that delimit binding sites S1–S4. Similar results were recently reported for ion conduction through the filter of TrkH, a membrane protein that participates in K+ uptake in bacteria (33). The filter of TrkH is characterized by three binding sites, and the free-energy barriers for conduction of K+ ions, Na+ ions, and Na+/K+ ion mixtures were identical, with Na+ ions always binding at the boundaries of binding sites (34). In contrast, in a K+-selective channel, the boundary between S2 and S3 does not constitute an energy minimum for a permeating Na+ ion. The lack of a Na+-binding site at the boundary between S2 and S3 in K+-selective channels is consistent with the reduction in the number of protein oxygen atoms coordinating the ion at this position, which is not compensated by an increase in the number of coordinating oxygen atoms from water molecules. In this nonselective channel, the number of coordinating oxygen atoms from the protein at the boundary between S2 and S3 is close to four, and two additional coordinating oxygen atoms are provided by water molecules, defining a perfect coordination shell for a Na+ ion even at this position of the pore (Fig. 5).
Figure 4.
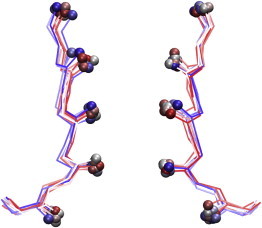
Backbone atoms (residues 62–66) of two opposite subunits of the SF of NaK-CNG from the energy minima I–XI. The last frames of the umbrella-sampling trajectories with harmonic restraints closer to the energy minima are superimposed. Spheres are used to highlight the positions of the carbonyl oxygen atoms. Colors range from red (trajectory closer to minimum I) to blue (trajectory closer to minimum XI).
Figure 5.
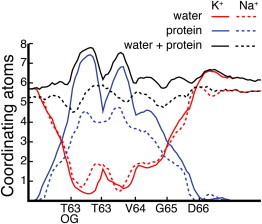
K+ and Na+ coordination number for ions inside the filter. The atoms coordinating K+ and Na+ ions were calculated by collecting the data from all the umbrella-sampling simulations. Oxygen atoms were considered part of the coordination shell if they were <2.8 Å from a Na+ ion, and <3.2 Å from a K+ ion.
Conclusions
From various studies on how ion selectivity is achieved in ion channels, it has been concluded that a combination of several aspects are essential. These factors are not exclusively structural or energetic, and they involve both the ion and the ion-coordinating ligands, either water or protein, the dehydration penalty of the permeating cations, the electrostatic interactions and redistribution of charge between the cation and the channel dipoles, the architecture of the ion-binding site, and the pore size and flexibility (35–41). Thompson et al. suggested that selectivity is linked to the multi-ion conduction mechanisms of K+ channels (18). More recently, Derebe et al. (5) proposed that ion selectivity of tetrameric cation channels could be tuned by changing the number of ion-binding sites. To understand the underlying principles of ion selectivity in tetrameric cation channels, they engineered a set of cation channel pores based on the nonselective NaK channel and determined their structures at high resolution. In the case of one of these mutants, NaK-CNG, although it maintains three contiguous cation-binding sites in the filter, it is virtually nonselective. In the free-energy maps presented here, the maximum energy barriers for the permeation of a single Na+ ion through a pore occupied by K+ ions are ∼6 kcal/mol. The same energy barriers were estimated for the permeation of K+ ions in NaK-CNG in a previous study (21). The situation is radically different in K+-selective channels (6,19). The highest energy barriers for conduction of K+ ions in the KirBac1.1 or KcsA K+ channels are ∼4 kcal/mol, and they become >10 kcal/mol for the conduction of a Na+ ion in the context of a pore occupied by K+ ions. These results are in agreement with experimental findings that NaK mutated channels with less than four cation-binding sites are not selective for K+ over Na+ ions (5).
The strategy adopted in this work is subject to several limitations inherent to MD simulations and free-energy calculations. First of all, the force field employed does not account for polarization effects and this could have an impact on the behavior of the ions in the SF (42,43). In the absence of a polarizable force field for proteins, lipids, and ions, the calculations presented here represent an approximation, which has proved appropriate in several related studies. The conclusions of this study are based on a comparison of two ion configurations, either K+ alone or Na+/K+ mixtures, in two channels, one selective and one nonselective. In the case of the nonselective channel, the energy barriers associated with ion permeation were identical for pure K+ and ion mixtures, whereas in the case of selective channels there was a threefold increase in the energy barriers. Since the free-energy maps were calculated in exactly the same way in both cases, the differences observed should be certainly meaningful.
The selectivity model that emerges from the data presented here and from previous theoretical and experimental studies is inherently related to the knock-on mechanism of K+ conduction. The preference of K+-selective channels for K+ ions, which is not fully understood yet, results in a pore occupied by K+ ions. Once the pore is in this state, the energy barriers for the conduction of K+ ions are much lower than the energy barriers for the conduction of a Na+ ion, which is consequently excluded from permeation events. The preference for K+ over Na+ at specific positions along the pore is not sufficient to explain selectivity. Indeed, although in the absence of K+ ions structural changes may take place in the pore region (44), leading to a nonconductive state (45), a subset of K+-selective channels are permeable to Na+ (46), and in these channels, Na+ ions can still bind inside the pore, only at different positions (47).
According to the data presented here, the differences between K+-selective and nonselective channels can be physically pinpointed at the boundary between S2 and S3 sites. When four cation-binding sites are available, as in selective potassium channels, the boundary between S2 and S3 is in the middle of the pore. During the permeation of a single Na+ ion in a pore occupied by K+ ions, configurations with the Na+ ion situated between two K+ ions will undoubtedly be anticipated, regardless of the permeation trajectory. Analysis of the MD trajectories and the free-energy maps for ion conduction in KirBac1.1 revealed that when the pore is occupied by two K+ ions and one Na+ ion, with the Na+ ion surrounded by the K+ ions, the boundary between S2 and S3 does not accommodate Na+ ions. That is, the octahedral coordination shell around a Na+ ion, with four oxygen atoms from the protein and two from water molecules, cannot be realized at this position. By contrast, the situation differs in a channel with three binding sites. In NaK-CNG, even when the Na+ ion is flanked by two K+ ions, the boundary between S2 and S3 can still provide a position reminiscent of a perfect binding site for Na+, characterized by an octahedral coordination shell. In the case where only three binding sites are available in the protein, the outermost K+ ion is more autonomous than the K+ ion bound to S0 in a four-binding-site K+-selective channel. Therefore, whereas in nonselective channels the outermost K+ ion can adjust its position to allow Na+ to bind to its preferred location, the same does not seem to be possible in K+-selective channels. The differences in water density between selective and nonselective channels in S1 could also contribute to the different behavior of Na+ at the boundary between S2 and S3.
Recently, the atomic structure of a Na+-selective channel, NavAb, from the bacterium Arcobacter Butzleri, was determined (2). Although Na+ ions were not observed in the crystallographic structure, due to its resolution, the presence of three Na+ binding sites was hypothesized in a SF much wider than that of known K+ channels (2). Residues Thr175 and Leu176 define two rings of carbonyl oxygen atoms at the intracellular entrance of the filter, and water molecules from the hydration shell of a Na+ ion may interact through hydrogen bonds with these two layers of carbonyl oxygen atoms that define two binding sites for hydrated Na+ ions. The third Na+ binding site is delimited by side chains of four glutamate residues, Glu177, from each of the four protein chains. From atomistic simulations and free-energy calculations, two Na+-binding sites were described in the SF of NavAb in simulations with either one or two permeating ions (49). These binding positions coincide with the sites hypothesized experimentally. In contrast, the experimentally speculated innermost binding site did not appear as a well defined energy minimum in the free-energy maps from atomistic simulations.
The ability of some channels to discriminate between ions, allowing some ions, and not others, to pass through the pore domain, has been experimentally associated with the number of consecutive sites in K+ channels. K+ channels have four contiguous binding sites. In contrast, NaK has two, and nonselective NaK mutants have three contiguous binding sites for a monovalent cation resembling the canonical filter of K+ channels. Conversely, NavAb has two ion binding sites, and it is still selective for Na+ ions. Therefore, it remains to be seen whether the connection between selectivity and the number of consecutive binding sites for cations can be also established in sodium channels. Although we can start studying the exact mechanism in great detail theoretically, new crystallographic structures, and functional data in particular, will be beneficial to validate the computational observations and provide a definite picture.
Acknowledgments
C.D. thanks The Royal Society for a University Research Fellowship. The work was supported by grants from the EPSRC. The Oxford Supercomputing Center, the National Service for Computational Chemistry Software, and HECToR are acknowledged for providing computational resources.
This work was supported by grants from the Engineering and Physical Sciences Research Council.
References
- 1.Doyle D.A., Morais Cabral J., MacKinnon R. The structure of the potassium channel: molecular basis of K+ conduction and selectivity. Science. 1998;280:69–77. doi: 10.1126/science.280.5360.69. [DOI] [PubMed] [Google Scholar]
- 2.Payandeh J., Scheuer T., Catterall W.A. The crystal structure of a voltage-gated sodium channel. Nature. 2011;475:353–358. doi: 10.1038/nature10238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Shi N., Ye S., Jiang Y. Atomic structure of a Na+- and K+-conducting channel. Nature. 2006;440:570–574. doi: 10.1038/nature04508. [DOI] [PubMed] [Google Scholar]
- 4.Alam A., Shi N., Jiang Y. Structural insight into Ca2+ specificity in tetrameric cation channels. Proc. Natl. Acad. Sci. USA. 2007;104:15334–15339. doi: 10.1073/pnas.0707324104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Derebe M.G., Sauer D.B., Jiang Y. Tuning the ion selectivity of tetrameric cation channels by changing the number of ion binding sites. Proc. Natl. Acad. Sci. USA. 2011;108:598–602. doi: 10.1073/pnas.1013636108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Furini S., Domene C. Selectivity and permeation of alkali metal ions in K+-channels. J. Mol. Biol. 2011;409:867–878. doi: 10.1016/j.jmb.2011.04.043. [DOI] [PubMed] [Google Scholar]
- 7.Aqvist J., Luzhkov V. Ion permeation mechanism of the potassium channel. Nature. 2000;404:881–884. doi: 10.1038/35009114. [DOI] [PubMed] [Google Scholar]
- 8.Bernèche S., Roux B. Energetics of ion conduction through the K+ channel. Nature. 2001;414:73–77. doi: 10.1038/35102067. [DOI] [PubMed] [Google Scholar]
- 9.Furini S., Domene C. Atypical mechanism of conduction in potassium channels. Proc. Natl. Acad. Sci. USA. 2009;106:16074–16077. doi: 10.1073/pnas.0903226106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Chung S.H., Corry B. Conduction properties of KcsA measured using brownian dynamics with flexible carbonyl groups in the selectivity filter. Biophys. J. 2007;93:44–53. doi: 10.1529/biophysj.106.098954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Burykin A., Schutz C.N., Warshel A. Simulations of ion current in realistic models of ion channels: the KcsA potassium channel. Proteins. 2002;47:265–280. doi: 10.1002/prot.10106. [DOI] [PubMed] [Google Scholar]
- 12.Domene C., Sansom M.S. Potassium channel, ions, and water: simulation studies based on the high resolution X-ray structure of KcsA. Biophys. J. 2003;85:2787–2800. doi: 10.1016/S0006-3495(03)74702-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Domene C., Vemparala S., Klein M.L. The role of conformation in ion permeation in a K+ channel. J. Am. Chem. Soc. 2008;130:3389–3398. doi: 10.1021/ja075164v. [DOI] [PubMed] [Google Scholar]
- 14.Furini S., Beckstein O., Domene C. Permeation of water through the KcsA K+ channel. Proteins. 2009;74:437–448. doi: 10.1002/prot.22163. [DOI] [PubMed] [Google Scholar]
- 15.Jensen M.O., Borhani D.W., Shaw D.E. Principles of conduction and hydrophobic gating in K+ channels. Proc. Natl. Acad. Sci. USA. 2010;107:5833–5838. doi: 10.1073/pnas.0911691107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Khalili-Araghi F., Tajkhorshid E., Schulten K. Dynamics of K+ ion conduction through Kv1.2. Biophys. J. 2006;91:L72–L74. doi: 10.1529/biophysj.106.091926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hodgkin A.L., Keynes R.D. The potassium permeability of a giant nerve fibre. J. Physiol. 1955;128:61–88. doi: 10.1113/jphysiol.1955.sp005291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Thompson A.N., Kim I., Nimigean C.M. Mechanism of potassium-channel selectivity revealed by Na+ and Li+ binding sites within the KcsA pore. Nat. Struct. Mol. Biol. 2009;16:1317–1324. doi: 10.1038/nsmb.1703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Egwolf B., Roux B. Ion selectivity of the KcsA channel: a perspective from multi-ion free energy landscapes. J. Mol. Biol. 2010;401:831–842. doi: 10.1016/j.jmb.2010.07.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Persson I. Hydrated metal ions in aqueous solution: how regular are their structures? Pure Appl. Chem. 2010;82:1901–1917. [Google Scholar]
- 21.Furini S., Domene C. Gating at the selectivity filter of ion channels that conduct Na+ and K+ ions. Biophys. J. 2011;101:1623–1631. doi: 10.1016/j.bpj.2011.08.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Phillips J.C., Braun R., Schulten K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.MacKerell A.D., Bashford D., Karplus M. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 24.Jorgensen W.L., Chandrasekhar J., Klein M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
- 25.Roux B., Bernèche S. On the potential functions used in molecular dynamics simulations of ion channels. Biophys. J. 2002;82:1681–1684. doi: 10.1016/S0006-3495(02)75520-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Feller S.E., Zhang Y.H., Brooks B.R. Constant-pressure molecular dynamics simulation: the Langevin piston method. J. Chem. Phys. 1995;103:4613–4621. [Google Scholar]
- 27.Essmann U., Perera L., Pedersen L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995;103:8577–8593. [Google Scholar]
- 28.Miyamoto S., Kollman P.A. Settle: an analytical version of the SHAKE and RATTLE algorithms for rigid water molecules. J. Comput. Chem. 1992;13:952–962. [Google Scholar]
- 29.Domene C., Furini S. Examining ion channel properties using free-energy methods. Methods Enzymol. 2009;466:155–177. doi: 10.1016/S0076-6879(09)66007-9. [DOI] [PubMed] [Google Scholar]
- 30.Torrie G.M., Valleau J.P. Monte Carlo free-energy estimates using non-Boltzmann sampling: application to sub-critical Lennard-Jones fluid. Chem. Phys. Lett. 1974;28:578–581. [Google Scholar]
- 31.Kumar S., Bouzida D., Rosenberg J.M. The weighted histogram analysis method for free-energy calculations on biomolecules. 1. The method. J. Comput. Chem. 1992;13:1011–1021. [Google Scholar]
- 32.Straatsma T.P., Mccammon J.A. Computational alchemy. Annu. Rev. Phys. Chem. 1992;43:407–435. [Google Scholar]
- 33.Cao Y., Jin X., Zhou M. Crystal structure of a potassium ion transporter, TrkH. Nature. 2011;471:336–340. doi: 10.1038/nature09731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Domene C., Furini S. Molecular dynamics simulations of the TrkH membrane protein. Biochemistry. 2012;51:1559–1565. doi: 10.1021/bi201586n. [DOI] [PubMed] [Google Scholar]
- 35.Noskov S.Y., Bernèche S., Roux B. Control of ion selectivity in potassium channels by electrostatic and dynamic properties of carbonyl ligands. Nature. 2004;431:830–834. doi: 10.1038/nature02943. [DOI] [PubMed] [Google Scholar]
- 36.Noskov S.Y., Roux B. Ion selectivity in potassium channels. Biophys. Chem. 2006;124:279–291. doi: 10.1016/j.bpc.2006.05.033. [DOI] [PubMed] [Google Scholar]
- 37.Luzhkov V.B., Aqvist J. K+/Na+ selectivity of the KcsA potassium channel from microscopic free energy perturbation calculations. Biochim. Biophys. Acta. 2001;1548:194–202. doi: 10.1016/s0167-4838(01)00213-8. [DOI] [PubMed] [Google Scholar]
- 38.Bostick D.L., Brooks C.L., 3rd Selectivity in K+ channels is due to topological control of the permeant ion’s coordinated state. Proc. Natl. Acad. Sci. USA. 2007;104:9260–9265. doi: 10.1073/pnas.0700554104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Burykin A., Kato M., Warshel A. Exploring the origin of the ion selectivity of the KcsA potassium channel. Proteins. 2003;52:412–426. doi: 10.1002/prot.10455. [DOI] [PubMed] [Google Scholar]
- 40.Thomas M., Jayatilaka D., Corry B. The predominant role of coordination number in potassium channel selectivity. Biophys. J. 2007;93:2635–2643. doi: 10.1529/biophysj.107.108167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Fowler P.W., Tai K., Sansom M.S. The selectivity of K+ ion channels: testing the hypotheses. Biophys. J. 2008;95:5062–5072. doi: 10.1529/biophysj.108.132035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Illingworth C.J.R., Furini S., Domene C. Computational studies on polarization effects and selectivity in K+ channels. J. Chem. Theory Comput. 2010;6:3780–3792. [Google Scholar]
- 43.Illingworth C.J., Domene C. Many-body effects and simulations of potassium channels. Proc. R. Soc. A Math. Phys. Eng. Sci. 2009;465:1701–1716. [Google Scholar]
- 44.Zhou Y., Morais-Cabral J.H., MacKinnon R. Chemistry of ion coordination and hydration revealed by a K+ channel-Fab complex at 2.0 Å resolution. Nature. 2001;414:43–48. doi: 10.1038/35102009. [DOI] [PubMed] [Google Scholar]
- 45.Domene C., Furini S. Dynamics, energetics, and selectivity of the low-K+ KcsA channel structure. J. Mol. Biol. 2009;389:637–645. doi: 10.1016/j.jmb.2009.04.038. [DOI] [PubMed] [Google Scholar]
- 46.Ye S., Li Y., Jiang Y. Novel insights into K+ selectivity from high-resolution structures of an open K+ channel pore. Nat. Struct. Mol. Biol. 2010;17:1019–1023. doi: 10.1038/nsmb.1865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Kim I., Allen T.W. On the selective ion binding hypothesis for potassium channels. Proc. Natl. Acad. Sci. USA. 2011;108:17963–17968. doi: 10.1073/pnas.1110735108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Reference deleted in proof.
- 49.Furini S., Domene C. On conduction in a bacterial sodium channel. PLOS Comput. Biol. 2012;8:e1002476. doi: 10.1371/journal.pcbi.1002476. [DOI] [PMC free article] [PubMed] [Google Scholar]


