Abstract
Nanophotonic structures with irregular symmetry, such as quasiperiodic plasmonic crystals, have gained an increasing amount of attention, in particular as potential candidates to enhance the absorption of solar cells in an angular insensitive fashion. To examine the photonic bandstructure of such systems that determines their optical properties, it is necessary to measure and model normal and oblique light interaction with plasmonic crystals. We determine the different propagation vectors and consider the interaction of all possible waveguide modes and particle plasmons in a 2D metallic photonic quasicrystal, in conjunction with the dispersion relations of a slab waveguide. Using a Fano model, we calculate the optical properties for normal and inclined light incidence. Comparing measurements of a quasiperiodic lattice to the modelled spectra for angle of incidence variation in both azimuthal and polar direction of the sample gives excellent agreement and confirms the predictive power of our model.
Coupled systems play a major role in nanophotonics and plasmonics. Plenty of applications such as optical nanosensors1,2,3 are based on Fano resonances4 which are due to interactions of different optical modes. The influence of planar periodic structures on particle plasmon resonances was studied by Lamprecht et al.5 and Auguié et al.6 Subwavelength holes in a metal film have been investigated by García-Vidal and coworkers7. All of the mentioned publications have only examined periodic structures. However, also planar aperiodic and disordered structures have been studied8,9,10,11. Even 3D photonic quasicrystals were investigated12,13. The coupling between particle plasmons and waveguide modes has been studied in periodic14,15,16 as well as in disordered17,18,19 systems. Additionally, nonlinear experiments have been performed20,21,22. These systems are used for intriguing applications such as enhancing the efficiency of solar cells23,24 as well as subwavelength focusing of light25. The latter application is based on a quasiperiodic structure. One of the key properties of such quasicrystalline systems is its more isotropic optical behaviour in comparison with periodic structures26. Therefore, the ability to model normally incident as well as angle-dependent optical properties is crucial. However, Fourier-periodic methods such as scattering-matrix calculations cannot predict the spectra of quasiperiodic and disordered structures. Therefore, the presented model of a previous paper for 2D plasmonic gold nanodot arrays on a slab waveguide for normal incidence27 has to be modified and expanded for oblique light incidence. Our model utilises the Fourier transform of the spatial lattice positions in combination with the dispersion of the slab waveguide. Additionally, elliptically shaped nanodots are taken into account. Experiments with different incident polarisations, different inclination angles as well as different azimuthal angles are compared to the theoretical curves, and excellent agreement is obtained. With the model presented in this paper, predictions of the optical properties of structures with a quasiperiodic gold disk arrangement are possible, which is confirmed by experiments. Therefore, the optical properties of future applications of these structures can be modelled and optimized by using this approach. Such applications include for example plasmon-assisted coatings for solar cells which would make their absorption more isotropic and polarisation insensitive.
Results
Modelling and simulations
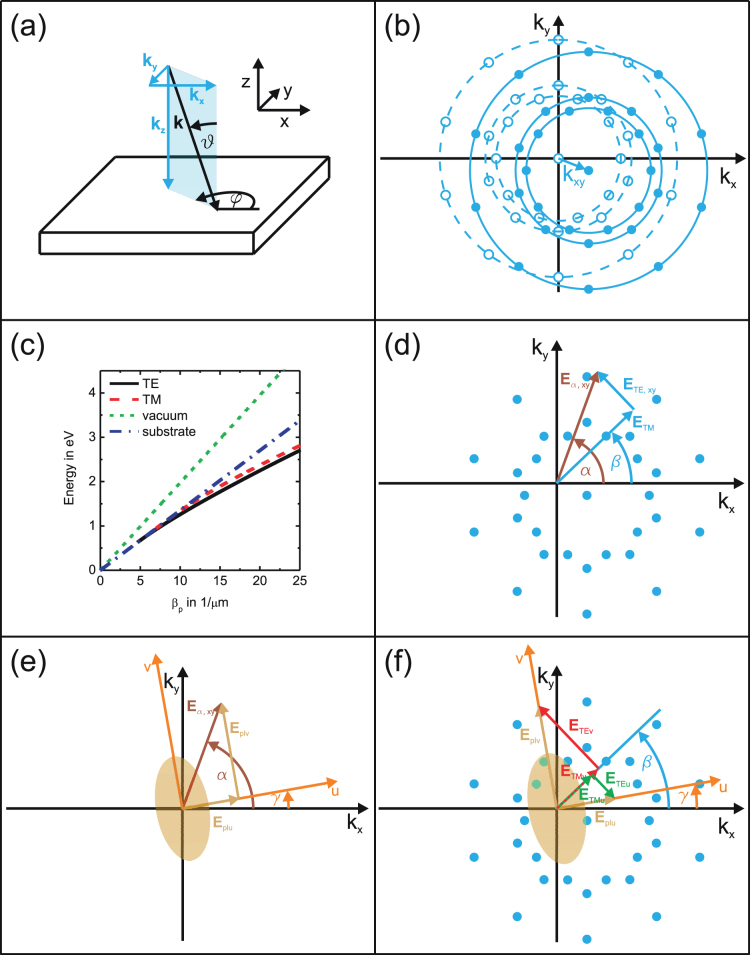
In the model as well as the experiment, a sample is used which consists of a 180-nm-thick HfO2 slab waveguide on a quartz substrate with plasmonic gold dots on top, arranged in a quasicrystalline Penrose tiling (see Fig. 1 and Methods for details). Light with the vector k incident on the sample is defined by the angle of incidence ϑ as well as the azimuth angle 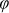 [see Fig. 2(a)]. In comparison with normal light incidence the incident k vector additionally possesses components parallel to the xy plane. Since the electric field vector Eα is always perpendicular to k, Eα can exhibit a component in z direction depending on
[see Fig. 2(a)]. In comparison with normal light incidence the incident k vector additionally possesses components parallel to the xy plane. Since the electric field vector Eα is always perpendicular to k, Eα can exhibit a component in z direction depending on 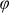 and on the polarisation angle α between the component Eα,xy and the x axis of the sample. Therefore, the theoretical model described in Ref. 27 has to be expanded. First, we start by calculating the 2D Fourier transform of the structure. This is carried out by setting a Dirac delta function at each coordinate of the nanodisks17,27 with xn and yn for the nth disk leading to a function
and on the polarisation angle α between the component Eα,xy and the x axis of the sample. Therefore, the theoretical model described in Ref. 27 has to be expanded. First, we start by calculating the 2D Fourier transform of the structure. This is carried out by setting a Dirac delta function at each coordinate of the nanodisks17,27 with xn and yn for the nth disk leading to a function
and then taking the 2D Fourier transform of f(x, y) by using the projection slice theorem (see Ref. 28 and 29):
Due to the structure design, namely a grating on top of a waveguide layer, it is possible to excite the waveguide modes. When a transverse electric (TE) or a transverse magnetic (TM) polarised waveguide mode propagates in the waveguide slab, its energy corresponds to a propagation constant βp defined by30
with g describing the location of the Fourier components. This indicates that, in order to calculate the angular propagation constants, it is possible to shift the 2D Fourier transform by the k component parallel to the xy plane, kxy, which is displayed as vectorially shifted circles in Fig. 2(b). However, each Fourier component as well as kxy are dependent on the energy of the incident light. Therefore, for a specific polar angle ϑ, the magnitude of the vector kxy is different for each Fourier component. In order to find the correct angular propagation constants, the TE and TM waveguide dispersion relations given in Refs. 31 and 32 have to be used. In these dispersion relations, which are plotted in Fig. 2(c) as black solid (TE) and red dashed (TM) curves, the absolute value of βp given by
is taken. This allows for calculation of βp in dependence on the corresponding k value of the incident beam for each Fourier component with distance g to the centre of the Fourier transform at an angle βFT between the direction of this Fourier component and the kx axis. The location of the angular propagation constants can then be easily calculated with Eq. (3). The directions of the waveguide modes are given as vectors starting from the centre of the Fourier transform and pointing to the different angular propagation constants. In each of these directions at angle β a TE as well as a TM mode can be guided, where the TE mode (TM mode) is defined with its electric (magnetic) field vector on a plane perpendicular to the direction of propagation. In order to find the correct amount of TE/TM waves propagating in direction β, the amplitudes of incident light with polarisation Eα have to be split into the components [see Fig. 2(d)]
with
The + sign in Eq. (5) belongs to the case when 0° ≤ α − β < 180°, whereas the – sign describes the case when 180° ≤ α − β < 360°. Cα is a factor that depends on the incident wave. Note that only CTE is dependent on Cα,z due to the fact that Eα,z is always on a plane perpendicular to the direction of propagation. For dielectric nanodisks these are the only waves propagating in the waveguide and, therefore, the total intensity of the waveguide modes is given by
where Sβ(kξ) describes the amplitude and phase information in direction β. The positive kξ axis of Sβ(kξ) is used for 0° ≤ β < 180° and the negative for 180° ≤ β < 360°.
Figure 1. SEM picture.

SEM picture of the Penrose tiling of the plasmonic gold nanodots on top of an HfO2 slab waveguide.
Figure 2. Simulation model.
(a) Illustration of the incident k-vector on the sample. (b) Angular Fourier transform (filled circles) shifted by kxy with respect to the Fourier transform for normal incidence (open circles). (c) Dispersion relations for vacuum (green short-dashed) and quartz (blue dash-dotted) as well as for TE (black solid) and TM waves (red dashed) propagating in a 180-nm-thick HfO2 layer on quartz. (d) TE and TM waveguide modes in direction β for incident polarisation Eα,xy. (e) Particle plasmon excitations along the particle main axes. (f) Additionally excited TE and TM waveguide modes in direction β due to the particle plasmons.
However, for metallic nanodisks we need to consider additional features, namely the particle plasmons. Light with an incident polarisation Eα can excite particle plasmons along the principal axes u, v, and z [see Fig. 2(e)]. This leads to the following components:
The values Cu, Cv, and Cz in Eqs. (11) – (13) are dependent on the eccentricity and the size of the particle. The three excited particle plasmons can be considered as independently polarised light, which is incident on the sample. These electric field vectors (Eplu, Eplv, and Eplz) can then excite waveguide modes in the same manner as explained above. Figure 2(f) shows how each of the electric field vectors of the particle plasmons Eplu and Eplv splits up into a TE polarised as well as a TM polarised wave in direction β leading to the components
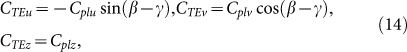 |
As above in Eqs. (5) and (6) for the electric field vector Eα,z, the particle plasmon in z direction can only excite a TE polarised waveguide mode. Note the – sign for the CTEu component which is due to the fact that ETEu points in the opposite direction than ETEv [Fig. 2(f)]. The complete components CTE,add and CTM,add are obtained by adding up the different components of Eqs. (5) and (14) for a TE wave as well as those of Eqs. (6) and (15) for a TM wave in β direction:
The total intensity of the waveguide modes for metallic nanodisks can now be calculated by using
As already explained above, the positive kξ axis of Sβ(kξ) is used for 0° ≤ β < 180° and the negative for 180° ≤ β < 360°.
Ftot,TE as well as Ftot,TM consist of amplitudes at specific k values. The corresponding energies are obtained by using the above-mentioned waveguide mode dispersion relations displayed in Fig. 2(c) as black solid (TE wave) and red dashed (TM wave) curves. As reference also the dispersion relations of the surrounding media are plotted (vacuum: green short-dashed, quartz: blue dash-dotted). The amplitudes Aj of the main waveguide mode resonances in Eqs. (18) and (19) at the energies Ej are used in order to describe the transmission amplitude t by a Fano model27,33,34
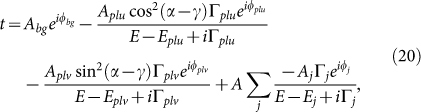 |
where the sum over j models the waveguide modes with spectral widths Γj and phase 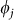 . The first term is due to the directly transmitted wave with amplitude Abg = 1 and phase
. The first term is due to the directly transmitted wave with amplitude Abg = 1 and phase 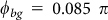 , whereas the second and third terms describe the particle plasmons in u and v directions with amplitudes Aplu/Aplv, spectral widths Γplu/Γplv = 0.15 eV, and phases
, whereas the second and third terms describe the particle plasmons in u and v directions with amplitudes Aplu/Aplv, spectral widths Γplu/Γplv = 0.15 eV, and phases 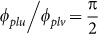 . Note that the particle plasmon in z direction is neglected since the height of the nanodisk is much smaller than the diameters in u and v direction. Therefore, the particle plasmon energy in z direction is in a different energy range as the measured spectra and the value Cz of Eq. (13) is much smaller than Cu and Cv. The amplitudes Aplu and Aplv as well as the value A are fitting parameters so that the particle plasmon amplitudes and the waveguide mode amplitudes possess the correct ratio. The phase of a waveguide mode not coupled to a particle plasmon is
. Note that the particle plasmon in z direction is neglected since the height of the nanodisk is much smaller than the diameters in u and v direction. Therefore, the particle plasmon energy in z direction is in a different energy range as the measured spectra and the value Cz of Eq. (13) is much smaller than Cu and Cv. The amplitudes Aplu and Aplv as well as the value A are fitting parameters so that the particle plasmon amplitudes and the waveguide mode amplitudes possess the correct ratio. The phase of a waveguide mode not coupled to a particle plasmon is 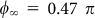 , which is the case when the energy of the waveguide mode is far away from the particle plasmon energy. For low energies the phase of the waveguide mode
, which is the case when the energy of the waveguide mode is far away from the particle plasmon energy. For low energies the phase of the waveguide mode 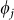 converges to
converges to 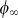 , whereas for large energies it converges to
, whereas for large energies it converges to 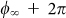 which corresponds to
which corresponds to 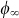 . If waveguide mode and particle plasmon possess the same energy,
. If waveguide mode and particle plasmon possess the same energy,  has a phase-shift of π with respect to the uncoupled phase
has a phase-shift of π with respect to the uncoupled phase 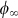 . Therefore, a phase behaviour of
. Therefore, a phase behaviour of
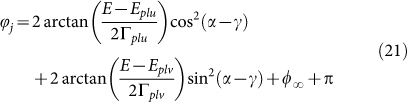 |
is assumed due to the two particle plasmons at energies Eplu and Eplv. The extinction spectra can then be obtained by calculating Ext = −ln(T) with the transmittance T = |t|2.
Experiments
The sample described in the Methods section was fabricated and then measured with a white light transmission setup15. The measurement principle is also described in the Methods section. The angle of incidence ϑ was varied between 0° and 6° in steps of 1° both in x (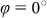 ) and in y direction (
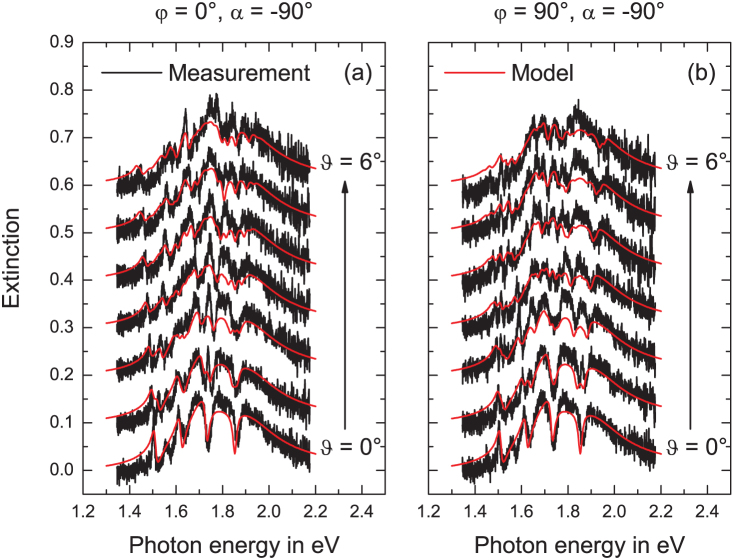
) and in y direction (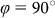 ) of the sample. All measurements, shown as black curves in Figs. 3 and 4, were performed for an incident polarisation with α = 0° and α = −90°, respectively. The curves on the bottom of Fig. 3(a) and (b) as well as those of Fig. 4(a) and (b) were measured at normal light incidence. The broad resonances visible in all spectra without the dips are the excited particle plasmons. Due to the fact that the short main axis of the gold disks is rotated by 40° around the sample x axis, the particle plasmon resonances along both main axes are excited for incident polarisations with α = 0° and α = −90°. However, by comparing Fig. 3 to Fig. 4, one recognises that the particle plasmons are located at slightly different energies. This means that either the plasmon along the short main axis (Fig. 3) or the plasmon along the long main axis (Fig. 4) is more pronounced. The sharp resonances at approximately 1.5 eV, 1.6 eV, 1.75 eV, and 1.85 eV are due to TE and TM waveguide modes propagating in the waveguide layer with a propagation constant equal to the inner ring of the Fourier components [see inner dashed circle in Fig. 2(b)] as well as those with a propagation constant equal to the outer ring of the Fourier components [see central dashed circle in Fig. 2(b)]. According to the energy position of the waveguide modes compared to the particle plasmons and thus to the degree of coupling between these resonances, the waveguide modes either appear as sharp peaks (decoupled, see resonance at 1.5 eV) or as sharp dips (coupled, see resonance at 1.85 eV). By tilting the sample, the waveguide modes split up into different components16,30 due to the different absolute values of the propagation constants for oblique light incidence. The behaviour for varying the inclination angle in x direction is different than that in y direction as expected. Additionally, we observe that this behaviour is dependent on the incident polarisation. This polarisation dependence has two reasons. First, the waveguide modes directly excited by the incident light show the same resonances with the same amplitudes for all spectra with
) of the sample. All measurements, shown as black curves in Figs. 3 and 4, were performed for an incident polarisation with α = 0° and α = −90°, respectively. The curves on the bottom of Fig. 3(a) and (b) as well as those of Fig. 4(a) and (b) were measured at normal light incidence. The broad resonances visible in all spectra without the dips are the excited particle plasmons. Due to the fact that the short main axis of the gold disks is rotated by 40° around the sample x axis, the particle plasmon resonances along both main axes are excited for incident polarisations with α = 0° and α = −90°. However, by comparing Fig. 3 to Fig. 4, one recognises that the particle plasmons are located at slightly different energies. This means that either the plasmon along the short main axis (Fig. 3) or the plasmon along the long main axis (Fig. 4) is more pronounced. The sharp resonances at approximately 1.5 eV, 1.6 eV, 1.75 eV, and 1.85 eV are due to TE and TM waveguide modes propagating in the waveguide layer with a propagation constant equal to the inner ring of the Fourier components [see inner dashed circle in Fig. 2(b)] as well as those with a propagation constant equal to the outer ring of the Fourier components [see central dashed circle in Fig. 2(b)]. According to the energy position of the waveguide modes compared to the particle plasmons and thus to the degree of coupling between these resonances, the waveguide modes either appear as sharp peaks (decoupled, see resonance at 1.5 eV) or as sharp dips (coupled, see resonance at 1.85 eV). By tilting the sample, the waveguide modes split up into different components16,30 due to the different absolute values of the propagation constants for oblique light incidence. The behaviour for varying the inclination angle in x direction is different than that in y direction as expected. Additionally, we observe that this behaviour is dependent on the incident polarisation. This polarisation dependence has two reasons. First, the waveguide modes directly excited by the incident light show the same resonances with the same amplitudes for all spectra with 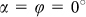 , 36°, 72°, 108°…. The location as well as the amplitudes of these waveguide modes differ from the spectra with
, 36°, 72°, 108°…. The location as well as the amplitudes of these waveguide modes differ from the spectra with  , 54°, 90°, 126°… due to the 10-fold symmetry of the Penrose tiling. Second, due to the fact that there are also waveguide modes present in the system that are excited by the particle plasmons, the amplitudes of the waveguide modes are also different for the spectra with for example
, 54°, 90°, 126°… due to the 10-fold symmetry of the Penrose tiling. Second, due to the fact that there are also waveguide modes present in the system that are excited by the particle plasmons, the amplitudes of the waveguide modes are also different for the spectra with for example 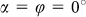 and
and 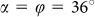 . However, the differences due to the second reason are only present, when the gold dots are elliptically shaped. The red curves in Figs. 3 and 4 are the spectra calculated with the simulation model presented in subsection Modelling and Simulations. A measured curve for one polarisation at normal light incidence was taken for fitting the theoretical spectrum to it. The fitting parameters obtained there were Aplu = 0.0735, Aplv = 0.1129, and A = 0.0016 and were used for calculating all other spectra. By comparing the measured and modelled spectra of Fig. 3, we observe an excellent agreement for both x and y variation of the inclination angle. The behaviour of the measured spectra of incident polarisation angle α = −90° (see Fig. 4) with the same fitting parameters is also well reproduced by the calculated spectra which confirms our model. Measured and modelled curves are shown here for incidence angles up to 6°. However, our model can easily predict the optical properties at larger angles.
. However, the differences due to the second reason are only present, when the gold dots are elliptically shaped. The red curves in Figs. 3 and 4 are the spectra calculated with the simulation model presented in subsection Modelling and Simulations. A measured curve for one polarisation at normal light incidence was taken for fitting the theoretical spectrum to it. The fitting parameters obtained there were Aplu = 0.0735, Aplv = 0.1129, and A = 0.0016 and were used for calculating all other spectra. By comparing the measured and modelled spectra of Fig. 3, we observe an excellent agreement for both x and y variation of the inclination angle. The behaviour of the measured spectra of incident polarisation angle α = −90° (see Fig. 4) with the same fitting parameters is also well reproduced by the calculated spectra which confirms our model. Measured and modelled curves are shown here for incidence angles up to 6°. However, our model can easily predict the optical properties at larger angles.
Figure 3. Measurements with polarisation α = 0°.
Measured (black) and modelled (red) curves for a Penrose tiling with edge length d = 530 nm. The angle of incidence was varied from 0° to 6° (from bottom to top) (a) along the sample x direction (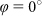 ) and (b) along the sample y direction (
) and (b) along the sample y direction (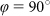 ). The incident polarisation was 0°. The curves are shifted upward for clarity.
). The incident polarisation was 0°. The curves are shifted upward for clarity.
Figure 4. Measurements with polarisation α = −90°.
Measured (black) and modelled (red) curves for a Penrose tiling with edge length d = 530 nm. The angle of incidence was varied from 0° to 6° (from bottom to top) (a) along the sample x direction (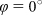 ) and (b) along the sample y direction (
) and (b) along the sample y direction (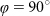 ). The incident polarisation was −90°. The curves are shifted upward for clarity.
). The incident polarisation was −90°. The curves are shifted upward for clarity.
Discussion
We have introduced a theoretical model for simulating the optical properties of 2D metallic photonic quasicrystals at normal and oblique light incidence for all polarisations. This model includes the Fourier transform of the structure shifted by the k vector component parallel to the structure surface and all possible waveguide modes as well as particle plasmon resonances. The energy spectrum is obtained by utilising the waveguide dispersion relations and a phenomenological model. We have measured a quasicrystalline plasmonic crystal sample by varying the angle of incidence as well as the light polarisation and obtained excellent agreement between the measured and the modelled spectra. Our model could find applications in plasmonic quasicrystalline super-oscillatory lenses35 as well as plasmonically enhanced solar cells using waveguide-plasmon geometries23,36.
Methods
Fabrication
The quasiperiodic lattice of the measured sample consists of 25-nm-high gold nanodisks which were placed on the vertices of a Penrose tiling with an edge length of 530 nm by using electron beam lithography. This arrangement is depicted in Fig. 1. Quartz (n = 1.46) with an 180-nm-thick HfO2 waveguide layer on top served as substrate. The refractive index of HfO2 is dispersive in the relevant spectral range and can be described by the following equation:
with λ as the wavelength of the incident light in µm. The gold disks are elliptically shaped (97 nm and 118 nm long main axis diameters) and rotated by an angle of 40° between the short main axis of the particle and the sample x axis.
Measurements
The light of a white light source was polarised and then focused on the sample by using a microscope objective (Zeiss, A-Plan, 10x, 0.25). The polariser was mounted on a rotation stage in order to change the incident polarisation. The light behind the sample was collimated and then focused on the slit of a spectrometer (Acton SpectraPro 500i with a CCD camera and a grating with 150 g/mm). A pinhole was used in the collimated beam after the sample in order to reduce the aperture angle of the beam below 0.2°15. The sample was placed on a rotation stage in order to perform measurements with different incidence angles on the sample.
Author Contributions
C.B. fabricated the sample, developed the simulation model, and carried out the measurements. G.K. helped developing the model. C.B. and H.G. wrote the manuscript. All authors contributed to scientific discussion and critical revision of the article. H.G. supervised the study.
Acknowledgments
The authors thank T. Weiss, J. Roth, P. Köberle, S. Tikhodeev, and C. Bechinger for useful discussions and suggestions. This work was financially supported by Deutsche Forschungsgemeinschaft (Open Access Publishing, SPP1391 and FOR557), by Landes-stiftung BW, and by BMBF (13N9155 and 13N10146).
References
- Lal S., Link S. & Halas N. J. Nano-optics from sensing to waveguiding. Nat. Phot. 1, 641–648 (2007). [Google Scholar]
- Liu N., Mesch M., Weiss T., Hentschel M. & Giessen H. Infrared perfect absorber and its application as plasmonic sensor. Nano Lett. 10, 2342–2348 (2010). [DOI] [PubMed] [Google Scholar]
- Yanik A. A., Huang M., Artar A., Chang T.-Y. & Altug H. Integrated nanoplasmonic-nanofluidic biosensors with targeted delivery of analytes. Appl. Phys. Lett. 96, 021101 (2010). [Google Scholar]
- Luk'yanchuk B. et al. The fano resonance in plasmonic nanostructures and metamaterials. Nat. Mater. 9, 707–715 (2010). [DOI] [PubMed] [Google Scholar]
- Lamprecht B. et al. Metal nanoparticle gratings: Influence of dipolar particle interaction on the plasmon resonance. Phys. Rev. Lett. 84, 4721–4724 (2000). [DOI] [PubMed] [Google Scholar]
- Auguié B. & Barnes W. L. Collective resonances in gold nanoparticle arrays. Phys. Rev. Lett. 101, 143902 (2008). [DOI] [PubMed] [Google Scholar]
- García-Vidal F. J., Martin-Moreno L., Ebbesen T. W. & Kuipers L. Light passing through subwavelength apertures. Rev. Mod. Phys. 82, 729–787 (2010). [Google Scholar]
- Matsui T., Agrawal A., Nahata A. & Vardeny Z. V. Transmission resonances through aperiodic arrays of subwavelength apertures. Nature 446, 517–521 (2007). [DOI] [PubMed] [Google Scholar]
- Rockstuhl C., Lederer F., Zentgraf T. & Giessen H. Enhanced transmission of periodic, quasiperiodic, and random nanoaperture arrays. Appl. Phys. Lett. 91, 151109 (2007). [Google Scholar]
- Zoorob M. E., Charlton M. D. B., Parker G. J., Baumberg J. J. & Netti M. C. Complete photonic bandgaps in 12-fold symmetric quasicrystals. Nature 404, 740–743 (2000). [DOI] [PubMed] [Google Scholar]
- Prikulis J., Hanarp P., Olofsson L., Sutherland D. & Käll M. Optical spectroscopy of nanometric holes in thin gold films. Nano Lett. 4, 1003–1007 (2004). [Google Scholar]
- Ledermann A. et al. Three-dimensional silicon inverse photonic quasicrystals for infrared wavelengths. Nat. Mater. 5, 942–945 (2006). [DOI] [PubMed] [Google Scholar]
- Ledermann A., Wegener M. & von Freymann G. Rhombicuboctahedral three-dimensional photonic quasicrystals. Adv. Mater. 22, 2363–2366 (2010). [DOI] [PubMed] [Google Scholar]
- Linden S., Kuhl J. & Giessen H. Controlling the interaction between light and gold nanoparticles: Selective suppression of extinction. Phys. Rev. Lett. 86, 4688–4691 (2001). [DOI] [PubMed] [Google Scholar]
- Christ A., Tikhodeev S., Gippius N. A., Kuhl J. & Giessen H. Waveguide-plasmon polaritons: Strong coupling of photonic and electronic resonances in a metallic photonic crystal slab. Phys. Rev. Lett. 91, 183901 (2003). [DOI] [PubMed] [Google Scholar]
- Christ A. et al. Optical properties of planar metallic photonic crystal structures: Experiment and theory. Phys. Rev. B 70, 125113 (2004). [Google Scholar]
- Nau D. et al. Disorder issues in metallic photonic crystals. phys. stat. sol. (b) 243, 2331–2343 (2006). [Google Scholar]
- Hughes S., Ramunno L., Young J. F. & Sipe J. E. Extrinsic optical scattering loss in photonic crystalwaveguides: Role of fabrication disorder and photon group velocity. Phys. Rev. Lett. 94, 033903 (2005). [DOI] [PubMed] [Google Scholar]
- Cao H. et al. Spatial confinement of laser light in active random media. Phys. Rev. Lett. 84, 5584–5587 (2000). [DOI] [PubMed] [Google Scholar]
- Zentgraf T., Christ A., Kuhl J. & Giessen H. Tailoring the ultrafast dephasing of quasiparticles in metallic photonic crystals. Phys. Rev. Lett. 93, 243901 (2004). [DOI] [PubMed] [Google Scholar]
- Utikal T., Stockman M. I., Heberle A. P., Lippitz M. & Giessen H. All-optical control of the ultrafast dynamics of a hybrid plasmonic system. Phys. Rev. Lett. 104, 113903 (2010). [DOI] [PubMed] [Google Scholar]
- Utikal T. et al. Towards the origin of the nonlinear response in hybrid plasmonic systems. Phys. Rev. Lett. 106, 133901 (2011). [DOI] [PubMed] [Google Scholar]
- Pala R. A., White J., Barnard E., Liu J. & Brongersma M. L. Design of plasmonic thin-film solar cells with broadband absorption enhancements. Adv. Mater. 21, 3504–3509 (2009). [Google Scholar]
- Spinelli P. et al. Optical impedance matching using coupled plasmonic nanoparticle arrays. Nano Lett. 11, 1760–1765 (2011). [DOI] [PubMed] [Google Scholar]
- Huang F. M., Zheludev N., Chen Y. & García de Abajo F. J. Focusing of light by a nanohole array. Appl. Phys. Lett. 90, 091119 (2007). [Google Scholar]
- Florescu M., Torquato S. & Steinhardt P. J. Complete band gaps in two-dimensional photonic quasicrystals. Phys. Rev. B 80, 155112 (2009). [Google Scholar]
- Bauer C., Kobiela G. & Giessen H. Optical properties of two-dimensional quasicrystalline plasmonic arrays. Phys. Rev. B 84, 193104 (2011). [Google Scholar]
- Kak A. C. & Slaney M. Principles of Computerized Tomographic Imaging. IEEE Press (1988). [Google Scholar]
- Mersereau R. M. & Oppenheim A. V. Digital reconstruction of multidimensional signals from their projections. Proc. IEEE 62, 1319–1338 (1974). [Google Scholar]
- Linden S., Christ A., Kuhl J. & Giessen H. Selective suppression of extinction within the plasmon resonance of gold nanoparticles. Appl. Phys. B 73, 311–316 (2001). [DOI] [PubMed] [Google Scholar]
- Tien P. K. Light waves in thin films and integrated optics. Appl. Opt. 10, 2395–2413 (1971). [DOI] [PubMed] [Google Scholar]
- Kogelnik H. & Ramaswamy V. Scaling rules for thin-film optical waveguides. Appl. Opt. 13, 1857–1862 (1974). [DOI] [PubMed] [Google Scholar]
- Fan S. & Joannopoulos J. D. Analysis of guided resonances in photonic crystal slabs. Phys. Rev. B 65, 235112 (2002). [Google Scholar]
- Christ A. et al. Controlling the fano interference in a plasmonic lattice. Phys. Rev. B 76, 201405(R) (2007). [Google Scholar]
- Rogers E. T. F. et al. A super-oscillatory lens optical microscope for subwavelength imaging. Nat. Mater. 11, 432–435 (2012). [DOI] [PubMed] [Google Scholar]
- Atwater H. A. & Polman A. Plasmonics for improved photovoltaic devices. Nat. Mater. 9, 205–213 (2010). [DOI] [PubMed] [Google Scholar]