Sources of fMRI signal fluctuations in the human brain at rest: a 7T study

Abstract

Signal fluctuations in functional magnetic resonance imaging (fMRI) can result from a number of sources that may have a neuronal, physiologic, or instrumental origin. To determine the relative contribution of these sources we recorded physiological (respiration and cardiac) signals simultaneously with fMRI in human volunteers at rest with their eyes closed. State-of-the-art technology was used including high magnetic field (7T), a multi-channel detector array, and high resolution (3 mm³) echo-planar imaging (EPI). We investigated the relative contribution of thermal noise and other sources of variance to the observed fMRI signal fluctuations both in the visual cortex and in the whole brain gray matter. The following sources of variance were evaluated separately: low frequency drifts due to scanner instability, effects correlated with respiratory and cardiac cycles, effects due to variability in the respiratory flow rate and cardiac rate, and other sources, tentatively attributed to spontaneous neuronal activity. We found that low-frequency drifts are the most significant source of fMRI signal fluctuations (3.0% signal change in the visual cortex, TE = 32 ms), followed by spontaneous neuronal activity (2.9%), thermal noise (2.1%) and effects due to variability in physiological rates (respiration 0.9%, heartbeat 0.9%) and correlated with physiological cycles (0.6%). We suggest the selection and use of four lagged physiological noise regressors as an effective model to explain the variance related to fluctuations in the rate of respiration volume change and cardiac pulsation. Our results also indicate that, compared to the whole brain gray matter, the visual cortex has higher sensitivity to changes in both the rate of respiration and in the spontaneous resting state activity. Under the conditions of this study, spontaneous neuronal activity is one of the major contributors to the measured fMRI signal fluctuations, increasing almost two-fold relative to earlier experiments under similar conditions at 3T.

Introduction

Several sources are responsible for fMRI signal fluctuations in the human brain at rest. Some of these fMRI resting-state fluctuations have a neuronal [1–3] and metabolic [4] correlate (spontaneous neuronal activity), and their apparent functional specificity has been exploited to study the functional connectivity of the brain at rest [5]. A large number of “resting-state” networks have been identified. Together they cover most of the brain, including the sensory areas, the fronto-parietal attentional system, the so-called “default-mode” network and frontal regions related to executive cognitive control [6].

Nevertheless, non-neuronal contributions to fMRI signal fluctuations can form a major confound to the study of functional connectivity [5, 7–9]. It has been shown that a substantial amount of the variance in the blood-oxygenation level dependent (BOLD) fMRI signal time course can be explained by a variety of physiological and instrumental sources. These include thermal noise (i.e. electrical noise inherent to nuclear magnetic resonance signal reception, with a “white” character, that is uniform power spectral density), and non-thermal sources (generally having a non-uniform power spectral density) related to cardiac and respiratory cycles, subject motion, and instrumental drift [7–13]. Spontaneous neuronal activity is also a non-thermal source and some of its spectral components overlap with those of physiological and instrumental sources. For proper interpretation of brain functional connectivity with fMRI, it is therefore crucial to identify, characterize and, ultimately, remove these confounds.

As a step towards this goal, the aim of the present study was to determine the variance explained by and the signal change attributable to thermal noise and non-thermal sources (including spontaneous activity) in resting-state fMRI data in the gray matter and particularly in the visual cortex at 7T. We considered several components [12, 14] of non-thermal sources of fluctuations separately: scanner instability (leading to signal drifts and other image artifacts), effects in phase with respiratory and cardiac cycles (e.g. pulsatility of blood flow, bulk motion of the head and local magnetic field changes in the head due to breathing [10–11]); effects of changes in physiological rates (e.g. fluctuations in arterial carbon dioxide (CO₂) concentration and arterial blood pressure, and hence in cerebral blood flow (CBF) and volume (CBV) [7–9]); and spontaneous neuronal activity. Because the exact timing and shape of effects due to changes in physiological rates [15] are not well known, we proposed an improved procedure for modeling these noise sources and compared it to methods developed in previous work [7, 9, 15].

Materials and Methods

Overview

We acquired fMRI images at 7 T and simultaneous physiological recordings of the cardiac and respiratory activity in eight healthy subjects during rest. First, the modeling of effects due to rate changes in respiration and cardiac pulsation (noise sources 3–4, see below) was studied and optimized. Specifically, an improved procedure for modeling these noise sources is proposed and compared with previously developed procedures [7, 9, 15]. Subsequently, the contribution of these and other noise sources to fMRI signal fluctuations was evaluated by estimating the explained variance and fMRI signal change in both the visual cortex and the total gray matter. We investigated the following sources: 1) low frequency drifts due to scanner instability and slow head motion; 2) signal fluctuations in phase with respiration and cardiac cycles; effects due to fluctuations in the rates of 3) respiration volume change and 4) cardiac pulsation; 5) thermal noise. Accounting for noise sources 1) –5) allowed us to estimate the potential contribution of spontaneous resting state neuronal activity (source 6)).

Paradigm

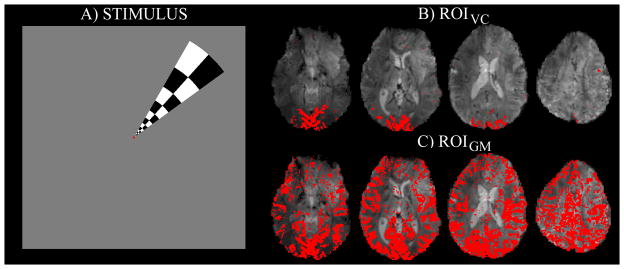
The functional paradigm employed two fMRI runs per subject. First, each subject was asked to rest with eyes closed throughout the scan, not to engage in any particular mental behavior, and to remain awake. Next, a polar-angle-mapping run, consisting of visual stimulation with a rotating wedge-shaped checkerboard (Figure 1A), was employed in order to functionally localize the visual cortex (see Figure 1B).

Figure 1.

A) The stimulus employed to functionally localize the visual cortex (polar-angle mapping run). The wedge-shaped checkerboard (contrast reversing at 7.5Hz) performed a full clock-wise rotation in 90s, covering 30 positions. For details, see Materials and Methods. B) Region of interest in the visual cortex (ROI_VC, for an example data-set), defined on the basis of the polar-angle mapping run. In particular, ROI_VC comprised the voxels in the visual cortex responding to the wedge-shaped checkerboard at any position in the visual field. C) Region of interest in the gray matter (ROI_GM, for the same data-set as shown in Figure 1B). ROI_GM was identified after regression of the signal of each voxel with a global regressor (average time-series across the whole brain), following a procedure developed in previous work [18]. Voxels with significant correlation (p < 0.001) were included in ROI_GM.

Subjects

Eight healthy subjects (mean age 33 years, standard error (s.e.) ± 4 years, 5 males) were included in the present analysis. The physiological and fMRI data acquired from these eight subjects, as part of a previous study [3], was complete and of high quality. All subjects received an explanation of the procedures and gave their written informed consent. The human subject protocol was approved by the Institutional Review Board of the National Institutes of Health.

Stimuli

Visual stimuli for the polar-angle mapping paradigm were presented by means of Presentation 11.0 software (http://www.neurobs.com/), which was synchronized with the MR scanner. Similar phase-encoding stimuli have been employed previously to map the visuotopic organization in multiple visual areas [16]. The stimuli were back-projected onto a translucent screen, positioned on the head coil, using a digital light processing (DLP) projector located outside the MR scanner room. The subject viewed the projection screen through a mirror and a prism (32° × 42° full field of view).

The wedge-shaped checkerboard used during the polar-angle-mapping run was 16° long (i.e. eccentricity 0–16°) and had a polar angle width of 24° (Figure 1A). It reversed its contrast at a rate of 7.5Hz. During each 3 s step the wedge consisted of black/white, red/green and blue/yellow checkers during the first, second, and third second of each step, respectively. Each wedge was superimposed on a gray background image with a central red dot and was isoluminant to the background.

To control subject attention and ensure fixation during the entire polar-angle-mapping run, subjects had to focus on a fixation dot displayed at the center of the screen and to press a button for any change in the dot color. The dot color was modified every 15 s on average, with the inter-stimulus interval in the range 10–20 s. The polar-angle-mapping paradigm began with 36s of gray field containing only the fixation dot, after which the wedge-shaped checkerboard appeared and started rotating in 30 steps of 12°.

Data Acquisition

fMRI was performed using a General Electric 7T MRI scanner (http://www.gehealthcare.com/) using 16 receive-only coil elements out of a 32-channel Nova detector array (http://www.novamedical.com/). Gradient-recalled echo-planar imaging (EPI) was used to obtain BOLD contrast. We acquired 36, 2 mm-thick, slices (slice spacing equal to 0.2 mm) in interleaved descending order, with the following parameters: repetition time (TR) of 3 s, flip angle (FA) of 75°, echo-time (TE) of 32 ms, bandwidth of 250 kHz, in-plane isotropic resolution of 1.25 mm (FOV = 240 x 180 mm²; matrix = 192 x 144) and a SENSE acceleration rate of 3.

We acquired 115 scans for the rest condition (345 s acquisition time), and 172 for the polar-angle-mapping run (516 s acquisition time). We used the first 10 images as a reference for coil sensitivity mapping and then discarded them from further fMRI analysis. To minimize head motion we placed foam pads in the space between the interior coating of the MRI detector array and the subject’s head. To further improve temporal signal stability, real-time modulation of B₀ shims (2^nd order) was carried out to compensate for respiration-induced magnetic field changes in the brain [17].

The timing of physiological cycles was recorded using the pulse-oximeter and respiratory bellows provided with the MR scanner and with a data acquisition card (National Instruments Corp., http://www.ni.com/) at a sampling rate of 250 Hz. This card also recorded the subjects’ button presses in response to the task and MR scanner triggers synchronized with the acquisition of each image volume.

Data Analysis

Pre-processing of fMRI data

We used a dedicated computer with code custom-written using IDL 7.0 software (ITT Visual Information Solutions, http://www.ittvis.com/) for coil sensitivity mapping and off-line SENSE image reconstruction. The FMRIB Software Library (FSL4.0, http://www.fmrib.ox.ac.uk/fsl/) was used for additional pre-processing steps, namely rigid body transformation to correct for head motion and spatial co-registration of the polar-angle-mapping data to that of the resting-state fMRI run. Next, time-series signals were converted to percentages by computing the ratio of the signal in each voxel at every time point to the signal in the same voxel at a reference time point (11^th scan after the beginning of the acquisition), and then multiplying by 100.

Localization of regions of interest

We identified a functional region of interest (ROI) in the visual cortex, ROI_VC (Figure 1B), and another ROI comprising all the gray matter, ROI_GM (Figure 1C).

To define ROI_VC we analyzed the functional localizer (polar-angle mapping) data-set as follows. Univariate regression analysis was performed with the Analysis of Functional NeuroImages tool (AFNI, http://afni.nimh.nih.gov/afni/) after high-pass filtering the data at 0.007Hz. This low frequency cut-off was chosen to preserve all stimulus-related signals. Thirty regressors were used, each modeling the BOLD fMRI response to the wedge-shaped checkerboard in one of the 30 partially overlapping positions occupied during its rotation. Each regressor was created by convolving the time at which the checkerboard reached each position with the Statistical Parameter Mapping (SPM2, http://www.fil.ion.ucl.ac.uk/spm/) standard hemodynamic response function (combination of two gamma-variate functions with a first positive peak at 5s, followed by an undershoot at 16s after the beginning of the stimulation). Voxels that were significantly activated during any wedge position (F-test, P < 0.0001) formed ROI_VC (Figure 1B).

To define ROI_GM we used a global signal regression procedure [18]. The signal in each voxel was correlated with the average time-series across the whole brain (after accounting for low frequency drifts with third-degree polynomials). Voxels with significant correlation (p<0.001) were included in ROI_GM.

On average across subjects ROI_VC was comprised of 8734±1094 voxels, and ROI_GM of 109110±10336 voxels.

Extraction of RVT regressor

The recorded respiratory signal (an offset added to make the signal positive) during the resting session was down-sampled to 10 Hz after neighborhood averaging. The cumulative integral (C) of the signal was computed. For each time-point (t, with t = 0 corresponding to the first MR trigger of the session), the respiration volume per unit time (RVt) was computed as the difference between C at t+TR/2 and at t-TR/2, divided by TR. The respiration volume per unit time (RVT) at each TR (defined as the interval between two consecutive MR scanner triggers), was computed by down-sampling RVt to 1/TR Hz after neighborhood averaging. This procedure to compute RVT is based on the method developed in [8], but it is slightly less computationally demanding.

Extraction of cardiac-rate regressor

The cardiac peaks in the pulse-oximeter signals were detected and the beat-to-beat cardiac rate was calculated (Hz) as the inverse of the beat-to-beat interval. Spurious, non-physiological ((p < 0.05, two sided t-test) beat frequencies were removed by rejecting any beat frequencies that were more than 1.96 standard deviations (calculated across the whole time-course) away from the median and replacing them with the mean of the two nearest non-spurious beat frequencies. A cardiac rate time-course with one time-point for every image volume was obtained by averaging the cardiac rate values falling within each TR. This procedure to compute the cardiac-rate regressor is based on the method developed in [9].

Model optimization for effects due to changes in physiological rates

Because the exact timing and shape of the effects due to changes in physiological rates on the BOLD signal are unclear [15], several models for cardiac and respiratory noise sources, 3) and 4), were tested. The variance explained by and the signal change attributable to each model (computed as described in paragraph “Relative contribution of each noise source and spontaneous activity to fMRI resting-state data”) were compared (Table 1).

Table 1.

The variance explained by and signal change attributed to different models of effects due to changes in the rates of respiration and cardiac pulsation (noise sources 3) and 4)) in the visual cortex (VC) and the total gray matter (GM) at the voxel and ROI level.

	VOXEL LEVEL		ROI LEVEL
	VC	GM	VC	GM
RVT⊗IRF1a) [7]	7.0 (1.6) 1.0 (0.1)	3.8 (0.5) 0.7 (0.1)	19.4 (4.5) 1.0 (0.1)	9.6 (2.5) 0.7 (0.1)
RVT⊗IRF2b) [15]	3.5 (1.3) 0.8 (0.2)	2.7 (0.9) 0.5 (0.1)	9.8 (3.9) 0.7 (0.2)	9.5 (4.3) 0.5 (0.1)
Dual-laggedc) RVT1d)	6.8 (2.0) 1.1 (0.2)	3.7 (1.0) 0.7 (0.1)	17.4 (5.2) 1.0 (0.2)	12.3 (4.4) 0.7 (0.1)
Dual-lagged Cardiac-rate2e)	3.0 (1.3) 0.7 (1.1)	1.7 (0.6) 0.5 (0.1)	6.1 (2.7) 0.5 (0.1)	2.5 (1.1) 0.3 (0.1)
Dual-lagged RVT2	5.1 (1.6) 0.9 (0.2)	2.6 (0.8) 0.6 (0.1)	14.3 (4.8) 0.8 (0.2)	8.6 (3.9) 0.5 (0.1)
Dual-lagged Cardiac-rate1	4.7 (2.0) 0.9 (0.3)	2.8 (0.9) 0.6 (0.1)	9.2 (4.0) 0.6 (0.2)	6.3 (2.2) 0.5 (0.1)
Multi-lagged f) RVT1 [9]	12.3 (2.8) 1.1 (0.2)	7.9 (1.6) 0.7 (0.1)	31.2 (5.4) 1.0 (0.2)	18.5 (6.6) 0.7 (0.1)
Multi-lagged Cardiac-rate2 [9]	3.7 (1.0) 0.7 (0.2)	2.4 (0.6) 0.5 (0.1)	6.3 (2.1) 0.5 (0.1)	4.1 (1.2) 0.3 (0.1)
Multi-lagged RVT2 [9]	9.2 (1.9) 1.4 (0.2)	5.9 (1.2) 1.0 (0.1)	23.9 (5.0) 1.1 (0.2)	14.1 (5.4) 0.8 (0.2)
Multi-lagged Cardiac-rate1 [9]	6.7 (2.5) 1.2 (0.3)	4.4 (1.3) 0.8 (0.2)	13.6 (5.5) 0.7 (0.2)	8.5 (3.4) 0.6 (0.2)

Percentage of variance explained (% VE), average (s.e.) across subjects, is given in bold (upper row). Percentage signal change (% SC), average (s.e.) across subjects, is given in italic (lower row). Noise sources 1) and 2) were accounted for in all the regression models included in the table (for example, in the Birn model [15] in the top row, the matrix of regressors used was X = [ Xpol Xretroicor RVT⊗IRF1]).

^a) IRF₁ = respiration impulse response function used in [7] (see also Methods)

^b) IRF₂ = respiration response function described in [15] (Eq. (3))

^c) The dual-lagged procedure corresponds to the model proposed in the present work, with RVT and cardiac-rate regressors shifted at two optimal time lags (lags = −9 s, +9 s and −3 s, +9 s respectively)

^d) RVT1 means that VE = R²_adj-1(Xrvt), see Eq. 2, and RVT2 means that VE = R²_adj-2(Xrvt))

^e) Cardiac-rate2 means that VE = R²_adj-2(Xcard-rate), see Eq. 2 (analogous for Cardiac-rate1). Note that since the sum of values of RVT1 and Cardiac-rate2 is the same as that of RVT2 and Cardiac-rate1, in the table we grouped RVT1 with Cardiac-rate2 and RVT2 with Cardiac-rate1

^f)The multi-lagged procedure corresponds to the model proposed in [9], with RVT and cardiac-rate regressors shifted at eight and five different time lags, respectively (lag range [−24 +18]s, and lag range [−12 +12]s, respectively, with step = 6 s)

All models employed respiration volume per unit time (RVT) [8] and cardiac rate [9] regressors, computed (using in-house code in IDL 7.0) from physiological recordings as explained above.

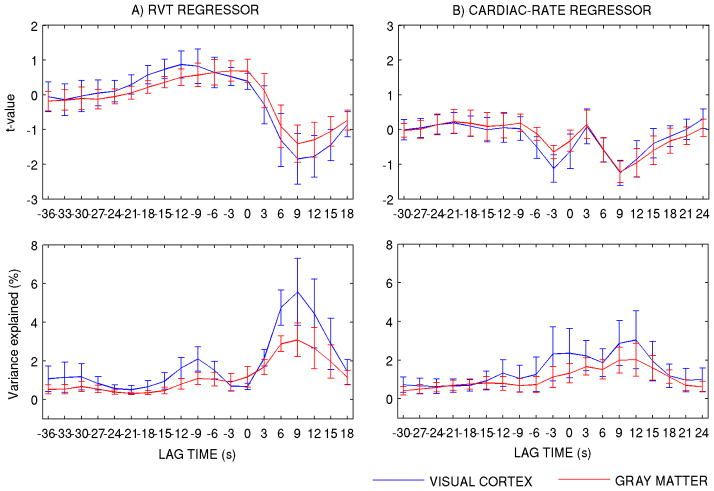
First, we explored the use of a RVT and a cardiac rate regressor, each shifted at two optimal time lags. This is referred to as the “dual-lagged procedure”. We fitted RVT and cardiac-rate regressors shifted over a range of lag times to the single-voxel time-series in each ROI (low frequency drifts with third-degree polynomials were also accounted for). We repeated the same analysis for ROI-averaged time-series in ROI_VC and ROI_GM. The adoption of two lags was inspired by the shape of the correlation (t-values and explained variance) of physiological regressors with fMRI signal fluctuations for different lag times, which displayed two maxima (in absolute value) for each regressor (Figure 2).

Figure 2.

A) t-value of the correlation between the RVT and cardiac-rate regressors (shifted over a range of lag times) and the single-voxel time-series. The results of averaging the t-values of correlation in each voxel over ROI_VC and ROI_GM are shown here. For the RVT, the time lags −9 s and +9 s correspond to the maximum and minimum t-values, respectively (positive time lags indicate that fluctuations in RVT predict future fMRI signal changes; viceversa for negative time lags). The Cardiac-rate regressor shows two (negative) peaks at time lags −3 s and +9 s. B) Variance (%) explained by each regressor at different delays. Mean values (of ROI-averaged values of VE) ± s.e. across subjects are displayed. In this computation, low frequency drifts were accounted for with third-degree polynomials (i.e., X = [Xpol Xrvt] or X = [Xpol Xcard-rate]).

As an alternative to the dual-lagged model we also considered the RVT time course convolved with a respiration impulse response function (IRF) for respiration effects. The IRF was equal to either: a) a single gamma-variate function having width 6 s and mean lag 6.3 s (IRF₁), valid for cerebral blood flow velocities in the middle cerebral artery, used in [7], and in agreement with previous transcranial Doppler ultrasound measurements [19]; or b) a combination of two gamma-variate functions (see Eq. (3) in [15]) peaking at 3 s followed by an undershoot peaking at 16 s (IRF₂), estimated from fMRI data in the gray matter during cued breathing [15].

Finally, we considered a procedure with 8 RVT and 5 cardiac-rate regressors [9], shifted at different time lags within a range of lags (–24 through 18 s and –12 through 12 s, respectively, with step = 6 s). This “multi-lagged procedure” [9] is the most conservative noise correction strategy of the four evaluated in this study. It allowed for the most comprehensive modeling of the targeted physiological noise sources, albeit with the most severe loss in degrees of freedom and the possible under-estimation of signals related to spontaneous neuronal activity.

Relative contribution of each noise source and spontaneous activity to fMRI resting-state data

The contribution of each noise source to fMRI resting-state signal fluctuations was evaluated in terms of the variance it explained and the signal change it caused in ROI_VC and ROI_GM.

The percentage fMRI signal variance explained (VE) by sources 1)−4) was computed as the coefficient of determination adjusted for the degrees of freedom (R²_adj), multiplied by 100. The R²_adj of a regression model measures the proportion of the fMRI signal variance that is explained by that model [20]. R²_adj has values between 0 and 1 and is adjusted to account for the different number of regressors in each model partition, enabling comparisons across model partitions. In particular, following the procedure developed by Shmueli [9], we used a set of 5 nested regression models X:

$$\begin{array}{l}\text{1)}\text{X}=[\text{Xpol}];\\ \text{2)}\text{X}=[\text{Xpol}\text{Xretroicor}];\\ \text{3)}\text{X}=[\text{Xpol}\text{Xretroicor}\text{Xcard}-\text{rate}];\\ \text{4)}\text{X}=[\text{Xpol}\text{Xretroicor}\text{Xrvt}];\\ \text{5)}\text{X}=[\text{Xpol}\text{Xretroicor}\text{Xrvt}\text{Xcard}-\text{rate}].\end{array}$$ (1)

Xpol is a third-order polynomial, modeling mainly low frequency drifts up to about 0.01 Hz, but also extending to higher frequencies. Xretroicor consists of eight RETROICOR regressors [11], including Fourier series expanded in terms of cardiac and respiratory phases up to the second-order, which explain fMRI signal fluctuations in phase with respiration and heartbeat cycles (the extraction of RETROICOR from physiological recordings acquired during the resting run was performed using the procedure (code written in C) of Glover et al. [11]). Xrvt and Xcard-rate comprise RVT and cardiac rate regressors determined using the “dual-lagged procedure” described above (or other models for noise sources 3) −4), when explicitly stated).

We evaluated the adjusted coefficient of determination (R²_adj) for each regression model (R²_adj(1–5)). We thereby computed R²_adj for each model partition (i.e. each group of noise regressors for noise sources 1) −4)) by subtracting the R²_adj of two consecutive regression models. For instance, we obtained:

$$\begin{array}{lll}{{\text{R}}^2}_{\text{adj}}(\text{Xpol})\hfill & ={{\text{R}}^2}_{\text{adj}}(1);\hfill & \hfill \\ {{\text{R}}^2}_{\text{adj}}(\text{Xretroicor})\hfill & ={{\text{R}}^2}_{\text{adj}}(2)-{{\text{R}}^2}_{\text{adj}}(1);\hfill & \hfill \\ {{\text{R}}^2}_{\text{adj}-1}(\text{Xrvt})\hfill & ={{\text{R}}^2}_{\text{adj}}(4)-{{\text{R}}^2}_{\text{adj}}(2);\text{and}{{\text{R}}^2}_{\text{adj}-2}(\text{Xrvt})\hfill & ={{\text{R}}^2}_{\text{adj}}(5)-{{\text{R}}^2}_{\text{adj}}(3);\hfill \\ {{\text{R}}^2}_{\text{adj}-1}(\text{Xcard}-\text{rate})\hfill & ={{\text{R}}^2}_{\text{adj}}(3)-{{\text{R}}^2}_{\text{adj}}(2);\text{and}{{\text{R}}^2}_{\text{adj}-2}(\text{Xcard}-\text{rate})\hfill & ={{\text{R}}^2}_{\text{adj}}(5)-{{\text{R}}^2}_{\text{adj}}(4).\hfill \end{array}$$ (2)

For RVT and cardiac-rate regressors, depending on which models were considered (with only one noise source at a time or both respiration and cardiac regressors together), two different values for the percentage fMRI signal variance explained could be obtained: the second value (e.g. R²_adj-2 (Xrvt)) was, in general, smaller than the first (e.g. R²_adj-1 (Xrvt), see also Table 1), due to some collinearity between Xrvt and Xcard-rate (see Figure 3).

Figure 3.

The correlation matrix (upper triangular matrix, r-value ranging from −1 to 1) of all noise regressors for noise sources 1) −4) is displayed, showing the collinearity between regressors. In the lower triangular matrix a contour plot highlighting regressors with significant collinearity (p < 0.05) is shown. At this statistical threshold (but not for p < 0.001) some regressors for different noise sources are collinear (see for example low frequency drifts and RVT regressors, or RVT regressors with cardiac-rate regressors).

The percentage signal change (SC) attributable to sources 1) −4) was computed from the signal variance (σ²) and VE of Eq. (2), as follows: SC = √(σ² · VE). Note that similar values are obtained if SC is computed as the standard deviation of the signal fitted by each model partition.

Sources 5) (thermal noise) and 6) (spontaneous neuronal activity) were not modeled with any regressor, but their contribution to fMRI signal fluctuations at rest in our experiments was estimated as follows. The SC due to thermal noise was estimated as the inverse of the image signal-to-noise ratio (SNR). The SNR was calculated by dividing the signal in each voxel at a fixed time point (11^th scan after the beginning of the acquisition) by the square root of the noise covariance in the same voxel. The noise covariance was computed from an extra acquisition with no radiofrequency (RF) excitation. The R²_adj and SC assumed to be due to spontaneous resting-state neuronal activity were determined from the residual signal variance after accounting for noise sources 1) −5).

We computed R²_adj and SC both for voxel time-courses (voxel level) and for signals averaged (ROI level) within the visual cortex and the total gray matter (ROI_VC and ROI_GM, respectively). Then, the R²_adj and SC mean ± s.e. across voxels were calculated and displayed (Figure 4 and Table 1).

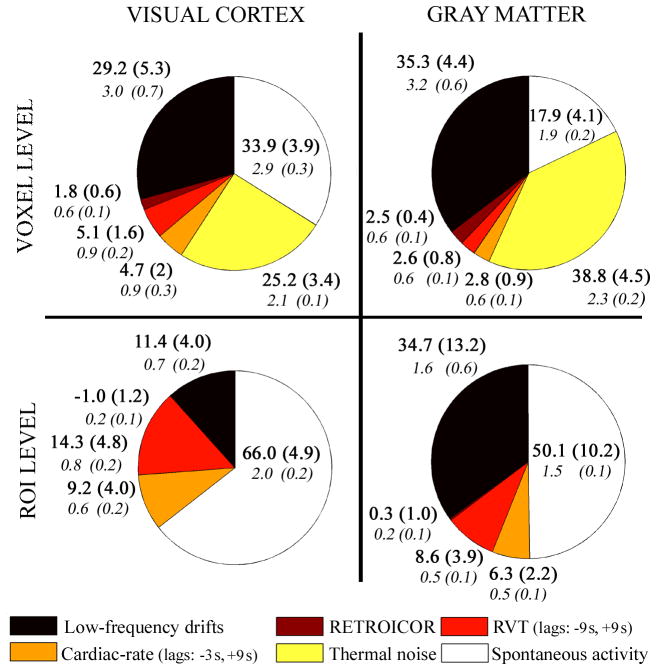
Figure 4.

Pie-charts showing the fMRI data variance explained (R²_adj, %, upper bold) by, and fMRI signal change (SC, %, lower italic) attributed to non-thermal noise sources 1) −4), thermal noise and spontaneous activity. Average (s.e) values across subjects are shown. The contribution of thermal noise at the ROI level was negligible.

Results

Optimization of the proposed model of effects due to changes in physiological rates

The computed t-values of the correlation between RVT (Figure 2A, upper row) and cardiac-rate regressors (Figure 2B, upper row), shifted over a range of lag times, and the single-voxel time-series in ROI_VC and ROI_GM (t-values averaged over ROIs) show a bi-modal distribution with the time lag. The variance explained by RVT and cardiac-rate regressors (Figure 2A-B, lower row) also display a similar distribution, with relevant delays for maximum explained variance (VE) at −9 s and +9 s for RVT and −3 s and +9 s for the cardiac-rate regressor. Similar trends were observed for signals in the visual cortex and in the whole gray matter (correlation between VE in the two ROIs: r > 0.9), and similar results for ROI-averaged signals with respect to single-voxel time-series (r > 0.87, results not shown). We therefore proposed and further investigated the use of a RVT and a cardiac rate regressor, each shifted at two optimal time lags (−9 s, +9 s and −3 s, +9 s, respectively).

Additional analysis of the autocorrelation between the time-lagged RVT (or cardiac-rate) regressors (Figure 3) showed that the use of only two time-lagged regressors to model RVT effects (or cardiac-rate effects) is sufficient to capture the inter-subject variability in the RVT (or cardiac-rate) response function. As visible from Figure 3, the use of shifts of a few seconds does not generate orthogonal regressors, and that the choice of only two time lags separated by at least 6–12 s is adequate. For example, a shift of 9 s of the RVT time series (and even more for the cardiac-rate regressor) does not generate an orthogonal regressor to the unshifted RVT regressors (p < 0.05, see Figure 3). To disclose the true autocorrelation order of RVT (cardiac-rate) regressors, we computed the partial autocorrelation function of RVT (cardiac-rate) regressor by the Yule-Walker equations procedure [21]. This procedure removes the contribution of lags lower than L from the computation of the autocorrelation at lag L (see also Figure 4SM, [3]). We found an autocorrelation order equal to one (3 s) and three (9 s) respectively for RVT and cardiac-rate regressors (p < 0.05), with RVT (or cardiac-rate) regressors becoming non-collinear when separated by at least two time lags, i.e. 6 s (or 4 time lags, i.e. 12 s).

Comparison with previous models of effects due to changes in physiological rates

In assessing the contribution of effects due to changes in the rates of respiration and cardiac pulsation to fMRI signal fluctuations at rest, we compared the two-time-lag RVT (or cardiac-rate) model (dual-lagged procedure) with three other models for noise sources 3) and 4). The explained variance (VE) and the signal change (SC) from the different models of noise sources 3) and 4) in the visual cortex and the gray matter are shown in Table 1.

Our results show that, in brain fMRI signals at rest (in the gray matter), the variance explained by and the signal change attributable to RVT convolved either with an impulse response function peaking at 6 s, obtained for cerebral flow velocities in the middle cerebral artery [7, 19], or with an impulse response function optimized for cerebral fMRI data [15] are comparable (in the visual cortex, the former performs better than the latter). The proposed dual-lagged procedure for selecting the optimal RVT (or cardiac-rate) regressors is a compromise between the more conservative multi-lagged model [9] (with eight and five lags for RVT and cardiac-rate regressor, respectively) and the procedures [7, 15] which employ an impulse response function to model signal fluctuations related to changes in respiration rate and volume.

Relative contribution of each noise source and spontaneous activity to the fMRI resting-state data

The VE and SC attributed to each noise-source (non-thermal and thermal) in the visual cortex and the gray matter are shown in Figure 4, both at the voxel level and at the ROI level. For RVT and cardiac-rate regressors, we used the dual-lagged procedure (see also Table 1), computing R² _adj-2 (Xrvt) and R²_adj-1(Xcard-rate) (“dual-lagged RVT2” and “dual-lagged Cardiac-rate1” in Table 1). For the calculation of the VE and SC of spontaneous neuronal activity, this is equivalent to using the procedures “dual-lagged RVT1” and “dual-lagged Cardiac-rate2”, because the sum of R²_adj-2(Xrvt) and R²_adj-1(Xcard-rate) is the same as that of R² _adj-1(Xrvt) and R²_adj-2(Xcard-rate). The R²_adj and SC of thermal noise at the ROI level were considered negligible, because averaging across voxels attenuated the SC by the square root of the total number of voxels (i.e., by a factor of ~93 and 330 for ROI_VC and ROI_GM, respectively).

The SNR (used to calculate the contribution of thermal noise) in the visual cortex and in the gray matter was equal to 70.7 ± 4.2 and 64.9 ± 4.2, respectively (mean ± s.e. across subjects, after averaging the SNR across voxels within ROIs).

Compared to the whole gray matter, the visual cortex showed larger signal fluctuations in response to variations in the rate of respiration volume change (source 3)) and greater spontaneous resting-state activity (source 6)), both at the voxel and ROI level (paired t-test, p < 0.05). This was not the case for either low frequency drifts (source 1), or for RETROICOR regressors (source 2). The difference between the signal change related to cardiac rate effects (source 4) in the visual cortex and the total gray matter was not significant, though it was close to significance at the voxel level.

Discussion

In this work we evaluated the relevance of different sources to fMRI signal fluctuations at 7T during rest, separating the contributions of signal drifts, effects related to physiological cycles, signal fluctuations related to changes in respiration and cardiac rates, thermal noise and signal changes tentatively attributed to spontaneous neuronal activity.

First, we discuss the contribution of non-thermal sources to fMRI signal fluctuations at 7T, and compare it to previous findings at 3T. We then address the differences in the amount of nonthermal noise between the visual cortex and the gray matter. Finally, we examine some issues linked to modeling non-thermal noise sources and, in particular, effects related to fluctuations in respiratory and cardiac rates.

Relative contributions of non-thermal noise at 7T

Our results demonstrate that low frequency drifts (mainly at frequencies < 0.01Hz) are a very important source (35.3 % of the total variance in the gray matter, at the voxel level, corresponding to a signal change of 3.2 %) of non-thermal noise and must be properly accounted for in studies of resting state activity. Potential contributors to this noise source are slow changes in head position, baseline physiology, and instrumental conditions such as slow drifts in gain and resonance frequency.

At the voxel level, RETROICOR regressors explained only 2.5 % of the signal variance (corresponding to a signal change of 0.6 %) in the gray matter. The observed contribution of physiological motion to fMRI signal fluctuations in the gray matter is smaller at 7T (2.5%) than at 3T (3.8% of the signal variance, as reported by Shmueli et al., [9]) and this could be the result of the use of real-time shimming at 7T [17] or of a stronger contribution from other sources to the measured signal. The contribution of RETROICOR regressors to fMRI ROI-averaged signals was negligible, suggesting a low spatial coherence of noise in phase with physiological cycles across the visual cortex and the gray matter in general.

A significant portion (9.8 % and 5.4 % in ROI_VC and ROI_GM, at the voxel level, see Figure 4) of the variance in fMRI signal fluctuations in the resting brain was explained by signal fluctuations induced by variations in the rates of respiration volume change and cardiac pulsation (sources 3) −4)). The exact amount of variance explained depends on how these noise sources are modeled (see Table 1 to compare different models), which is still a matter of controversy. Comparison of the current findings with previous results obtained at 3T [7, 9] is not straightforward as previous studies report on fluctuations in terms of explained variance (%) rather than signal change (%). The former is dependent on the contribution of other sources (for example thermal noise for results at the voxel level, or any other source at the ROI level), which generally differs across studies and thus precludes meaningful comparison. For example, the respiration-related variance reported by Wise in selected regions at 3T (R² = 24.1%, see Table 3 in [7]) is larger than the variance found here in gray matter-averaged signals (9.6%) at 7T; this discrepancy could be readily explained by differences in regions of interest and the contributions of other noise sources. In contrast, comparing the multi-lagged procedure with previous findings at 3T obtained at the single voxel level within the gray matter (Table 2 in [9]), the variance explained by RVT and cardiac-rate regressors is larger (about 4.9 and 2.7 times, respectively) at 7T (Table 1), as expected for higher field strengths. Nevertheless, some of this variation in single voxel analysis could be explained by differences in thermal noise levels across studies.

BOLD signal fluctuations are expected to increase at 7T with respect to 3T, as we observed for the effects due to spontaneous neuronal activity. Here, we observed residual fMRI signal changes attributed to spontaneous neuronal activity of 2.9 % in visual cortex (1.9 % in gray matter, TE = 32 ms) when analyzing on a voxel-by-voxel basis after removal of non-thermal and thermal noise sources. For ROI-averaged results we found residual signal changes of 2.0% and 1.5% for ROI_VC and ROI_GM, respectively. This is indeed 1.7 times larger than what was previously reported at 3T: 1.2 % and 0.9 % for average signals in the VC and GM respectively, during resting without sleeping for a voxel volume 1.85 times larger than that of the current study and an echo time of 43 ms optimized for fMRI at 3T, see Figure 4 in [22].

Non-thermal noise in the visual cortex and in the gray matter

It is not clear whether non-thermal noise, especially physiological noise, and spontaneous activity in fMRI signals are characterized by significant regional heterogeneity and how this might affect the identification of spontaneous resting activity in different brain areas. To clarify this issue, we compared the relative contribution of different non-thermal noise sources to the total fMRI signal fluctuations in the visual cortex with that in the whole brain gray matter.

Compared to the total gray matter, the greater amplitude of fMRI signal fluctuations due to RVT changes and to spontaneous activity observed in the visual cortex demonstrates this region’s high BOLD sensitivity to physiological changes and to neuronal activity. The greater physiological noise and spontaneous neuronal activity is consistent with regional differences in vascular regulation and metabolism within the brain: in the visual cortex the BOLD fMRI sensitivity to changes in cellular activity is higher than in neighboring areas [23], potentially due to its high concentration of venules [24]. Moreover, the BOLD fMRI signal in the visual cortex (together with that in the parietal and the temporal lobe) displays the highest reactivity in the brain to spontaneous fluctuations of arterial carbon dioxide level (CO₂) in volunteers at rest [7], and during CO₂ challenges such as hypo- and hypercapnia [25–27].

Non-thermal noise modeling

The contribution of spontaneous neuronal activity to resting state fMRI signal fluctuations depends strongly on the number of noise sources considered and on the approach employed to model each noise source.

In multiple regression analysis the degrees of freedom decrease with the number of regressors employed. Therefore, to avoid losing statistical power in the detection of spontaneous neuronal activity, one should keep the number of regressors modeling different noise sources well below the number of independent time points. Note that in addition to the above-mentioned noise sources, for data heavily compromised by head motion, it is common to use an extra six regressors to model head motion (unrelated to physiological cycles), which further exacerbates this issue.

The number of regressors used to model low frequency drifts depends only on the scan length (i.e. increases with it), and once the frequencies of interest and the model are defined, some room for optimization is available. Polynomial modeling is preferable to finite impulse-response high-pass filtering since the frequency content of the polynomials is very similar to that of low-frequency drifts and also includes their contribution at frequencies higher than any filter cut-off (even though these tails explain no more than 1% of the signal variance). Note that much of the typical “1/f” shape of fMRI noise can be accounted for simply by modeling a linear drift. In addition, the choice of a polynomial model for low frequency drifts can help in reducing the number of regressors. For a 315 s acquisition and a high-pass limit of 0.01 Hz (spontaneous neuronal activation is usually investigated above this frequency, [5]) we employed a third-degree polynomial fit (three regressors). If a Fourier basis set had been chosen to remove frequencies below 0.01 Hz for a TR of 3 s, it would have required functions up to third-order i.e. six regressors which is double the number needed for the polynomial model.

Motion due to respiration and cardiac cycles is usually modeled with eight regressors: four for fluctuations in phase with the respiration and cardiac cycles, and four for fluctuations at twice that phase [10–11]. In our data, the contribution of the second harmonic of the physiological motion to the total fMRI signal variance (0.5 %) was much smaller than the contribution of the first harmonic (2.0 %). Therefore, when the number of degrees of freedom is of concern, this suggests that using only four RETROICOR regressors instead of eight may be most efficient.

Noise components related to changes in physiological rates are the most difficult to characterize in terms of both their number and their dynamics. Little is known about the effects of respiration and cardiac rates on the timing and shape of CBF, CBV and BOLD signal changes. Depending on the brain region, different response delays and dispersion might occur, due to differences in local vascular properties and in the transport of CO₂. Nevertheless, from our results (Figure 2), the visual cortex behaved very similarly to the total gray matter, except for an increased contribution of physiological noise regressors for lags in the range [–6 0] s (cardiac rate regressors) and [−12 −6] s (RVT regressors).

Various approaches have been adopted previously to model signal changes related to respiration rate fluctuations [7–9, 15]. Wise et al. [7] used, for each brain region, a single convolution kernel of the BOLD response to CO₂ changes induced by respiration depth and rate. In their approach, the kernel is optimized for the middle cerebral artery [7, 19], and not necessarily accurate for the cerebral cortex. Our results show that, in the gray matter, the amount of variance explained by the adoption of such a kernel is similar to that explained by an impulse response function optimized for cortical fMRI signals [15]. The latter approach, i.e. the adoption of an independently measured respiratory response function obtained by experiments using cued breathing [15], is theoretically the most favorable approach. However, it gives disappointing results when applied to spontaneous breathing (i.e. that usually employed resting condition) unless a lag optimization procedure at the voxel level is employed [15]. Optimization at the voxel level has certain drawbacks, since it would require a separately acquired dataset on the same subject. Since neuro-vascular control and hemodynamic delays are unlikely to dramatically vary at the voxel level, local optimization over bigger areas might be a suitable compromise.

Shmueli et al. [9] use for each voxel the same regressor derived from the respiration belt measurement shifted at different time lags. The same approach is used for cardiac noise modeling. This method seems very conservative in terms of physiological noise removal and probably overestimates the physiological noise contribution to the total signal. Assuming that in the fMRI signal in a brain area only few lagged noise regressors (one, or two if feedback loops are included) explain physiological noise, the use of the remaining time-shifts will incorrectly remove spontaneous resting-state activity with the same spectral amplitude of physiological noise but with a different phase. In the current study, discarding a single-voxel approach, we adopted a region-based double-lagged approach to optimize physiological noise modeling, to be used for future studies in the visual cortex (or in the gray matter in general). While the amount of variance explained with the dual-lagged procedure was larger (especially in the visual cortex) than that of some procedures used previously [7, 15], it did not reach that level achieved with the multi-lagged procedure [9]. The flipside of this is that the latter required a large number (13) of regressors, which can substantially reduce efficiency for the detection of spontaneous activity, in particular for brief experimental sessions.

Our result for respiration-related effects qualitatively agrees with a previous study [8], showing a bi-modal distribution of the correlation of the RVT regressor with fMRI signal fluctuations. With respect to cardiac-rate related effects, our study indicated that negative correlations between the cardiac-rate regressor and the fMRI signal occur in the [−6 15] s range of time lags, and that two lags separated by 12 s are sufficient to describe most of the variance in this range. This result partially agrees with previous work [9] at lower temporal resolution (TR = 6 s), which shows a negative correlation of cardiac-rate regressor with fMRI signal fluctuations in the range 6–18s; however, a double peak in the correlation was not found previously [9]. This discrepancy may have various origins, including experimental differences and differences across volunteers. Investigation of the origin of this double-peak behavior requires further study.

Limitations

Because of the many possible contributions to fMRI temporal signal variability, some of which strongly depend on experimental conditions, our results are not directly generalizable to all resting conditions and functional brain regions outside the two regions studies here. The impact of non-thermal noise (more specifically physiological noise) on fMRI signal fluctuations is expected to depend on the breathing conditions and might increase considerably in special circumstances (sleep, anxiety studies, experiments involving children). Future work might extend our findings to other resting-state networks (e.g. auditory system, sensory-motor areas, attentional system etc) and different conditions or patients.

Conclusions

The results presented in this study underline the importance of modeling non-thermal noise and especially low frequency drifts to define resting-state activity in the visual cortex and in the gray matter as a whole. Our findings demonstrate the usefulness of 7T studies of spontaneous neuronal activity, which is a major contributor to the signal variance and causes increased signal fluctuations with respect to those measured at 3T. Compared to the gray matter in general, the visual cortex showed increased signal fluctuations due to both physiological noise and spontaneous neuronal activity. We provide guidelines for selecting an appropriate model (number and time-shifts of lagged regressors) for the effects due to respiration volume and cardiac rate changes. More work is needed to better elucidate the shape of the BOLD response functions related to these physiological fluctuations.