Abstract
Pleiotropy is the property of genes affecting multiple functions or characters of an organism. Genes vary widely in their degree of pleiotropy, but this variation is often considered a by-product of their evolutionary history. We present a functional theory of how pleiotropy may itself evolve. We consider genes that contribute to two functions, where contributing more to one function detracts from allocation to the second function. We show that whether genes become pleiotropic or specialize on a single function depends on the nature of trade-offs as gene activities contribute to different traits and on how the functionality of these traits affects fitness. In general, when a gene product can perform well at two functions, it evolves to do so, but not when pleiotropy would greatly disrupt each function. Consequently, reduced pleiotropy should often evolve, with genes specializing on the trait that is currently more important to fitness. Even when pleiotropy does evolve, not all genes are expected to become equally pleiotropic; genes with higher levels of expression are more likely to evolve greater pleiotropy. For the case of gene duplicates, we find that perfect subfunctionalization evolves only under stringent conditions. More often, duplicates are expected to maintain a certain degree of functional redundancy, with the gene contributing more to trait functionality evolving the highest degree of pleiotropy. Gene product interactions can facilitate subfunctionalization, but whether they do so depends on the curvature of the fitness surface. Finally, we find that stochastic gene expression favors pleiotropy by selecting for robustness in fitness components.
Keywords: multifunctionality, promiscuous enzyme, gene sharing, redundancy, model
PLEIOTROPY is the property whereby a gene affects more than one function or phenotypic character of an organism. Gene-knockout studies in yeast indicate that deleting genes with higher degrees of pleiotropy has, on average, a more harmful effect on fitness (Salathé et al. 2006; Cooper et al. 2007). This negative relationship with fitness is expected given that most mutational changes are deleterious so that the more characters are affected by a mutation, the more likely the net effect on fitness is harmful, even if the mutation is beneficial for a subset of characters. This claim has been verified in theoretical studies based on Fisher’s geometrical model (Chevin et al. 2010; Lourenço et al. 2011). Pleiotropy is consequently seen as a constraint on evolution because it reduces the adaptive capacity of an organism (Orr 2000; Welch and Waxman 2003).
Recent observations in a variety of species have found that the extent of pleiotropy varies among genes and is often limited, with a majority of genes influencing a small set of traits while a few genes affect many traits (Dudley et al. 2005; Albert et al. 2008; Wagner et al. 2008; Wang et al. 2010; Wagner and Zhang 2011). This is in direct opposition to the historical assumption of universal pleiotropy underlying most population and quantitative genetics approaches to the joint evolution of multiple characters (Fisher 1930; Lande 1979; Orr 1998). It has been suggested that selection may favor reduced pleiotropy to improve the capacity of a population to respond to selective challenges, that is, to improve its evolvability (Hansen 2003). Because selection on evolvability would act at the population level, however, it is likely weak compared to selection acting at the level of the pleiotropic genes themselves. It is thus not yet clear whether selection pressures have substantially shaped the distribution of pleiotropic effects among genes and what mechanisms account for the observed variability in pleiotropy. In this article, we explore the fate of genetic modifiers that alter the degree of pleiotropy to determine whether and when this expectation for reduced pleiotropy is likely to hold.
The nature of pleiotropy
A gene may have pleiotropic effects on different traits for a variety of reasons. For example, pleiotropy may stem from (i) the activity of two different enzymatic products coded by the gene (e.g., from alternative splicing of the coding sequence), which catalyze different reactions, (ii) different substrate affinities of a single enzymatic product catalyzing different reactions, (iii) the differential allocation of the same gene product to two functions in different cell compartments, or (iv) two different biochemical properties of the same gene product [e.g., eye crystallins that are also metabolic enzymes (Piatigorsky and Wistow 1989)]. Although these cases differ in the precise mechanism of their action, we treat them equivalently by considering that their alternate activities trade off; increasing activity in one compartment comes at an activity cost in the other compartment. If this were not the case (i.e., if increasing one activity would benefit or hurt both traits), then we would expect the system to evolve accordingly, until reaching a point where a trade-off is observed.
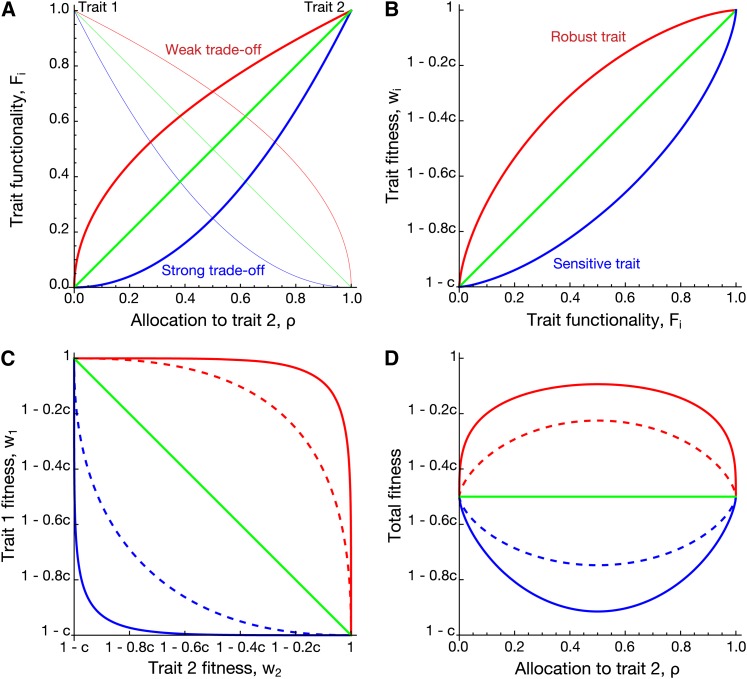
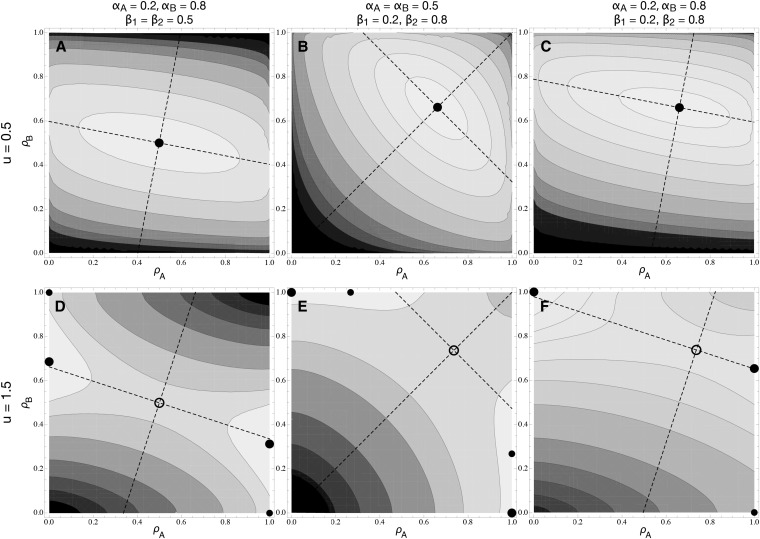
As we shall see, selection on the degree of pleiotropy depends critically on the shape of trade-offs that arise as gene products are allocated to different traits and these traits contribute differentially to organismal fitness. The shape of trade-offs is similarly important in ecological models exploring the evolution of specialists vs. generalists (Levins 1968; Egas et al. 2004; Ravigné et al. 2009; Débarre and Gandon 2010). Indeed, the topics are intricately related, as genes with high degrees of pleiotropy can be thought of as generalists. We thus explore how the mappings that relate gene activity onto trait functionality (Figure 1A) and then trait functionality onto fitness (Figure 1B) combine together to determine the overall shape of the trade-off between fitness contributions from different traits (Figure 1C). As a result of these trade-offs, organismal fitness may be maximized either when genes are pleiotropic (red curves in Figure 1D) or when they specialize on a single trait (blue curves). We call the trade-off between gene activity and trait functionality (Figure 1A) weak when the mapping function is concave (or saturating; red curves) and strong when the function is convex (or accelerating; blue curves); a weak trade-off implies that shifting some gene products away from their current primary role leads to minor losses in functionality of that primary trait relative to gains in a secondary trait. Furthermore, we say that fitness is robust when changes in functionality have relatively minor effects on trait fitness (concave mappings in Figure 1B; red curves) and is sensitive when changes in functionality have relatively major effects on trait fitness (convex mappings; blue curves). For example, the fitness of traits associated with metabolic enzymes may often be robust because flux through an enzymatic pathway typically saturates at high enzyme activities (Dykhuizen et al. 1987; Dekel and Alon 2005). On the other hand, catalytically less efficient proteins may fail unless fully functional, leading to sensitive fitness functions, as seen in some cases of enzyme-mediated drug resistance (Zimmermann and Rosselet 1977; O’Loughlin et al. 2006; Brown et al. 2009).
Figure 1 .
Relationship between gene activity, trait functionality, and fitness. (A) Mapping between activity of gene product allocated to trait 2 (ρ) and the functionality of trait 1 (F1: thin lines) or trait 2 (F2: thick lines). Red curves represent weak trade-offs (u = 1/2), blue curves represent strong trade-offs (u = 2), and the green line represents a linear trade-off (u = 1). (B) Mapping between the functionality of a trait (Fi) and trait fitness (wi). Fitness may be robust (red curve, v = 2/3), sensitive (blue curve, v = 3/2), or proportional (green line, v = 1) to changes in functionality. (C) The combination of these two mappings generates a trade-off between the two trait fitnesses, w1 and w2. The red curves assume fitness is robust (v = 2/3), with either a weak (solid: u = 1/2) or a linear (dashed: u = 1) activity–functionality trade-off. The blue curves assume fitness is sensitive (v = 3/2), with either a strong (solid: u = 2) or a linear (dashed: u = 1) activity–functionality trade-off. The green line assumes linear activity–functionality (u = 1) and trait–fitness (v = 1) relationships. (D) The two trait fitnesses combine to determine organismal fitness, W, here assumed to be additive and equally affected by both traits (β1 = β2 = 1/2). A–D assume αA = 1 for a single locus A, while the strength of selection (c) was kept general.
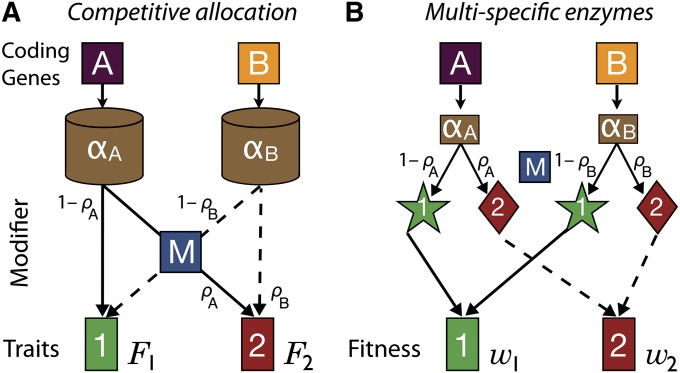
As motivating examples, we consider two specific scenarios. In the first, a gene product (cylinders in Figure 2A) is divvied up among the traits, such that the proportions of gene products allocated to each trait sum to one. If trait functionality depends only on the total amount of gene product allocated to a trait, then there will be a linear trade-off between the functioning of the traits (green line in Figure 1A). Because the traits are essentially competing for the same gene product, we call this the competitive allocation scenario. Examples include pigment production in flowers where a precursor compound is used to produce different pigments [e.g., flower anthocyanin pigments differentiate from the single product of the flavanone-3-hydroxylase (F3H) enzyme, DH-kaempferol, in angiosperms (Rausher 2008)], alternative splicing of pre-mRNA where the spliced products are functionally distinct and the modifier locus affects the relative amount of iso-proteins produced (Black 2003), or any case where the functionality of a trait (its phenotypic value) depends linearly on the amount of gene product allocated to that trait.
Figure 2 .
(A) Cartoon illustrating the competitive allocation scenario, where a proportion ρ of the total gene product (cylinder) is allocated to trait 2, and the remainder (1 − ρ) to trait 1. (B) Cartoon illustrating the multispecific scenario, where each gene product has two distinct properties (e.g., substrate specificities), with one affecting trait 1 (stars) and the other affecting trait 2 (diamonds).
In the second scenario, a single gene has more than one biochemical property and can, for instance, catalyze two different reactions or interact with two substrates with different affinities (stars and diamonds in Figure 2B). The functionality of a trait then becomes a measure of the specificity of the gene product for the substrate associated with that trait. Because the two traits depend on different properties of the gene product, we call this the multispecific scenario. Examples include cases of “gene sharing” (Piatigorsky and Wistow 1989), where a gene product is co-opted for a secondary use that depends on a different biochemical property than its original function. A classic example is eye crystallin proteins that also act as metabolic enzymes (e.g., δ-crystallin as arginosuccinate lyase). Other examples are “promiscuous enzymes” (Aharoni et al. 2005; Khersonsky and Tawfik 2010) that catalyze different reactions but with large differences in their substrate specificities; they are often highly specific for one primary substrate but show low specificity to one or more secondary substrates. Under the multispecific scenario, the nature of the trade-off in functionality depends on what aspects of the gene product have to change to improve the functioning of a trait. In some cases, the optimal conformation of the entire protein might be different for the two functions, so that improving one function would substantially disrupt its original function (a strong trade-off, blue curve in Figure 1A). On the other hand, when two active sites of an enzyme are physically separated, it may be possible to increase the functioning of one site with little cost to the functioning of the other (a weak trade-off, red curve in Figure 1A). Indeed, substrate affinities of many multispecific enzymes have been shown to trade off weakly (Khersonsky and Tawfik 2010). We return to these scenarios in the Discussion, applying our results to these cases.
Previous models
Previous population genetic models have considered modification of pleiotropy mostly as a by-product of gene duplication (Wagner 2000). A gene copy may acquire a novel function (neofunctionalization), either by adding to the set of ancestral functions (increased pleiotropy) or by substituting one function for another (no change in pleiotropy). Alternatively, the pleiotropic degree of a coding gene may decrease because of the appearance of degenerative mutations in a subset of its regulatory sequences [subfunctionalization (Force et al. 1999; Lynch and Force 2000)]. The total expression domain over both copies remains the same, however. Because subfunctionalization, either with or without neofunctionalization, is often observed (He and Zhang 2005), gene duplication is viewed as a mechanism that lessens the degree of pleiotropy.
Counteracting this decline, pleiotropy is thought to increase as organisms face new selective challenges, with existing genes providing the raw material from which evolution molds additional functions. For example, using the software platform, Avida, within which digital organisms compete for computer resources (CPU cycles), Lenski et al. (2003) found that complex features generally evolved out of simpler functions, with some mutations adding functionality to existing code. Such “addition exaptations” have been shown to play an important role in the evolution of novel traits, such as defense and attraction systems in Dalechampia vines (Armbruster et al. 2009).
A further mechanism affecting the evolution of pleiotropy is selection for robust genetic systems. Robustness is the capacity of an organism to resist noisy gene expression and to produce stable phenotypes. Noise in expression may be of developmental or mutational origin (McAdams and Arkin 1997; Elowitz et al. 2002; Ozbudak et al. 2002). Developmental noise is predicted to be counterselected in a stable environment (Swain 2004; Raser and O’Shea 2005; Lehner 2008), although possibly not under unpredictable and/or stressful conditions (Thattai and Van Oudenaarden 2004; Acar et al. 2008; Ratcliff and Denison 2010). Mutational noise stems from the constant input of random genetic changes and is mostly deleterious (Eyre-Walker and Keightley 2007). As such, nonadaptive stochastic gene expression is thought to select for phenotypic robustness (de Visser et al. 2003). Pleiotropy could provide such a buffering mechanism if multiple genes contribute pleiotropically to a trait rather than a single gene targeted solely to that trait, because the functioning of the trait would not be entirely dependent on the activity of a single gene. Robustness is itself related to the curvature of the fitness function, with concave fitness curves yielding higher robustness to stochastic noise (Gros et al. 2009). Nevertheless, the connection between robustness and the evolution of pleiotropy has yet to be explored explicitly.
In this study, we use a population genetic approach to explore the evolution of pleiotropy by determining the nature of selection acting on any site that alters the set of functions performed by a gene; we refer to such a site as a “modifier” of pleiotropy. We show that weak functional trade-offs and robust trait fitnesses promote the evolution of generalist genes with higher degrees of pleiotropy, while strong functional trade-offs and sensitive trait fitnesses promote the evolution of specialist genes with lower degrees of pleiotropy. At an intuitive level, pleiotropy evolves when performing multiple functions moderately well still yields high fitness, whereas specialized (or modular) genes evolve when high fitness is attained only by concentrating gene products on a particular trait.
The evolution of pleiotropy can thus be seen in the broader context of the evolution of specialists vs. generalists (Levins 1968; Egas et al. 2004; Ravigné et al. 2009; Débarre and Gandon 2010; Rueffler et al. 2012). The recent study by Rueffler et al. (2012) is particularly closely related. They examined the evolution of specialist vs. generalist modular structures, which could be physical structures (e.g., limbs) or genetic structures (e.g., duplicate genes). We clarify the parallels and differences between the two models during the analysis, especially when we consider how pleiotropy may evolve in the context of gene duplicates. Overall, our work indicates that variation in the nature of fitness trade-offs among genes and functions may predict the degree to which the underlying genes display pleiotropy.
The Model
We model the evolution of the degree of pleiotropy of genes whose products influence the performance of two phenotypic traits in an organism. The activities of these genes are adjusted by a regulatory site, the modifier locus M, which may or may not be linked to the focal gene(s) and may even lie within the coding region of the gene(s). To describe a wide class of trade-off functions, we use a general mapping of gene activity onto trait functionality and ultimately onto organismal fitness, illustrating our results with specific trade-off functions. We begin with a model that describes the evolution of pleiotropy of a single gene and then consider two genes.
General mapping between genes and fitness
Trait functionality, Fi, is modeled as a function of gene activity and can be viewed as the phenotypic value of the trait. Genes are haploid with total activity level αj for gene j, which represents the activity level if the gene were specialized on one or the other trait. We scale this activity relative to one, which represents the activity of a fully functioning gene (αj ≤ 1). Activity can be interpreted as the level of expression of a gene (e.g., number of proteins produced) or as the catalytic activity of the gene product (enzyme). The modifier locus M changes the targeting of gene activity to the different traits and can be seen as a cis- or a trans-acting regulatory sequence. The functionality, Fi(ρj), of a trait i depends on how much of the activity of the product of gene j is allocated to that trait, ρj, which can be altered by the modifier [where it improves clarity, we drop the (ρj) notation]. With two traits, F1 and F2 change in opposite directions when the modifier alters the targeting of gene activities, because we assume a trade-off among the two functions (Figure 1A). We thus let ρj measure the degree of allocation to the second trait, so that F1 is a decreasing and F2 is an increasing function of ρj,
| (1) |
for any coding gene j. We further say that a gene is pleiotropic when 0 < ρj < 1, so that its activity is apportioned to both functions, while it is perfectly specialized to trait 1 (trait 2) for ρj = 0 (ρj = 1) (see Figure 1).
The total fitness of an individual depends on how variation at the regulatory and coding sequences influences trait functionality and how this functionality in turn affects fitness. Total fitness is thus given as a generic function of the contributions to fitness coming from the two traits, W(w1, w2), with the fitness contribution of a trait given as an arbitrary function of that trait’s functionality, wi(Fi). We naturally assume that total fitness is an increasing function of the contributions of each trait to fitness, with
| (2) |
As the two traits may not be equally critical to survival and reproduction, we introduce the terms, β1 and β2, which weight the relative importance of the two traits to total fitness (with β1 + β2 = 1).
We first analyze the general model delineated here based only on the conditions (1) and (2) and then illustrate our results using the specific functional relationships described below.
Specific mapping between genes and fitness
For the mapping of gene activity onto trait functionality (Fi(ρj)), the specific function that we use is a power trade-off describing how a gene’s activities are apportioned among the two traits:
| (3) |
This satisfies condition (1). To express the trade-off between allocating the products of a gene to traits 1 and 2, we measure functionality relative to αj (its value if all gene products were allocated to the trait) and define the trade-off function, t(x), as F2(ρj)/αj = t(F1(ρj)/αj), where
| (4) |
The parameter u (u > 0) determines the curvature of the trade-off curve (Figure 1A). A linear trade-off function (Figure 1A, green: u = 1) describes cases where increasing allocation to trait 1 proportionately reduces functionality of trait 2, as in the competitive allocation scenario. Trade-offs are strong when the curve is convex (Figure 1A, blue: u > 1) and weak when the curve is concave (Figure 1A, red: u < 1) (following Ravigné et al. 2009; Débarre and Gandon 2010).
We assume that the fitness contribution of each trait depends on that trait’s functionality according to the “power” function (Egas et al. 2004; Ravigné et al. 2009),
| (5) |
which we assume is the same function for both traits 1 and 2 (but see Discussion). The constant c determines the importance of trait i to fitness, with fitness reduced to wi(0) = 1 − c when there is no gene product allocated to the trait (Fi = 0). If c = 1, the organism dies if the trait is nonfunctional, whereas if c is small, variation in the performance of the trait matters little to fitness (e.g., a trait involved in capturing one type of prey may not matter much when other food sources are available). The parameter v (v > 0) sets the convexity of the fitness curve (Figure 1B). Trait fitness is sensitive to the functioning of a trait when wi(Fi) is convex (Figure 1B, blue: v > 1) and robust when wi(Fi) is concave (Figure 1B, red: v < 1). This power function implies that the fitness trade-off curves that emerge among the two traits (Figure 1C) will be monotonic, such that w1 always decreases and w2 always increases with increasing allocation to trait 2 (increasing ρ). As the maximum activity is defined as αj = 1, trait functionality Fi lies between 0 and 1, which ensures that w(Fi) ∈ [0, 1].
Finally, we consider two specific functions relating the fitness effect of a trait to the total fitness of an individual, W(w1, w2), additive or multiplicative, with
| (6a) |
| (6b) |
The additive case may be more biologically appropriate if, for example, each trait contributes to energy reserves, the sum of which determines the number of offspring, while the multiplicative case may be more biologically appropriate if each trait contributes to survival at different stages, where reproduction occurs only if death has not occurred in any previous stage.
Given these functional relationships, we track evolutionary changes at the modifier locus, M, using a model of a single large population of haploids that mate at random, with selection after reproduction. We initially consider models where expression levels (αj) are the same for each individual within the population, later relaxing this assumption and considering noise and variation in expression levels.
Results
Evolutionarily stable pleiotropy at a single locus
We investigate the evolution of the targeting locus M by introducing a modifier allele m that changes the allocation of gene products by an amount Δρj relative to the wild-type allele M (with (ρj + Δρj) ∈ [0, 1]). We first assume that a single pleiotropic gene A is fixed for a certain level of activity, αA. Because only the modifier is polymorphic, standard population genetics theory can be used to show that the modifier allele m will spread if and only if it increases fitness relative to the wild-type allele, ΔW > 0, regardless of the recombination rate between the modifier and the focal locus. In this case, the fitness difference between the mutant and the wild-type modifier alleles is
| (7) |
with
| (8) |
Plugging (8) into (7), and assuming that Δρ is small, the difference in fitness between m and M carriers is
| (9) |
Whether a modifier spreads in this one-locus case thus depends on the sign of the term in parentheses. A potential evolutionary stable strategy (ESS) is found by setting ΔW = 0 and solving for the pleiotropic value, ρ*, that resists invasion by modifiers of pleiotropy. In general, this requires a numerical solution. We can obtain an ESS solution in the perfectly symmetrical case, where the fitness functions are identical in their rate of change relative to changes in their arguments close to ρ* (i.e., ∂W/∂w1 = ∂W/∂w2 = ∂W/∂w, which implies that β1 = β2, and ∂w1/∂F1 = ∂w2/∂F2 = ∂w/∂F). A symmetrical ESS then occurs at the point where ∂F2/∂ρ = −∂F1/∂ρ, that is, where any further change in gene allocation would improve the functioning of one trait to the same extent that it harms the other (see Rueffler et al. 2012, for a similar and independently derived result in the context of generalist/specialist evolution). Using the specific function (3), we find ρ*=1/2, independently of the form of the trade-offs and how these traits influence organismal fitness (i.e., independently of the values of u and v).
General convergence properties (one gene):
The system will converge toward ρ* if mutants increasing (decreasing) ρ are able to invade when ρ is initially below (above) ρ*. This requires that the derivative of equation (9) with respect to ρ is negative [recall that (9) will equal zero at ρ*] (Eshel 1983). In the opposite scenario (with a positive derivative), ρ* will be repelling, with modifier alleles being favored that reduce ρ when ρ < ρ* and vice versa. Starting from points near the ESS, the condition for convergence stability (dΔW/dρ < 0) is thus
| (10) |
where each of the derivatives is evaluated at the ESS, ρ*. The term in brackets equals the curvature of the fitness function W at ρ*, as expected for a fitness surface. The convergence properties of the ESS level of pleiotropy, ρ*, thus depend on exactly how the curvatures of the different fitness and activity trade-off functions combine. For the case where each trait’s effect on total fitness adds together (Equation 6a), several terms cancel and we are left with
| (11) |
Therefore, in the additive case, the relative importance of each trait to total fitness (given by β1, β2) plays a key role in the convergence properties of the ESS whenever the parenthetical terms have opposite signs. More importantly, Equations 10 and 11 show that selection may favor the evolution of increased or decreased levels of pleiotropy, depending on the nature of the trade-offs experienced. Assuming that fitness of the traits rises with functionality (∂wi/∂Fi > 0), concave trait functionality and fitness relationships (∂2Fi/∂ρ2 < 0 and ) facilitate the evolution of pleiotropy, yielding a convergence stable ESS, whereas the ESS is repelling when both of these functions are convex, favoring the specialization of both genes on the same function. To obtain more detailed predictions, especially when the curvatures differ in sign, requires that we specify the nature of these functions.
Exploring specific mapping functions (one gene):
Using the specific functions relating gene activity to trait functionality (Equation 3) and trait functionality to trait fitness (Equation 5), Equation 9 for a single gene A becomes
| (12) |
for additivity of fitness components (Equation 6a), and
| (13) |
for multiplicativity of fitness components (Equation 6b). Because, by definition, αA ≤ 1, the terms multiplying β1 and β2 are non-negative. In the symmetrical case where both traits have similar importance to total fitness (β1=β2=1/2), a potential ESS, where ΔW=0, occurs when ρ*=1/2, regardless of u and v. In asymmetrical cases, the exact position of ρ* needs to be found numerically (see Figure 3).
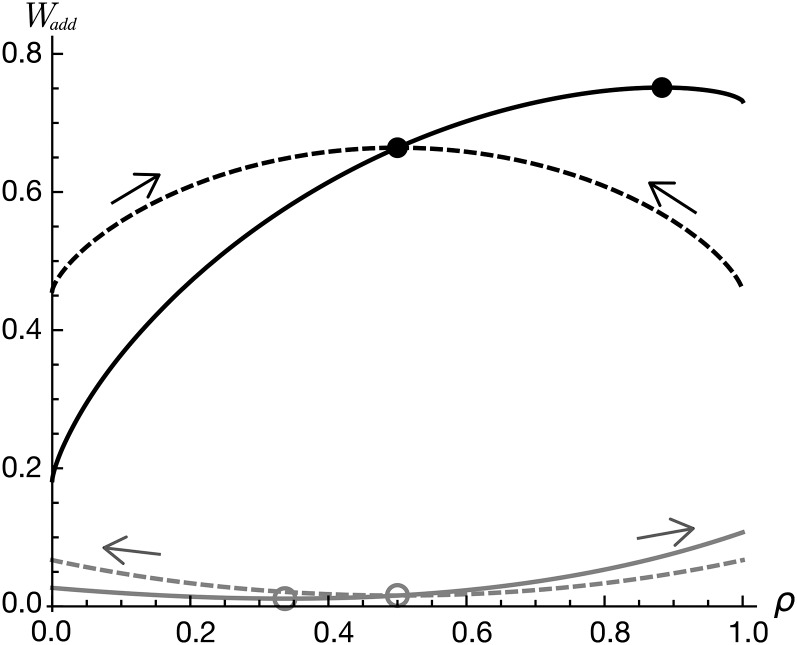
Figure 3 .
Fitness landscape of genotype M in the one-locus model as a function of trait allocation ρ at locus A. Total fitness in the additive case, Wadd is plotted against gene allocation to trait 2, ρ. Solid curves illustrate a robust trait–fitness relationship (v = 1/2), while shaded curves illustrate a sensitive relationship (v = 2), both assuming a strong activity–functionality trade-off (u = 1.5). The dashed curves correspond to traits equally important to fitness β1 = β2 = 0.5, while solid curves correspond to β1 = 0.2 and β2 = 0.8. Circles represent singular points where ΔW in Equation 12 is zero. For the value of u used here, the solid circles are attracting for robust traits (corresponding to an evolutionary stable state), while the hollow circles are repelling for sensitive traits. Pleiotropy is maintained when the ESS value of ρ lies between 0 and 1 and is absent otherwise. Other parameters are c = 1 and αA = 1/2.
Convergence properties with the specific mapping functions (one gene):
With β1 = β2 = 1/2, convergence to the singular point at ρ*=1/2 from initial values nearby requires that , which for the specific trade-off functions (3) and (5) equals
| (14) |
for Δρ > 0. This result holds exactly when total fitness is an additive function of trait fitnesses (Equation 6a) and holds approximately when fitness is multiplicative (Equation 6b) if selection is weak (for small c), which we assume henceforth unless explicitly mentioned. Because is always <2uv under our assumptions, ρ* is attracting when both trade-off functions Fi(ρ) and wi(Fi) are concave (0 < u, v < 1) and repelling when both functions are convex (u, v > 1), regardless of the value of αA (detailed proofs are available in supporting information, File S2 and File S3). If the trade-off functions have opposite curvatures, then the singular point will be convergence stable only if the net result causes the total fitness function, W, to be concave near ρ*=1/2 [this is mathematically equivalent to requiring (14)]. Even when the curvatures are opposite, ρ* is guaranteed to be an attractor when 1 < u ≤ 1/v and a repeller when 1 > u ≥ 1/v.
Summary of one-gene results:
Our analyses demonstrate that weak activity–functionality trade-offs [concave Fi(ρ) with u < 1] and robust trait fitnesses [concave wi(Fi) with v < 1] favor the evolution of pleiotropy, while complete specialization of the gene product on only one trait (ρ = 0 or 1) is expected to evolve when activity–functionality trade-offs are strong and trait fitnesses are sensitive (see Figure 3). At an intuitive level, if the product of a gene can perform well at two functions, it evolves to do so, but not if pleiotropy would greatly disrupt each function. Finally, because polymorphism is present only at the modifier, the location of the modifier in the genome is immaterial and can include alterations to the coding gene itself.
Evolution of pleiotropy at two coding loci
Regulatory sequences often affect the expression of multiple genes within a gene family. We thus model the evolution of a modifier locus affecting the pleiotropic degree of two protein-coding sequences, loci A and B, with activity levels αA and αB, respectively. This model allows us to address how pleiotropy evolves in the context of gene duplication. With allele M initially present at the modifier locus M, the pleiotropic degrees of loci A and B are ρA and ρB, respectively. We proceed as previously by introducing a modifier mutant allele m that changes the pleiotropic levels at loci A and B by ΔρA and ΔρB, respectively, and assume total fitness is additive (Equation 6a) (or multiplicative with weak selection, c small). We then ask under what circumstances the modifier is able to spread, assuming that the Δρ’s are of small order. Again, because the A and B loci are initially assumed fixed, the spread of the modifier allele m depends only on its effect on total fitness, ΔW. The difference in fitness between m and M carriers is now
| (15) |
Under the assumption of a symmetrical system, where the fitness effect of each trait influences organismal fitness to the same extent (i.e., ∂W/∂w1 = ∂W/∂w2 = ∂W/∂w), and the fitness of each trait is equally sensitive to that trait’s functionality (∂w1/∂F1 = ∂w2/∂F2 = ∂w/∂F), we find that ΔW = 0, regardless of the mutational effects of the modifier (ΔρB and ΔρA), when ∂F2/∂ρA = −∂F1/∂ρA and ∂F2/∂ρB = −∂F1/∂ρB. Thus, again, a potential symmetrical ESS, (), occurs where the functionality of trait 2 increases with increased allocation of gene product to trait 2 by an amount exactly equal to how much the functionality of trait 1 decreases for both genes A and B (see proofs in File S2 and File S3). To simplify the following presentation, we discuss functionality in reference to trait 2, defining F(ρA, ρB) = F2(ρA, ρB).
General convergence properties (two genes):
To determine the convergence properties of the singular point in a symmetrical system (), we need to evaluate the rate of change in fitness close to that point on the fitness surface. We assess convergence to the ESS by examining the topology of the total fitness function, Wadd, on the (ρA, ρB) plane, as described by the Hessian matrix H evaluated at () (see Appendix A and more extensive derivations in File S2 and File S3). As illustrated in Figure 4, a concave fitness surface at (), representing a local optimum that favors the evolution of two pleiotropic generalist genes, occurs when both eigenvalues of H (λ1 and λ2) are negative. Alternatively, when at least one of the eigenvalues of H is positive, indicating convexity of the fitness surface along the corresponding eigenvector (see dashed lines in Figure 4), the singular point is an evolutionary repeller favoring the evolution of specialist strategies. Generally, the signs of the eigenvalues are given by the combination of the curvature of the functionality and trait-fitness mapping functions (∂2F/∂ρ2, ∂2w/∂F2, respectively) and of the way the gene products interact to determine trait functionality (∂2F/(∂ρA∂ρB)). The full derivation of the general results is presented in Appendix A (see also File S2 and File S3). The results indicate that we cannot always expect the system to evolve toward increased pleiotropy or subfunctionalization; the predicted outcome depends on the overall shape of the fitness surface. For more detailed predictions, we next apply these general results, using a specific set of activity–functionality mapping functions.
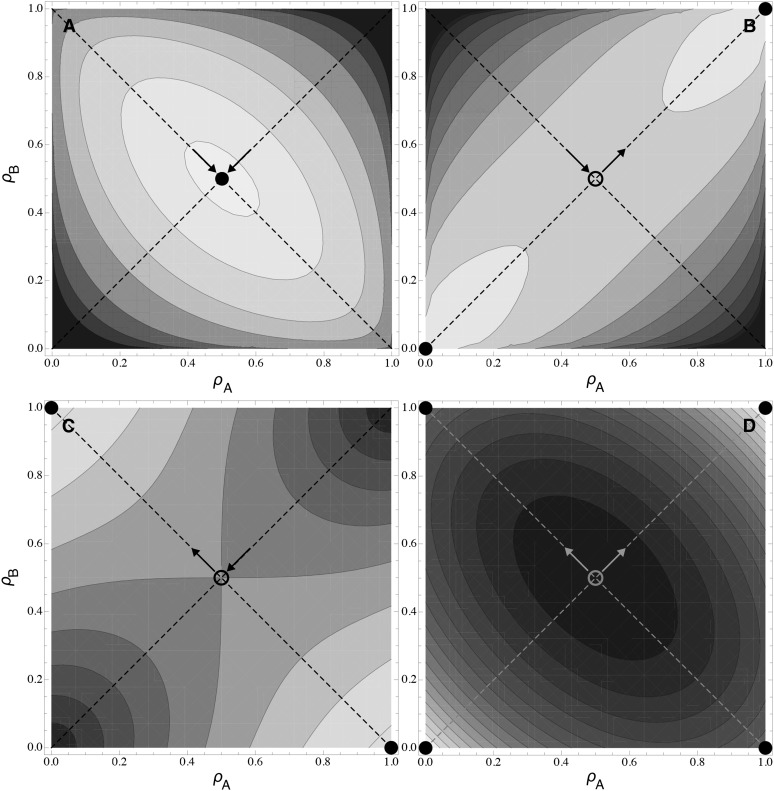
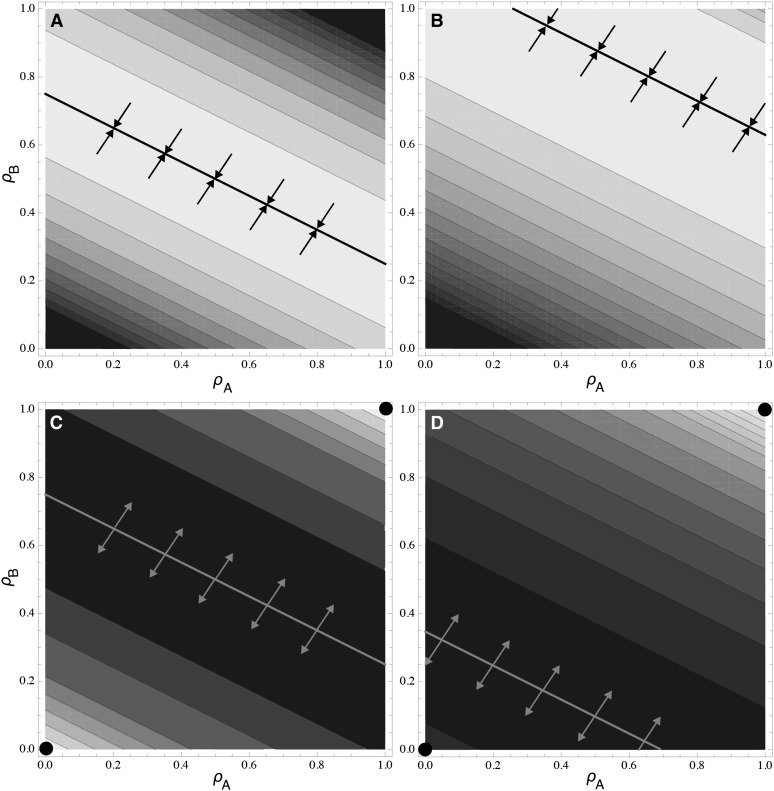
Figure 4 .
Fitness surface in the two-locus model. Contours represent fitness isoclines as a function of ρA and ρB. Darker colors represent lower fitness values. Circles represent singular points, which are either repelling states (open circles) or evolutionary stable states (solid circles). The orientations of the eigenvectors of the Hessian matrix are indicated by dashed lines, and the arrows indicate the convergence stability of the singular point and the sign of the associated eigenvalue; a positive eigenvalue is indicated by an arrow pointing toward the singular point, while a negative eigenvalue points away from it. The four graphs correspond to the four cells of Table 1. (A) u, v = 0.5; (B) u = 1/v = 0.5; (C) u = 1/v = 2; (D) u, v = 2. Other parameters are c = 1, αA = αB = 0.5, and β1 = β2 = 0.5, and total fitness is additive.
Exploring specific mapping functions (two genes):
To simplify the presentation, we assume that the products of the two genes do not interact [∂2F/(∂ρA∂ρB) = 0] and let
| (16) |
This assumption is reasonable as long as the functionality trade-offs occur at the level of each gene product separately, without interactions between the gene products (e.g., trade-offs in affinity given changes in protein configuration). We also assume that both genes have similar activity trade-off curves, with u identical for genes A and B, as may be the case for two newly duplicated genes. The levels of activity of the duplicates (αA and αB, with 0 < αA + αB ≤ 1) are, however, allowed to differ and may result from differences in promoter sequences flanking the two genes. Finally, we assume that total fitness is additive (Equation 6a) and that the contribution of each trait to fitness is given by Equation 4.
Because of the symmetry of these specific functions, the potential ESS always occurs on the diagonal where , and it lies exactly midway () when both traits are equally important to fitness (β1 = β2; see File S2 and File S3). In either case, the convergence properties of the singular point can be directly obtained from Appendix A [definition (16) satisfies the symmetry assumptions made there about the curvature of the trait–functionality relationship], and the results are summarized in Table 1. The singular point is attracting in all directions if u, v > 1 (Table 1A) or repelling if u, v < 1 (Table 1D), as in the one-gene case.
Table 1 . The evolutionarily stable strategy for a modifier affecting pleiotropy at two genes.
| v < 1 (robust trait fitness) | v > 1 (sensitive trait fitness) | |
|---|---|---|
| u < 1 (weak trade-off) | (A) λ1,λ2 < 0; pleiotropy maintained (Figure 4A) | (B) λ1 < 0, λ2 > 0 if ; specialization (Figure 4B) [Behaves as in (A) if ] |
| u > 1 (strong trade-off) | (C) λ1 > 0, λ2 < 0 if ; subfunctionalization (Figure 4C) [Behaves as in (D) if ] | (D) λ1,λ2 > 0; specialization or subfunctionalization (Figure 4D) |
Assuming a symmetrical system with αA ≈ αB, an analysis of the shape of the fitness surface at the singular point , predicts that selection favors (A) the maintenance of pleiotropy for both genes (convergence to the singular point), (B) two genes that specialize on the same trait (λ1 < 0, λ2 > 0), (C) two genes that specialize each on a different trait (subfunctionalization), or (D) two genes that specialize either on the same or on two different traits, depending on the parameters and initial conditions (λ1 > 0, λ2 > 0; see Figure 4D). When αA ≠ αB, the corners representing specialization on the same trait or subfunctionalization are no longer maxima on the fitness surface, so that the ESS always involves one pleiotropic gene and one specialized gene—a mixture of specialization and subfunctionalization (see Figure 5). The expression for Ccrit is given by Equation A2 in Appendix A.
When the curvatures of the functionality and the trait–fitness relationships are opposite, and unlike our one-gene analysis, the potential ESS can sit on a saddle-shaped surface. Using the specific functions (Equation 16), the requirements for a saddle-shaped topology are
| (17a) |
| (17b) |
These conditions are equivalent to requiring in the general analysis (see Equation A2). A saddle necessarily results when 1/v > u > 1 (favoring specialization of the two genes on different traits, i.e., subfunctionalization; Figure 4C) or when 1/v < u < 1 (favoring specialization of the two genes on the same trait; Figure 4B). In other cases, Equation 17 must be evaluated numerically to determine whether a saddle is present.
Implications for the evolution of pleiotropy after gene duplication (two genes):
When the functionality and trait–fitness relationships are both concave functions (u, v < 1; Figure 4A), we expect from our one-gene analysis that pleiotropy will be favored (see black lines in Figure 3), so that the genes, once duplicated, will start close to and then approach the central ESS, where both genes will remain pleiotropic, according to Table 1A. Conversely, when the relationships are both convex (u, v > 1; Figure 4D), we expect the ancestral gene to be originally specialized on one of the traits (see gray lines in Figure 3), in which case the duplicated system is likely to start near (ρA, ρB) = (0, 0) or (1, 1) and approach the closest of these two corners after duplication (Table 1D).
When the two relationships have opposite curvatures, the central ESS will represent a saddle point as long as condition (17) is satisfied. In this case, depending on the orientation of the saddle, the duplicate copies will either start as two pleiotropic genes close to the central ESS and evolve toward subfunctionalization (if u > 1, v < 1; Table 1C) or start close to one of the specialized corners and remain specialized on the same trait (if u < 1, v > 1; Table 1B). If, however, the functional trade-offs between the two traits are too strong or too weak, then the condition (17) for a saddle will not be met. If the trade-off is too strong (; that is, u ≫ 1), the singular point will repel in all directions despite v < 1, leading to specialization even before the gene duplicates arise. If the trade-off is too weak (; that is, u ≪ 1), the singular point will sit on a maximum of the fitness surface despite v > 1, and the duplicate system will start near that point, leading to functional redundancy and the maintenance of pleiotropy. It may thus not be easy, given these restrictions, to evolve toward subfunctionalization of the gene copies.
Connections with Rueffler et al. (2012):
Rueffler et al. (2012) recently analyzed the conditions under which generalist or specialist structures would evolve in a model exploring the evolution of repeated modules within an organism, discussing duplicated genes as a special case. While similar in many respects, they assume robustness of fitness to changes in identical modules (∂2W/∂ρ2 < 0 when ρA = ρB; their constrained trait space) and identical activity levels of the modules (in terms of the specific model introduced above, this implies αA=αB). They also find that modules can evolve either to subfunctionalize on different tasks or to generalize on multiple tasks, depending on how performance affects fitness and on how the modules (our genes) interact to affect performance of two tasks (our traits). They find that negative interactions among the gene products [∂2F/(∂ρA∂ρB) < 0] favor the evolution of specialization on different tasks (subfunctionalization), which we also find (see analysis in Appendix A). Our analysis shows, in addition, that positive interactions tend to facilitate specialization of both genes on the same trait, rather than pleiotropy or subfunctionalization, a result that is consistent with the results of Rueffler et al. (2012) but lies outside of their constrained trait space. Our model also allows us to explore how initial differences in expression (αA ≠ αB) might influence the evolution of pleiotropy (see next section).
On the role of αA and αB:
Assuming the total expression level of the two coding genes is held constant (αA+αB), changing the relative expression levels of genes A and B has no effect on the position of the potential ESS (see proof in File S2 and File S3 and Figure 5). Similarly, the stability properties of this point remain unchanged by slight changes in relative expression levels [whether an eigenvalue is below or above one is not affected by a small enough change in the parameters (Karlin and Mcgregor, 1972a,b)]. Consequently, the primary effect of altering the relative expression levels of the two coding genes is to shift the orientation of the fitness surface, causing the eigenvectors of H to rotate as indicated by the dashed lines in Figure 5. In particular, when the singular point is a saddle point that favors subfunctionalization (Equation 17a; Figure 5D), the eigenvector associated with the positive eigenvalue no longer aligns with the {−1, 1} diagonal line, moving the attracting points away from complete subfunctionalization (e.g., with ρA = 0, ρB = 1) and toward more central points on the borders of the (ρA, ρB) plane. The gene with higher expression level then evolves some degree of pleiotropy while the less expressed gene becomes specialized on a single function (Figure 5D).
Figure 5 .
Functional redundancy and subfunctionalization of two coding genes with asymmetric expression levels and unequal trait importance to fitness. Compared to the symmetrical cases considered in Figure 4, asymmetry of gene expression levels (αA = 0.2, αB = 0.8 in A, C, D, and F) causes a tilt in the eigenvectors (dashed lines in A and D), away from the diagonals of the ρA, ρB plane. Asymmetry in the importance to fitness of the traits, with trait 2 mattering more than trait 1 (β1 = 0.2, β2 = 0.8 in B, C, E, and F), causes a shift of the singular point (open and solid circles) toward specialization on trait 2 in the upper right corner whenever v < 1 (as here, v = 0.5 in all panels) and away from it otherwise. With a weak activity–functionality trade-off (u = 0.5 in A–C), the central ESS remains stable but shifts toward greater specialization on the trait that is more important to fitness. With a strong activity–functionality trade-off (u = 1.5 in D–F), the central ESS is an unstable saddle, and subfunctionalization evolves. In D–F, there are two sets of local maxima on the fitness surface: higher ones indicated by larger solid circles and lower ones by smaller solid circles. Thus, in these cases, either partial or complete subfunctionalization may evolve, depending on the initial conditions and the nature of the mutations that arise. Total fitness is additive (Equation 6a).
The orientation of the fitness surface is particularly important when the activity–functionality relationship is linear, as in the competitive allocation scenario where a gene product must be allocated to one or the other function (i.e., ∂2F/∂ρ2 = 0 or, using the specific functions, u = 1). As shown in Appendix A, one eigenvalue is zero in this linear case (Equation A7), yielding a fitness surface with a ridge of equal fitness (Equation A10; Figure 6). The orientation of this ridge is given by the eigenvector associated with λ= 0, which depends only on the relative values of αA and αB (Equation A9). Consequently, when the genes differ in their inherent activity level (αA ≠ αB), the eigenvectors point less in the diagonal directions and more in the horizontal and vertical directions (Figure 6). Thus, in the competitive allocation scenario, when the ridge is attracting (v < 1), the gene having the highest expression level always evolves some degree of pleiotropy, while the other gene evolves to any point along the ESS ridge, including edge cases without pleiotropy.
Figure 6 .
Fitness surface and ESS ridges in the two-locus model with competitive allocation (u = 1). Parameters are αA = 1/4, αB = 1/2 with β1 = β2 = 1/2 in A and C and β1 = 0.2, β2 = 0.8 in B and D. Trait fitness is robust (v = 1/2) in A and B and sensitive (v = 2) in C and D. The ridge is presented as a solid line, using Equation A10 when β1 = β2 or determined numerically otherwise. Darker colors represent lower fitness values. The ESS ridge is attracting in A and B and favors the evolution of some degree of pleiotropy at both genes, while specialist strategies are favored in C and D, with both genes specialized on the same trait, denoted by the circles and the arrows pointing away from the ridge.
On the role of β1 and β2:
The main effect of having the traits affect fitness to different degrees is to shift the singular point away from the center of the (ρA, ρB) plane (see Figures 5 and 6). When trait 2 becomes increasingly important to fitness (β2 rises relative to β1) and when the singular point is attracting, the ESS moves toward the specialized corner ρA = ρB = 1 (compare Figure 5, B and C, to 5A). This movement to the corners is even more pronounced when the fitness trade-off is nearly linear (v nearer one), with the activities of both genes evolving to the point where they are primarily, but not exclusively, targeted to trait 2 when β2 > β1 (Figure S1 and Figure S2 in File S1). In such cases, it may be difficult to maintain the functioning of trait 1 in the face of mutation pressure, and even if pleiotropy is maintained, it may be difficult to detect. In cases where the singular point is repelling and v > 1, increasing β2 relative to β1 moves the singular point in the opposite direction, away from the ρA = ρB = 1 corner, which increases the basin of attraction to this corner, making it more likely for specialization to evolve to the more important trait (see Figure S3 in File S1).
Strong selection:
In the above, we have assumed that it is possible for the organism to function even if there is no allocation of gene product to a trait. In some cases, however, the two traits may be essential to fitness. If those traits require allocation of gene product to be functional, then the organism would die without any allocation from at least one of the genes. Such cases can continue to be modeled within our framework, but the possibility of lethality in the absence of a functional trait requires strong selection (c = 1) and implies that total fitness is multiplicative and so drops to zero if one of the traits becomes nonfunctional (i.e., wi = 0 in Equation 6b). In essence, such a scenario causes the fitness surface at the two specialist corners (ρA, ρB) = (0, 0) and (1, 1) to be pulled down to zero. This converts all cases like those in Figure 4, B and D, into cases like Figure 4, A and C. Specializing both gene products solely on one of the traits is then no longer viable, and the system can evolve only toward a pleiotropic state (Figure 4A) or a subfunctionalized state (Figure 4C).
Adding developmental noise
Gene expression is known to be a highly stochastic process (McAdams and Arkin 1997; Elowitz et al. 2002; Ozbudak et al. 2002). To describe the type of noise in gene expression, we borrow from literature in ecology on adaptation in variable environments (Levins 1968) and define fine and coarse-grained noise. Expression noise is fine-grained when the gene expression level varies over a single generation such that a given individual experiences a mix of expression levels. By contrast, coarse-grained noise is expressed at the among-individual level, where individuals in a population are found in different states characterized by different expression levels.
Coarse-grained noise can arise stochastically during development (nonheritable) or it can result from genetic variation within a population (heritable). With heritable variation in expression levels among individuals, we must technically track the frequency of each genotype and account for linkage disequilibrium that builds up between the selected loci and the modifier of pleiotropy. If the rate of recombination between these loci is high relative to selection, however, linkage disequilibrium has a weaker effect on a modifier than direct fitness differences (Kirkpatrick et al. 2002). Consequently, to leading order, we need only track the frequencies of different types of individuals within a population, regardless of whether variants arise by developmental noise or mutation.
In all cases, we consider two alternate states or alleles at each coding locus, with the wild-type state occurring with probability 1−p and having expression level αj and the alternate deleterious state occurring with probability p and contributing in a reduced way to expression, αj − Δαj. Conceptualized in this way, developmental and mutational noise is seen to perturb a system from its optimal state, reducing expression of these genes.
Fine-grained noise:
If expression levels vary at a sufficiently fine-grained scale, introducing such noise simply results in an altered average amount of gene product, with αA and αB replaced by (αA−p ΔαB) and (αB−p ΔαB), respectively. Consequently, we can apply the results of section “on the role of αA and αB.” In particular, such noise tends not to alter the position of the singular point or its stability properties, unless expression levels are so altered that the conditions in Equation 14 for the one-gene case or Equation 17 for the two-gene case are affected (see File S2 and File S3). Fine-grained noise does, however, alter the orientation of the fitness surface (the eigenvectors) in the two-gene case, especially when the product of one gene is more subject to noise than that of the other. As described previously, we then expect the gene that is less affected by noise (highest αi − p Δαi) to remain pleiotropic, either when subfunctionalization is expected or in the competitive allocation scenario (u = 1), improving the robustness of the two traits to noise. While we have modeled developmental noise here as switching between two states, the above discussion applies to noise generating a variety of states experienced by a single individual, with p Δαj then representing the average reduction in gene expression across all perturbed states.
Coarse-grained noise:
With coarse-grained noise, we must average the fitness effect of a modifier over the different types of individuals within a population. For the one-locus case, using (12), we find that the change in mean fitness caused by a substitution at the modifier is, to leading order,
| (18) |
with
| (19a) |
| (19b) |
Selection on a modifier of pleiotropy is then intermediate between the same model in the absence of noise (i.e., setting p = 0 in Equation 18, we recover Equation 12) and the model with fine-grained developmental noise when p = 1 and αA is replaced with (αA − p ΔαA). The ESS value of ρ* is thus bounded by the values obtained in these two models (but remains at ρ* = 1/2 when β1 = β2 = 1/2; see File S2 and File S3). The difference between these models is small, however, with Equation 12 yielding slightly smaller (greater) ESS values than fine-grained noise for ρ* when v < 1 (v > 1).
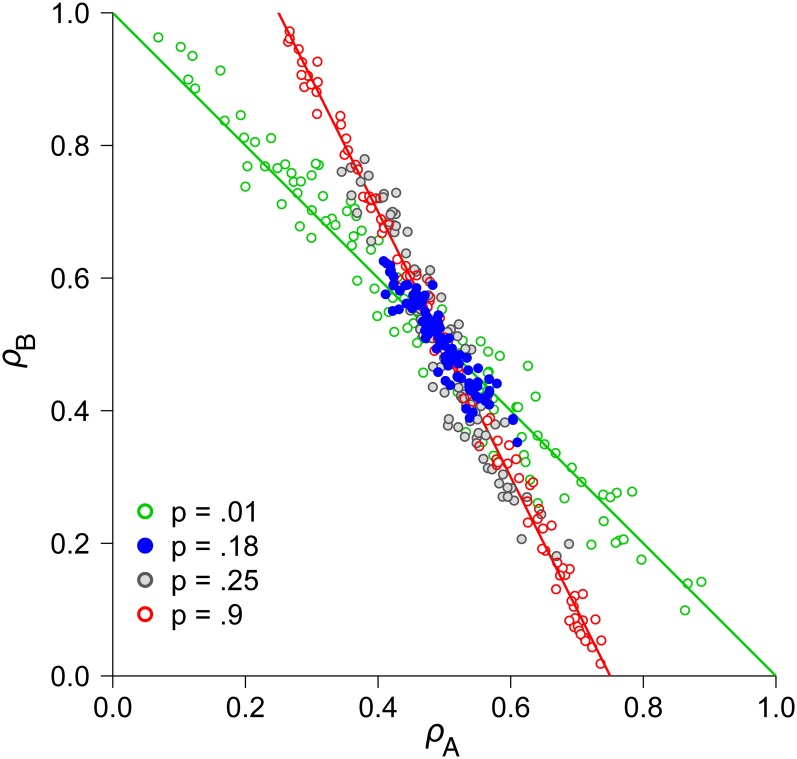
For two loci, results are similar when we assume that individuals have probability pApB of having both coding genes in the deleterious state, probability (pA(1−pB)+(1−pA)pB) of having one of the two genes in the deleterious state, and probability (1−pA)(1−pB) of being in the wild-type state. The main difference is that the eigenvectors fall in slightly different locations depending on the relative effects of each modifier allele on pleiotropy at loci A and B (ΔρA vs. ΔρB). In the competitive allocation case (u = 1), this means that the ridge lines shift, depending on the exact nature of the modifier mutations that arise. When the ridge is attracting (v < 1), these slight shifts in the location of the ridge tend to draw the system inward, toward complete pleiotropy (see File S2 and File S3). Simulations of this coarse-grained model show that its behavior indeed converges toward more central values for ρA and ρB, leading to increased pleiotropy of both genes (Figure 7; see Appendix B for simulation procedures). This tendency is pronounced only for intermediate expression noise (p ∼10% − 20%, with pA = pB = p). If p is near zero or one, the system instead aligns with the ridge expected under the highest (p = 0) or lowest (p = 1) expression levels.
Figure 7 .
Evolution of pleiotropy in two-locus simulations with coarse-grained noise and robust traits. The level of expression at each coding locus is αA = αB = 0.5, with noise reducing gene expression in some individuals by ΔαA = 0.1 and ΔαB = 0.3. The green line is the ESS ridge line in the absence of noise (p = 0) while the red line represents the expectation for expression levels reduced by ΔαA and ΔαB in every individual (p = 1), as given by numerically solving Equation 18. Each point on the graph represents a different simulation, with 100 replicates per parameter set, for various values of p (see inset key). Mutations drive the system inward toward pleiotropy at both genes when there are low to intermediate levels of noise (particularly with p = 0.18). The population size is N = 5000, β1 = β2 = 0.5, u = 1, and v = 0.5.
Discussion
Why do genes vary in their degree of pleiotropy? This fundamental question has not previously received much attention, with pleiotropy often considered to be an immalleable side-product of a gene’s evolutionary history. Our model explores how the degree of pleiotropy may itself evolve and provides some clues as to why we might expect pleiotropy to vary among genes (as shown by Dudley et al. 2005; Albert et al. 2008; Wagner et al. 2008; Wang et al. 2010). Most importantly, the degree to which a gene specializes on a given function depends on the trade-offs that arise when dedicating gene products to different functions and on the relationship between those functions and fitness. We show that selection favors generalist, pleiotropic genes when improving one gene function comes at little costs to other functions, particularly when activity–functionality (Fi) and trait–fitness (wi) relationships are concave (red curves in Figure 1, A and B). Pleiotropy is thus intimately linked to the robustness of phenotypes and organismal fitness to variation in expression of the underlying genes. In addition, the expression level of a gene plays an important role, as we found that more highly expressed genes (those with higher αj) evolve a greater degree of pleiotropy whenever pleiotropy is favored (e.g., Figure 6). Evidence consistent with this prediction has been found recently in yeast gene deletion experiments where genes with a high degree of pleiotropy were found to have significantly higher per-trait effects (Wang et al. 2010; see Wagner and Zhang 2011, for a synthesis including other organisms). Moreover, we find a positive but weak correlation between the expression level and the pleiotropic degree of genes in the budding yeast Saccharomyces cerevisiae, using four different data sets, as shown in Table 2. These empirical patterns are tantalizing and suggest that pleiotropy and gene expression may coevolve, although the direction of causality is not settled. It might be, for instance, that more pleiotropic genes evolve higher expression levels to maintain functionality at the traits they affect. Finally, we have also shown that variation in the degree of noise in expression among genes can facilitate the maintenance of pleiotropy in cases where complete subfunctionalization (Figure 5) or a neutrally stable ridge (Figure 7) would have arisen otherwise.
Table 2 . The correlation between gene expression and pleiotropy in Saccharomyces cerevisiae.
| Data set | rSpearman | P | rPearson | P | ngenes | ntraits |
|---|---|---|---|---|---|---|
| Dudley et al. (2005) | 0.059 | 0.116 | 0.071 | 0.119 | 698 | 21 |
| Ohya et al. (2005) | 0.077 | 0.0004 | 0.087 | 0.0002 | 1792 | 254 |
| CYGD: phenotypic | −0.017 | 0.52 | 0.0095 | 0.56 | 1381 | 142 |
| CYGD: functional | 0.046 | 0.0006 | 0.027 | 0.104 | 5192 | 456 |
| GO: biological processes | 0.059 | <0.0001 | 0.034 | 0.030 | 5160 | 2294 |
| GO: molecular functions | 0.064 | <0.0001 | 0.033 | 0.037 | 5160 | 1747 |
| GO: cellular components | 0.193 | <0.0001 | 0.173 | <0.0001 | 5160 | 649 |
| GO: all categories | 0.127 | <0.0001 | 0.106 | <0.0001 | 5160 | 4690 |
Estimates of gene pleiotropy are obtained from different sources (leftmost column). Dudley et al. (2005) report significant growth defects for 774 nonessential gene knockout strains in 21 different environments. Ohya et al. (2005) report significant effects of 2059 haploid knockout strains on 254 morphological traits. Literature-curated phenotypic effects (physiological) and functional categories of yeast genes are reported in the Comprehensive Yeast Genome Database (CYGD) (http://mips.helmholtz-muenchen.de/genre/proj/yeast/). Further gene functional annotation is provided by the Gene Ontology (GO) database (http://www.geneontology.org/), accessed on August 16, 2012, where pleiotropy is assessed by counting the number of (nonredundant) GO categories associated with each gene, considering three main functional categories or their union. Genome-wide gene expression levels are provided by Holstege et al. (1998) for 5449 yeast genes. We assessed the correlation between the log-transformed expression level and pleiotropic degree using Spearman’s rank correlation (rSpearman) and Pearson’s (rPearson) estimates. Because of a lack of normality, significance was assessed by randomization, permuting the pleiotropic degree among genes randomly 10,000 times. We report the two-tailed P-values (P). ngenes reports the number of genes present in both the pleiotropy and gene expression data set, and ntraits is the total number of traits affected by the genes in each analysis. All significant correlations are positive.
Exploring two motivating examples of specific functional trade-offs
As mentioned in the Introduction, pleiotropy can arise in a myriad of ways (e.g., Hodgkin 1998; He and Zhang 2006). To place our results in context, we now explore the implications of our results in the competitive allocation and multispecific scenarios, which motivate particular mappings of gene activity onto trait functionality and ultimately fitness.
Competitive allocation scenario:
The first scenario assumes that the product of a gene is allocated to one trait or the other trait (e.g., proteins targeted to different structures; see cartoon in Figure 2A). In this case, if the functioning of each trait is directly proportional to the amount of gene product allocated to that trait, then we would expect the functional trade-off relationship, Fi, to be linear (i.e., ∂2F/∂ρ2 = 0 as in the green curve in Figure 1A). As shown in Appendix A (Equations A7–A10; see also File S2 and File S3), a ridge of equal fitness then results on the fitness surface (Figure 6). When fitness is robust to changes in gene allocation [concave wi(Fi), implying v < 1 using our specific functions], the ridge is an evolutionary attractor. As evolution along the equilibrium ridge is neutral, genetic drift can lead to the evolution of a large range of outcomes, from complete pleiotropy of both genes to subfunctionalization of one of the genes (Figure 6, A and B), with subfunctionalization of both genes expected only in the symmetric case (αA = αB and β1 = β2) where the ridge line passes through the points (ρA, ρB) = (0, 1) and (1, 0). Alternatively, when fitness is an accelerating function of trait performance [convex wi(Fi), implying v > 1], the two genes tend to specialize on the same trait (Figure 6, C and D). In either case, subfunctionalization is not an attracting state, at best being neutrally stable with respect to pleiotropy.
Multispecific scenario:
Gene products often have more than one biochemical property and can, for instance, catalyze two different reactions or interact with two substrates with different affinities (see cartoon in Figure 2B). Mutations at the modifier locus then change the biochemical properties of the gene product(s), instead of changing the allocation of the product as in the previous case. In this multispecific scenario, functionality (Fi) then becomes a measure of the specificity of the gene product for substrate i, and the strength of the trade-off in gene activities depends on u ≠ 1. As mentioned in the Introduction, multispecific genes may exhibit strong functional trade-offs (u > 1), when functioning well for one trait requires conformational changes that greatly disrupt the other trait, or weak functional trade-offs (u < 1), when traits depend on different aspects of the gene product that can be altered fairly independently (e.g., distinct active sites). If we focus this second example on enzyme affinities for alternate substrates, then trait performance and thus fitness can be measured in terms of enzymatic fluxes. Enzymatic flux classically depends on the kinetic properties of the enzyme involved in the conversion of a given substrate into a product and is well described by Michaelis–Menten kinetics for a large proportion of known enzymes (Cornish-Bowden 2004). Rueffler et al. (2012) use a similar example to illustrate the evolution of specialization of duplicated genes; we have thus not repeated their derivations here. The main qualitative point is that enzymatic flux is typically a saturating function of gene affinity for a given substrate. It follows, with the additional assumption that trait fitness is directly proportional to flux, that fitness will be robust to declines in trait functionality ( or, using the specific functions, v < 1). Subfunctionalization may then evolve if there are strong trade-offs between the functioning of the two traits [u greater than one but not so large that condition (17a) is not satisfied; see Table 1 and Figure 4C] or if there are interfering interactions among gene products (Appendix A), as shown recently by Rueffler et al. (2012). They argue that such interactions would, for instance, arise when heterodimers are more stable than homodimers, favoring specialization of duplicated genes on different subcomponents. Nevertheless, specialization should not always be expected, and there are numerous cases that might yield the type of weak activity–function trade-offs (u < 1) that facilitate the evolutionary maintenance of pleiotropy, as evidenced by the many examples of gene sharing and enzyme promiscuity. It is also important to note that examples of accelerating enzymatic flux functions exist (see, e.g., Zimmermann and Rosselet 1977; Brown et al. 2009), which would tend to cause fitness to be sensitive to trait functionality (v > 1) and could help explain the existence of genes that are highly specialized on the same trait. Finally, while we considered two mapping levels, from activity to functionality, and from functionality to fitness, specific cases might necessitate more levels. For instance, in the multispecific scenario, mapping of flux to fitness may be nonlinear and require an additional mapping [e.g., from affinity to functionality (say Km of an enzyme), from functionality to flux, and from flux to fitness].
Evolution by gene duplication and the rise of two specialists
Gene duplication is seen as a major mechanism driving the evolution of pleiotropy, with the common view being that gene duplication generally reduces the degree of pleiotropy. The argument usually invoked is that pleiotropy represents a constraint on the evolution of independent gene functions, and specialization is seen as a way of escaping adaptive conflicts caused by multifunctionality (Hughes 1994; des Marais and Rausher 2008). From our perspective, specialization is not a necessary outcome of gene duplication. Importantly, if conditions that prevail prior to the duplication event favor the maintenance of a single multifunctional gene with u, v < 1 (see Table 1) and those conditions continue to apply after duplication, then we would expect pleiotropy to be maintained at both genes, essentially because the genes can perform both functions well and there are diminishing returns with respect to fitness of specializing further on either trait (as in Figure 4A). Only if there is a convex activity–functionality relationship (u > 1) and there is a sufficiently concave trait–fitness relationship (v < 1, such that Equation 17a is satisfied) or there are interfering interactions would we expect the system to evolve toward a generalist state when only one gene is present (as in Figure 3), but to branch after gene duplication into two subfunctionalized genes (as in Figure 4C). On the other hand, with a convex trait–fitness relationship (v > 1), we would expect the single gene to have specialized to one or the other trait before duplication, and this specialist state would likely be subsequently maintained by the duplicated genes, essentially because continuing to perform that one trait very well is most conducive to high fitness (see Figure 4, B and D).
Our conclusions may seem at odds with established models of the evolution of subfunctionalization by gene duplication, which suggest subfunctionalization as a likely outcome of the duplication of originally multifunctional genes. Our results can, however, be aligned with established models given special choices of the parameters, clarifying the underlying assumptions of these models. In particular, we consider two opposing views, neutralist and adaptationist, about the evolutionary forces acting on young paralogs (Hahn 2009; Innan and Kondrashov 2010). The neutralist view (Ohno 1970; Nowak et al. 1997; Force et al. 1999) classically assumes a period of relaxed selection after duplication for one gene copy that can neutrally evolve toward a pseudogene (no expression), a subfunctional gene (Force et al. 1999), or a new form, eventually co-opted into a new function (Ohno 1970). In contrast, the adaptationist view considers the retention of the duplicate copies as a result of positive selection for increased gene dosage, with the subsequent evolution into subfunctional genes driven by a release of selective constraints [i.e., the escape from adaptive conflict hypothesis (see Hughes 1994; des Marais and Rausher 2008; Rueffler et al. 2012)].
First, nearly neutral evolution allowing subfunctionalization of pleiotropic genes can be achieved in our model by making the fitness surface extremely robust to declines in functionality. Setting v small, the fitness surface is virtually flat as long as some gene product is allocated to the trait, so that the duplication itself and a null mutation in one of the gene copies (e.g. setting ρA = 0) become effectively neutral (similar to the model of Force et al. 1999). Once subfunctionality is achieved through the degeneration of a particular function in one coding locus (say trait 1 in gene A), a null mutation for that same function in the other gene (causing F1 = 0) would be selected against. Selection would then lead gene B toward increased allocation to this function, although such selection would be very weak when v is small. Even then, complete subfunctionalization, with gene B fully specialized on the function that gene A no longer performs, is expected only in the perfectly symmetrical case with β1=β2 and αA=αB (see Figure 6). Otherwise, some degree of pleiotropy is maintained at the second coding locus.
Second, under the adaptationist view, selection would drive the spread of the gene duplicate when the total gene product, αA + αB, is greater than the amount of gene product from a single gene, α. This will not always be true if other factors (such as substrate availability) limit the total amount of gene product. Assuming that the gene duplicate has spread because of selection for increased dosage, then our model reveals the condition for subfunctionalization to result. Specifically, when there is a slightly convex activity–functionality trade-off () and the trait–fitness relationship is sufficiently robust (such that ∂2w/∂F2 < Ccrit < 0 or, equivalently, Equation 17a), then we would expect the two genes to exhibit pleiotropy initially but then become subfunctionalized, representing an escape from adaptive conflict. As mentioned earlier, this scenario is especially likely when selection is strong and each trait must function for survival, as this tends to drive down the fitness near the corners where both genes are specialized on the same trait (making it more likely that ∂2w/∂F2 < Ccrit < 0 is satisfied).
To sum up, only under very specific conditions do we expect the two gene copies to become perfectly subfunctionalized, each contributing independently to different functions, or perfectly pleiotropic, contributing equally to both functions. More generally, we expect gene duplicates to remain specialized on the same trait (because of the advantage of increased dosage) or to exhibit a certain degree of functional redundancy, with the gene contributing more to trait functionality and/or more to fitness exhibiting the highest degree of pleiotropy.
Indeed, functional redundancy among pairs of duplicated genes is commonly observed in many different organisms (He and Zhang 2005; Dean et al. 2008; Farré and Albà 2010; Qian et al. 2010; Liu et al. 2011), even after prolonged periods of evolution (Dean et al. 2008; Farré and Albà 2010). Furthermore, it is common for expression intensity to differ between newly duplicated genes (Farré and Albà 2010; Qian et al. 2010; Liu et al. 2011), which, based on our model, tends to favor the evolution of only partial functional redundancy, with pleiotropy maintained for the more highly expressed gene (i.e., when αA ≠ αB; see Figure 5). That said, partial functional redundancy can also result from neutral processes [e.g., incomplete complementary degeneration (Force et al. 1999)].
Caveats
While we have attempted a fairly general analysis of the evolution of pleiotropy at one or two genes, with or without developmental noise, we should close by emphasizing that our main results were simplified by focusing on potential ESS points that arise in symmetrical cases, where the benefits of allocating gene products to either trait 1 or trait 2 were equivalent. Furthermore, our figures were all generated assuming specific functional equations (e.g., Equations 5 and 16) that forced the total fitness surface to exhibit smooth shapes, with at most one internal maximum for total fitness, W. In particular, we ignored the possibility of having stabilizing selection for intermediate levels of functionality or trait fitness, assuming that the functioning of a trait, Fi, was a monotonically increasing function of the amount of gene product allocated to that trait and that trait fitness, wi, was a monotonically increasing function of Fi. Such assumptions may have important implications for the evolution of pleiotropy of duplicated genes. Would selection for optimal dosage after duplication then favor subfunctionalization or would it instead favor decreased expression of each gene (decreased αj), as sometimes observed (Qian et al. 2010)? Further work on the evolution of pleiotropy may profitably shed light on such questions.
In addition, we assumed that each trait exhibited a similar relationship between allocation and function and between function and fitness. Real fitness surfaces are likely more complex. For example, traits may differentially affect fitness or may vary in their sensitivity to products of different genes. Such asymmetries could be modeled by letting the v coefficients differ for different traits (or the u coefficients). Preliminary results (see Figure S4 in File S1) suggest that changing the fitness curve for one of the traits from a concave to a convex one (e.g., v1 > 1, v2 < 1) may lead to increased specialization to the more sensitive trait with higher v. Combinations of concave and convex curves lead to highly nonlinear fitness surfaces and a thorough investigation of the dynamics is awaited.
Finally, we have ignored the possibility that the nature of the trade-off may itself evolve. For example, structural mutations may change the efficacy with which a gene product could perform a certain task (changing u or v), as suggested by experimental studies (Brown et al. 2009), turning a weak trade-off into a strong one, or vice versa. Empirical work grounding our understanding of the nature of the functional trade-offs and trait–fitness relationships will improve our understanding of what is possible and what is likely when it comes to the evolution of pleiotropy.
Conclusions
Taken together, our results suggest that pleiotropy and specialization of all genes on the trait particularly important to fitness are two common outcomes of the evolution of multifunctional genes under functional trade-offs. By contrast, subfunctionalization is expected only under more stringent conditions, requiring slightly convex trade-offs between gene-product allocation and functionality as well as a sufficiently robust relationship between fitness and trait functionality. Even then, complete and reciprocal specialization of two genes on two different functions is selectively favored only when the two traits are equally important to fitness and the two genes are equally expressed. These results could thus help explain why complete subfunctionalization is a less common outcome than theory predicts (e.g., Hughes 1994; Force et al. 1999; Innan and Kondrashov 2010; Proulx 2012). Furthermore, our results indicate that variation in the degree of pleiotropy among genes should be the norm. In particular, genes that contribute more to trait functionality (higher αj) are expected to evolve a higher degree of pleiotropy, all else being equal. Conversely, an increased degree of specialization of genes is expected when one trait matters substantially more to fitness (Figure 5). These results are in line with the more general literature on the evolution of specialization, mostly studied in an ecological context and at the level of individuals rather than genes (Levins 1968; Egas et al. 2004; Ravigné et al. 2009; Débarre and Gandon 2010). Our results also agree with and extend independently derived results from a recent model on the evolution of the division of labor (Rueffler et al. 2012).
In conclusion, variation in pleiotropy is multifactorial and depends not only on variation in the biochemical properties of coding genes but also on variation in selection pressures among traits, on variation in expression level of the genes, on stochastic noise, on drift, and on variation in the evolutionary history of the genes, where processes such as duplication and regulatory mutations are expected to play a leading role. A few empirical studies have started exploring the functional causes of variation in pleiotropy, and we hope this study will motivate more theoretical and empirical work to come.
Supplementary Material
Acknowledgments
We thank Florence Débarre, Leithen M’Gonigle, and Sam Yeaman for discussions and comments on earlier drafts that helped improve the manuscript and the reviewers and editor, whose suggestions strengthened this article. We are particularly grateful to Claus Rüffler for sharing an unpublished manuscript and encouraging us to think about gene product interactions and to Robert Polster for compiling and sharing the data used in Table 2. This work was supported by a Swiss National Science Foundation Ambizione grant (PZ00P3_121697) (to F.G.) and a Natural Sciences and Engineering Research Council Discovery grant (to S.P.O.).
Appendix A
Eigen-Decomposition of the Hessian Matrix
We derive the Hessian matrix H of the fitness surface at () and determine the sign of the eigenvalues and orientation of the eigenvectors of H. We focus on the stability properties of the symmetrical ESS (), which can be found under the symmetry assumptions ∂W/∂w1 = ∂W/∂w2 = ∂W/∂w and ∂w1/∂F1 = ∂w2/∂F2 = ∂w/∂F. To simplify the analysis of the eigensystem near this ESS, we make the additional symmetry assumptions that trait 1 and trait 2 are equally sensitive to variation in ρA and ρB () and similarly for trait fitnesses , while assuming that total fitness is additive (Equation 6a). Under these assumptions, we are able to derive a workable expression for the eigenvalues (λ1, λ2) of H. To determine their sign, we use the fact that the characteristic polynomial of H (calculated as def[λI − H]) has a quadratic form with a positive λ2 term (see File S2 and File S3). Consequently, the roots of this quadratic are the eigenvalues, and their signs depend on the slope and intercept of the characteristic polynomial at λ = 0:
| (A1a) |
| (A1b) |
When the intercept is positive, both eigenvalues will have the same sign, yielding an ESS that is attracting from all directions (two negative eigenvalues when the slope is positive) or repelling in all directions (two positive eigenvalues when the slope is negative). Conversely, when the intercept is negative, the potential ESS sits on a saddle, attracting along one eigenvector and repelling along the other.
In the absence of gene interactions [∂2F/(∂ρA∂ρB) = 0], the intercept of the characteristic polynomial is always positive when the trait functionality and fitness relationships are curved in the same way. When they are both negatively curved (, ∂2w/∂F2 < 0), the slope of the characteristic polynomial must be positive (so that λ1, λ2 < 0), indicating that () represents a local fitness maximum. In this case, we expect each gene to remain pleiotropic, even after gene duplication, because of the diminishing returns with respect to both functionality and fitness if either gene allocates more to a particular trait, at the cost of the other trait. Conversely, when both relationships are positively curved (, ∂2w/∂F2 < 0), the slope of the characteristic polynomial must be negative (so that λ1, λ2 > 0), indicating that is a repelling point, and the system will evolve increased specialization, because of the accelerating functionality and fitness benefits of doing so. Even when the curvatures are opposite at these two levels, the above slope and intercept results continue to hold (with the behavior depending on the sign of ) if the activity–functionality relationship is highly curved while the trait–fitness curvature is sufficiently mild that ∂2w/∂F2 lies between 0 and Ccrit, where
| (A2) |
Thus, when the trade-off between allocation of the gene product to two traits and functionality of these traits is very weak or very strong , Ccrit will be large in magnitude, and the singular point will tend to sit on a maximum (pleiotropy favored if ) or a minimum (specialization favored if ), rather than a saddle.
Only when the relationship between fitness and functionality is strongly curved and opposite in sign to , such that the magnitude of ∂2w/∂F2 is greater than the magnitude of Ccrit, does the total fitness surface become saddle shaped. To assess the orientation of the saddle, we can determine the curvature of the total fitness surface along the diagonal connecting specialization on trait 1 (ρA = ρB = 0) and specialization on trait 2 (ρA = ρB = 1):
| (A3) |
Again ignoring gene-product interactions, the saddle will represent a maximum along this diagonal when the trait–fitness relationship is negatively curved (∂2w/∂F2 < 0). Thus, when is positive yet ∂2w/∂F2 is negative and less than Ccrit, the system will tend to evolve toward increased pleiotropy along this diagonal line and then be repelled toward subfunctionalization of the two genes on opposite traits, at least in the vicinity of ().
Gene-product interactions
The topology of the fitness surface is also influenced by the way the products of the two genes interact [i.e., ∂2F/(∂ρA∂ρB) ≠ 0 in Equation A1b]. A positive interaction implies that increasing both gene products improves trait functionality more than the individual contributions of each product would predict. The sign of the intercept (A1b), but not the slope, depends on the interaction term. If the interaction (∂2F/∂ρA∂ρB) and the curvature of the fitness function (∂2w/∂F2) are both positive or both negative, then the intercept becomes more negative (more likely to be saddle shaped in the vicinity of ). When they are both negative, the saddle is declining toward the (0, 0) and (1, 1) corners [i.e., (A3) is negative]; such interactions thus facilitate evolutionary branching and subspecialization, essentially because fitness is maximized by investment in both traits but the negative interactions among the gene products favor the specialization of each gene on different traits. The interactions continue to contribute negatively to the intercept if ∂2F/(∂ρA∂ρB) and ∂2w/∂F2 have opposite signs but the functionality interactions are stronger:
| (A4) |
Examining Equation A3 when (A4) is satisfied, the total fitness surface will be curved downward along the diagonal between specialization on trait 1 (0, 0) and specialization on trait 2 (1, 1) if ∂2F/∂ρA∂ρB < 0 and curved upward otherwise. Thus, strong negative interactions facilitate subspecialization, with evolution along the diagonal toward () followed by specialization of each gene on different traits, regardless of the sign of ∂2w/∂F2 as long as (A4) is satisfied. By contrast, when the interactions are weak and opposite in sign to the curvature of the trait–fitness relationship, so that (A4) is not satisfied, the interactions make the intercept of the characteristic polynomial more positive, favoring a stable ESS [if the slope (A1a) is positive] or a repelling point [if the slope (A1a) is negative].
Eigenvalues and eigenvectors
The eigenvalues are obtained by solving the characteristic polynomial for λ (see File S2 and File S3),
| (A5) |
and their corresponding eigenvectors equal
| (A6) |
We next consider some limiting cases of relevance.
Special case of a linear functional trade-off:
When gene products are allocated to one or another function, the functionality relationship may become linear, with . In this competitive allocation scenario, the eigenvalues simplify to
| (A7) |
with corresponding eigenvectors
| (A8) |
Thus, with linear allocation of gene products to the two traits, one eigenvalue becomes zero, and it can be shown that this occurs because the fitness surface contains a neutral ridge of equal fitness, which is either an attracting ridge with maximal fitness if ∂2w/∂F2 < 0 (so that λ2 < 0) or a repelling ridge with minimal fitness if ∂2w/∂F2 > 0 (so that λ2 > 0). Using the specific functional relationships (5) and (16), these eigenvectors become
| (A9) |
The first eigenvector, associated with λ1 = 0, describes a ridge of equal fitness on the fitness surface that passes through the ESS point. In the symmetrical case where β1 = β2, this ridge passes through the midpoint, , and is given by
| (A10) |
For other values of βi, the ridge must be numerically calculated, but it can be shown that it remains a line whose slope depends only on the relative expression levels of αA and αB (see File S2 and File S3). This ridge is an evolutionary attractor when v < 1 (the fitness surface is concave across the ridge; λ2 < 0), in which case any combination of the pleiotropic degrees of the two genes that brings the system to the ridge is neutrally stable with respect to any other point on the ridge (Fig. 6, A and B). When v > 1, the ESS ridge becomes an evolutionary repeller, and the two specialized states (ρA, ρB) = (0, 0) and (1, 1) become the stable equilibria of the system (Fig. 6, C and D). Which trait becomes more “functional” then depends on their relative contributions to fitness (the β-coefficients) and on the current state of the system, where evolution is likely to lead both genes to specialize on the initially more functional and more important trait.
Special case of equal expression levels:
While the general analysis allowed the genes A and B to differ in expression levels, the analysis simplifies greatly when the two genes have equal expression levels (αA = αB), which might occur initially following gene duplication if gene regulation is unaffected. With equal expression levels, trait functionality is equally sensitive to changes in either gene, with and . Further assuming that there are no interactions between the gene products (∂2F/∂ρA∂ρB = 0), the eigenvalues simplify to
| (A11) |
and their corresponding eigenvectors equal
| (A12) |
The first eigenvector points to the two corners corresponding to subfunctionalization, with one gene specialized on trait 1 and the other gene specialized on trait 2, while the second eigenvector points to the two corners where both genes are specialized on the same trait. For subspecialization to evolve over either specialization on the same trait or pleiotropy thus requires that ∂2F/∂ρ2 > 0 so that λ1 is positive, while ∂2w/∂F2 is sufficiently negative that λ2 is negative (this is equivalent to the general requirement that ∂2w/∂F2 be greater in magnitude than Ccrit for a saddle-shaped topology and, using the specific functions, to Equation 17a). In cases where the expression levels of genes A and B are not equal, however, the eigenvectors will not line up along the diagonals, so that even when is evolutionarily unstable, the system can evolve in directions that maintain pleiotropy in one gene (see, for example, Figure 5).
Appendix B
Individual-Based Simulations
We implemented the haploid model with coarse-grained noise in the Nemo individual-based simulation platform (Guillaume and Rougemont 2006). Each individual carried two expression loci and one modifier locus. Mutations affecting ρA and ρB at the modifier locus were randomly drawn from a bivariate Gaussian distribution with mean of 0 and standard deviation equal to 0.05, with mutational effects added to the allelic values already present at the locus. Such mutations occurred at rate μρ = 10−4. Mutational covariance of the effects of a mutation on ρA and ρB was set to zero. The initial allelic values at the modifier locus were set randomly in the first generation by drawing each individual from a uniform distribution, for each replicate, ensuring an initially large phenotypic variance to avoid strong effects of initial allelic values. Because we model coarse-grained noise, each locus in a new individual had probability p to be in the more deleterious state (αj−Δαj). Random mating (with probability 1/N of self-fertilization) and free recombination among all three loci were assumed. A single large panmictic population of size N = 5000 was modeled. Individuals were subject to viability selection at birth with fitnesses given by Equation 6a. Enough surviving offspring were produced each generation to fill the population to its carrying capacity. A total of 100 replicates were run for 500,000 generations for each parameter set, and the results presented are the averages over the last 20,000 generations, recorded every 100 generations.
Footnotes
Communicating editor: L. M. Wahl
Literature Cited
- Acar M., Mettetal J. T., van Oudenaarden A., 2008. Stochastic switching as a survival strategy in fluctuating environments. Nat. Genet. 40: 471–475 [DOI] [PubMed] [Google Scholar]
- Aharoni A., Gaidukov L., Khersonsky O., Gould S. M., Roodveldt C., et al. , 2005. The ‘evolvability’ of promiscuous protein functions. Nat. Genet. 37: 73–76 [DOI] [PubMed] [Google Scholar]
- Albert A. Y. K., Sawaya S., Vines T. H., Knecht A. K., Miller C. T., et al. , 2008. The genetics of adaptive shape shift in stickleback: pleiotropy and effect size. Evolution 62: 76–85 [DOI] [PubMed] [Google Scholar]
- Armbruster W. S., Lee J., Baldwin B. G., 2009. Macroevolutionary patterns of defense and pollination in Dalechampia vines: adaptation, exaptation, and evolutionary novelty. Proc. Natl. Acad. Sci. USA 106: 18085–18090 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Black D. L., 2003. Mechanisms of alternative pre-messenger rna splicing. Annu. Rev. Biochem. 72: 291–336 [DOI] [PubMed] [Google Scholar]
- Brown K. M., DePristo M. A., Weinreich D. M., Hartl D. L., 2009. Temporal constraints on the incorporation of regulatory mutants in evolutionary pathways. Mol. Biol. Evol. 26: 2455–2462 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chevin L.-M., Martin G., Lenormand T., 2010. Fisher’s model and the genomics of adaptation: restricted pleiotropy, heterogenous mutation, and parallel evolution. Evolution 64: 3213–3231 [DOI] [PubMed] [Google Scholar]
- Cooper T. F., Ostrowski E. A., Travisano M., 2007. A negative relationship between mutation pleiotropy and fitness effect in yeast. Evolution 61: 1495–1499 [DOI] [PubMed] [Google Scholar]
- Cornish-Bowden A., 2004. Fundamenals of Enzyme Kinetics, Ed. 3 Portland Press, London [Google Scholar]
- Dean E. J., Davis J. C., Davis R. W., Petrov D. A., 2008. Pervasive and persistent redundancy among duplicated genes in yeast. PLoS Genet. 4: e1000113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Débarre F., Gandon S., 2010. Evolution of specialization in a spatially continuous environment. J. Evol. Biol. 23: 1090–1099 [DOI] [PubMed] [Google Scholar]
- Dekel E., Alon U., 2005. Optimality and evolutionary tuning of the expression level of a protein. Nature 436: 588–592 [DOI] [PubMed] [Google Scholar]
- des Marais D. L., Rausher M. D., 2008. Escape from adaptive conflict after duplication in an anthocyanin pathway gene. Nature 454: 762–765 [DOI] [PubMed] [Google Scholar]
- de Visser J. A. G. M., Hermisson J., Wagner G. P., Meyers L. A., Bagheri H. C., et al. , 2003. Perspective: evolution and detection of genetic robustness. Evolution 57: 1959–1972 [DOI] [PubMed] [Google Scholar]
- Dudley A. M., Janse D. M., Tanay A., Shamir R., Church G. M., 2005. A global view of pleiotropy and phenotypically derived gene function in yeast. Mol. Syst. Biol. 1: 2005.0001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dykhuizen D. E., Dean A. M., Hartl D. L., 1987. Metabolic flux and fitness. Genetics 115: 25–31 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Egas M., Dieckmann U., Sabelis M. W., 2004. Evolution restricts the coexistence of specialists and generalists: the role of trade-off structure. Am. Nat. 163: 518–531 [DOI] [PubMed] [Google Scholar]
- Elowitz M. B., Levine A. J., Siggia E. D., Swain P. S., 2002. Stochastic gene expression in a single cell. Science 297: 1183–1186 [DOI] [PubMed] [Google Scholar]
- Eshel I., 1983. Evolutionary and continuous stability. J. Theor. Biol. 103: 99–111 [DOI] [PubMed] [Google Scholar]
- Eyre-Walker A., Keightley P. D., 2007. The distribution of fitness effects of new mutations. Nat. Rev. Genet. 8: 610–618 [DOI] [PubMed] [Google Scholar]
- Farré D., Albà M. M., 2010. Heterogeneous patterns of gene-expression diversification in mammalian gene duplicates. Mol. Biol. Evol. 27: 325–335 [DOI] [PubMed] [Google Scholar]
- Fisher R. A., 1930. The Genetical Theory of Natural Selection. Clarendon Press, Oxford [Google Scholar]
- Force A., Lynch M., Pickett F. B., Amores A., Yan Y. L., et al. , 1999. Preservation of duplicate genes by complementary, degenerative mutations. Genetics 151: 1531–1545 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gros P.-A., Le Nagard H., Tenaillon O., 2009. The evolution of epistasis and its links with genetic robustness, complexity and drift in a phenotypic model of adaptation. Genetics 182: 277–293 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guillaume F., Rougemont J., 2006. Nemo: an evolutionary and population genetics programming framework. Bioinformatics 22: 2556–2557 [DOI] [PubMed] [Google Scholar]
- Hahn M. W., 2009. Distinguishing among evolutionary models for the maintenance of gene duplicates. J. Hered. 100: 605–617 [DOI] [PubMed] [Google Scholar]
- Hansen T. F., 2003. Is modularity necessary for evolvability? remarks on the relationship between pleiotropy and evolvability. Biosystems 69: 83–94 [DOI] [PubMed] [Google Scholar]
- He X. L., Zhang J. Z., 2005. Rapid subfunctionalization accompanied by prolonged and substantial neofunctionalization in duplicate gene evolution. Genetics 169: 1157–1164 [DOI] [PMC free article] [PubMed] [Google Scholar]
- He X. L., Zhang J. Z., 2006. Toward a molecular understanding of pleiotropy. Genetics 173: 1885–1891 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hodgkin J., 1998. Seven types of pleiotropy. Int. J. Dev. Biol. 42: 501–505 [PubMed] [Google Scholar]
- Holstege F. C., Jennings E. G., Wyrick J. J., Lee T. I., Hengartner C. J., et al. , 1998. Dissecting the regulatory circuitry of a eukaryotic genome. Cell 95: 717–728 [DOI] [PubMed] [Google Scholar]
- Hughes A. L., 1994. The evolution of functionally novel proteins after gene duplication. Proc. Biol. Sci. 256: 119–124 [DOI] [PubMed] [Google Scholar]
- Innan H., Kondrashov F., 2010. The evolution of gene duplications: classifying and distinguishing between models. Nat. Rev. Genet. 11: 97–108 [DOI] [PubMed] [Google Scholar]
- Karlin S., Mcgregor J., 1972a Application of method of small parameters to multi-niche population genetic models. Theor. Popul. Biol. 3: 186–209 [DOI] [PubMed] [Google Scholar]
- Karlin S., Mcgregor J., 1972b Polymorphisms for genetic and ecological systems with weak coupling. Theor. Popul. Biol. 3: 210–238 [DOI] [PubMed] [Google Scholar]
- Khersonsky O., Tawfik D., 2010. Enzyme promiscuity: a mechanistic and evolutionary perspective. Annu. Rev. Biochem. 79: 471–505 [DOI] [PubMed] [Google Scholar]
- Kirkpatrick M., Johnson T., Barton N., 2002. General models of multilocus evolution. Genetics 161: 1727–1750 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lande R., 1979. Quantitative genetic analysis of multivariate evolution, applied to brain: body size allometry. Evolution 33: 402–416 [DOI] [PubMed] [Google Scholar]
- Lehner B., 2008. Selection to minimise noise in living systems and its implications for the evolution of gene expression. Mol. Syst. Biol. 4: 170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lenski R. E., Ofria C., Pennock R. T., Adami C., 2003. The evolutionary origin of complex features. Nature 423: 139–144 [DOI] [PubMed] [Google Scholar]
- Levins R., 1968. Evolution in Changing Environments. Princeton University Press, Princeton, NJ [Google Scholar]
- Liu S.-L., Baute G. J., Adams K. L., 2011. Organ and cell type-specific complementary expression patterns and regulatory neofunctionalization between duplicated genes in Arabidopsis thaliana. Genome Biol. Evol. 3: 1419–1436 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lourenço J., Galtier N., Glémin S., 2011. Complexity, pleiotropy, and the fitness effect of mutations. Evolution 65: 1559–1571 [DOI] [PubMed] [Google Scholar]
- Lynch M., Force A., 2000. The probability of duplicate gene preservation by subfunctionalization. Genetics 154: 459–473 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McAdams H. H., Arkin A., 1997. Stochastic mechanisms in gene expression. Proc. Natl. Acad. Sci. USA 94: 814–819 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nowak M. A., Boerlijst M. C., Cooke J., Maynard Smith J., 1997. Evolution of genetic redundancy. Nature 388: 167–171 [DOI] [PubMed] [Google Scholar]
- Ohno S. 1970. Evolution by Gene Duplication. Springer-Verlag, New York [Google Scholar]
- Ohya Y., Sese J., Yukawa M., Sano F., Nakatani Y., et al. , 2005. High-dimensional and large-scale phenotyping of yeast mutants. Proc. Natl. Acad. Sci. USA 102: 19015–19020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Loughlin T. L., Greene D. N., Matsumura I., 2006. Diversification and specialization of HIV protease function during in vitro evolution. Mol. Biol. Evol. 23: 764–772 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orr H. A., 1998. The population genetics of adaptation: the distribution of factors fixed during adaptive evolution. Evolution 52: 935–949 [DOI] [PubMed] [Google Scholar]
- Orr H. A., 2000. Adaptation and the cost of complexity. Evolution 54: 13–20 [DOI] [PubMed] [Google Scholar]
- Ozbudak E. M., Thattai M., Kurtser I., Grossman A. D., van Oudenaarden A., 2002. Regulation of noise in the expression of a single gene. Nat. Genet. 31: 69–73 [DOI] [PubMed] [Google Scholar]
- Piatigorsky J., Wistow G. J., 1989. Enzyme crystallins—gene sharing as an evolutionary strategy. Cell 57: 197–199 [DOI] [PubMed] [Google Scholar]
- Proulx S. R., 2012. Multiple routes to subfunctionalization and gene duplicate specialization. Genetics 190: 737–751 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qian W. F., Liao B. Y., Chang A. Y. F., Zhang J. Z., 2010. Maintenance of duplicate genes and their functional redundancy by reduced expression. Trends Genet. 26: 425–430 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raser J. M., O’Shea E. K., 2005. Noise in gene expression: origins, consequences, and control. Science 309: 2010–2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff W. C., Denison R. F., 2010. Individual-level bet hedging in the bacterium Sinorhizobium meliloti. Curr. Biol. 20: 1740–1744 [DOI] [PubMed] [Google Scholar]
- Rausher M. D., 2008. Evolutionary transitions in floral color. Int. J. Plant Sci. 169: 7–21 [Google Scholar]
- Ravigné V., Dieckmann U., Olivieri I., 2009. Live where you thrive: joint evolution of habitat choice and local adaptation facilitates specialization and promotes diversity. Am. Nat. 174: E141–E169 [DOI] [PubMed] [Google Scholar]
- Rueffler C., Hermisson J., Wagner G. P., 2012. Evolution of functional specialization and division of labor. Proc. Natl. Acad. Sci. USA 109: E326–E335 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salathé M., Ackermann M., Bonhoeffer S., 2006. The effect of multifunctionality on the rate of evolution in yeast. Mol. Biol. Evol. 23: 721–722 [DOI] [PubMed] [Google Scholar]
- Swain P. S., 2004. Efficient attenuation of stochasticity in gene expression through post-transcriptional control. J. Mol. Biol. 344: 965–976 [DOI] [PubMed] [Google Scholar]
- Thattai M., van Oudenaarden A., 2004. Stochastic gene expression in fluctuating environments. Genetics 167: 523–530 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner A., 2000. The role of population size, pleiotropy and fitness effects of mutations in the evolution of overlapping gene functions. Genetics 154: 1389–1401 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner G. P., Zhang J., 2011. The pleiotropic structure of the genotype-phenotype map: the evolvability of complex organisms. Nat. Rev. Genet. 12: 204–213 [DOI] [PubMed] [Google Scholar]
- Wagner G. P., Kenney-Hunt J. P., Pavlicev M., Peck J. R., Waxman D., et al. , 2008. Pleiotropic scaling of gene effects and the ‘cost of complexity’. Nature 452: 470–472 [DOI] [PubMed] [Google Scholar]
- Wang Z., Liao B.-Y., Zhang J., 2010. Genomic patterns of pleiotropy and the evolution of complexity. Proc. Natl. Acad. Sci. USA 107: 18034–18039 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Welch J. J., Waxman D., 2003. Modularity and the cost of complexity. Evolution 57: 1723–1734 [DOI] [PubMed] [Google Scholar]
- Zimmermann W., Rosselet A., 1977. Function of the outer membrane of Escherichia coli as a permeability barrier to beta-lactam antibiotics. Antimicrob. Agents Chemother. 12: 368–372 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.