Estimate of the Spontaneous Mutation Rate in Chlamydomonas reinhardtii

Abstract

The nature of spontaneous mutations, including their rate, distribution across the genome, and fitness consequences, is of central importance to biology. However, the low rate of mutation has made it difficult to study spontaneous mutagenesis, and few studies have directly addressed these questions. Here, we present a direct estimate of the mutation rate and a description of the properties of new spontaneous mutations in the unicellular green alga Chlamydomonas reinhardtii. We conducted a mutation accumulation experiment for ∼350 generations followed by whole-genome resequencing of two replicate lines. Our analysis identified a total of 14 mutations, including 5 short indels and 9 single base mutations, and no evidence of larger structural mutations. From this, we estimate a total mutation rate of 3.23 × 10⁻¹⁰/site/generation (95% C.I. 1.82 × 10⁻¹⁰ to 5.23 × 10⁻¹⁰) and a single base mutation rate of 2.08 × 10⁻¹⁰/site/generation (95% C.I., 1.09 × 10⁻¹⁰ to 3.74 × 10⁻¹⁰). We observed no mutations from A/T → G/C, suggesting a strong mutational bias toward A/T, although paradoxically, the GC content of the C. reinhardtii genome is very high. Our estimate is only the second direct estimate of the mutation rate from plants and among the lowest spontaneous base-substitution rates known in eukaryotes.

NEW mutations are the ultimate source of the genetic variation necessary for adaptation via natural selection. Moreover, the mutation rate has profound consequences for a myriad of disciplines, including conservation, genetics, medicine, and evolution. The rate of new mutations influences both the speed at which populations respond to natural selection and the rate at which fitness may decline due to inbreeding. The rate, strength, and sign of fitness effects of new mutations are critical parameters of models of the evolution and maintenance of sexual reproduction. Currently, however, characterization of the rates, causes, and effects of different kinds of mutations is lacking.

Although mutation is fundamentally important for adaptive change, the vast majority of mutations influencing fitness are generally believed to be deleterious (Keightley and Lynch 2003; but see Shaw et al. 2002; Rutter et al. 2010). For this reason, most theory, especially in recombining populations, predicts that selection will drive mutation to lower and lower rates (Kimura 1967; Kondrashov 1995; Dawson 1999; Lynch 2008). Even when a mutator allele increasing the mutation rate arises and produces a beneficial mutation, recombination will tend to disassociate the mutator from the beneficial mutation, eliminating any benefit it may gain from hitchhiking (for example, Raynes et al. 2011). Although selection is expected to drive the mutation rate toward zero, the mutation rate remains detectably above zero.

Relatively few studies have estimated the spontaneous mutation rate directly through the sequencing of a large fraction of the genome (see below). Accurate estimation of the mutation rate is made difficult by the very low rate of spontaneous mutagenesis, so most estimates have been indirect, relying on DNA divergence at putatively neutral sites between species or on phenotypic screens. These approaches make several assumptions that are difficult to validate (including evolutionary divergence dates and generation intervals), limiting their precision and accuracy (reviewed by Kondrashov and Kondrashov 2010). Recently, a few studies have begun to estimate the mutation rate through direct sequencing of lines that have accumulated mutations for multiple generations or by the sequencing of parents and their offspring (Caenorhabditis elegans, Denver et al. 2009; Drosophila melanogaster, Haag-Liautard et al. 2007; Keightley et al. 2009; Saccharomyces cerevisiae, Lynch et al. 2008; Arabidopsis thaliana, Ossowski et al. 2010; Homo sapiens, Xue et al. 2009; Roach et al. 2010; Conrad et al. 2011; Kong et al. 2012). With sufficient depth of coverage and cross-validation, direct sequencing of MA lines with new sequencing technologies has proven to be highly accurate, producing few false positives. These studies have confirmed that mutation rates per generation vary by more than 2 orders of magnitude among taxa. However, estimates are sparse and unevenly distributed across taxa, limiting our understanding of the forces governing the evolution of the mutation rate. In this study, our aim is to characterize spontaneous mutation and estimate its rate in Chlamydomonas reinhardtii.

Chlamydomonas reinhardtii is a single-celled chlorophyte that has been extensively used as a model organism in plant physiology. It is a member of a large and distinct group of microorganisms within the plant kingdom that has been separated from land plants by roughly 1 billion years of evolution, and its reproductive and cell biology are well understood. The microalgae are critical to the ecology of the planet, as they are thought to carry out half of all photosynthesis (Beardall and Raven 2004). With the exception of a study in A. thaliana (Ossowski et al. 2010), relatively little work has been done to directly estimate the spontaneous mutation rate in plants. C. reinhardtii has a rapid generation time, making it feasible to carry out hundreds of generations of mutation accumulation (MA) in the laboratory, and is also facultatively sexual, and therefore amenable to genetic experimentation. The genome of C. reinhardtii is relatively compact, comprising ∼120 Mb (Merchant et al. 2007), which is similar to that of A. thaliana and D. melanogaster. It contains a diversity of genomic elements common to eukaryotes, and this may help to elucidate the nature of spontaneous mutation across site types in the genome. Interestingly, Chlamydomonas is a free-living microbe with relatively high genetic diversity (Smith and Lee 2008), suggesting that the species has large effective population size, leading to the prediction that it should have a low mutation rate (Lynch 2010; 2011). Additionally, the expected consistency of mutations per cell division per genome, known as Drake’s rule (Drake 1991), and the large genome of C. reinhardtii compared to other microbes predicts a low mutation rate.

We conducted a MA experiment followed by whole-genome sequencing to characterize spontaneous mutation in Chlamydomonas reinhardtii. Our aims were to estimate the rate of mutation, mutational bias in base composition, and the relative frequency of different kinds of mutations, such as point mutations, indels, and larger structural changes.

Materials and Methods

Mutation accumulation

We allowed mutations to accumulate in two replicate lines of Chlamydomonas reinhardtii strain CC-2937 that were maintained asexually for approximately 350 generations. We obtained CC-2937, a natural isolate from Quebec, Canada (Sack et al. 1994), from the Chlamydomonas Resource Centre. To initiate the MA lines, we streaked a liquid suspension of cells onto a Bold’s agar plate and grew them for 4 days. Plates were maintained at 25° under white light unless otherwise stated. Two separate colonies, each derived from a single cell, were chosen at random as the starting points of the two MA replicates. To propagate the replicate lines, a colony was picked at random and streaked onto a fresh Bold’s agar plate. We retained agar plates from four previous transfers as backups in dim light at room temperature. Colonies were selected by marking a spot using random coordinates on the base of the plate prior to streaking. At the next transfer, we chose the colony closest to the marked spot. If there were no colonies on the plate, we picked a new colony at random from the backup plate. Over the whole experiment, we needed to do this seven times for MA line 1 and four times for MA line 2.

In a study such as this, minimizing the transfer length is important, because it reduces potential competition between a newly arising genotype and its parent genotype within a colony and increases the number of generations over which mutations can accumulate, since growth slows down as the colony size increases. However, the transfer time should not be so short as to select against slow-growing colonies. Preliminary work in which individuals cells were spread on Bold’s agar plates, and colonies counted daily, showed that of 532 colonies that were present after 9 days of growth, 531 (99.8%) were visible on day 3 and all by day 4. Thus, we chose a protocol in which the period of growth between transfers alternated between 3 and 4 days. However, after 18 transfers it became apparent that the growth rate of some lines had slowed, and colonies were becoming harder to see after 3 days of growth. A repeat of the preliminary work for these lines showed that on some plates only 97% of colonies were visible after 3 days of growth; therefore, we changed our procedure with transfers occurring on a 4-day, 5-day, 5-day cycle. This 4–5–5-day regime was continued to the end of the experiment (34 transfers, 137 days for line 1; 37 transfers, 151 days for line 2).

Estimation of the number of generations of mutation accumulation

To estimate the total number of generations of MA, we measured the number of generations undergone by the ancestral genotype between transfers. Because our transfer protocol involved a mixture of three different transfer periods (3 days, 4 days, or 5 days), and generation time is likely to increase as colonies become larger, it was necessary to estimate growth independently for the three transfer periods. Furthermore, growth rate may change during MA, so we also carried out these measurements for cells from both MA lines taken from the end of the experiment for 4-day and 5-day transfer periods. Evolved lines were not measured over 3-day transfers, as this transfer period was used only at the beginning of the experiment.

We streaked the ancestor and each MA line onto separate Bold’s agar plates and allowed these to grow for 4 days. Individual colonies were selected at random from each of the lines and allocated to grow for 3, 4, or 5 days. There were six replicates for each combination of line and transfer period, giving a potential total 42 growth estimates. However, 5 of these replicates failed, giving a final number of 37 estimates. After growth for the allotted number of days, a single random colony was taken from each plate by removing an agar plug containing the colony and a surrounding piece of agar. Each plug was placed into separate 500-μl volume of Bold’s medium, vortexed, and left for 3–4 hr to allow the cells to disperse off the surface of the agar. These were further vortexed and serially diluted, and each dilution was plated on to Bold’s agar. The algae were allowed to grow for 4 days, at which point the number of colonies on the plate was counted. Counts were multiplied by the dilution factor to provide an estimate of the total number of cells in the original colony.

We calculated the number of generations over the course of colony growth (G) from the following equation

$$G=\frac{\left(\text{log}{N}_{\text{f}}-\text{log}{N}_0\right)}{\text{log}2}$$, (1)

where N_f represents the final number of cells in colony and N₀ represents the number of cells initially in the colony; in all cases here this is 1, since colonies were initiated from a single cell. Estimates of the number of generations for each 3-day, 4-day, and 5-day transfer period for the ancestor of the MA lines and 4 days and 5 days for each MA line are shown in Table 1. Finally, using the average number of generations per transfer we can calculate the effective population size as the harmonic mean of colony sizes through each generation.

Table 1 . Estimates of the mean number of generations (+/− SE) for each transfer period at the start of the MA experiment (i.e., for the ancestor) and for the two MA lines at the end of MA.

Transfer period (days)	Number of generations per transfer period
	Ancestor	MA line 1	MA line 2
3	8.49 (0.41)
4	11.41 (0.44)	10.92 (0.37)	8.18 (0.48)
5	11.53 (0.84)	9.89 (0.24)	9.54 (0.46)

DNA sequencing

To extract DNA, we grew cells on 1.5% Bold’s agar for 4 days until there was a high density of cells, at which point the cells were collected and frozen at −80°. We disrupted the frozen cells using glass beads and extracted DNA using a standard phenol-chloroform extraction (http://www.plantlab.sssup.it/chlamydomonas-protocols).

Whole-genome resequencing was conducted using the Illumina GAII platform at the Beijing Genomics Institute (BGI-HongKong Co., Hong Kong). The sequencing protocol was modified to accommodate the unusually high GC content of the C. reinhardtii genome (mean GC = 63.9%). Variation in GC content is known to cause uneven representation of sequenced fragments, especially when GC > 55% (Aird et al. 2011). We therefore used a modified PCR step in sequencing library preparation, according to Aird et al. (2011) (3 min at 98°; 10 × [80 sec at 98°, 30 sec at 65°, 30 sec at 72°]; 10 min at 72°, with 2 M betaine and slow temperature ramping 2.2°/sec). We obtained ∼5 Gbp of 100-bp paired-end sequence from each of the two MA lines.

Sequence alignment and mutation identification

Reads were aligned to the Chlamydomonas reference genome (version 4) using BWA 0.5.9 (Li and Durbin 2009). We tested a variety of values for the fraction of mismatching bases allowed in alignments, but variation about the default (n = 0.04) did not improve the number of high-quality reads mapped or genome coverage (results now shown). To avoid calling false variants due to alignment errors, we used the Genome Analysis Toolkit, GATK v. 1.4-37 (McKenna et al. 2010; Depristo et al. 2011) to realign reads flanking potential insertions and deletions. We realigned the two samples together to ensure that the same alignment solutions were chosen in both genotypes. The final alignments were then used to jointly call genotypes using the UnifiedGenotyper from GATK after filtering bases with a PHRED scaled quality below Q15 and reads where mapping quality was less than Q20. The UnifiedGenotyper uses a Bayesian multisample genotyping method, which employs a prior probability of a site being variable defined by the parameters “–heterozygosity” and “–indel_heterozygosity.” We tested the effect of altering these parameters across 3 orders of magnitude (0.01, 0.001 and 0.0001) but found no major impact on our findings (see supporting information, File S1 and Figure S1) and therefore proceeded with the default values.

We identified novel mutations as high-quality positions where the two samples differed from one another. The two MA lines were genetically identical at the beginning of the experiment; therefore, all differences are candidate new mutations. However, inaccuracy in the alignment and sequencing process can lead to uncertainty in the genotype calls. We explored a variety of quality filters to attempt to minimize both false positives and false negatives. We found that the best quality statistic to identify novel mutation was genotype quality (GQ), which is the PHRED scaled probability that the genotype of each sample is correct. GQ was more useful for identifying new mutations than the PHRED scaled probability that a reference of alternate polymorphism exists (QUAL), because it provides a score for each sample. We examined this by confirming candidate mutations using Sanger sequencing and visually inspecting alignments to the reference (see below for details).

To calculate the mutation rate, we also needed to know the total number of sites of equivalent quality to the novel mutations. However, GQ is not defined for invariant sites. We therefore inferred a measure of quality comparable to GQ for invariant sites as follows. At sites where the genotype of the two samples differed, we extracted the QUAL (invariant QUAL) and GQ score for the individual sample that matched the reference. The individual QUAL was recalculated for the reference sample using the UnifiedGenotyper from the GATK. We then estimated the relationship between the QUAL and GQ using a linear model, (r = 0.91, P < 0.001) and used this to calculate appropriate QUAL values to count the number of invariant sites for a given GQ threshold. Additionally, we excluded heterozygous sites, because C. reinhardtii is haploid and these sites likely represent alignment or sequencing errors. To assess the effect of varying quality cutoffs, we calculated the mutation rate across a range of quality thresholds (GQ > 5, 10, 15, 20, 30, 40, 50, 60, 70, 80, 90). We found that GQ of 20 or greater was the optimal threshold for minimizing both false positives and negatives (see Results). To confirm our candidate mutations, we visually examined alignments from all sites identified with GQ > 5 using the Integrated Genomics Viewer (IGV) (Thorvaldsdóttir et al. 2012). This allowed inspection of how each individual read maps to a particular genomic region. Common alignment problems are easily identified (discussed below in Results). Additionally, we Sanger sequenced all sites with GQ > 15. In addition to identifying novel single base mutations and short indels, we used the software PINDEL (Ye et al. 2009) to look for novel structural mutations such as inversions, tandem duplication, and large insertions/deletions. However, although there was evidence of structural variation between the reference genome and CC-2937, there was no evidence for novel mutations beyond short indels already identified using GATK.

To test the accuracy of our mutation rate estimation process, we simulated 1000 random mutations throughout the genome and tested whether our method recovered the expected mutation rate. We simulated independent mutations in two copies of the reference genome such that new mutations would be positions where one MA sample matched its reference and the other did not (for details see File S1). We then aligned the original reads of each sample to the two “mutated” reference genomes. From this, we calculated the expected mutation rate to be (4.49 × 10⁻⁶ mutations/position). Using the same quality criteria outlined above, we were able to call genotypes at 62 Mb of 105 Mb of the genome and therefore expected to find 560 of the simulated mutations. Our method recovered a simulated mutation rate of 4.48 × 10⁻⁶ mutations/position and 558 of the simulated mutations. Moreover, there was little effect of GC content on whether a mutation was discovered, suggesting that the GC bias in Illumina sequencing did not substantially influence our results (for full details of this exercise see File S1).

Results

Estimation of number of generations of mutation accumulation

Estimates of the numbers of generations between transfers for the different transfer periods are shown for the ancestral strain and the two MA lines at the end of the experiment in Table 1. To examine whether the growth rate of our lines had changed during our experiment, we fitted a general linear model with MA line, transfer period, and ancestral or evolved line as factors. Data from the 3-day transfers were not included, since this was estimated only for the ancestor. Growth rate dropped during the experiment (F_1,21 = 17.60, P = 0.001), but there was no evidence that the change in growth rate differed between the two MA lines (F_1,21 = 1.84, P = 0.190) or between the two transfer periods (F_1,21 = 0.03, P = 0.854).

To estimate the total number of generations undergone by each MA line, we multiplied the number of generations of growth over each transfer period for that line by the number of times that this transfer period occurred during MA. To account for an effect of change in growth rate, we used the growth-rate estimates for the ancestor for the first 18 transfers (up to the point when we switched from a 3- to 4-day cycle to a 4–5–5-day cycle) and the estimates from the MA lines at the end of the experiment for the remaining transfers. We infer that MA line 1 underwent ∼343 generations, and MA line 2 underwent ∼351 generations. Finally, using the average number of generations (G) per transfer we calculated N_e as the harmonic mean of colony sizes throughout a transfer period (i.e., 2°, 2¹, 2²…, 2^G). Across the entire experiment there were 2.41 generations/day, or approximately 12 generations in a 5-day transfer period, resulting in N_e ≈ 6.

Mutation identification

Whole-genome resequencing generated 5.2 and 4.6 × 10⁹ bp of DNA sequence in MA lines 1 and 2, respectively. After alignment to the reference genome, removal of PCR duplicates, and filtering of low quality reads, the mean coverage in MA lines 1 and 2 were 33.6× and 29.7×, respectively. These averages exclude the mitochondrial and chloroplast genomes, which have multiple copies per cell and therefore had much higher mean coverage (mean depth of cpDNA = 557× and mtDNA = 3991×). The GC content of the high-quality sites called in our study is 0.9% lower than the GC content of the Chlamydomonas reference genome and the low-quality sites were 1.4% higher than the genome average. The difference in GC between high- and low-quality sites is likely due to lower coverage at high GC sites. The small overall effect of GC suggested that the modification of the Illumina library preparation accounted well for the GC-biased C. reinhardtii genome.

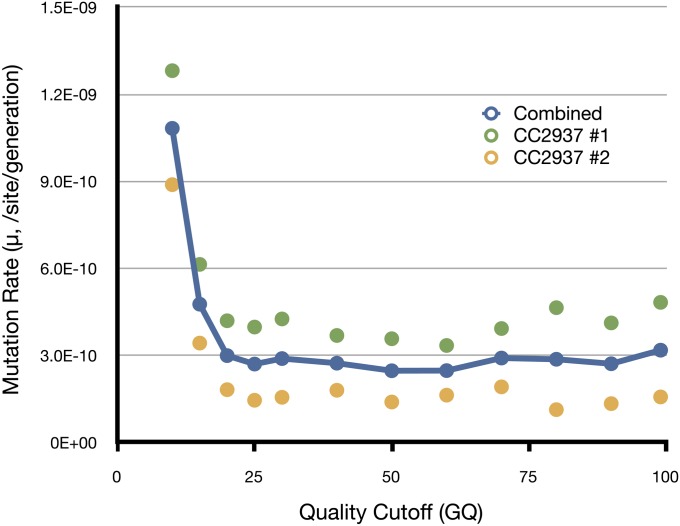
We tested the effect of varying the minimum GQ cutoff across the two replicates on our estimate of the mutation rate. We found that by increasing the stringency of the minimum GQ (and corresponding minimum QUAL value for invariant sites) the mutation rate estimate leveled off at ∼3×10⁻¹⁰ /generation/bp when GQ exceeded 20 (see Figure 1). With the exception of one mutation, all of the mutations, identified with GQ < 20, were likely false positives caused by read-mapping errors. The most common cause of these errors appeared to be repeats not present in the reference genome where reads derived from distinct loci mapped to the same region of the genome. An overrepresentation of opposite read types from the repeat copy appeared as novel mutations. These errors were easily identified, because there was typically a cluster of mutations and the opposite read type could be seen in both samples at low frequencies. By increasing the GQ threshold above 20 we excluded known mutations, but the effect on the total number of callable sites was proportional and, therefore, had little effect on the final estimate of the mutation rate (Figure 1).

Figure 1 .

Estimate of mutation rate as a function of quality cutoff. The GQ is the PHRED scaled confidence that the genotype of each sample is correct. The mutation rate levels off at ∼GQ > 20. For each GQ cutoff we applied an equivalent cutoff to determine the total number of callable sites.

We used PCR and Sanger sequencing to check all 23 mutations where GQ > 15. In this set, only one mutation out of 14 with GQ > 20 was a false positive and one mutation out of 10 with GQ between 15 and 20 was genuine. This leaves a total of 14 novel mutations identified in both samples of this study (8 in MA line 1 and 6 in MA line 2; Table 2). Assuming that the reference sequences represent the ancestral state, there were 4 deletions and 1 insertion. All of the indels were short (1–3 bp) and 4 of 5 indels appear to be a consequence of slippage in short simple sequence repeats. Based on all confirmed mutations in 62,292,728 bp (QUAL cutoff 57.2) and a mean generation number of 329, the mutation rate per generation per site is 3.23 × 10⁻¹⁰. Assuming that mutation is a Poisson process, the 95% C.I. around our estimate is 1.82 × 10⁻¹⁰–5.23×10⁻¹⁰ /site/generation. Similarly, considering only a single base mutation, we estimate the per-base pair rate as 2.08 × 10⁻¹⁰ /base/generation (95% C.I., 1.00 × 10⁻¹⁰–3.74 × 10⁻¹⁰ /site /generation).

Table 2. New mutations identified in this study.

Position	MA line	Mutation	Mutation site	Mutation type	Site type
Chr 1: 2,483,232	2	-GAC	GGAAATGGACGACGA	Deletion	Coding (in frame)
Chr 10: 3,513,120	1	-AGC	TCTGAGGAGCGCTGT	Deletion	Intron
Chr 10: 5,070,869	1	-C	AAGGAAGCCCCCCCC	Deletion	Intron
Chr 3: 8,791,984	2	-GT	TGTGTCAGTGTGTGT	Deletion	Intron
Chr 4: 2,443,951	2	+GCT	CCATGCGGGCTGCTG	Insertion	Intron
Chr 8: 2,234,083	1	T	CACGCTGCCATCCGA	Transition	Intergenic
Chr 10: 3,513,125	1	T	AGGAGCGCTGTTGAG	Transition	Intron
Chr 9: 3,469,066	1	A	GAGTTTGGCGGGCCC	Transition	Synonymous
Chr 10: 5,826,273	2	A	CGGAAGAGCGTTCCT	Transition	Synonymous
Chr 3: 3,303,576	1	A	CTCCTGCGCGGGGCC	Transition	Intron
Chr 2: 4,718,895	2	A	CTATCGGCGGTGCAG	Transversion	Nonsynonymous
Chr 7: 4,075,424	1	A	TGGCACTCGGCTGTG	Transversion	Intergenic
Chr 2: 6,925,830	1	G	CTACACGCCCAGTCA	Transversion	Intergenic
Chr 11: 2,535,739	1	T	CCTGCCCGCGCTCAT	Transversion	Nonsynonymous

Coordinates provided are from the Chlamydomonas reinhardtii genome version 5. The annotation for each mutation was manually adapted from the version 4 annotation. For each mutation we provide the unmutated sequence where the site of the mutation is underlined and boldface.

Among our nine point mutations we found 8 G/C → A/T mutations and no A/T → G/C mutations (the ninth was GC → CG). Although our sample is quite small, there is a clear pattern of mutational bias for G/C → A/T, since the probability of observing 8/8 G/C → A/T mutations in the absence of mutational bias (controlling for GC content) is 0.025. To assess whether there was a bias in the base composition of new mutations we calculated the likelihood of observing our data under a range of potential biases from 0 to 100% G/C → A/T. Assuming a binomial distribution, and accounting for GC content, we can say with 95% confidence that the mutational bias GC → AT is between 68.4% and 100%.

Of the 14 novel mutations identified here, 3 were in intergenic DNA, 6 were in introns, 5 were in coding exons and none were in UTRs. This distribution is not significantly different from random, based on the fraction of positions included in our high-quality sites (χ² = 2.43, d.f. = 3, P = 0.49). The 5 exonic mutations included one indel, which was in frame as part of a trinucleotide repeat. Two mutations were synonymous and two were nonsynonymous. These nonsynonymous mutations were in the genes flagellar outer dynein arm heavy chain gamma (Chlamydomonas JGI protein ID 155136) and a small ARF-related GTPase (Chlamydomonas JGI protein ID 93550). There was no discernible pattern to the spatial distribution of mutations across the genome.

Discussion

Here, we report an estimate of the mutation rate from genome sequencing in a chlorophyte, C. reinhardtii. Our estimate of the total mutation rate is 3.23 × 10⁻¹⁰/site/generation, and, excluding insertions and deletion events, the mutation rate is 2.08 × 10⁻¹⁰/base/generation. Shotgun sequencing of the whole genome of MA lines allowed us to survey a large fraction of the genome and resulted in an estimate of the per-site mutation rate with reasonably narrow confidence limits. The mutations were randomly distributed with respect to site type (coding, noncoding), consistent with selection not having preferentially removed coding mutations. Our estimate of the per-site mutation rate per generation is among the lowest recorded in eukaryotes, it is an order of magnitude lower than most multicellular eukaryotes, including the flowering plant A. thaliana (6.5×10⁻⁹, Ossowski et al. 2010), and is marginally, but not significantly, lower than the yeast, S. cerevisiae (3.3 × 10⁻¹⁰; Lynch et al. 2008). However, to calculate the mutation rate per cell division of multicellular organisms we must divide the per-generation rate by the number of reproductive cell divisions per generation. For example, assuming 30–40 divisions per generation in A. thaliana the mutation rate per cell division is 2 × 10⁻¹⁰ (Ossowski et al. 2010), which is comparable to C. reinhardtii.

Through whole-genome resequencing, we were able to call mutations in both samples with high confidence across >62 Mbp of the 104 Mbp of completed sequence in the C. reinhardtii genome (>8 Mb of the 112-Mbp nuclear genome is scaffolded with N_s). In our analysis, we required the presence of high-quality genotype calls in both replicates to distinguish between SNPs differentiating the reference and our ancestral CC-2937 strain and novel mutations. Including additional samples or sequencing to a greater depth may have allowed us to assay more sites. However, many regions of the genome sequenced at low coverage were subject to alignment problems corresponding to regions with high repeat content. This creates ambiguity in alignments or attracts reads from paralogous regions that are absent from the reference genome. These problems make it difficult to use simple quality criteria, such as the presence of a certain fraction of concordant reads, because sampling of alternate paralogs in each line can lead to false-positive mutation calls. This problem could also be mitigated by sequencing more lines or to a greater depth. Our method uses all the information available, including base quality, mapping quality, depth, and purity, and we found that increasing the stringency above GQ of 20 did not substantially alter our estimate of the mutation rate, suggesting that it is reasonably unbiased. Additionally, by simulating 1000 random mutations throughout the genome we were able to demonstrate that our method accurately recovered the expected number and rate of mutations.

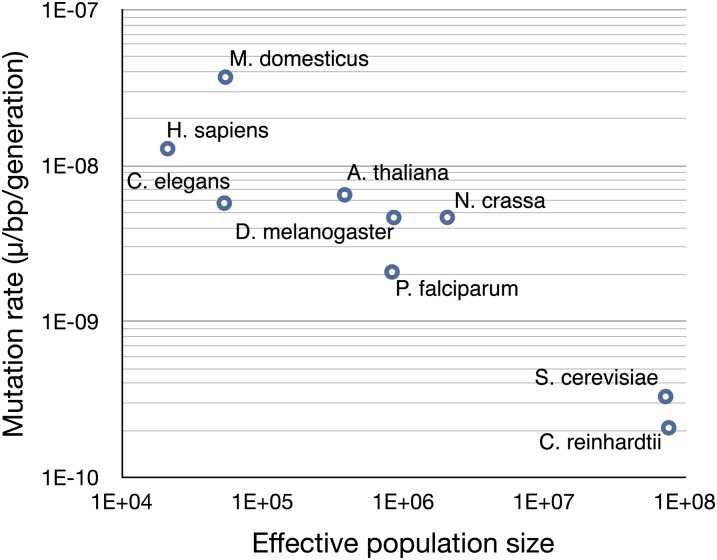
A variety of hypotheses to explain why the mutation rate does not evolve to zero have been proposed. These hypotheses generally invoke physiological constraint to further reduction in the mutation rate or a trade-off in terms of the cost of increasing fidelity by diminishing amounts (Kimura 1967; for a review see Baer et al. 2007). Alternatively, the lower bound for the mutation rate may depend on the efficacy of selection on vanishingly small fitness benefits from improvements to replication fidelity (Lynch 2010, 2011). Under the “drift hypothesis,” as the product of the selective advantage for reducing the mutation rate (s) and the population size (N_e) approaches 1 the action of genetic drift will dominate. This force would act on the per-generation mutation rate because it is the rate that drives selection on sites linked to the mutator. One would therefore predict that species with large N_e will tend to have the lowest mutation rates. Assuming that neutral diversity reflects the product of population size and mutation rate (2N_eµ = 0.032; Smith and Lee 2008) N_e of C. reinhardtii = 0.032/(2 × 2.08×10⁻¹⁰) = 7.6 × 10⁷. This very large N_e is consistent with its relatively low mutation rate compared to other eukaryotes and is very similar to yeast, which also has a large N_e (7.2 × 10⁷, Figure 2). However, the few natural isolates of C. reinhardtii are scattered across eastern North America, and the extent of genetic structure among populations is unknown. Therefore, if the mutation rate evolves quickly, the size of the local population will determine the efficacy of selection. However, no estimates of variation in the mutation rate among closely related taxa or within species have been made, and we cannot as yet address the rate at which the mutation rate evolves.

Figure 2 .

Plot of base substitution rate per generation (µ) by the effective population size (N_e). N_e is calculated from neutral genetic diversity, π = 2N_eµ (haploid) or 4N_eµ (diploid). Data for species other than C. reinhardtii were adapted from Lynch et al. (2006) and Lynch (2010).

The downward evolutionary pressure on the mutation rate derives from mutator alleles creating linked deleterious alleles. Therefore, the number of mutations per genome rather than the rate per site is more relevant for mutation rate evolution, because it more accurately reflects the number of potentially linked deleterious mutations creating selection against the mutator. Under this framework, our analysis gives a rate in C. reinhardtii of 0.038 mutations/genome/generation or one mutation every 26 generations. This estimate is substantially lower than in other eukaryotes with similar genome sizes, such as D. melanogaster (0.560; Keightley et al. 2009) and A. thaliana (0.875; Ossowski et al. 2010) and is consistent with the large N_e of C. reinhardtii allowing selection to operate on antimutator alleles with very small effects. However, the rate per genome is about an order of magnitude higher than in S. cerevisiae (0.004; Lynch et al. 2008), which has an ∼10-fold smaller genome (12 Mbp). According to the drift hypothesis, species with similar effective population sizes should have similar per-genome mutation rates. However, this assumes that a similar fraction of the genome in each species is evolutionarily constrained and is therefore a target for deleterious mutations. Drake et al. (1998) introduced the concept of effective genome size, which is the portion of the genome that, if mutated, could have an effect on fitness. Interestingly, although the C. reinhardtii genome is much larger than the yeast genome, there is less than three times as much coding sequence, which implies that it may have a lower effective genome size and may partly explain the higher per-genome mutation rate. However, determining the effective genome size requires knowledge of the function of the noncoding fraction of the genome and would demand a more thorough comparative genomic investigation among chlorophytes than has been done.

The interpretation of the negative relationship between µ and N evident in Figure 2 depends on the accuracy with which nucleotide diversity (θ_π) reflects the product of N_e and µ. Factors such as genetic draft or background selection may strongly constrain θ_π, especially in species with large N_e, where selection operates more efficiently (Gillespie 2000). Therefore, if diversity does not reflect 2N_eµ (4N_eµ in diploids) we might expect a negative scaling between mutation rate and N_e simply as an artifact of N_e increasing for a given θ_π as the value of µ decreases. Unfortunately, distinguishing between these alternatives would require an independent estimate of the long term N_e of a species, which is currently not possible.

Although the rate of mutation per generation varies greatly across known eukaryotes, mutation rate per cell division is more consistent (Drake et al. 1998). The per-generation rate is important in an evolutionary context because it controls what parents pass on to their offspring and is therefore the rate that is acted upon by selection. In single-celled organisms such as C. reinhardtii or S. cerevisiae, the number of generations and cell divisions are equivalent, but in larger, multicellular organisms there are often tens to hundreds of cell divisions per generation. If we were to compare the same taxa as shown in Figure 2 the mutation rate per division would vary from 1.2 × 10⁻¹⁰ to 47 × 10⁻¹⁰, and there is no obvious trend with population size. Moreover, studies that have used mutation accumulation or sequencing of parent–offspring trios only record variation in the per-division mutation rate from 1.2 × 10⁻¹⁰ in H. sapiens to 6.4 × 10⁻¹⁰ in C. elegans. The relative consistency of the per division mutation rate across a broad (albeit small) sample supports the idea of a constraint on the fidelity of replication machinery.

If the genome were at equilibrium with respect to base composition, we would expect the number of G/C → A/T mutations to be equal to the number of A/T → G/C mutations, regardless of the underlying bias in the mutational process. Using a simple likelihood approach, we calculated the lower bound to the mutational bias from A/T → G/C to be 68.4%. Even at the minimum mutational bias, we expect the neutral equilibrium GC content of Chlamydomonas to be <32%, but the GC content in C. reinhardtii is strongly GC biased (GC_nuclear = 64.1%), suggesting strong selection for GC variants or widespread biased gene conversion (BGC). Distinguishing between these two possible forces would require further work, because the population genetic signature of selection and BGC is indistinguishable. Interestingly, the two organellar genomes of C. reinhardtii do not share the high GC content of the nuclear genome (GC_chloroplast = 34.5% and GC_{mitochondrion} = 45.2%). We did not detect any mutations in these genomes, but if they share the mutational bias found in the nuclear genome, the fact that they are largely nonrecombining and have lower GC is consistent with a strong role of BGC in the nuclear genome.

In this study, we have presented an estimate of the spontaneous mutation rate in Chlamydomonas reinhardtii. The total mutation rate was 3.23 × 10⁻¹⁰/site/generation and the single base rate was 2.08 × 10⁻¹⁰/base/generation, the lowest measured in a eukaryote. Given the large N_e of C. reinhardtii, this result is consistent with the lower bound of the mutation rate being defined by the efficacy of selection on antimutators of small effect (Lynch 2010, 2011). Kondrashov and Kondrashov (2010) pointed out that to date there are no published replicated MA with resequencing studies. Consequently, the degree to which the estimated mutation rate depends on subtle changes in the environment, experimental design, and the extent of within-species variation for mutation rate are unknown. We are aware of a parallel study in C. reinhardtii by S. Miller, M. Ackerman, T. Doak, and M. Lynch (unpublished results) with a different genotype and experimental design; our studies combined may therefore help to shed light on these potential influences. With advancing DNA sequencing technology, future studies should be able to include multiple genotypes, under a variety of environments to address these questions.