A new infectious disease model for estimating and projecting HIV/AIDS epidemics

Abstract

Objectives

As the global HIV pandemic enters its fourth decade, countries have collected longer time series of surveillance data, and the AIDS-specific mortality has been substantially reduced by the increasing availability of antiretroviral treatment. A refined model with a greater flexibility to fit longer time series of surveillance data is desired.

Methods

In this article, we present a new epidemiological model that allows the HIV infection rate, r(t), to change over years. The annual change of infection rate is modelled by a linear combination of three key factors: the past prevalence, the past infection rate and a stabilisation condition. We focus on fitting the antenatal clinic (ANC) data and household surveys which are the most commonly available data source for generalised epidemics defined by the overall prevalence being above 1%. A hierarchical model is used to account for the repeated measurement within a clinic. A Bayesian approach is used for the parameter estimation.

Results

We evaluate the performance of the newly proposed model on the ANC data collected from urban and rural areas of 31 countries with generalised epidemics in sub-Sahara Africa. The three factors in the proposed model all have significant contributions to the reconstruction of r(t) trends. It improves the prevalence fit over the classic Estimation and Projection Package model and provides more realistic projections when the classic model encounters problems.

Conclusions

The proposed model better captures the main pattern of the HIV/AIDS dynamic. It also retains the simplicity of the classic model with a few interpretable parameters that are easy to interpret and estimate.

Introduction

Combating the AIDS epidemic requires quantitative analysis because countries need to ground their AIDS strategies in an understanding of their own epidemics and their national responses. Due to the paucity of reliable information on the incidence of AIDS in developing countries, sentinel surveillance systems for HIV are designed to provide information on prevalence trends to policy makers and programme planners. For the purpose of surveillance, UNAIDS and WHO suggest a classification that describes the epidemic by its current state, that is, generalised, concentrated or low level. In generalised epidemics, HIV prevalence is consistently over 1% in pregnant women in urban areas. The percentage of HIV positive cases are often estimated among antenatal clinic (ANC) patients to represent the general population. In low level or concentrated epidemics, HIV infection has never expanded to a significant level in the general population. The surveillance data are often gathered from each identified most-at-risk population, for example, sexually transmitted diseases clinic patients, injecting drug users and men who have sex with men.

To fill in the information gap on the number of individuals living with HIV/AIDS, the rate of new infections, and the need for intervention and treatment, WHO proposed the AIDS epidemic software called EpiModel in the early 1990s when few surveillance data were available. EpiModel constructs HIV incidence curves based on two inputs: start year of epidemic and recent national adult prevalence. It uses a two-parameter γ function to describe the shape of the HIV incidence curve.^{1 2}

Since more data have become available in the 1990s, the UNAIDS Reference Group has developed the Estimation and Projection Package (EPP), which uses a generic epidemiological model. The epidemiological model in EPP 2009 incorporates population change over time by fitting four input parameters: r, the rate of infection; t₀, the start year of the epidemic; f₀, the initial fraction of the adult population at risk of infection; and φ, a behaviour change parameter.^3–8 The output ρ(t) is a sequence of yearly HIV prevalence rates at the national level. The uncertainty analysis is produced by using a Bayesian method with an appropriate prior distribution for the input parameters.⁹

As the global HIV pandemic enters its fourth decade, countries have collected longer time series of antenatal surveillance data. With the current EPP model, it has been found that some patterns are hard to reproduce.^{6 10 11} A flexible epidemiological model is thus needed to improve the fit to recently observed prevalence trends. Instead of assuming a constant infection rate, three refined models were developed to allow the infection rate vary across years: r-jump model, r-spline model and r-stochastic model. The infection rate, r(t), is the average number of infections caused by one HIV+person at year t, and it represents the behaviour change over time. The r-jump model allows a one-time change in the infection rate.⁶ However, it is hard to justify why there should be a sudden change of infection rate in a specific year. The spline model and stochastic model both assume that the infection rate has been changing since the starting year of the epidemic. The spline model fits the sequence of infection rates by using penalised B-splines.¹⁰ The stochastic model assumes the infection rates follow a Gaussian random walk with mean zero.¹¹ They both offer more flexible structures that can fit the prevalence data better when EPP encounters challenges. Note that the four-parameter classic EPP model truncates the prevalence space, and thus imposes a strong structure on the prevalence patterns that is shared by all countries. As long as the desired prevalence curve falls into that truncated space, the classic EPP model is accurate and computationally efficient. Unlike the classic EPP model, the spline model and stochastic model do not impose any common pattern of HIV prevalence across countries, and the fitted curve is completely driven by the observed data within each country. As a result, the computational efficiency may become an issue due to the increased degrees of freedom. Moreover, the spline model projection is too sensitive to the last couple of years of data, and additional constraints are needed to eliminate epidemiologically unrealistic projections in some cases.¹²

Here, we describe a flexible epidemiological model that can both fit the data well and yield realistic projections. In the Methods section we review the EPP model and describe the proposed alternative epidemiological model. In the Results section, we present results for 31 countries with generalised epidemics. In the Discussion section, we offer some conclusions.

Methods

The UNAIDS EPP, EPP 2011, is based on a simple susceptible–infected–removed epidemiological model.¹² The population being modelled is aged 15+, and the population at time t is divided into two groups: Z(t) is the number of uninfected individuals, and Y(t) is the number of infected individuals. The rates at which the sizes of the groups change are described by the following differential equations:

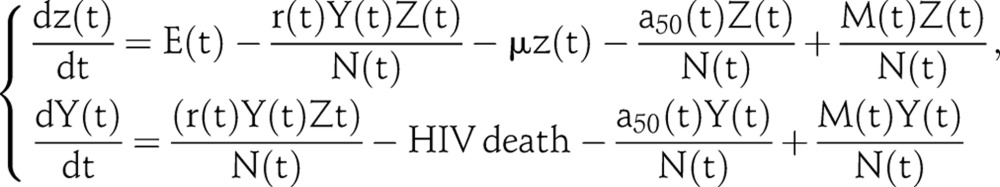1

The number of new adults entering the population at time t, E (t), depends on the population size of 15 years ago, the birth rate and the survival rate from birth to age 15. r(t) Is the average infection risk, µ is the non-AIDS death rate, −a₅₀(t) is the number of adults exit the model after attaining age 50 and M(t) is the number of net migration into the population. Because of the increasing coverage of antiretroviral therapy (ART), the infected group Y(t) is further decomposed according to the CD4 counts. As implemented in this manuscript, we divide Y(t) into three compartments: those at early-stage of infection, those eligible for the first line ART (eg, those having CD4 counts between 200 cells/mm and 350 cells/mm) and those eligible for the second line ART (eg, those having CD4 counts below 200 cells/mm). The survival rates of those eligible for ART also depend on whether they receive the treatment.⁸

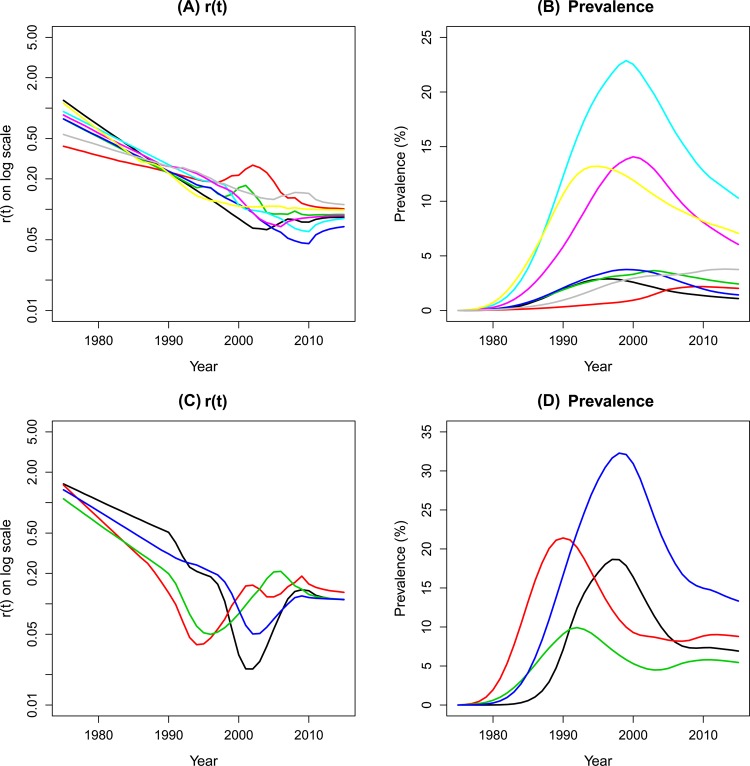
From EPP 2011 implementation experience, we find the Gaussian random walk model provides similar trends of r(t) across countries with generalised epidemics (see figure 1 for examples). Based on this observation, we propose a more informative structure for the time-varying infection rate parameter r(t) than the spline model and the stochastic model, so that it can represent the common pattern of HIV epidemics across countries. HIV and population dynamics are always intertwined, for example, HIV infection reduces fecundability.¹³ The widespread availability of ART also alters the course of HIV epidemics. ART has substantially increased survival rate for people living with HIV, and also can lower the HIV incidence for a given prevalence level through decreases in viral load reducing individuals’ infectiousness. Built upon model (1), we further assume that the yearly change of infection rate, r(t), can be related to some known factors driving the HIV/AIDS epidemic. It assumes a systematic shift of log r(t) has the following form:

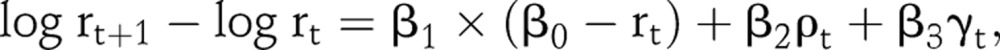2

where β₃<0. β₀ can be interpreted as an equilibrium condition at which the current infection rate does not lead to any shift of log(r_t). β₁ Describes how log(r_t) changes when the current infection rate differs from its equilibrium value. For positive β₀ and β₁, r(t) increases if its current value is less than β₀, and decreases otherwise. The mean shift is also related to the prevalence. β₂ Is the expected change of log(r_t) given a unit increase of the prevalence and we expect β₂<0 so that the higher prevalence, the more likely the infection rate decreases. Since we have observed longer time series data, and for many countries their prevalence has stabilised, we want to restrict the change of r(t) for the later period of the epidemic. With β₃<0, the third term γ_t=(ρ_t + 1−ρ_t) (t−t₀−t₁)⁺/ρ_t is the relative change of prevalence times the positive part of t−t₀−t₁, and it implies that the prevalence tends to stabilised after t₀+t₁. We refer to the above models (1) and (2) together as the r-trend model.

Figure 1.

The r(t) trends and prevalence trends fitted by the Gaussian random walk model. Different colours represent the different posterior median prevalence from different countries. (A) r(t) Starts with a high value to initiate the epidemic and then declines; (B) the corresponding prevalence reaches the peak and then gradually declines; (C) and (D) r(t) has a turnover when the prevalence levels off or increases after a steady declining period.

The newly proposed r-trend model requires seven parameters. They are the starting year of the epidemic t₀, the number of years that the epidemic takes to stabilise t₁, the initial infection rate r₀, and four βs describing how the relative infection rate changes with prevalence, incidence and stabilisation stage. We carry out Bayesian estimation with the following prior distributions:

3

The lower bound of r₀ for generalised epidemics is set at 1/11.5 because 11.5 is the expected length of the infectious period so the epidemic would not spread if r₀ were smaller than 1/11.5. A lower bound of 1/11.5+1/d is recommended for concentrated epidemics, where d is the mean duration that people stay in the at-risk category.

The ANC data consist of the number of infected women, Y_st, and the number of women tested, N_st, for clinic s in year t. Let ρ_t be the overall population prevalence in year t, X_st=(Y_st+0.5)/(N_st+1). A hierarchical model is used to define the likelihood with a random clinic effect b_s accounting for the repeated measurement within clinic:⁹

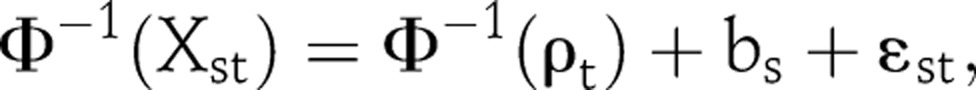4

where Φ⁻¹ is the standard normal cumulative distribution function, and ɛ_st are independent normal errors.

To evaluate the goodness of fit and predictive validity of the r-trend model, we fit models based on the full data time series as well as assessing 5-year out-of-sample projections from models fit to truncated data.^{9 12} We calculate the coverage and the width of the 95% clinic-specific credible intervals, the mean absolute errors (MAE) of the clinic-specific posterior median and the mean error which is the clinic-specific posterior median subtracted by the observed values. The coverage of clinic-specific intervals is defined as the proportion of ANC data that fall within the corresponding clinic-specific intervals.

The most commonly available ANC data tend to be biased upwards because the pregnant women are more sexually active. Many countries with generalised HIV/AIDS epidemics also have a couple of national representative household-based Demographic and Health Surveys (DHS) that include HIV tests. DHS can serve as approximately unbiased estimates of HIV prevalence, and thus can be used to adjust the bias of ANC data. We can incorporate the DHS HIV prevalence, denoted by X_dhs,t, into the likelihood as follows:

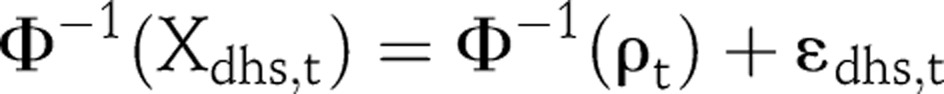5

We assume that the clinic effects b_s in equation (4) follows non-centred normal distributions to reflect the bias in ANC data:

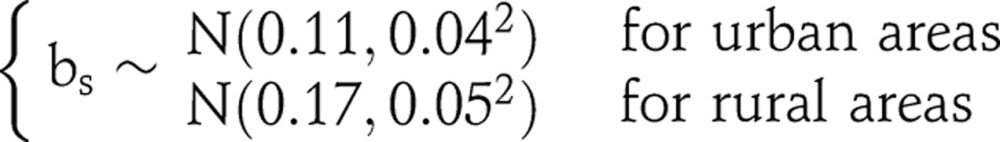6

Results

We evaluate the r-trend model using the data from urban and rural areas of the following 31 countries:

• Eastern Africa: Burundi, Ethiopia, Eritrea, Kenya, Malawi, Rwanda, United Republic of Tanzania, Uganda, Zambia

• Central Africa: Cameroon, Central African Republic (RCA), Chad, Congo, Democratic Republic of the Congo (RDC), Equatorial Guinea, Gabon

• Southern Africa: Botswana, Lesotho, Namibia, Zimbabwe

• Western Africa: Benin, Burkina Faso, Cote d'Ivoire (RCI), Gambia, Ghana, Guinea, Liberia, Mali, Nigeria, Sierra Leone, Togo.

We fit the r-trend model to 62 datasets by using priors: β_i∼N(0, 0.2). All of the β_is are significant under 0.05 level. Moreover, the signs of the coefficients are as expected. We get positive β₀ and β₁, negative β₂ and β₃ for each individual dataset. The mean and SD of estimates from 62 datasets are shown in table 1. It supports that the βs are useful parameters describing the trend of r(t). To make the sampling more efficient, we recommend the use of normal distributions with mean and SD taken from table 1 as the default prior distributions of βs, t₁ and log r₀ for countries with generalised epidemics. The default prior distribution of t₀ is still uniform (1970, 1990).

Table 1.

Summary of parameter estimates across 62 datasets

	β0	β1	β2	β3	t0	t1	log r0
Mean	0.46	0.17	−0.68	−0.038	1978	20	0.42
SD	0.12	0.07	0.24	0.009	4.3	4.5	0.23

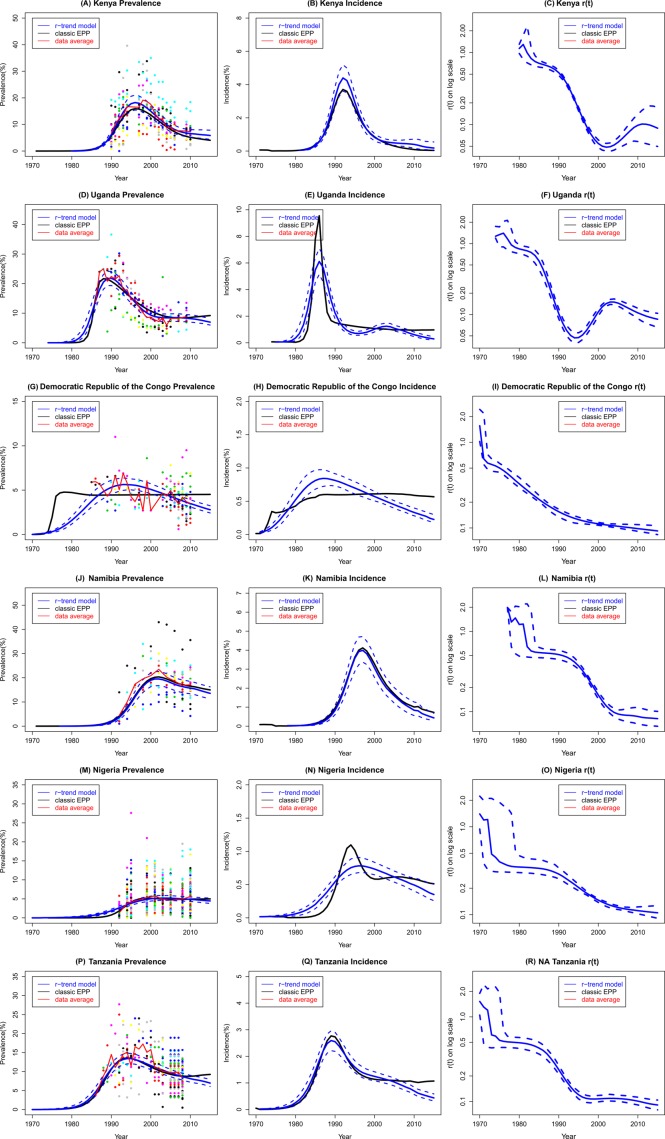
The proposed r-trend model has yielded satisfactory results on each dataset. Figure 2 presents the urban area results from six countries that have the largest population sizes in this study: Kenya, Uganda, Democratic Republic of the Congo, Namibia, Nigeria and Tanzania. Kenya and Uganda are the cases where the EPP model encounters the greatest challenges. For Kenya, the average ANC prevalence declined quickly and then levelled off (figure 2A). For Uganda, the ANC data revealed declines in the mid and late 1990s, followed by stabilisation between 2000 and 2005, and then modest ascent since 2007 due to the great reduction in AIDS-related deaths (figure 2D). The classic EPP model produced a slow decline after the prevalence peak in both examples. The r-trend model is flexible enough to capture the stabilisation in Kenya and the uptick in Uganda after the significant decline of prevalence. The incidence rate estimated by the classic model approaches 0% in 2015 in Kenya which overoptimistic. The r-trend model gives a gentle decline of incidence (figure 2B). Note that the φ parameter of the original Reference Group model implies a stronger decline postpeak, while the β₃ parameter of the r-trend model assumes more stable prevalence that has been most commonly observed across countries. For Democratic Republic of the Congo, the classic EPP fits a straight line through the data period. The median prevalence of r-trend model better captures the quadratic curve of observed data (figure 2G). For Namibia, Nigeria and Tanzania, the classic EPP and the r-trend model provide similar median prevalence within the data period, but the r-trend model tends to forecast a lower incidence than the classic EPP model.

Figure 2.

Continued.

Figure 2.

Results from Kenya, Uganda, Democratic Republic of the Congo, Namibia, Nigeria and Tanzania: coloured dots are observed prevalence from different sites; the black line is the classic model trajectory; the blue solid line is the median trajectory of the proposed model; the dashed blue lines are the 95% credible intervals of the proposed model; and the red solid line is the data trend averaged over all clinics at each year. Note that the infection rate of the classic model is a constant and hence not shown in the figure.

For each dataset, we calculate the coverage and the width of the 95% clinic-specific intervals, the MAE, the mean errors and the computing time. Table 2 summarises those statistics averaged across all datasets. Rural datasets from Guinea, Central African Republic, Liberia and Sierra Leone are excluded for the out-of sample projection because there are no data left after removing the last 5 years in those areas. For the insample fit, the r-trend model offers marginal improvements over the classic EPP model; it converges 38% slower than the classic EPP model. For the out-of-sample projection, the r-trend model substantially increases the coverage, and reduces the width of predictive interval and MAE over the classic EPP model. The r-trend model is less biased than the classic EPP model which tends to overestimate the prevalence.

Table 2.

Comparisons between the clinic-specific posterior median and the clinic data: coverage and width of 95% CI, mean absolute error (MAE) and mean error (ME).

	Insample fit		Out-of-sample projection
	Classic EPP	r-Trend model	Classic EPP	r-Trend model
Coverage	86.7%	87.7%	76.5%	80.1%
Width	0.071	0.070	0.097	0.077
MAE	0.017	0.016	0.029	0.023
ME	0.002	0.002	0.008	−0.002
Computing time	1.28 h	1.76 h	1.34 h	1.50 h

The results of insample fit are evaluated through the entire data period and the results of out-of-sample projection are evaluated in the 5-year projection period.

EPP, Estimation and Projection Package.

In table 3, we also provide the evaluation statistics of the classic EPP model and r-trend model in the last data year. For the insample fit, the coverage, interval width and MAE of classic EPP and r-trend model are both improved when we focus on the most recent year of data. The benefit of using r-trend over the classic EPP is more obvious in terms of the coverage. It suggests that the r-trend model tends to fit the most recent data better. The out-of-sample projection becomes more challenging because we are projecting the epidemic 5 years ahead.

Table 3.

Last data year comparisons between the clinic-specific posterior median and the clinic data: coverage and width of 95% CI, mean absolute error (MAE) and mean error (ME).

	Insample fit		Out-of-sample projection
	Classic EPP	r-Trend model	Classic EPP	r-Trend model
Coverage	87.4%	89.4%	74.9%	79.0%
Width	0.067	0.065	0.108	0.080
MAE	0.015	0.013	0.028	0.024
ME	0.002	0.001	0.011	−0.003

The results are evaluated only in the last data year.

EPP, Estimation and Projection Package.

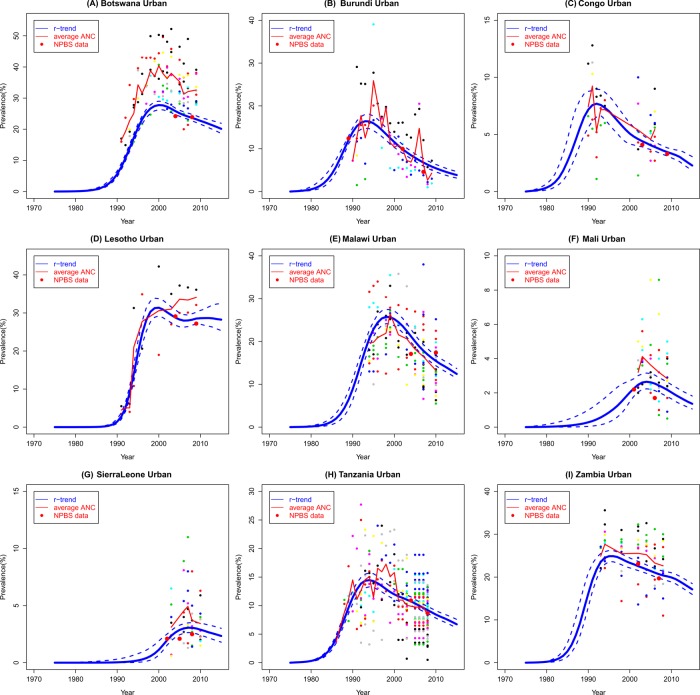
Finally, the r-trend estimates of HIV prevalence in nine countries with multiple national population-based surveys are shown in figure 3. The national population-based survey estimates are more precise than the ANC estimates, that is, they tend to have a larger sample size and a lower variance. Incorporating the national population-based survey data reduces both bias and uncertainty.

Figure 3.

Estimates of prevalence from the r-trend models incorporating national population-based surveys: the blue solid line is the median trajectory of the proposed model; the dashed blue lines are the 95% credible intervals of the proposed model; the red solid line is the data trend averaged over all clinics at each year; and red dots are the estimates from national population-based surveys.

Discussion

In the last decade, the classic EPP model fitted the data trends well for countries with generalised epidemics. However, as countries have obtained longer time series of data, a number of countries have proved challenging to fit using EPP. The classic EPP model imposes a strong structure of HIV prevalence trend: the epidemic spreads out, declines after a spike and then either levels off or keeps declining towards extinction. It is hard for the classic EPP curves to fit a second peak of prevalence after a steady decline of prevalence.

Here, we propose a new model in which the infection rate depends on the development of the epidemic and prevention systems. It offers greater flexibility than the classic EPP model, and it can also be parsimonious through careful variable selection. The new model proposed here combines the advantages of the previous models. It will retain the simplicity of EPP so that the parameters are easy to interpret and estimate. It will also add some flexibility to EPP to represent country-specific structure. An attractive feature of the proposed parsimonious model is that it allows imposing a hierarchical structure for areas within a country and for countries within a region, so that the area or country with fewer observations can borrow strength from its neighbours. We will present a more comprehensive analysis of the hierarchical model in another article.

Note that the results are based on illustrative HIV prevalence data for these countries, which may not be complete. These results should therefore not be seen as replacing or competing with official estimates regularly published by countries and UNAIDS.

Key messages.

• Countries have obtained longer time series of HIV surveillance data in recent years. The patterns of HIV epidemics become more complex.

• The four-parameter model in the UNAIDS Estimation and Projection Package does not have enough flexibility to capture some new patterns, for example, prevalence rises after a steady declining period.

• A seven-parameter model is proposed in which the changes of infection rates are modelled parsimoniously. It yields more satisfactory results than the classic model.