Abstract
Mechanical function of the annulus fibrosus of the intervertebral disc is dictated by the composition and microstructure of its highly ordered extracellular matrix. Recent work on engineered angle-ply laminates formed from mesenchymal stem cell (MSC)-seeded nanofibrous scaffolds indicates that the organization of collagen fibers into planes of alternating alignment may play an important role in annulus fibrosus tissue function. Specifically, these engineered tissues can resist tensile deformation through shearing of the interlamellar matrix as layers of collagen differentially reorient under load. In the present work, a hyperelastic constitutive model was developed to describe the role of interlamellar shearing in reinforcing the tensile response of biologic laminates, and was applied to experimental results from engineered annulus constructs formed from MSC-seeded nanofibrous scaffolds. By applying the constitutive model to uniaxial tensile stress–strain data for bilayers with three different fiber orientations, material parameters were generated that characterize the contributions of extrafibrillar matrix, fibers, and interlamellar shearing interactions. By 10 weeks of in vitro culture, interlamellar shearing accounted for nearly 50% of the total stress associated with uniaxial extension in the anatomic range of ply angle. The model successfully captured changes in function with extracellular matrix deposition through variations in the magnitude of model parameters with culture duration. This work illustrates the value of engineered tissues as tools to further our understanding of structure–function relations in native tissues and as a test-bed for the development of constitutive models to describe them.
Keywords: Intervertebral disc, Nanofibers, Structure–function, Mesenchymal stem cells, Hyperelastic model
1 Introduction
The intervertebral disc permits a wide range of spinal motions while maintaining stability and resisting large multidirectional loads. The disc is able to fulfill this demanding mechanical function through the interaction of its two primary substructures, the central gelatinous nucleus pulposus, and the surrounding annulus fibrosus. The annulus fibrosus is a multilamellar fibrocartilage, with highly aligned collagen fibers residing within discrete lamellae and the direction of collagen alignment alternating above and below the transverse axis of the spine by 30–45° (Marchand and Ahmed 1990). Understanding the relation between this highly ordered structure and mechanical function is an area of active experimental and theoretical investigation (Guerin and Elliott 2006, 2007; O’Connell et al. 2009; Smith and Fazzalari 2009; Sun and Leong 2004; Wagner and Lotz 2004). While such endeavors have focused on the study of either healthy or degenerate annulus fibrosus tissue, engineered tissue analogs also represent a useful tool for understanding how form and function are coupled in these systems (Nerurkar et al. 2011). This stems from recent advances in tissue engineering that have enabled the formation of engineered constructs in vitro that mimic the composition, multiscale organization, and mechanical function of the annulus fibrosus and other load-bearing soft tissues (Mauck et al. 2009; Nerurkar et al. 2009, 2010).
We have recently employed electrospun nanofibrous scaffolds coupled with mesenchymal stem cells (MSCs) to engineer nanofibrous biologic laminates that replicated the angle-ply organization of the annulus fibrosus and, after 10 weeks of in vitro culture, developed uniaxial tensile properties commensurate with the native annulus fibrosus (Nerurkar et al. 2009). Native tensile properties were only achieved when fibers in adjacent lamellae were aligned along opposing orientations (+/−30°); parallel alignment of fibers (+/+30°) resulted in significantly lower tensile moduli. These results indicated that shearing interactions across the lamellae may act to strengthen the macroscopic tensile response of biologic laminates (Fig. 1a). This mechanism of reinforcement, whereby opposing fiber reorientations shear the interlamellar matrix, was confirmed using an acellular nanofiberhydrogel system (Nerurkar et al. 2009).
Fig. 1.
Proposed mechanism of interlamellar reinforcement of the tensile response of two opposing fiber populations, shown schematically (a). Nanofibrous biologic laminates were constructed in three ply angles; e1 and e2 indicate the Cartesian coordinate system where axes are parallel to the orthonormal base vectors e1 and e2, respectively (b). The change in ply angle with deformation was chosen as a kinematic input for the strain energy function to describe interlamellar shearing interactions (c). L1, 2 Lamella 1, 2; IL Interlamellar matrix; ao, bo undeformed fiber directions; a, b deformed fiber directions. F deformation gradient tensor; 2ϕo undeformed angle between fiber populations; 2ϕ deformed angle between fiber populations; Wm, W f, and Wint are the strain energy density functions associated with matrix, fibers, and interlamellar interactions, respectively
Constitutive models are an important tool for studying the evolving mechanical function of growing engineered tissues (Nerurkar et al. 2007, 2008) and for the comparison of these tissues with native ones, where it is critical to account for nonlinearity, anisotropy, and finite elastic deformations (Fung 1982). Previously, we modeled cell-seeded electrospun scaffolds consisting of a single layer of unidirectionally aligned fibers with a hyperelastic model, accounting for anisotropy using the methodology described by Spencer (Spencer 1972). In this approach, a fiber-reinforced composite is modeled by the additive decomposition of the strain energy function into the sum of an isotropic matrix with a fiber phase. This method has been widely used for the study of many fiber-reinforced tissues and of the annulus fibrosus in particular (Guerin and Elliott 2007; Guo et al. 2006; O’Connell et al. 2009; Wagner and Lotz 2004; Wagner et al. 2006). Unfortunately, this approach cannot account for interactions between the two fiber populations, a phenomenon shown to be important for the function of engineered biologic laminates (Nerurkar et al. 2009). While additional strain energy terms have been added to the ‘fiber plus matrix’ model to account for various interactions between fibers and matrix, prior continuum models of the annulus fibrosus have simplified the multilamellar architecture by assuming both fiber populations coexist at each point in the material. Under such conditions, it is not possible to account any interlamellar effects, including shearing of the interlamellar matrix as fibers reorient under tensile load. Therefore, the objective of the present work was to extend the existing theoretical framework to account for interlamellar shearing interactions in order to understand the role of this phenomenon in the evolving function of nanofibrous biologic laminates with extracellular matrix deposition in vitro. This was accomplished through a two-tiered approach, beginning first with experimental investigations into the behavior of nanofibrous laminates with varying ply angles and second by applying a constitutive model to these experimental data that explicitly accounts for interlamellar interactions.
2 Materials and methods
2.1 Engineering MSC-seeded nanofibrous biologic laminates
Oriented nanofibrous mats were electrospun as described previously (Baker and Mauck 2007; Nerurkar et al. 2009). Rectangular samples (5 × 30 mm2) approximately 250 μm in thickness were cut from the electrospun mat with the long axis rotated either by 30° or 90° with respect to the prevailing fiber direction (Nerurkar et al. 2007). Scaffolds were stored in a dessicator until use, at which point they were sterilized, rehydrated, and incubated in fibronectin (20 μg/ml) overnight prior to seeding (Nerurkar et al. 2007).
MSCs were isolated from the tibial and femoral bone marrow of juvenile bovine knee joints and expanded to passage 2 (Mauck et al. 2007). Cells were then seeded on scaffolds with either 30° or 90° fiber orientations as described previously (Baker et al. 2009). Briefly, cells in basal media (DMEM with 10% FBS and 1% PSF) were seeded onto scaffolds at a concentration of 500,000 cells per side. Cell-seeded scaffolds were maintained in 4 mL of basal media overnight and then switched to chemically defined, serum-free growth media supplemented with 10 ng/mL TGF-β3 (Mauck et al. 2006). After 2 weeks of pre-culture as single lamellar strips, bilayers were formed by layering two strips between two pieces of porous polypropylene and wrapping with a foil sleeve (Nerurkar et al. 2009). Three bilayer orientations were constructed: transverse (+/+90°), parallel (+/+30°), and opposing (+/−30° Fig. 1b). These orientations were selected to accentuate certain specific contributions to mechanical functions for material property determination, as outlined below. After 2 weeks of culture as bilayers, the surrounding foil sleeve and polypropylene pieces were removed. Bilayers were cultured for up to 10 weeks with media changes twice weekly.
2.2 Measuring functional growth of nanofibrous biologic laminates
At 2, 4, and 10 weeks, bilayers from transverse, parallel, and opposing orientations were subjected to uniaxial tensile testing along the sample long axis (n = 5, Fig. 1b) or histologic analyses (n = 2). Mechanical testing was carried out by first measuring cross-sectional area using a noncontact laser system (Peltz et al. 2009), after which samples were speckle-coated with black enamel paint and loaded into custom serrated grips for tensile testing. Grips were fitted into an Instron 5542 testing system and, after preload (0.1 N for 300 s) and preconditioning (15 cycles to 0.1% at 0.05% per second), were ramped to failure at 0.1% strain per second (Guerin and Elliott 2006). During the ramp, images of the sample midsubstance were captured using a camera with magnifying lens (one image per 5 s). Images were post-processed with Vic-2D image correlation software to compute 2-D Lagrangian strains (E). Modulus was computed as the slope of the linear region of the stress–strain curves by linear regression. Histologic samples were embedded in OCT freezing medium, cryo-sectioned, and stained with Alcian Blue and Picrosirius Red to visualize glycosaminoglycan (GAG) and collagen, respectively.
2.3 Formulating a hyperelastic term for interlamellar interactions
Work in the present study builds on a prior model that was used to characterize the mechanics of single lamellar constructs (Nerurkar et al. 2008). Because the single lamellar model, which consisted of a Neo-Hookean matrix reinforced by exponential fibers, has been discussed in depth previously, the present work will focus only on its expansion to the study of biologic laminates with two opposing fiber populations. Additional details are available in the Appendix.
2.3.1 A hyperelastic model for interlamellar shearing of biologic laminates
The decomposition of W, the total composite strain energy function, into fiber and matrix strain energy functions can be interpreted as a base isotropic response, the extrafibrillar matrix (Wm, Appendix, Eq. A2), with an added energetic cost associated with stretching the material along the direction prescribed by a unit vector representing a fiber direction (Wf, Appendix, Eq. A3). Similarly, the role of interlamellar shearing interactions is incorporated here as an additional energetic cost that is associated with changing the relative angle between two fiber populations (Wint, Fig. 1b, c). Therefore, the total composite strain energy function, W, is given by:
| (1) |
The expression of each component of the strain energy function in terms of strain invariants ensures objectivity of the material definition, and therefore, the following invariants of the Right Cauchy Green tensor (C = FTF where F is the deformation gradient tensor) are introduced (Ogden 1997; Spencer 1972):
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
where ao and bo are unit vectors along the directions of fiber alignment in the undeformed state (Fig. 1c):
| (7) |
| (8) |
Here, ei are the orthonormal bases of a Cartesian coordinate system and ϕo is the ply angle. Throughout, uniaxial extension is applied along the e1 direction, bisecting the angle 2ϕo formed between the two fiber populations.
To define the energetic cost associated with interlamellar shearing, it was necessary to first identify a kinematic event that describes this phenomenon (Fig. 1a) (Nerurkar et al. 2009). Because interlamellar shearing was assumed to result from fibers reorienting in opposing directions under load, the change in angle between the two fiber populations was selected as the kinematic variable (Fig. 1c). To express this mathematically, Wint was chosen to follow the form:
| (9) |
where a and b are unit vectors defining the fiber orientations in the deformed configuration. In other words, the strain energy of interlamellar shearing is a function of the change in angle between two fiber populations as the fibers reorient under load. As shown in the Appendix, Eq. (9) can be rewritten in terms of strain invariants as:
| (10) |
Because experimental results suggested that interlamellar shearing is nonlinear, playing a larger role with increasing strain magnitudes (Nerurkar et al. 2009), an exponential form of Wint was adopted, analogous to Wf such that two parameters (κ, δ) could be used to define its role:
| (11) |
where κ defines the magnitude of the interlamellar interaction and δ defines the degree of stress–strain nonlinearity. Note that when F = I, Wint = 0, indicating that this particular form of strain energy function is consistent with a stress-free reference configuration. Further, for all deformations F, W (F) ≥ 0.
2.3.2 Defining the constitutive law of nanofibrous biologic laminates
To arrive at the constitutive law, Eqs. (A2), (A3), and (11) were substituted into Eq. (1) to provide the full strain energy function of the composite:
| (12) |
The first Piola–Kirchoff stress tensor was then computed by substituting Eq. (12) into:
| (13) |
The resulting constitutive relation for the nanofibrous biologic laminate is thus:
| (14) |
where each component stress is given by:
| (15) |
| (16) |
| (17) |
In summary, the model contains six material parameters, with two parameters associated with each the extrafibrillar matrix (μ and ν), fibers (γ and ξ), and interlamellar shearing (κ and δ).
2.4 Implementing the hyperelastic model to quantify the role of interlamellar shearing
The full stress–strain Eqs. (14–17) were applied to experimentally measured stress–strain curves for transverse (+/+ 90°), parallel (+/+30°), and opposing (+/−30°) bilayers in order to generate values for the six material constants. This was done by performing least-squares curve fits to the experimental data using a custom MATLAB code (Nerurkar et al. 2008). Because the model consists of six constants, fitting a single curve would generate multiple solutions, removing the physical meaning associated with these parameters. Therefore, the model was sequentially fit to data sets in order to determine the constants two at a time, using average values of the first pair in the determination of the next pair and so on. This was possible because each orientation of bilayer relies on a different combination of mechanisms to resist deformation. For instance, when fibers within each layer are parallel, as is the case for transverse and parallel bilayers, a = b, and therefore Wint = 0. Because fibers are assumed to bear only tensile loads, uniaxial loading of transverse bilayers produces a matrix-only response, as and Wf = 0 (Appendix).
Fitting of the constitutive equation to the stress–strain data from transverse bilayers was first performed and yielded values of matrix parameters μ and ν. The average values of each constant were computed, and their values were used in fitting Eqs. (14–17) to parallel bilayer data in order to provide values of the fiber parameters γ and ξ. Finally, with four of the six parameters determined, Eqs. (14–17) were fit to opposing bilayer data, making use of the average values of matrix and fiber constants to determine interlamellar shear interaction parameters κ and δ. This tiered curve fitting approach was chosen so that properties could be determined for the simplest case—transverse bilayers representing only the matrix—and then progressively add more properties with each fit (Fig. 1b). This permitted the determination of explicit values for each of the six parameters in unique combinations that best fit the dataset. The fitting approach was repeated for each time point, so that the changes in material parameters could be examined as cells deposited extracellular matrix with increasing culture duration.
The relative contributions of matrix, fibers, and interlamellar shearing interactions to the overall mechanics of biologic laminates after 10 weeks of culture were determined for uniaxial extension by computing the stresses tm, tf, and ti nt, respectively. Contributions were computed for uniaxial extension with the average material parameters obtained from fitting experimental data for Poisson’s ratio v12 = 1, and ϕ = 30°.
2.5 Simulating the mechanics of cell-seeded nanofibrous biologic laminates
To probe the behavior of the interlamellar shearing component of the model, simulations were performed for uniaxial extension of a fiber-reinforced laminate. Because the matrix and fiber terms have been used extensively in previous studies—which included sensitivity analyses—the simulations carried out here were focused on the behavior of the interlamellar shearing term, which has not appeared previously (Eberline et al. 2001; Guerin and Elliott 2007; Wagner and Lotz 2004). Except where noted, simulations were carried out for the case of an angle-ply laminate with ϕ = +/− 30° fiber orientations with respect to the loading axis and a Poisson’s ratio ν = 1.0 (determined experimentally). The effects of strain (E11), ply angle (ϕ), and Poisson’s ratio (ν) on strain energy and stress were examined. An additional simulation was carried out using the material parameters obtained from each time point to examine how interlamellar shearing reinforces the tensile response of biologic laminates for a range of deformation magnitudes and ply angles in the specific context of cell-mediated matrix deposition.
2.6 Statistics
Significance (p ≤ 0.05) was evaluated by two-way ANOVA with a Tukey’s post hoc test for the variables of culture duration and bilayer orientation (transverse, parallel, and opposing). For comparison of model parameters across time points, one-way ANOVAs with Tukey’s post hoc were used. Goodness of model fits are reported in R2 and Bland–Altman limits of agreement (bias ± standard dev), presented in MPa (Bland and Altman 1986).
3 Results
3.1 Experimental results
Consistent with previous findings, biologic laminates seeded with MSCs accumulated abundant GAG and collagen (Fig. 2a, b). Staining of both GAG and collagen was observed throughout each lamella as well as along the boundary between layers. This biologic interface was shown previously to be the operative structure in interlamellar shearing of nanofibrous biologic laminates (Nerurkar et al. 2009). No differences in staining were observed between transverse, parallel, and opposing bilayers, indicating similar quantities and localization of GAG and collagen between these three orientations.
Fig. 2.
Alcian Blue (a) and Picrosirius Red (b) staining of opposing bilayers after 10 weeks of culture demonstrates abundant deposition of GAG and collagen, respectively, within the lamellae and at the lamellar boundaries. No differences in staining were observed between transverse, parallel, and opposing bilayers. L1, 2 Lamella 1, 2; IL interlamellar matrix. Linear region modulus (c) increased with time for transverse, parallel, and opposing bilayers. p ≤ 0.05 indicated by overbars (vs. 2, 4 weeks), + (vs. transverse) and # (vs. parallel). Scale 250 μm
Tensile testing of biologic laminates revealed significant increases in tensile modulus with culture duration for transverse, parallel, and opposing bilayers (Fig. 2c). At 10 weeks, opposing bilayers were significantly stiffer than parallel bilayers, confirming the findings of our previous study (and motivation for the present one) that interlamellar shearing reinforces angle-ply biologic laminates.
3.2 Model results
Equations (14–17) were successfully fit to experimental data for transverse bilayers at each time point to obtain the Neo-Hookean material parameters μ and ν (Table 1; Fig. 3a, b). A significant increase in the matrix modulus-like parameter μ was observed with culture duration, indicating an increase in the isotropic response with extracellular matrix deposition (Fig. 3a). Large sample-to-sample variations in ν precluded any significant changes with culture duration (Fig. 3b), although this parameter trended upwards with culture duration. Significant changes in both fiber parameters were observed with culture duration (Fig. 3c, d). The fiber modulus-like term γ steadily declined (Fig. 3c), in contrast to a pronounced increase in the fiber nonlinearity parameter ξ (Fig. 3d). Additionally, while no significant changes were observed in the interlamellar shearing modulus-like term κ (Fig. 3e), the associated nonlinearity term δ increased by fourfolds during the 10-week culture period (Fig. 3f).
Table 1.
R2 and Bland–Altmann (BA) limits of agreement for fits to transverse, parallel, and opposing bilayers at 2, 4 and 10 weeks of culture
| R2
|
BA (MPa)
|
|||||
|---|---|---|---|---|---|---|
| 2 | 4 | 10 | 2 | 4 | 10 | |
| Transverse | 0.93 ± 0.05 | 0.93 ± 0.06 | 0.94 ± 0.03 | 0.002 ± 0.007 | 0.003 ± 0.013 | 0.002 ± 0.025 |
| Parallel | 0.99 ± 0.0 | 0.99 ± 0.0 | 0.98 ± 0.0 | 0.0011 ± 0.004 | 0.002 ± 0.007 | 0.015 ± 0.039 |
| Opposing | 0.98 ± 0.03 | 0.99 ± 0.005 | 0.98 ± 0.008 | 0.002 ± 0.009 | 0.004 ± 0.011 | 0.01 ± 0.033 |
Fig. 3.
Model fits to data from transverse, parallel, and opposing bilayers generated matrix (a, b), fiber (c, d), and interlamellar interaction (e, f) parameter values at each time point, respectively. Over-bars indicate p < 0.05
At 10 weeks, the contribution of matrix, fiber, and interlamellar interactions varied with strain for opposing bilayers (Fig. 4). While at small strains the behavior was dominated by matrix, with increasing strain the contribution of fibers and interlamellar interactions increased. At 0.1 strain, stress was accounted for primarily by interlamellar shearing (49%), with additional stress contribution from the matrix (36%) and fibers (14%) (Fig. 4).
Fig. 4.

Percent of total stress attributed to matrix (M, blue dashed line), fibers (F, black dotted line), and interlamellar interactions (I, red solid line) as a function of applied uniaxial strain E11. Values were computed for opposing bilayers after 10 weeks of in vitro culture
3.3 Model simulations
Simulations were performed to interrogate the behavior of the interlamellar interaction term. To understand first how ply angle changes with uniaxial extension, the change in fiber orientation, denoted by dot products of the unit vectors associated with each population, was computed for a number of ply angles as the laminate is extended along the x1 direction, which bisects the angle between the two fiber populations. The change in ply angle with uniaxial extension depended on the undeformed ply angle (Fig. 5a). For instance, when the two fiber populations are parallel to one another, or when both fiber populations are parallel (0°) or perpendicular (90°) to the direction of loading, there is no change in ply angle, as there is no rotation of one fiber population relative to the other. The degree of fiber reorientation, and therefore the change in ply angle, is also dependent on the Poisson’s ratio of the material (Fig. 5b). An increase in lateral contraction under uniaxial load generated increased fiber rotation and therefore greater changes in ply angle.
Fig. 5.
The angle change between two fiber populations was chosen as the kinematic measure to represent interlamellar shearing. This measure, represented by the difference between the dot products of the deformed and undeformed fiber directions, varies with ply angle (a) and in-plane Poisson’s ratio (b). E11 Lagrangian strain along the direction of applied strain. Each simulation assumes uniaxial extension along the x1 direction, bisecting the angle between the two fiber populations. Poisson’s ratio is 1.0 in (a); ply angle is 30° in (b)
The strain energy due to interlamellar shearing as defined by Eq. (11) was computed for a range of ply angles (Fig. 6a). Values were normalized to the pre-multiplier κ for simplicity. The strain energy is a constant zero for the case where the fiber populations are parallel to one another at 0° and 90°. Magnitude and slope of the strain energy density increased with ply angle up to 45°, beyond which strain energy decreased with increasing ply angle. Notably, strain energy curves were not symmetric about the 45° ply angle; complimentary angles do not produce identical curves.
Fig. 6.
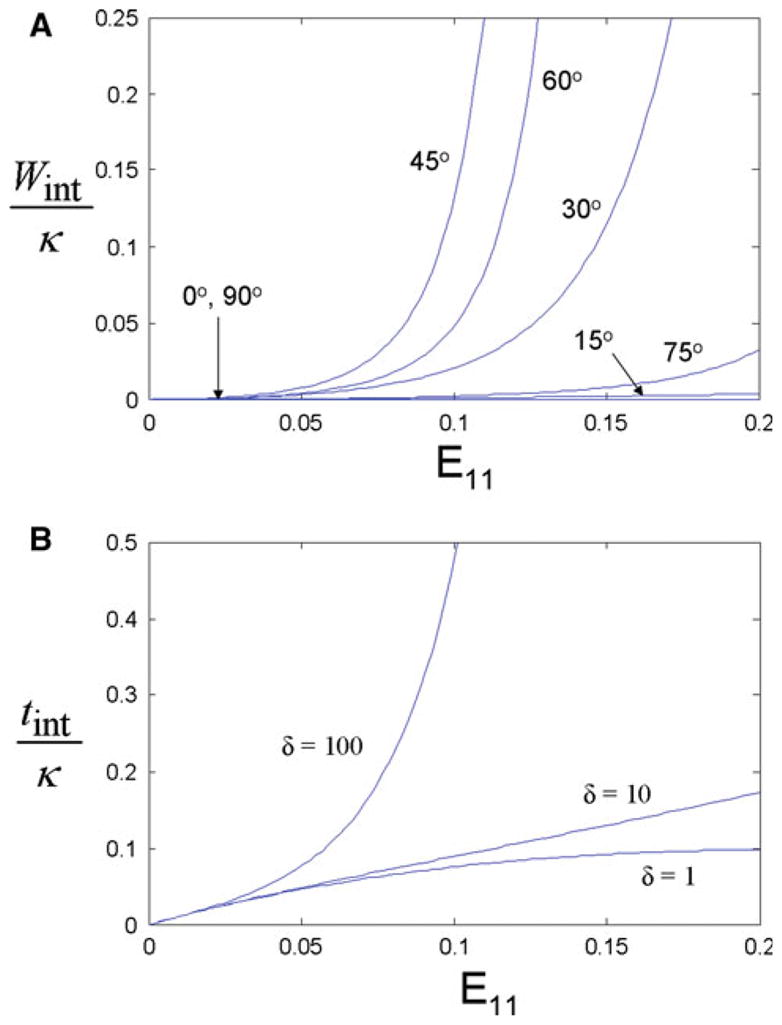
For the interlamellar shearing interactions, strain energy is computed as a function of applied uniaxial tensile strain for a range of fiber ply angles (a). The first Piola–Kirchoff stress associated with interlamellar shearing interactions, tint (b) is shown for three values of non-linearity parameter δ; ply angle = 30°. The y-axes are normalized to the modulus-like scalar κ
Stress due to the interlamellar shearing term was computed according to Eq. (17) (Fig. 6b); the stress was normalized to κ. Shape of the stress–strain curve was strongly influenced by the nonlinearity parameter δ. Because under uniaxial extension, fibers oriented 30° from the loading axis rotate progressively less with increasing strain, a competing effect was observed between this kinematic measure and the nonlinearity of the constitutive relation in which it appears. Specifically, at δ = 1, the stress–strain curve demonstrated decreasing slope with increasing strain, similar to the curve in Fig. 5b. However, as δ is increased, the stress–strain curve passes through a linear phase before becoming increasingly nonlinear with an increasing slope. In this way, modulation of δ dictates not only the degree of nonlinearity of the curve, but its general shape as well.
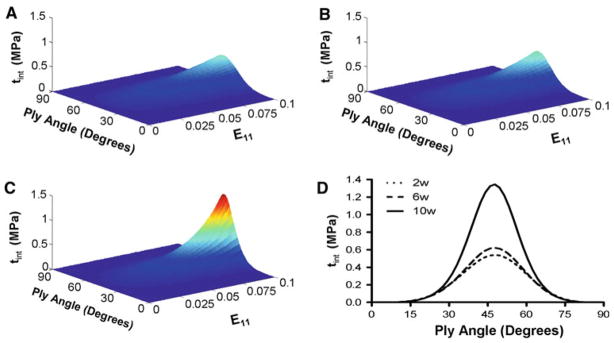
Finally, using the average parameter values obtained from fitting the experimental results, the stress–strain curves associated with the interlamellar shearing term were computed for a range of ply angles at each 2, 4, and 10 weeks. In each, the stress and modulus (Fig. 7a–c) were strain dependent. Importantly, the effect of interlamellar shearing was maximized in the range of ply angles near 45° (Fig. 7d). The overall magnitude of interlamellar shearing-induced tensile stress was highest at 10 weeks (Fig. 7c, d), indicating that with increased matrix deposition the effects of interlamellar shearing on tensile behavior were magnified.
Fig. 7.
Simulation of interlamellar shearing-induced tensile stresses at 2 (a), 4 (b), and 10 (c) weeks. Cross-sections from each contour are shown for E11 = 0.1 (d)
4 Discussion
In the present work, a hyperelastic model was formulated and applied to experimental data obtained from the mechanics of engineered nanofibrous biologic laminates. As in previous work, MSC-seeded biologic laminates accumulated considerable GAG and collagen (Fig. 2a, b), two of the primary ECM components of the annulus fibrosus. Concomitantly, the tensile modulus of these laminates increased with culture duration for each of the three orientations examined (Fig. 2c). The model successfully characterized the role of interlamellar shearing and how this reinforcement mechanism is progressively enhanced with extracellular matrix deposition (Figs. 3, 7). The model fit the stress–strain curves of opposing bilayers and produced nonzero values for the interlamellar shearing parameters κ and δ (Fig. 3; Table 1), suggesting that the particular form of the interaction term was able to characterize this reinforcement. Moreover, the model resolved functional growth of opposing bilayers through the time-varying material parameters that independently describe changes in matrix, fibers, and interlamellar shearing reinforcement with extracellular matrix deposition (Fig. 3). Interestingly, variability in the value of certain parameters, such as ν and ξ, increased with culture duration (Fig. 3b, d). This may reflect the experimental variability that accompanies extracellular matrix deposition during in vitro growth of bilayers (Nerurkar et al. 2009). Effectively, these material parameters serve as functional metrics of growth, demonstrating quantitatively the physical mechanisms that underlie enhanced tissue function.
Parameters describing the extrafibrillar matrix were obtained from transverse bilayers and demonstrated a culture-dependent increase in isotropic behavior. The magnitude of matrix parameters and how they changed with culture is consistent with our prior work with single lamellar constructs (Nerurkar et al. 2008), indicating that the tensile properties of the disorganized interlamellar ECM are similar to the extrafibrillar matrix within lamellae. In previous work using agarose hydrogel-nanofiber composites, we showed that even relatively soft (~ kPa) interlamellar material can strongly reinforce angle-ply biologic laminates in tension through the interlamellar shearing mechanism (Nerurkar et al. 2009). While aligned electrospun PCL scaffolds are structurally and mechanically anisotropic, they are less so than many native fiber-reinforced soft tissues, with anisotropy ratios (fiber : transverse direction modulus) of approximately 10:1 for scaffolds (Nerurkar et al. 2007) compared to upward of 1,000:1 in the annulus fibrosus (Holzapfel et al. 2005). This explains the relatively large contribution of matrix to the total stress of constructs with a 30° ply angle (36%) when compared to similar approximations in native annulus fibrosus (5–20%) (Elliott and Setton 2001; O’Connell et al. 2009). Nonetheless, degradation of the PCL scaffold over a sufficiently large time scale may result in anisotropy ratios that more closely resemble native tissues.
Fiber parameters were obtained from parallel bilayers where extension oblique to the unidirectionally aligned fibers is resisted by a combination of matrix and fibers. While the fiber nonlinearity parameter ξ increased by nearly five-folds by 10 weeks of culture, the pre-multiplier γ decreased (Fig. 3c, d). Together these observations suggest a potential reduction in stiffness at small strains that is offset by a pronounced stiffening at larger strains. These fiber parameters describe the combined effect of PCL nanofibers and cell-generated collagen, and so these changes may indicate a progressive shift in load-bearing from the linear elastic PCL to nonlinearly elastic collagen fibers. Predictions of the contribution of fiber stretch to total stress under uniaxial tension (~10–15% for ϕ = +/− 30°, Fig. 4) are similar to estimates generated previously for the native annulus fibrosus (20%) (Elliott and Setton 2001).
The interlamellar interaction pre-multiplier κ was unchanged throughout culture while the nonlinearity parameter δ increased significantly. In fact, by 10 weeks nearly 50% of the total stress was contributed by interlamellar interactions (Fig. 4), underscoring the importance of this mechanism of reinforcement for biologic laminates. Such findings demonstrate the utility of constitutive modeling for engineered tissues, whereby it is possible to discern not only how ECM deposition alters the bulk response of a tissue, but also how the fundamental mechanisms by which loads are resisted are altered in these evolving structures.
Simulations of stress due to interlamellar shearing indicated that the extent of tensile reinforcement increases with extracellular matrix deposition during culture and depends on the angle-ply alignment of the bilayers, as well as the magnitude of applied strain (Fig. 7). The contribution of interlamellar shearing is maximized in the range of +/−40° to +/−45°; this is similar to the anatomic range of ply angles found within the native annulus fibrosus, +/−30–45° (Cassidy et al. 1989; Marchand and Ahmed 1990). Given this coincidence, it is possible that interlamellar shearing plays an important role in the ability of the native tissue to withstand tensile loads in vivo. These findings may elucidate the ways in which the annulus fibrosus is structurally optimized to withstand the loading environment of the spine.
While it is possible to make inferences about the function of annulus fibrosus from the analysis of engineered biologic laminates, the proposed model can be applied directly to the annulus fibrosus as well. It has previously been demonstrated that a simple ‘fiber plus matrix’ model is not capable of capturing the uniaxial tensile properties of the native annulus fibrosus (Guerin and Elliott 2007; O’Connell et al. 2009). Other strain energies have been introduced to describe the contribution of interconnections between parallel fibers and interactions between the fibers and matrix (Guerin and Elliott 2005, 2007; Guo et al. 2006; Wagner and Lotz 2004; Wagner et al. 2006). However, these works were not intended to account for the organization of collagen fiber populations into discrete, alternating planes. We demonstrated here and previously (Nerurkar et al. 2009) that this organization provides an important functional reinforcement mechanism for resisting tensile stresses in engineered biologic laminates. However, the present study does not discount the potential importance of fiber–matrix interactions in the more complex native annulus fibrosus, and a rigorous material definition may require the incorporation of both terms. If such a model can be successfully implemented to characterize annulus fibrosus function, it will serve as an important tool in the comparison of engineered and native tissue function and in the quantification of changes in annulus function with degeneration.
While the present work advances the application of constitutive models for the study of engineered and native fiber reinforced tissues, there are certain limitations that will be addressed in future work. The present model successfully fit datasets in a tiered fitting approach and generated single, repeatable values for each material parameter. However, the model has not been tested in a predictive capacity; model-based predictions for the mechanical behavior of a bilayer with ply angles untested in the present study could be compared to experimentally measured stress–strain curves to validate the model. This illustrates the value of engineered tissues as a test-bed for constitutive model development, as there is considerable flexibility in the construct design and the associated type of data that can be generated for analysis when compared to native tissue. The tiered curve fitting approach used here and in many investigations of native tissue mechanics (Guerin and Elliott 2005, 2007; Klisch and Lotz 1999; O’Connell et al. 2009; Wagner and Lotz 2004) is a powerful tool for the study of such tissues, as a single type of test can be used to generate sufficient data to derive the values of multiple material parameters. However, there are also limitations to this approach that bear consideration. For instance, it is typically assumed that in each of the different orientations tested, the physical tissue components interact in similar ways; matrix in a transverse test behaves the same as it does in a test where fibers are also in tension. While this appears a reasonable assumption, it is difficult to prove directly. Second, properties to describe the bilayer come from several different samples. A more rigorous material definition would require obtaining all six model parameters from a single test on a single sample. This is unlikely for a uniaxial tensile test, but may be possible for tests that generate more information about the sample, such as biaxial tensile testing or combined loading modalities (e.g. tension-shear) (Driscoll et al. in press; O’Connell et al. 2007). The interlamellar shearing model proposed here will be applied to biaxial tests of annulus fibrous and engineered biologic laminates in future work.
In the present study, a new hyperelastic model was proposed for biologic laminates to account for and evaluate the role of interlamellar shearing in reinforcing the tensile response of these tissues. This approach is distinct from prior models of the annulus, where it is typically assumed that fibers are not in discrete alternating planes, an assumption that does not account for interactions between these layers. The model successfully characterized the evolving mechanical function of engineered nanofibrous biologic laminates and provides new insight into the reinforcing role of interlamellar shearing and how it depends on ply angle, strain, and culture duration. This work illustrates the value of tissue engineering not only as a means to eventually replace damaged tissues, but as a tool to instruct the understanding of structure–function relations in native tissues, and as a test-bed for the development of constitutive models to describe them.
Acknowledgments
This work was funded by National Institutes of Health grants AR 056624 and EB 02425. Additional support was provided by the Penn Center for Musculoskeletal Disorders (AR 050950).
Appendix A
A.1 Continuum modeling of fiber-reinforced soft tissues
Following the theory of strongly anisotropic solids outlined by Spencer (Spencer 1972), the total strain energy of a material can be decomposed into an isotropic response due to the extrafibrillar matrix and an anisotropic response resulting from the fibers. The fibers are modeled as energetic penalties along directions specified by unit vectors describing the fiber orientations. Therefore, the composite strain energy function (W) is additively decomposed into:
| (A1) |
where Wm and Wf are strain energy density functions representing the matrix and fiber phases, respectively. The matrix was assumed to be of a compressible, Neo-Hookean form:
| (A2) |
where μ and are the two scalar material parameters that characterize the matrix mechanics.
The fiber strain energy used here is modified from our previous work to account for two fiber populations, but returns to its prior form for ao = bo. Accounting for these features and the need to capture the stress–strain nonlinearity typical of collagenous tissues under tension, an exponential form of fiber strain energy function that is widely used for the study of annulus fibrosus was chosen (Eberline et al. 2001; Guerin and Elliott 2007; O’Connell et al. 2009; Wagner et al. 2006):
| (A3) |
| (A4) |
where γi and ξi are material parameters. By assuming that the two fiber populations differ only in orientation, Eq. (A3) simplifies with γi = γ and ξi = ξ; these parameters are associated with fiber modulus and nonlinearity, respectively (Eberline et al. 2001; Fung 1982; Guerin and Elliott 2007; Holzapfel 2000; O’Connell et al. 2009). The distinction between and I4/6 is made in order to restrict the contribution of fibers to purely tensile stresses, a practice common in the modeling of collagenous soft tissues (Ateshian 2007).
A.2 Hyperelastic model for interlamellar shearing of biologic laminates
The interlamellar shearing term is based on the kinematic variable of change in angle between two vectors as a material deforms. Accordingly, objectivity of such a strain energy function can be demonstrated by defining a second material frame A* related to the original frame A by a rotation Q, such that the fiber orientations are defined in A* by
| (A5) |
Frame indifference is then demonstrated by substitution of a* and b* into (8):
| (A6) |
making use of the orthogonality of the tensor Q, which requires that QTQ = QQT = I, the identity tensor.
The kinematic measure given in Eq. (9) can be rewritten in terms of strain invariants (Spencer 1972):
| (A7.1) |
| (A7.2) |
| (A7.3) |
| (A7.4) |
This final expression in terms of I4, I6, and I8 is the deformational input for the interaction strain energy Wint in Eq. (10).
Contributor Information
Nandan L. Nerurkar, Department of Orthopaedic Surgery, University of Pennsylvania, 424 Stemmler Hall, 36th Street and Hamilton Walk, Philadelphia, PA 19104-6081, USA. Department of Mechanical Engineering and Applied Mechanics, University of Pennsylvania, Philadelphia, PA 19104, USA
Robert L. Mauck, Department of Orthopaedic Surgery, University of Pennsylvania, 424 Stemmler Hall, 36th Street and Hamilton Walk, Philadelphia, PA 19104-6081, USA. Department of Bioengineering, University of Pennsylvania, Philadelphia, PA 19104, USA
Dawn M. Elliott, Email: delliott@mail.med.upenn.edu, Department of Orthopaedic Surgery, University of Pennsylvania, 424 Stemmler Hall, 36th Street and Hamilton Walk, Philadelphia, PA 19104-6081, USA. Department of Bioengineering, University of Pennsylvania, Philadelphia, PA 19104, USA
References
- Ateshian GA. Anisotropy of fibrous tissues in relation to the distribution of tensed and buckled fibers. J Biomech Eng. 2007;129:240–249. doi: 10.1115/1.2486179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker BM, Mauck RL. The effect of nanofiber alignment on the maturation of engineered meniscus constructs. Biomaterials. 2007;28:1967–1977. doi: 10.1016/j.biomaterials.2007.01.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker BM, Nathan AS, Huffman GR, Mauck RL. Tissue engineering with meniscus cells derived from surgical debris. Osteoarthr Cartil. 2009;17:336–345. doi: 10.1016/j.joca.2008.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986;307(310):307–310. [PubMed] [Google Scholar]
- Cassidy JJ, Hiltner A, Baer E. Hierarchical structure of the intervertebral disc. Connect Tissue Res. 1989;23:75–88. doi: 10.3109/03008208909103905. [DOI] [PubMed] [Google Scholar]
- Driscoll TD, Nerurkar NL, Jacobs NT, et al. Shear mechanics of electrospun scaffold for annulus fibrosus tissue engineering. J Mech Behav Biomed Mater (in press) [Google Scholar]
- Eberline R, Holzapfel GA, Schulze-Bauer CA. An anisotropic constitutive model for annulus tissue and enhanced finite element analyses of intact lumbar disc bodies. Comput Methods Biomech Biomed Eng. 2001;4:209–230. [Google Scholar]
- Elliott DM, Setton LA. Anisotropic and inhomogeneous tensile behavior of the human anulus fibrosus: experimental measurement and material model predictions. J Biomech Eng. 2001;123:256–263. doi: 10.1115/1.1374202. [DOI] [PubMed] [Google Scholar]
- Fung YC. Biomechanics: mechanical properties of livign tissues. (2) 1982:568. [Google Scholar]
- Guerin HA, Elliott DM. The role of fiber-matrix interactions in a nonlinear fiber-reinforced strain energy model of tendon. J Biomech Eng. 2005;127:345–350. doi: 10.1115/1.1865212. [DOI] [PubMed] [Google Scholar]
- Guerin HA, Elliott DM. Degeneration affects the fiber reorientation of human annulus fibrosus under tensile load. J Biomech. 2006;39:1410–1418. doi: 10.1016/j.jbiomech.2005.04.007. [DOI] [PubMed] [Google Scholar]
- Guerin HL, Elliott DM. Quantifying the contributions of structure to annulus fibrosus mechanical function using a nonlinear, anisotropic, hyperelastic model. J Orthop Res. 2007;25:508–516. doi: 10.1002/jor.20324. [DOI] [PubMed] [Google Scholar]
- Guo ZY, Peng XQ, Moran B. A composites-based hyperelastic constitutive model for soft tissue with application to the human annulus fibrosus. J Mech Phys Solids. 2006;54:1952–1971. [Google Scholar]
- Holzapfel GA. Nonlinear solid mechanics: a continuum approach for engineering. Wiley; West Sussex: 2000. p. 455. [Google Scholar]
- Holzapfel GA, Schulze-Bauer CA, Feigl G, Regitnig P. Single lamellar mechanics of the human lumbar anulus fibrosus. Biomech Model Mechanobiol. 2005;3:125–140. doi: 10.1007/s10237-004-0053-8. [DOI] [PubMed] [Google Scholar]
- Klisch SM, Lotz JC. Application of a fiber-reinforced continuum theory to multiple deformations of the annulus fibrosus. J Biomech. 1999;32:1027–1036. doi: 10.1016/s0021-9290(99)00108-6. [DOI] [PubMed] [Google Scholar]
- Marchand F, Ahmed AM. Investigation of the laminate structure of lumbar disc annulus fibrosus. Spine. 1990;15:402–410. doi: 10.1097/00007632-199005000-00011. [DOI] [PubMed] [Google Scholar]
- Mauck RL, Yuan X, Tuan RS. Chondrogenic differentiation and functional maturation of bovine mesenchymal stem cells in long-term agarose culture. OA&C. 2006;14:179–189. doi: 10.1016/j.joca.2005.09.002. [DOI] [PubMed] [Google Scholar]
- Mauck RL, Byers BA, Yuan X, Tuan RS. Regulation of cartilaginous ECM gene transcription by chondrocytes and MSCs in 3D culture in response to dynamic loading. Biomech Model Mechanobiol. 2007;6:113–125. doi: 10.1007/s10237-006-0042-1. [DOI] [PubMed] [Google Scholar]
- Mauck RL, Baker BM, Nerurkar NL, et al. Engineering on the straight and narrow: the mechanics of nanofibrous assemblies for fiber-reinforced tissue regeneration. Tissue Eng Part B Rev. 2009;15:171–193. doi: 10.1089/ten.teb.2008.0652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nerurkar NL, Elliott DM, Mauck RL. Mechanics of oriented electrospun nanofibrous scaffolds for annulus fibrosus tissue engineering. J Orthop Res. 2007;25:1018–1028. doi: 10.1002/jor.20384. [DOI] [PubMed] [Google Scholar]
- Nerurkar NL, Mauck RL, Elliott DM. ISSLS prize winner: integrating theoretical and experimental methods for functional tissue engineering of the annulus fibrosus. Spine (Phila Pa 1976) 2008;33:2691–2701. doi: 10.1097/BRS.0b013e31818e61f7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nerurkar NL, Baker BM, Sen S, et al. Nanofibrous biologic laminates replicate the form and function of the annulus fibrosus. Nat Mater. 2009;8:986–992. doi: 10.1038/nmat2558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nerurkar NL, Sen S, Huang AH, et al. Engineered disc-like angle-ply structures for intervertebral disc replacement. Spine (Phila Pa 1976) 2010;35:867–873. doi: 10.1097/BRS.0b013e3181d74414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nerurkar NL, Han W, Mauck RL, Elliott DM. Homologous structure-function relationships between native fibrocartilage and tissue engineered from MSC-seeded nanofibrous scaffolds. Biomaterials. 2011;32:461–468. doi: 10.1016/j.biomaterials.2010.09.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Connell GD, Sen S, Baker BM, et al. Biaxial mechanics of native and engineered fiber-reinforced musculoskeletal tissues. Proceedings of ASME 2007 summer bioengineering conference; Keystone, CO. 2007. [Google Scholar]
- O’Connell GD, Guerin HL, Elliott DM. Theoretical and uniaxial experimental evaluation of human annulus fibrosus degeneration. J Biomech Eng. 2009;131:111007. doi: 10.1115/1.3212104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogden RW. Non-linear elastic deformations 1997 [Google Scholar]
- Peltz CD, Perry SM, Getz CL, Soslowsky LJ. Mechanical properties of the long-head of the biceps tendon are altered in the presence of rotator cuff tears in a rat model. J Orthop Res. 2009;27:416–420. doi: 10.1002/jor.20770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith LJ, Fazzalari NL. The elastic fibre network of the human lumbar anulus fibrosus: architecture, mechanical function and potential role in the progression of intervertebral disc degeneration. Eur Spine J. 2009;18:439–448. doi: 10.1007/s00586-009-0918-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spencer AJM. Deformations of fibre-reinforced materials. Oxford University Press; 1972. p. 128. [Google Scholar]
- Sun DD, Leong KW. A nonlinear hyperelastic mixture theory model for anisotropy, transport, and swelling of annulus fibrosus. Ann Biomed Eng. 2004;32:92–102. doi: 10.1023/b:abme.0000007794.87408.1e. [DOI] [PubMed] [Google Scholar]
- Wagner DR, Lotz JC. Theoretical model and experimental results for the nonlinear elastic behavior of human annulus fibrosus. J Orthop Res. 2004;22:901–909. doi: 10.1016/j.orthres.2003.12.012. [DOI] [PubMed] [Google Scholar]
- Wagner DR, Reiser KM, Lotz JC. Glycation increases human annulus fibrosus stiffness in both experimental measurements and theoretical predictions. J Biomech. 2006;39:1021–1029. doi: 10.1016/j.jbiomech.2005.02.013. [DOI] [PubMed] [Google Scholar]