Haplotype-based methods for detecting uncommon causal variants with common SNPs

Abstract

Detecting uncommon causal variants (minor allele frequency (MAF) < 5%) is difficult with commercial single-nucleotide polymorphism (SNP) arrays that are designed to capture common variants (MAF > 5%). Haplotypes can provide insights into underlying linkage disequilibrium (LD) structure and can tag uncommon variants that are not well tagged by common variants. In this work, we propose a wei-SIMc-matching test that inversely weights haplotype similarities with the estimated standard deviation of haplotype counts, to boost the power of similarity-based approaches for detecting uncommon causal variants. We then compare the power of the wei-SIMc-matching test with that of several popular haplotype-based tests, including four other similarity-based tests, a global score test for haplotypes (global), a test based on the maximum score statistic over all haplotypes (max), and two newly proposed haplotype-based tests for rare variant detection. With systematic simulations under a wide range of LD patterns, the results show that wei-SIMc-matching and global are the two most powerful tests. Among these two tests, wei-SIMc-matching has reliable asymptotic P values, whereas global needs permutations to obtain reliable P values when the frequencies of some haplotype categories are low or when the trait is skewed. Therefore, we recommend wei-SIMc-matching for detecting uncommon causal variants with surrounding common SNPs, in light of its power and computational feasibility.

Introduction

In the past few years, genome-wide association studies (GWAS) have identified hundreds of common genetic variants (minor allele frequency (MAF) > 5%) for complex human diseases. However, these common variants can only explain a small proportion of heritability [Manolio, et al. 2009]. Uncommon variants (MAF < 5%) are likely to play an important role in the missing heritability that cannot be explained by common variants. In this work, we call the variants with MAF < 5% ‘uncommon variants’, including the so-called ‘rare variants’ (MAF < 1%) and ‘low-frequency variants’ (MAF 1%–5%) [Zeggini 2011]. Searching for uncommon variants that are responsible for complex diseases is now attracting more attention [Zeggini 2011]. However, this topic remains challenging. When sequencing data are available, pooling signals of multiple uncommon variants and testing the association of this pooled set with the disease [Han and Pan 2010; Li and Leal 2008; Madsen and Browning 2009; Morris and Zeggini 2010; Price, et al. 2010] is an attractive strategy [Lin, et al. 2011]. However, due to the high cost of sequencing [Sboner, et al. 2011], GWAS data are still the most commonly available data in the current stage [Li, et al. 2010; WTCCC 2007]. For GWAS using commercial single-nucleotide polymorphism (SNP) arrays, the pooling methods are underpowered in detecting uncommon causal variants as they pool signals of common SNPs that cannot well represent the information of uncommon variants (this argument should be apparent and the pooling methods were mainly proposed for sequencing data with rare variants, but we still include them into the following comparisons). Similarly, conventional single-marker analysis is also underpowered because markers in commercial SNP arrays cannot be good surrogates for causal variants that are too rare [Gusev, et al. 2011].

Haplotypes can provide insights into underlying linkage disequilibrium (LD) structure and can tag uncommon causal variants that are not well tagged by common SNPs [Gusev, et al. 2011; Li, et al. 2010]. For some complex diseases such as hypertension, rare haplotypes have been shown to influence the disease susceptibility [Kitsios and Zintzaras 2010; Liu, et al. 2005; Zhu, et al. 2005]. A recent study has shown that identical-by-descent haplotype mapping is powerful for tagging rare variants [Gusev, et al. 2011]. In addition, similarity-based approach has been used in uncommon and common variant detection [Tzeng, et al. 2011]. These studies suggest that similarity-based approaches might be also useful, to some extent, in detecting uncommon causal variants using nearby common SNPs.

In this work, we propose a ‘wei-SIMc-matching’ test, to capture the signals of uncommon causal variants using haplotype information. We inversely weight haplotype similarities with the estimated standard deviation of haplotype counts, to boost the power of similarity-based approaches for detecting uncommon causal variants. We then compare the performance of wei-SIMc-matching with that of several popular haplotype methods. We show that although commercial SNP arrays are not designed to capture uncommon causal variants, some haplotype methods including the proposed wei-SIMc-matching test have a better ability to complement this.

Methods

(I) Similarity-based tests

Statistical model

Let y_i be the phenotype of the i^th subject (i = 1, …, N), and let Γ(h_i) be a k×1 vector coding the frequencies of all ‘haplotype categories’ for the i^th subject, where k is the number of ‘haplotype categories’ (i.e., unique haplotypes in the sample, two haplotypes are classified into a same category if all observed alleles on the two haplotypes are the same). For example, if there are three categories of haplotypes {h¹,h²,h³} and both of the haplotypes of the i^th subject are h¹, then Γ(h_i)^T = [1 0 0], where Γ(h_i)^T is the transpose of Γ(h_i). If one haplotype is h² and the other is h³, then Γ(h_i)^T = [0 0.5 0.5]. When the haplotype phase is uncertain, statistical methods such as the expectation-maximization (EM) algorithm [Dempster, et al. 1977] can be used to infer the haplotype frequency vector, under the assumption of Hardy-Weinberg equilibrium (HWE) [Excoffier and Slatkin 1995; Hawley and Kidd 1995; Long, et al. 1995].

We consider a generalized linear model:

$$g(E(\mathit{Y}))=\mathit{C}\mathit{\alpha }+\mathit{x}\beta ,$$ (1)

where g(·) is a link function, Y is an N-length vector of phenotypes, C is an N×(m+1) matrix with the i^th row of c_i^T = [1 c_i,1 c_i,2 ⋯ c_i,m] coding 1 (for the intercept term) and m covariates (e.g., age, gender, ethnicity, etc.) of the i^th subject, α is the (m+1) -element vector of covariate effects including the intercept term, x is an N-length vector with the i^th element of x_i = γ^T · S · Γ(h_i) coding the genetic information (regarding the region under investigation) of the i^th subject, and β is the regression coefficient of the genetic information coded by x. The scalar x_i = γ^T · S · Γ(h_i) is a quantity comparing the i^th subject’s haplotypes against haplotypes of all the other subjects, in which Γ(h_i) is the haplotype frequency vector of the i^th subject, γ is a specified vector aggregating the haplotype information of all the N subjects, and S is a k×k matrix whose (υ, ν) element is the similarity between the υ^th and ν^th categories of haplotypes. The canonical link is the logit function $(g(\mu )=\text{log}\frac{\mu }{1-\mu })$, the identity function (g(μ) = μ), and the log function (g(μ) = log μ) given binary traits, normally-distributed traits, and traits with Poisson distribution, respectively [Nelder and Wedderburn 1972].

Test statistics

Based on the model in Eq. (1) and under the assumption of gene-covariate independence, the score statistic is

$$U={\mathit{\gamma }}^{\mathbf{T}}·\mathrm{S}·{\displaystyle \sum _{i=1}^N}\frac{(y_i-{\mathrm{\mu ̂}}_i)}{a(\varphi )}\mathbf{\Gamma }(h_i),$$ (2)

where μ̂_i = c_i^T (C^TC)⁻¹ (C^TY) is the fitted value of the i^th subject according to the covariates; a (ϕ) is the mean square error (MSE) if the trait distribution is normal, and is 1 if the trait distribution is Bernoulli or Poisson [Nelder and Wedderburn 1972]. With different specification of γ, the score statistic can result in different tests.

When we specify $\mathit{\gamma }=\frac{1}{N}{\displaystyle {\sum }_{i=1}^N}\mathbf{\Gamma }(h_i)\equiv \mathit{p̂}$, where p̂ is the vector of the average haplotype frequencies of all the N subjects, the resulting test is called SIMp with the test statistic

$$T_{\mathit{\text{SIMp}}}=\frac{{[{\mathit{p̂}}^{\mathbf{T}}\mathrm{S}{\displaystyle \sum _{i=1}^N}\frac{(y_i-{\mathrm{\mu ̂}}_i)}{a(\varphi )}\mathbf{\Gamma }(h_i)]}^2}{{\mathit{p̂}}^{\mathbf{T}}\mathrm{S}\mathrm{\Omega ̂}\mathrm{S}\mathit{p̂}},$$ (3)

where Ω̂ is the estimated variance-covariance matrix of ${\displaystyle \sum _{i=1}^N}\frac{(y_i-{\mathrm{\mu ̂}}_i)}{a(\varphi )}\mathbf{\Gamma }(h_i)$ [Lin, et al. 2012] and

$$\mathrm{\Omega ̂}={\displaystyle \sum _{i=1}^N}[\frac{(y_i-{\mathrm{\mu ̂}}_i)}{a(\varphi )}\mathbf{\Gamma }(h_i)]{[\frac{(y_i-{\mathrm{\mu ̂}}_i)}{a(\varphi )}\mathbf{\Gamma }(h_i)]}^{\mathbf{T}}-\frac{1}{N}[{\displaystyle \sum _{i=1}^N}\frac{(y_i-{\mathrm{\mu ̂}}_i)}{a(\varphi )}\mathbf{\Gamma }(h_i)]{[{\displaystyle \sum _{i=1}^N}\frac{(y_i-{\mathrm{\mu ̂}}_i)}{a(\varphi )}\mathbf{\Gamma }(h_i)]}^{\mathbf{T}}.$$

Because T_SIMP is the square of a standard normal variable, it has an asymptotic χ² distribution with one degree of freedom.

When we specify $\mathit{\gamma }={\displaystyle \sum _{i=1}^N}\frac{(y_i-{\mathrm{\mu ̂}}_i)}{a(\varphi )}\mathbf{\Gamma }(h_i)$, the resulting test is called SIMc with the test statistic

$$T_{\mathit{\text{SIMc}}}={[{\displaystyle \sum _{i=1}^N}\frac{(y_i-{\mathrm{\mu ̂}}_i)}{a(\varphi )}\mathbf{\Gamma }(h_i)]}^{\mathbf{T}}\mathrm{S}[{\displaystyle \sum _{i=1}^N}\frac{(y_i-{\mathrm{\mu ̂}}_i)}{a(\varphi )}\mathbf{\Gamma }(h_i)].$$ (4)

By the theory of quadratic forms of normal variables [Scheffe 1959], T_SIMc is asymptotically distributed as ${\displaystyle {\sum }_{i=1}^{\varpi }}{\lambda }_i{\chi }_{1,i}^2,\text{ where }{\chi }_{1,i}^2$ ’s are independent χ² variables with one degree of freedom, and λ₁ ≥ λ₂ ≥ ⋯ ≥ λ_ϖ are the ordered eigen values of the matrix Ω̂S (ϖ is the rank of the matrix Ω̂S). The distribution of T_SIMc can be approximated by the three-moment approximation method [Allen and Satten 2007; Allen and Satten 2009; Imhof 1961; Tzeng, et al. 2009]. The P value of the observed SIMc test statistic is given by

$$P({\chi }_b^2>(T_{\mathit{\text{SIMc}}}-c_1)\times \sqrt{\frac{b}{c_2}}+b),$$

where $c_j={\displaystyle {\sum }_{i=1}^{\varpi }}{\lambda }_i^j,b=\raisebox{1ex}{$c_2^3$}\!\left/ \!\raisebox{-1ex}{$c_3^2$}\right.,\text{ and }{\chi }_b^2$ is the χ² distribution with b degrees of freedom.

The similarity matrix S can be constructed based on metrics such as the counting measure or the matching measure [Tzeng, et al. 2003]. The counting measure calculates the percentage of alleles in common between any two haplotypes; the matching measure treats each haplotype as a distinct category and is defined as 1 if two haplotypes match and 0 otherwise. Therefore, the similarity matrix S is a matrix with all diagonal elements of 1 and all off-diagonal elements of 0, if the matching measure is employed. Both the two similarity-based tests (SIMp and SIMc) can be respectively equipped with the counting measure and the matching measure, resulting in four tests (SIMp-counting, SIMp-matching, SIMc-counting, and SIMc-matching).

Weighting similarities

Previous studies show that uncommon causal variants usually have larger effect sizes compared to common causal variants [Bodmer and Bonilla 2008]. Moreover, uncommon variants are more likely to be tagged by uncommon haplotypes than by common haplotypes. Therefore, up-weighting uncommon haplotypes may facilitate the discoveries of uncommon variants. Li et al. [2010] defined S_h = [N_ct · f_ct,h · (1 − f_ct,h)]^−½ (h=1, …, k, in which k is the number of haplotype categories), where N_ct is the number of controls; f_ct,h is the adjusted frequency of haplotype h among controls and is quantified as $f_{\mathit{\text{ct}},h}=\frac{(C_{\mathit{\text{ct}},h}+1)}{(2N_{\mathit{\text{ct}}}+2)}$, in which C_ct,h is the number of haplotype h among controls. We let the k×k similarity matrix S be a diagonal matrix with the h^th diagonal element of S_h = [N_ct · f_ct,h · (1 − f_ct,h)]^−½, where h=1, 2, …, k. When continuous traits are analyzed, we let S_h = [N · f_ct,h · (1 − f_h)]^−½, where N is the total number of subjects and $f_h=\frac{(C_h+1)}{(2N+2)}$, in which C_h is the number of haplotype h among all the N subjects.

We plug this similarity matrix S into Eq. (4), and the resulting test is referred to as the wei-SIMc-matching test. It is based on the SIMc test with the matching measure inversely weighted by the estimated standard deviation of haplotype counts. The weighting scheme given to haplotypes is inspired from Madsen and Browning’s weights for SNPs [Madsen and Browning 2009]. Using this weight in S implies that we up-weight the similarities contributed by uncommon haplotypes but down-weight the similarities contributed by common haplotypes. Presumably, wei-SIMc-matching can boost the power of similarity-based approaches for detecting uncommon causal variants. We will evaluate its performance with simulations.

(II) Standard haplotype regression tests

A global score test for haplotypes (global) and a test based on the maximum score statistic over all haplotypes (max) have been widely used for detecting common variants [Schaid, et al. 2002]. The global test is regarded as a standard haplotype regression and is usually compared with similarity-based tests [Lin and Schaid 2009; Lin, et al. 2012; Tzeng, et al. 2009; Tzeng, et al. 2011]. The global and max tests are based on a generalized linear model:

$$g(E(\mathit{Y}))=\mathit{C}\mathit{\eta }+\mathbf{\Im }\mathit{\psi },$$ (5)

where g(·) is a link function, ℑ is an N×k matrix with the i^th row of Γ(h_i)^T (the transpose of the haplotype-frequency vector of the i^th subject), η is the (m+1) -element vector of covariate effects including the intercept term, and ψ is the k-element vector of the regression coefficients for the k categories of haplotypes in the region. Let U_ψ be the score vector of ψ, and V_ψ be the variance-covariance matrix of U_ψ. The global score statistic is $T_{\mathit{\text{global}}}={\mathit{U}}_{\mathit{\psi }}^{\mathit{T}}{\mathit{V}}_{\mathit{\psi }}^{\mathit{-}\mathit{1}}{\mathit{U}}_{\mathit{\psi }}$, which has an asymptotic χ² distribution with degrees of freedom equal to the rank of V_ψ [Schaid, et al. 2002].

The maximum score statistic over all haplotypes is $T_{\text{max}}=\underset{k}{\text{max}}\left(\raisebox{1ex}{${\mathit{U}}_{\mathit{\psi },\mathit{\kappa }}^{\mathit{2}}$}\!\left/ \!\raisebox{-1ex}{${\mathit{V}}_{\mathit{\psi },\mathit{\kappa },\mathit{\kappa }}$}\right.\right)$, where U_ψ,κ is the k^th element of U_ψ and V_ψ,κκ is the (k, k) element of V_ψ. There is no analytic form for the distribution function of the max test statistic, so permutation P values are used in practice [Schaid, et al. 2002].

(III) Haplotype-based tests to detect rare variants

Recently, two haplotype-based tests were proposed for rare variant detection. Both the two tests split the data into a training set and a testing set. Zhu et al.’s haplotype grouping test (referred to as ‘HG’) classifies haplotypes as risk or non-risk with the training set (the co-classification stage), and then tests for associations by performing a Fisher’s exact test with the testing set (the association stage) [Zhu, et al. 2010]. This method has been applied to the Wellcome Trust Case Control Consortium (WTCCC) data [Feng and Zhu 2010]. Li et al.’s weighted haplotype test on genotyped SNPs (referred to as ‘WHG’) is based on a similar procedure. The WHG further boosts power to detect rare variants by weighting haplotypes according to their frequencies [Li, et al. 2010]. For both HG and WHG, we followed Li et al. [2010] to randomly select 30% of the sample as the training set and let the remaining 70% be the testing set.

Simulation study

Following Li et al.’s simulation [2010], we first generated 200 data sets each containing 10,000 chromosomes of 1 Mb regions with the Cosi program [Schaffner, et al. 2005]. The chromosomes were generated in consistency with the HapMap CEU (CEPH people from Utah, U.S.A., http://hapmap.ncbi.nlm.nih.gov/) samples. For each data set, we randomly picked an ~50 kb region as the causal region, within the 1 Mb region. Within each causal region, we randomly selected d variants with population MAF between 0.1% and 5% (d=5, 10, 20, 30, or 40), and we treated these variants as causal variants that might increase or decrease the disease risk (or the value of a continuous trait). Among the d causal variants, we let r% of them increase the disease risk while the remaining (100 − r)% decrease the disease risk (or the value of a continuous trait). The value of r was specified at 5, 20, 50, 80, and 100, respectively. In each data set, we randomly chose 120 from the 10,000 chromosomes to mimic the Phase II HapMap CEU data, and these 120 chromosomes were randomly paired to form 60 subjects. Based on the LD patterns of the 60 subjects, tag SNPs were selected according to the conventional criterion of r² = 0.8 and MAF > 5% (many association studies for complex human diseases tend to use SNPs with MAF > 5% due to a power consideration [Barrett and Cardon 2006; Keating, et al. 2008]), with the H-clust method [Rinaldo, et al. 2005; Roeder, et al. 2005]. These tag SNPs were served as markers used in our simulations.

Binary traits

When evaluating the type-I error rates, the population attributable risk (PAR) was set at 0%. When evaluating the power, the PAR of each causal variant was set at 0.2%, 0.4%, 0.6%, 0.8%, and 1.0%, respectively. We follow previous studies [Li, et al. 2010; Madsen and Browning 2009] to assign larger genetic effects to rarer variants, because rare variants with a chance to be detected usually have larger effect sizes compared to common variants [Bodmer and Bonilla 2008]. The genotype relative risk (GRR) of a causal variant j with PAR of PAR_j and MAF of MAF_j is

$${\mathit{\text{GRR}}}_j={(\frac{{\mathit{\text{PAR}}}_j}{(1-{\mathit{\text{PAR}}}_j)·{\mathit{\text{MAF}}}_j}+1)}^{{(-1)}^{I({\xi }_j=1)}},$$ (6)

where I(ξ_j = 1) is the indicator function with a value of 1 or 0 according to whether the causal variant j decreases the disease risk or not. Given a value of PAR, the relationship between MAF and GRR depicted by Eq. (6) is shown in our supporting information (Supplementary Figures S1 and S2). In addition, we also show the distributions of MAFs and GRRs of the causal variants in our 200 simulated data sets in Supplementary Figures S3 and S4, respectively.

To generate chromosomes of one individual, we randomly selected two chromosomes from the remaining 9,880 (= 10,000 − 120) chromosomes. The disease status of an individual possessing two chromosomes {H₁,H₂} was determined by

$$P(\mathit{\text{affected}}|\{H_1,H_2\})=f_0\times {\displaystyle \prod _{k=1}^2}{\displaystyle \prod _{j=1}^d}{\mathit{\text{GRR}}}_j^{I(H_{k,j}=a_j)},$$ (7)

in which f₀ is the baseline penetrance, and a_j is the rare allele of the causal variant j. Following Li et al. [2010], we fixed f₀ at 10%. In each replication, we continued the sampling procedure until 1,000 cases and 1,000 controls were reached. After generating the disease status based on Eq. (7), the genotypes of all the causal variants were removed from our data sets. For each data set, we selected an analysis region with 20 tag SNPs, to encompass the d causal variants.

To account for the haplotype ambiguity, we first inferred haplotype phases from unphased multimarker genotypes with the EM algorithm, by using the ‘haplo.em’ function in the ‘haplo.stats’ package [Schaid, et al. 2002]. Note that all phasing algorithms assume Hardy-Weinberg equilibrium (HWE) [Excoffier and Slatkin 1995; Hawley and Kidd 1995; Long, et al. 1995], including the ‘haplo.em’ function. Following Schaid et al. [2002], we assumed HWE in the pooled sample of cases and controls, and then phased cases and controls together (phasing cases and controls together provides a better control of type-I error rates than phasing cases and controls separately [Lin and Huang 2007]). All possible haplotype pairs were considered with their posterior probabilities by treating the posterior probabilities as weights.

In addition to the nine haplotype-based tests, we also used the variable-threshold (VT) test program (http://genetics.bwh.harvard.edu/rare_variants/) to perform four pooling tests, including the fixed-threshold test with two thresholds of 1% and 5% [Morris and Zeggini 2010], the weighted-sum test [Madsen and Browning 2009], and the VT test [Price, et al. 2010]. With a preliminary simulation, we found that the VT test was generally the most powerful test among the four pooling tests. Therefore, in the following comparisons, we only present the result of the VT test [Price, et al. 2010] as a representative of the four pooling tests.

Continuous traits

We further generated a continuous trait (Y) by

$$Y=10C_1+10C_2+{\beta }_1{g}_1+{\beta }_2{g}_2+\cdots +{\beta }_d{g}_d+e,$$ (8)

where C₁ was a continuous covariate generated from a standard normal distribution, C₂ was a dichotomous covariate taking a value of 0 or 1 each with a probability of 0.5, g_j was the number of causal allele on the j^th causal variant (g_j = 0, 1, or 2), β_j was the effect size of the j^th causal variant, and e was the random error. The random error, e, was assumed to have a normal distribution with a mean of zero and a variance of V_e. The effect sizes β’s and V_e were determined so that the heritability of each variant (we call it ‘marginal heritability’) was fixed at 0.05%, 0.1%, 0.15%, or 0.2% under the alternative hypothesis. The relationship between MAFs and β’s was shown by our Supplementary Figure S5. The total sample size was set at 2,000. After generating the traits, the genotypes of all the causal variants were removed from our data sets. HG [Zhu, et al. 2010] and WHG [Li, et al. 2010] were proposed for case-control studies and so they were not included in the comparisons for analyzing continuous traits.

In addition to specifying a normally distributed error term (e), we also studied the situation when the random error came from a Gamma distribution with a shape parameter of 1 and a scale parameter of $\sqrt{V_e}$. The V_e and the effect sizes β’s (see Eq. (8)) were determined so that the marginal heritability was fixed at 0.05%, 0.1%, 0.15%, or 0.2% under the alternative hypothesis.

Simulation results

Type-I error rates

By setting the PAR or the marginal heritability at exactly 0%, we used the 200 simulated data sets to evaluate the type-I error rates. For each data set, 200 replications were performed. In the package ‘haplo.stats’, the default of the minimum number of counts for a haplotype to be included in the model is 5. Therefore, by default, haplotypes with frequencies less than ${\alpha }_0=0.125\%(=\raisebox{1ex}{$5$}\!\left/ \!\raisebox{-1ex}{$(2\times 2000)$}\right.$, where 2000 is the total number of subjects) would be lumped into a single baseline group when using the ‘haplo.stats’ package. To evaluate the influence of the choice of α₀, we specified α₀ = 0.125%, 0.25%, and 1%, respectively. The corresponding minimum numbers of counts for a haplotype to be included in the model were 5, 10, and 40, respectively.

For similarity-based tests, following a practical strategy to provide robustness to genotyping errors [Lin and Lee 2010; Lin and Schaid 2009; Sha, et al. 2007], we merged a haplotype with frequency less than a cutoff value α₀ with its most similar haplotype with frequency larger than α₀. This α₀ is not necessary to be identical to the α₀ used in ‘haplo.stats’. However, to have a parallel comparison, we here also let α₀ = 0.125%, 0.25%, and 1% (where 1% is the cutoff value suggested by Sha et al. [2007]), respectively.

Figure 1 presents the type-I error rates under various nominal significance levels, based on the 40,000 replications across the 200 simulated data sets, for each trait distribution and each α₀. When α₀ = 0.125% or 0.25%, the asymptotic results of the global test are somewhat conservative for binary trait (panels A and D), but anticonservative for the continuous trait with a normally distributed error term (panels B and E) and the continuous trait with a Gamma-distributed error term (panels C and F). When α₀ = 1%, the asymptotic results of the global test are valid for binary trait (panel G) and the continuous trait with a normally distributed error term (panel H), but still somewhat anticonservative for the continuous trait with a Gamma-distributed error term (panel I). All the other tests, including the global test based on permutation P values, are valid in the sense that their type-I error rates correspond to the nominal significance levels. To have a fair comparison in power, we use permutations to evaluate the statistical significance for the global test (permutations are also required for max and VT). In the following simulations, the significances of global and max are obtained with 1,000–20,000 permutations by a sequential Monte Carlo algorithm [Besag and Clifford 1991], according to the default of the package ‘haplo.stats’ [Schaid, et al. 2002]. Moreover, α₀ is specified at 0.125% in the following simulations (as the default cutoff value in ‘haplo.stats’) for the global, max, and the similarity-based tests.

Figure 1. Type-I error rates.

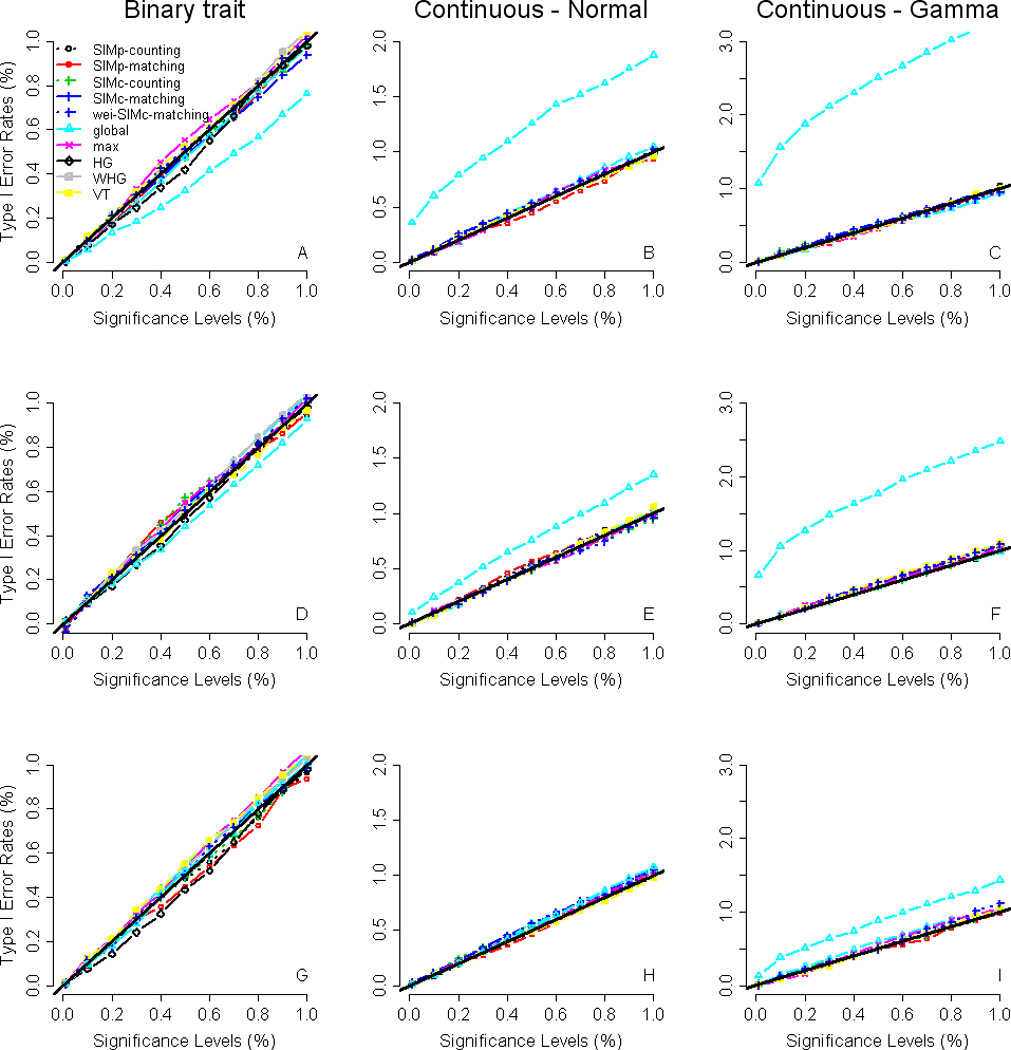
The x-axis is the nominal significance level (where the left-most point is 10⁻⁴ and the right-most point is 10⁻²), and the y-axis is the type-I error rate. The different panels in the figure are arranged such that the cutoff value of haplotype frequencies is 0.125%, 0.25%, and 1% (from top to bottom) and the trait is binary, continuous with a normally distributed error term, and continuous with a Gamma-distributed error term (from left to right). In each panel, there are two curves for the global test (one is based on asymptotic P values whereas the other is based on permutation P values). For panels G and H, both the two curves for the global test are on the line y = x (the black bold line). For other panels, the one on the line y = x is for the global test based on permutation P values and the one off the line y = x is for the global test with asymptotic P values. Note that the ranges of the y-axis for the three trait distributions are different in order to present the curve of the global test based on asymptotic P values.

Power comparisons - binary traits

Figure 2 presents the power averaged over the 200 data sets representing a wide range of LD patterns, when the trait is binary. For each scenario (each combination of r, PAR, and d) within each simulated data set, we performed 100 replications. The results show that the pooling methods such as the VT test are underpowered because they pool signals of common SNPs that do not well represent the information of uncommon variants. The global, wei-SIMc-matching, and max tests are the three most powerful tests. Specifically, the max test is slightly more powerful than the other two competitors when the PAR of each causal variant is smaller than or equal to 0.4% (the middle column of Figure 2) or when the number of causal variants is smaller than 20 (the right column of Figure 2). When there are more causal variants (d ≥ 20), there are usually more categories of disease-contributing haplotypes. In this situation, global, an omnibus test of all haplotype categories, is more powerful than max.

Figure 2. Comparison of power by r (the percent of high-risk variants among the d causal variants), PAR, and d (the number of causal variants), given a binary trait.

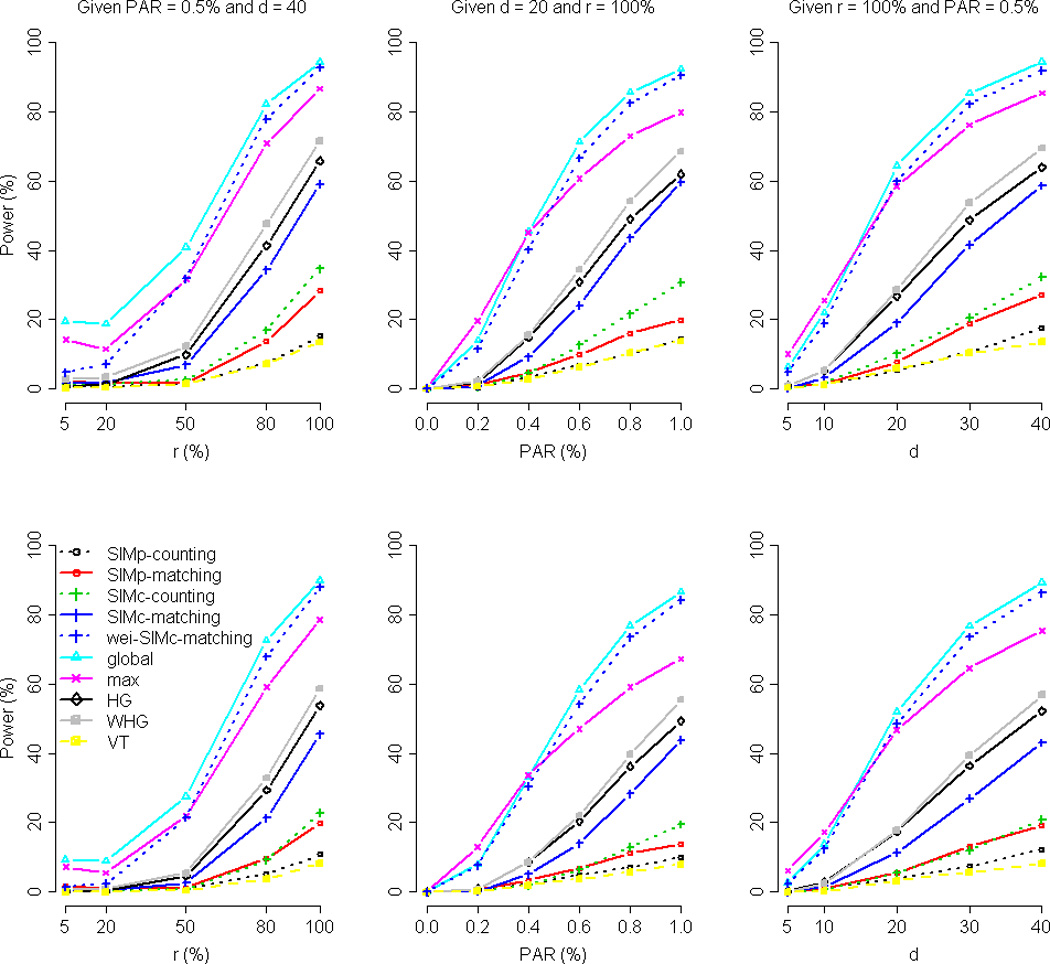
The figure shows the power comparison by r (the left column, given PAR = 0.5% and d = 40), PAR (the middle column, given d = 20 and r = 100%), and d (the right column, given r = 100% and PAR = 0.5%), respectively. The nominal significance levels were set at 10⁻³ (top row) and 10⁻⁴ (bottom row), respectively.

Overall, global is slightly more powerful than wei-SIMc-matching. The test statistic of SIMc is a summed product of genomic similarities and covariate-adjusted phenotypes (see Eq. (4)). When the causal variants are all uncommon (MAF < 5%), SIMc is underpowered because few subjects have the causal variants and most subjects are similar by having no causal variants. By contrast, global lets each haplotype category (common or uncommon, as long as the frequency is larger than the cutoff α₀) account for an equal ONE degree of freedom (see Eq. (3) of [Schaid, et al. 2002]). Therefore, the association of uncommon haplotypes is more likely to be detected by global, rather than by SIMc.

The wei-SIMc-matching test, a variant of SIMc, is thus developed to enhance the ability of similarity-based approach to detect uncommon causal variants. The weight used in the wei-SIMc-matching test is in the order of ½ from the binomial standard deviation viewpoint. Through this work, we see that the SIMc test with this weight on haplotypes still cannot compete with the global test, when all the causal variants are uncommon (MAF < 5%). A larger order of weight can further boost the power to detect uncommon causal variants, however it will inevitably suffer from power loss if there are some common causal variants in that region [Tzeng, et al. 2011].

Comparing SIMc with SIMp, the former is more powerful because it takes not only the within-group similarity but also the between-group similarity into considerations [Allen and Satten 2009; Lin, et al. 2012; Nolte, et al. 2007; Sha, et al. 2007]. SIMp has good power only when the causal variant was introduced at a common haplotype [Lin, et al. 2012]. In our simulations, the disease status was influenced by multiple variants that usually resulted in multiple disease-contributing haplotypes with low frequencies. Therefore, SIMp was underpowered in this situation. Comparing the counting measure with the matching measure, the latter is more powerful because it captures the information of identical-by-descent sharing more precisely [Lin and Lee 2010; Lin and Schaid 2009; Tzeng, et al. 2009].

HG [Zhu, et al. 2010] and WHG [Li, et al. 2010] were not as powerful as the global, wei-SIMc-matching, and max tests. A main reason is that the data were split into a training set and a testing set. Both HG and WHG can be improved by using the entire sample for the co-classification stage and the same entire sample for the association stage, with permutations to adjust for the statistical significance. This strategy is computationally feasible when handling only top genes [Feng and Zhu 2010]. However, it is computationally demanding for our comprehensive simulations.

Power comparisons - continuous traits

Figure 3 presents the power averaged over the 200 data sets when the trait is continuous (100 replications for each scenario within each data set), given the nominal significance level of 10⁻³. The result given the nominal significance level of 10⁻⁴ is presented in Supplementary Figure S7. When the error term is simulated from a normal distribution, the wei-SIMc-matching, global, and max tests are, again, the three most powerful tests. The global test is more robust to the percent of variants among the d causal variants that increase the trait value (the left upper panel of Figure 3). The global and max tests are slightly more powerful than the wei-SIMc-matching test when the marginal heritability of each causal variant is smaller than or equal to 0.1% (the middle upper panel of Figure 3) or when the number of causal variants is smaller than or equal to 20 (the right upper panel of Figure 3).

Figure 3. Comparison of power by r (the percent of variants among the d causal variants that increase the trait value), the marginal heritability, and d (the number of causal variants), given a continuous trait.

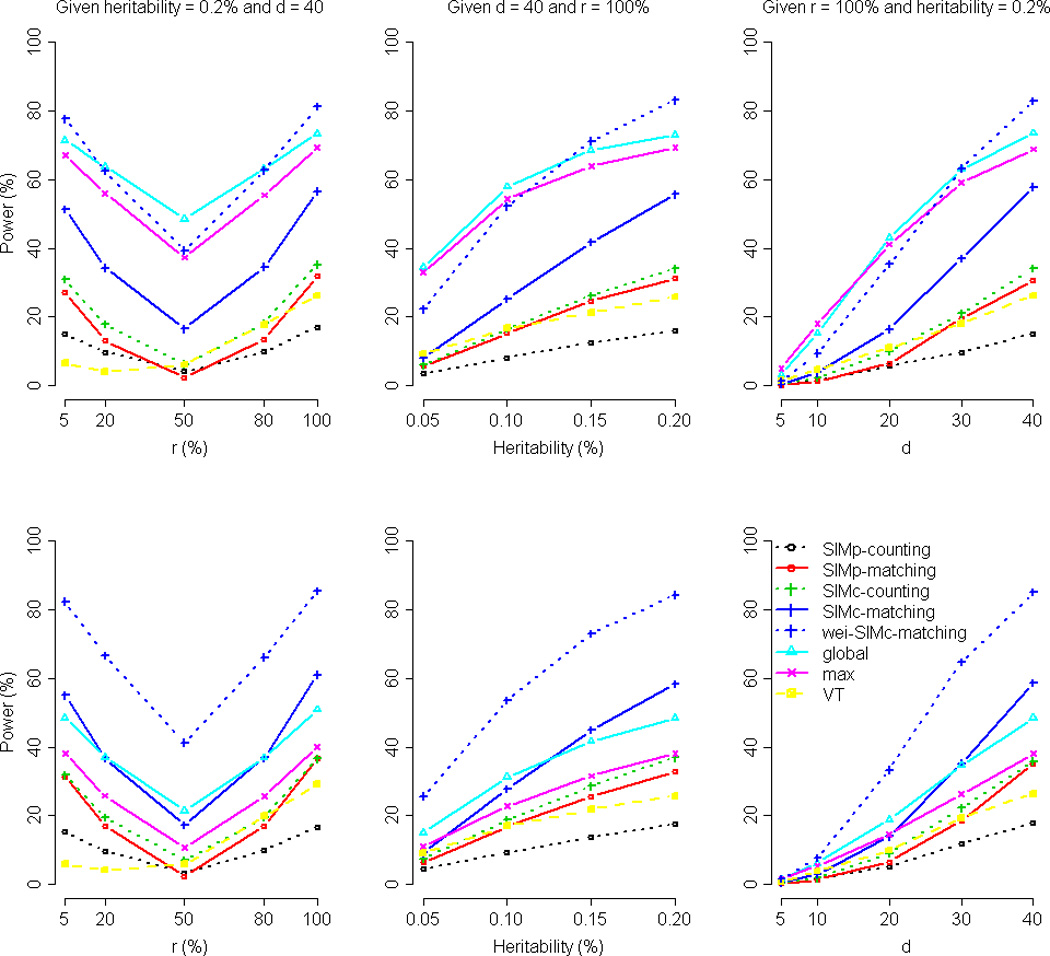
The figure shows the power comparison by r (the left column, given the marginal heritability = 0.2% and d = 40), the marginal heritability (the middle column, given d = 40 and r = 100%), and d (the right column, given r = 100% and the marginal heritability = 0.2%), respectively. The nominal significance level was set at 10⁻³. The trait is continuous with a normally distributed error term (top row) and continuous with a Gamma-distributed error term (bottom row), respectively. The result given the nominal significance level of 10⁻⁴ is shown by Supplementary Figure S7.

Note that different from other tests, the power of the VT test is not V-shaped, when the x-axis is the percent of variants among the d causal variants that increase the trait value (the first columns of Figure 3 and Supplementary Figure S7). This is because VT performs a right-tailed test in the program (http://genetics.bwh.harvard.edu/rare_variants/). Revising it to a two-tailed test can improve its power under a small r (the percent of variants among the d causal variants that increase the trait value).

When the error term is simulated from a Gamma distribution, wei-SIMc-matching is consistently the best method under all scenarios we evaluated (the bottom rows of Figure 3 and Supplementary Figure S7). In the package ‘haplo.stats’, the only choice of trait type for a continuous trait is ‘gaussian’. Therefore, we also specify ‘gaussian’ as the trait type, when analyzing the continuous trait with a Gamma-distributed error term. Because the trait is skewed and is not following the normal (gaussian) distribution, the global and max tests (both performed with the package ‘haplo.stats’) suffer from power loss. This problem can be remedied by taking a logarithmic transformation on the trait. However, the skewness of an error term is not always easy to be recognized from the observed trait values. By contrast, the performances of the similarity-based tests are robust to the distribution of the traits (comparing the top rows and the bottom rows of Figure 3 and Supplementary Figure S7).

We also present the power stratified by the marginal heritability (given d = 40, and r = 100%) and then sorted by the percent of rare causal variants with MAF < 0.5% (top rows of Supplementary Figures S10–S11). Given many rare causal variants (MAF < 0.5%), wei-SIMc-matching is underpowered because very few subjects have the causal variants and most subjects are similar by having no causal variants. Furthermore, we also sorted the power by the LD pattern between the causal variants and the surrounding markers (bottom rows of Supplementary Figures S10–S11). As expected, the power of all the tests improves as the average r² increases. Generally speaking, global is more powerful than wei-SIMc-matching when the average r² is smaller, whereas wei-SIMc-matching is more powerful when the average r² is larger (d = 40, the average r² was obtained by averaging the 40×20 r²’s of any one causal variant and each of the 20 surrounding markers).

Choice of the cutoff valueα₀

In the above power comparisons, the cutoff value for haplotype frequencies was set at α₀ = 0.125%, the default value used in ‘haplo.stats’. The haplotypes with frequencies less than α₀ were pooled into a single baseline group when we used ‘haplo.stats’. Besides, in the similarity-based tests, a haplotype with frequency less than α₀ was merged with its most similar haplotype with frequency larger than α₀. Because the matching measure is a phase-dependent metric, the choice of α₀ may affect the performance of the SIMp-matching, SIMc-matching, and wei-SIMc-matching tests. To evaluate the influence on power of the five tests (global, max, SIMp-matching, SIMc-matching, and wei-SIMc-matching tests) with a different α₀, we further performed simulations with α₀ = 1%. In Supplementary Figures S12–S14, we compare the result given α₀ = 0.125% with that given α₀ = 1%.

When analyzing binary traits (Supplementary Figures S12), all the five tests (global, max, SIMp-matching, SIMc-matching, and wei-SIMc-matching tests) became less powerful given an increased α₀ of 1%. As shown by Supplementary Figures S3, among all the causal variants in our simulation, the percent of rare causal variants (MAF < 1%) is 73.7%, whereas the percent of extremely rare causal variants (MAF < 0.125%) is 18.5%. The power loss given an increased α₀ of 1% is expected because haplotypes with frequencies less than 1% are more likely to tag the rare causal variants (MAF < 1%). However, they are lumped into a single baseline group when performing global and max, or merged with other commoner haplotypes when performing the SIMp-matching, SIMc-matching, and wei-SIMc-matching tests.

When analyzing continuous traits, again, similarity-based tests have a decrease in power when α₀ is increased to 1%, especially for the wei-SIMc-matching test whose power is boosted from up-weighting the similarities contributed by uncommon haplotypes. For global and max, however, generally the power improves when α₀ is increased to 1%. This contradicts the previous result for binary traits. Scoring many rare haplotypes (frequencies between 0.125% and 1%) in a model may weaken the power of the global and max tests, although we are unclear why this phenomenon only appears in analyzing continuous traits. On average, in each replication, ~18 haplotypes with frequencies larger than 1% and ~20 haplotypes with frequencies between 0.125% and 1% (see Supplementary Figures S15–S16). Therefore, compared with α₀ = 1%, ~20 more haplotypes need to be scored in the model given α₀ = 0.125%. The many rare haplotypes (frequencies between 0.125% and 1%) may cause unstable estimation of the score vector U_ψ and/or the variance-covariance matrix V_ψ.

Computational burden

The computational burden to perform the wei-SIMc-matching test is reasonable because no permutation is required. When analyzing binary traits given PAR = 0.2%, d = 20, r = 100%, and the cutoff values for haplotype frequencies α₀ = 0.125%, the wei-SIMc-matching test on average takes respectively 0.9, 6.9, and 23.3 seconds for a 20-SNP multimarker set on 1000, 2000, and 3000 subjects, given an Intel Xeon workstation with 3.0 GHz of CPU and 2.0 GB of memory. The global test with 1,000–20,000 permutations on average takes 13.6, 61.3, and 145.9 seconds, for analyzing 1000, 2000, and 3000 subjects, respectively. The range of the required time for the global test is quite large (shown in Supplementary Figure S17), depending on the number of permutations (may range from 1,000 to 20,000) in each replication.

Summary of simulation results

The purposed wei-SIMc-matching test is among the most powerful tests for detecting uncommon causal variants (MAF < 5%), although it still cannot compete with the global test when most causal variants are very rare (MAF < 0.5%) or when the average r² between the causal variants and the surrounding markers is extremely low (≤ 0.01), as clearly shown by Supplementary Figure S10. However, the performance of the wei-SIMc-matching test is more robust to the trait distributions and the cutoff values for haplotype frequencies (α₀). Furthermore, it does not require permutations to obtain reliable statistical significance.

Application to a population-based resequencing study for the ANGPTL4 gene

We then applied the eight (for a continuous trait) or ten (for a binary trait) tests to a population-based resequencing study for the ANGPTL4 gene [Romeo, et al. 2007; Romeo, et al. 2009]. To understand the role of ANGPTL4 in lipid metabolism, Romeo et al. [2007; 2009] sequenced seven exons and the intron-exon boundaries of ANGPTL4. There were 3,551 subjects coming from a population-based probability sample of Dallas County residents, including 1,830 African Americans, 601 Hispanics, 1,045 European Americans, and 75 other ethnicities. In our analysis, we evaluated the performance of the various tests to detect associations between the plasma triglyceride levels and the uncommon variants in ANGPTL4, pretending that all the uncommon variants were not genotyped. We excluded the 75 subjects of other ethnicities from our analysis. Among the 93 variants, we kept two variants with MAF > 5% in the sample of the 3,476 (3,551 − 75 other ethnicities) subjects: P307P (MAF=6.6%) and P389P (MAF=6.5%). We deliberately excluded the variants with MAF less than 5% in order to mimic a commercial SNP array. To the best of our knowledge, E40K (MAF = 0.73%) and R278Q (MAF = 3.1%) are the only two variants reported to be associated with plasma triglyceride levels, based on the analyses for this resequencing data set [King, et al. 2010; Maxwell, et al. 2010; Romeo, et al. 2007; Yi, et al. 2011]. Our objective is to see whether the haplotype-based methods can detect the signal caused by the two reported uncommon variants (MAF < 5%), E40K and R278Q, which were both deliberately excluded from our analyses.

The log-transformed plasma triglyceride levels were first adjusted for age, sex, body-mass index (BMI), and ethnicity (including three levels: African American, Hispanic, and European American), by performing a linear regression of log-transformed plasma triglyceride levels on these four covariates. The residuals (y_i − μ̂_i) ’s were treated as continuous traits used in Eq. (3) and (4) to perform the similarity-based tests. Because there were 468 subjects missing in age or BMI, the actual number of subjects for the analysis of the continuous trait was 3,008 (= 3,551 − 75 − 468). Following Romeo et al. [2007], we also created a binary trait by coding subjects in the top and bottom quartiles of the residuals as 1 (755 subjects) and 0 (744 subjects), respectively. The remaining subjects were excluded from the analysis. Therefore, the number of subjects for the analysis of the binary trait was 1,499 (= 755+744). We then tested for the association between the continuous / binary trait and the haplotypes formed by the two variants (P307P and P389P). There were 93 variants, generating $4,278(=\left(\begin{array}{c}\hfill 93\hfill \\ \hfill 2\hfill \end{array}\right))$ possible combinations of any two variants. We set the significance level at $1.16\times {10}^{-5}(=\raisebox{1ex}{$0.05$}\!\left/ \!\raisebox{-1ex}{$4278$}\right.)$. The tests yielding significant results included SIMc-counting (P value of the analysis for the continuous / binary trait = 3.6×10⁻¹⁰ / 2.2×10⁻⁹), global (<10⁻⁶ / <10⁻⁶, with 10⁶ permutations), max (6×10⁻⁶ / 5×10⁻⁶, with 10⁶ permutations), and wei-SIMc-matching (6.3×10⁻⁶ / 1.8×10⁻⁵). The above four tests can detect the association between the plasma triglyceride levels and the uncommon variants in ANGPTL4 (E40K and R278Q [King, et al. 2010; Maxwell, et al. 2010; Romeo, et al. 2007; Yi, et al. 2011]), even when the uncommon variants were not genotyped. The results for the continuous trait and the binary trait were very similar.

Discussion

When performing haplotype-based tests, the question of how to choose the size of a multimarker set is still open [Schaid 2004]. Although we let 20 SNPs form a multimarker set in our simulations, we also performed simulations by using only 10 SNPs to form a set (Supplementary Figures S18–S20). The relative power performances were very similar to the results by using 20 SNPs, but generally each test was less powerful than that by using 20 SNPs in a multimarker set. This is because larger multimarker sets may allow for measuring sharing over longer genomic sequences and lead to more power gains [Allen and Satten 2009; Lin, et al. 2012].

Through systematic simulations while considering a wide range of LD patterns, we find that although wei-SIMc-matching cannot compete with global in some situations (especially when most causal variants are very rare (MAF < 0.5%) or when the average r² between the causal variants and the surrounding markers is extremely low (≤ 0.01), as shown by Supplementary Figure S10), it is one of the best approaches for detecting uncommon causal variants (MAF < 5%) with surrounding common SNPs (MAF > 5%). In addition to the power, the merits of wei-SIMc-matching also include its robustness to the trait distributions and the cutoff values for haplotype frequencies (α₀). Furthermore, it is computationally feasible in the sense that no permutation is required to obtain reliable P values.

Although max is slightly more powerful than global and wei-SIMc-matching under certain situations when analyzing binary traits, there is no analytic form for the distribution function of the max test statistic and permutation P values are required. Permutation procedure is also required to obtain more reliable P values for global, when the frequencies of some haplotype categories are low or when the trait is skewed (see our Figure 1 or [Schaid, et al. 2002]). When the significance level is much smaller than 0.05 as in whole-genome association studies, the estimation of P values with permutation procedures can be computationally challenging [Tong, et al. 2010]. By contrast, wei-SIMc-matching provides reliable asymptotic P values. As shown by Figure 1, its type-I error rates exactly correspond to the nominal significance levels.

The max test may not be very ideal because it evaluates the significance of a haplotype by assuming no effect of other haplotypes on the trait. Recall that the statistic for global is $T_{\mathit{\text{global}}}={\mathit{U}}_{\mathit{\psi }}^{\mathit{T}}{\mathit{V}}_{\mathit{\psi }}^{\mathit{-}\mathit{1}}{\mathit{U}}_{\mathit{\psi }}$, where U_ψ is the score vector evaluated at ψ = 0 (ψ_k = 0 for all k, in which ψ_k is the kth element of ψ). When performing max with the package ‘haplo.stats’, the test statistic is $T_{\text{max}}=\underset{k}{\text{max}}\left(\raisebox{1ex}{${\mathit{U}}_{\mathit{\psi },\mathit{\kappa }}^{\mathit{2}}$}\!\left/ \!\raisebox{-1ex}{${\mathit{V}}_{\mathit{\psi },\mathit{\kappa },\mathit{\kappa }}$}\right.\mathit{\right)}$, where U_ψ,κ is the k^th element of U_ψ that is evaluated at ψ_k = 0 for all k. It will be more precise to calculate the test statistic of max based on ${\mathit{U}}_{\mathit{\psi },\mathit{\kappa }}^{*}$ (instead of U_ψ,κ), where ${\mathit{U}}_{\mathit{\psi },\mathit{\kappa }}^{*}$ is evaluated at ψ_k = 0 and ψ_l = ψ̂₁ (l ≠ k, ψ̂_l is the maximum likelihood estimate of the effect of haplotype l in the unconstrained model). That is, ${\mathit{U}}_{\mathit{\psi },\mathit{\kappa }}^{*}$ evaluates the significance of haplotype k while leaving the effects of the rest of haplotypes unconstrained.

In conclusion, compared with the other tests considered in this work, the wei-SIMc-matching test is to be recommended for the detection of uncommon causal variants with surrounding common SNPs, in light of its power and computational feasibility.