Abstract
Dysregulated remodeling of the cervix precedes preterm birth, a major cause of infant mortality and morbidity. The goal of this work was to identify changes in the mechanical properties of the cervix in late gestation. The tensile and load relaxation properties of cervices from rats 15 days to 21 days (full term) post-conception were measured. Stiffness and load at 25% circumferential strain decreased with gestational age and correlated with the initial circumference of the cervix. Load-relaxation curves were accurately described by a seven parameter quasi-linear viscoelastic model, where three parameters associated with stiffness and load capacity decrease with gestational age and correlate with initial circumference. Time-dependent parameters did not depend on age or structure. Mechanical properties correlated with water content, but unexpectedly not with measures of collagen content, solubility, or organization. Quantitative measurements of cervical stiffness and structure will lead to a more accurate description of cervical remodeling and prediction of preterm birth.
Keywords: cervix, mechanical properties, stiffness, load relaxation, gestational age, structure
1. Introduction
Preterm birth is the leading contributor to infant mortality and morbidity. 12% of US births in 2010 delivered preterm, a moderate decline from 2006 levels but still well above rates in 1981 (Hamilton et al., 2011). The total societal cost of preterm birth was estimated in 2006 to be over $26 billion annually (Berhman and Butler, 2007). Preterm birth is a syndrome with a variety of causes. Mechanical failure of the cervix (called cervical incompetence or insufficiency) is one cause of preterm birth (Timmons et al., 2010). The cervix is the fibrous tissue at the base of the uterus. It serves two functions: first as a barrier between the developing fetus and the outside world, and second to maintain the fetus within the uterine cavity until the fetus is mature. At term, this tissue must deform to allow the fetus to pass. In the past decade, many studies have suggested that the cervix may be an important factor leading to successful outcome. The mechanical properties of the cervix are therefore one focus of strategies to predict preterm cervical remodeling leading to birth (McFarlin, 2009).
Multiple investigators have demonstrated that the cervix begins to transform early in pregnancy and continues to transform through delivery when it reverts back to its non-pregnant state. A variety of remodeling events occur with changes in macrostructure, microstructure, and biochemical makeup that are thought to contribute to changes in its mechanical properties (House et al., 2009b) (Timmons et al., 2010) (Mahendroo, 2012). The proteoglycan and water content increase with gestational age, while the total amount of collagen remains the same but is remodeled, resulting in a softer tissue (House et al., 2009b) (Mahendroo, 2012). The most established method to assess cervical remodeling in humans is also one of the oldest, most subjective, and least technological. The Bishop score (Bishop, 1964), obtained via a digital examination of the cervix, measures five characteristics: cervical position, softness, effacement (thinning and shortening), dilation, and fetal station (descent of the fetus into the pelvis), three of which relate to cervical remodeling: softness, effacement, and dilation (Bishop, 1964). The Bishop score was proposed as a way to predict the success of labor induction in multiparous women. It can be highly variable due to the subjective nature of each component (effacement, dilation, station, consistency, and position) and lack of precision.
More quantitative measures of cervical remodeling are necessary. Transvaginal ultrasound examinations and MRI of the human cervix indicate that the cervix begins to shorten from the internal os outwards (Hassan et al., 2000) (Hassan et al., 2006) (House et al., 2009a) (Iams, 2003). Thus, it is diffeicult for a clinician to detect some changes by digital examination. Transvaginal ultrasound measurements of cervical length have been used to identify cervical remodeling (Crane and Hutchens, 2008) (Chiossi et al., 2006) (Gomez et al., 2005) (Gramellini et al., 2007) (Hassan et al., 2000) (Hassan et al., 2006) (Iams et al. 1996) (Iams, 2003) (Newman et al., 2008) (Schmitz et al., 2008). Although ultrasound measurements of cervical structure (length and funneling) are useful for determining the risk of preterm delivery (Gomez et al., 1994) (Gomez et al., 2005) (Honest et al. 2003), these measurements alone have low positive predictive value (Gramellini et al., 2007) (Iams, 2003) and in many cases did not outperform the Bishop score in predicting preterm birth (Newman et al., 2008) (Schmitz et al., 2008). There is a need to develop techniques that detect tissue remodeling in the pregnant cervix before effacement and dilation occur.
Due to the risks of cervical tissue sampling during pregnancy, animal models have been used as surrogates for understanding physiological changes in the cervix associated with parturition (Mahendroo, 2012). As far back as the 1950s, Harkness and Harkness conducted tensile tests in load-control on pregnant rat cervices (Harkness and Harkness, 1959). A number of papers since then have reported mechanical properties of cervical tissue from rats (Hollingsworth et al., 1979) (Clark et al., 2006) (Drzewiecki et al., 2005), mice (Read et al., 2007) (Kokenyesi et al., 2004), sheep (Owiny et al., 1991), and humans harvested by biopsy (Rechberger et al., 1988) (Oxlund et al., 2010) or hysterectomy (Myers et al., 2008) (Myers et al. 2010). The wide range of testing procedures, time points, and measured properties make comparisons across the literature difficult. Furthermore, there is little direct comparison between mechanical, biochemical, and structural properties in the same sample.
The goal of this study was to identify the relationship between the mechanical properties of the rat cervix with measurements of structure and biochemical composition. The entire cervix was harvested from pregnant rats between days 15 and 21 (term) of gestation, a period comparable to the third trimester of pregnancy in humans. The lower half the cervix underwent displacement-controlled tensile and load-relaxation tests. The structural mechanical properties measured in these tests were compared with gestational age and structure (initial inner circumference). The results were also correlated with biochemical composition using the upper half of the cervix, including measures of water content, collagen content, soluble (uncrosslinked) collagen content, and collagen organization.
2. Methods
2.1 tissue collection
All procedures were approved by the Institutional Animal Care and Use Committee at the University of Illinois at Urbana-Champaign and by the Animal Care Committee at the University of Illinois at Chicago. After euthanasia with carbon dioxide, cervical tissue was immediately harvested from timed-pregnant Sprague-Dawley rats at 15 (n=6), 17 (n=7), 19 (n=7), and 21 (n=11) days post-conception, as defined by the breeder (Harlan Labs). The cervix was excised from the uterus at the transition zone where the more muscular lower segment transitions to a pale fibrous tissue. Each cervix was cut in half transversely, perpendicular to the cervical canal. The portion containing the internal os was sent for biochemical analysis (water and collagen), while the portion with the external os was used for mechanical testing (Figure 1a). All tissue was frozen at −80C.
Figure 1.
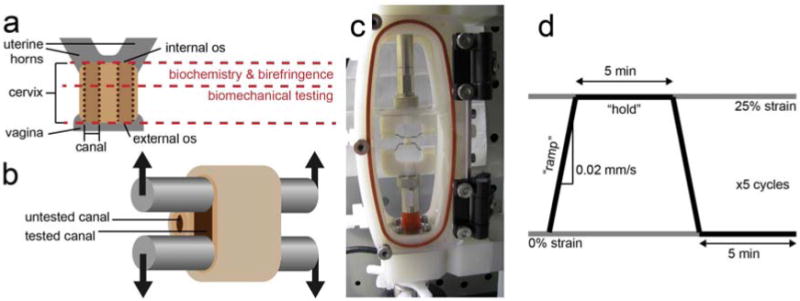
Illustration of the rat cervix (a). The cervix was removed and cut in half, perpendicular to the canals. The section near the internal os was used for biochemical composition and collagen organization using birefringence measurements, while the section near the external os was used for biomechanical testing. The rat cervix has two canals, indicated by the vertical dotted lines, one leading to each uterine horn. For biomechanical testing, stainless steel rods were threaded through a single canal (b). A photograph of the cervix positioned in the custom-designed fixture attached to the Bose Biodynamic test system, submerged in phosphate buffered saline (c). The displacement waveform applied to each specimen, where 25% circumferential strain was calculated from the distance between the rods (d). Samples were stretched at 0.02 mm/s in the “ramp” section, then kept at 25% strain for 5 min during the “hold.”
2.2 mechanical testing, initial circumference measurement
Cervices were thawed, brought to room temperature, and weighed before mechanical testing. A pair of 1.2 mm-diameter bent stainless steel rods (McMaster Carr) were threaded through a single canal of the cervix (Figure 1b). The rods were placed into a custom made fixture fabricated from VeroWhite polymer with an Eden 350 3D printing system (Objet Inc.). The fixture was designed to fit within an Electroforce Biodynamic test frame (Bose Corp.). The Electroforce system was fitted with a 1000 g load cell and sealed sample chamber for submerged testing. Testing was conducted within a 37°C incubator. Once the cervix was placed in the fixture, the distance between the rods was measured with calipers and the fluid chamber was filled with 37°C phosphate buffered saline (Lonza).
The test was conducted in displacement control using WinTest control software (Bose). The sample was preloaded to approximately 1 g above the load cell noise floor. At this point, the initial circumference was calculated from the measured rod spacing d0, the distance added with the control software d+, and the diameter of the rods: c0 = 2(d0 + d+) + 1.2π.
The testing protocol is illustrated in Figure 1c. Following 60 s of baseline recording, samples were stretched to 25% circumferential strain without preconditioning (Δd = .125c0) at a rate of 0.02 mm/s with data collection at 20 Hz (defined as the “ramp” section). A preconditioning cycle was not used because the majority of the cervix is not loaded in vivo, simulating the physiological state; a prestretched cervix in vivo would result in premature delivery. These data were used to calculate stiffness. To analyze load-relaxation properties, the displacement was then held for 5 min with data collection at 5 Hz (defined as the “hold” section), before ramping down at 0.02 mm/s and holding for another 5 min. Five cycles were recorded in total.
2.3 mechanical analysis
Load, time, and displacement data were imported into Matlab (The Mathworks) for analysis with custom-written code. Stiffness was defined as the linear region of the load-displacement curve at the end of each ramp and defined as force/displacement (g/mm). The linear region was automatically identified and fit using a least-squares approach with a custom-written Matlab program. The load-relaxation data were fit to a quasi-linear viscoelastic (QLV) model (Abramowitch and Woo, 2004) (Nekouzadeh et al., 2007) (Yang et al., 2006) using a least-squares method with a custom-written Matlab program. Further details are provided in Supplementary Materials. Because the data are in terms of force and displacement rather than stress and strain, the results below represent structural properties --inseparable from geometry -- rather than intrinsic material properties.
2.4 biochemical analysis
Tissue samples were thawed and weighed to determine the wet weight, then dehydrated in a freeze dryer for 24 h. The dry weight was obtained to determine water content.
Collagen solubility was determined by first freezing and pulverizing tissue samples. Extractable collagen was determined using the methods of Faris et al. (Faris et al., 1978). Weak acid extraction of non-crosslinked collagen was performed with approximately 20 mg of tissue (wet weight) suspended in 25 volumes of 0.5 M acetic acid in Tris-buffered saline for 24 h at 4°C. The supernatant containing weak acid extractable collagen was recovered by centrifugation at 15,000 g for 15 min. Pepsin extractable collagen was determined by suspending the remaining pellet in 0.5 M acetic acid with 1 mg/ml pepsin for 24 h at 4°C. The supernatant containing pepsin extractable collagen was recovered by centrifugation at 15,000 g for 15 min. The residual pellet was assayed for hydroxyproline as described below. Solubilized collagen was determined using Sircol Soluble Collagen Assay (Biocolor) according to manufacturer's instructions.
Nonsoluble collagen was determined using the method of Stegemann and Stalder to determine hydroxyproline content (Stegemann and Stalder, 1967). Briefly, the residual pellet was solubilized in 6 N HCl (100 μl/10 mg) at 110°C for 16 h. The solubilized hydroxyproline was determined by the DMB assay [ref different than above]. Collagen content was determined with the assumption that 13.4 wt % of collagen is hydroxyproline.
A subset of the samples (15 day n = 4, 17 day n = 6, 19 day n = 5, 21 day n = 7) were embedded in OCT, frozen, and sectioned in 7-8 μm slices with a Microm HM 505 N cryostat onto Superfrost Plus microscope slides (Cole-Parmer). The sections were stained with picrosirius red and analyzed via polarized light microscopy. Collagen birefringence was determined using an Olympus BX50 microscope with a polarizer/analyzer combination at 40× magnification. Two random images were taken from each quadrant of the cervix. The degree of organization as a percent area of the total image was determined using Metamorph software (Molecular Devices).
2.5 statistical analysis
All statistical analyses were computed using R software (R Development Core Team, 2010). Comparisons across gestational ages were made using one-way analysis of variance with Tukey post-hoc means comparison. These data were represented graphically with box plots, where horizontal bars indicate pairwise statistical differences with p < .05. The p value returned by the analysis of variance test is also displayed on each box plot. Pearson product moment correlations were used to compare measured mechanical, biochemical, and geometric properties with each other. These data were represented graphically with scatter plots, with the Pearson product moment correlation (denoted as ‘r’) and p value included on each plot. Again, p < .05 was considered statistically significant. In some cases, noted below, measured properties were log10-transformed prior to statistical analysis where doing so resulted in normally-distributed data and eliminated large differences in variance. Plots were created using the ggplot2 plugin (Wickham, 2009). Some labels and legends were modified and indicators for statistical significance were added with Illustrator (Adobe Systems Inc.). Where means are reported in the text, ± indicates standard deviation.
3. Results
3.1 geometry and mass
The mass of the portion of the cervix used for mechanical testing increased with gestational age (F = 11.776, p < .0001), from 45.50 mg ± 8.04 mg at 15 days to 84.53 mg ± 11.42 mg at 21 days. Tukey means comparison revealed that 15 day cervices weighed less than all other time points, but the mean mass of the 17, 19, and 21 day cervices were statistically indistinguishable (Figure 2a). Analysis of variance also showed that circumference increased with gestational age (F = 40.978, p < .0001), averaging 6.93 mm ± 0.62 mm at 15 days and increasing to 13.02 mm ± 1.63 mm at 21 days, with the means of 17 and 19 day samples statistically indistinguishable (Figure 2b). The gestational ages were supplied by the breeder, and some uncertainty regarding the exact time of conception must be considered in addition to expected variation from animal to animal. The initial circumference is a structural measure independent of reported gestational age but still representative of progress in pregnancy, analogous to dilation measured clinically. Circumference correlated with the mass of each sample (r = +.6694, p < .0001, Figure 2c).
Figure 2.
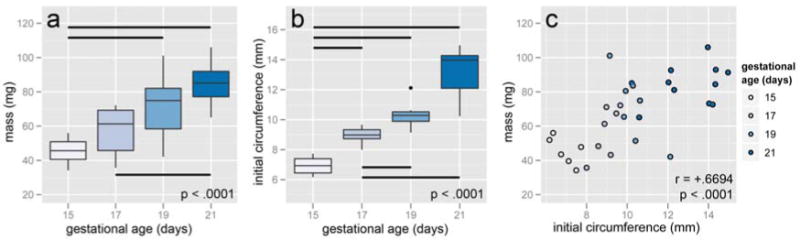
Mass (a) and initial circumference (b) increased with gestational age. Horizontal bars show pairwise statistical significance at p < .05. Mass and initial circumference were strongly correlated (c).
3.2 stiffness and load at 25% strain
The stiffness and load at 25% strain decreased with gestational age and with cervical circumference. Stiffness was defined as the linear region for the force-displacement curve as the sample approaches 25% circumferential strain (Figure 3a). This value for strain was chosen because some 15 day samples tore at higher strains in preliminary tests. A relatively large variance observed in 15 day samples was accounted for by using log10-transformed stiffness prior to statistical analysis. Stiffness decreased with gestational age (F = 21.999, p < .0001), though 19 and 21 day samples were statistically equivalent. A comparison between log10-transformed stiffness and circumference revealed a strong negative correlation (r = −.7338, p < .0001). When the data were not transformed, 17-21 day samples were no longer different with 95% confidence. Though stiffness here is expressed in g/mm, most of the statistically significant comparisons are the same when expressed in g/% strain (Supplementary Figure S2). The load at 25% circumferential strain (also log10-transformed) similarly decreased with gestational age (F = 8.9889, p = .0003) and negatively correlated with initial circumference (r = −.5471, p = .0014). Both stiffness and peak load decreased dramatically from day 15 to 17, then continued to decrease at a slower rate after that.
Figure 3.
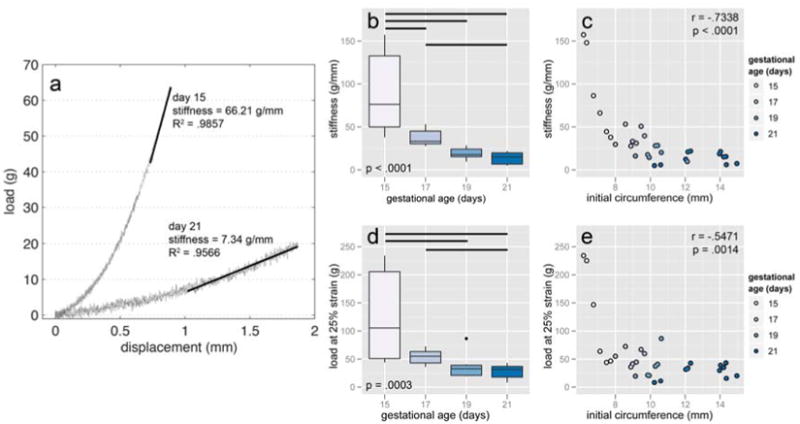
Representative load-displacement data with stiffness indicated (a). The maximum displacement for each test was set at 25% circumferential strain. Stiffness decreased with gestational age (b) and showed a strong negative correlation with initial circumference (c). In addition to the pairwise differences shown, the mean stiffness of day 17 and 19 samples just missed statistical significance (p = .0516). The load at 25% strain also decreased with gestational age (d) and negatively correlated with initial circumference (e). Horizontal bars show pairwise statistical significance. All values were log10-transformed prior to running statistics.
3.3 load-relaxation
The instantaneous load response (Abramowitch and Woo, 2004) was described by the following equation as a function of displacement (x):
where A and B are structural properties related to stiffness. A five-parameter relaxation function was chosen because in a preliminary analysis, it closely fit the load of the ‘hold’ section without the “ramp.” The relaxation function was defined as
where the parameters k0, k1, τ1, k2, τ2 were unknowns. The QLV theorem was used to describe both the elastic response during the ‘ramp’ and the relaxation response during the following “hold” by convolving the two functions (Abramowitch and Woo, 2004) (Nekouzadeh et al., 2007) (Yang et al., 2006):
The resulting, seven parameter function was fit to load-time data from the first ramp and hold by least-squares method using the Levenberg-Marquart algorithm. Further details are provided in the supplementary materials.
The ramp and hold data were well described by the QLV model, with an average coefficient of determination (R2) of .9596. The two parameters that describe stiffness, A and B (Figure 4b and c), depended on gestational age (F = 4.5979, p = .0100 and F = 6.5059, p = .0019, respectively) correlated with initial circumference (r = −.4092, p = .0223 and r = −.6721, p < .0001, respectively). The parameter k0 (Figure 4d), which represents the load approached as time continues towards infinity, also depended on gestational age (F = 5.8070, p = .0034) and correlated with initial circumference (r = −.6763, p < .0001). In each case, day 17, 19, and 21 samples were not statistically different at 95% confidence according to Tukey tests post-ANOVA. However, the means of B and k0 decrease with both age and circumference, as indicated in scatter plots (Supplementary Figure S4).
Figure 4.
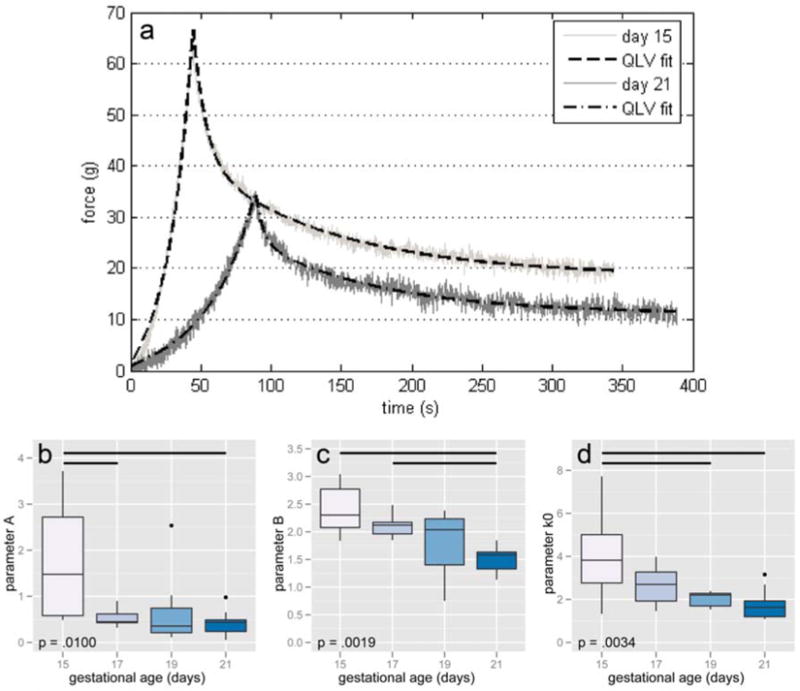
Representative load-relaxation data from 15 and 21 day samples with lines of best fit according to a quasi-linear viscoelastic (QLV) model (a). Best-fit parameters A (b), B (c), and k0 (d) all decreased with age. Horizontal bars show pairwise statistical significance.
3.4 change in load at 25% strain over multiple cycles
The decrease in load at 25% strain (immediately after the “ramp”) from cycle-to-cycle was used as a measure of non-recoverable deformation. On the second cycle, 15 day cervices reached a mean load 59.19% ± 8.31% of the magnitude reached on the first, compared to a mean of 43.00% ± 6.08% for all other days. Results were consistent through subsequent cycles. At 25% strain on the fifth cycle, 15 day samples were 33.22% ± 7.73% from their initial loads compared with a 22.12% ± 7.74% for all other samples (F = 3.2406, p = .0376, Figure 5c). The decrease in load at the maximum strain also correlated with circumference (r = -.4176, p = .0194, Figure 5d). These lower loads were attributed to the toe region, which began at larger strains and persisted to larger strains with each cycle. In other words, 15 day samples were able to recover from the prescribed strain more quickly, while 17-21 day cervices may have accumulated damage or simply recover over much larger time scales.
Figure 5.
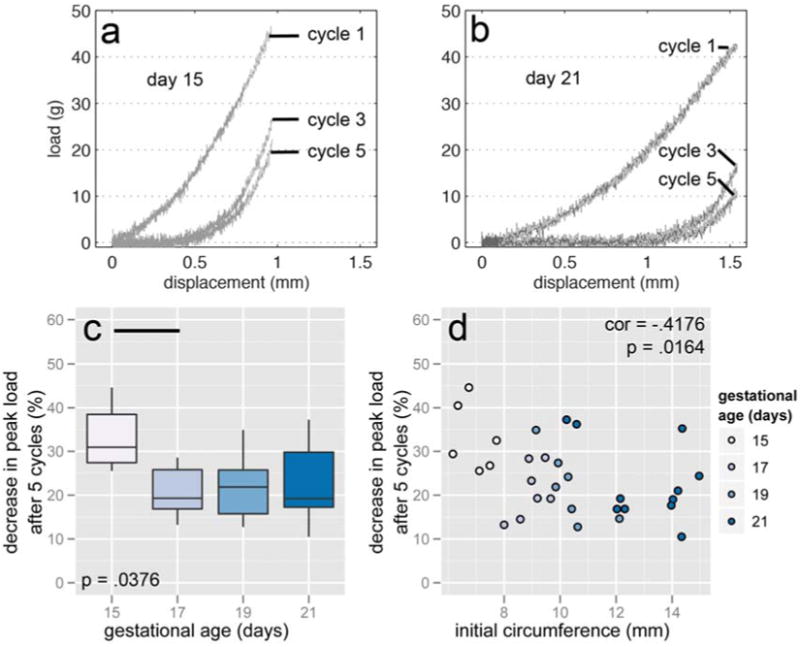
Representative load-displacement curves from cycles 1, 3, and 5 from 15 day (a) and 21 day (b) cervices. The load at 25% strain decreased less in 15 day samples than in other gestational ages after 5 cycles (c) and negatively correlated with initial circumference (d). In addition to the pairwise difference illustrated in (c), the means comparison of day 15 with days 19 and 21 approached statistical significance (p = .0701 and .0826, respectively). A 50% decrease is equivalent to the load at cycle 5 being half what it was in cycle 1. Horizontal bars show pairwise statistical significance.
3.5 biochemistry
The water content of samples, with two outliers omitted because testing reported <70% water, increased with gestational age (F = 12.627, p < .0001, Figure 6a). However, the only time point with a statistically significant difference from the others was day 15, with a mean of 84.18% ± 1.56%. Days 17, 19, and 21 averaged 85.92% ± 9.53%. Water content strongly correlated with initial circumference (r = .7473, p < .0001, Figure 6b). It follows that water content was negatively correlated with stiffness (r = −.6691, p < .0001), the load at 25% strain in the first cycle (r = −.6068, p = .0005), and the QLV best-fit parameters A (r = -.5873, p = .0008), B (r = -.4201, p = .0233) and k0 (r = -.5624, p = .0015).
Figure 6.
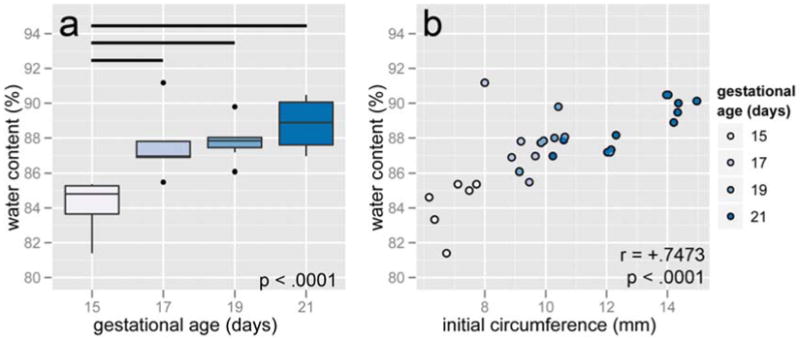
Water content increased after 15 days (a) and was positively correlated with initial circumference (b). Horizontal bars show pairwise statistical significance.
Total collagen content was independent of gestational age (F = 0.4245, p = .7370), averaging 5.89 mg ±1.76 mg. Additionally, neither measure of soluble collagen, pepsin-digested uncrosslinked collagen or tropocollagen, showed any statistical difference across gestational ages (49.1 μg ± 16.8 μg, F = 0.4901, p = .6922 and 1.0 μg ± 0.9 μg, F = 1.2437, p = .3150, respectively). These measured properties did not correlate with initial circumference, stiffness, load at 25% strain, or any load-relaxation parameters. Finally, birefringence measurements also showed no relationship to gestational age (F = 1.0159, p = .4087), averaging 32.76% ±17.62% alignment, nor did they correlate with any other mechanical measurement.
4. Discussion
An important goal of this study was to establish links between the structure, extrinsic mechanical properties, and biochemical composition of rat cervices in late-stage pregnancy. Increasing cervical circumference with gestational age has been noted in previous work (Harkness and Harkness, 1959) (Drzewiecki et al., 2005) (Read et al., 2007), but to our knowledge this was the first work to actually test the correlation of initial circumference with other measured properties. These experiments indicated that changes in cervical structure (circumference) were more apparent than changes in extrinsic, structural mechanical properties over the last days of term. The mean stiffness and load of day 19 and day 21 cervices at 25% strain were statistically equivalent, but circumference increased from a mean of 10.34 mm ±0.92 mm to 13.02 mm ±1.63 mm (p = .0002 according to Tukey means comparison). However, we emphasize that these are one-dimensional, extrinsic measures and not true material properties. The intrinsic properties could be determined if an accurate measure of the cross-sectional area could have been determined for each sample. The cervices enlarge with gestational age, as evidenced by mass, circumference, and water content measurements. An intrinsic measure of stiffness like Young's modulus would likely decrease even from day 19 to day 21. Thus, it may be that our reported differences of extrinsic properties are conservative relative to the intrinsic ones.
Our measurements were consistent with literature that has shown a decrease in stiffness with gestational age in sheep (Owiny et al., 1991) and mice (Read et al., 2007). Studies reporting the stiffness of rat cervices indicate significant decreases in stiffness at gestational ages of 10 (Drzewiecki et al., 2005) and 16 (Buhimschi et al., 2004) days, with no further statistically significant softening after gestational day 16. In this study, the wide variance in stiffness of 15 day samples at 25% strain compared to later time points may be indicative of an abrupt softening at that age. Significant differences were likely observed in this work for two reasons. First, by log-transforming the data - necessary to satisfy the requirement that variances across groups are equal - differences at low stiffness became more apparent. The mean stiffness values of all gestational ages were statistically different from each other with the exception of days 19 and 21. Second, the equipment used in this study has much higher precision than that used in previous work (Read et al., 2007) (Drzewiecki et al., 2005) (Buhimschi et al., 2004), where displacement was added in discrete increments rather than as a continuous ramp.
Creep tests, in which a constant load is applied to the cervix and deformation is measured, are much more common in the literature. An abrupt increase in extensibility in cervices from mice (Kokenyesi et al., 2004) and rats (Harkness and Harkness, 1959) (Hollingsworth et al., 1979) (Clark et al., 2006) has been observed mid-gestation (12-16 days). An increase in extensibility in creep may be related to the reduced QLV parameter k0 observed in this study.
The load during “ramp” and “hold” sections were well-described by a 7-parameter QLV model. The most interesting result from this model is the fact that neither the time constants (τ1 and τ2) or the constants that scale the time-dependent exponentials (k1 and k2) change with gestational age or with cervical circumference. This may reflect some fundamental properties of the extracellular matrix such as the rate at which water is squeezed out of the protein and proteoglycan network or the forces between sliding macromolecules. The relaxation function (G(t)) can be interpreted as a constitutive model consisting of a spring and two Maxwell elements in parallel (Fung, 1993). Similar one-dimensional lumped-parameter models have been proposed to describe the load-relaxation behavior of human cervices in compression (Myers et al. 2010) (Jordan et al., 2011) and fibroblast-populated collagen rings in tension (Nekouzadeh et al., 2007).
The parameters that reflect stiffness (A and B) and the parameter that represents the minimum load supported by the cervix under a given deformation (k0) all decrease with gestational age. The ability to resist deformation and the ability to maintain load-bearing capacity are of great importance in earlier gestational ages when cervical dilation would increase the risk of a poor outcome. In contrast, at term decreased elasticity is desirable to provide a more efficient labor process. Further work is necessary to establish these connections, as differences in biochemical structure and composition were not observed in this study (see further discussion below).
One limitation of this study was the fact that each cervix was divided in two in order to have tissue for mechanical and biochemical analysis. A pregnant rat cervix measures approximately 7 mm length × 6 mm width × 2.5 mm thick. The upper (uterine) portion was sent for biochemical analysis while the lower (vaginal) portion was used for mechanical testing. In this study, the biochemical content and microstructure unexpectedly did not change with gestational age. Other researchers have shown that mechanical properties (Owiny et al., 1991) and tissue composition (Harkness and Harkness, 1959) change along the length of the cervical canal. Owiny et al. (1991) suggest that cervical remodeling begins at the internal os, while Read et al. (2007) have shown that collagen solubility increases in rat cervices before softening but levels off at later time points.
An additional limitation of the work was related to the test equipment. The sealed sample chamber was too small to allow manual measurement of cervix geometry before testing. Additionally, only two of the four sidewalls of the chamber were transparent, so measurement with imaging was not possible. Accurate measurement of cross-sectional area would enable calculation of intrinsic material properties like the Young's modulus. Still, even without controlling for geometry after manual bisection of the tissue, the differences observed in tensile stiffness and load-relaxation are illuminating and will inform future work. Strain measurement, perhaps by digital image correlation (Andonian, 2008) would be particularly valuable for identifying differences in properties in different locations of the cervix.
Additionally, the use of smaller but stronger rods (Webster et al., 2011) would enable testing at earlier time points with smaller diameter cervices.
5. Conclusion
The purpose of this work was to characterize the uniaxial tensile and relaxation mechanical behavior of the rat cervix tissue between 15 and 21 days post-conception. The resting circumference of the cervical canal increased significantly with gestational age. Tensile tests to 25% circumferential strain showed that the cervix softens as term nears, and that this softening also strongly correlates with the initial circumference. The load during the initial ramp and hold cycle was accurately described by a seven parameter QLV model. Three parameters related to stiffness and load capacity decreased as term approached, while four parameters that relate to relaxation over time did not. In subsequent loading cycles, cervices at 15 days sustained less unrecoverable damage than 17-21 day cervices. These mechanical properties, particularly in conjunction with structural measures like circumference, may be useful measures for predicting the timing of birth.
Supplementary Material
Research Highlights.
Late-term rat cervical tissue was subjected to tension and load-relaxation tests.
Extrinsic measures of stiffness decreased with gestational age and circumference.
Time-dependent relaxation properties did not change with gestational age.
Load-relaxation was well-described by a quasi-linear viscoelastic (QLV) model.
Water content correlated with age. Collagen composition and organization did not.
Acknowledgments
This project was supported by National Institutes of Health grant R21HD058705. The authors would like to thank Dr. William D. O'Brien and Ellora Sen-Gupta for their assistance.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Abramowitch SD, Woo SLY. An improved method to analyze the stress relaxation of ligaments following a finite ramp time based on the quasi-linear viscoelastic theory. J Biomech Eng. 2004;126:92–97. doi: 10.1115/1.1645528. [DOI] [PubMed] [Google Scholar]
- Andonian AAT. Optical methods. In: Shaepe WN, editor. Handbook of Experimental Solid Mechanics. Springer; New York, NY: 2008. pp. 823–837. [Google Scholar]
- Behrman RE, Butler AS. Institute of Medicine Committee on Understanding Premature Birth and Assuring Healthy Outcomes. The National Academies Press; Washington, DC: 2007. [accessed April, 2012]. Preterm birth: causes, consequences, and prevention; p. 31. http://www.ncbi.nlm.nih.gov/pubmed/20669423. [PubMed] [Google Scholar]
- Bishop EH. Pelvic scoring for elective induction. Obstet Gynecol. 1964;24:266–268. [PubMed] [Google Scholar]
- Buhimschi IA, Dussably L, Buhimschi CS, Ahmed A, Weiner CP. Physical and biomechanical characteristics of rat cervical ripening are not consistent with increased collagenase activity. Am J Obstet Gynecol. 2004;191:1695–1704. doi: 10.1016/j.ajog.2004.03.080. [DOI] [PubMed] [Google Scholar]
- Chiossi G, Verocchi G, Venturini P, Facchinetti F. Changes in cervical nitric oxide concentration correlate with bishop score and cervical length modifications in prostaglandin E2-mediated induction of labor. J Soc Gynecol Invest. 2006;13:203–208. doi: 10.1016/j.jsgi.2006.01.001. [DOI] [PubMed] [Google Scholar]
- Clark K, Ji H, Feltovich H, Janowski J, Carroll C, Chien EK. Mifepristone-induced cervical ripening: structural, biomechanical, and molecular events. Am J Obstet Gynecol. 2006;194:1391–1398. doi: 10.1016/j.ajog.2005.11.026. [DOI] [PubMed] [Google Scholar]
- Crane JM, Hutchens D. Use of transvaginal ultrasonography to predict preterm birth in women with a history of preterm birth. Ultrasound Obstet Gynecol. 2008;32:640–645. doi: 10.1002/uog.6143. [DOI] [PubMed] [Google Scholar]
- Drzewiecki G, Tozzi C, Yu SY, Leppert PC. A dual mechanism of biomechanical change in rat cervix in gestation and postpartum: applied vascular mechanics. Cardiovasc Eng. 2005;5:187–193. [Google Scholar]
- Faris B, Moscaritolo R, Levine A, Snider R, Goldstein R, Franzblau C. Isolation of purified insoluble aortic collagen. Biochim Biophys Acta. 1978;534:64–72. doi: 10.1016/0005-2795(78)90476-2. [DOI] [PubMed] [Google Scholar]
- Fung YC. Biomechanics: Mechanical Properties of Living Tissues. second. Springer; New York, NY: 1993. pp. 41–48. [Google Scholar]
- Gomez R, Galasso M, Romero R, Mazor M, Sorokin Y, Gonçalves L, Treadwell M. Ultrasonographic examination of the uterine cervix is better than cervical digital examination as a predictor of the likelihood of premature delivery in patients with preterm labor and intact membranes. Am J Obstet Gynecol. 1994;171:956–964. doi: 10.1016/0002-9378(94)90014-0. [DOI] [PubMed] [Google Scholar]
- Gomez R, Romero R, Nien JK, Chaiworapongsa T, Medina L, Kim YM, Yoon BH, Carstens M, Espinoza J, Iams JD, Gonzalez R. A short cervix in women with preterm labor and intact membranes: a risk factor for microbial invasion of the amniotic cavity. Am J Obstet Gynecol. 2005;192:678–689. doi: 10.1016/j.ajog.2004.10.624. [DOI] [PubMed] [Google Scholar]
- Gramellini D, Fieni S, Kaihura C, Modena AB. Cervical length as a predictor of preterm delivery: gestational age-related percentiles vs fixed cut-offs. Acta Biomed. 2007;78:220–224. [PubMed] [Google Scholar]
- Hamilton BE, Martin JA, Ventura SJ. National Vital Statistics Reports. Vol. 60. National Center for Health Statistics; Hyattsville, MD: 2011. [accessed on April 1, 2012]. Births: preliminary data for 2010; p. 5. http://www.cdc.gov/nchs/data/nvsr/nvsr60/nvsr60_02.pdf. [PubMed] [Google Scholar]
- Harkness MLR, Harkness RD. Changes in the physical properties of the uterine cervix of the rat during pregnancy. J Physiol. 1959;148:524–547. doi: 10.1113/jphysiol.1959.sp006304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hassan SS, Romero R, Berry SM, Dang K, Blackwell SC, Treadwell MC, Wolfe HM. Patients with an ultrasonographic cervical length < or =15 mm have nearly a 50% risk of early spontaneous preterm delivery. Am J Obstet Gynecol. 2000;182:1458–1467. doi: 10.1067/mob.2000.106851. [DOI] [PubMed] [Google Scholar]
- Hassan S, Romero R, Hendler I, Gomez R, Khalek N, Espinoza J, Nien JK, Berry SM, Bujold E, Camacho N, Sorokin Y. A sonographic short cervix as the only clinical manifestation of intra-amniotic infection. J Perinat Med. 2006;34:13–19. doi: 10.1515/JPM.2006.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hollingsworth M, Isherwood CN, Foster RW. The effects of oestradiol benzoate, progesterone, relaxin and ovariectomy on cervical extensibility in the late pregnant rat. J Reprod Fertil. 1979;56:471–477. doi: 10.1530/jrf.0.0560471. [DOI] [PubMed] [Google Scholar]
- Honest H, Bachmann LM, Coomarasamy A, Gupta JK, Kleijnen J, Khan KS. Accuracy of cervical transvaginal sonography in predicting preterm birth: a systematic review. Ultrasound Obstet Gynecol. 2003;22:305–322. doi: 10.1002/uog.202. [DOI] [PubMed] [Google Scholar]
- House M, Bhadelia RA, Myers K, Socrate S. Magnetic resonance imaging of three-dimensional cervical anatomy in the second and third trimester. Eur J Obstet Gynecol Reprod Biol. 2009a;144:S65–S69. doi: 10.1016/j.ejogrb.2009.02.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- House M, Kaplan DL, Socrate S. Relationships between mechanical properties and extracellular matrix constituents of the cervical stroma during pregnancy. Sem Perinatol. 2009b;33:300–307. doi: 10.1053/j.semperi.2009.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iams JD, Goldenberg RL, Meis PJ, Mercer BM, Moawad A, Das A, Thom E, McNellis D, Copper RL, Johnson F, Roberts JM National Institute of Child Health and Human Development Maternal Fetal Medicine Unit Network. The length of the cervix and the risk of spontaneous premature delivery. N Engl J Med. 1996;334:567–572. doi: 10.1056/NEJM199602293340904. [DOI] [PubMed] [Google Scholar]
- Iams JD. Prediction and early detection of preterm labor. Obstet Gynecol. 2003;101:402–412. doi: 10.1016/s0029-7844(02)02505-x. [DOI] [PubMed] [Google Scholar]
- Jordan P, Kerdok AE, Howe RD, Socrate S. Identifying a minimal rheological configuration: a tool for effective and efficient constitutive modeling of soft tissues. J Biomech Eng. 2011;133:041006. doi: 10.1115/1.4003620. [DOI] [PubMed] [Google Scholar]
- Kokenyesi R, Armstrong LC, Agah A, Artal R, Bornstein P. Thrombospondin 2 deficiency in pregnant mice results in premature softening of the uterine cervix. Biol Reprod. 2004;70:385–390. doi: 10.1095/biolreprod.102.014704. [DOI] [PubMed] [Google Scholar]
- Mahendroo M. Cervical remode ling in term and preterm birth: insights from an animal model. Reproduction. 2012;143:429–438. doi: 10.1530/REP-11-0466. [DOI] [PubMed] [Google Scholar]
- McFarlin BL. Solving the puzzle of prematurity: healthy infancy starts with a healthy woman. Am J Nurs. 2009;109:60–63. doi: 10.1097/01.NAJ.0000344041.49768.ec. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myers KM, Paskaleva AP, House M, Socrate S. Mechanical and biochemical properties of human cervical tissue. Acta Biomat. 2008;4:104–116. doi: 10.1016/j.actbio.2007.04.009. [DOI] [PubMed] [Google Scholar]
- Myers KM, Socrate S, Paskaleva A, House M. A study of the anisotropy and tension/compression behavior of human cervical tissue. J Biomech Eng. 2010;132:021003. doi: 10.1115/1.3197847. [DOI] [PubMed] [Google Scholar]
- Nekouzadeh A, Pryse KM, Elson EL, Genin GM. A simplified approach to quasi-linear viscoelastic modeling. J Biomech. 2007;40:3070–3078. doi: 10.1016/j.jbiomech.2007.03.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newman RB, Goldenberg RL, Iams JD, Meis PJ, Mercer BM, Moawad AH, Thom E, Miodovnik M, Caritis SN, Dombrowski M National Institute of Child Health and Human Development Maternal-Fetal Medicine Units Network. Preterm prediction study: comparison of the cervical score and Bishop score for prediction of spontaneous preterm delivery. Obstet Gynecol. 2008;112:508–515. doi: 10.1097/AOG.0b013e3181842087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Owiny JR, Fitzpatrick RJ, Spiller DG, Dobson H. Mechanical properties of the ovine cervix during pregnancy, labour and immediately after parturition. Br Vet J. 1991;147:432–436. doi: 10.1016/0007-1935(91)90085-2. [DOI] [PubMed] [Google Scholar]
- Oxlund BS, Ørtoft G, Brüel A, Danielsen CC, Bor P, Oxlund H, Uldbjerg N. Collagen concentration and biomechanical properties of samples from the lower uterine cervix in relation to age and parity in non-pregnant women. Reprod Biol Endocrinol. 2010;8:82. doi: 10.1186/1477-7827-8-82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Development Core Team. R Foundation for Statistical Computing. Vienna, Austria: 2010. R: A language and environment for statistical computing. http://www.R-project.org. [Google Scholar]
- Read CP, Word RA, Ruscheinsky MA, Timmons BC, Mahendroo MS. Cervical remodeling during pregnancy and parturition: molecular characterization of the softening phase in mice. Reproduction. 2007;134:327–340. doi: 10.1530/REP-07-0032. [DOI] [PubMed] [Google Scholar]
- Rechberger T, Uldbjerg N, Oxlund H. Connective tissue changes in the cervix during normal pregnancy and pregnancy complicated by cervical incompetence. Obstet Gynecol. 1988;71:563–567. [PubMed] [Google Scholar]
- Schmitz T, Kayem G, Maillard F, Lebret MT, Cabrol D, Goffinet F. Selective use of sonographic cervical length measurement for predicting imminent preterm delivery in women with preterm labor and intact membranes. Ultrasound Obstet Gynecol. 2008;31:421–426. doi: 10.1002/uog.5297. [DOI] [PubMed] [Google Scholar]
- Stegemann H, Stalder K. Determination of hydroxyproline. Clin Chim Acta. 1967;18:267–273. doi: 10.1016/0009-8981(67)90167-2. [DOI] [PubMed] [Google Scholar]
- Timmons B, Akins M, Mahendroo M. Cervical remodeling during pregnancy and parturition. Trends Endocrinol Metab. 2010;21:353–361. doi: 10.1016/j.tem.2010.01.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Webster MR, De Vita R, Twigg JN, Socha JJ. Mechanical properties of tracheal tubes in the American cockroach (Periplaneta Americana) Smart Mater Struct. 2011;20:1–7. [Google Scholar]
- Wickham H. ggplot2: Elegant Graphics for Data Analysis. Springer; New York, NY: 2009. [Google Scholar]
- Yang W, Fung TC, Chian KS, Chong CK. Viscoelasticity of esophageal tissue and application of a QLV model. J Biomech Eng. 2006;128:909–916. doi: 10.1115/1.2372473. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


