Phenomenological consequences of sectioning and bathing on passive muscle mechanics of the New Zealand white rabbit tibialis anterior

Abstract

Skeletal muscle tissue provides support and mobility of the musculoskeletal system. Numerical modeling of muscle tissue aids in understanding disease pathophysiology, however, the effectiveness is dependent on accurately accounting for various tissue phenomena. Muscle modeling is made difficult due to the multitude of constituents that contribute to elastic and viscous mechanisms. Often, deterministic single fiber or fiber bundle studies are undertaken to examine these contributions. However, examination of whole, intact and structurally altered tissue and comparison to findings at the myofibril scale can help elucidate tissue mechanics. Stress relaxation tests at 10% strain were performed on 28 New Zealand White rabbits tibialis anterior muscles for whole, intact muscle and sub-sectioned muscle samples. Additionally, to aid in examining viscous effects sub groups were tested with and without a phosphate buffered saline bath. The steady-state elastic modulus was not significantly different between groups. Interestingly, sectioning did result in a negative Poisson’s ratio. Additionally, sectioning resulted in altering the viscous tissue response as the time to reach steady-state was significantly faster than whole muscle samples (p < 0.05), as well as the linear relaxation rate from 0 to 0.1 (p < 0.01), 1 to 10 (p < 0.05), and 10 to 100 seconds (p < 0.05). Bathing tissue resulted in a significantly greater amount of percent stress relaxation for whole muscle (p < 0.01). These findings provide new insight into the differing mechanical characteristics of whole and sectioned muscle tissue.

1. Introduction

Passive muscle mechanics play an important role in support and mobility of the musculoskeletal system. Numerical modeling of muscle mechanics has the potential to aid in providing rapid estimates of degenerative pathophysiology. While modeling approaches range from simplistic Hill-type (Hill, 1938) to micro-mechanical phenomenologically driven (Sharafi and Blemker, 2010; Winters et al., 2011) or continuum based hyperelastic muscle models (Blemker and Delp, 2005; Odegard et al., 2008), the accuracy of all models hinges on experimental validation. Notably, skeletal muscle tissue mechanics research lags behind classical collagenous (e.g. ligament, tendon, cartilage) tissue investigations. Often elegant architectural studies examine the viscous and/or elastic contribution(s) of individual muscle constituents (Gregory et al., 2007; Linke and Leake, 2004; Proske, 1999; Toursel et al., 2002); however, these results do not necessarily encapsulate passive whole muscle behavior when scaled accordingly (Winters et al., 2011).

Complicating skeletal muscle modeling is the tissue’s elaborate hierarchical structure containing various extensible constituents. Consequently, seldom does muscle mechanics research focus on aggregate effects due to the difficulty in interpreting the results. However, it has been shown that while extracellular matrix (ECM) tensile compliance is significantly greater than that of myofibrils, force transmission is accomplished through shearing mechanisms (Purslow and Trotter, 1994; Sharafi and Blemker, 2010; Trotter and Purslow, 1992). Recent investigation of the ECM also indicates a previously unconsidered role in the structural mechanics of muscle tissue by applying a transverse strain during loading (Smith et al., 2011). Also, while intrinsic viscous contributions of load bearing proteins have been documented, it has been suggested that extracellular fluid movement has an effect on the apparent viscoelastic behavior in passive myocardial tissue (Yang and Taber, 1991).

Subjecting muscle tissue to various mechanical stimuli under a multitude of conditions can aid in elucidating differences in the multi-scale behavior of this tissue. Therefore, the aim of this study was to examine how material properties ascertained from experimental testing are influenced by external conditions. Specifically, it was expected that differences in time-dependent mechanical behavior would exist between whole and sectioned muscle. It was hypothesized that by sectioning muscle tissue and disrupting the compliant ECM (Purslow and Trotter, 1994) there would be no change in steady-state elastic modulus for a certain level of strain, however, transverse strains would be greatly reduced without an intact matrix-fiber network (Smith et al., 2011). Additionally, due to the instrumental role fluid flow can play in dictating viscoelastic mechanics, differences between bathed and open air samples would exist.

2. Materials and methods

2.1. Sample preparation

Whole New Zealand White rabbit hind limbs (n = 28), removed at the hip joint, were procured with institutional animal care and use committee approval and stored intact, pre-rigor mortis, at −20°C. Prior to dissection specimens were allowed to thaw overnight at 4°C. The tibialis anterior muscles, selected for their relatively uniform cross section and low pennation angle (Lieber and Blevins, 1989), were dissected out at room temperature, keeping the epimysium intact. Specimens were divided into two groups: whole muscle and sectioned muscle, with the latter being excised from the central axis of the muscle body using a custom drop cutter mounted with two high profile microtome blades (EXTREMUS, C.L. Sturkey, Lebanon, PA) spaced 3.3mm apart. Slices were made parallel to muscle fiber axis. A waterproof ink speckle pattern was applied to the surface of the specimens using a gravity fed paint sprayer backed by 10psi of air pressure (Fig. 1). Sample cross sectional area was determined using images captured using two orthogonally mounted CCD’s (Flea3, Point Grey, Scottsdale, AZ) and ImageJ image processing software (Abramoff et al., 2004).

Figure 1.

Whole muscle sample in the test apparatus with a waterproof ink speckle pattern applied to the surface. The strain region of interest, taken in the specimen mid-substance to avoid edge effects due to gripping, is shown in the rectangular box.

2.2. Mechanical testing

Muscle groups were further subdivided into specimens tested with and without a phosphate buffered saline (PBS) bath, yielding four test groups examined: whole-with a bath, whole-without a bath, sectioned-with a bath, and sectioned-without a bath. Specimens were subjected to uniaxial tension, parallel to the fiber direction, using a hydraulic test stand (Mini-Bionix II 831, MTS, Eden Prarie, MN) coupled with thin-film grips (FC-20, Imada, Northbrook, IL) and a 100N load cell (661.09B-21, MTS, Eden Prairie, MN) (Abraham et al., 2011). A steady-state tare stress of 0.1% of the predetermined average failure stress (Morrow et al., 2010) was slowly applied to the specimen such that:

$$0.001{\sigma }_{\mathit{ult}}=\frac{F}{A}=\frac{\mathit{Preload}}{\pi d_{\mathit{maj}}/2d_{\mathit{min}}/2}or\frac{\mathit{Preload}}{\mathit{width}\mathit{thickness}}$$

where σ_ult is the assumed to be 163 MPa and d_min and d_maj correspond to the measured major and minor axes of the elliptical muscle tissue for whole muscle specimens. For sectioned muscle, the cross sectional area was determined assuming rectangular geometry rather than elliptical. The specimens were then strained to 10% strain at a rate of 1% sec⁻¹ and held for 5 minutes. Images of the speckled surface as well as the plane perpendicular to the image were recorded. Bathed specimens were kept completely submerged in PBS (Ca and Mg free) while specimens without a bath were wetted using a spray bottle immediately prior to testing with PBS.

2.3. Data analysis

2^nd Piola-Kirchoff stress, σ, was calculated using the applied load, F, and the original cross-sectional area, A_i, such that

$$\sigma =\frac{F}{A_i}$$

The experimental strains and Poisson’s ratio were obtained from the applied inkspeckle pattern using digital image correlation (DIC) (Opticist v0.948). A subset window size of 21 pixels² and the zero-normalized sum of squared differences processing algorithm, selected for its relative immunity to changes in light conditions and lens effects, were found to produce reliable results (Pan et al., 2009). To reduce any effects bathing may have on using optical strain determination the bath viewing window was mounted perpendicular camera to mitigate refraction. High uniformity acrylic was also selected to limit any distortion effects. Pilot testing comparing acquisition with and without a bath for speckled patterned rubber sheets revealed no significant differences. A strain region of interest (ROI) was defined as the specimen mid-substance where a quality speckle pattern could be visualized and avoided any edge effects due to gripping. The mean strain for the ROI was then taken as the Cauchy strain. The mean Cauchy strain, ε_C, was then converted to Green Strain, ε_G, using

$${\epsilon }_G=\frac{1}{2}\left({\left(1+{\epsilon }_C\right)}^2-1\right)$$

The drained/steady-state elastic modulus was ascertained from the final stress value during the relaxation phase divided by the Green strain. Poisson’s Ratio, ν, was determined by acquiring both the longitudinal and transverse strains from the speckle pattern DIC. The mean strain for each direction in the ROI was then used to compute the ratio using

$$\nu =-\frac{\delta {\epsilon }_{\mathit{trans}}}{\delta {\epsilon }_{\mathit{long}}}$$

To verify findings of Poisson’s ratio for additional analysis of the camera images was performed by a blinded reviewer. Supplied with a coded and randomized stack of images and using ImageJ image processing software they measured frontal area immediately prior to testing and at peak stress.

To examine changes in viscous behavior, whether due to fluid movement or intrinsic viscoelasticity, time to steady-state, percent stress relaxation, and stress relaxation rate were determined. Time to steady-state was ascertained by applying a moving average smoothing filter to the stress relaxation data to remove random noise components and then defining steady-state when the change in stress was below 0.001%. The smoothing filter was leveraged as the algorithm to determine steady-state compared nearest neighbor data points and located the time when the change was below the predetermined threshold. Broadband noise components in the load data generate sharp peaks that could potentially result in the algorithm missing the true change in load. Ideally, the stress relaxation would be recorded as a monotonically decreasing function, however, this is not necessarily possible due to various acquisition phenomena, including but not limited to load cell sensitivity, discretization, and analog to digital bit error. Percent relaxation between peak stress and steady-state was then computed at this point. Linear stress relaxation rates were computed post-peak stress for four time periods of 0 to 0.1, 0.1 to 1, 1 to 10, and 10 to 100 seconds (Hakim and Grange, 2011).

2.4. Statistics

Steady-state and elastic modulus, Poisson’s ratio, time to steady-state, percent relaxation, and relaxation rate were compared between groups using a two-factor ANOVA with sectioning and bathing as the independent variables. Explicit comparisons were made post-hoc using a student’s t-test. Significant differences were identified at p < 0.05. All data is presented as mean value ± standard deviation.

3. Results and discussion

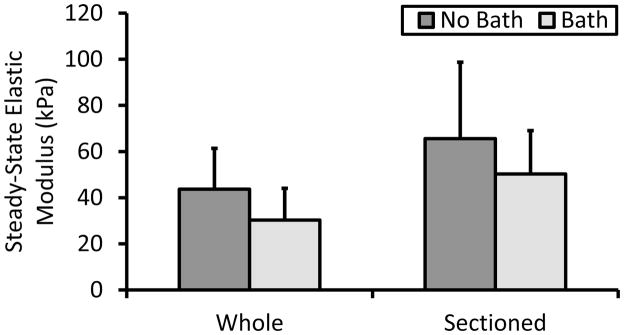
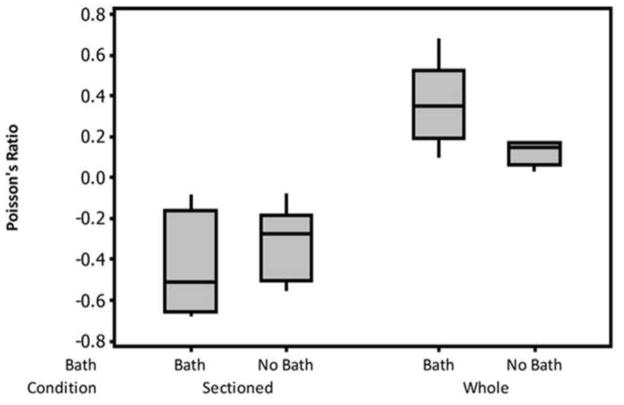
As expected, disruption of the ECM-fiber network due to sectioning did not change elastic behavior (Fig. 2). In particular, sectioning of the epimysium and muscle fascicles did not alter the microstructure to significantly affect the steady-state response. Within the tissue it is known that various matrix components aid in contractile load transmission primarily through shearing mechanisms (Purslow and Trotter, 1994; Trotter and Purslow, 1992). However, in passive extension, with no contractile forces generated, the surrounding matrix seemingly acts more as a compliant retainer for maintaining muscle shape. This is affirmed by analyzing the two-dimensional strain of sectioned muscle which resulted in a negative Poisson’s ratio after deformation that was significantly and structurally difference from whole muscle (Fig. 3). The additional analysis performed by the blinded reviewer (not shown) confirmed these findings as they showed an increase in frontal area due to loading for the sectioned specimens only. This finding supports the work of Smith et. al. that compared single fibers to fiber bundles and concluded that the ECM applies a transverse strain during longitudinal loading (Smith et al., 2011). While their finding implicates the importance of the endomysium, the work here indicates that the epimysium may function similarly, though on a grander scale. The demonstrable lateral expansion after sectioning is typical of auxetic materials, such as engineered foams, which are known to possess high amounts of energy absorption, in and of itself an important facet of skeletal muscle. This behavior is not unique within the body as it is believed that skin and living bone may also exhibit auxetic behavior (Veronda and Westmann, 1970; Williams and Lewis, 1982). Physiologically, this may attributed to “unfolding” of the Z-disc at the titin anchorage points during loading, however, more detailed in situ imaging modalities would be required to verify this hypothesis. Values for Poisson’s ratio of intact muscle were comparable to Van Loocke et al. as they reported a value of 0.5 along the main fiber axis, well within the variance for whole, bathed tissue (Van Loocke, Lyons, & Simms, 2006). It should be noted, however, that samples in their study were in fact sectioned from pelvic and thoracic limbs from porcine, bovine, and ovine samples. Thus, their findings for what would be comparable to our sectioned group do not agree. Mechanical testing protocols did, however, differ between studies as they subjected the tissue to uniaxial compression. Although special care was taken in their study to minimize potential buckling of the muscle fibers, loss of ECM integrity, leading to loss of structural retention, may also have influenced their findings. Comparison between sectioned and whole muscle in compression may help to further elucidate this phenomena and the role of the ECM in skeletal muscle tissue.

Figure 2.

Elastic modulus calculated from the steady-state portion of the relaxation phase of the stress-relaxation test. This parameter is analogous to the steady-state or drained modulus for viscoelatic and poroelastic models. No significant differences were evident due to either sectioning or bathing.

Figure 3.

Boxplot of Poisson’s ratio. Sectioned muscle samples had a negative Poisson’s ratio, implicating that disruption of the extracellular matrix results in a loss of structural retention.

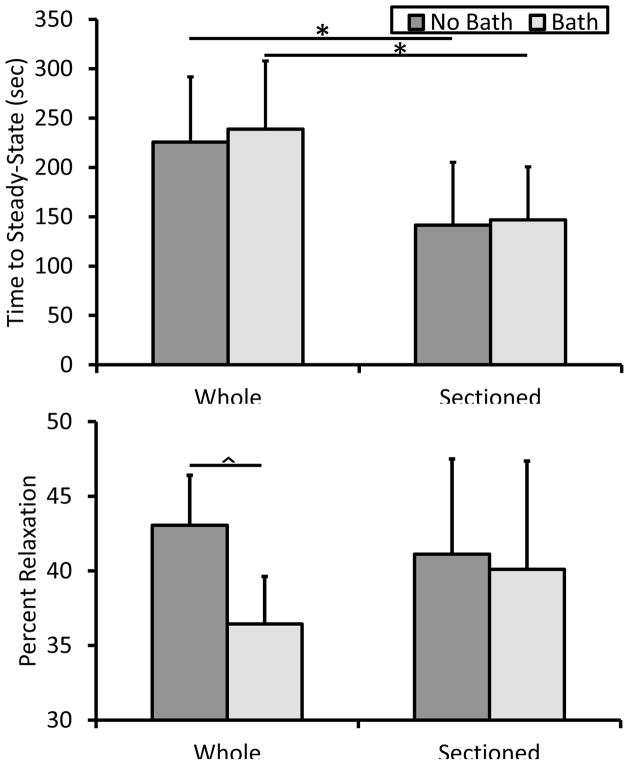
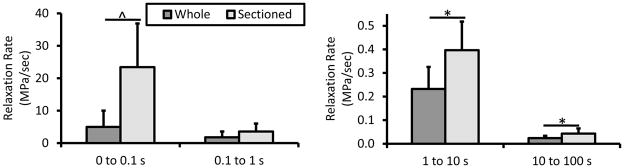
Sectioning tissue did result in significantly decreasing the time required to achieve steady-state behavior both with and without a bath (Fig. 4a). In ligament and tendon, collagen is known to possess intrinsic energy dissipation due to fibril and fiber bundle sliding during tensile deformation (Mow and Huiskes, 2005). In muscle, at the myofibril level stress-relaxation is thought to be a function of titin-Ig domain unfolding, Z-disc and A-band anchorage points, as well as sliding motion of load bearing proteins through liquid (Linke and Leake, 2004). With the inclusion of the intact epimysium there appears to be a significantly damped relaxation response (Fig. 5). In assessing the viscoelastic properties of muscle in compression, Van Loocke et al. showed that 80% of the stress relaxation occurred during the first 100 sec of the hold phase, agreeing with data from our intact muscle samples (Fig. 5) (Van Loocke et al., 2008). Once again, however, in the sectioned group the tissue relaxed far faster as exhibited by the significant greater relaxation rate for 0 to 0.1, 1 to 10, and 10 to 100 seconds (Fig. 6). Overall percent stress relaxation of 40–45% was also comparable to Van Loocke et al. who showed approximately a 50% reduction in stress over 300 seconds. Only whole, bathed tissue appeared to be impacted according to this metric, potentially implicating a significant fluid effect (Fig. 4b).

Figure 4.

Viscous properties of muscle tissue. Time to achieve steady-state behavior was significantly greater in whole muscle samples indicating that the extracellular matrix has a dramatic effect on the energy disspation during relaxation. * p < 0.05. The amount of stress relaxation was significantly less for bathed, whole muscle specimens. ^ p < 0.01.

Figure 5.

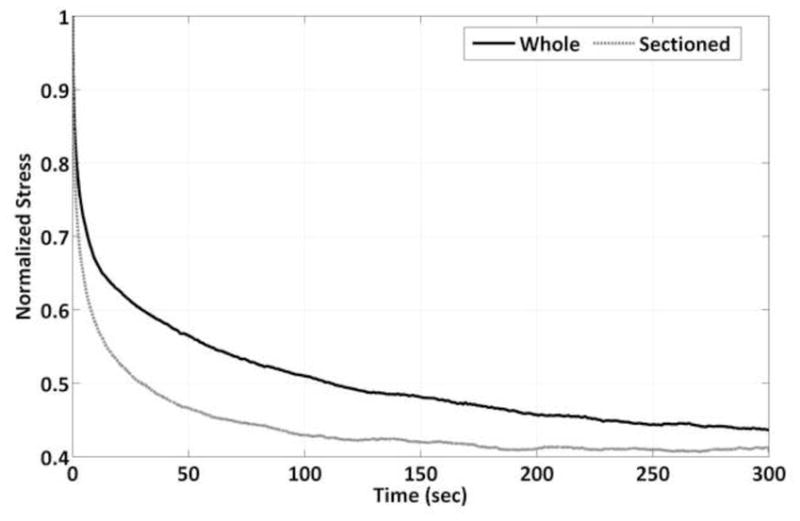
Representative stress relaxation for whole and sectioned muscle samples. Sectioned muscle samples have a more dramatic initial relaxation period resulting in a faster time to steady-state behavior.

Figure 6.

Linear stress relaxation rate was significantly greater for sectioned muscle samples from 0 to 0.1, 1 to 10, and 10 to 100 seconds. * p < 0.05. ^ p < 0.01.

Assuming the muscle ECM is fully free draining, the open air specimens may have lost a substantial amount of fluid pressure over the 300 second duration of the relaxation phase. In contrast bathed specimens likely retained their fluid content due to hydrostatic forces and hence a higher amount of internal stress. Additionally, significant fluid-matrix-fiber interactions are implicated by Van Loocke et al. as they witnessed differences in viscoelastic behavior for compression along and across the muscle fiber axis. They postulate that fluid more freely flows along the fiber axis within fascicles, whereas in the case of compression across the fiber axis the fluid remains constrained by the endoymsium and perimysium (Van Loocke et al., 2008). Sectioning may have resulted in a higher rate of fluid expulsion due to loading. It remains difficult, however, to completely decouple time-dependent behavior in skeletal muscle due to fluid effects and intrinsic material viscoelasticity.

One trend that must be addressed is the relatively higher amount of variability in the sectioned muscle properties. The sectioning technique performed here ensured that a constant sample width was removed from each whole muscle specimen. This approach does not account for animal to animal size variability and may result in differences of fiber packing density. An increase in the number of muscle fibers could potentially increase the steady-state moduli as the ECM is thought to contribute less to tensile stiffness (Purslow & Trotter, 1994). Additionally, fiber packing density would influence viscoelastic effects as fluid flow within the fascicles would be altered. Lastly, while extreme care was taken to align the longitudinal muscle fibers parallel with the cutting blades, some out of plane sectioning may have occurred, potentially reducing the tensile load carrying capacity, though this did not seem to be the evident in our data as there were no significant differences between whole and sectioned muscle for steady-state modulus.

A shortcoming of this study is the use of fresh-frozen tissue. While freeze/thaw cycles have minimal effect on ligament mechanics, evidence for muscle is confounding. While failure properties are reduced (Leitschuh et al., 1996; Van Ee et al., 2000) the elastic modulus has been reported to increase in arterial muscle tissue (Venkatasubramanian et al., 2010) but decrease in supraspinatus bone-muscle-bone units (Gottsauner-Wolf et al., 1995). Additionally, the collagenous extracellular matrix has been shown to undergo microstructural changes during freeze/thaw cycles in engineered biomaterials, indicating the significant impact this process can have on tissue mechanics (Teo et al., 2011). For this research all samples were frozen pre-rigor with surrounding tissue intact, thawed, and then tested without preconditioning, analogous to previous work in skeletal muscle that showed the modulus to not be significantly different from live tissue by this process (Van Ee et al., 2000). Thus, the data presented here may provide a good approximation of live passive tissue properties, however, should be primarily considered in the context of comparing between the testing groups.

Lastly, skeletal muscle does exhibit material anisotropy (Morrow et al., 2010, Van Loocke et al., 2006); however, at this time we chose to focus along the primary loading axis of low pennation angle tissue. Future investigation of sectioning and bathing tissue and subjecting it to tensile and/or compressive loading along various axes may help to further elucidate muscle fiber-matrix-fluid interactions.

4. Conclusions

Sectioning whole rabbit tibialis anterior muscles and disrupting the matrix-fiber network was shown to have minimal effect on tissue elastic modulus, however, deleterious effects on viscous tissue mechanics. Importantly, structural alteration resulted in a negative Poisson’s ratio following tensile loading, corroborating evidence that the extracellular matrix applies a transverse strain during loading. Bathing tissue with phosphate buffered saline during testing resulted in significantly less tissue relaxation in whole muscle samples, potentially due to hydrostatic pressure created by the surrounding fluid volume. These findings provide a new understanding of the multiscale behavior of skeletal muscle. This information can be coupled with future numerical modeling techniques to examine muscle performance and degeneration.

Highlights.

• We examine changes in passive muscle mechanics due to sub-sectioning and/or bathing.

• Sectioning resulted in a negative Poisson’s ratio.

• Elastic modulus was not affected by sectioning or bathing.

• Viscous tissue response was affected by both sectioning and bathing.

• Provides new insight into the differing mechanical characteristics of muscle tissue.