Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2014 Jan 15.
Published in final edited form as: J Neurosci Methods. 2012 Sep 29;212(1):43–55. doi: 10.1016/j.jneumeth.2012.09.018

Adaptive prior probability and spatial temporal intensity change estimation for segmentation of the one-year-old human brain

Sun Hyung Kim 1,!, Vladimir Fonov 2, Cheryl Dietrich 1, Clement Vachet 1, Heather C Hazlett 1, Rachel G Smith 1, Mike Graves 1, Joseph Piven 1, John H Gilmore 1, D Louis Collins 2; The IBIS network, Guido Gerig 3, Martin Styner 1,4
PMCID: PMC3513941  NIHMSID: NIHMS411536  PMID: 23032117

Abstract

The degree of white matter (WM) myelination is rather inhomogeneous across the brain. White matter appears differently across the cortical lobes in MR images acquired during early postnatal development. Specifically at 1-year of age, the gray/white matter contrast of MR T1 and T2 weighted images in prefrontal and temporal lobes is reduced as compared to the rest of the brain, and thus, tissue segmentation results commonly show lower accuracy in these lobes. In this novel work, we propose the use of spatial intensity growth maps (IGM) for T1 and T2 weighted images to compensate for local appearance inhomogeneity. The IGM captures expected intensity changes from 1 to 2 years of age, as appearance homogeneity is greatly improved by the age of 24 months. The IGM was computed as the coefficient of a voxel-wise linear regression model between corresponding intensities at 1 and 2 years. The proposed IGM method revealed low regression values of 1–10% in GM and CSF regions, as well as in WM regions at maturation stage of myelination at 1 year. However, in the prefrontal and temporal lobes we observed regression values of 20–25%, indicating that the IGM appropriately captures the expected large intensity change in these lobes mainly due to myelination. The IGM is applied to cross-sectional MRI datasets of 1-year-old subjects via registration, correction and tissue segmentation of the IGM-corrected dataset. We validated our approach in a small leave-one-out study of images with known, manual ‘ground truth’ segmentations.

Keywords: Myelination, Expectation Maximization algorithm, Tissue segmentation, Intensity growth map, and Partial volume estimation

INTRODUCTION

Image segmentation methods are widely used in neurodevelopmental analyses to study anatomical differences and functionalities across all ages (Gilmore et al., 2010; Gilmore et al., 2007; Hazlett et al., 2011; Knickmeyer et al., 2008; Shaw et al., 2006). Many proposed methods segment MR images into tissue classes of white matter (WM), gray matter (GM) and cerebrospinal fluid (CSF). Common approaches for segmentation include Expectation Maximization (EM) (Roche et al., 2011), Artificial Neural Network (Perez de Alejo et al., 2003) and fuzzy classification-based algorithms (Shen et al., 2005). These methods work well on images from subjects older than 2 years of age, a point in development when the WM of the brain is mature enough to appear mostly homogenous across the brain. Consequently, volumetric studies evaluating GM and WM maturation changes in full-term children have been conducted mainly in subjects older than 2 years of age (Caviness et al., 1996; Giedd et al., 1996; Sowell et al., 2004). However, they fail to accurately represent WM around 1 year of age due to the progress of myelination in WM. The progress of WM maturation is inhomogeneous across the brain, following a pattern of posterior-to-anterior lobes and superior to inferior progression (Colby et al., 2011; Tzarouchi et al., 2009). The intensity of late myelinating WM often appears similar to GM intensity, strongly affecting MRI appearance. Consequently, at 1 year of age, the prefrontal lobes and inferior temporal pole show a reduced WM/GM contrast as compared to other lobes (Figure. 1). Not surprisingly, standard tissue segmentation methods, which assume homogeneous within-class appearance across the image produce incorrect results within the prefrontal and temporal lobes even after correcting intensity nonuniformity. Commonly, white matter is under-segmented in inferior temporal and prefrontal lobe. In order to address this issue, the addition of a mixed WM/GM class or the use of regional/lobar atlases was previously proposed, often with limited success, unless paired longitudinal datasets existed (Merisaari et al., 2009; Shi et al., 2010a; Shi et al., 2010b). For the reminder of this paper, WM regions that are comparatively under-myelinated will be called immature WM.

Figure 1.

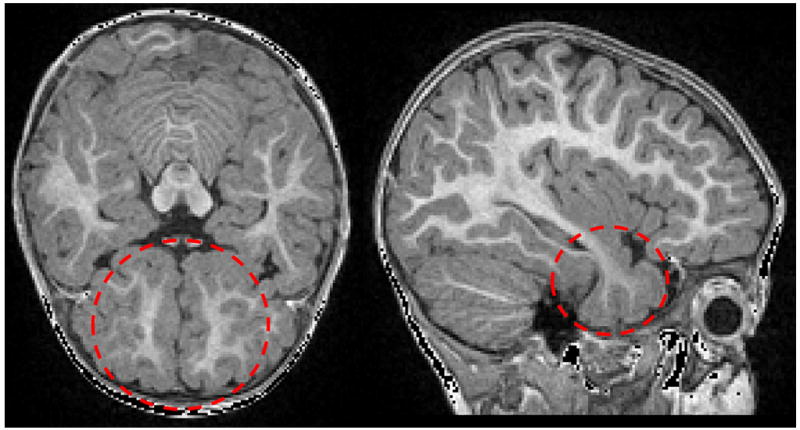
Figure 1

Open in a new tab

WM in early postnatal stage undergoes myelination that strongly affects MR appearance. The intensity of immature WM (red circles) often appears similar to GM intensity within the temporal (left: sagittal slice) and prefrontal lobes (right: transverse slice).

Related studies

There are two main categories for methods compensating of immature WM in MRIs of 1-year-olds: a classifier-based approach and an atlas-based approach. (Claude et al., 2004) proposed a classifier-based approach by segmenting immature WM parts of premature brain using a semi-automatic strategy including the pixel-wise region growing method and a novel method of image intensity gradient generation. The myelination intensity correction inside the WM was used to update Gaussian mixture model parameters for the WM cluster computation. After myelination correction, segmentation is achieved via combining several segmentation methods from a watershed segmentation-based method, rigid transformation and combination with prior probability images in the SPM2 package, and a Hidden Markov Random Field method. This method and most such classifier-based segmentation methods tend to overestimate the intensity compensation due to local over-fitting.

To reduce such overestimation, atlas-based approaches define spatial tissue priors for white matter regions at different stage of white matter maturation in a known brain atlas space. Such a brain atlas represent typical subjects at similar developmental age with a large number of often manually determined regional tissue class priors. The brain atlas image template, as well as the tissue priors, are registered and transferred to the subject image being segmented. In (Weisenfeld and Warfield, 2009), which focused on newborn MRI scans, the registration of atlas and priors are used to automatically learn subject-specific class-condition density functions, which are then fused to form an optimal estimate of the targets’ segmentation. (Shi et al., 2010a) applied an approach using atlas-based segmentation from a later time-point image of the same subject also for neonatal brain segmentation. This approach takes advantage of the fact that brain gyrification remains mainly stable during postnatal development for full-term infants. However, these segmentation results fully depend on availability of longitudinal datasets. To overcome this limitation, (Shi et al., 2010b) proposed a multi-region-multi-reference framework for atlas-based neonatal brain segmentation parcellating the average atlas into multiple regions, and applying an exemplar for image clustering into different sub-populations.

Motivation of current study

The white matter maturational process in the first few years of postnatal human life shows a relatively large degree of regional inhomogeneity (Murakami et al., 1999). At one year of age, the white matter in the prefrontal and inferior temporal lobes is at a reduced level of myelination and consequently shows reduced WM/GM contrast as compared to other cerebral regions. The purpose of this study is to develop a novel brain tissue segmentation method for cross-sectional 1-year-old MRI datasets using a novel spatial intensity growth map (IGM) that compensates for the white matter intensity appearance inhomogeneity. The proposed method is evaluated on selected T1-weighted images of 1-year-old subjects with manual ‘ground truth’ segmentations.

METHOD

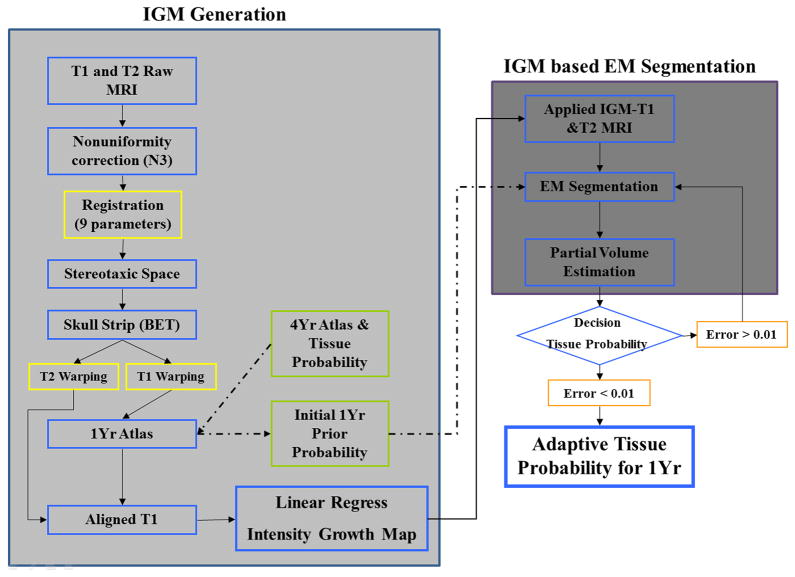
The proposed segmentation procedure is based on a local intensity changes that captures expected intensity changes from 1 to 2 years of age (see Figure 2 for an overview of the methods), The IGM is applied to MRI images by deformable registration and subsequent intensity correction (section 2.3). The modified image is then segmented with an enhanced EM-based tissue segmentation method (section 2.4). In order to achieve optimal tissue priors, we further employed an EM-like optimization of existing prior tissue probability maps to fit known expert rater segmentations (section 2.5).

Figure 2.

Figure 2

Open in a new tab

Overview of proposed IGM based segmentation method. T1 and T2 images underwent several preprocessing steps such as correction of non-uniformities, registration into common space with affine transformation and skull stripping. The IGM was calculated via regression on the paired and aligned voxels (left shaded box). Initial prior probability obtained from a deformably mapped 4-year-old atlas was adapted. These priors were finally employed for the final IGM-EM segmentation method.

Training data

The subject population employed for the creation of the proposed IGM method consisted of fourteen subjects with paired longitudinal T1− (160 slices with TR=2400ms, TE=3.16 ms, flip angle=8, field of view 256 × 256) and T2-weighted (160 slices with TR=3200ms, TE=499ms, flip angle=120, field of view 256 × 256) MR scans at 12 and 24 months. The subject scans were selected from scans acquired as part of the IBIS (Infant Brain Imaging Study) network (http://www.ibis-network.org) at 4 different sites (University of North Carolina, University of Washington at Seattle, Washington University at Saint Louis and the Children’s Hospital of Philadelphia. All datasets were acquired on 3T Siemens Tim Trio scanners at 1 × 1 × 1 mm3 resolution.

Preprocessing

The fourteen-paired T1- and T2-weighted images were first separately corrected for geometric distortions (Fonov V, 2010) as well as intensity non-uniformity (Sled et al., 1998). All T2-weighted images were rigidly registered to the corresponding T1-weighted images via mutual information registration. For cases where the automatic co-registration failed we manually initialized the registration procedure. Then both T1 and T2 were transformed to stereotaxic space based on the registration of the T1 scan. Intensity histogram equalization to reference image, 1-year-old template, was then performed on these registered images (Nyul et al., 2000). Next, the skull was extracted using FSL’s BET (Brain Extraction Tool) on all T1w images (Smith, 2002), The computed T1 brain mask was applied to the T2 image. Corresponding 1 and 2-year-old skull-stripped T1w images were next aligned with nine parameters similarity registration. The 1-year-old T1 data was then aligned with an affine followed by a thin-plate spline based deformable registration into a prior 1-year-old template data set (Collins et al., 1994; Fonov et al., 2011). Finally, the concatenated registration transformation matrix was applied to each of the T2-weighted 1-year-old image and the T1- and T2-weighted 2-year-old images. The prior atlas space employed here is an unbiased, age-appropriate (1-year) atlas template computed via joint deformable registration that simultaneously minimizes the differences of intensity and transformation from 104 training images from the 1-year-old dataset within the IBIS study (Fonov et al., 2011).

Spatial prior intensity growth map (IGM) generation

While MRI images of 1 year old subjects exhibit myelination related regional WM intensity inhomogeneity, by 2-years of age, the white matter has almost reached maturity and exhibits less intensity variation on MRI. We propose to compute a spatial prior intensity growth map (IGM) that aims at capturing this change in MR intensity from 1 to 2 years. In the preprocessing described above we established voxel-wise correspondence across subjects at 1 year of age as well as within subjects from 1 to 2 years of age in the average template space. Employing this voxel-wise correspondence, we compute the IGM in template space as the local coefficient map from a voxel-wise linear regression model between the local intensity changes at the paired 2 year and 1-year-old data in each voxel. While the common linear regression model also includes a constant term, we did not consider such a constant, as we assume consistent zero intensity for the image background at both ages.

∑j=06Yvj=αv∑j=06Xvj

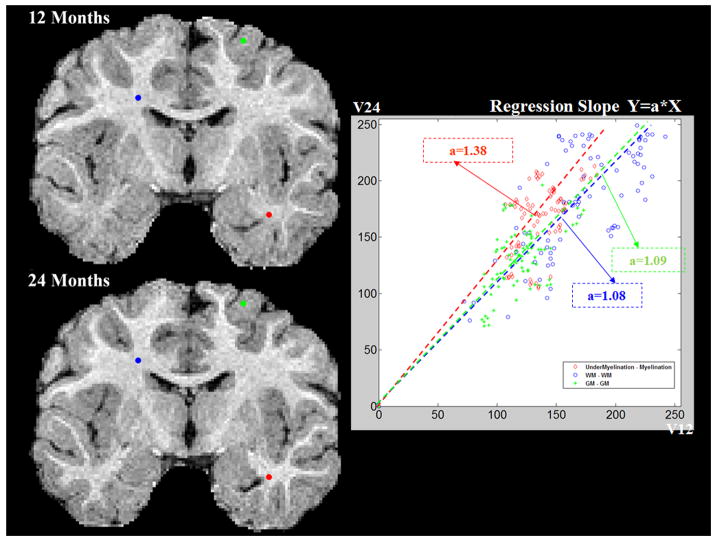
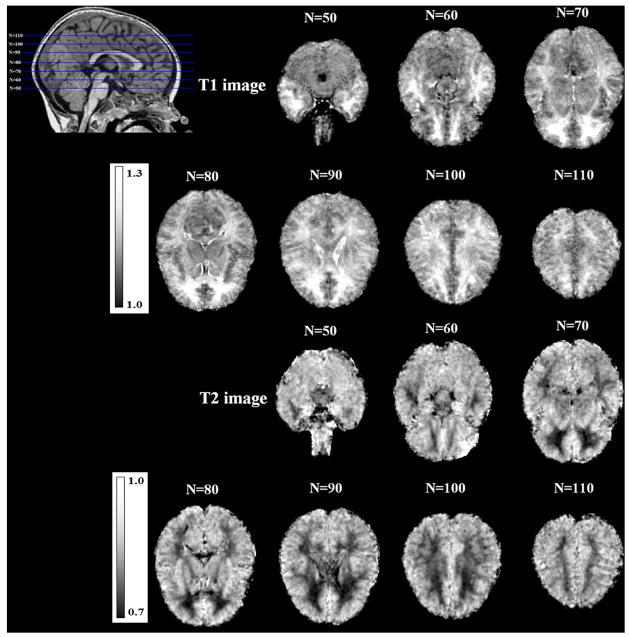
‘Yv’ denotes the intensity at 2-years of age, and ‘Xv’ at 1-year. The estimated local regression coefficients, αv, voxel v were computed over their six connected neighborhood, j, to reduce variability of the regression coefficients due to registration errors. It is noteworthy, that the proposed IGM is not directly applied as part of the tissue classification step, but rather serves as a correction factor of the original image intensities. Thus, each local coefficient was estimated voxel-wise from 7 (6+1) voxels and 14 datasets with a total of 98 samples. For T1w images, the coefficient αv is expected to show high values in areas of high intensity change and low values for those regions of moderate intensity change from 1- to 2-years of age (see Figure 3 and 4). The results for T2 images are expected to show the inverse behavior.

Figure 3.

Figure 3

Open in a new tab

Regression plots from three selected voxels. Low coefficient values are observed in gray matter areas (in green) and fully developed white matter areas (blue) between 1- and 2-year-olds, whereas high coefficient values are found in immature WM areas (red).

Figure 4.

Figure 4

Open in a new tab

The generated spatial intensity growth maps for T1 and T2 images. The dominant intensity changes are observed in the temporal and pre-frontal lobes, where the IGM shows regression coefficients of about 25%.

Enhanced EM-segmentation via IGM and WM skeletonization (IGM-EM)

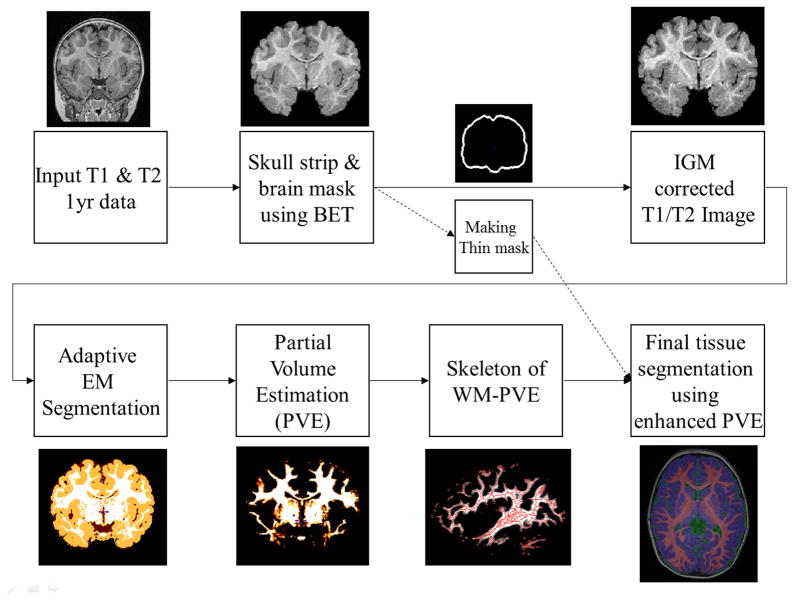
The overview of proposed IGM segmentation method is shown in Figure 5. Like most atlas based segmentation approaches, our EM segmentation registers a prior atlas template to a new subject’s T1 or T2 datasets and maps the atlas tissue priors to the subject space. Registration is achieved via a deformable, b-spline based registration optimizing local mutual information (Collins et al., 1994). In our approach, we also map the IGM map into the subject image space. The mapped T1 and T2 IGMs are then multiplied with each T1 and T2 weighted image to yield intensity corrected T1 and T2 images to serve as input to our EM-based tissue segmentation (Delignon et al., 1997). The EM framework was applied with the mapped tissue probability priors to the subject’s T1 and T2 weighted images after voxel-wise multiplication with the local IGM coefficients. The expectation step started with given Pk(0),mk(0),σk(0) from the mapped 1-year-old atlas, and we compute the probability density as Gaussian mixture model with 4 classes (WM (mature + immature WM), GM, CSF and background).

Figure 5.

Figure 5

Open in a new tab

Segmentation pipeline: Following skull stripping, the atlas template with its tissue priors and IGM map is registered into the subject image space using deformable registration. After IGM based intensity correction, partial volume estimates (PVE) are computed via adaptive EM segmentation. The skeleton of the binarized PVE map and a thin inner brain mask is employed to compute the final tissue segmentation. The inner brain mask is used to prevent WM over-estimation, especially for superior areas.

XvT1=IvT1×αvT1XvT2=IvT2×αvT2

For X =(X1, X2,…., XN) is a sample of N independent observations from a mixture of two multivariate Gaussian model (Van Leemput et al., 1999).

P(i)(k∣v)=Pk(i)g(Xv;mk(i),σk(i))∑m=1kPk(i)g(Xv;mk(i),σk(i))

Where class is represented by k (k=1,2,3,4) at EM iteration (i). This step is iterated until convergence to a local maximum of the likelihood function (D = dimension):

mk(i+1)=∑v=1NP(i)(k∣v)Xv∑v=1NP(i)(k∣v)σk(i+1)=1D∑v=1NP(i)(k∣v)||Xv-mk(i+1)||2∑v=1NP(i)(k∣v)Pk(i+1)=1N∑v=1NP(i)(k∣v)

In addition to the posterior WM, GM and CSF probability maps, our EM segmentation approach also provides a partial volume estimation map (PVE) for each tissue type (Tohka et al., 2004). As the WM is often thin and highly variable in the temporal pole and posterior occipital lobes, the application of the proposed IGM can leave those WM areas under-segmented and can lead to disconnected WM parts. To correct for this, we employed a thinning-based 1D-skeleton of the WM-PVE map binarized at an empirical threshold of 40% to further enhance the posterior WM probability by setting the WM posterior probability at the WM-PVE-skeleton Sv to 1 (Figure 6). This process did little to the overall volume (less than 1% change), but provided considerable enhancement to any potential cortical thickness analysis following the tissue segmentation.

Figure 6.

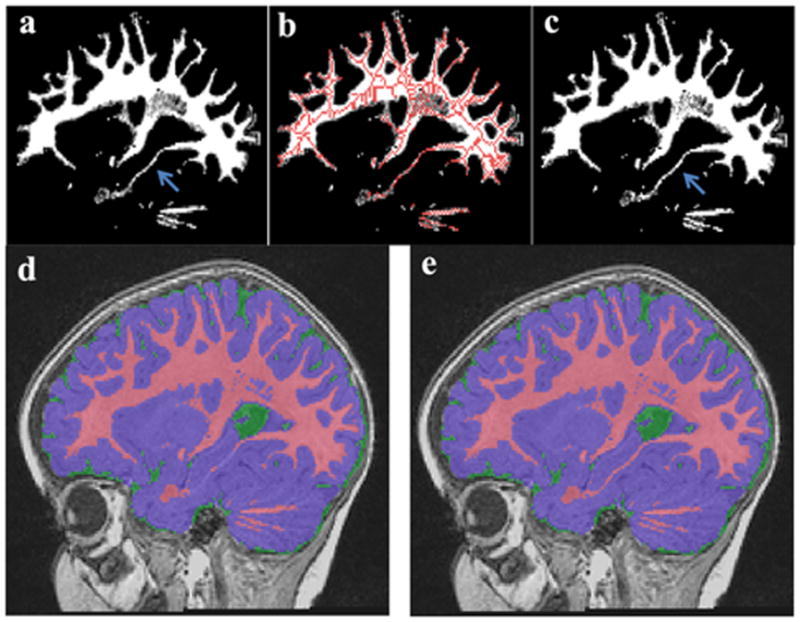
Figure 6

Open in a new tab

Partial volume estimation of WM was enhanced using skeletonization of WM with threshold 40%. The original PVE-WM (a) and the skeletonization of PVE overlap into original PVE-WM (b). Blue arrow indicates little changes in temporal areas (c). There are some missing WM areas in mid teporal lobe (d), but enhaced PVE-WM using skeltonization PVE-WM shows accurates segmentation results in mid temporal areas (e).

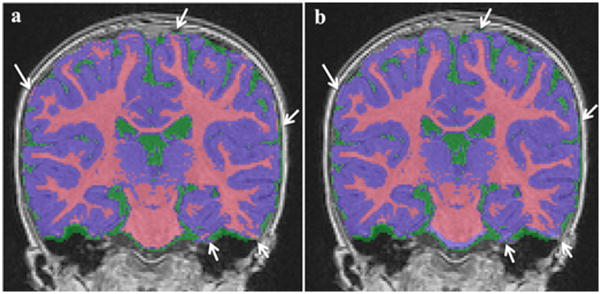
Since the topology of cerebral WM is assumed to be simply one-connected, i.e., of spherical topology, when disregarding subcortical structures, we further eliminated isolated WM voxel regions. We also observed that ringing artifacts due to motion combined with the expected, reduced GM/WM contrast in 1-year olds could lead to over-corrections during the intensity non-uniformity pre-processing step, which subsequently resulted in WM being over-segmented in superior cortical regions. To prevent such over-corrections, we employed a conservative, minimal cortex GM+CSF mask to reserve a thin layer towards the inside starting at the inner skull surface (WM+GM+CSF) only for GM and CSF. The thickness of this minimal cortex mask thickness is conservatively set at 3 mm given an expected CSF contribution of 1–2 mm in most cortical regions. Figure 7 shows the effects of cortex mask. WM segmentation errors are visible in superior parts and lateral temporal areas without the cortex mask.

Figure 7.

Figure 7

Open in a new tab

WM over-segmentation example (white arrows) without minimal cortical mask (a), corrected with cortical mask (b).

Thus, the final hard segmentation map K(v) was then computed as follows:

PVEvnewWM=min(PVEvWM+Sv,1)Sv∈{0,1}ifPVECSF(v)>0&PVECSF(v)>PVEGM(v)→K(v)=CSF,elseifM(v)>0&PVEGM(v)>0&PVEGM(v)>PVECSF(v)→K(v)=GM,elseifM(v)>0&PVEnewWM(v)>0→K(v)=GM,elseifPVEGM(v)>PVEnewWM(v)→K(v)=GM,elseifPVEnewWM(v)>0→K(v)=WM,elseK(v)=Background

Optimization of prior tissue probability maps

As is the case for all atlas based tissue classification methods, the tissue segmentation result of our IGM–EMS method is strongly dependent on the prior tissue probability maps defined in the atlas template space. In our application, the initial tissue class priors in the atlas space were determined by deformable registration of an existing 4-year-old atlas (Hazlett et al., 2011) with known probability priors into the 1-year-old atlas. Figure. 2 shows an overview of generating adapted prior probabilities for the 1-year-old atlas. The 1-year-old atlas image was created via an unbiased age-appropriate atlas building (Fonov et al., 2011) from 104 subject dataset available as part of the IBIS network (see section 2.1). The 4-year-old atlas image was then registered to this 1-year-old image via Automatic Nonlinear Image Matching and Anatomical Labeling (Collins D.L., 1995) and tissue priors were propagated to the 1-year-old atlas space. Due to the differences in local image WM/GM contrast at 1 and 4 years of age, small registration errors resulted in insufficient tissue segmentation quality especially in the prefrontal and temporal lobes. Thus, an additional step was performed to improve the prior tissue probability maps using expert manual segmentations of additional datasets.

Specifically, we selected 5 further cases from the same IBIS network study to be segmented manually by the same expert (MG) for all cases and form a standard “ground truth” dataset. These segmentation were established by extensive manual adaptation of segmentation maps computed with another atlas based EM segmentation method called ABC (http://www.nitrc.org/projects/abc/) (Prastawa et al., 2003). Using the interactive segmentation tool ITK-SNAP (http://www.itksnap.org), the expert determined manual segmentations of WM, GM and CSF on the T1 weighted images.

As the first step though to improve the propagated 4-year-old probability priors, we employed the proposed IGM-EMS segmentation of the 14 training subjects already employed in the IGM computation. The resulting segmentation maps were mapped back in the atlas space, where they were averaged voxel-wise to represent a first updated prior probability maps. Then, we employed the above described ground truth to iteratively improve the atlas tissue prior maps. For each iteration, we computed the IGM-EMS segmentations, as well as resulting difference maps to the ground truth for each tissue class (0 = correct segmentation; +q = false positive; −q = false negative, q was set at 1.0). The difference maps were transformed back to atlas space, where they were voxel-wise averaged across the 5 cases. The updated atlas prior maps were finally computed by straightforward subtraction of the difference maps. This procedure was iterated until the prior maps showed less than 1% cumulative change across all priors.

Evaluation EM segmentation with IGM

Our proposed IGM-EM segmentation method was evaluated using the same five selected datasets with expert segmentations (ground truths). In order to compare our methods against previous methods, these images were also segmented with a conventional EM approach (Delignon et al., 1997), FSL-FAST method based on a hidden Markov random field model and an associated EM algorithm (Zhang et al., 2001), and Artificial Neural Network method of the constrained Laplacian-based automated segmentation with proximities (CLASP) pipeline (Kim et al., 2005). The conventional EM method is the same basic EM method that we employed within IGM-EM (see 2.4). To allow for a fair comparison, we generated optimized prior tissue probability maps by applying the above method for each method separately. Furthermore, all segmentations were computed using a leave-one-out strategy over the prior maps, rendering the proposed evaluation fully unbiased. Thus, in order to compute the set of segmentations, we generated separate optimized prior tissue probability maps for each method and for each image using the expert segmentations in the remaining ground truth cases only. As the evaluation criterion we selected the Dice error: 1 − 2 × |X ∩ Y|/(|X| + |Y|) and Tanimoto error: 1 − |X ∩ Y|/(|X| + |Y| − |X ∩ Y|). Both of these measurements have been suggested and successfully employed in recent segmentation challenges at MICCAI conferences (Heimann et al., 2009; Styner M, 2008; van Ginneken B, 2007)

RESULTS

Intensity growth map (IGM) for correcting the intensity in immature white matter regions

As can be seen in Figure 4, the computed T1 IGM reflects the expected maturation-related MR intensity changes between 1 and 2 years. Figure. 3 represents different coefficients dependent on tissue types between 1- and 2-year-old data. GM and CSF regions, which should remain mainly unaffected by the myelination process, reveal relatively low regression coefficients αv between 1.0 and 1.1 in the T1 image. In WM regions that already underwent considerable myelination, we measured a similar coefficient αv to those in GM and CSF regions. However, in those WM areas that are known to exhibit a comparatively lower stage of myelination at 1 year of age, we observe 20–30% intensity differences between 1- and 2-year-olds (i.e. coefficients αv around 1.25). The IGM coefficients for the T2 weighted images provide the same interpretations, although inversely related to the T1 weighted IGM values. In both T1 and T2 IGMs, the superior frontal lobe, inferior temporal lobe and temporal pole changed the most. GM maturation occurs throughout the brain from inferior to superior and from posterior to anterior (Tzarouchi et al., 2009). Also, WM increase and myelination progress follow similar pattern of age-related changes (Neil et al., 2002; Xydis et al., 2006a; Xydis et al., 2006b). Finally, IGM corrected MR images of 1-year-old subjects appear visually similar to the appearance of a 2-year-old MR image (Figure 8).

Figure 8.

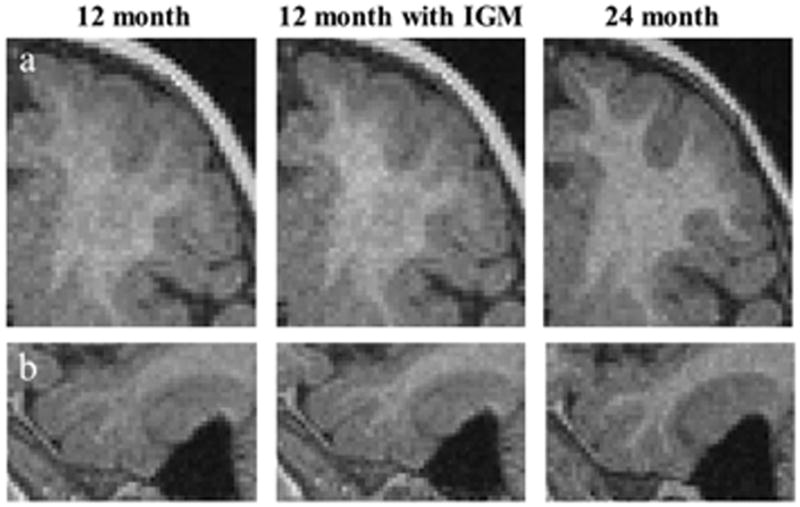
Figure 8

Open in a new tab

Applied IGM to T1 image of 12 month data (middle column) and compared with 24 month of same subject. The contrast between GM and WM improved in prefrontal area (a) and mid temporal area (b).

Prior probability for the one year old atlas

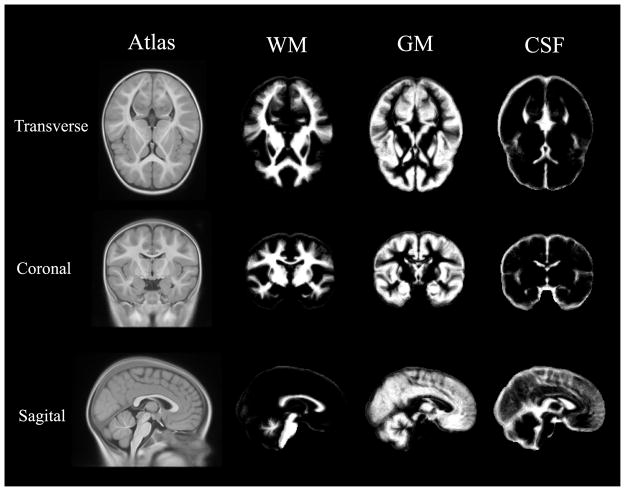
The optimized prior GM, WM and CSF probabilities converged within four iterations of the prior probability optimization procedure. The coronal view displays the optimized prior probability maps in Figure 9.

Figure 9.

Figure 9

Open in a new tab

The average 1-year-old atlas computed from IBIS data (Fonov et al, 2011) with updated tissue priors optimized for the proposed IGM enhanced segmentation method using five datasets with known ground truth segmentations.

EM segmentation with IGM

We validated the accuracy of the IGM-EM segmentation methods via five datasets with known manual segmentations employing a leave-one-out scheme for all parts of the validation. In comparison to conventional EM segmentation, a clear improvement in the inferior frontal, temporal and posterior occipital lobes is visible in Figure 10. These regions are at a lower stage of myelination and a higher anatomical variation at 1 year of age. The conventional EM without IGM tends to underestimate WM in pre-/superior frontal and inferior temporal areas due to the observed immature myelination. In contrast, our IGM-EM method appropriately segments WM in these areas. This is also visible in Figure 11, which shows the detailed performance of our proposed IGM-EM versus that of the conventional EM, FSL’s FAST and the Artificial Neural Network methods.

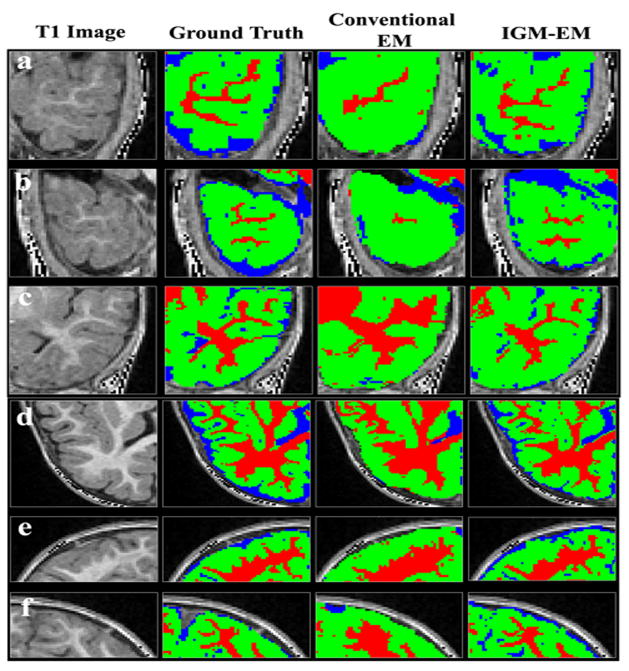
Figure 10.

Figure 10

Open in a new tab

Visual comparison of segmented results. The WM was under-estimated in prefrontal and inferior temporal lobes using the conventional EM (third column) algorithm as compared to the IGM-EM (fourth column) results and the expert ground truth. First column is the original T1 image and second column shows the ground truth. Our proposed IGM-EM obtained more accurate segmentation results in right (a) and left (b) inferior temporal lobe, right middle/superior temporal lobe (c), left superior frontal lobe (d), right (e) and left (f) occipital lobe.

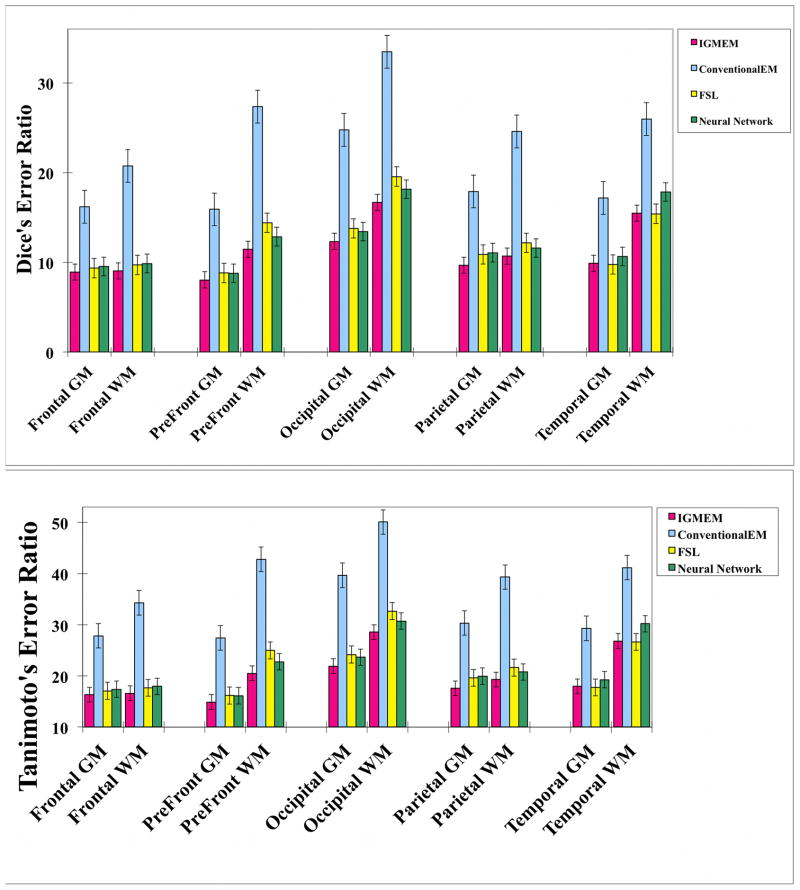
Figure 11.

Figure 11

Open in a new tab

Dice’s and Tanimoto’s coefficient error ratio was used to validate our results to the ground truth, and compared with FSL’s FAST and CLASP’s Artificial Neural Network. The IGM-EM errors are consistently lower than the ones of the other methods. The error bar shows standard error of the mean.

Overall, our proposed method provides the lowest error of all segmentation methods tested in our study. Furthermore, in areas with expected comparatively low anatomical variation, Tissue segmented results of IGM-EM have overall low Dice errors such as in the frontal (GM: 8.904, WM: 9.052), prefrontal (GM: 8.038, WM: 11.438) and parietal lobes (GM: 9.658, WM: 10.684). On the other hand, the occipital lobe (GM: 12.324, WM: 16.668) and the temporal lobe (GM: 9.872, WM: 15.48) show slightly higher error scores than the other regions.

The average Dice and Tanimoto error ratio of our proposed method has lower mean and standard deviation (GM: 9.75±1.00 and WM: 12.66±0.87) than the other algorithms: conventional EM (GM: 18.38±1.76 and WM: 26.41±3.59), FSL’s FAST (GM: 10.51±1.42 and WM: 14.24±2.34) and neural network (GM: 10.69±1.21 and WM: 14.06±1.43). FLS’s FAST also provides generally good segmentation results, though still often insufficient in handling immature WM areas. As can be seen in Figure 12, while the volumetric measurements from FSL’s FAST are closest to those of the ‘ground truth’ the Dice error is greater than for IGM-EM. For the Artificial Neural Network method, relatively low Dice and Tanimoto error ratio are observed (as compared to traditional EM) with relatively high volumetric measurement errors though.

Figure 12.

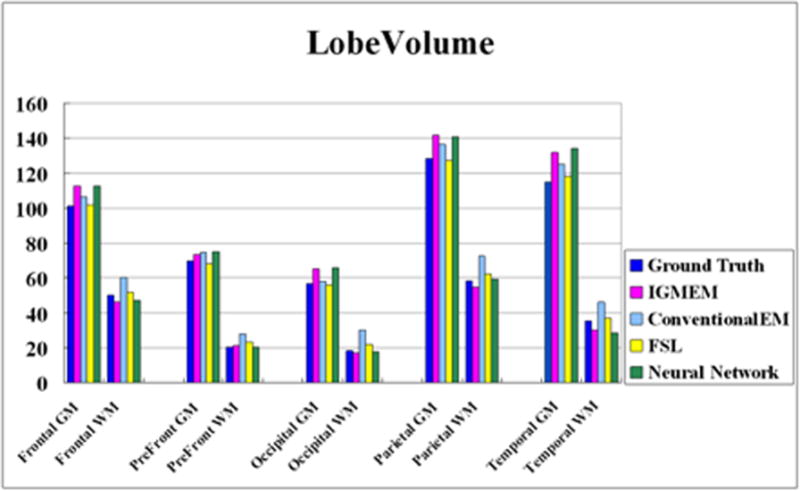
Figure 12

Open in a new tab

Lobe volume differences across the methods. All segmented lobe volumes are quite similar to those of the ground truth even if similarity scores are variable. In average, FSL’s FAST shows the most similar volume results to those of ground truth. As Dice’s and Tanimoto’s error ratios for FAST are greater than for IGM-EM or CLASP’s neural network method, FAST likely compensates false positives with false negative errors.

Using paired t-test statistics, we observed that our IGM method shows significantly higher performance than all other methods in all lobar regions except in the temporal lobe where the result of FSL is a similar with that of our proposed method. However, if all lobes are incorporated in the statistical analysis, IGM significantly outperforms FSL, whether we analyze the performance on WM (p = 0.002) and GM (p = 0.003) separately or jointly (p = 0.00004). Even though the performance of IGM and FSL is not statistically different within temporal lobe, this is likely due to the low sample size (n=5) as IGM has overall higher dice scores, as well as a lower standard deviation than FSL even within the temporal lobe (see Table 1).

Table 1.

P value indicates statistical difference of dice error ratio among the methods.

Conventional EM FSL Neural Network
IGM-EM
Total Brain (GM+WM) <0.00001 0.00004 <0.00001
Total GM <0.00001 0.00293 <0.00001
Total WM <0.00001 0.00214 <0.00001
Frontal GM+WM 0.00001 0.03338 0.00204
Prefrontal GM+WM 0.00003 0.02390 0.00015
Occipital GM+WM <0.00001 0.01076 0.00296
Parietal GM+WM 0.00002 0.01888 0.00003
Temporal GM+WM <0.00001 0.84185 0.01348
Open in a new tab

It is important to note that for all approaches evaluated here, including our IGM method, the white matter segmentation in the temporal lobe is the most challenging. In addition, IGM was additionally evaluated on 288 datasets from IBIS network study with a 93.3% success rate without need for manual correction. The main source of errors in this study is motion artifacts leading to segmentation errors in several lobes.

DISCUSSION

Accurate brain segmentation of MR datasets of subjects at 1 year of age is an important task. For example, infants, who will be diagnosed with autism at a later age, display early symptoms already at 1 year of age such as significantly less eye contact or less responsiveness to their name being called, as well as impairments in attention behaviors. Recently, researchers have shown that these symptoms closely relate to brain morphometry in lateral-temporal, superior-frontal and lateral-frontal areas using lobar volume and cortical thickness (Ozonoff et al., 2010; Yirmiya and Charman, 2010; Zwaigenbaum et al., 2005). Therefore, brain tissue volume and cortical thickness measurements, which are main components of most traditional anatomical MRI studies, need the accurate brain tissue segmentations to understand the developed brain changes at this period. However, in postnatal development, such tissue segmentation is very challenging. Here, we propose a correction and tissue segmentation methodology that allows a standard brain tissue segmentation method to handle areas at comparatively low stages of myelination in 1-year-old brain MRIs. An advantage of our proposed methods is that the effect of such late myelination is approximately corrected, resulting in more accurate segmentations.

The developmental trajectory of WM has been shown to be temporally complex and a regionally dynamic function of age. There is significant background information for the development of WM. In prior DTI studies, inferior areas have displayed lower fractional anisotropy and higher diffusivity than superior areas, indicating that myelination processes follow an inferior to superior and posterior to anterior myelination trajectory (Colby et al., 2011). Similar patterns are clearly visible in our computed IGMs. This suggests that the major intensity changes estimated in the IGMs are likely due to white matter myelination processes from 1 to 2 years of age.

Even though T1w and T2w images were obtained using same machine type and MRI protocol, image intensity variations caused by image devices itself, radio frequency field and human body are expected (Axel et al., 1987). These variations have a direct impact on any intensity-based analysis, such as the IGM segmentation method. Furthermore, the IGMs were directly calculated by regressing intensity. Therefore, to generate accurate IGMs, intensity normalization is a necessity.

When inspecting the residual errors of the IGM-EM method (Figure 13), the thalamic sub-cortical GM regions show relatively large errors. It has been demonstrated by SPECT and perfusion studies in full-term infants that the basal ganglia mature earlier than motor and sensory cortex (Takahashi et al., 1999; Tokumaru et al., 1999). In another study, slower development trajectory was observed in the thalamus compared to the basal ganglia (Tzarouchi et al., 2009). The IGM map indicates low values of intensity change from 1 to 2 year of age. Consequently, the mislabeling of thalamic areas in IGM-EM is unlikely due to a potentially uncorrected myelination effects, but rather likely due to the ambiguous intensity boundary, generally present in MR T1/T2 imagery of the thalamus.

Figure 13.

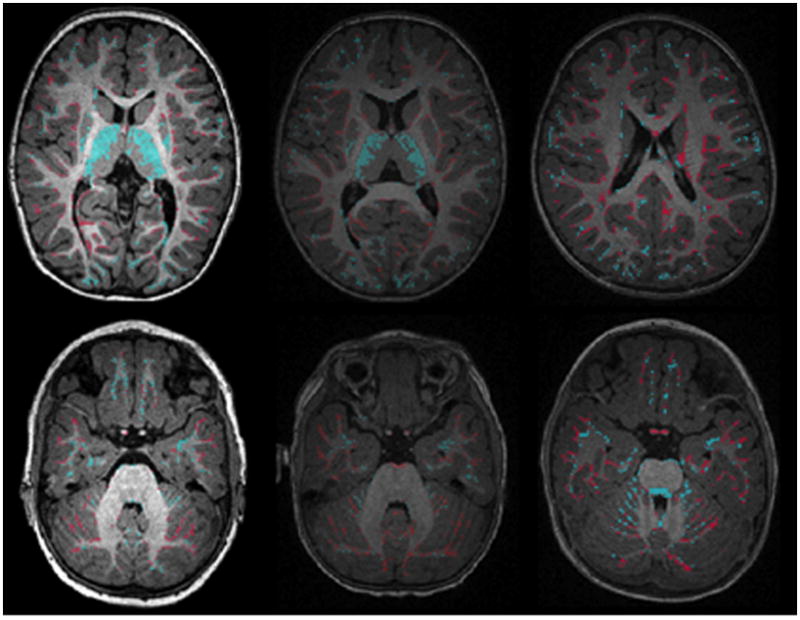
Figure 13

Open in a new tab

The difference of segmentation results between ground truth and IGM-EM. Blue areas highlight regions with white matter under-segmentation and red areas show regions of over-segmentation. The sub-cortical area, especially thalamus areas, shows mislabeling of under-estimation (blue).

Since WM maturation changes in full-term children have been conducted mainly in subjects older than 2 years of age, conventional segmentation approaches commonly show good performance in that age range, though not at the younger age of 1-year. While our IGM-method has been developed specifically for the appropriate segmentation of immature WM regions in MR images of 1-year-old subjects, a similar approach could be employed for the segmentation of datasets in younger ages, potentially up to 6–8 months. It is though unlikely that this method could be straightforwardly extended to even younger ages due the age related white-gray matter contrast inversion.

It further noteworthy, that through the use of a prior atlas with expected intensity changes, the proposed IGM approach introduces a segmentation bias towards the average brain morphometry. This bias is expected to be present in IGM results in addition to existing biases originating from the standard atlas based EM scheme. In most current neuroimaging studies, tissue segmentation methods employ atlases with its tissue prior probabilities, which introduces a well-known, inherent bias towards average morphometry, such as in the widely used FSL and ABC packages. Even small changes to the tissue priors or the atlas anatomical image will result in potentially considerable changes in the segmentations. While the additional intensity change prior in IGM provides further bias in a similar sense, we expect its effects to be considerably smaller than the known bias in standard atlas based tissue segmentation methods. When we tested IGM vs non-IGM versions of the same EM algorithm, we could not detect (visually) any consistent additional bias towards the average morphometry.

We are currently extending the proposed IGM by selectively applying an IGM to white-matter only local intensity correction (based on the observed WM posterior) that is incorporated into the EM segmentation loop, as the major contrast changes are limited to the white matter. Such a scheme would not provide a direct additional bias to non-white matter tissue classes, such as CSF and GM.

In summary, we have presented and validated an IGM method for segmentation in MRIs of 1-year-old. This strategy is a straightforward, but effective method. The method is original in that a prior training map, which was calculated using the paired MRIs, is applied for the compensation of intensity values in immature WM regions. Novelty is also present in the adaptive morphological segmentation post-processing designed for 1-year-old MRI.

Highlights.

  1. We propose the intensity growth maps (IGM) to perform segmentation of one-year old data.

  2. The IGM captured intensity changes of 20–25% in immature WM regions.

  3. We generate adaptive tissue probability map of one-year old data using IGM.

  4. IGM-EM has a dice error ratio, GM: 9.75 and WM: 12.66.

  5. The results of IGM-EM show good performance in temporal and prefrontal lobe areas.

Acknowledgments

Funding was provided primarily from the IBIS (Infant Brain Imaging Study) Network, an NIH funded Autism Center of Excellence (HDO55741) that consists of a consortium of 7 Universities in the U.S. and Canada. Clinical Sites: University of North Carolina: J. Piven (IBIS Network PI), H.C. Hazlett, C. Chappell; University of Washington: S. Dager, A. Estes; Washington University: K. Botteron, R. McKinstry, J. Contstantino, L. Flake; Children’s Hospital of Philadelphia: R. Schultz, S. Paterson; University of Alberta: L. Zwaigenbaum. Data Coordinating Center: Montreal Neurological Institute: A. Evans, L. Collins, B. Pike, R. Aleong, S. Das. Image Processing Core: University of Utah: G. Gerig; University of North Carolina: M. Styner. Statistical Analysis Core: University of North Carolina: H. Gu. Genetics Analysis Core: University of North Carolina: P. Sullivan, F. Wright.

Additional support is provided by the following grants: NIH grants P50 MH 064065 (JHG, MAS), MH070890 (JHG, MAS), HD053000 (JHG), and UNC Intellectual and Developmental Disabilities Research Center P30 HD03110 (MAS, SJS), R01 MH091645 (MAS), NIH Roadmap Grant U54 EB005149-01 (MAS).

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Axel L, Costantini J, Listerud J. Intensity correction in surface-coil MR imaging. AJR American journal of roentgenology. 1987;148:418–20. doi: 10.2214/ajr.148.2.418. [DOI] [PubMed] [Google Scholar]
  2. Caviness VS, Jr, Kennedy DN, Richelme C, Rademacher J, Filipek PA. The human brain age 7–11 years: a volumetric analysis based on magnetic resonance images. Cereb Cortex. 1996;6:726–36. doi: 10.1093/cercor/6.5.726. [DOI] [PubMed] [Google Scholar]
  3. Claude I, Daire JL, Sebag G. Fetal brain MRI: segmentation and biometric analysis of the posterior fossa. IEEE transactions on bio-medical engineering. 2004;51:617–26. doi: 10.1109/TBME.2003.821032. [DOI] [PubMed] [Google Scholar]
  4. Colby JB, Van Horn JD, Sowell ER. Quantitative in vivo evidence for broad regional gradients in the timing of white matter maturation during adolescence. NeuroImage. 2011;54:25–31. doi: 10.1016/j.neuroimage.2010.08.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Collins DLHCJ, Peters TM, Evans AC. Automatic 3D model-based neuroanatomical segmentation. Human brain mapping. 1995;3:190–208. [Google Scholar]
  6. Collins DL, Neelin P, Peters TM, Evans AC. Automatic 3D intersubject registration of MR volumetric data in standardized Talairach space. Journal of computer assisted tomography. 1994;18:192–205. [PubMed] [Google Scholar]
  7. Delignon Y, Marzouki A, Pieczynski W. Estimation of generalized mixtures and its application in image segmentation. IEEE transactions on image processing: a publication of the IEEE Signal Processing Society. 1997;6:1364–75. doi: 10.1109/83.624951. [DOI] [PubMed] [Google Scholar]
  8. Fonov V, Evans AC, Botteron K, Almli CR, McKinstry RC, Collins DL. Unbiased average age-appropriate atlases for pediatric studies. NeuroImage. 2011;54:313–27. doi: 10.1016/j.neuroimage.2010.07.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Fonov VJA, Caramanos Z, Arnold D, Narayanan S, Pike G, Collins D. Improved Precision in the Measurement of Longitudinal Global and Regional Volumetric Changes via a Novel MRI Gradient Distortion Characterization and Correction Technique. MIAR 2010. 2010 [Google Scholar]
  10. Giedd JN, Snell JW, Lange N, Rajapakse JC, Casey BJ, Kozuch PL, Vaituzis AC, Vauss YC, Hamburger SD, Kaysen D, Rapoport JL. Quantitative magnetic resonance imaging of human brain development: ages 4–18. Cereb Cortex. 1996;6:551–60. doi: 10.1093/cercor/6.4.551. [DOI] [PubMed] [Google Scholar]
  11. Gilmore JH, Kang C, Evans DD, Wolfe HM, Smith JK, Lieberman JA, Lin W, Hamer RM, Styner M, Gerig G. Prenatal and neonatal brain structure and white matter maturation in children at high risk for schizophrenia. The American journal of psychiatry. 2010;167:1083–91. doi: 10.1176/appi.ajp.2010.09101492. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Gilmore JH, Lin W, Prastawa MW, Looney CB, Vetsa YS, Knickmeyer RC, Evans DD, Smith JK, Hamer RM, Lieberman JA, Gerig G. Regional gray matter growth, sexual dimorphism, and cerebral asymmetry in the neonatal brain. The Journal of neuroscience: the official journal of the Society for Neuroscience. 2007;27:1255–60. doi: 10.1523/JNEUROSCI.3339-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Hazlett HC, Poe MD, Gerig G, Styner M, Chappell C, Smith RG, Vachet C, Piven J. Early brain overgrowth in autism associated with an increase in cortical surface area before age 2 years. Archives of general psychiatry. 2011;68:467–76. doi: 10.1001/archgenpsychiatry.2011.39. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Heimann T, van Ginneken B, Styner MA, Arzhaeva Y, Aurich V, Bauer C, Beck A, Becker C, Beichel R, Bekes G, Bello F, Binnig G, Bischof H, Bornik A, Cashman PM, Chi Y, Cordova A, Dawant BM, Fidrich M, Furst JD, Furukawa D, Grenacher L, Hornegger J, Kainmuller D, Kitney RI, Kobatake H, Lamecker H, Lange T, Lee J, Lennon B, Li R, Li S, Meinzer HP, Nemeth G, Raicu DS, Rau AM, van Rikxoort EM, Rousson M, Rusko L, Saddi KA, Schmidt G, Seghers D, Shimizu A, Slagmolen P, Sorantin E, Soza G, Susomboon R, Waite JM, Wimmer A, Wolf I. Comparison and evaluation of methods for liver segmentation from CT datasets. IEEE transactions on medical imaging. 2009;28:1251–65. doi: 10.1109/TMI.2009.2013851. [DOI] [PubMed] [Google Scholar]
  15. Kim JS, Singh V, Lee JK, Lerch J, Ad-Dab’bagh Y, MacDonald D, Lee JM, Kim SI, Evans AC. Automated 3-D extraction and evaluation of the inner and outer cortical surfaces using a Laplacian map and partial volume effect classification. NeuroImage. 2005;27:210–21. doi: 10.1016/j.neuroimage.2005.03.036. [DOI] [PubMed] [Google Scholar]
  16. Knickmeyer RC, Gouttard S, Kang C, Evans D, Wilber K, Smith JK, Hamer RM, Lin W, Gerig G, Gilmore JH. A structural MRI study of human brain development from birth to 2 years. The Journal of neuroscience: the official journal of the Society for Neuroscience. 2008;28:12176–82. doi: 10.1523/JNEUROSCI.3479-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Merisaari H, Parkkola R, Alhoniemi E, Teras M, Lehtonen L, Haataja L, Lapinleimu H, Nevalainen OS. Gaussian mixture model-based segmentation of MR images taken from premature infant brains. Journal of neuroscience methods. 2009;182:110–22. doi: 10.1016/j.jneumeth.2009.05.026. [DOI] [PubMed] [Google Scholar]
  18. Murakami JW, Weinberger E, Shaw DW. Normal myelination of the pediatric brain imaged with fluid-attenuated inversion-recovery (FLAIR) MR imaging. Ajnr. 1999;20:1406–11. [PMC free article] [PubMed] [Google Scholar]
  19. Neil J, Miller J, Mukherjee P, Huppi PS. Diffusion tensor imaging of normal and injured developing human brain - a technical review. NMR in biomedicine. 2002;15:543–52. doi: 10.1002/nbm.784. [DOI] [PubMed] [Google Scholar]
  20. Nyul LG, Udupa JK, Zhang X. New variants of a method of MRI scale standardization. IEEE transactions on medical imaging. 2000;19:143–50. doi: 10.1109/42.836373. [DOI] [PubMed] [Google Scholar]
  21. Ozonoff S, Iosif AM, Baguio F, Cook IC, Hill MM, Hutman T, Rogers SJ, Rozga A, Sangha S, Sigman M, Steinfeld MB, Young GS. A prospective study of the emergence of early behavioral signs of autism. Journal of the American Academy of Child and Adolescent Psychiatry. 2010;49:256–66. e1–2. [PMC free article] [PubMed] [Google Scholar]
  22. Perez de Alejo R, Ruiz-Cabello J, Cortijo M, Rodriguez I, Echave I, Regadera J, Arrazola J, Aviles P, Barreiro P, Gargallo D, Grana M. Computer-assisted enhanced volumetric segmentation magnetic resonance imaging data using a mixture of artificial neural networks. Magnetic resonance imaging. 2003;21:901–12. doi: 10.1016/s0730-725x(03)00193-0. [DOI] [PubMed] [Google Scholar]
  23. Prastawa M, Bullitt E, Moon N, Van Leemput K, Gerig G. Automatic brain tumor segmentation by subject specific modification of atlas priors. Academic radiology. 2003;10:1341–8. doi: 10.1016/s1076-6332(03)00506-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Roche A, Ribes D, Bach-Cuadra M, Kruger G. On the convergence of EM-like algorithms for image segmentation using Markov random fields. Medical image analysis. 2011;15:830–9. doi: 10.1016/j.media.2011.05.002. [DOI] [PubMed] [Google Scholar]
  25. Shaw P, Greenstein D, Lerch J, Clasen L, Lenroot R, Gogtay N, Evans A, Rapoport J, Giedd J. Intellectual ability and cortical development in children and adolescents. Nature. 2006;440:676–9. doi: 10.1038/nature04513. [DOI] [PubMed] [Google Scholar]
  26. Shen S, Sandham W, Granat M, Sterr A. MRI fuzzy segmentation of brain tissue using neighborhood attraction with neural-network optimization. IEEE transactions on information technology in biomedicine: a publication of the IEEE Engineering in Medicine and Biology Society. 2005;9:459–67. doi: 10.1109/titb.2005.847500. [DOI] [PubMed] [Google Scholar]
  27. Shi F, Fan Y, Tang S, Gilmore JH, Lin W, Shen D. Neonatal brain image segmentation in longitudinal MRI studies. NeuroImage. 2010a;49:391–400. doi: 10.1016/j.neuroimage.2009.07.066. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Shi F, Yap PT, Fan Y, Gilmore JH, Lin W, Shen D. Construction of multi-region-multi-reference atlases for neonatal brain MRI segmentation. NeuroImage. 2010b;51:684–93. doi: 10.1016/j.neuroimage.2010.02.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Sled JG, Zijdenbos AP, Evans AC. A nonparametric method for automatic correction of intensity nonuniformity in MRI data. IEEE transactions on medical imaging. 1998;17:87–97. doi: 10.1109/42.668698. [DOI] [PubMed] [Google Scholar]
  30. Smith SM. Fast robust automated brain extraction. Human brain mapping. 2002;17:143–55. doi: 10.1002/hbm.10062. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Sowell ER, Thompson PM, Leonard CM, Welcome SE, Kan E, Toga AW. Longitudinal mapping of cortical thickness and brain growth in normal children. J Neurosci. 2004;24:8223–31. doi: 10.1523/JNEUROSCI.1798-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Styner MLJ, Chin B, Chin MS, Commowick O, Tran H-H, Markovic-Plese S, Jewells V, Warfield S. 3D Segmentation in the Clinic: A Grand Challenge II: MS lesion segmentation. Insight Journal. 2008:1–6. http://hdl.handle.net/10380/1509.
  33. Takahashi T, Shirane R, Sato S, Yoshimoto T. Developmental changes of cerebral blood flow and oxygen metabolism in children. Ajnr. 1999;20:917–22. [PMC free article] [PubMed] [Google Scholar]
  34. Tohka J, Zijdenbos A, Evans A. Fast and robust parameter estimation for statistical partial volume models in brain MRI. NeuroImage. 2004;23:84–97. doi: 10.1016/j.neuroimage.2004.05.007. [DOI] [PubMed] [Google Scholar]
  35. Tokumaru AM, Barkovich AJ, O’Uchi T, Matsuo T, Kusano S. The evolution of cerebral blood flow in the developing brain: evaluation with iodine-123 iodoamphetamine SPECT and correlation with MR imaging. Ajnr. 1999;20:845–52. [PMC free article] [PubMed] [Google Scholar]
  36. Tzarouchi LC, Astrakas LG, Xydis V, Zikou A, Kosta P, Drougia A, Andronikou S, Argyropoulou MI. Age-related grey matter changes in preterm infants: an MRI study. NeuroImage. 2009;47:1148–53. doi: 10.1016/j.neuroimage.2009.03.072. [DOI] [PubMed] [Google Scholar]
  37. van Ginneken BHT, Styner MA. Segmentation in the Clinic: A Grand Challenge. Workshop on 3D Segmentation in the Clinic. MICCAI. 2007:7–15. [Google Scholar]
  38. Van Leemput K, Maes F, Vandermeulen D, Suetens P. Automated model-based tissue classification of MR images of the brain. IEEE transactions on medical imaging. 1999;18:897–908. doi: 10.1109/42.811270. [DOI] [PubMed] [Google Scholar]
  39. Weisenfeld NI, Warfield SK. Automatic segmentation of newborn brain MRI. NeuroImage. 2009;47:564–72. doi: 10.1016/j.neuroimage.2009.04.068. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Xydis V, Astrakas L, Drougia A, Gassias D, Andronikou S, Argyropoulou M. Myelination process in preterm subjects with periventricular leucomalacia assessed by magnetization transfer ratio. Pediatric radiology. 2006a;36:934–9. doi: 10.1007/s00247-006-0235-x. [DOI] [PubMed] [Google Scholar]
  41. Xydis V, Astrakas L, Zikou A, Pantou K, Andronikou S, Argyropoulou MI. Magnetization transfer ratio in the brain of preterm subjects: age-related changes during the first 2 years of life. European radiology. 2006b;16:215–20. doi: 10.1007/s00330-005-2796-8. [DOI] [PubMed] [Google Scholar]
  42. Yirmiya N, Charman T. The prodrome of autism: early behavioral and biological signs, regression, peri- and post-natal development and genetics. Journal of child psychology and psychiatry, and allied disciplines. 2010;51:432–58. doi: 10.1111/j.1469-7610.2010.02214.x. [DOI] [PubMed] [Google Scholar]
  43. Zhang YY, Brady M, Smith S. Segmentation of brain MR images through a hidden Markov random field model and the expectation-maximization algorithm. IEEE transactions on medical imaging. 2001;20:45–57. doi: 10.1109/42.906424. [DOI] [PubMed] [Google Scholar]
  44. Zwaigenbaum L, Bryson S, Rogers T, Roberts W, Brian J, Szatmari P. Behavioral manifestations of autism in the first year of life. International journal of developmental neuroscience: the official journal of the International Society for Developmental Neuroscience. 2005;23:143–52. doi: 10.1016/j.ijdevneu.2004.05.001. [DOI] [PubMed] [Google Scholar]

RESOURCES