The Extrinsic and Intrinsic Functional Architectures of the Human Brain Are Not Equivalent

Abstract

The brain's intrinsic functional architecture, revealed in correlated spontaneous activity, appears to constitute a faithful representation of its repertoire of evoked, extrinsic functional interactions. Here, using broad task contrasts to probe evoked patterns of coactivation, we demonstrate tight coupling between the brain's intrinsic and extrinsic functional architectures for default and task-positive regions, but not for subcortical and limbic regions or for primary sensory and motor cortices. While strong correspondence likely reflects persistent or recurrent patterns of evoked coactivation, weak correspondence may exist for regions whose patterns of evoked functional interactions are more adaptive and context dependent. These findings were independent of task. For tight task contrasts (e.g., incongruent vs. congruent trials), evoked patterns of coactivation were unrelated to the intrinsic functional architecture, suggesting that high-level task demands are accommodated by context-specific modulations of functional interactions. We conclude that intrinsic approaches provide only a partial understanding of the brain's functional architecture. Appreciating the full repertoire of dynamic neural responses will continue to require task-based functional magnetic resonance imaging approaches.

Introduction

Large-scale functional systems revealed by task-based and task-free (“resting state”) functional magnetic resonance imaging (fMRI) appear strikingly similar, despite marked differences in the phenomena they measure. The strong correspondence between the brain's extrinsic (task-evoked) and the intrinsic (task-free, spontaneous) architecture suggests that the brain's intrinsic functional architecture provides a framework for its moment-to-moment responses to the external world (Fox et al. 2006; Raichle 2010). Accordingly, Smith et al. (2009, p. 13040) proposed that “the full repertoire of functional networks utilized by the brain in action is continuously and dynamically ‘active’ even when at ‘rest’.” Such assertions raise classic cognitive neuroscience questions about the extent to which functional interactions among brain regions are fixed and invariant or dynamic and flexible.

Evidence for the linkage between the brain's intrinsic and extrinsic architectures remains preliminary. Initial studies suggested strong correspondence between intrinsic connectivity networks derived on the basis of resting-state data and task-evoked coactivation networks detected using large-scale meta-analytic approaches (Toro et al. 2008; Smith et al. 2009). Although powerful, task-based meta-analytic approaches cannot capture covariation in task-evoked hemodynamic responses across trials, which would more closely parallel the temporal phenomena that form the basis of intrinsic connectivity approaches. Building on these findings, recent studies have documented the relationship between intrinsic connectivity networks and task-evoked activation at the individual participant level (Mennes et al. 2010; Gordon et al. forthcoming). These studies focused on intrinsic connectivity at a macro network level, investigating networks that were data driven (Gordon et al. forthcoming) or derived from a priori selected regions of interest (Mennes et al. 2010).

Here, we investigated regional variation in the degree to which patterns of task-evoked functional interactions mirror the brain's intrinsic functional architecture, using a voxelwise approach. This was accomplished at the participant level by computing the spatial correlation between patterns of intrinsic functional connectivity (iFC) and patterns of task-evoked functional connectivity (or coactivation; eFC) for each voxel in the brain. iFC was defined as the correlation between each gray matter voxel's resting-state time series and that of every other gray matter voxel in the brain. Likewise, eFC was defined as the pairwise correlation between each voxel's trialwise task-evoked hemodynamic responses. Trialwise task-evoked responses were estimated using regression, where individual trials were modeled as independent predictors, yielding a time series of evoked response estimates (Rissman et al. 2004). Finally, we correlated iFC-eFC patterns on a within-subject voxelwise basis quantifying the similarity between patterns of intrinsic and task-evoked functional interactions.

To ensure generalizability, we applied this approach to 3 data sets each including a resting-state scan and specific task: 1) an “Eriksen Flanker” task, 2) a “Simon Stimulus-Response Compatibility” task, and 3) a “Risky Decision-Making” task (for details, see Supplementary Methods and for task-evoked activity maps, see Supplementary Fig. 1). Twenty-one participants in the “Flanker” and “Decision-Making” data sets overlapped. The “Simon” data set constituted an independent sample. Finally, we assessed iFC-iFC similarity using resting-state scans collected ∼45 min and 5–16 months apart in the same participants (Shehzad et al. 2009).

Materials and Methods

Participants

We included 3 task data sets that differed with respect to task paradigm and participant sample. All participants were adults without a history of psychiatric or neurological illness as confirmed by psychiatric assessment. Written informed consent was obtained prior to participation as approved by the institutional review boards of New York University (NYU) and the NYU School of Medicine.

Twenty-six participants (mean age 28.5 ± 8.5 years, 11 males) completed a slow event-related Eriksen Flanker task scan, 21 participants (mean age: 30.5 ± 7.3 years, 12 males) completed a rapid event-related Simon stimulus-response compatibility task scan, and 24 participants (mean age: 29.9 ± 8.5 years, 16 males) completed a rapid event-related Risky Decision-Making task scan. In addition, all participants completed a brief (6.5 min) resting-state scan during which they were asked to relax while keeping their eyes open. The order of the resting-state and task scans was counterbalanced across participants. A subset of 21 participants (including 6 participants who did not complete any task scans) completed 3 resting-state scans (test–retest resting state). Two scans were completed in the same session (i.e., ∼45 min apart), while the third scan was completed 5–16 months prior to the first 2. In total, task data were collected from 50 unique participants. The 21 participants who completed the Simon task did not complete the Eriksen Flanker or Risky Decision-Making tasks. Five participants completed only the Eriksen Flanker task, while 3 completed only the Risky Decision-Making task. Of the 21 participants who completed the test–retest resting-state scans, 6 did not complete any of the task scans. Additional details on the task paradigms and participant overlap between data sets are available in Supplementary Methods.

Image Acquisition

All scans were acquired using a standard Siemens head coil on a Siemens Allegra 3.0-T scanner. fMRI scans were collected as contiguous echo planar imaging whole-brain volumes, and for spatial normalization and localization we obtained a high-resolution T₁-weighted magnetization prepared gradient echo sequence from each participant. Acquisition and image preprocessing details are provided in Supplementary Methods.

General Analyses Description

We defined iFC as the temporal correlation between voxels’ resting-state fMRI time series and eFC as the correlation between voxels’ task-evoked hemodynamic responses across trials. Only voxels that had a probability of being gray matter exceeding 25% in the FSL avg152 gray matter tissueprior were included in our analyses. Preprocessing and analysis specifics are provided in Supplementary Methods.

eFC Time Series extraction

After preprocessing the task scans, we conducted a participant-level multiple regression for each task, modeling trials as individual predictors (Rissman et al. 2004; see Supplementary Methods) and comparing them to all remaining activity (i.e., fixation or intertrial intervals, hereafter referred to as “baseline”). Using this method, we obtained an estimated evoked response (beta value) for each trial that was used to construct a time series of estimated trialwise evoked responses. This time series allowed us to calculate voxelwise eFC maps. Only correctly answered trials were modeled in the participant-level multiple regression. For the Eriksen Flanker, this procedure resulted in beta values for each of 24 congruent and 24 incongruent trials if all trials were answered correctly. The method developed by Rissman et al. (2004) was originally devised for the analysis of slow event-related designs but can be applied to rapid event-related designs. However, applying this method to rapid event-related designs may lead to inadequate beta estimation for consecutive trials due to summation of the blood oxygen–level dependent (BOLD) signal, especially when trials are closely spaced in time. To minimize estimation losses due to BOLD signal overlap inherent to the rapid event-related designs employed for the Simon and Risky Decision-Making tasks, we optimized response estimation by randomly grouping 4 trials of the same type into a predictor instead of modeling each trial separately. Each trial was included only once. In the Simon task, we randomly grouped trials counterbalancing for the previously presented trial, resulting in beta values for each of 24 congruent and 24 incongruent “trials.” In the Risky Decision-Making task, beta values were obtained for 42 decision and 42 feedback predictors, each including 4 randomly selected decision or feedback events. Beta value time series were registered to 3 mm Montreal Neurological Institute (MNI)152 standard space prior to eFC calculations.

iFC-eFC Relationship Computations

After registering each participant's preprocessed resting-state scan to 3 mm MNI152 standard space, we generated each voxels’ iFC map by correlating its resting-state time series with that of every other gray matter voxel. Similarly, we calculated the eFC map for each gray matter voxel, by correlating each voxel's beta value time series quantifying the magnitude of task-evoked responses with the beta value time series of every other gray matter voxel.

Subsequently, for each participant, we calculated the spatial correlation between each voxel's iFC and eFC map. This analysis resulted in a map for each participant that indexed for every voxel how similar its pattern of task-evoked functional interactions (eFC map) was to its intrinsic functional architecture (iFC map).

For the Risky Decision-Making task, we calculated eFC maps for the decision and feedback trials separately (decision vs. baseline; feedback vs. baseline). For the Eriksen Flanker and Simon task we included eFC maps calculated across congruent and incongruent trials (congruent + incongruent vs. baseline) as well as iFC-eFC relationships obtained using eFC maps calculated for each trial type separately and for “tight” comparisons. For the latter, we calculated eFC maps for incongruent versus congruent by subtracting each voxel's eFC map obtained for congruent trials from the eFC map obtained for incongruent trials.

To identify those voxels whose iFC-eFC correlation was significantly different from 0 across participants, we conducted group-level analyses for every data set using FSL FEAT. The resulting zstat maps were corrected for multiple comparisons using Gaussian Random Field theory (Z > 2.3, P < 0.05 corrected). Overall mean iFC-eFC relationships were compared between data sets in a one-way analysis of variance including data set as factor (P < 0.05).

Finally, we assessed the generalizability of the iFC-eFC relationship topography by calculating the spatial correlation between the mean iFC-eFC correlation maps obtained for each data set.

iFC-eFC Relationship versus Noise

We confirmed that the observed iFC-eFC relationships were not driven by regional differences in temporal signal-to-noise ratio (SNR) or by differences in SNR between the resting-state and the task scans. To investigate regional differences in temporal SNR, we calculated the relationship across voxels between the mean iFC-eFC map (averaged across participants) and the mean SNR map (averaged across participants). For the resting-state scan and task-based beta time series of each participant, we calculated SNR maps by dividing the mean of the time series by their standard deviation (SD). After z-transforming the participant-level SNR maps, we created mean SNR maps by averaging across participants within each sample. To assess the influence of regional differences in SNR between the resting-state and the task scans on the iFC-eFC relationship, we performed paired t-tests comparing for each sample the resting-state SNR maps with the task-based beta time series SNR maps. Next, we calculated the relationship across voxels between the obtained t-scores and the mean iFC-eFC map.

Beyond considering potential relationships between the regional variation in SNR and the iFC-eFC topography, we also considered possible relationships between the iFC-eFC topography and the fractional amplitude of low-frequency fluctuations (fALFF). fALFF is an index of the temporal dynamics of spontaneous BOLD fMRI activity, with robust regional variation independent of vascular effects (Zuo, Di Martino, et al. 2010). Specifically, fALFF expresses the power of the low-frequency fluctuations (0.01–0.1 Hz) as a proportion of the power of the total frequency range available in the BOLD signal (Zuo, Di Martino, et al. 2010). After calculating an fALFF map for each participant's resting-state scan, we correlated each sample's mean fALFF map (averaged across participants) with that sample's mean iFC-eFC map (averaged across participants).

Results

Significant iFC-eFC correlations were ubiquitous. Regardless of task, group-level analyses revealed significant iFC-eFC relationships for >96% of voxels (Z > 2.3, P < 0.05 corrected for multiple comparisons). Overall mean iFC-eFC correlations did not vary significantly between task data sets but were significantly lower than the mean iFC-iFC correlations obtained by comparing the resting-state data sets (P < 0.001; Fig. 1).

Figure 1.

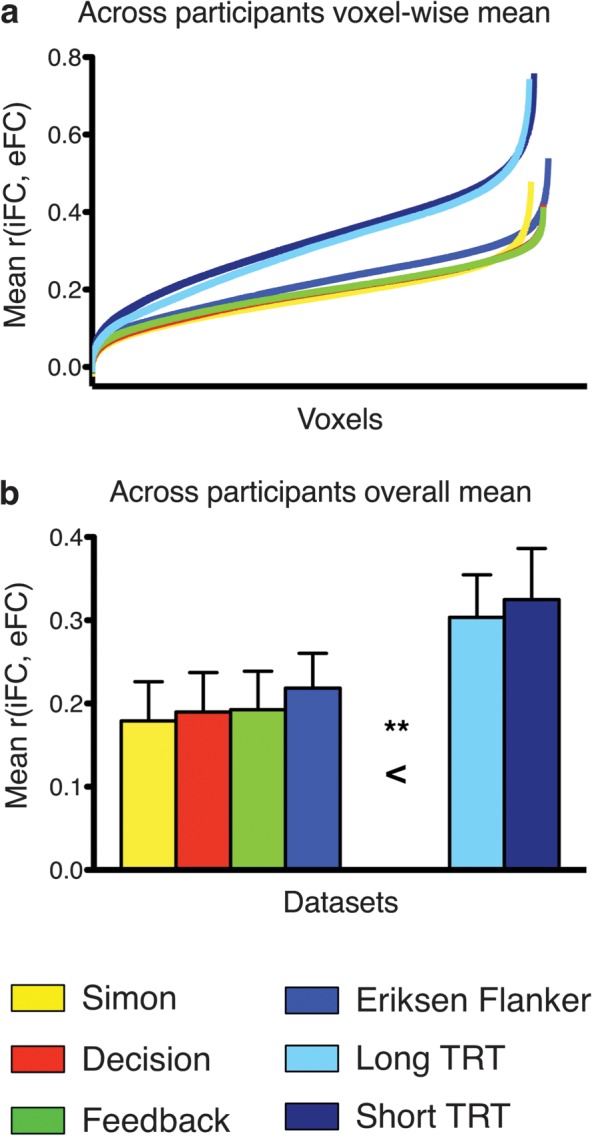
Distribution and overall mean of iFC-eFC correlations observed for each data set. (a) iFC-eFC correlation for each voxel in each data set sorted from weakest to strongest. (b) Mean iFC-eFC correlation across voxels for each data set. A one-way analysis of variance including data set as factor indicated that the overall mean iFC-eFC correlations did not vary significantly between task data sets but were significantly lower than the mean iFC-iFC correlations obtained for the resting-state data sets (**P < 0.001). TRT: resting-state Test–ReTest data set.

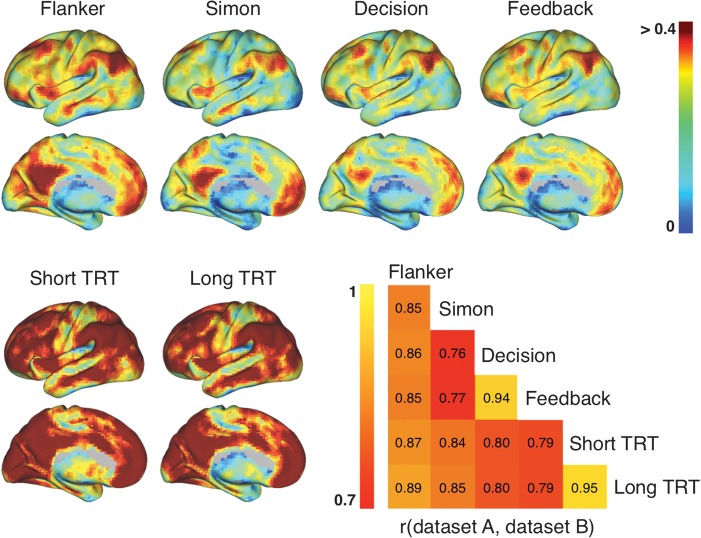
Although ubiquitous, the strength of the iFC-eFC relationships varied markedly across the brain. Mean correlations across participants ranged among −0.01 and 0.54 for the task data sets (mean: 0.19–0.22; SD: 0.06–0.08) and −0.01 and 0.76 for the iFC-iFC correlations in the resting-state only data sets (mean: 0.30–0.32; SD: 0.12–0.13). Despite large regional variation in strength, the topography of iFC-eFC relationships was remarkably similar across data sets (Fig. 2; between-data set correlations ranged from 0.76 to 0.95, see Supplementary Table 1). Core regions of the frequently described “task-positive” and “default” networks (Fox et al. 2005; Kelly et al. 2008) exhibited the strongest iFC-eFC correlations (Supplementary Fig. 2). In contrast, subcortical, limbic, and primary sensory motor areas exhibited more variable patterns of functional interactions across task-active and resting states (see hierarchical characterization in Supplementary Figs 3 and 4). Figure 3 illustrates iFC and eFC maps in a single participant for regions showing respectively weak and strong iFC-eFC relationships. While overall mean iFC-eFC correlation strength did not differ between data sets, we did observe a limited number of local voxelwise differences in iFC-eFC correlation strength. This result indicates that the specific requirements of each task influenced the strength of the iFC-eFC relationship for specific voxels (Supplementary Fig. 5).

Figure 2.

Surface topography showing the mean voxelwise iFC-eFC correlations obtained for each data set. All surface maps are scaled identically (r = 0–0.4). As is clear from the surface maps, the iFC-eFC topography generalized across data sets. Between-data set correlations ranged from 0.76 to 0.95 and are illustrated in the correlation matrix. See Figure 3 for single participant iFC and eFC maps obtained for 2 regions showing respectively weak and strong iFC-eFC correlations.

Figure 3.

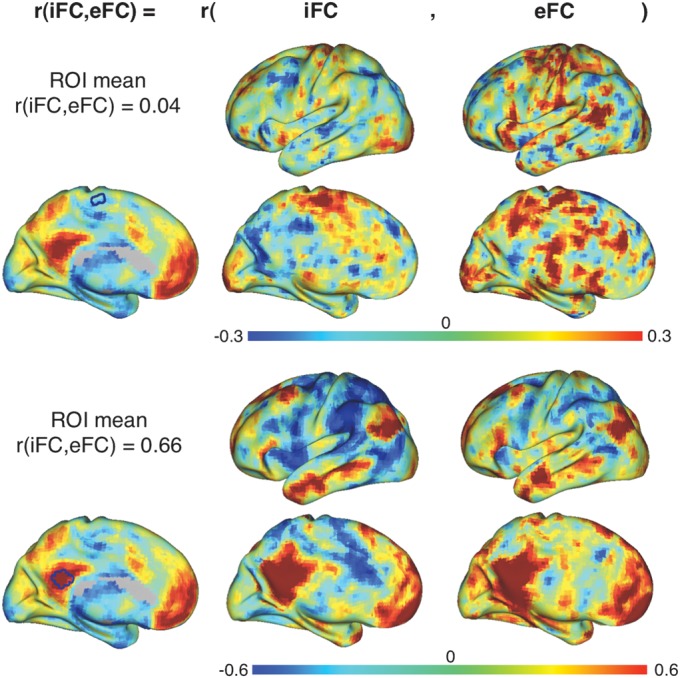
Illustration of weak versus strong iFC-eFC correlations in a single participant. For a participant from the Simon data set, we calculated iFC and eFC maps for a seed region in supplementary motor cortex (top) and posterior cingulate cortex (bottom). These seed regions exhibited respectively weak and strong iFC-eFC correlations. Of note, for illustration purposes, we used seed regions of interest (ROIs) comprising 33 voxels for calculating the iFC and eFC maps shown in this figure, all other analyses were done for each voxel individually.

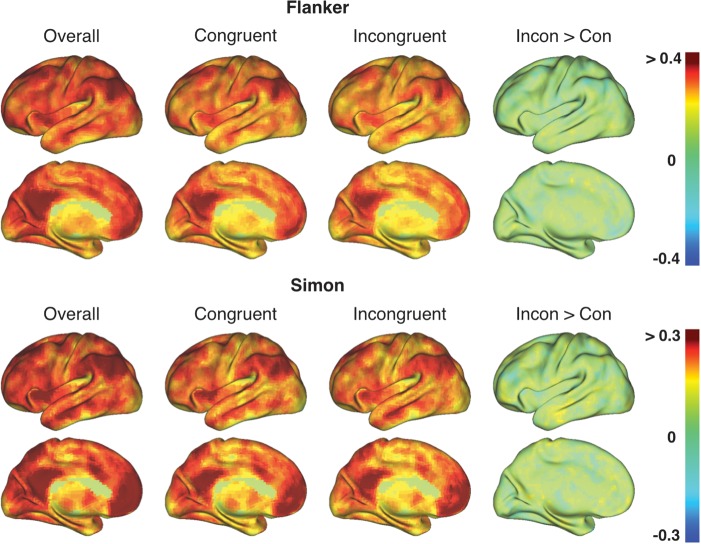
In the Flanker and Simon data set, the topography obtained using all trials was preserved when eFC calculations were limited to either congruent or incongruent trials (Fig. 4). However, in contrast to our findings for the “broader” task contrasts (i.e., congruent + incongruent > baseline), mean iFC-eFC relationships for tight task contrasts (i.e., incongruent > congruent) were weak (range: −0.1 to 0.1) and did not show a distinct topography (Fig. 4).

Figure 4.

The topography of iFC-eFC correlations calculated using eFC based on the individual trial types (congruent or incongruent) in the Flanker and Simon task was similar to the iFC-eFC topography obtained when calculating eFC based on all trials (Overall = congruent + incongruent > baseline). However, when iFC-eFC correlations were calculated using eFC based on the “tight” incongruent > congruent contrast (Incon > Con), mean iFC-eFC correlations were low and yielded no specific spatial topography. See Supplementary Table 2 for between-data set correlations.

When considering our results, one concern is that our findings might merely reflect regional or paradigm-related variation in SNR. Voxelwise correlations between the resting-state scan SNR maps and the mean iFC-eFC maps were moderate, ranging between 0.21 and 0.27 depending on the participant sample (see Supplementary Fig. 6 and Supplementary Table 3). SNR maps obtained for the beta value time series used to obtain the eFC maps did not correlate with the mean iFC-eFC maps (correlations ranged between −0.04 and 0.06 depending on the task paradigm and task condition). In addition, we confirmed that lower task-based SNR values were not contributing to weak iFC-eFC relationships as we observed moderate correlations between the mean iFC-eFC maps and the t-score maps indexing differences between the resting-state and the task-based SNR maps (range: 0.16–0.25). Regions exhibiting higher SNR values for the resting-state scan also exhibited stronger iFC-eFC relationships, while regions exhibiting higher SNR values for the task-based time series exhibited weaker iFC-eFC relationships. In contrast to the SNR results, we observed strong correlations between the iFC-eFC topography and the regional variation in fALFF, an index of the relative strength of low-frequency fluctuations in the fMRI BOLD signal (see Supplementary Fig. 6). Correlations ranged between 0.58 and 0.66 depending on the participant sample. These results suggest that regional differences in the temporal dynamics of the low-frequency fluctuations, which a recent arterior spin labeling-based study linked to brain metabolism (Zou et al. 2009), appear to better account for regional variation in the strength of the iFC-eFC relationship compared to simple metrics of signal/noise.

A second concern is that our analyses could have been biased toward the detection of stronger iFC-eFC relationships for voxels within larger networks. For example, a voxel in posterior cingulate cortex is significantly correlated with a larger number of other voxels (the widespread default network) than a voxel in motor cortex with a more circumscribed pattern of iFC. However, we obtained practically identical results when spatial iFC-eFC overlap was assessed using the Dice coefficient (see Supplementary Methods), suggesting that network size is unlikely to explain regional differences in iFC-eFC correspondence (Supplementary Fig. 7).

Finally, although global signal regression is commonly performed during processing of resting-state fMRI data, its use and implications are much debated (Murphy et al. 2009; Anderson et al. 2011; He and Liu 2012). Accordingly, we examined whether the iFC-eFC topography was independent of global signal regression applied to the resting-state scan (it was not applied to the task scans). Supplementary Figure 8 shows that the iFC-eFC topography and hierarchy remained intact when global signal regression was omitted.

Discussion

Our results show that the brain's intrinsic functional architecture does not provide a complete representation of its repertoire of extrinsic responses. In particular, for subcortical and limbic areas as well as for primary sensory and motor cortices, we observed weak correspondence between functional interactions embedded in patterns of correlated intrinsic activity and patterns of task-evoked coactivation. In contrast, multimodal association areas in the default and task-positive networks exhibited consistent patterns of interactions across their intrinsic and extrinsic functional architectures.

This pattern of results was observed across tasks probing a variety of cognitive functions: cognitive control, stimulus response mapping, decision-making, and feedback processing. As such, our results suggest a generalized topography in the strength of the relationship between the brain's intrinsic and the extrinsic functional architectures. This conclusion must remain tentative, however, until our findings are replicated across other task domains, such as social cognitive and affective processing, task switching, or error monitoring. Beyond the limited number of cognitive functions, sample sizes in the present study were relatively moderate (smallest n = 21), with partial overlap in participants across tasks. This limitation may have weakened our ability to detect relationships between the brain's intrinsic architecture and the measures of eFC derived from tight comparisons (e.g., incongruent vs. congruent).

Strongly related to the topography of fALFF, an index of BOLD signal dynamics (Zou et al. 2009), our observations on iFC-eFC relationships derived from broad task contrasts (e.g., incongruent + congruent vs. baseline) spark 2 important questions: 1) How does the brain establish and maintain veridical intrinsic representations of certain patterns of evoked interactions? 2) Why are patterns of evoked functional interaction for subcortical and limbic areas as well as primary sensory and motor cortices not accurately represented in the brain's intrinsic architecture?

Structural connections between regions are obvious contributors to establishing and maintaining the intrinsic connectivity networks that represent task-evoked patterns of coactivation (Honey et al. 2007). However, structural connections and patterns of functional connectivity do not exhibit a 1:1 relationship. Instead, it is hypothesized that intrinsic functional networks are sculpted by repeated evoked coactivation of regions (Kenet et al. 2003; Foster and Wilson 2006; Fox and Raichle 2007; Deco and Corbetta 2011; Deco et al. 2011) and thus extend beyond existing structural connections.

Consistent with this hypothesis, it has been repeatedly observed that the regions that constitute the task-positive and default intrinsic networks are jointly activated or deactivated, respectively, during task performance (Gusnard et al. 2001; Fox et al. 2005; Sridharan et al. 2008). Indeed, we found that these regions showed the strongest relationship between their intrinsic and extrinsic functional architectures. In addition, it is of interest that the topography of the strongest iFC-eFC relationships closely parallels the distribution of regions exhibiting elevated resting levels of aerobic glycolysis (Vaishnavi et al. 2010), which is thought to index metabolic processes beyond basal levels, including learning- or activity-related biosynthesis (Vaishnavi et al. 2010; Vlassenko et al. 2010). Furthermore, we found that regions exhibiting strong similarity between their intrinsic and extrinsic functional architecture also exhibited high fALFF. Given the relationship between amplitude of low-frequency fluctuations and cerebral blood flow at rest (Zou et al. 2009), this finding is also consistent with our observation that iFC-eFC topography paralleled the topography of the brain's resting metabolism. As such, our data suggest that the brain invests considerable resources into maintaining a veridical intrinsic representation of certain patterns of evoked interactions.

Our results indicate that the brain does not maintain accurate intrinsic representations of patterns of evoked functional interaction for subcortical and limbic areas. One possible explanation is that the functional interactions of these regions are more variable, accommodating specific task demands by flexibly interacting with demand-specific regions for short periods of time (Deco et al. 2011). This hypothesis is consistent with models of basal ganglia and thalamic anatomical connectivity that emphasize parallel but integrated cognitive, emotional, and motor circuits supporting flexible adaptation to internal and external demands (Alexander et al. 1990; Haber 2003).

In task-based fMRI studies, subcortical networks have been shown to adaptively accommodate different stages of learning new motor sequences (Doyon and Benali 2005; Bapi et al. 2006; Tunik et al. 2007), and striatal structures are thought to influence visual-oculomotor decisions by constantly updating higher order regions with the latest sensory information (Ding and Gold 2010). Furthermore, subcortical networks associated with “hub” regions such as the thalamus and cerebellum exhibit a larger number of short-range functional connections and greater overlap with one another compared with cortical networks such as the default network (Tomasi and Volkow 2011). Finally, subcortical and paralimbic iFC exhibits strong developmental effects. While subcortical iFC decreases significantly from childhood to adulthood, paralimbic iFC increases significantly (Supekar et al. 2009).

Together, these characteristics may confer less stability (or greater flexibility) on patterns of subcortical interactions, thereby decreasing the extent to which their evoked functional interactions are represented in the intrinsic brain. This speculation is consistent with the observation that test–retest reliability for striatal and cerebellar intrinsic connectivity networks ranked among the lowest in the brain and was markedly lower than that of the default and task-positive networks (Zuo, Kelly, et al. 2010).

Studying the iFC-eFC topography in Figure 2 reveals that regions in the so-called “sensorimotor strip” as well as primary visual cortical areas (V1, V2) also exhibited relatively weak correspondence between their intrinsic and extrinsic functional interactions. This observation is not immediately evident in the hierarchy plots in Supplementary Figure 4, which is likely due to the coarse nature of the anatomical parcellation employed for the hierarchical classification. The lack of intrinsic representations in these areas might be explained by the idea that sensorimotor regions exhibit strong local iFC but weak iFC with the rest of the brain (i.e., they are more globally isolated; Power et al. 2011). As such, their communications with the rest of the brain may be less predetermined and more influenced by factors, such as attentional state or arousal. In addition, we observed low Dice coefficients for the primary sensorimotor areas indicating limited spatial overlap between their iFC and eFC networks. This finding suggests that the local and homotopic interactions of these areas are modulated as well. For instance, in the primary sensory and motor cortices, Power et al. (2011) distinguished a ventral network involved in processes related to facial sensations and a dorsal network related to sensory processing for the rest of the body (Power et al. 2011). Interactions among such subnetworks during task performance may be dependent on stimulus properties and/or task demands (Tunik et al. 2007).

Our conclusions regarding regional variation in iFC-eFC relationships must be considered in the context of broad task contrasts (e.g., congruent + incongruent vs. baseline). When evoked coactivation patterns for tight task contrasts (e.g., incongruent vs. congruent trials) were examined, we found no relationship with the brain's intrinsic architecture. Consistent with demonstrations in the task-based literature, this result suggests that high-level task or stimulus demands are accommodated by context-specific modulations of functional interactions. For example, unilateral task-evoked activations can be observed in functional networks containing bilateral regions (e.g., unilateral evoked motor activity, while the intrinsic motor network is bilateral), and voxels in regions activated by multiple demands exhibit a specific task preference (Haynes et al. 2007; Stiers et al. 2010). This phenomenon is capitalized on by studies applying multivoxel pattern analysis (e.g., Kahnt et al. 2011), which demonstrate that task demands can be decoded from context-specific patterns of evoked activity.

It is worth noting that, although considerably weaker than the relationship with fALFF, the iFC-eFC topography was moderately related to the topography of SNR values derived from the resting-state scan. The fact that both fALFF and resting-state SNR were related to the iFC-eFC topography is not surprising given the properties of SNR and fALFF. While SNR is calculated as the temporal mean divided by the temporal SD of the resting-state time series, ALFF is equivalent to the temporal SD of the resting-state time series, restricted to the lower frequency bands (Zuo, Di Martino, et al. 2010). In turn, fALFF expresses ALFF as a fraction of the power across all frequencies present in the resting-state BOLD signal. As such, these measures are mathematically related (positively correlated), which likely explains their common relationship with the iFC-eFC topography. However, the fact that fALFF is a more specific measure of low-frequency oscillatory phenomena (Zuo, Di Martino, et al. 2010) than resting-state SNR might explain its stronger relationship with the iFC-eFC topography relative to that of the resting-state SNR values. Interestingly, we observed no relationship between the iFC-eFC topography and the SNR values derived from the task-evoked beta value time series. In contrast to the ongoing signal fluctuations recorded during the resting-state scan, the beta value time series reflect trial-related activity. As such, the lack of a relationship between the task-evoked SNR values and the iFC-eFC topography could be attributed to the spatial distribution of the task-evoked SNR values. Their distribution matches the spatial distribution of task activations rather than large-scale network definitions or the intrinsic topography. In addition, it is important to note that variability in task-evoked responses across trials is more likely governed by state-related factors (e.g., level of attention, error-related activity, impact of one trial on the next) than by inherent trait factors that exhibit less variability over time.

In conclusion, we have provided a detailed topography of the correspondence between task-evoked interaction patterns associated with broad task contrasts and the brain's intrinsic functional architecture. While strong correspondence was demonstrated for default mode and task-positive regions, weak correspondence was demonstrated for subcortical and limbic regions, as well as for primary sensory and motor cortices. In addition, we observed that evoked interaction patterns for tight task contrasts did not relate to the brain's intrinsic architecture. Accordingly, we conclude that intrinsic approaches provide only a partial understanding of the brain's functional architecture. Appreciating the full repertoire of dynamic neural responses will continue to require task-based approaches.

Supplementary Material

Supplementary material can be found at: http://www.cercor.oxfordjournals.org/

Funding

This research was partially supported by grants from National Institute of Mental Health (R01MH083246), Autism Speaks, the Stavros Niarchos Foundation, the Leon Levy Foundation, and the endowment provided by Phyllis Green and Randolph Cowen. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.