Diffusion model drift rates can be influenced by decision processes: An analysis of the strength-based mirror effect

Abstract

Improving memory for studied items (targets) often helps participants reject non-studied items (lures), a pattern referred to as the strength-based mirror effect (SBME). Criss (2010) demonstrated the SBME in diffusion model drift rates; that is, the target drift rate was higher and the lure drift rate was lower for lists of words studied five times versus lists of words studied once. She interpreted the drift rate effect for lures as evidence for the differentiation process, whereby strong memory traces produce a poorer match to lure items than weak memory traces. However, she notes that strength may have also affected a model parameter called the drift criterion – a participant-controlled decision parameter that defines the zero point in drift rate. We directly contrasted the differentiation and drift-criterion accounts by manipulating list strength either at both encoding and retrieval (which produces a differentiation difference in the studied traces) or at retrieval only (which equates differentiation from the study list but provides the opportunity to change decision processes based on strength). Across three experiments, results showed that drift rates for lures were lower on strong tests than on weak tests, and this effect was observed even when strength was varied at retrieval alone. Therefore, results provided evidence that the SBME is produced by changes in decision processes, not by differentiation of memory traces.

What makes us confident that an event did not occur? That is, what types of evidence support a statement such as “I am certain that I did not go to the grocery yesterday”? One possibility is that the candidate event is inconsistent with general knowledge or with other memories. For example, one might remember the general timeline of activities from the day before and note that a trip to the grocery cannot fit in anywhere. The candidate event might also be dismissed in light of a revealing lack of evidence. For example, one might imagine all of the memories that should have been established by the proposed trip to the grocery – the smell of the produce, the interaction with the cashier, etc. – and note that these memories are absent.

In the laboratory, research on the strength-based mirror effect (SBME) offers insights into the factors that affect the rejection of non-experienced events (e.g., Stretch & Wixted, 1998). The SBME was discovered using a paradigm in which participants study a list of items and are later asked to discriminate the studied items (“targets” or “old” items) from non-studied items (“lures” or “new” items). The proportion of targets called “old” is the hit rate, and the proportion of lures called “old” is the false-alarm rate. In such experiments, strengthening memory for the studied words – say, by presenting them repeatedly instead of just once – increases performance for both the target and lure items. That is, people who study a strong list are not only better able to recognize the studied items themselves, but also better able to reject the non-studied items (Criss, 2006, 2009, 2010; Ratcliff, Clark, & Shiffrin, 1990; Starns, White, & Ratcliff, 2010; Stretch & Wixted, 1998). The term “mirror effect” refers to the finding that the increase in the hit rate is mirrored by a decrease in the false-alarm rate (Glanzer & Adams, 1985).

The SBME was initially explained in terms of changes in decision processes (Brown, Lewis, & Monk, 1977; Hirshman, 1995; Stretch & Wixted, 1998). This idea is most commonly expressed in terms of Signal Detection Theory, which assumes that memory strength varies along a single dimension for both targets and lures (McNicol, 1972). Targets have higher strength values on average, but there is considerable overlap in the target and lure strength distributions. A criterion along the strength dimension determines the response on each trial, with strength values above the criterion producing an “old” response and strength values below the criterion producing a “new” response. When the list words are learned more effectively, the target distribution shifts to a higher average strength value, which leads to a higher hit rate. Moreover, people who study a strong list expect to have strong memories for encountering the studied items, so they are only willing to say “old” for items with high memory strength values. In other words, the response criterion shifts to a more conservative position (Hirshman, 1995; McCabe & Balota, 2007; Singer, 2009; Singer & Wixted, 2006; Starns, Hicks, & Marsh, 2006; Stretch & Wixted, 1998; Verde & Rotello, 2007). Fewer lure items pass the more stringent criterion, leading to a lower false-alarm rate for strong lists. Although the decision-based account is usually discussed in terms of a criterion shift, the Bind-Cue-Decide Model of Episodic Memory (BCDMEM) also produces the SBME in terms of decision processes by incorporating an estimate of the strength of the studied items into the retrieval equations (Dennis & Humphreys, 2001; Starns et al., 2010).

Contrasting the decision-based account, some computational memory models produce the SBME based on the inherent properties of memory traces (McClelland & Chappell, 1998; Shiffrin & Steyvers, 1997; see also Shiffrin, Ratcliff, & Clark, 1990). These models incorporate a property called differentiation, whereby strong memory traces are less confusable with other items than weak traces. For example, the Retrieving Effectively from Memory (REM) model produces memory decisions by matching the test item to all memory traces from the target context (e.g., the study list). Additional learning creates memory traces with a stronger match to the studied item itself, leading to a higher hit rate. Strengthening a trace also decreases its match to any other item. Thus, lure items produce a poorer match across the traces from a strong list than traces from a weak list, leading to a lower false alarm rate (see Criss, 2006 and Starns et al., 2010 for more detailed simulations).

Our goal was to discriminate the differentiation and decision accounts of the SBME by isolating retrieval and encoding influences. Our experiments included pure list conditions that followed the standard SBME paradigm: all of the studied words were presented once for the weak lists and five times for the strong lists. With this design, both differentiation and strength-based adjustments in decision processes can contribute to the SBME. That is, strong lists have better differentiated traces than weak lists, but participants also know that exclusively strong or weak items will appear on the test and can adjust their decision processes accordingly. We compared the pure results to a condition in which each study list was a mixture of items studied once (weak) and items studied five times (strong). In contrast to standard mixed list conditions, the tests were still pure with regard to target strength, with only strong targets on half of the tests and only weak targets on the other half. Participants were informed of the target strength just before each test began. Because encoding was held constant, differentiation from the traces established at encoding could not create differences between the strong and weak tests. Therefore, any effects produced by differentiation should be observed with pure lists but not with mixed lists. In contrast, effects produced by changes in decision processes should be observed with both pure and mixed lists, as both allow participants to adjust their decision making based on the expected strength of the targets.

A recent study with a design similar to the current experiments challenged the role of differentiation in the SBME (Starns et al., 2010). Results showed that the SBME could be produced by correctly informing participants that only weak or only strong items would be tested following mixed-strength study lists. In contrast, when participants knew that only weak targets would be tested, increasing the differentiation of strong items had no effect on the false-alarm rate. In the current study, we extend the Starns et al. results by applying the diffusion model (Ratcliff, 1978) to both response proportion and RT data from new experiments in which participants were asked to balance speed and accuracy in their responding. Criss (2010) recently used this model to support the differentiation account of the SBME, so it is critical to evaluate diffusion model results in a paradigm that explicitly separates differentiation and decision processes. In the following sections, we review the diffusion model and describe how Criss used the model to explore the SBME. Finally, we describe how our own design can clarify the significance of diffusion model results for the different accounts of the SBME.

Diffusion Model

The diffusion model can be characterized as a dynamic version of signal detection theory (Ratcliff, 1978). Signal detection models assume that decisions are made by comparing a single evidence value to a response criterion. The diffusion model assumes that decisions are based on a number of evidence samples that vary from moment to moment. Evidence from the samples is accumulated over time until the total evidence reaches one of two response boundaries. As in signal detection theory, a criterion determines whether each sample supports an “old” or “new” response, and this is referred to as the “drift criterion” (Ratcliff, 1978; Ratcliff, Van Zandt, & McKoon, 1999). Specifically, the accumulated evidence takes a step toward the “old” boundary if the sample falls above the drift criterion or toward the “new” boundary is the sample falls below. In addition to varying from moment-to-moment within a trial, evidence also varies from one trial to the next. For example, for a poorly-learned target item, the evidence samples might be nearly as likely to fall below the drift criterion as above, resulting in a slow average approach to the “old” boundary. For a well-learned target, most of the evidence samples should fall above the drift criterion, resulting in a fast average approach to the “old” boundary. The diffusion model assumes that evidence samples are taken continuously in time, producing a continuous drift rate in the evidence accumulation process.

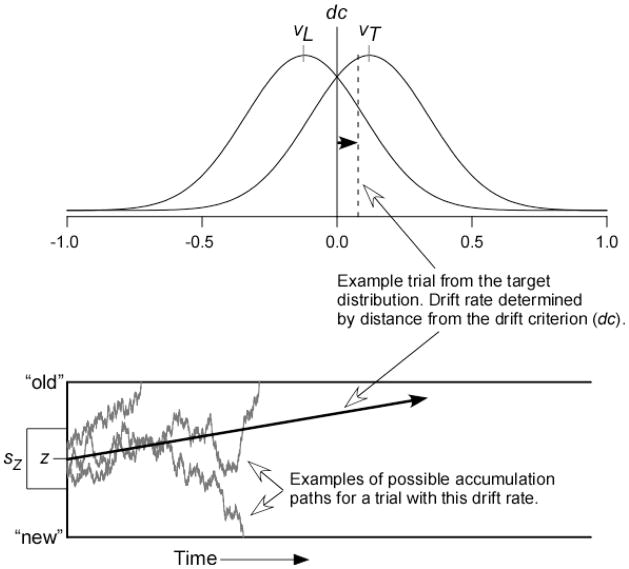
The dynamic signal detection process described above results in the model displayed in Figure 1. The distributions in the top panel show the between-trial variation in drift rate for lures and targets. These drift distributions have a standard deviation η and means v_L and v_T, respectively. The drift rate on each trial is determined by taking a sample from the drift distribution and evaluating the deviation between this value and the drift criterion, with positive drift rates above the criterion and negative drift rates below. The dashed line shows the position of one particular trial in the target drift distribution, and the black arrows show how the position relative to the drift criterion translates to the average drift rate in the diffusion process. The drift criterion is placed at zero in the figure, but readers should keep in mind that this is arbitrary. Just as in signal detection models, only the the relative position of the criterion and the distributions can be defined, so one of them can be set to zero without loss of generality.

Figure 1.

The diffusion model for two-choice responding. The top panel shows distributions of drift rates across test trials for both targets (mean = v_T) and lures (mean = v_L). The vertical line is the drift criterion (dc), and the drift rate on each trial is determined by the distance between the drift criterion and a sample from the drift distribution, as shown with the dashed line. The bottom panel shows three examples of accumulation paths for a trial with the sampled drift rate. The starting point of accumulation is a random draw from a uniform distribution with mean z and range s_Z. Paths terminating on the top boundary lead to “old” responses, and paths terminating on the bottom boundary lead to “new” responses.

The wandering lines in the bottom panel show three potential accumulation paths with the displayed drift rate. The within-trial variation in drift results in processes that finish at different times and can even terminate on the boundary opposite the direction of drift, leading to errors. Errors can also arise based on the between-trial variation in drift; for example, some target items will actually have an average drift toward the “new” boundary (represented by the proportion of the target drift distribution that falls below the drift criterion). The starting point of the accumulation process varies across trials with mean z and a uniform range s_Z. The different finishing times give RT distributions from the decision process, and these distributions are convolved with a uniform distribution of non-decision times with mean T_er and range s_T. The non-decision component accommodates the time needed to form a memory probe for the test word and to press a response key once the decision has been made.

Figure 2 shows three possible mechanisms for producing the strength-based mirror effect with the standard pure-list paradigm, as discussed by Criss (2009). The top-left panel shows performance on the weak lists, and the remaining panels show strong lists under the differentiation, drift criterion, and starting point accounts of the strength-based mirror effect. The differentiation account proposes that strong memory traces produce a poorer match to lure items than weak traces, so strengthening studied words both increases evidence for targets and decreases evidence for lures. In the bottom-left panel, the drift distribution for targets shifts to the right and the lure distribution shifts to the left with no change in the drift criterion, resulting in higher drift rates for targets and lower drift rates for lures. The drift criterion account proposes that repeating items increases evidence for targets without affecting evidence for lures; therefore, the lure drift distribution is in the same position as the weak panel. However, when participants know that only strong items will be tested, they shift the drift criterion closer to the midpoint of the target and lure distributions, producing lower drift rates for lures. So the drift criterion account proposes that target drift rates increase based on changes in evidence and lure drift rates decrease based on decision processes. The starting point account proposes that strengthening the targets affects neither the lure distribution nor the drift criterion. Instead, participants shift the starting point closer to the “new” boundary on strong lists to cancel out the higher drift rates for targets than for lures.

Figure 2.

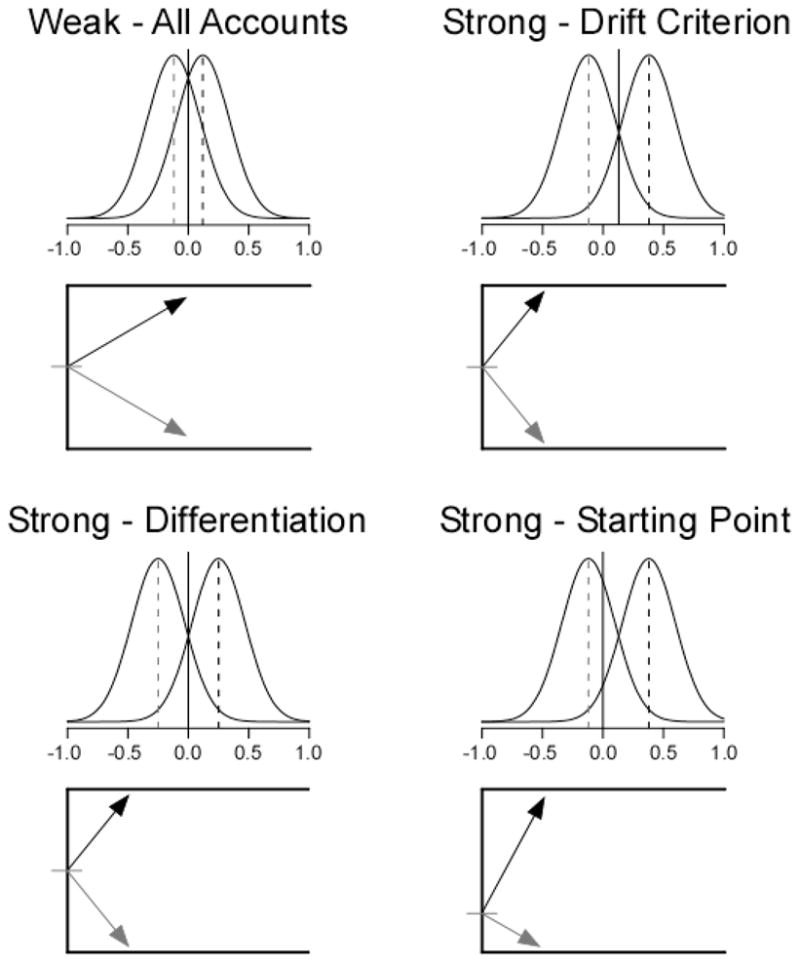
Possible mechanisms for the SBME in the diffusion model. The top left panel shows example parameters from a weak list, and the remaining panels show parameters from a strong list under the differentiation (bottom left), drift criterion (top right), and starting point (bottom right) accounts. The distributions in each panel are the drift distributions, with the mean of the lure distribution marked with a gray dashed line and the target mean marked with a black dashed line. The solid vertical line is the drift criterion. The bottom panel shows the average drift rates for targets and lures based on the distance of each drift distribution from the drift criterion. See the text for detailed discussion of the different accounts.

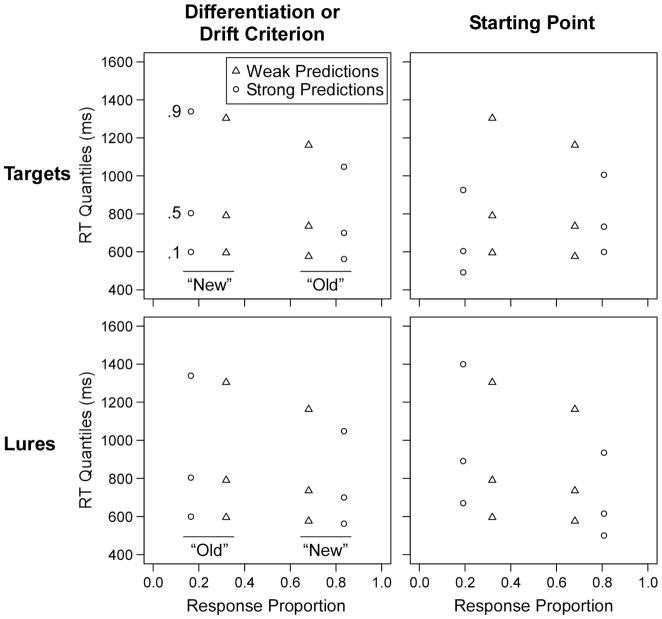
Figure 3 shows model predictions for each of the potential mechanisms of the SBME. The predictions are shown in quantile-probability plots to display all aspects of the data in a concise form (Ratcliff, 2001; Ratcliff & McKoon, 2008). Each vertical column of plotting points shows the .1, .5, and .9 quantiles of the RT distribution (the .1 quantile is the point at which 10% of responses have already been made, etc.). The model predicts that RT distributions are positively skewed; thus, the distributions are more compact below the median (.5 quantile) than above. Both “old” and “new” responses are displayed on each plot, and the position of each column on the x-axis is the proportion of trials on which the response was made. For targets, proportions above .5 are generally “old” responses and proportions below .5 are generally “new” responses, and the opposite pattern holds for lures (that is, people tend to make more correct than incorrect responses). Variables that increase performance will move the plotting points closer to the edges of the plot. Therefore, the plots show a mirror effect in that performance improves for both targets and lures from weak to strong. We adjusted parameters to yield unbiased performance in all conditions; thus, the proportion of correct responses for lures is the same as for targets. However, readers should note that this is not a general prediction of the model.

Figure 3.

Quantile-probability plots showing diffusion model predictions for the drift-based (differentiation and drift criterion shift) and starting point accounts of the SBME. The sets of 3 points are the .1, .5, and .9 quantiles of the RT distributions, and they are plotted on x-values equal to the probability of the response. Values above .5 are “old” responses on the target plots (top row) and “new” responses on the lure plots (bottom row).

The first column in Figure 3 shows predictions based on changes in either differentiation or the drift criterion. The RT distributions are slower for errors than correct responses, especially in the higher quantiles. Such slow errors are seen in a variety of tasks, and the model produces this pattern based on the between-trial variation in drift rates (Ratcliff & McKoon, 2008; Ratcliff et al., 1999). For correct responses, the tails of the distributions (.9 quantiles) are faster for strong than weak; however, there is very little change in the leading edge of the distributions (the .1 quantiles). The second column shows the predictions for the starting point account. Although changing the starting point produces an identical SBME in terms of probabilities, the RT predictions clearly differ from the drift-based accounts. For weak lists, “old” and “new” responses have similar RT distributions, whereas “new” responses are much faster than “old” responses in the strong condition. For targets, the starting point shift leads to faster error responses than correct responses for strong lists. The RT differences are seen even in the leading edges of the distributions, contrasting the relatively constant leading edges for the drift-based accounts.

Criss (2010) recently explored these alternative mechanisms for the SBME. In the critical experiment, participants completed multiple study/test cycles with words studied once on half of the cycles and five times on the other cycles. Results showed the standard SBME effect for recognition performance, with higher hit rates and lower false-alarm rates for the strong versus the weak lists. Fitting the response proportions and RT distributions with the diffusion model revealed essentially no change in starting point between the strong and weak lists but a substantial change in both the target and lure drift rates. Thus, the results supported either the differentiation or the drift-criterion accounts. To discriminate these alternatives, Criss explored the effects of changing the proportion of targets on the test in a separate experiment. The goal was to see how the model parameters responded to a manipulation that unquestionably influenced decision processes. Target proportion had a large effect on starting point and a much smaller and inconsistent effect on the drift criterion, and other studies reinforce this relatively selective effect on starting point (Ratcliff, 1985; Ratcliff et al., 1999; Ratcliff & Smith, 2004; Wagenmakers, Ratcliff, Gomez, & McKoon, 2008). Criss concluded that decision manipulations influence starting point with little influence on drift rates; therefore, the strength effect on lure drift rates is best interpreted as a change in evidence for lures produced by differentiation.

Our primary goal is to determine if drift rates can be affected by strength-based changes in decision processes, or if drift rates offer a unique signature of differentiation. One possibility is that decision processes affect the starting point with little or no effect on drift rates. In this scenario, differences in lure drift rates should be obtained when differentiation differs between weak and strong tests (the pure condition) but not when differentiation is held constant and only retrieval expectations change (the mixed condition). In other words, lure drift rates will only change when differentiation directly affects the evidence distribution for lures as shown in the bottom-left panel of Figure 2. If the mixed condition shows a change in false-alarm rate between weak and strong tests, then modeling should show that this difference is based on changes in starting point bias. A second possibility is that drift rates are influenced by retrieval expectations via changes in the drift criterion. In this scenario, a strength effect on lure drift rates would be expected in both the pure and mixed conditions. That is, both pure and mixed participants will shift their drift criterion to a higher value when they know that only strong versus weak items will be tested, as depicted in the top-right panel of Figure 2.

Experiment 1

Method

Design and Participants

Participants were undergraduates at Ohio State University who were compensated with extra credit in their psychology courses. List condition was manipulated between subjects with the levels pure-between, pure-within, and mixed. We ran the pure list condition in both between-subject and within-subject versions to investigate the role of matches to previous lists. For the pure-within condition, participants completed multiple study/test cycles with exclusively strong items on half of the study lists and exclusively weak items on the other lists. At test, this creates a differentiation difference between strong and weak for the most recent study list, but these differences may be diluted if participants also match to traces of previous lists. That is, traces from a previous strong list may be matched while a weak list is being tested, or vice versa. There was no reason for participants to match to previous lists (words from previous study/test cycles were never re-tested), but the contextual similarity between lists may have made it difficult to isolate traces from the most recent list. To address this possibility, we designed the pure-between condition to preserve a differentiation difference regardless of the ability to isolate the most recent list. One group of participants studied strong lists and another group studied weak lists on all study/test cycles. Therefore, even if traces from previous lists sometimes made it into the match set, the strong group would be matching to more differentiated traces than the weak group. For the pure-between condition, 22 participants were randomly assigned to the weak list group and 20 were assigned to the strong list group. The pure within-condition included 20 participants who studied half strong lists and half weak lists, and the mixed condition included 19 participants who always studied a mixed list but had the strong targets on half of the tests and the weak targets on the other half. None of the participants contributed data to more than one list condition.

Materials

For each participant, the words used on the study and test lists were randomly sampled from a pool of 729 words with natural-language frequencies between 60–10,000 occurrences/million (Kucera & Francis, 1967). The study lists always contained 24 unique words. For entirely weak lists, each word was presented only once. For entirely strong lists, each word was presented five times for a total of 120 presentations. For mixed lists, 12 words were presented once and 12 were presented five times for a total of 72 presentations. Across all conditions, at least one different word intervened before the same word was repeated. All tests included 12 words from the last study list along with 12 lures. A unique set of words was sampled for each study/test cycle (i.e., words never repeated across cycles), and the order of each list was randomized independently for each participant.

Experimental Procedure

The initial instructions informed participants that they would study multiple lists with a memory test after each. They were informed that they would only have to recognize words from the very last list they studied. At learning, each word remained on the screen for 800 ms with 150 ms of blank screen between words. We used a two-back task as a distractor between study and test (participants were not informed that this task was just a filler). For the task, each stimulus was a random selection from the digits 1–9. Participants were asked to press the ‘/’ key each time the current digit was the same as the digit that was presented two items back in the sequence. Each digit remained on the screen for 900 ms, with 100 ms of blank screen between digits. After 30 digits were presented, participants saw feedback on the number of targets that occurred in that cycle and the number of times they correctly hit the key when a target appeared. After this feedback, participants were prompted to begin the recognition test under instructions to balance the speed and accuracy of their responding. They were informed that the test would include words studied once (weak tests) or words studied five times (strong tests), and participants had to press either “1” or “5” to ensure that they attended to this message. After this response, participants were asked to place their fingers on the “z” and “/” keys, which were used to make “new” and “old” responses, respectively. They hit the space bar with their thumb to begin the test. No error feedback was provided, but the participants saw a “TOO FAST” message for any RT under 250 ms.

All participants completed 12 study/test cycles. The first two cycles were practice cycles to familiarize participants with the task, and they were not included in the analyses. In the pure-between condition, all 12 cycles for a given participant were either pure-weak or pure-strong lists. For pure-within condition, the study/test cycles were evenly divided between pure-weak and pure-strong lists. For the mixed condition, all of the study lists were mixed, with only the weak targets tested on half of the study/test cycles and only the strong targets tested on the other half. The sequence of weak and strong study/test cycles was separately randomized for each participant in the pure-within and mixed conditions under the constraint that the first two (practice) cycles had one weak and one strong test.

Statistical Procedure

We used the Bayesian t-test developed by Rouder, Speckman, Sun, Morey, and Iverson (2009) for all comparisons. The test yields a Bayes factor (BF), which is the ratio of the marginal likelihoods for the null hypothesis and the alternative hypotheses (null/alternative).¹ The marginal likelihood for the null is simply the likelihood for an effect size of zero. The marginal likelihood for the alternative is the average likelihood across all possible effect sizes weighted by a prior distribution. Specifically, the likelihood for each effect size is multiplied by the corresponding density on the prior distribution and the products are integrated across all effect sizes. For non-directional tests, we used a normal distribution with M = 0 and SD = 1 as the prior (this is Rouder et al.’s unit information prior). The normal prior places higher weights on smaller effect sizes: the highest weight is for an effect size of zero with weights dropping to nearly half of this value at standardized effect sizes of −1 and 1 and to nearly a tenth of this value at effect sizes of −2 and 2. For directional tests, we used a folded normal distribution with M = 0 and SD = 1 to concentrate the density above zero (all of our directional tests evaluated positive effects).

Bayes factors above 1 indicate that the null hypothesis in more likely than the alternative given the data, and vice versa. Following the suggestions of Jeffreys (1961), we will consider the results suggestive if one hypothesis is between 3 and 10 times more likely than the other (3 < BF < 10 for the null or .100 < BF < .333 for the alternative), strong if one hypothesis is between 10 and 30 times more likely (10 < BF < 30 for the null or .033 < BF < .100 for the alternative), and very strong if one hypothesis is greater than 30 times more likely (BF > 30 for the null or BF < .033 for the alternative).

Results and Discussion

Recognition Performance

Table 1 reports the recognition hit rate (HR) and false-alarm rate (FAR) data from each of the conditions. As expected, words studied five times had a higher HR than words studied once in each of the list conditions. The FAR data showed the mirror pattern across all list conditions; that is, there were fewer false alarms for strong than weak tests. The size of the effect was similar across the list conditions. Non-directional Bayesian t-tests on the FAR data found strong evidence for a strength effect in the pure-between condition (BF = 0.09234) and very strong evidence for an effect in the pure-within and mixed conditions (BF = 0.0090 and 0.0005, respectively).

Table 1.

Recognition memory data across all experiments

Measure and Strength	Experiment and List Condition
	Ex. 1			Ex. 2			Ex. 3
	PB	PW	M	PB	PW	M	M
HR
Weak	.63	.58	.48	.59	.58	.54	.64
Strong	.77	.75	.70	.80	.80	.76	.84
FAR
Weak	.27	.26	.25	.23	.20	.22	.36
Strong	.15	.16	.12	.14	.12	.13	.20

Note:

HR = hit rate; FAR = false alarm rate; PB = pure between; PW = pure within; M = mixed.

Standard errors ranged from .02 to .05 across the displayed means.

Replicating previous work (Hirshman, 1995; Marsh et al., 2009; McCabe & Balota, 2007; Starns et al., 2010), the current recognition results show that the SBME can be produced with a purely retrieval-based manipulation. In the mixed condition, testing exclusively strong or weak items and informing participants which it would be produced a robust FAR effect. Interestingly, the size of the strength effect on FAR in the mixed condition was similar to the pure conditions. The pure conditions had the same test manipulation as the mixed condition – exclusively strong or weak items were tested and participants were aware of which it would be – with an additional manipulation of the degree of differentiation from the study list. Thus, the results give no indication that differentiation contributes to a larger strength effect in the FAR data, suggesting that the effect was driven purely by retrieval factors. To investigate this further, we calculated the difference between the weak and strong FAR for each participant in the pure-within and mixed conditions. With a directional test, we compared the null hypothesis that the FAR effect was the same size in the mixed and pure condition to the alternative hypothesis that the effect was larger in the pure condition. The results provided suggestive, but not strong, evidence that differentiation plays no role in the effect (BF = 5.22; remember that values above 1 indicate support for the null hypothesis).

Diffusion Model Analyses

To explore whether the FAR effects were produced by changes in lure drift rate or starting point, we fit the diffusion model to the data in each condition. To prepare the data for modeling, we calculated the .1, .3, .5, .7, and .9 quantiles for both “old” and “new” responses in each condition for each participant. The response frequencies were broken into six RT bins using these quantiles. For example, if there were 500 total “old” responses, then there would be 50 (10%) below the .1 quantile, 100 (20%) between the .1 and .3 quantiles, 100 between the .3 and .5 quantiles, and so forth. There were 12 response frequencies for each condition (six RT bins for both “old” and “new” responses), so each condition contributes 11 degrees of freedom (one degree of freedom is lost because the frequencies must sum to the total number of trials for the condition). The model was fit to the frequencies in the RT bins; thus, to match the data the model had to match both the overall proportion of “old” versus “new” responses and the appropriate RT distributions for both. The observed and predicted frequencies were used to compute the G² statistic, and model parameters were adjusted to minimize G² using the SIMPLEX routine (Nelder & Mead, 1957).

We fit both the group data and data from each individual participant, and in all cases parameters from the group fits were very close to the average parameter values across participants. For the individual participant fits, any conditions with fewer than five observations were fit for probability but not RT quantiles (five quantile RTs cannot be estimated with fewer than five observations). For the group data, we averaged quantile values across participants excluding any conditions with fewer than five responses. Trials with RTs less than 300 ms or greater than 3000 ms were trimmed from the data. This eliminated less than 1% of trials across all experiments and conditions except for the mixed condition in Experiment 2, in which 1.5% of trials were eliminated.

To contrast the differentiation and drift-criterion accounts, we allowed both lure drift rate and starting point to vary across strength and tested for differences in these parameters across participants. For the pure-between condition, we performed separate fits for the weak and strong groups. Each fit had two conditions (targets and lures), yielding a total of 22 degrees of freedom in the data. The data were fit with 9 free parameters: boundary separation (a), starting point (z), starting point variability (s_Z), average drift rates for targets (v_T) and lures (v_L), across-trial standard deviation in drift (η), mean non-decision time (T_er), range in non-decision time (s_t), and proportion of RT contaminants (p_O). The last parameter estimates the proportion of trials affected by RT delays from task-unrelated factors, and it was very low across all of our experiments and conditions. For the pure-within and mixed conditions, the weak and strong data were fit simultaneously. Thus, there were four total conditions (strong and weak targets and lures) and 44 degrees of freedom in the data. Four model parameters varied across the strength variable: boundary separation, starting point, and the average drift rates for targets and lures.² The remaining parameters were fixed across strength. Thus, there were 13 free parameters total. Again, only the relative positions of the drift distributions and drift the criterion can be estimated, so we followed convention by setting the drift criterion to zero for both levels of strength. Readers should keep in mind that differences in v_L can be produced either by changing the position of the lure drift distribution or by a shift in the drift criterion (as shown in the bottom-left and top-right panels of Figure 2, respectively).

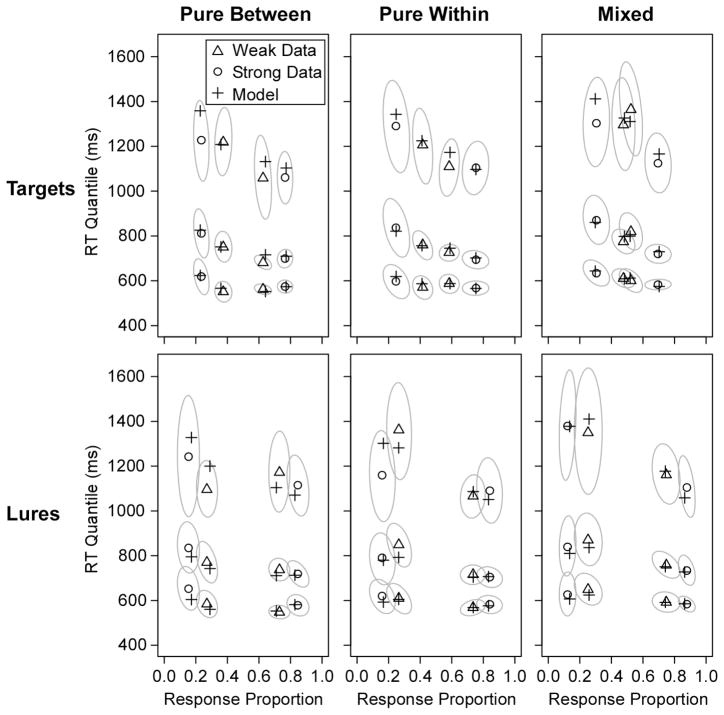
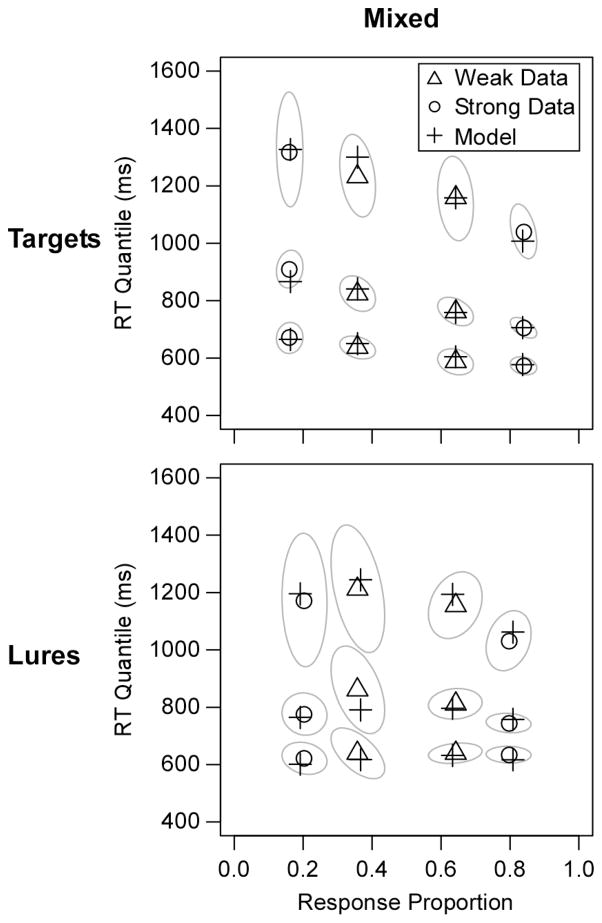
Figure 4 shows the data and model predictions for the group data across all of the conditions, and Table 2 reports the G² values from the fits. All of the RT distributions showed a pronounced positive skew; that is, the quantiles were much more spread above the median (.5 quantile) than below the median (as is almost always observed). The plot reveals a mirror effect in all conditions in that performance improved for both targets and lures from the weak to strong tests. The model predictions captured the mirror effect in the response proportions as well as the positive skew in the RT distributions. Nearly all of the predicted points fell within the 95% confidence ellipses around the data points (the light grey ovals; see the figure caption for details on how the confidence ellipses were produced).

Figure 4.

Quantile-probability plots for group data from Experiment 1 with the predicted points of the best-fitting diffusion model (predictions are from the fits with both lure drift and starting point varying across strength). The sets of 3 points are the .1, .5, and .9 quantiles of the RT distributions, and they are plotted on x-values equal to the probability of the response (the .3 and .7 quantiles were also fit, but they are omitted from the plot to avoid clutter). The gray ovals show 95% confidence ellipses estimated with a bootstrap procedure (Efron & Tibshirani, 1985). For the bootstraps, 500 simulated datasets were created by randomly sampling participants with replacement, and response proportions and RT quantiles were calculated for each simulated dataset. The plot shows the smallest ellipses that contained 95% of the points across the bootstrap runs.

Table 2.

G² values for the diffusion model with both lure drift rate and starting point free to vary by strength

Condition	Experiment and Type of Fit
	Experiment 1		Experiment 2		Experiment 3
	Overall	Ind.	Overall	Ind.	Overall	Ind.
Pure-between
Weak	93	16	105	21	-----	-----
Strong	47	19	39	14	-----	-----
Pure-within	88	38	105	33	-----	-----
Mixed	78	33	90	36	111	39

Note: The “Overall” column gives the G² values from the fits to the overall data, and the “Ind.” column gives the median G² value across the individual-participant fits. The weak and strong fits in the pure-between condition each have 13 degrees of freedom (22 free response frequencies minus 9 free parameters). The pure-within and mixed fits each have 31 degrees of freedom (44 free response frequencies minus 13 free parameters).

Table 3 reports the average parameter values from the individual-participant fits. Replicating Criss (2010), both of the pure conditions showed a mirror pattern in the drift rates: from weak to strong, target drift rates increased and lure drift rates decreased. Critically, a similar mirror pattern arose in the mixed condition, which demonstrates that lure drift rates are sensitive to differences in decision processes at retrieval. Non-directional Bayesian t-tests supported the alternative hypothesis of a lure-drift effect in all of the list conditions (BF = 0.3432, 0.0116, and 0.0002 for pure-between, pure-within, and mixed). Results from the mixed condition provide strong evidence that lure drift rates can change without changing the degree of differentiation in the encoded traces.

Table 3.

Average parameter values from the individual participant fits

Parameter and Strength	Experiment and List Condition
	Ex. 1			Ex. 2			Ex. 3
	PB	PW	M	PB	PW	M	M
a
Weak	.134	.142	.150	.155	.155	.175	.138
Strong	.136	.152	.150	.140	.151	.164	.135
z/a
Weak	.523	.496	.521	.546	.541	.505	.590
Strong	.517	.541	.546	.562	.577	.575	.602
sz
Weak	.033	.029	.019	.030	.006	.019	.016
Strong	.026	.029	.019	.012	.006	.019	.016
vT
Weak	.099	.064	−.016	.060	.051	.034	.059
Strong	.207	.200	.141	.237	.264	.204	.245
vL
Weak	−.172	−.194	−.192	−.250	−.255	−.210	−.147
Strong	−.273	−.335	−.325	−.360	−.386	−.348	−.305
η
Weak	.198	.233	.214	.253	.267	.227	.223
Strong	.189	.233	.214	.237	.267	.227	.223
Ter
Weak	499	513	522	513	541	509	558
Strong	527	513	522	503	541	509	558
sT
Weak	172	183	205	129	181	190	214
Strong	175	183	205	115	181	190	214
pO
Weak	.002	.002	<.001	.009	<.001	.005	<.001
Strong	.013	.002	<.001	<.001	<.001	.005	<.001

Note: Parameters in italics were fixed across strength.

PB = pure between, PW = pure within, M = mixed.

The size of the strength effect on lure drift rates was quite consistent across the list conditions. As we did with the false alarm rates, we directly compared the size of the strength effect for the pure-within and mixed conditions with a directional test. The test found support for the null hypothesis over the hypothesis that the strength effect was larger in the pure-within condition, although the evidence favoring the null was weak (BF = 2.7833). Thus, there was again no evidence that differentiation produced a larger effect with pure versus mixed study lists.

We also evaluated the effect of strength on the relative starting point (z/a). A relative starting point of .5 indicates unbiased responding, i.e., the starting point is equidistant from the “old” and “new” boundaries. Values above .5 reflect a bias to say “old,” and values below .5 represent a bias to say “new.” Non-directional tests favored the null hypothesis in the pure-between and mixed conditions, with the former passing the criterion for suggestive evidence (BF = 3.3184) and the latter falling just short of this benchmark (BF = 2.6278). Results for the pure-within condition weakly favored the alternative hypothesis (BF = 0.5585); however, Table 3 shows that the starting point was slightly closer to the “old” boundary for strong versus weak lists, the opposite of the effect predicted by the starting point account. Thus, the fitting results showed no evidence that changes in the starting point explain the lower FAR on strong versus weak tests.

Model Comparison

The analyses above suggest that the drift rate for lures changes even in the mixed condition. That is, lure drift rates can change with no difference in differentiation of the encoded traces, supporting the drift criterion account. To further test the drift criterion account, we compared the fit of two constrained models to ensure that differences in lure drift rate are required to adequately fit the data from the mixed condition (we ignored the pure list data because both the differentiation and drift criterion accounts predict changes in lure drift rates for this condition). In the lure drift model, we allowed the drift rate for lures to change between weak and strong tests with a constant starting-point value. In the starting point model, we fixed lure drift rates across strength and allowed the position of the starting point to vary. All other model parameters matched the fits above, which gave both models 12 free parameters. According to the drift criterion hypothesis, lure drift rates should change across strength even in the mixed condition; thus, the starting point model should not be able to accommodate the data. However, if changes in lure drift rates can only be produced by differentiation, then the FAR effects in the mixed condition must reflect changes in starting point, the parameter that Criss (2010) suggests is uniquely sensitive to decision biases. Thus, the drift criterion account predicts a superior fit for the lure drift model, and the differentiation account predicts a superior fit for the starting point model.

Table 4 reports G² values for the constrained models fit to both the group and individual data (values were summed across participants for the individual fits). The lure drift model produced a better fit than the starting point model at both levels. The basis for the poor fit of the starting point model is clear when one compares the starting point predictions in Figure 3 to the mixed data in Figure 4. The data show no hint of the predicted changes in the leading edge of the RT distributions. Also contrary to predictions, error responses are not made faster than correct responses for targets on the strong tests. In fact, to match the RT distributions, the starting point model had to propose very similar values of starting point bias for strong and weak tests (in the group fit, z/a was .54 for weak tests versus .53 for strong). As a result, the model completely missed the decrease in false alarm rate from weak to strong tests, predicting a false alarm rate of .19 in both cases. In other words, if the model had adjusted the starting point to accommodate the false alarm rate difference, the resulting misses to the RT distributions would have produced an even worse fit than a model with a constant starting point. In contrast, the lure drift model accommodated the false-alarm rate difference while maintaining a good fit to the RT distributions. The lure drift model predicted false-alarm rates of .25 and .14 for the weak and strong conditions, quite close to the data values of .25 and .12. Clearly, data from the mixed condition can only be accommodated by proposing changes in the lure drift rate.

Table 4.

G² values for the lure drift and starting point versions of the diffusion model fit to data from the mixed condition

Experiment and Condition	Type of Fit and Model
	G2 Group Fits		Σ(G2) Individual Fits
	Lure Drift Model	Starting Point Model	Lure Drift Model	Starting Point Model
Experiment 1	89	149	709	754
Experiment 2	106	125	759	821
Experiment 3	117	188	858	914

Note: In the lure drift model, drift rate for lures freely varied across test strength with the starting point held constant. In the starting point model, drift rate for lures was fixed across strength and starting point bias was free to vary. Each model had 12 free parameters to fit 44 freely varying response frequencies. There were 19 participants in Experiment 1, 20 in Experiment 2, and 21 in Experiment 3 (all data are from the mixed condition).

Summary

The most important finding from the first experiment is that drift rates for lures were affected by strength-based changes in decision processes as proposed by the drift criterion account. In the mixed condition, correctly informing participants that only weak or only strong items would be tested produced the same mirror effect in drift rates observed by Criss (2010). Differentiation from the study list was controlled in the mixed condition, so the drift rate results cannot be interpreted as a unique signature of this mechanism. Moreover, comparing the size of the strength effect across the mixed and pure conditions revealed no evidence of a contribution from the differentiation process; that is, the effect was as large when test expectations changed without a differentiation difference (mixed condition) as when expectations and differentiation both changed (pure condition). This pattern held for both the false-alarm rate and the lure drift rate. Finally, we found no evidence that biases in the starting point produce the lower FAR on strong versus weak tests.

Experiment 2

In Experiment 1, we matched the length of the distractor task across all conditions. However, the study lists had different numbers of presentations, which created differences in the average retention interval. Although this does not affect conclusions about the effect of strength within any of the list conditions, it could cloud comparisons across conditions. In the second experiment, we matched the average retention interval across conditions by adjusting the length of the distractor phase.

Method

Design and Participants

The design was the same as Experiment 1. For the pure-between condition, there were 21 participants in the weak group and 21 in the strong group. The pure-within condition had 18 participants, and the mixed condition had 20. None of the participants contributed data to more than one list condition or to the previous experiment.

Materials

All materials were the same as those in Experiment 1.

Procedure

The procedures matched Experiment 1 with two exceptions. First, we adjusted the length of the two-back task to equate the average retention interval for weak items between the pure-weak and mixed lists as well as the average retention interval from the last presentation of the strong items across the pure-strong and mixed lists. Specifically, participants saw 30 digits after mixed lists, 22 after pure-strong lists, and 53 after pure-weak lists. Second, the number of study/test cycles changed in all of the list conditions. In the pure-within and mixed conditions, there were 11 cycles. The first two were practice cycles, and they were followed by eight critical cycles. Both the practice and critical cycles were evenly split between the strong and weak conditions. The final cycle did not contribute data to the analyses.³ In the pure-between condition, the number of cycles was reduced to eight, with two practice cycles followed by five critical cycles. The last cycle was not included in analyses for consistency with the other conditions.

Results and Discussion

Recognition Performance

The HR and FAR data across all conditions are shown in Table 1. We succeeded in equating the strength effect on memory sensitivity across the list conditions: the increase in d′ from weak to strong was 1.12 for pure-between, 1.03 for pure-within, and 1.08 for mixed [d′ = z(HR) − z(FAR) where z is the inverse cumulative distribution function for a unit normal distribution]. As in Experiment 1, a mirror pattern arose for all of the list conditions. That is, the HR increased and the FAR decreased from weak to strong tests. As in Experiment 1, we evaluated strength-based differences in FAR using Bayesian t-tests. These analyses found evidence for an FAR effect that ranged from suggestive to very strong across the list conditions (BF = .3125, .0051, and .0925 for pure-between, pure-within, and mixed). Also replicating Experiment 1, the false-alarm rate effect was similar in size in the pure and mixed conditions, which suggests that differentiation plays little or no role in producing the effect. A directional Bayesian t-test found suggestive support for the null hypothesis over the hypothesis of a larger FAR effect in the pure condition (BF = 4.0878).

Diffusion Model Analyses

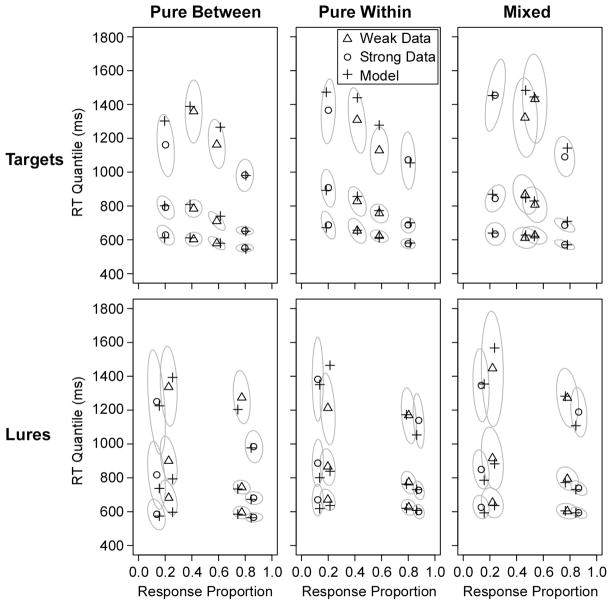
Figure 5 shows the fit to the overall data for the 13-parameter diffusion model (with both lure drift and starting point varying across strength), and Table 2 reports the G² values. Once again, the model matched both the RT distributions and the mirror pattern in the response frequencies. Nearly all of the predicted points fell within the 95% confidence ellipses around the data. As in Experiment 1, we performed analyses on the lure drift rate and starting point results.

Figure 5.

Quantile-probability plots for group data from Experiment 2 with the predicted points of the best-fitting diffusion model (predictions are from the fits with both lure drift and starting point varying across strength). The sets of 3 points are the .1, .5, and .9 quantiles of the RT distributions, and they are plotted on x-values equal to the probability of the response (the .3 and .7 quantiles were also fit, but they are omitted from the plot to avoid clutter). The gray ovals show 95% confidence ellipses estimated with a bootstrap procedure (Efron & Tibshirani, 1985). For the bootstraps, 500 simulated datasets were created by randomly sampling participants with replacement, and response proportions and RT quantiles were calculated for each simulated dataset. The plot shows the smallest ellipses that contained 95% of the points across the bootstrap runs.

Table 3 reports the average drift rates from the individual-participant fits. Drift rates for targets studied five times were higher than drift rates for targets studied once. Moreover, drift rates were lower for lures that were tested with strong targets than lures tested with weak targets, showing a mirror pattern. Tests produced suggestive evidence for a strength effect on lure drift rates in the pure-between condition (BF = 0.3259) and very strong evidence in the pure-within and mixed conditions (BF = 0.0057 and 0.0009, respectively). The hypothesis that the strength effect on lure drift rates was the same across the pure-within and mixed conditions was favored over the hypothesis that the effect was larger with pure lists, but the support for the former hypothesis was only suggestive (BF = 3.7169).

The starting points were generally near the unbiased value (.5), although they showed a consistent slight bias toward the “old” response. In the pure-within and pure-between conditions, results showed slight to suggestive evidence for a null strength effect (BF = 3.0664 and 2.1355, respectively). The test for the mixed condition found evidence in favor of a strength effect (BF = 0.0040). However, this effect arose because the starting point was slightly more biased toward “old” responses on strong versus weak tests, the opposite of the shift needed to account for the SBME (see Figure 2). Thus, the results indicate that starting point differences play no role in the decreased FAR on the strong tests, and might have even worked against this decrease in the mixed condition.

Model Comparison

As in the first experiment, we further tested the drift criterion account by contrasting the fit of the lure drift model versus the starting point model to data from the mixed condition. The lure drift model again produced a better fit at both the group and individual-participant level (see Table 4). As in Experiment 1, the starting point model failed because the RT distributions were inconsistent with the predicted changes in leading edge and the relative speed of error and correct responses. Again, to match the distributional characteristics, the starting point model had to maintain a relatively constant bias across strength (in the group fit, z/a was .53 for weak lists and .54 for strong) and missed the change in false alarm rate as a result. In fact, the starting point model produced a slightly lower false-alarm rate for the weak lists (.18) than for the strong lists (.20). In contrast, the lure drift model matched the false alarm rate difference, producing weak and strong false-alarm rates of .22 and .16 (the observed values were .22 and .13). Again, given the RT data, the diffusion model simply could not accommodate the strength-based change in false alarm rate in terms of starting point bias without changes in lure drift rates.

Summary

The results closely replicated those of Experiment 1. In the mixed condition, differences in lure drift rate were produced by changes in the expected target strength at test with no differentiation difference. This pattern is consistent with a strength-based shift in the drift criterion. Results in the pure conditions once again replicated the Criss (2010) result but showed no evidence that differentiation produced a larger strength effect on false-alarm rate or lure drift rate compared to the mixed condition.

Experiment 3

When we displayed the predictions of the drift-based and starting-point mechanisms, we assumed unbiased performance (Figure 3). In the first two experiments, participants had an overall bias to say “new” resulting in higher performance for lures than for targets. Starns et al. (2010) also observed general conservativeness in experiments without response feedback, but participants were closer to unbiased performance when feedback was provided. In Experiment 3, we replicated the mixed condition from the second experiment with performance feedback at test. If we replicate the difference in lure drift rates found in the mixed conditions of Experiments 1 and 2, then the results will further strengthen the evidence that drift rates can change based on decision processes. In contrast to the previous experiments, performance for targets and lures should be similar and the results should closely match the drift predictions in Figure 3.

Method

All methodological details were identical to the mixed condition from Experiment 2, except that the word “ERROR” appeared on the screen for 1 s after each incorrect response on the recognition test. This experiment included 21 participants who did not contribute data to any of the previous experiments.

Results and Discussion

Recognition

The recognition results showed a clear mirror effect: the HR was higher for strong versus weak targets, and the FAR was lower (Table 1). The FAR effect was larger than any of the conditions in the first two experiments, perhaps indicating that feedback facilitates strength-based changes in decision processes. A Bayesian t-test found overwhelming evidence for a strength effect in the FAR data (BF = 0.00005).

Diffusion Model Analyses

Figure 6 shows the fit of the 13 parameter diffusion model (with both lure drift rate and starting point varying across strength), and Table 2 reports G² values from the fits. The model closely matched the data, and for this experiment none of the predictions fell outside the 95% confidence ellipses. The response probabilities line up much more closely for targets and lures than in the previous experiments, indicating relatively unbiased performance. Overall, the data closely matched the predictions of the drift-based accounts shown in Figure 3. For correct responses to both targets and lures, RTs were lower for strong than for weak lists, with the difference primarily in the distribution tails (.9 quantiles) and not the leading edges (.1 quantiles). Error RTs were slower than correct and were relatively constant across weak and strong tests. In contrast, the plots clearly mismatch the predictions of the starting point account. There is no evidence that “new” responses are generally faster on strong than weak lists.

Figure 6.

Quantile-probability plots for group data from Experiment 3 with the predicted points of the best-fitting diffusion model (predictions are from the fits with both lure drift and starting point varying across strength). The sets of 3 points are the .1, .5, and .9 quantiles of the RT distributions, and they are plotted on x-values equal to the probability of the response (the .3 and .7 quantiles were also fit, but they are omitted from the plot to avoid clutter). The gray ovals show 95% confidence ellipses estimated with a bootstrap procedure (Efron & Tibshirani, 1985). For the bootstraps, 500 simulated datasets were created by randomly sampling participants with replacement, and response proportions and RT quantiles were calculated for each simulated dataset. The plot shows the smallest ellipses that contained 95% of the points across the bootstrap runs.

Table 3 reports the parameter values. As in the previous experiments, target drift rates increased and lure drift rates decreased from the weak to strong tests. A Bayesian t-test yielded very strong evidence for a strength effect in the lure drift rates (BF = 0.000007). Thus, the results again demonstrate that drift rate results are sensitive to decision processes.

Table 3 shows that the starting point was slightly biased toward “old” responses for both weak and strong tests, and there was suggestive evidence in support of the null hypothesis (BF = 4.1074). Again, the numeric difference was in the direction of more liberal responding on the strong test, so the results are inconsistent with a role of starting point in the reduced FAR on strong tests. Interestingly, the model results suggest that the unbiased responding in terms of hit and false alarm rates was produced by offsetting biases in starting point (slightly biased toward “old”) and the drift criterion (slightly biased toward “new,” producing drift rates farther from zero for lures than targets). However, this result may simply reflect tradeoffs between the bias parameters in fits.

Model Comparison

Table 4 shows fitting results from the lure-drift and starting-point versions of the diffusion model. As in the first two experiments, the lure drift model provided a superior fit. Again, the problem for the starting point model was that the RT distributions were inconsistent with large changes in starting point, leaving this model with no mechanism to accommodate false-alarm rate differences between the weak and strong tests. For the group fit, the starting-point bias (z/a) was .60 on weak tests versus .55 on strong tests, leading to a fairly constant false-alarm rate (.28 weak versus .27 strong). Again, the lure drift model produced a much larger FAR effect (.35 weak versus .20 strong) that was more in line with the effect seen in the data (.36 versus .20).

General Discussion

The results convincingly demonstrate that diffusion model drift rates can be influenced by strength-based changes in decision processes. In the mixed condition from all three experiments, correctly informing participants that weak versus strong targets would be tested produced a substantial difference in drift rates for lure items, with lure drifts more quickly approaching the “new” boundary on strong tests. These differences were observed even though the strong and weak tests followed identical study lists; thus, the effects cannot be attributed to differences in the memory traces established at encoding. The results are consistent with a conservative shift in the drift criterion from weak to strong tests. That is, when participants know that targets will be strong, they require higher evidence values to move the accumulation process toward the “old” boundary. This shift is directly analogous to the criterion shift account of the SBME proposed within the signal detection framework (e.g., Hirshman, 1995; Stretch & Wixted, 1998). Results showed no evidence that the lower false-alarm rate on the strong test resulted from a change in starting point. Therefore, the experiments are inconsistent with the proposal that decision manipulations selectively influence the starting point.

Critically, by showing that drift rates are sensitive to decision processes, the results demonstrate that observing the SBME in terms of drift rates does not provide evidence for differentiation. The first two experiments offered a chance to assess any additional role for differentiation. That is, the pure conditions offered the same opportunity to adjust decision processes from strong to weak tests with an additional manipulation of the level of differentiation for the studied items. Results showed no evidence that the added differentiation difference produced a bigger strength effect for either false-alarm rates or lure drift rates. In contrast, the Bayesian t-test results consistently provided weak to suggestive support for the hypothesis that the strength effect was the same size in the pure and mixed conditions, and none of the tests favored the hypothesis that the strength effect was larger with pure lists. Although we cannot confidently conclude that differentiation plays no role in the SBME, the clear effects in the mixed condition show that differentiation from the study list is certainly not necessary to produce the effect (also see Hirshman, 1995; Marsh et al., 2009; McCabe & Balota, 2007; Starns et al., 2010). Moreover, all of the studies used to support the role of differentiation in the SBME used paradigms in which participants could adjust their decision processes from strong to weak lists (Criss, 2006, 2009, 2010). Therefore, there are no positive results that uniquely support the role of differentiation in the SBME.

Our results also highlight a more general message: because drift rates can be affected by both evidence and decision processes, the two must be separately manipulated at the experimental level for researchers to draw firm conclusions. This is certainly possible in many situations. For example, if strong and weak targets are randomly mixed at test with no distinguishing characteristics other than the number of times they were studied, then participants have no opportunity to change their decision standards based on strength (the number of times a word was studied cannot affect criteria for deciding whether a word was studied or not). In this case, a higher drift rate for strong versus weak targets can be unambiguously attributed to a change in evidence. In contrast, consider two groups of participants who study identical lists, but one group is asked to be careful to never make false alarms at test whereas the other is asked to be careful to never miss a target item. If drift rates differed between the two groups, then the difference could be confidently attributed to decision processes given that learning was held constant.

Differentiation at Retrieval

Recent work on the decline in accuracy across test trials has applied a version of REM in which memory traces are updated throughout the recognition test (Criss, Malmberg, & Shiffrin, 2011). These studies also use a version of the model that decides whether to store each item in an existing trace or a new trace based on the match to memory. That is, if the model decides that the item has been previously presented, then the trace with the highest match to the item is updated. If the model decides that this is the first presentation for the item, then a new trace is formed (Shiffrin & Steyvers, 1997). With such a model, it is possible for differentiation differences to arise at test even with the design used in our mixed condition. At the start of the test, differentiation would be equal for strong and weak tests, as each followed a list of half strong and half weak items. However, as targets are tested, a higher proportion of them would be recognized and added to a previous trace on strong tests than on weak tests. Therefore, lures occurring at the end of a weak test might actually be matched to less differentiated traces compared to lures on a strong test.

Although differentiation at test is theoretically possible, comparing the pure and mixed conditions still provides strong evidence against the proposition that differentiation underlies the false-alarm rate and lure drift rate differences. The pure condition had an identical test structure to the mixed condition, so any differentiation arising at test should have been equivalent between the two. However, the degree of differentiation from the studied traces varied dramatically between pure and mixed. These large differences in differentiation at study did not produce a bigger strength effect for the pure conditions. Therefore, extending differentiation to retrieval cannot explain the full pattern of results across conditions.

A more recent study directly investigated the role of differentiation at retrieval (Starns & Hicks, 2011). Participants studied mixed lists of strong and weak words, and then they completed a test that was organized into blocks based on target strength. For example, the first 20 items of the test might contain only strong targets and lures, the next 20 only weak targets and lures, and so forth. For some of the participants, strong and weak blocks were marked by different colors, whereas blocks were not demarcated in any way for the remaining participants. Critically, both groups encountered the same study and test structure, so the level of differentiation was equated even if traces were also established at test. However, marking the blocks gave participants a chance to adjust their decision standards based on strength. Results showed that the strong FAR was significantly lower than the weak FAR for the marked condition, but there was no FAR difference with umarked blocks. Thus, contrary to the differentiation-at-test account, the critical factor was not the structure of the test but the opportunity to adjust decision processes based on strength.

Different Types of Criteria in RT Models

The diffusion model has multiple parameters that accommodate decision biases: the starting point and the drift criterion. This might seem superfluous, especially for theorists who are accustomed to the single criterion parameter in signal-detection theory. However, changes in the starting point and the drift criterion have distinct signatures in terms of RT distributions, with much larger changes in the leading edge of the distributions based on changes in starting point (Figure 3 herein; Ratcliff et al., 1999; Ratcliff & McKoon, 2008). Different decision manipulations show these characteristic patterns; thus, they cannot all be modeled with one decision parameter. For example, target proportion manipulations cannot be modeled solely with the drift criterion without changes in starting point (Criss, 2010; Ratcliff, 1985; Ratcliff et al., 1999; Ratcliff & Smith, 2004; Wagenmakers et al., 2008), whereas the strength-based changes in decision processes that we observed could not be modeled in terms of the starting point without changes in the drift criterion.

More critically, the different decision parameters have different interpretations that meaningfully relate to the types of manipulations found to affect them. The starting point represents an a priori preference for one of the responses before any evidence samples have been observed. For example, if a test is 80% target items, then it is natural to lean toward the “old” response independent of the evidence from memory. In contrast, the drift criterion determines whether each evidence sample supports an “old” or “new” response. In other words, it determines how strong the evidence must be to take a step toward the top boundary. Thus, it is not surprising that changes based on the expected strength of the target items affect the drift criterion instead of the starting point. The pattern across different decision manipulations highlights the importance of RT data and demonstrates that evaluating accuracy alone conflates different underlying decision mechanisms. Notably, the need for different types of decision criteria is almost completely unaddressed by current computational models of recognition memory, largely because these models are just beginning to tackle the accumulation of evidence over time (e.g., Malmberg, 2008; Nosofsky & Stanton, 2006).

Models for Decision Processes

An important goal for future work is specifying the mechanism by which expected strength impacts drift rates. The effect can be modeled in terms of the drift criterion, but a full explanation would require a model for how the drift criterion is set and adjusted based on strength. One possibility is that the drift criterion serves as a proxy for a likelihood assessment at retrieval (Glanzer, Hilford, & Maloney, 2009). That is, each incoming sample leads to a step toward the “old” boundary if it was more likely to be produced by a target than a lure, and vice versa. The critical question in such accounts is how participants assess these likelihoods; that is, how do they gain knowledge of the distributional form of evidence samples for targets and lures? One possibility is that participants develop estimates of these distributions based on direct experience with the test items (Turner, Van Zandt, & Brown, in press), but they would have to maintain separate values of these distributions for tests with weak versus strong targets in the mixed list design. Also, extending this idea to RT models will require substantial theoretical development.

An alternative approach is to posit that likelihoods are directly computed by the memory system based on information in the probe and in memory traces (Dennis & Humphreys, 2001; McClelland & Chappell, 1998; Shiffrin & Steyvers, 1997). A key innovation in models of this sort is the ability to produce positive evidence that an item is a lure, eliminating the need to place a criterion at an arbitrary position on the strength continuum. The BCDMEM model, for example, assesses the likelihood that each test item is a target versus a lure based on the matches and mismatches between the context retrieved by the item and a context representing the study list. To achieve this, the memory system needs an estimate of how well the items would have been linked to the studied context if they were indeed on the list. Therefore, BCDMEM directly incorporates strength-based changes in decision processes: if stronger targets are expected at retrieval, then mismatching features produce stronger evidence that the test item is a lure (Dennis & Humphreys, 2001; Starns et al., 2010).

To avoid confusion, we should note that expressing memory matches in terms of likelihoods is a property shared by a number of current models, including REM. However, the likelihood calculations in REM are not influenced by the expected strength of the targets. Instead, target strength affects the actual matches and mismatches for targets and lures, so the SBME is produced based on the properties of the traces themselves and not changes in the decision process (Criss, 2006; Shiffrin & Steyvers, 1997; Starns et al., 2010). Therefore, the current class of likelihood models subsumes both models that explain the SBME in terms of differentiation (such as REM) and models that produce the effect via decision processes (such as BCDMEM).

Conclusion

The current results add to a growing body of evidence that the SBME is properly explained in terms of decision processes (Hirshman, 1995; McCabe & Balota, 2007; Singer, 2009; Singer & Wixted, 2006; Starns et al., 2006, 2010; Stretch & Wixted, 1998; Verde & Rotello, 2007). Differentiation is not required to produce the effect, and to date no results demonstrate an effect of differentiation independent of decision processes. The results also highlight an important caveat in interpreting diffusion model parameters: drift rates can be affected both by changes in evidence and by changes in decision processes, and these possibilities can only be discriminated when they are de-confounded by the experimental design. Thus, the drift criterion is a critical parameter of the diffusion model, and one that deserves closer attention.