Tangential Tether Extraction and Spontaneous Tether Retraction of Human Neutrophils

Abstract

Membrane tethers are extracted when neutrophils roll on the endothelium to initiate their transendothelial migration. Tether extraction from both neutrophils and endothelial cells stabilizes neutrophil rolling, so it has been studied extensively and the force-velocity relationship for tether extraction is of great interest. Due to limitations of the techniques used in previous studies, this relationship has been obtained only from tethers perpendicular to the cell surface. Here, with the microcantilever technique, where latex beads affixed on silicon cantilevers were used as the force transducer, we extracted tethers either perpendicular or tangential to the neutrophil surface. We found that the force-velocity relationship was not sensitive to tether pulling direction. Little movement of the tether-cell junction was observed during tangential tether extraction, and no coalescence was observed during multiple tether extraction. Following adhesion rupture, spontaneous tether retraction was visualized by membrane staining, which revealed two phases: one was fast and exponential, whereas the other was slow and linear. Both phases can be reproduced with a mechanical model. These results show for the first time, to our knowledge, how neutrophil tethers shorten upon instantaneous force removal, and furthermore, they illustrate how membrane tethers contribute to neutrophil rolling stability during the inflammatory response.

Introduction

To fight against invading microorganisms, circulating neutrophils first roll on the endothelium and then migrate across the endothelium to infection sites. Stable rolling of neutrophils, which is a prerequisite for their successful transmigration, is mediated by selectins (L-selectin on neutrophils and P- and E-selectin on endothelial cells) (1). To achieve stable rolling, neutrophils exploit not only molecular features of selectins but also cellular mechanical properties, such as tether extraction (2–8), surface protrusion (6,9), and cell deformation (10,11). It has been shown that tether extraction acts to effectively relieve disruptive forces on selectin bonds and in so doing increases selectin-bond lifetime, hence stabilizing neutrophil rolling. Therefore, it is imperative to know how fast a tether grows (U_t) at a certain pulling force (F).

Several models have been proposed to describe how F relates to U_t, and they have been applied to tether extraction from neutrophils and endothelial cells (1–4,6,12–16). In earlier experiments where U_t was <20 μm/s, it was found that the F-U_t relationship can be well described by the linear equation (15,17–19)

$$F=F_0+2\pi {\eta }_{eff}{U}_t,$$ (1)

where F₀ is the threshold force and η_eff is the effective viscosity. Probed at a larger velocity range (0.4 < U_t < 150 μm/s), tether extraction exhibited significant shear thinning, so the F-U_t data can be fitted better with the power-law equation (13)

$$F=\alpha U_t^{\beta },$$ (2)

where α and β are two constants. One shortcoming of the power-law model is that the pulling force vanishes at zero tether velocity, so a more general but complex model was proposed based on the assumption of hydrodynamic narrowing of the tether radius (12). More recently, another power-law equation was proposed (20,21):

$$F=\alpha {\left(U_t-U_0\right)}^{\beta },$$ (3)

where α and β are two constants and U₀ (<0) is the tether velocity when F = 0. This equation captures all known characteristics of tether extraction, including nonlinearity, nonzero threshold force, and possible retraction (U_t < 0), but it is phenomenological by nature.

Limited by the techniques in previous studies, tethers were always extracted with pulling forces perpendicular to the cell surface. The F-U_t relationship obtained as such has been assumed to be applicable in vivo, in flow-chamber studies, and in mathematical models (6,8). However, after a tether is extracted during neutrophil rolling, the pulling force changes its direction continuously, and it is rarely perpendicular to the cell surface, as shown in flow-chamber studies (5). It is unknown whether different pulling directions affect the F-U_t relationship.

On a related note, a pulling force nonperpendicular to the cell surface may cause lateral movement of the tether-cell junction on the cell surface, as observed on lipid vesicles (22). On the cell surface, this lateral movement has to overcome the energy barrier presented by the membrane-cytoskeleton association. Whether the tether-cell junction can move on the cell surface during neutrophil rolling is unknown. Moreover, the mobility of the tether-cell junction is related to another question important for studying cell rolling dynamics, i.e., whether multiple tethers can coalesce on the cell surface. For lipid vesicles, because the tether-vesicle junction can move freely on the vesicle surface (22), multiple tethers spontaneously coalesce when the distance separating the junctions becomes smaller than a threshold value (23). As a result, the overall force imposed on the vesicle by the coalesced tethers becomes only a fraction of the precoalescence value. Both tether coalescence and tether-cell junction movement can potentially alter cell rolling dynamics.

Membrane tethers can also retract. For example, upon breakage of the selectin-ligand bonds during neutrophil rolling, extracted tethers (especially those with short adhesion lifetime) may retract back to the cell body. Ramachandran et al. postulated that incompletely retracted tethers contribute to rolling stabilization by allowing an easier second-round extraction (5). Another example is simultaneous tether extraction (two tethers, one from a neutrophil and the other from an endothelial cell, linked in series by a receptor-ligand bond), which has been shown to be more effective than single-tether extraction for stabilizing rolling (4,8). Because the threshold forces for tether extraction from neutrophils and endothelial cells are not equal, when the pulling force falls below the larger threshold force, one tether will retract even as the total tether length still increases. In addition, membrane tethers extracted from platelets (24) or neuronal growth cones (17) and those connecting cultured T-cells (25) have also been observed to retract. In a broad sense, both extraction and retraction are integral parts of force-modulated tether dynamics. Yet in contrast to the extensive studies of tether extraction, much less is known about tether retraction. Retraction of rapidly extracted and ultralong (hundreds of micrometers or longer) tethers from giant vesicles has been studied both experimentally and theoretically (26), but the results cannot be readily applied to cells where complex membrane-cytoskeleton interactions are involved and tethers are much shorter and extracted at much lower speeds. A recent study on erythrocytes showed that extracted tethers retracted slowly back to the cell body after the pulling force was suppressed (27), but the study was largely qualitative in regard to tether retraction. To our knowledge, no quantitative data are available for tether retraction from human neutrophils at present.

Materials and Methods

Neutrophil isolation and membrane staining

Neutrophils from healthy donors (recruited with a protocol approved by the Washington University Institutional Review Board) were prepared similarly, as described elsewhere (6,16). Briefly, cells collected by finger prick were isolated by density-gradient centrifugation and suspended in 0.5% human serum albumin (Fisher Scientific, Hampton, NH) in Hank’s buffered salt solution (Sigma, St. Louis, MO). For membrane staining, isolated neutrophils were suspended in 1 mL 1% bovine serum albumin (Fisher Scientific) in phosphate-buffered saline (PBS) and gently mixed on a shaker at room temperature for 5 min. The sample was then centrifuged at 200 × g for 5 min. The cell pellet was resuspended in 1 mL 0.5% human serum albumin in Hank’s buffered salt solution. Then, 20 μL 2.5 mg/mL DiO (a lipophilic carbocyanine membrane dye; Invitrogen, Carlsbad, CA) solution in dimethylsulfoxide (Sigma) was added and the mixture was incubated on a shaker at 37°C for 20 min.

Bead preparation

Latex beads (Bangs Laboratories, Fishers, IN) were coated with mouse anti-human CD162 or CD44 (BD Biosciences, San Jose, CA) by two methods. Passive adsorption was used for cantilever-attached beads. For each cantilever (Veeco Probes, Camarillo, CA), a plain dry latex bead was affixed onto its tip by a tiny drop of UV curing adhesive (Norland Products, Cranbury, NJ). The whole chip was then immersed in 0.1 μg/μL anti-CD162 solution for 4 h at room temperature. For latex beads precoated with goat anti-mouse antibody (Bangs Laboratories), they were first washed with PBS twice and then incubated with 0.01 μg/μL anti-CD162 (or CD44) in PBS at 37°C for 1 h.

The microcantilever technique (MCT)

Our experimental chamber was formed by a 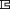-shaped plastic block sandwiched between two glass coverslips. As shown in Fig. 1 a, the chamber (the glass coverslips on the top and bottom are omitted for clarity) has an opening on the right side, where a micropipette is inserted into the chamber. The horizontal movement of the pipette is controlled by a piezo stage (not shown; Model P-517.3CL, Physik Instrumente, Karlsruhe, Germany). The pressure in the pipette is controlled by a water reservoir (not shown) mounted on a vertical motorized stage (Model M501.1PD, Physik Instrumente). The pipette can be used for holding and moving a cell or for imposing pushing or pulling forces, as used frequently in the micropipette aspiration technique (MAT). To the left of the pipette is an atomic force microscope cantilever chip that is glued into a rectangular cut in the chamber wall. A latex bead is affixed to the tip of the softest cantilever on the chip (Fig. 1 b). This bead serves two purposes: it bears proteins that interact with other beads or cells and functions as a displacement marker for the cantilever-tip deflection. The bead displacement is tracked with the algorithm developed by Gelles et al. (28). The cantilevers used in this study were calibrated in situ with the MAT (29) (Fig. 1 b). During calibration, the bead on the cantilever tip is pressed by the bead inside the micropipette, which is the force transducer of the MAT. The calibrated stiffness was 16.5 ± 6.0 pN/nm (mean ± standard deviation; n = 10) compared with their nominal stiffness of 10 pN/nm.

Figure 1.

The microcantilever technique. (a) Schematic. (b) Cantilever calibration. Dotted lines show how the enlarged cantilever corresponds to the small rectangular area in a. The cantilever stiffness was calibrated by pushing it with a known force, imposed by the bead inside the micropipette. The cantilever deflection was tracked using the single-particle tracking algorithm (28).

Tangential and perpendicular tether extraction

The procedures for both tangential and perpendicular tether extraction are illustrated in Fig. 2. A passive neutrophil held by the micropipette was brought into contact with the antibody-coated bead and then pulled back to the right. This process was repeated many times before another cell-bead pair was studied. By placing the micropipette at different positions, tethers were extracted either perpendicularly (Fig. 2 a) or tangentially (Fig. 2 b) to the cell surface. The whole experiment was recorded with a digital camera (Model Phantom v4.2, Vision Research, Wayne, NJ) and analyzed later. The pulling speed was controlled by the piezo stage that controls the micropipette (the speed range was 5–50 μm/s) and the pulling force was calculated by the product of the cantilever stiffness and the cantilever-tip deflection.

Figure 2.

Microscopic view of perpendicular (a) and tangential (b) tether extraction. The bead affixed on the cantilever tip was coated with antibodies against proteins on the cell, which was held by the micropipette. The cell was moved to contact the right side (a) or the top (b) of the bead, then pulled to the right to allow perpendicular (a) or tangential (b) tether extraction from the cell. If a tether was extracted, the cantilever would deflect to the right.

Fluorescent observation of membrane tethers

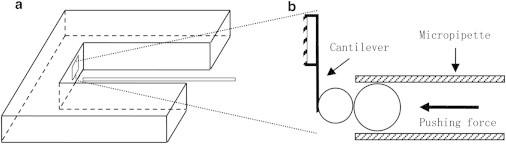
In our experiments carried out with the MCT, the cantilever tip was usually tens of micrometers above the chamber bottom. That was not an ideal location for fluorescent imaging. Thus, we used a two-micropipette system so that we could extract membrane tethers close to the chamber bottom for fluorescent visualization. For studying tether-cell junction movement, tethers were either extracted tangentially (Fig. 3 a) or obliquely (Fig. 3 b). For studying tether retraction, a perpendicular tether was extracted by moving the bead continuously to the left in Fig. 3 b, until the tether detached from the bead and retracted to the cell body. The whole experiment was recorded on DVD with an analog camera (Model WV-BP330, Panasonic, Secaucus, NJ) and digitalized with Scion Image (Scion, Frederick, Maryland) for postanalysis.

Figure 3.

Tether-cell junction mobility in tangential and oblique tether extraction. Dotted circles represent the bead position when it was in contact with the cell. (a) After making contact with the top of the cell, the bead was moved to the left. (b) After making contact with the left side of the cell, the bead was moved briefly to the left and then upward. φ is the angle between the tether and the cell surface (φ = 0° and 90° for tangential and perpendicular tethers, respectively). θ is the angle defined by the tether-cell junction, the upper micropipette corner (the vertex of θ), and the cell center, so the change in θ represents the movement of the tether-cell junction. (c) Fourteen consecutive images (0.033 s between adjacent frames) showing a tangential tether being extracted from a neutrophil, only part of which is shown (the black cap). Fluorescent images are inverted for clarity herein and below. The membrane tether is shown as the faint black shadow emanating from the cell. Note that the bead is invisible. The black dotted line indicates the left end of the growing tether. The tether-cell junction stayed on the vertical white dotted line, showing its immobility. (d) A tether being extracted obliquely from a neutrophil. The black circle shows the position of the bead. (e) Quantification of the lateral mobility of the tether-cell junction on the cell surface for tethers extracted in different pulling directions (φ). The vertical arrow indicates the frame number at which the pulling bead started moving upward (refer to b). Obviously, the angle θ remained nearly constant, indicating that no sliding of the tether-cell junction occurred.

Results

Tangential tether extraction

Using the MCT, we extracted both tangential and perpendicular tethers from human neutrophils with anti-CD162-coated beads affixed on the cantilever tip (Fig. 2). Fig. 4 shows a typical force curve for tangential tether extraction. For perpendicular tether extraction, the shape of the force curve is similar (data not shown). As shown in Fig. 4, when the cell was pulled by a point force mediated by CD162, a crossover force of ∼700 pN needed to be overcome before tether extraction could occur. This behavior has been observed in several other studies of neutrophils and other cell types (21,30–33). Once the crossover force was overcome, the force dropped to a constant until the tether detached from the bead and the force returned to zero. In most cases, there was a single force plateau, as shown in Fig. 4, corresponding to single-tether extraction. Occasionally, multiple force plateaus were observed (data not shown), representing multiple-tether extraction in parallel.

Figure 4.

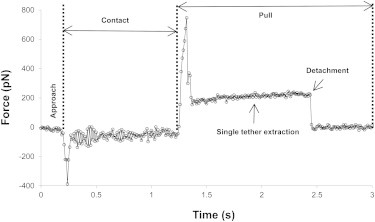
A typical force curve for tangential tether extraction. The approach, contact, and pull are marked, as are the single-tether extraction and detachment. The pulling speed was 25 μm/s.

The force magnitude (F) during single-tether extraction depends on the pulling speed, which is equal to the tether-growth velocity (U_t). Seven pulling speeds were used in this study: 5, 10, 15, 20, 25, 30, and 50 μm/s. A total of 371 perpendicular tethers and a total of 357 tangential tethers from 27 cells were collected. For both cases, the relationships between F and U_t are shown in Fig. 5. The excellent agreement between our results and the results of Heinrich et al. (13) shows that 1), the MCT is reliable, since our perpendicular tether extraction yielded an almost identical relationship between F and U_t; and 2), the relationship between F and U_t does not depend on pulling direction, since our perpendicular and tangential tether extraction yielded almost indistinguishable results.

Figure 5.

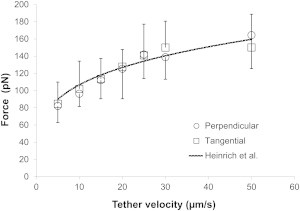
The relationships between F and U_t for both perpendicular and tangential tether extraction. Each point represents an average of ∼50 tether extractions (error bars denote standard deviations).

Tether-cell junction mobility

In our tangential-tether-extraction experiments, we assumed that the pulling speed was equal to U_t, which implied that the tether-cell junction did not move laterally on the cell surface. This is indeed the case, as shown in Fig. 3 c (obtained with the setup shown in Fig. 3 a), where lateral movement (sliding) of the tether-cell junction was not discernible. This experiment was repeated with seven other tether-cell pairs, and the same behavior was observed.

Using the setup shown in Fig. 3 b and anti-CD162- or anti-CD44-coated beads, we also examined the mobility of the tether-cell junction with oblique tether extraction, which is more analogous to tether extraction in vivo during neutrophil rolling. Compared with tangential tether extraction (Fig. 3 a), oblique tether extraction imposes a larger torque on the cell body around the center of the pipette opening (Fig. 3 b), so it becomes more likely to produce cell-body rotation or deformation. In 65 of the 74 cases studied with anti-CD162-coated beads, the cell body outside the pipette remained nearly spherical and rotated without noticeable body deformation (Fig. 3 d). One such case is shown in Fig. 3 e, where φ decreased from ∼80° to ∼30°, but constant θ was found, corresponding to no sliding of the tether-cell junction. In seven other cases, where significant cell-body deformation was observed, especially when φ was small, measuring θ became unreliable and unmanageable, so these few cases were excluded from analysis. However, even in these few cases, θ was a constant when φ was large where no significant cell-body deformation was present (data not shown). In only two cases, the tether-cell junction slid to a new position over a small distance and stayed there during the latter stage of tether extraction (the sliding distances for these two cases were ∼0.5 and ∼0.3 μm in ∼0.5 and ∼0.3 s, respectively). Out of a total of 35 oblique and eight tangential tethers studied with anti-CD44-coated beads, no sliding of the tether-cell junction was ever observed. This is very likely a reflection of the fact that both CD162 and CD44 are distributed on the nonmicrovillar cell surface of human neutrophils (34,35). When oblique tether extraction was carried out with dying cells (characterized by smooth peripheries and more vibrant granular fluctuation), tethers slid freely (i.e., always perpendicular to the cell surface) as if they were on lipid vesicles.

In the experiments described above, multiple tethers were occasionally extracted. Since tether coalescence requires the mobility of the tether-cell junction, we examined whether tether coalescence occurred in these cases. In 47 out of 48 cases of multiple tether extraction, no coalescence was observed (Fig. 6). In one case only, one of the initially parallel tethers partially slid on the cell surface (over a distance of ∼0.4 μm in ∼0.1 s), but no coalescence occurred (data not shown).

Figure 6.

Multiple tether visualization. No coalescence was observed when double tether extraction was performed. Only part of the cell is shown on the right.

Spontaneous tether retraction

As shown in Fig. 4, membrane tethers would eventually detach from the bead because of bond dissociation, receptor extraction, or antibody dislodgment. These tethers would then retract as a consequence. By staining the cell membrane with DiO, we studied tether retraction after single tethers were extracted at four different velocities, 1, 5, 10, and 25 μm/s. A representative case of tether retraction is shown in Fig. 7 a. Usually, retracting tethers would lose their straight shape and adopt a wavy contour in <0.1 s. During this period of time, tethers shortened rapidly. Thermal fluctuation could be visualized at the tether tip and then on the whole tether, indicating relaxation of membrane tension. After the initial fast retraction, tethers would continue to shorten, but at a slower and more steady pace. Coincident with the initial fast shortening, there was always an increase in fluorescence intensity on retracting tethers, despite photobleaching, showing an increase in membrane area/unit of tether length (Fig. 7) and indicating an expansion of tether diameter.

Figure 7.

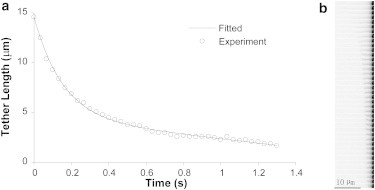
Retraction of a tether extracted at 5 μm/s. (a) Tether length measured over time (circles). The solid curve is the best fit with the model described in the Appendix. (b) Video frames (0.033 s between adjacent frames) corresponding to the length measurements in a.

Tethers extracted at small velocities appeared to be either straight or curved cylindrical tubes at any given instant during retraction (Fig. 7 b). However, at larger U_t, we observed the formation of pearl-like structures more and more frequently at the tips of the retracting tethers: 0% at 1 μm/s, 17% at 5μm/s, 76% at 10 μm/s, and 100% at 25 μm/s. At 1, 5, and 10 μm/s, ∼12 tethers were obtained and their changes in length over time were measured and fitted with the model described in the Appendix. Because of the faster tether retraction at 25 μm/s, we could not measure enough points to achieve reliable fitting. According to our model, the initial fast tether retraction is dominated by elastic deformation recovery, and the later slow tether retraction is dominated by membrane flow due to far-field membrane tension on the cell body and the membrane-cytoskeleton adhesion. At larger U_t, the retraction started at smaller tether radii because of the larger pulling force (hydrodynamic narrowing), and the initial retraction velocity was always larger. For retraction of tethers extracted at 1, 5, and 10 μm/s, we found that R_∞ = 0.074 ± 0.006 μm, t_c = 0.10 ± 0.01 s, and νη_e = 262 ± 45 pN·s/μm³ (mean ± SE for n = 39 tethers), where R_∞ is the terminal value that the tether radius (R_t) approaches during tether retraction, t_c is the characteristic time for elastic energy recovery, v is the surface density of integral proteins, and η_e is the surface viscosity.

Discussion

Most studies of tether extraction have been performed with the MAT (2–4,7,14,16,18,19,36), the biomembrane force probe (BFP) (13), and the optical trap (OT) (17,30). However, these techniques cannot be easily applied to tether extraction at a controlled pulling angle. Both the MAT and the BFP take advantage of a micropipette manipulation system with two opposing coaxial pipettes, one holding the force transducer and the other holding the object of interest (a cell or a protein-coated bead). By design, they impose/measure forces along the pipette axis, which is perpendicular to the cell surface. Because the force transducer of the OT can rotate freely around the trap center, tangential tether extraction (including both direction and velocity) cannot be controlled well. For example, the tether velocity is not constant due to the rotation of the force transducer, even when the cell is pulled away at a constant velocity. Therefore, we developed the micropipette-based MCT with both the convenience of micropipette manipulation and the ability to impose forces at an arbitrary pulling angle.

The F-U_t relationship for tether extraction is essential for a systematic understanding of the physiological processes related to membrane tethers, including neutrophil rolling. In previous studies, this relationship was obtained by pulling membrane tethers perpendicular to the cell surface. In this study, we showed that this relationship did not change for tethers pulled tangentially to the cell surface. Therefore, this relationship may hold for tethers pulled at any angle to the cell surface. Also in this study, we showed that, in the context of cell rolling, the mobility of the tether-cell junction can be neglected at physiological rolling velocities (37). Even in the three cases where we saw lateral movement, the maximal displacement of the tether-cell junction was only ∼0.5 μm, which should not have much of an impact on rolling dynamics. We believe that the major resistance to the tether-cell junction movement comes from the membrane-cytoskeleton association, since tethers can readily move on apoptotic cells or lipid vesicles (22,23).

The mobility of the tether-cell junction is required for tether coalescence. Theoretical work by Derényi et al. predicted that multiple extracted tethers naturally attract each other due to energy minimization, hence coalescing in the absence of any pinning force (38). After tether coalescence, the overall force imposed on the cell or vesicle body becomes only a fraction of the precoalescence magnitude. Therefore, the force drop observed during multiple-tether extraction (3,7,23,39) may be attributed to either tether coalescence or tether detachment. However, the fact that no coalescence was observed in ∼50 cases of multiple tether extraction in this study shows clearly that on neutrophils, multiple tethers do not coalesce during extraction, and the force drop during multiple tether extraction is thus due to tether detachment.

After a membrane tether is extracted, more and more energy is stored in it (mainly due to membrane bending and stretching) as it is pulled longer by force, so the tether is expected to retract to release the stored energy once the pulling force is removed. Although Eq. 3 can be used to describe tether retraction, it can only be applied to the cases where the pulling force decreased gradually (i.e., the force unloading rate was finite). It cannot be applied to this study, where the pulling force was removed instantaneously (i.e., the force unloading rate was infinite). Consequently, we developed a mechanical model for spontaneous tether retraction (Appendix) that fit well with our experimental results (Fig. 7 a). The model postulates that the retraction is driven by the sum of two principal driving forces, the recovery of elastic energy stored as a result of the radius of the tether being less than its resting radius, and the far-field membrane tension and adhesion to the cytoskeleton, which tend to draw the tether back onto the cell surface. Elastic recovery appears to dominate the early phase of the recovery, and the far-field membrane tension/adhesion appears to dominate at longer times. The fitted value of νη_e (262 pN·s/μm³) is close to what was obtained by Brochard-Wyart et al. (12). The fitted value of R_∞ (0.074 μm) is a parameter likely determined by the inherent mechanical properties like the far-field membrane tension and the bending modulus. With the fitted value of t_c (0.1 s), we can calculate the value of the damping coefficient, μ, which is 0.02 pN·s·μm. Since $\mu \dot{C}=\mu \dot{L}/\left(\text{tether}\text{surface}\text{area}\right)$, where C is tether curvature and L is tether length, and the tether surface area is on the order of LR_t (∼1 μm²), the equivalent drag coefficient should be ∼0.02 pN·s/μm for tether retraction. From low-Reynolds-number hydrodynamics, we can find the drag coefficient for the fluid flow induced by tether retraction, which is on the order of Lη_f (26,40,41), where η_f is the fluid viscosity and its value should be close to the viscosity of water, 10⁻³ pN·s/μm². Since L is typically tens of micrometers, the value of 0.02 pN·s·μm for μ strongly indicates that the resistance for tether curvature change comes from the fluid inside and outside the tether.

The two phases of spontaneous tether retraction (fast and exponential followed by slow and linear) are similar to what was observed from erythrocyte tethers (27) but markedly different from what was observed from lipid-vesicle tethers, where the retraction velocity was more or less a constant (26). In these two earlier studies, the tether did not retract freely, because the tether tip was connected to either a cell or a bead, which slowed down tether retraction hydrodynamically. Even for neutrophil tethers, when the pulling force was decreased gradually rather than removed instantaneously, tether retraction exhibited quite different characteristics (20). Therefore, the force unloading rate is the dominating factor for determining how tether retraction occurs.

Conclusion

In this work, we have shown that the constitutive equation (F-U_t relationship) of tether extraction from human neutrophils is the same for tethers extracted perpendicularly and tangentially to the cell surface. This is consistent with another key observation that the tether-cell junction does not move on the cell surface. Consistent with the tether-cell junction immobility, we did not observe tether coalescence when multiple tethers were extracted from neutrophils. Furthermore, we found that dissociated tethers retracted spontaneously. The retraction starts from a fast exponential phase, followed by a slow linear phase. According to our mechanical model, the initial fast phase was dominated by elastic deformation recovery and the latter slow phase was driven by the far-field membrane tension and the membrane-cytoskeleton adhesion.

Appendix A: A Mechanical Model of Tether Retraction

A membrane tether undergoes hydrodynamic narrowing and experiences larger tension while being extracted by a pulling force (f) (12). As a result, once the pulling force is removed, the tether radius (R_t) should increase and the tension-generated membrane strain should decrease to release the stored elastic energy. These two processes are impeded by the resistance from membrane flow, interbilayer slip, cytoplasmic flow, membrane slip over the cytoskeleton, and surrounding fluid flow. Therefore, they can be simulated by viscously damped free vibration. Because of the large area compressibility modulus of cell membrane, little strain was generated by the tension in the tether during extraction, so its contribution to tether retraction can be ignored. Since mass is too small to matter, the change in the tether radius can be described by

$$\mu \dot{C}+kC=0,$$ (A1)

where C (1/R_t) is the curvature, k is the bending modulus of the cell membrane (0.2 pN·μm), and μ is the damping coefficient, which accounts for the total resistance encountered during tether radius increase. The terminal tether radius that R_t approaches is represented by R_∞. The characteristic time (t_c) of this process is μ/k. At the start of tether retraction (or the end of tether extraction), the initial tether radius (R₀) can be calculated from (12)

$$R_0=\sqrt{\frac{k}{2{\sigma }_t}},$$ (A2)

where σ_t is the membrane tension in the tether. It can be shown that (12)

$${\sigma }_t={\sigma }_0+W_0+v{\eta }_e{U}_t{R}_0\text{ln}\left(\frac{R}{R_0}\right),$$ (A3)

where σ₀ is the far-field membrane tension on the cell body, W₀ is the adhesion energy between the membrane and cytoskeleton (σ₀ + W₀ = 127.5 pN/μm for human neutrophils (15,19)), v is the surface density of integral proteins, η_e is the surface viscosity, U_t is the tether velocity at the tether-cell junction, and R (4.5 μm) is the cell radius.

Simultaneously, the tether flows back to the cell body because of adhesion and membrane tension, which can be described by (12)

$$\frac{d\sigma }{dr}=-v{\eta }_e{U}_t\frac{R_t}{r},$$ (A4)

where σ is the membrane tension on the cell body and r is the cylindrical coordinate. Integrating Eq. A4 from R_t to R yields

$${\sigma }_0+W_0=-v{\eta }_e{U}_t{R}_t\text{ln}\left(\frac{R}{R_t}\right),$$ (A5)

which allows us to obtain

$$U_t=-\frac{{\sigma }_0+W_0}{v{\eta }_e{R}_t\text{ln}\left(\frac{R}{R_t}\right)}.$$ (A6)

During tether retraction, we assume that the tether retains its cylindrical shape (refer to Fig. 7 b) and the membrane surface area should be conserved. Therefore,

$$\dot{L}=U_t-\frac{L{\dot{R}}_t}{R_t}.$$ (A7)

The tether length (L) can be numerically solved from Eqs. A1, A6, and A7. With R_∞, t_c, and vη_e as three parameters, the numerical solution can then be fitted to the experimental data using the least-square method.