A Cell-Level Biomechanical Model of Drosophila Dorsal Closure

Abstract

We report a model describing the various stages of dorsal closure of Drosophila. Inspired by experimental observations, we represent the amnioserosa by 81 hexagonal cells that are coupled mechanically through the position of the nodes and the elastic forces on the edges. In addition, each cell has radial spokes representing actin filaments on which myosin motors can attach and exert contractile forces on the nodes, the attachment being controlled by a signaling molecule. Thus, the model couples dissipative cell and tissue motion with kinetic equations describing the myosin and signal dynamics. In the early phase, amnioserosa cells oscillate as a result of coupling among the chemical signaling, myosin attachment/detachment, and mechanical deformation of neighboring cells. In the slow phase, we test two ratcheting mechanisms suggested by experiments: an internal ratchet by the apical and junctional myosin condensates, and an external one by the supracellular actin cables encircling the amnioserosa. Within the range of parameters tested, the model predictions suggest the former as the main contributor to cell and tissue area reduction in this stage. In the fast phase of dorsal closure, cell pulsation is arrested, and the cell and tissue areas contract consistently. This is realized in the model by gradually shrinking the resting length of the spokes. Overall, the model captures the key features of dorsal closure through the three distinct phases, and its predictions are in good agreement with observations.

Introduction

Dorsal closure (DC) is an important process during the embryonic development of Drosophila. After germband retraction, an epidermal opening appears on the back of the embryo, which is covered by an extraembryonic epithelium, the amnioserosa (AS). The AS contracts and eventually disappears inside the embryo so that the two opposing epithelia fuse at the dorsal midline to establish epidermal continuity. Aside from its biological significance, DC of Drosophila provides a fascinating example of tissue morphogenesis that couples cell and tissue mechanics with intra- and intercellular structural remodeling. Thus, it has received much attention in the recent literature (e.g., (1–3)).

DC is a complex and multifaceted process. A consensus is taking shape regarding the most general features. On the finer and deeper details, however, conflicting results abound and numerous questions remain. In general, the process consists of the following phases (4–6):

• 1.Early phase. This is characterized by persistent oscillation of AS cells and no net contraction of cell area and the area of the AS tissue. Strictly speaking, this oscillatory, pre-DC phase is not part of the closure process. However, the oscillation of AS cells is believed to be a major factor in subsequent DC. There are then two important and related questions: what is the cause of the oscillation (3), and how is it correlated among cells in the tissue? Recent studies indicate that the cyclic apical constriction correlates strongly with the assembly and disassembly of myosin condensates or foci on the apical surface (2,6–10). Solon et al. (4) reported in-phase and anti-phase correlations between neighbors, with apparently random switching between the two. On the other hand, Gorfinkiel et al. (2) observed strings of AS cells contracting and expanding in unison.
• 2.Slow phase. This is with the AS cell oscillation decreasing in amplitude and period, and the onset of net shrinkage in cell area (6). In the meantime, a supracellular actin cable (AC) forms along the leading edge of the epidermis (4). The key question is: what causes the net area shrinkage? Earlier work has suggested that the AC acts as a purse-string to constrict the AS (11,12). More recently, the idea of a ratchet has gained currency. There are two competing hypotheses for the ratchet (1,13). Solon et al. (4) argued that the AC serves as a ratchet over the entire AS tissue, such that when the oscillating AS shrinks in area, the AC remodels and shortens in length so as to allow the AS to return only to a somewhat smaller area. This is supported by the observation that the onset of DC coincides with the formation of the AC, and that the reduction in oscillation amplitude seems to initiate with the cells next to the leading edge and then propagate inward in the dorsal direction. However, Gorfinkiel, Blanchard, and co-workers (2,6,13) found that the AS cells can contract completely in mutants not having a functional AC. Following earlier work on Drosophila mesoderm invagination (8,14), they advocate an internal-ratchet based on the apical and junctional actomyosin stabilizing the cell cortex between contractions. Possibly both AC ratcheting and internal ratcheting are at work as redundant mechanisms.
• 3.Fast phase. This is the phase in which the rate of AS area contraction accelerates markedly, and most cells contract consistently with little fluctuation. This is apparently related to the elevated density of the apical actomyosin foci, which intensify during the slow and fast phases to eventually form a continuous network covering the entire apical surface (6). This arrests the AS oscillation and straightens the cell edges. Near both canthi, the protrusion and interdigitation of epidermal filopodia produce the so-called zippering, leading to fusion between the opposing leading edges (5,15). Finally, zippering and the closure are also known to be assisted by AS cell apoptosis (5,16) and active elongation of the epidermis (2).

From the above, one can identify five major players in DC: AS contraction, AC constriction, filopodia-based zippering, AS apoptosis, and epidermal expansion. Despite certain inconsistencies, the experimental observations so far can be tentatively summarized into the following picture. The AS oscillation in the early phase is caused by the periodic assembling and disassembling of apical medial actomyosin foci, which pull the adherens junctions inward, contract the cell, and ruffle the membrane. In the slow phase, a ratcheting mechanism kicks in, from the actomyosin in each cell (internal ratcheting) or the supracellular AC lining the leading edge, or even both. The fast phase features rapid contraction of AS cells, due apparently to a dense and sustained actomyosin network covering the apical surface. Finally, zippering, apoptosis, and epidermal expansion conspire to complete the closure. Experimental evidence points to the first two, AS contraction and the AC constriction, as the dominant factors, with the rest playing secondary roles (8,11,17). From a cell-mechanical viewpoint, the two outstanding questions are: what causes the AS oscillation in the early phase, and what is the ratcheting mechanism in the slow phase?

So far, physical modeling of DC consists mostly of calculations of how the AS tissue, as an elastic continuum, reacts to a prescribed tension in the actin cables that enclose the tissue (17–19). As such, they do not bear on the two questions asked above. Solon et al. (4) explicitly accounted for the AS cells as polygons with vertices connected by elastic springs. Cell oscillation was reproduced by applying a sinusoidal or area-based contractile force on each spring. As this force is imposed from the outside, it offers no insight on the underlying mechanisms for the oscillation. However, their results suggest that the oscillation is not cell-autonomous but depends on intercellular coupling. Sokolow et al. (3) further surmised an intercellular feedback mechanism for the AS oscillation, and considered it a major unresolved question. Regarding the ratchet, the only quantitative exploration so far is that of Solon et al. (4), who applied an increasing contraction force on the AC to produce AS contraction.

This article reports an attempt to model the DC process on a more fundamental level. We focus on the AS oscillation and ratcheting mechanisms, and ignore for the time being apoptosis, zippering, and epidermal expansion. Guided by the experimental observations and insights, we propose a plausible biochemical model with myosin assembly and disassembly governed by a signaling molecule and tension in the actin filament. The coupling among the signaling molecule concentration, myosin recruitment onto actin filaments, and cell deformation and movement produces an oscillatory behavior similar to observations. Furthermore, we test the internal and AC ratchets, and explore their individual and joint contributions to arresting cell oscillation during DC. The model predicts a more important role for the internal ratchet; the AC serves in a secondary role to reinforce the contraction.

Model Formulation

We consider an AS tissue shown in Fig. 1 composed of 81 hexagonal cells. Each cell is represented by six nodes on the periphery and one central node, connected by edge segments and spokes. We adopt a two-dimensional representation of the cell because the AS tissue is thin with squamous cells, and most of the dynamics take place on the apical surface. The configuration of the AS tissue is modeled after that of Solon et al. (4), and the edge-spoke structure of each cell is inspired by the following considerations. During the AS pulsation in the early phase, Martin (8) and Blanchard et al. (6,20) noted that myosin foci concentrate on two areas: in the middle of the apical surface forming an apical medial network, and along the circumferential actin belt. Because the apical constriction coincides with coalescence of the apical medial network, and is accompanied by wiggles in the cell membrane, they have come to the conclusion that the cyclic contraction is driven by the medial network pulling on the adherens junctions rather than the circumferential belt tightening as a purse string (14). We use the spokes and the edge segments to represent the medial and junctional actin assembly. Onto the spokes myosins can attach and detach, modeling the formation and disassembly of the apical medial actomyosin foci (2,6,20). Thus, the force on the spokes comprises a passive elastic force and an active tensile force due to the myosin,

$$f_{ij}=\mu \left(l_{ij}-l_{0ij}\right)+\beta m_{ij},$$ (1)

where μ is the elastic modulus, and l_ij is the length of the spoke connecting nodes i and j, whose resting length is l_0ij. The value β is the tensile force per myosin motor, and m_ij is the number of motors attached on the spoke. The edges, on the other hand, are taken to be passively elastic (i.e., β = 0 in Eq. 1), with no myosin-induced contraction. We should note that the linear elasticity for the edges and spokes is a simplification. The resting length l_0ij is assumed to be a constant at the beginning of our simulation. In reality, this quantity is difficult to define and may depend on, e.g., the local strain and Ca²⁺ concentration (21). We take the elastic modulus μ to be a constant, but in reality it may depend on the actin concentration, myosin concentration, and cortical tension τ. For example, a power-law μ ∼ τ^3/2 has been proposed (22,23). For simplicity, we have neglected the actin turnover and focused on the myosin dynamics.

Figure 1.

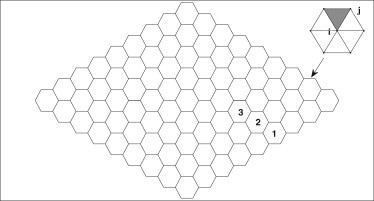
Model of the AS tissue composed of 81 hexagonal cells. (Inset) Each cell has six edges and six spokes. (Shaded area) Local triangle to the spoke ij.

In Fig. 1, we take the horizontal direction to be the anterior-posterior (AP) axis, and the vertical the medial-lateral (ML) axis. The two nodes at the left and right tips are fixed in space, representing the two canthi. The other nodes move according to the elastic and myosin forces on all the edges and spokes attached to it,

$$\begin{array}{c}\eta \frac{d{\mathit{x}}_i}{dt}={\mathit{f}}_i,\\ {\mathit{f}}_i=\sum _j{f}_{ij}\frac{{\mathit{x}}_j-{\mathit{x}}_i}{\left|{\mathit{x}}_j-{\mathit{x}}_i\right|},\end{array}$$ (2)

where η is the friction factor and f_i sums up the forces f_ij exerted by all segments connecting node i to an adjacent node j. Note that the geometric setup for the AS tissue is symmetric about both the AP and ML axes, though the solution may develop asymmetry under dynamic forcing as happens during DC (3,5).

To model the dynamics of myosin attachment onto the spokes, we recognize that this is controlled by various signaling molecules. The exact pathways are not clear at present, but experiments have suggested that several proteins may be involved. For example, Dawes-Hoang et al. (24) show that the protein Twist, mediated by Rho GTPase, acts through the Fog signaling pathway to localize myosin apically during ventral furrow formation. A similar pathway may underlie the myosin localization in dorsal closure. Martin et al. (14) has shown that the protein Snail is required for initiating cell pulsation, and Twist is required for stabilizing the pulsatile behavior. The PAR complex and Dpp are believed to play important roles in tissue contraction as well (10,13). In our model, we use a single variable s to represent the signaling proteins, and write the following kinetic equation for the number of attached motors on each spoke:

$$\frac{d{m}_{kj}}{dt}=k^{+}{s}_k{h}_{kj}-k^{-}{m}_{kj}.$$ (3)

Here s_k is the signal level in the k^th cell, m_kj is the myosin number on the j^th spoke of this cell, and h_kj is a geometric factor that distributes s_k to the different spokes. It is taken to be the average area of the two local triangles that border on the spoke divided by the area of the entire cell (compare to Fig. 1). The increase of m due to s represents the condensation of myosin foci observed in the experiments (2,6,20,25). The association/dissociation constants k^± in general may be load-dependent. For example, tension in the actin stress fiber is known to inhibit motor detachment (26,27). In our model, k⁺ is taken to be a constant while k⁻ is expressed in the Arrhenius form

$$k^{-}=k_1{e}^{-k_2\left[\mu \left(l_{kj}-l_{0kj}\right)+\beta m_{kj}\right]}.$$ (4)

Note that for convenience of narration, we have referred to a spoke by the end nodes in Eqs. 1 and 2, but by the cell and node in Eqs. 3 and 4. Lacking detailed knowledge of the signaling pathways, we write a simple equation for s by assuming constant production inside the cell at rate q and exhaustion due to myosin activity,

$$\frac{d{s}_k}{dt}=q-k_0{M}_k,$$ (5)

where $M_k={\sum }_j{m}_{kj}$ is the total number of myosin motors in the cell.

To the greatest extent possible, we have chosen the parameter values based on measurements and estimations reported in the literature. The other parameters are determined by the need to predict certain experimental observations quantitatively. The mechanical parameters η = 100 nN·s/μm and μ = 1 nM/μm are taken from the recent study of Solon et al. (4) (see the Supplemental Data therein). Specifically, the friction factor η was deduced from measured cell viscosities (28,29) and a characteristic intracellular length scale. Then the elastic modulus μ was determined so as to produce a characteristic relaxation time of η/μ ∼ 100 s. The resting length 1_0ij = 5 μm is also taken from Solon et al. (4). The myosin force constant β = 0.75 nM/μM is chosen such that the two forces on the right-hand side of Eq. 1 are roughly on the same order of magnitude; this turns out to be essential for maintaining the integrity of the cell during dynamic simulations.

For the rate constants, Kovács et al. (30) reported a range for myosin II release rates: 0.2 ∼ 0.36 s⁻¹, from which we have chosen k₁ = 0.25 s⁻¹. Our choice of k₂ = 1.33 nN⁻¹ is small so that the myosin dissociation rate k⁻ remains relatively high in Eq. 3. This gives myosin dissociation an important role in moderating the myosin oscillation. Otherwise s tends to oscillate excessively and even falls below zero. The rest of the parameters are chosen to produce desirable oscillatory behavior in the early phase: q = 0.05 μM/s, k₀ = 0.0083 s⁻¹, and k⁺ = 0.25 s⁻¹. This has been partly guided by a bifurcation analysis of the coupled ordinary differential equations (Eqs. 2, 3, and 5) that suggests parameter ranges for steady-state and oscillatory solutions. A bifurcation diagram is included as Fig. S1 in the Supporting Material. In particular, the association constant k⁺ is adjusted to match the oscillation period observed in experiments; increasing k⁺ shortens the period. At the start of the simulation, we set a uniform signal level in all cells: s₀ = 10 μM and a uniform myosin level on all spokes: m₀ = 1 μM (hence M₀ = 6 μM per cell). The system of equations is solved using a MATLAB (The MathWorks, Natick, MA) ODE solver with the fourth-order Runge-Kutta method.

Results

With the model parameters selected as above, we have explored the predictions of the model in each of the three phases of DC. The results are discussed in the following subsections.

Early phase

The focus of this subsection is on the cause of the sustained oscillation of the AS cells. We found that cell-cell coupling is able to produce sustained oscillation in the amnioserosa, not only in the cell area, but also in the signal s and myosin number m. From a uniform initial condition, the cells spontaneously develop a phase difference between neighbors, and eventually enter into a quasiperiodic state with characteristic spatial correlations similar to experimental observations (2,4,6).

Fig. 2 shows the oscillation of the cell area (thin line) and the total myosin level (thick line) of a representative cell, the one labeled “3” in Fig. 1, up to 50 min before the onset of dorsal closure (t = 0). The oscillation of the entire tissue is shown in Movie S1 in the Supporting Material. The AS cells and the tissue as a whole show no net area contraction, and this corresponds to the early phase described in Blanchard et al. (6) that starts at the end of germ-band retraction and lasts 40 ∼ 50 min in the experiment. Three observations can be made:

• 1.The sustained oscillation in Fig. 2 arises from the coupling among three dynamically changing quantities in our model: the signal s, the myosin number m, and the deformation of each cell (whose node motion is determined by myosin-generated forces). This differs from the previous predictions of Solon et al. (4), where area oscillation is maintained by an externally imposed time-dependent forcing. In addition, at the parameters used, an isolated cell will tend to a steady-state shape (see Fig. S1). Thus the oscillation relies on the mechanical coupling among neighboring cells, in agreement with prior arguments (4,6). In fact, we have found that parameter values at which a single cell oscillates do not necessarily produce sustained oscillation for the multiple cell tissue. Our model thus provides a version of the intercellular feedback mechanism that Sokolow et al. (3) hypothesized.
• 2.The period of oscillation T = 4 ∼ 5 min matches experimental observations closely (3,4,6). As mentioned above, this has been achieved by adjusting the myosin association rate k⁺.
• 3.The cell area oscillates nearly in anti-phase with the myosin number. This agrees with observations (6,10), and underscores the fact that myosin assembly on the spokes drives the cell contraction. In particular, Blanchard et al. (6) noticed that the contraction is a faster and more active process than the expansion, the former being a result of the myosin foci actively pulling on the cell cortex while the latter is a return to equilibrium governed more by the passive elasticity of the cortex. Our model predicts the same trend, as illustrated in Fig. 3 by the distribution of the expansion/contraction time ratio among all the cells. Our simulation also shows that the peak of myosin intensity precedes the valley of the cell area (Fig. 2), in agreement with experimental observations for the wild-type Drosophila embryo (6). This is because the peak myosin level produces maximum tensile forces in the spokes, which contract the cell at a finite speed against viscosity. In turn, the peaks of s precede those of m, reflecting the signaling mechanism of Eq. 3 (see Fig. S2).

Figure 2.

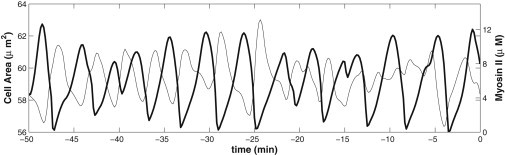
Early phase: fluctuation of the cell area (thin line) and myosin level (thick line) in cell 3 of Fig. 1. Time t = 0 is set to be the onset of net AS contraction, i.e., the end of the early phase and start of the slow phase.

Figure 3.

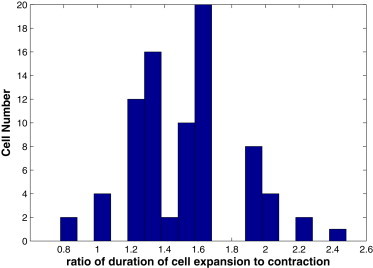
Distribution of the expansion/contraction time ratio among all cells in the tissue. For most cells, the contraction happens more rapidly than the expansion.

The AS oscillation also exhibits interesting spatial correlations. The oscillation is predominantly anti-phase between neighboring cells, as demonstrated in Fig. 4 by the cross-correlation of the area variation between neighbors. The cross-correlation is calculated by using the MATLAB (The MathWorks) function xcorr, integrated over 2000 s, and averaged over all neighboring cell pairs in the tissue. The negative peak at time lag ΔT = 0 and the positive ones at ΔT = ±T/2 indicate the anti-phase oscillation between neighbors. Fig. 4 is inspired by a similar plot that Solon et al. (4) constructed from experimental measurements (see their Fig. 5C). The two agree in the position of the positive and negative peaks. However, our model does not predict the observation of Solon et al. (4) that cells near the edge of the tissue oscillate with smaller amplitude. Our cells 1, 2, and 3 (Fig. 1) have comparable amplitudes.

Figure 4.

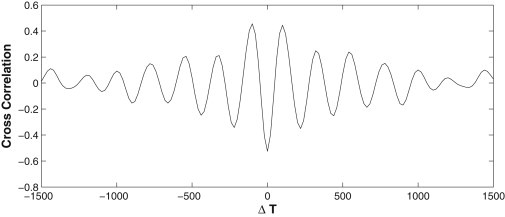
Cross-correlation of the cell area variation among neighbors in the AS tissue. ΔT is the time lag used in computing the cross-correlation, and the negative peak at ΔT = 0 indicates anti-phase oscillation between neighbors.

Figure 5.

Rate of area contraction (negative) and expansion (positive) for each cell in the AS tissue. The rate is normalized by the cell area and has unit of s⁻¹, with the grayscale assigned according to the scale bars to the right of each plot. (Top panel) The two snapshots are at (a) t = −39.2 min and (b) −25.2 min. The apparent symmetry in the patterns is due to the initially uniform s and m distributions. (Bottom panel) Asymmetric patterns predicted from nonuniform initial conditions. The two snapshots are at (c) t = −40.5 min and (d) −22.5 min.

Following Gorfinkiel et al. (5), we have further calculated the expansion or contraction rate for each cell in the tissue, and plotted two snapshots in Fig. 5, a and b. Although the cross-correlation of Fig. 4 shows that over time, the neighboring cells mostly oscillate in anti-phase, the snapshots indicate that at some instants of time, certain neighbors may be expanding or contracting in unison. In fact, one may identify at t = −39.2 min vertical lines of cells that are contracting in synchrony, and similarly arched strings of expanding cells at t = −25.2 min. This pattern of organization resembles the supracellular ribbons seen by Gorfinkiel, Blanchard, and co-workers (2,6) in experiments—strings of AS cells that contract and expand in synchrony in the early phase. The apparent symmetry in the patterns of Fig. 5, a and b, is due to the initially uniform s and m distributions. Using nonuniform initial conditions to break the symmetry, we have also generated asymmetric patterns and ribbons (Fig. 5, c and d), which more closely resemble the observations. In our model predictions, such patterns appear, evolve, and disappear in time (see Movie S2), much as in the experiments.

Slow phase: ratcheting

Experiments show that after the onset of DC, the AS cells oscillate with decreasing amplitude and experience a net contraction in area. Meanwhile, the area of the whole tissue contracts as well. Two ratcheting mechanisms have been proposed as explanations: an internal ratchet that relies on the cell cortex and apical medial network remodeling themselves during each oscillation (6,8,14), and an external ratchet due to the supracellular actomyosin cable around the epidermis (4).We have tested each separately using our model, and then combined both, in each case aiming to represent the ideas proposed from experiments. The model predictions are compared with experimental observations.

The internal ratchet, as illustrated by Martin (8) using cartoons, consists of two coordinated structural remodelings of the actomyosin machinery: first, the myosin condenses into medial foci on the apical surface, which pull inward on the spot junctions to keep the cortex from expanding after a contraction; second, the cortical actin ring restructures to straighten the cell edges. Thus, the cell has shrunk its area and is ready for the next cycle of contraction. The molecular mechanisms for the medial and cortical restructuring are unclear at present. But a buckling mechanism recently proposed by Soares e Silva et al. (25) provides an attractive candidate. The main idea is that actin filaments easily buckle under compression and the resulting slack areas can be removed by bridging or pulling during subsequent tension. This simple scenario can explain both apical and cortical remodeling in the internal ratchet. In our model, we mimic the effect by shortening the resting length l₀ of each segment—both cell edges and spokes—by a small amount δl₀ when the cell area reaches its minimum of each oscillatory cycle. This way, the cell will expand in the following cycle to a smaller size than the last, hence realizing a ratcheting effect.

Fig. 6 shows the time evolution of the normalized cell area for the cells labeled 1 and 2 in Fig. 1, together with the evolution of the overall tissue area. The evolution of the entire tissue is shown in Movie S3. The internal ratcheting is activated at t = 0 by reducing the resting length l₀ of each cellular segment by δl₀ = 0.03 l₀ in each cycle. The immediate effect is that, for each cell, the amplitude and the mean value of the area fluctuation both start to decline in time. Cells to the anterior and posterior of the tissue stop oscillating first, and those closer to the ML axis stop at a later time. This is borne out by the behavior of cells 1 and 2 in Fig. 6. Overall, the arrest of cell pulsation appears to propagate from the anterior and posterior toward the middle. This pattern resembles the experimental observation of Solon et al. (4) that the oscillation of peripheral cells is arrested earlier than that of interior cells. They attributed this to the effect of the AC cable. We see that the internal ratchet may produce spatially differentiated arrest of oscillation as well. Note, however, that Sokolow et al. (3) did not see such spatial patterns in the onset of net cell area contraction. At ∼t = 80 min, roughly $45\text{\%}$ of all the cells, accounting for 50 ∼ 60% of the tissue area, has been arrested; we consider this the end of the slow phase of DC in our simulation. At this time, the middle of the tissue still undergoes small-scale fluctuation; the snapshot of the tissue in the inset shows a few cells contracting strongly at the moment. During the entire process, the tissue area contracts monotonically, and the rate of change decreases in time.

Figure 6.

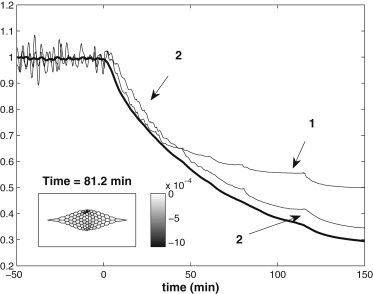
Temporal evolutions of the normalized cell area for cells 1 and 2 (see Fig. 1, thin lines) and the normalized tissue area (thick line). The internal ratcheting is modeled by reducing the resting length of the edges and spokes of a cell by 3% in each oscillation cycle. Cells 1 and 2 stop oscillating at ∼t = 50 and 80 min, respectively. (Inset) Snapshot of the tissue at the end of the slow phase, with the grayscale marking the rate of normalized area change in unit of s⁻¹.

In the experiments, the end of the slow phase is defined as the point at which the net contraction of AS accelerates dramatically, with the cessation of oscillation for most AS cells (6). This typically happens some 80 min after the onset of DC, by which time the AS tissue area has reduced by ∼50% (6,31). In Fig. 6, our model predicts a tissue area reduction of 56% at t = 80 min, in rough agreement with experiments, for δl₀ = 0.03 l₀. Of course, in the model the rate of tissue area reduction and the arrest of cell oscillation both depend on δl₀, which may be viewed as the strength of the internal ratcheting. Obviously, smaller δl₀ leads to milder area shrinkage and the oscillation will persist longer in the tissue (see Fig. S3). In fact, for δl₀ < 0.01 l₀, the internal ratchet is too weak to arrest tissue oscillation completely.

Now we disable the internal ratchet and turn to the extracellular ratcheting mechanism based on the outer AC enclosing the AS tissue (4,32). We implement the AC by activating at t = 0 two elastic bands along the outer boundary of the amnioserosa. Each is an elastic spring of modulus K and resting length L₀ = 125 μm, which is much shorter than the arc length of the AS tissue between the canthi so that the AC springs are in tension. As the AS tissue oscillates, so does the total length of the AC. The ratchet is realized by reducing L₀ by a small amount δL₀ each time the tissue area A_t reaches a minimum. This is again motivated by the idea of actin cable buckling (25). Little data is available on the elastic modulus of the AC. We have tested a range of values, 0.01 ≤ K ≤ 0.2 nM/μm and 0.005 ≤ δL₀/L₀ ≤ 0.05. Fig. 7 depicts the effects of the AC ratchet for K = 0.1 nM/μm and δL₀ = 0.01 L₀ (see also Movie S4). The total AS area A_t drops by some 3% immediately upon activation of the ratchet. Afterwards the fluctuations in A_t persist and show no signs of dying out. In addition, the mean value of A_t decreases very slowly, by only 6% at 150 min after the onset of DC. The most visible effect of the AC is to smooth the edges of the tissue, as shown by the insets. The bottom panel of Fig. 7 compares area oscillations for cells 1 and 2 marked in Fig. 1. Again the AC does not suppress the cell area fluctuation, nor cause a considerable net contraction in time. Cell 1, on the edge of the tissue and immediately next to the AC, experiences a sudden decrease in cell area when the AC cable is activated, but cell 2, one row away from the AC, hardly shows any effect. Apparently, the AC ratcheting effect is too weak.

Figure 7.

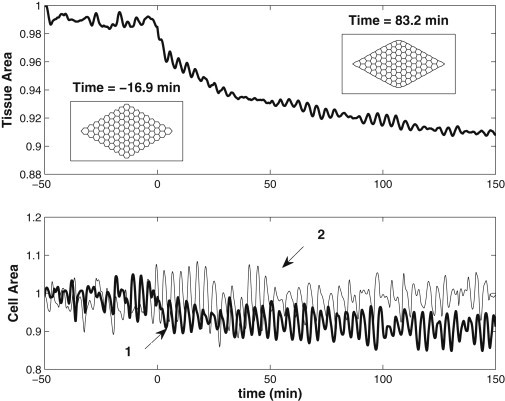
AC ratcheting with K = 0.1 nN/μm and δL₀ = 0.01 L₀. (Top panel) Evolution of the normalized tissue area. (Insets) Tissue shape before and after AC ratcheting is activated. (Lower panel) Area oscillation for cells 1 and 2.

Naturally, we have tested larger δL₀ and larger K to boost the AC ratcheting effect. Initially, increasing these values slightly enhances cell and tissue area reduction. But there is no arrest of pulsation. Then at a threshold value, the model prediction changes abruptly, with topological inversion of the cells at the edge and onset of unphysical dynamics. Take K = 0.2 nN/μm and δL₀ = 0.01 L₀, for example. The two outmost cells in the ML direction experience such strong deformation that they flip, with the edge nodes abruptly jumping into the interior and the spokes lying outside of tissue domain. A similar scenario occurs when increasing δL₀ = 0.05 L₀ while keeping K = 0.1 nN/μm. With this model, therefore, we cannot reproduce strong but physically reasonable AC ratcheting by increasing K or δL₀.

The ineffectiveness of the AC ratchet is due to the presence of the spokes in our cell model, which, aside from generating contractile force through the myosin motors, also resist compression through their passive elasticity when the cells are compressed by the AC. The cellular distortion at larger K or δL₀ can be attributed to the conflict between the compressive force due to the AC and the resistance of the intracellular spokes. It seems that without internal ratchet, AC alone is not sufficient to reduce tissue area as observed in experiments. In fact, the undesirable consequence of the resistance of the spokes suggests that the internal and external ratchets need to cooperate for proper behavior to be produced. This conclusion differs from the argument of Solon et al. (4) that AC suppresses the AS oscillation and produces its net area reduction. In their model, area reduction is achieved by a tension-induced-contraction scheme; when an edge cell is compressed by the AC, it loses its internal tension and stops contraction and pulsation.

Finally, we simulated the slow phase with both the AC cable and the internal ratchet activated, and the result can be seen from Movie S5. The internal ratchet dominates for the parameters we tested, and the AC ratchet makes an insignificant contribution to area reduction. With δl₀ = 0.03 l₀, K = 0.1 nN/μm, and δL₀ = 0.01 L₀, the tissue area reduction at the end of the slow phase (t = 80 min) is 56% without the AC and 59.5% with it. Hence AC speeds up the process somewhat. In addition, AC cable tends to smooth the outer boundary of the AS tissue. Overall, in the debate between the internal and AC ratchets, our model favors the former over the latter, although in reality, they probably act in coordination and cooperation (4,6).

Fast phase

In the fast phase, the medial actomyosin network becomes denser and more pervasive, eventually covering the entire apical surface (2,6). This is believed to produce sustained contractile force on the cell cortex and realize the further reduction in AS area. In our model, the simple signal-myosin dynamics postulated in Eqs. 3 and 5 reproduces the oscillatory behavior in the early and slow phases, but is unable to predict the upsurge of apical myosin density in the fast phase. Thus, we have chosen to represent this effect mechanically by shortening the resting length l₀ progressively. This strengthens the contractile elasticity of the edges and spokes, and serves as an ad hoc model for the intensifying medial actomyosin network.

The evolution of the normalized tissue area is shown in Fig. 8 through all the three phases, with the insets showing the tissue shape and the strain rate distribution at two times. Movie S6 gives a dynamic depiction of the process. At the start of DC (t = 0), internal and AC ratchets are activated together using parameters tested in the last subsection (δl₀ = 0.03 l₀, δl₀ = 0.01 L₀, and K = 0.1 nN/μm). Thus, the behavior in the slow phase is as explained before. In the fast phase that starts at t = 80 min, we reduce l₀ by 5% and L₀ by 1% once every fixed time interval δt = 50 s. This time is chosen to be half of the relaxation time of the cells (4). The greater reduction δl₀ = 0.05 l₀ in the fast phase, compared with 0.03 l₀ per cycle in the slow phase, reflects the higher myosin concentration in the medial network and the cortex that is observed in this stage (6). This produces a sustained and relatively rapid decrease in the tissue area from t = 80 to 200 min, when the tissue area falls below 10% of the original area. Because zippering is absent from the model, it is reasonable to consider this level of area reduction to be complete closure. In this process, the tissue retains a smooth and symmetric shape and becomes progressively narrower (insets to Fig. 8). For the amount of decrease in the resting length described above, the duration of the fast phase, roughly 120 min, matches the experimental observations (3,31). With stronger or weaker δl₀, this period will be shorter or longer, respectively. In addition, simulation with the same implementation but without the AC ratchet also leads to DC as expected (6); the tissue area reduces to $10\text{\%}$ of the original area at t = 238 min (data not shown).

Figure 8.

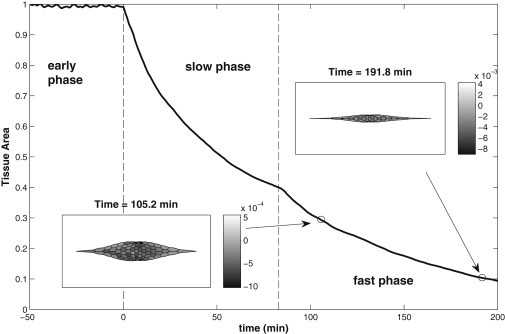
Time evolution of the normalized tissue area through the three phases. (Insets) Tissue shape and area contraction rate distribution (in grayscale) at t = 105.2 and 191.8 min. Internal and AC ratchets are both activated at the onset of DC (t = 0). After the start of the fast phase (t = 80 min), the resting length of the cellular segments and the AC cable are reduced at regular periods.

In the fast phase, the myosin level m fluctuates around its equilibrium value (1 μM per spoke and 6 μM per cell) with amplitude <0.005 μM. Because the cellular area is shrinking, the myosin concentration may be said to rise in time. Inside each cell, however, the total amount of myosin M does not increase as observed in the experiments (6). Instead M approaches a steady-state level after its oscillation is dampened by the ratcheting (see Fig. S4). This is because, in our model, Eq. 5 dictates an equilibrium value of cellular myosin M^e = q/k₀. The equilibrium myosin level will increase only if q/k₀ grows in time, which may occur if the signal becomes more active as the local supply rate q increases. One is tempted to hypothesize that some such process happens in reality. Perhaps at the start of the fast phase, certain additional signaling pathways are turned on that lead, ultimately, to the sustained intensification of the actomyosin network in the apical surface (2,6). Such pathways remain to be determined. Without this knowledge, our model could only predict the fast-phase dynamics phenomenologically, through shortening of the resting lengths.

From the insets to Fig. 6 and Fig. 8, it is obvious that most of the AS cells contract anisotropically. This is well known from experimental observations (5,11). In particular, Gorfinkiel et al. (5) noted that the cells contract predominantly in the ML direction, with AP contraction becoming appreciable only toward the end of the fast phase. This trend is captured by our model, as can be discerned from the cell and tissue shapes in Figs. 6 and 8. To be more precise, we plot in Fig. 9 the strain rates along the ML and AP directions averaged over all the cells during the slow and fast phases of DC. The ML contraction is roughly twice as strong as the AP contraction, and tends to grow in time. These features agree with the experiment (see Fig. 3 of Gorfinkiel et al. (5)), but the intensification in time is not as pronounced in the model prediction.

Figure 9.

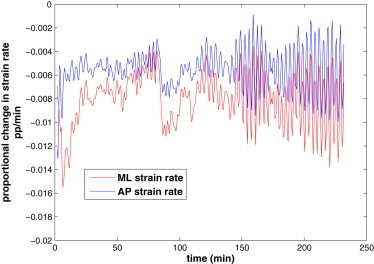
Anisotropic contraction of the AS tissue indicated by the strain rates along the medial-lateral (ML) and anterior-posterior (AP) directions. The ML contraction is twice as strong as the AP contraction, and becomes especially active toward the late stage of DC.

Conclusion

We have modeled dorsal closure by a dissipative system with simple kinetic equations describing the attachment and detachment of myosin onto actin filaments controlled by a certain signaling molecule. The model qualitatively reproduces the features of the early, slow, and fast phases of dorsal closure. In the early phase, coupling among the signal, myosin dynamics, and mechanical deformation produces sustained oscillation of individual cells and of the whole tissue, with no net reduction of area. This agrees qualitatively with experimental results. In the slow phase, we have tested two ratcheting mechanisms that have been proposed to explain the arrest of cell oscillation and onset of net area reduction—one due to the apical and junctional actomyosin condensates (internal ratchet), and the other due to the supracellular actin cable that encloses the amnioserosa tissue (AC ratchet). Within the range of parameters tested, the model suggests that the internal ratchet plays a major role, with the AC ratchet being supplemental. This is consistent with the recent experiment observations (6). Then, in the fast phase, we realize sustained contraction of the cells and the tissue by periodically shrinking the resting length of the edges and spokes of the cell.

A weakness of the model we discuss here is the lack of a clear representation of the signaling pathways. This precludes, for example, the prediction of a sustained intensification of the actomyosin network in the fast phase. As a result, the continual and rapid cell and tissue contraction in this phase has to be modeled phenomenologically. In addition, the onsets of the slow and fast phase are almost certainly controlled by the signaling molecules, whereas in our model they are specified rather than predicted. The signals probably also play important roles in both ratcheting mechanisms, although tension-driven myosin accumulation and adherens-junction reinforcement may be implicated as well. Finally, the AS cells tend to show great diversity in behavior (3), which may again be due to chemical signaling but cannot be rationalized at present. Of course, the above reflects our lack of understanding, as of the time of this writing, of the signaling pathways. In this regard, the modeling has to await the advent of more detailed and definitive experimental data.