Quantitative Analysis of Approaches to Measure Cooperative Phosphate Release in Polymerized Actin

Abstract

We use stochastic simulations that treat several experimental probes of actin dynamics to explore the extent to which phosphate dissociation in filamentous actin may be cooperative. Phosphate time-courses from polymerization and copolymerization experiments of ATP- and ADP-actin are studied, including the effects of variations in filament-number concentration as well as single-filament depolymerization time-courses. We find that highly cooperative models are consistent with the treated experimental data. We also find that some types of experiments that are believed to provide strong constraints on the cooperativity of actin hydrolysis models do not provide such constraints.

Introduction

The polymerization kinetics of actin depends strongly on the chemical state of the bound nucleotide (1). Actin has at least three chemical states: ATP-actin, which has a tightly bound ATP; ADP-Pi-actin, which has a bound ADP and a trapped or loosely bound inorganic phosphate; and ADP-actin, which has only a bound ADP (2,3). The transition from ATP-actin to ADP-Pi-actin is called phosphate cleavage, and the transition from ADP-Pi-actin to ADP-actin is called phosphate dissociation or phosphate release. Quantitative understanding of actin dynamics in cells requires a detailed understanding of these transitions. Efforts to obtain such understanding have mainly compared predictions from various hydrolysis models with a range of experiments performed in vitro.

Such models must at least describe the conditions and rates for phosphate cleavage and dissociation, though other transitions, such as ADP-actin to ADP-Pi-actin through phosphate association, may also be present. The actin hydrolysis model most frequently used for analysis of experimental data is the uncorrelated, three-state model, which is generally referred to as the random model. This model assumes that state transitions depend only on the state of the protomer undergoing the transition. The random model has just two parameters that describe the rates of the transitions: the cleavage rate, r_c; and the phosphate dissociation rate, r_d.

The random model does not contain the correlations between transitions in neighboring protomers that are suggested by the observed conformational variations of actin protomers in filaments (4). Because transition rates are exponentially related to changes in activation energies, even subtle changes in activation energies caused by these conformational changes may have a significant effect on the rate of cleavage or phosphate dissociation within a protomer. Such effects are included in the other widely used, three-state model with only two parameters, i.e., the vectorial model (5). In this model, cleavage events occur in an F-ATP-actin protomer only when its pointed-end neighbor is either an F-ADP-Pi-actin or an F-ADP-actin protomer, and phosphate dissociation events occur in an F-ADP-Pi-actin protomer only when its pointed-end neighbor is an F-ADP-actin protomer. The random and vectorial models are the limiting cases most amenable to analytic analysis, and have thus received the most theoretical scrutiny (6–8).

The simplest generalization of these models is a first-order (nearest neighbor), correlated model called the cooperative model (9). Cooperative models can be used to describe either hydrolysis or phosphate dissociation, though we will only consider cooperative phosphate dissociation in this work. This generalization requires a single additional parameter, the phosphate dissociation cooperativity, ρ_d, such that the dissociation rate at a boundary between ADP-Pi-actin and ADP-actin subunits, R_d, is

$$R_d={\rho }_d{r}_d,$$ (1)

where r_d is the nonboundary phosphate-dissociation rate. Cooperative cleavage can also be considered, but our focus here is on dissociation. The additional parameter allows the strength of correlations to be varied smoothly from the random model at ρ_d = 1 to the vectorial model where ρ_d → ∞. In the case of actin, negatively correlated models (those with 0 ≤ ρ_d < 1) are not generally considered (9). Note that models with large ρ_d can still be qualitatively different from the vectorial model, because cooperative models have a chance to spontaneously nucleate a boundary between the ADP-Pi and ADP states of F-actin. This boundary then allows rapid state transitions to propagate along the filament.

Three notable experiments using different methods have been used to support the random models in Carlier and Pantaloni (2), Pieper and Wegner (10), and Jégou et al. (11). In Carlier and Pantaloni (2), polymerization of doubly radioactive labile actin was monitored using glass fiber filtration to separate filaments from released inorganic phosphate. Phosphate time-courses were compared for two different filament-number concentrations (1.1 nM and 20 nM). It was assumed that in a vectorial, or strongly cooperative model, increasing the filament-number concentration would increase the apparent phosphate dissociation rate by a corresponding factor of ∼18. However, the resulting difference in lag-time between polymerization and phosphate dissociation was approximately a factor of four, which corresponded to a change in the apparent phosphate dissociation rate of approximately two. Because this change was relatively small compared to the expected factor of 18 for the vectorial model, it was taken to mean that significantly cooperative models (especially the vectorial model) were excluded.

The first quantitative attempt to constrain cooperative models comes from Pieper and Wegner (10). Here, G-ATP-actin and G-ADP-actin were polymerized together in various fractions while the inorganic phosphate concentration was monitored. In cooperative models, increasingly rapid phosphate dissociation was expected as the G-ADP-actin fraction increased. This experiment is important, but was designed to measure hydrolysis rather than dissociation, and thus its data cannot be used to directly constrain ρ_d.

Recently, in Jégou et al. (11), time-courses of the length of depolymerizing single filaments were measured via total internal reflection fluorescence microscopy. The simplified theoretical analysis of the work considered only the random and vectorial models, and concluded that the random model must be correct because the data did not exhibit the shoulder that the analysis predicted for the vectorial model.

In the work described here, we performed fully stochastic simulations of these key experiments in Carlier and Pantaloni (2), Pieper and Wegner (10), and Jégou et al. (11), to quantitatively evaluate the bounds they could place on the phosphate dissociation cooperativity, ρ_d. These simulations included the behaviors shown in Fig. 1, as well as polymerization and depolymerization at both ends (where appropriate), and phosphate association throughout the filament. We found that the data from Carlier and Pantaloni (2) and Jégou et al. (11) are better fit by highly cooperative models than by random models. Although the experimental design of Pieper and Wegner (10) precludes extraction of meaningful bounds on ρ_d, we present results that could be used to extract ρ_d from future experiments of a similar type.

Figure 1.

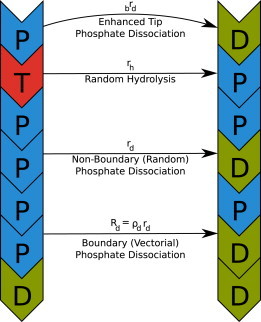
Schematic of the treatment of actin transitions in our simulations. An example of each type of hydrolysis and phosphate dissociation event, along with its associated rate, is shown.

Materials and Methods

Simulation procedure

The results in this article were produced by stochastic simulation using a modified Gillespie algorithm (12) written in the softwares Python (13) and C++. The algorithm used is similar to the third algorithm discussed in Schulze (14). The software is available under the GNU General Public License Ver. 3 at http://github.com/mark-burnett/filament-dynamics.

Except for single-filament simulations of depolymerization, each simulation began with 1000 ADP-actin seed filaments of equal size. Polymerization kinetics and conditions appropriate to each experimental procedure were used along with appropriate transitions depicted in Fig. 1. All simulations incorporated a full, three-state actin hydrolysis model. Because the process of cleavage is much quicker than phosphate dissociation, we assumed random cleavage for simplicity. Phosphate dissociation was modeled with random, vectorial, or cooperative transitions. Polymerization and depolymerization were allowed at both ends, except in the case of the single-filament depolymerization simulations (11), where the pointed-ends were considered static. Enhanced phosphate dissociation at both the barbed- and pointed-ends of filaments was included, and phosphate association at all ADP-actin subunits was allowed.

Parameter values and simulation conditions

The widely used random and vectorial models each have 16 parameters when including enhanced phosphate dissociation at filament-ends. The full cooperative model discussed here adds a single parameter to describe correlations in phosphate dissociation between neighboring protomers, bringing the total parameter count to 17. To avoid a global search of this large parameter space, we took most parameter values from previous data analyses, some of which assumed random models for both cleavage and phosphate dissociation. Simulation parameters used are given in Table 1.

Table 1.

Simulation parameters taken from external analysis of experimental results

Parameter		Value [μM−1 s−1]	Ref.
Association rate constants
Barbed G-ATP	bk+T	11.6	Pollard (32)
Barbed G-ADPPi	bk+P	3.4	Fujiwara et al. (1)
Barbed G-ADP	bk+D	2.9	Fujiwara et al. (1)
Pointed G-ATP	pk+T	1.3	Pollard (32)
Pointed G-ADPPi	pk+P	0.11	Fujiwara et al. (1)
Pointed G-ADP	pk+D	0.14	Fujiwara et al. (1)
Parameter		Value [s−1]	Ref.
Dissociation rates
Barbed F-ATP	bk−T	1.4	Pollard (32)
Barbed F-ADPPi	bk−P	0.2	Fujiwara et al. (1)
Barbed F-ADP	bk−D	5.4	Fujiwara et al. (1)
Pointed F-ATP	pk−T	0.8	Pollard (32)
Pointed F-ADPPi	Pk−P	0.02	Fujiwara et al. (1)
Pointed F-ADP	Pk−D	0.25	Fujiwara et al. (1)
Barbed Pi	brd	2	Fujiwara et al. (1)
Pointed Pi	prd	2	Fujiwara et al. (1)
Other parameters
Cleavage rate	rc	0.3	Blanchoin and Pollard (33)

Note that the barbed-end Pi dissociation rate was varied for some simulations.

Conditions for each set of simulations were matched to experiment as closely as possible. For phosphate time-course simulations (15), G-ATP-actin concentration was 30 μM with F-ADP-actin seed concentration of 6 μM at a filament-number concentration of 1.67 nM, which was fit using our stochastic models.

For the simulations corresponding to Carlier and Pantaloni (2), G-ATP-actin concentration was 40 μM and F-ADP-actin seed concentration was 55 nM. The filament-number concentration was varied from 1.1 nM to 20 nM. This amount of seed actin at these high filament-number concentrations would have dissipated in an experiment due to many filaments having fewer than four protomers. Our simulations did not allow this dissipation, because the experiment actually began with longer seed filaments, then fragmented them using sonication while polymerization was taking place (2).

For the copolymerization simulation, the experimental conditions of Melki et al. (15) were re-used for simplicity. As the G-ADP-actin fraction increased, the amount of G-ATP-actin was decreased so that the total amount of G-actin remained 30 μM. The phosphate concentration half-time was measured when the phosphate concentration reached half its possible maximum or, equivalently, half of the original G-ATP-actin concentration.

For the single-filament depolymerization simulations corresponding to Jégou et al. (11), we simulated short seed filaments in an infinite volume. Pointed-ends were not allowed to polymerize or depolymerize for these simulations. A G-ATP-actin concentration of 1.5 μM was maintained for 300 s, then forced to zero to observe depolymerization.

Choice of experimental data for fitting

We considered two sets of [Pi] time-course data for use in fitting phosphate dissociation rates: those from Blanchoin and Pollard (16) and those from Melki et al. (15). The relevant differences between the [Pi] time-course data sets that we considered are that Blanchoin and Pollard (16) provides access to actual recordings, whereas Melki et al. (15) only provides access to smoothed data. The experimental duration of Melki et al. (15) was 2500 s, whereas Blanchoin and Pollard (16) only provides data for 1200 s. Extracting average filament lengths from Melki et al. (15) yields ∼50 μm, whereas from Blanchoin and Pollard (16) we obtain ∼180 μm. Analysis of Blanchoin and Pollard (16) would have been complicated by severing, because the accepted spontaneous rate from Sept et al. (17) would lead to more than one expected severing event per filament.

Though Blanchoin and Pollard (16) provided unsmoothed data, extracting those noisy data by hand from the published figure would bias statistics (toward the extrema of the noise), providing a poor fitting target. Blanchoin and Pollard (16) also did not provide F-actin concentration data beyond the point where F-actin overshoot would diminish—reporting only fit results beyond that point. There was not a clear correct choice between these two data sets, but the complicating effect of the large expected filament length of Blanchoin and Pollard (16) led us to choose Melki et al. (15).

Fitting procedure and error estimation

The quality of fit metric minimized was

$${\Delta }^2=\sum _{i=1}^N\frac{{\left(x_s-x_d\right)}^2}{N},$$ (2)

where x_d is the value of observable x from the data, x_s is its corresponding value from the simulation, and N is the number of measurements.

To obtain r_d from the time-course data of Melki et al. (15), we first performed exploratory simulations of 100 filaments to find the neighborhood of the best fit. Then the final value was fit by running at least 100 simulations of 1000 filaments in the neighborhood of the final fit value. The r_d dependences of the Δ² values of those simulations were fit using a parabola. The minimum of that parabola was taken to be the best value of r_d. Confidence intervals were extracted from these parabolic fits using a t-test with α = 0.01 (18), and were all <1%.

The filament-number concentration for the data from Melki et al. (15) was fit iteratively with r_d for the random model, and the final fit value of the filament-number concentration of $n=1.67\text{nM}$ was used to fit the phosphate dissociation rates for the cooperative and vectorial models. Values for the dissociation rates can be found in Table 2.

Table 2.

Nonboundary (r_d) and boundary (R_d) phosphate dissociation rates used for various stochastic models

Model	rd[s−1]	Rd[s−1]	Statistical error [%]
Random	1.628 × 10−3	1.628 × 10−3	0.021
ρd = 101	6.031 × 10−4	6.031 × 10−3	0.073
ρd = 102	2.120 × 10−4	2.120 × 10−2	0.098
ρd = 103	6.924 × 10−5	6.924 × 10−2	0.15
ρd = 104	2.150 × 10−5	0.2150	0.21
ρd = 105	6.394 × 10−6	0.6394	0.26
ρd = 106	1.790 × 10−6	1.790	0.34
ρd = 107	4.494 × 10−7	4.494	0.71
ρd = 108	7.942 × 10−8	7.942	0.85
ρd = 109	9.146 × 10−9	9.146	0.40
ρd = 1010	9.271 × 10−10	9.271	0.47
Vectorial	0	9.312	0.41

These rates were extracted by fitting to data from Melki et al. (15). Errors are 99% confidence intervals that include all statistical errors in the simulation.

Confidence intervals for the quality of fit to data from Carlier and Pantaloni (2) and Jégou et al. (11) were extracted from 10 to 100 runs of 1000 filaments (at both 1.1 nM and 20 nM in the case of Carlier and Pantaloni (2)) using a simple t-test with α = 0.01. All experimental data were extracted from figures using the program DataThief (http://www.datathief.org/).

Key assumptions

Our main assumptions are the following:

Assumption 1

The first assumption is that correlations are first-order in nature, i.e., phosphate dissociation at a given protomer depends only on the nearest-neighbor protomer. The physical justification for considering second-order single-strand models is that each protomer is in direct physical contact with four other protomers in the double-strand filament (two in each direction), and these interactions correspond to second-order interactions in single-strand models. Second-order models are not considered here for two reasons: 1), additional parameters would be required, and 2), first-order models have not yet been fully explored. Most theoretical studies of actin dynamics use simplified, noncooperative first-order models (6–8,19), and this work is, to our knowledge, the most complete quantitative treatment of general first-order models (9,10) of the system at this time. Furthermore, second-order models would probably give results equivalent to first-order models with different parameters. Consider an extreme case where the second-nearest neighbor boundary dissociation rate, R_d⁽²⁾, substantially exceeds the first-order rate, R_d. The ADP-Pi-/ADP-actin boundary would move at a velocity of 2R_d⁽²⁾ protomers per unit time, which would be equivalent to a first-order model with R_d = 2R_d⁽²⁾.

Assumption 2

The substance of this assumption is that actin conformational states are determined by chemical state. At least two conformational states appear to exist (4,20,21) for ADP-actin. Therefore, our assumption does not have solid physical justification. However, we have chosen the simplest approach—to first ignore the possible independence of conformational state transitions and see how well models with few parameters can reproduce the existing data.

Assumption 3

This assumption is that severing and annealing are not significant. One might expect significant severing when fitting the data from Melki et al. (15), because the expected filament length was quite long (50 μm compared to the equilibrium severing-limited length of 7 μm). However, the severing rate measured in Sept et al. (17) is 1.1 × 10⁻⁸ subunit⁻¹ s⁻¹, which yields a mean filament-severing time of ∼4200 s⁻¹. The duration of the actual experiment was only 2500 s; thus, we expect the effects of severing to be moderate in this case. Further, one theoretical study found that the effects of severing and annealing were not significant for polymerization studies (22), though these did not directly consider cooperative models.

We also assumed that state transitions in cooperative models depend only on the state of the pointed-end neighbor of a protomer, but our simulations (not shown) showed that the results did not differ significantly for polymerization experiments when this dependence was reversed.

Results and Discussion

[Pi] Time-course observations: constraining r_d as a function of ρ_d

To compare phosphate dissociation models in terms of cooperativity, ρ_d, we constrained the nonboundary phosphate dissociation rate, r_d, using phosphate time-course data from Fig. 3B of Melki et al. (15). We first discuss these results before turning to analysis of Carlier and Pantaloni (2), Pieper and Wegner (10), and Jégou et al. (11).

Figure 3.

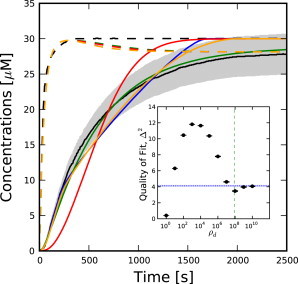
(Dashed lines) [F-actin] time-courses; (solid lines) [P_i] time-courses. (Shaded area) Within 10% of [Pi] time-course data from Melki et al. (15). Shown are data from Melki et al. (15) (black), random model (green), vectorial model (blue), ρ_d = 10⁴ (red), and ρ_d = 10⁸ (orange). (Inset) Quality of fit, Δ², to data from Melki et al. (15). (Dotted blue line) Quality of fit for the vectorial model (blue-shaded region represents statistical errors). (Dashed green line) Corresponds to ρ^∗_d from Eq. 4. Error bars represent statistical errors.

Time-courses of phosphate concentrations measured during actin polymerization provide strong constraints on the phosphate dissociation rate. We chose to use the data from Melki et al. (15) to constrain r_d for reasons detailed above. We varied the rate, r_d, for each value of the cooperativity, ρ_d, and chose the value of r_d that provided the best fit to the phosphate time-course data from Melki et al. (15). Fig. 2 shows the decreasing r_d-versus-ρ_d relationship extracted from these fits. Without this decrease, the effective phosphate dissociation rate would increase with increasing ρ_d, because the boundary dissociation rate, R_d, would increase. Thus, fitting the data of Melki et al. (15) requires r_d to decrease with increasing ρ_d. We emphasize that the plot of r_d and R_d versus ρ_d is obtained by minimizing residual error between simulation results and experimental data without the use of approximate analytical theory. However, simplified calculations based on rate equations (see Section A in the Supporting Material) suggest a relationship between r_d and ρ_d when ρ_d is not too large, but still >1,

$$r_d=\frac{1}{t_{1/2}^{\text{Pi}}\sqrt{{\rho }_d}},$$ (3)

where $t_{1/2}^{\text{Pi}}$ is the measured phosphate dissociation half-time of the data (433 s in Melki et al. (15)). Note that the boundary dissociation rate, R_d = ρ_dr_d, increases rapidly up to ∼ρ_d = ρ_d^∗ ≈ 10⁸, then slowly approaches the value for the vectorial model as ρ_d → ∞. Equation 13 of Ohm and Wegner (9),

$$R_d>r_d{\left(\frac{G_0}{n}\right)}^2,$$

describes the domain of r_d and R_d for which cooperative models behave like the vectorial model. Thus, we define the point where cooperative models change from mostly randomlike behavior to mostly vectorial-like behavior to be the critical cooperativity, ρ_d^∗,

$${\rho }_d^{\ast }={\left(\frac{G_0}{n}\right)}^2,$$ (4)

where G₀ is the initial G-actin concentration (30 μM), and n is the filament-number concentration (1.67 nM). The red line in Fig. 2 shows that this theory captures the overall behavior when 1 ≪ ρ_d ≪ ρ_d^∗, but diverges significantly outside that domain.

Figure 2.

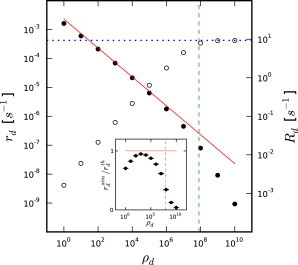
Fit nonboundary (r_d, solid circles, left scale) and boundary (R_d, open circles, right scale) phosphate dissociation rates versus phosphate dissociation cooperativity as fit to data from Melki et al. (15). (Red line) Data obtained from Eq. 3. (Dotted blue line) R_d for the vectorial model (ρ_d → ∞). (Dashed green line) ρ^∗_d from Eq. 4. (Inset) Rescaled view of differences between simulations and theory from Eq. 3 showing a systematic deviation from theory. Error bars represent statistical errors.

Previous work on vectorial models has mainly used only two-state models (5,7,8,19,23) In the limit ρ_d → ∞, our fit gave R_d = 9.3 s⁻¹, much larger than the value of 0.3 s⁻¹ estimated in Stukalin and Kolomeisky (7) and used in some subsequent theoretical studies (8,19). To match the $t_{1/2}^{\text{Pi}}$ measured in Melki et al. (15) using the value of R_d from Stukalin and Kolomeisky (7), one would require a filament-number concentration of roughly 115 nM, based on the following formula (see Eq. S12 in the Supporting Material),

$$n=\frac{G_0}{2t_{1/2}^{\text{Pi}}{R}_d},$$ (5)

where n is the filament-number concentration, and G₀ is the initial G-actin concentration (30 μM. This large filament-number concentration is inconsistent with the [F-actin] curve from Melki et al. (15), which suggests a filament-number concentration of 1.67 nM.

In addition to constraining the phosphate dissociation rate for each cooperativity, [Pi] time-course data can be used to constrain the cooperativity directly. Fig. 3 shows simulated time-courses for selected values of ρ_d along with the data from Melki et al. (15). Because the data appear to have been significantly smoothed and no error estimates are provided, a 10% error band has been added to these data as an aid in evaluating the significance of the fits. To justify this error estimate, we note that in Melki et al. (15), parameters fit to comparable assays for tubulin varied by as much as 30%. Furthermore, the overshoot of [F-actin] seen in our simulations is completely absent from the data. This overshoot is physical (24), and suggests nearly 10% error in the [F-actin] time-course alone. Because the [F-actin] time-course is subtracted from the absorbance measurement at 360 nm to yield the [Pi] time-course, any error in the [F-actin] time-course would translate directly to an error in the [Pi] result. Finally, similar data from Blanchoin and Pollard (16) exhibit as much as 20% noise; because we have no information about the noise in Melki et al. (15), we assume that it is comparable to that in Blanchoin and Pollard (16).

The inset of Fig. 3 shows the quality of fit as a function of cooperativity. The best fit is obtained for ρ_d = 1, but another minimum in Δ² is found at ρ_d = 10⁸, close to ρ_d^∗. This surprising nonmonotonic behavior results from different ADP-Pi-/ADP-actin boundary nucleation mechanisms dominating in different regions of ρ_d. For ρ_d = 1, [Pi] grows linearly at small times, as expected for a first-order reaction. At ρ_d = 10⁴, nucleation of ADP-Pi-/ADP-actin boundaries within filaments is slow, but still exceeds the impact of the initial boundaries caused by polymerizing onto ADP-actin seeds. Because R_d = 0.22 s⁻¹ is relatively small, as many as 20 ADP-Pi-/ADP-actin boundaries per filament are required for the apparent phosphate dissociation rate to approach a rate commensurate with the data. This results in quadratic short-time behavior while the necessary additional boundaries are being created, giving a poor fit to the data. As ρ_d increases further, the time-course becomes more linear at short times because the number of ADP-Pi-/ADP-actin boundaries in each filament becomes dominated by its initial boundary from the ADP-actin seed.

Based on just these data and our 10% error estimate, which corresponds to Δ² = 5.3, we would reject models with cooperativity between 10² and 10⁶.

Dependence of Pi dissociation kinetics on filament-number concentration

One experimental justification for the random model came from Carlier and Pantaloni (2), in which phosphate concentrations were monitored using radioisotopes during polymerization of Ca-actin at two different filament-number concentrations, 1.1 nM and 20 nM. The key observation was that the lag-time between polymerization and phosphate dissociation,

$$t_{\text{lag}}=t_{1/2}^{\text{Pi}}-t_{1/2}^{\text{F}},$$

where $t_{1/2}^{\text{F}}$ is the half-time for actin polymerization, was roughly a factor of four smaller at n = 20 nM than at n = 1.1 nM. This observation is generally thought to support the random model, because one would expect the lag-time of a purely vectorial system to change by a factor of ∼18. This expectation is based on the assumption that a single filament has a single boundary between ADP-Pi- and ADP-actin, so increasing the filament-number concentration increases the number of such boundaries proportionally. Equation 6, which follows from Eq. S12 in the Supporting Material, assuming that polymerization is much faster than phosphate dissociation, shows the lag-time behavior of the vectorial model expected on the basis of a simplified analytic theory:

$$t_{\text{lag}}=\frac{G_0}{2n{R}_d},$$ (6)

where n is the filament-number concentration, and G₀ is the initial G-actin concentration. Because of the enhanced barbed-end phosphate dissociation rate, _br_d = 2 s⁻¹, which creates additional boundaries during polymerization, lag-times for simulations of the vectorial model, shown in Fig. 4, are smaller than this expectation by ∼30%.

Figure 4.

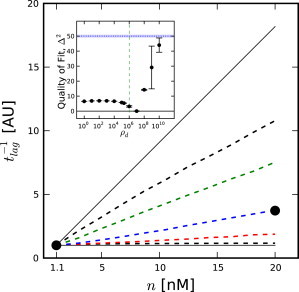
Dependence of t⁻¹_lag on n (arbitrary units). Results have been scaled by their values at n = 1 nM. (Solid circles) Scaled data from Carlier and Pantaloni (2). (Solid black lines) Theoretical expectations for the random and vectorial models (vectorial on top) based on Eqs. 3 and 6, respectively. (Dashed black lines) Simulation results for the random and vectorial models (vectorial on top). (Colored dashed lines) Simulation results for cooperative models (red, ρ_d = 10⁶; blue, ρ_d = 10⁷; green, ρ_d = 10⁸). (Inset) Quality of fit of simulations to Carlier and Pantaloni (2). (Dotted blue line) Quality of fit for the vectorial model. (Dashed green line) Corresponds to ρ^∗_d from Eq. 4.

The lag-times of stochastic simulations of cooperative models performed for Mg-actin under the conditions from Carlier and Pantaloni (2) are shown in Fig. 4 as a function of filament-number concentration, along with the experimentally measured lag-times from Carlier and Pantaloni (2) for Ca-actin. We have scaled both the data and our results, because we are comparing Ca-actin experiments with Mg-actin simulations. This was done because better data were available to constrain the rate parameters for Mg-actin than for Ca-actin, but the data from Carlier and Pantaloni (2) are only for Ca-actin. Our simulation results and theoretical calculations (see Section A in the Supporting Material) confirm the work done by Ohm and Wegner (9), which shows the independence of the cooperative model on filament-number concentration for cooperativities smaller than the critical cooperativity, which is ρ_d^∗ = 10⁶ for these conditions. As seen in Fig. 4, there would likely be no way to distinguish the random model from any cooperative model up to ρ_d ≈ 10⁶ using this type of experiment.

Thus, these data do not appear to support the hypothesis of random phosphate dissociation; instead, Fig. 4 shows that the scaled data are most consistent with a very high phosphate dissociation cooperativity, ρ_d = 10⁷, which is, again, close to ρ_d^∗. Further, both our simulations and analytic theory suggest that this type of experiment is not capable of providing a strong constraint on the phosphate dissociation cooperativity, except at extremely large values of ρ_d.

Dependence of [Pi] half-time on G-ADP-actin fraction

The copolymerization experiments performed in Pieper and Wegner (10) could, in principle, be used to constrain ρ_d. However, because the measured quantity is the remaining ATP, the reported [F-ADP-actin] concentrations in their Figs. 1 and 2 actually correspond to

$$\left[\text{F-ADP-Pi-actin}\right]+\left[\text{F-ADP-actin}\right],$$

ignoring the phosphate dissociation step entirely. Thus, these data cannot be used directly to constrain cooperative dissociation models.

Motivated by Pieper and Wegner (10), we performed simulations of actin filaments polymerizing with a mixture of free ATP-actin and free ADP-actin. Copolymerizing with ADP-actin creates additional boundaries between ADP-Pi-actin and ADP-actin that should enhance the apparent rate of phosphate dissociation in cooperative systems. This larger effective rate should allow us to distinguish between models.

Unlike the experimental procedure of Carlier and Pantaloni (2), which (as shown above) does not provide a sensitive measurement of the cooperativity, the experimental idea of copolymerization from Pieper and Wegner (10) can strongly constrain the cooperativity. Fig. 5 shows how the half-times for different cooperative models vary as a function of ADP-actin fraction in copolymerization experiments. For highly cooperative models, the half-time drops rapidly with increasing ADP-actin concentration. Using this method, one could reasonably constrain the cooperativity even at values as small as ρ_d = 100 using 10% ADP-actin during polymerization.

Figure 5.

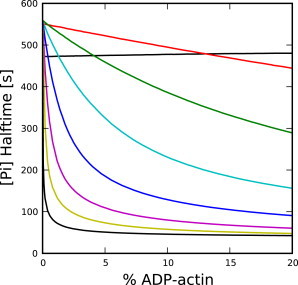
Dependence of [Pi] half-time on initial ADP-actin percentage for different values of ρ_d, in copolymerization experiments. Simulations performed using 30 μM total G-actin at 1.67-nM filament-number concentration. Values for ρ_d are: 1 (black, top), 10 (red), 10² (green), 10³ (cyan), 10⁴ (blue), 10⁵ (magenta), 10⁶ (yellow), and ∞ (black, bottom).

Single-filament depolymerization

More recent evidence used to support the random model comes from Jégou et al. (11). In this experiment, the length of a single filament was monitored as it depolymerized in solution without G-actin. As shown in Fig. 6 A, our stochastic simulations of both the random and vectorial models that include enhanced phosphate dissociation at the barbed-end using standard parameters are inconsistent with these data.

Figure 6.

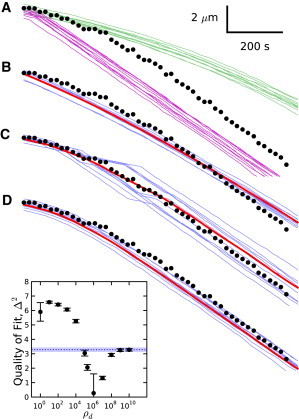
Comparison of filament length time-course data from Jégou et al. (11) (black) with stochastic treatments of several models. All models use an enhanced barbed-end phosphate dissociation rate of 2 s⁻¹ unless otherwise specified. (A) (Green lines) Sample filament trajectories from the random model using standard parameters. (Purple lines) Sample filament trajectories from the vectorial model. (B–D) (Red line) Mean filament time-course; (blue lines) sample filament traces. (B) Random model with _br_d = 7.5 s⁻¹. (C) Cooperative model with ρ_d = 1 × 10⁶. (D) Random model with r_d = 0.0074 s⁻¹. (Inset) Quality of fit for cooperative models to the data from Jégou et al. (11). (Dotted blue line) Δ² for the vectorial model; (blue shaded area) statistical errors for the vectorial model. Error bars represent statistical errors.

The vectorial theory of Jégou et al. (11) assumes a piecewise, linear time-dependence of the length as the filament tip transitioned from ADP-Pi-actin to ADP-actin. Our simulations reproduce this piecewise linear behavior if enhanced phosphate dissociation at the tip (1) is ignored. However, inclusion of this effect has significant impact on the predicted measurements from vectorial and cooperative models, drastically shortening the slow depolymerization phase and broadening the transition to the faster depolymerization phase. One reason is that the rapid barbed-end phosphate dissociation rate creates ADP-actin subunits at the tip during polymerization, according to the equation (see Section B in the Supporting Material)

$$\ell \approx \frac{{\left(k_T^{+}G\right)}^2}{r_c{\cdot }_b{r}_d},$$ (7)

where ℓ is the average number of protomers between ADP-actin protomers created due to rapid phosphate dissociation at the barbed-end, r_c is the ATP-actin cleavage rate (0.3 s⁻¹), _br_d is the barbed-end phosphate dissociation rate (2 s⁻¹), and G is the monomer concentration at which the filament is polymerizing (1.5 μM). This equation predicts the creation of a new state boundary approximately every 500 subunits under the conditions of Jégou et al. (11) (compared to the 600 subunit spacing seen in our simulations), providing enough ADP-Pi-actin/ADP-actin boundaries for the phosphate dissociation to be nearly complete as polymerization ends. For example, we find that when polymerization is complete under the conditions of Jégou et al. (11), 86% of the actin subunits are ADP in the vectorial model when enhanced tip-release is included. The effects of enhanced tip-release on the subsequent depolymerization dynamics are seen in Fig. S4 in the Supporting Material.

Though the data cannot be reproduced with the random model using standard parameters, they can be fit in three ways:

• Approach 1, using an especially high barbed-end phosphate dissociation rate, _br_d;

• Approach 2, using a large ρ_d = 10⁷; and

• Approach 3, using an unusually large value of r_d.

We were unable to fit these data simultaneously with the data from Melki et al. (15) without including enhanced phosphate dissociation at the tip.

For Approach 1, the data are best-fit using _br_d ≈ 7.5 s⁻¹, which is high, but apparently consistent with Fujiwara et al. (1). The primary shortcoming of this correction is that the simulated time-courses have visibly less curvature than the observed data, as shown in Fig. 6 B.

For Approach 2, the average trajectory, found using a high phosphate-dissociation cooperativity of ρ_d = 10⁶, provides a good fit to the data, as shown in Fig. 6 C. The figure also shows that cooperative models with high ρ_d generally have a large amount of length variation among filaments over time. At this point, there are not enough data available to say whether such variations are observed. As shown in the inset of Fig. 6, ρ_d = 10⁶ gives a pronounced minimum in Δ² using values of r_d fit to the data of Melki et al. (15).

For Approach 3, filament trajectories using r_d = 0.0074 s⁻¹, as proposed by Jégou et al. (11), instead of the accepted value of roughly 0.002 s⁻¹, are shown in Fig. 6 D. They fit the depolymerization data well; however, simulations using this rate under the conditions of Melki et al. (15) yield $t_{1/2}^{\text{Pi}}=146\text{s}$ instead of the measured 433 s. This difference seems larger than the likely errors of the two experiments, suggesting that r_d is unlikely to be large enough to fit the data from Jégou et al. (11) directly.

Additional filament depolymerization simulations using the conditions of Jégou et al. (11) with various free actin concentrations are shown in Fig. 7. These simulations show that the filament length time-courses for depolymerization of the random model are relatively independent of the free actin concentration during polymerization. The vectorial and cooperative models, however, show a measurable dependence. Thus, repeating the experiment of Jégou et al. (11) with varying G should provide additional constraints on the cooperativity.

Figure 7.

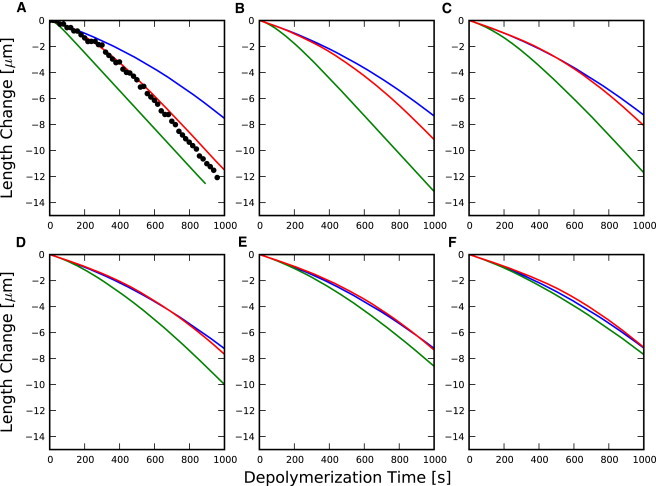
Mean depolymerization time-courses for the random model (blue), cooperative model with ρ_d = 10⁶ (red), and vectorial model (green) models with rapid phosphate dissociation at the tip. (Black dots) Data from Jégou et al. (11). Polymerization phase was 300 s with G-ATP-actin concentration, G maintained at (A) G = 1.5 μM, (B) G = 2.5 μM, (C) G = 3.5 μM, (D) G = 4.5 μM, (E) G = 5.5 μM, and (F) G = 6.5 μM.

Conclusion

The main finding of this work is that highly cooperative models of phosphate dissociation are not excluded by data used in the literature to justify the random model. Fig. 8 provides a visual comparison of the quality of fit of our simulations of cooperative models to several types of experimental data (2,11,15) as a function of ρ_d. All three data sets have a minimum at large ρ_d. Only Melki et al. (15) seems to provide support for the random model. However, this support may be weaker than it appears, because there are no reported error estimates for the data (only a mean time-course was reported). This makes it difficult to know whether key features of the various models, such as the shoulder near 1600 s in the vectorial model, are simply below the noise of the data. We also found that existing data for filament elongation rate as a function of free actin concentration can be fit by random, cooperative, and vectorial models (see Section C in the Supporting Material). Additionally, the effects of severing and annealing (excluded from this work) could nucleate additional state boundaries, making cooperative and vectorial models appear more like the random model at long times—though this effect may be small (22).

Figure 8.

Apparent experimental constraints on phosphate dissociation cooperativity. Jégou et al. (11) provides single-filament depolymerization data. Carlier and Pantaloni (2) varied filament-number concentration while monitoring polymerization. Melki et al. (15) monitored free phosphate during polymerization.

Based on our results, performing experiments similar to Pieper and Wegner (10) while measuring released phosphate should yield significant constraints on actin hydrolysis models. Additional stochastic simulations (not shown) also indicate that performing copolymerization with nonhydrolyzable ATP-actin should yield constraints on the cooperativity similar to those found using copolymerization with ADP-actin. We also found that performing experiments based on Jégou et al. (11) using different concentrations of free actin during the polymerization phase could help discriminate between different models. The time-course of depolymerization shows almost no dependence on the concentration of free actin during polymerization for the random model, whereas both the cooperative model (using ρ_d = 10⁶) and the vectorial model show measurable dependence.

If phosphate dissociation from F-actin is strongly cooperative, this will strongly affect the apparent rate of phosphate dissociation in cells. Consider a typical cortical actin filament of length 100 subunits. If such a filament has a free pointed-end, it will rapidly dissociate its Pi (1), creating an ADP-Pi-/ADP-actin boundary. At ρ_d = 10⁷, R_d ≈ 4.5 s⁻¹ (see Table 2), and the propagation of this boundary would cause the entire filament to release half of its Pi in ∼10 s. Free pointed-ends would be plentiful in branched cortical actin networks, as the lifetime of the Arp2/3 complex stabilizing the branches is <2 s (25). Such rapid apparent dissociation was assumed in Berro et al. (26) to fit experimental results for yeast, indicating that phosphate dissociation in cells is more rapid than expected, based on contemporary random hydrolysis models.

Parameters from the literature are often extracted using procedures that assume both random cleavage and random phosphate dissociation, rendering unbiased comparison of models more difficult. To differentiate actin hydrolysis models without bias, a global fit of general models across a wide range of experimental data will ultimately be required. The data from Jégou et al. (11) illustrate this need quite clearly, because these data can be fit by adjusting any of three parameters.

The chemical models considered here may be insufficient to explain some controversial phenomena. Two experiments have observed actin filaments undergoing depolymerization suddenly entering a phase of extremely slow depolymerization (11,27). Despite analysis (28) showing that hand-selected trajectories of highly cooperative models can match some of the observed trajectories from Kueh et al. (27), our simulations (not shown) suggest that first-order, correlated, three-state models are incapable of reproducing the corresponding bulk measurements shown in Fig. 1G of Kueh et al. (27) (a measurement not addressed in Li et al. (28)). Recent work suggests that this observed dynamic stabilization may be due to fluorophore dimerization rather than intrinsic properties of actin (29). In addition, filament-length diffusion coefficients (30,31) at approximately twice the critical concentration are an order-of-magnitude larger than calculations based on the random (6,8) and vectorial (7,8) models, which obtained large tip-diffusion coefficients very near the critical concentration and below it. If these measurements are accurate, we may be forced to seriously explore other possibilities such as extending models of actin dynamics to treat conformational states explicitly.