Conformational coupling in BK potassium channels

Abstract

Large conductance calcium- and voltage-dependent BK potassium channels (aka BK_Ca, MaxiK, Slo1, KCa1.1, and KCNMA1) are expressed in a wide variety of tissues throughout the body and are activated by both intracellular Ca²⁺ and membrane depolarization. Owing to these properties, BK channels participate in diverse physiological processes from electrical excitability in neurons and secretory cells, and regulation of smooth muscle tone to tuning of auditory hair cells (Vergara et al., 1998; Ghatta et al., 2006). The response to voltage and Ca²⁺ allows BK channels to integrate electrical and calcium signaling, which is central to their physiological role. Understanding how BK and other multimodal channels are regulated by and integrate diverse stimuli is not only physiologically important but also relevant to the topic of conformational coupling. As a voltage- and ligand-dependent channel, BK channels contain both voltage-sensor and ligand-binding domains as well as a gate to regulate the flow of K⁺ through the pore. Coupling of conformational changes in one domain to another provides the basis for transducing voltage and ligand binding into channel opening and, therefore, defines, together with the functional properties of the gate and sensors, the signal transduction properties of the channel. The goal of this perspective is to provide an overview on the role and molecular basis of conformational coupling between functional domains in BK channels and outline some of the questions that remain to be answered.

BK channel structure

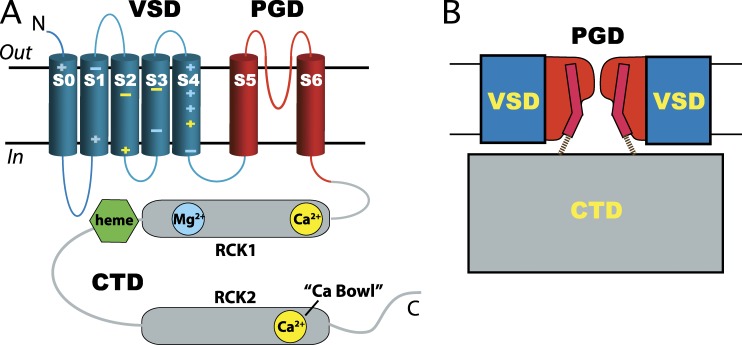
The BK channel is a member of the superfamily of voltage-gated channels that assembles as a homotetramer of pore-forming Slo1 (α) subunits. Each subunit contains seven transmembrane segments (S0–S6), including an S5–S6 pore gate domain (PGD) and voltage-sensor domain (VSD) that is likely to include S0–S4 segments (Liu et al., 2008) with charged voltage-sensing residues in S2, S3, and S4 (Fig. 1 A; Ma et al., 2006). In addition, a large C-terminal cytoplasmic domain (CTD) consisting of two homologous regulator of K⁺ conductance domains (RCK1 and RCK2) contains binding sites for Ca²⁺ and other ligands (Hou et al., 2009). The CTDs form a tetrameric gating-ring structure whose conformation changes upon Ca²⁺ binding. Crystal structures of the isolated BK channel gating ring and related prokaryotic Ca²⁺-activated K⁺ channel MthK have been solved in the presence and absence of Ca²⁺ (Jiang et al., 2002; Ye et al., 2006; Wu et al., 2010; Yuan et al., 2010, 2012). The atomic structure of the transmembrane domain has yet to be determined but is assumed to be homologous with that of voltage-gated potassium (K_V) channels, consistent with a low resolution cryo-EM structure of the entire channel(Wang and Sigworth, 2009). Although BK channels formed from Slo1 alone are fully functional, each channel may also coassemble with up to four regulatory subunits of which several subtypes exist (β1–4 and γ1–4; Brenner et al., 2000; Yan and Aldrich, 2012). Regulatory subunits tune BK channel function in different tissues, contain one or two transmembrane segments, occupy sites adjacent to the VSD (Liu et al., 2010), and act in part to regulate voltage-dependent gating (Bao and Cox, 2005; Yan and Aldrich, 2010).

Figure 1.

BK channel structure. (A) Topology of the pore-forming Slo1 subunit, including VSD, PGD, and CTD. Charged residues in the VSD that are important for voltage sensing are highlighted in yellow. The CTD contains binding sites for Ca²⁺, Mg²⁺, and heme. (B) Schematic organization of functional domains in the tetrameric channel. S6 segments in the PDG are connected to the CTD gating ring through S6-RCK1 linkers.

BK channel function

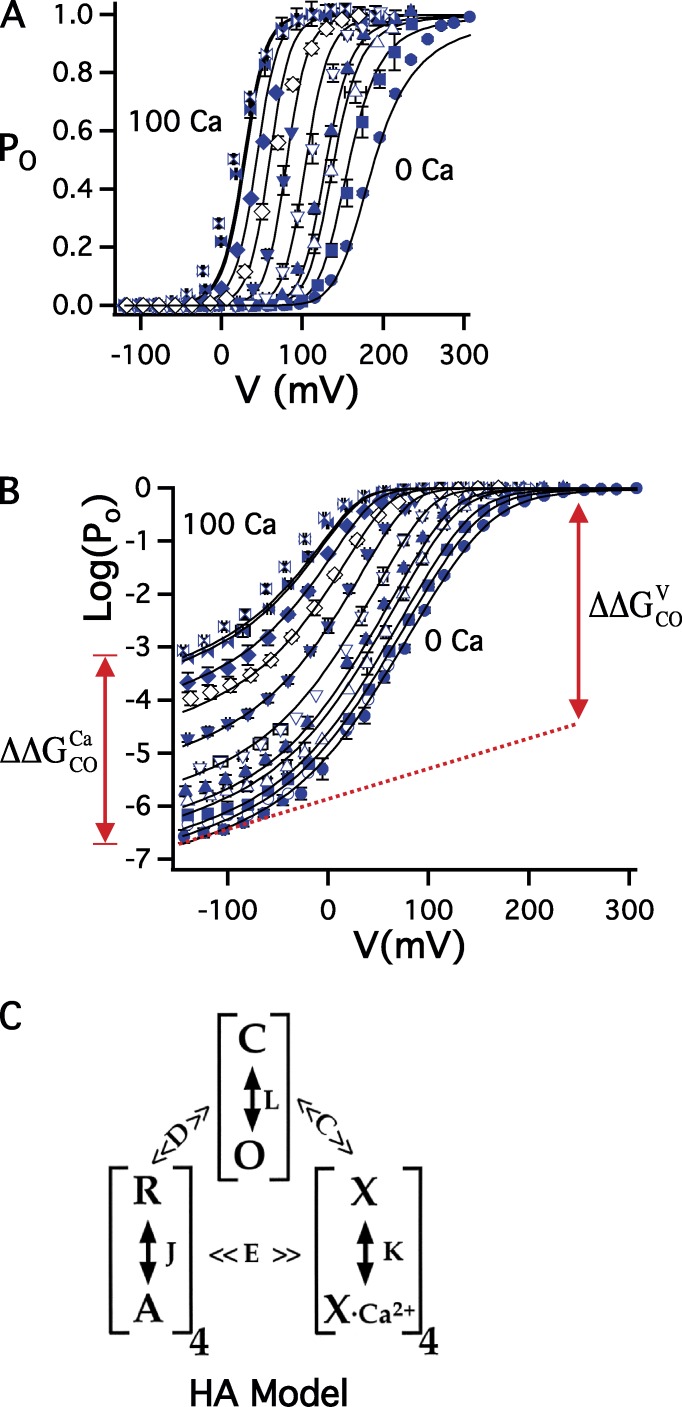
The response of BK channels to voltage and Ca²⁺ is illustrated in Fig. 2 by plotting steady-state open probability (P_O; Fig. 2 A) and Log(P_O) (Fig. 2 B) versus voltage at different [Ca²⁺]_i (0–100 µM) for heterologously expressed Slo1 channels (Horrigan and Aldrich, 2002). The P_o-V relation in 0 Ca²⁺ (∼0.5 nM) shows channels can be fully activated in the absence of Ca²⁺ binding, but only at voltages approaching +300 mV. Calcium, to a first approximation, shifts P_o-V to more negative voltages (Fig. 2 A), allowing the channel to activate in a physiological voltage range. However, plotting the data on a log scale reveals that Ca²⁺ does not simply shift the curve but rather increases Log(P_O) in a nearly voltage-independent manner until P_O saturates (Fig. 2 B). This response indicates that BK channels are activated independently by voltage- and Ca²⁺-sensors. Furthermore, Log(P_O) becomes almost voltage independent at extreme negative voltages indicating that channels can open in the absence of voltage-sensor activation, a conclusion supported by gating current measurements (Horrigan and Aldrich, 1999).

Figure 2.

Voltage- and Ca²⁺-gating of BK channels. (A) P_O-V relations for mSlo1 estimated as G_K/G_Kmax from macroscopic tail currents after 30 ms voltage pulses in 0–100 µM Ca²⁺. (B) Log(P_o)-V relations extend P_O to <10⁻² using steady-state unitary current recordings from macropatches. A and B represent mean ± SEM and are fit (solid curves) by the HA model (Horrigan and Aldrich, 2002). The increase in Log(P_o) from 0 Ca²⁺ to saturating 100 µM Ca²⁺ at −120 mV (where voltage-sensors are in the resting state) reflects Ca²⁺-sensor/gate coupling energy ($\Delta \Delta {\mathrm{G}}_{\text{CO}}^{\text{Ca}}$). The increase in Log(P_o) in 0 Ca²⁺ from −120 mV to ∼+300 mV (where voltage sensors are fully activated) reflects voltage-sensor/gate coupling ($\Delta \Delta {\mathrm{G}}_{\text{CO}}^{\mathrm{V}}$). The values of $\Delta \Delta {\text{G}}_{\text{CO}}^{\text{Ca}}$ and $\Delta \Delta {\text{G}}_{\text{CO}}^{\text{V}}$ are determined from the change in the free energy of the gate (e.g., $\Delta \Delta {\text{G}}_{\text{CO}}^{\text{Ca}}=\Delta {\text{G}}_{\text{CO}}\left[100\hspace{0.17em}\text{Ca}\right]-\Delta {\text{G}}_{\text{CO}}\left[0\hspace{0.17em}\text{Ca}\right]$, where $\Delta {\text{G}}_{\text{CO}}=\mathit{kT}\text{ln}\left[{\text{P}}_{\text{O}}/\left(1-{\text{P}}_{\text{O}}\right)\right]$), and, in the case of $\Delta \Delta {\text{G}}_{\text{CO}}^{\text{V}}$, the measurement at −120 mV must be extrapolated to positive voltages (dashed line) to correct for the weak voltage dependence of the C-O transition (z_L = 0.3 e). (C) Allosteric model indicates the possible conformations of the gate (C and O), voltage sensors (R and A), and Ca²⁺ sensors (X and X-Ca²⁺) in each of four subunits and allosteric factors (C, D, and E) that describe the energetic coupling between these three parts of the channel. J and L are voltage-dependent equilibrium constants with zero-voltage values J₀ and L₀ and partial charges (z_J, z_L), K = [Ca²⁺]/K_D, where K_D is the elementary Ca²⁺ dissociation constant for the closed channel.

An allosteric mechanism of BK channel gating

That BK channels exhibit basal activity in the absence of voltage-sensor activation and Ca²⁺ binding implies that sensor/gate coupling is not an obligatory process. That is, sensor activation promotes but is not required for channel opening. The ability of voltage or Ca²⁺ sensors in different subunits to influence a concerted conformational change (opening) in a nonobligatory fashion is well described in terms of allosteric mechanisms (Monod et al., 1965). A dual allosteric model (Fig. 2 C, HA model) was used to fit the steady-state data in Fig. 2 (A and B, curves), accounts for many other features of Slo1 gating (Horrigan and Aldrich, 1999, 2002; Horrigan et al., 1999), and provides a useful framework for analyzing BK channel gating in terms of domain/domain interactions. The HA (Horrigan-Aldrich) model asserts that the channel gate can undergo a closed to open (C-O) conformational change that is regulated by four independent and identical voltage- and Ca²⁺-sensors. Voltage sensors can be in a resting (R) or activated (A) conformation, whereas Ca²⁺ sensors can be Ca²⁺ free (X) or Ca²⁺ bound (X-Ca²⁺). The function of each domain is defined by equilibrium constants for gate opening (L), voltage-sensor activation (J), and Ca²⁺ binding (K). The coupling, or energy transfer, between domains is represented by allosteric factors (C, D, and E) which define the ability of a transition in one domain to affect the equilibrium constant in another.

The energetics of conformational coupling

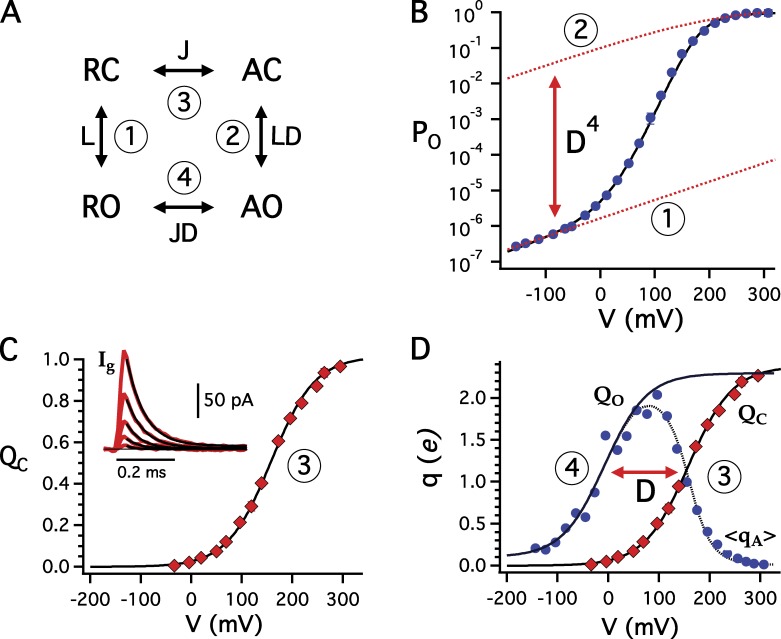
The structures of BK and homologous channels provide important clues concerning the molecular basis of conformational coupling, as discussed below. However, many features of coupling can only be resolved through structure-function analysis using site-directed mutagenesis. A prerequisite to such analysis is to quantify coupling interactions represented by allosteric factors C, D, and E in the HA model. Mutations that alter channel activity may perturb sensors, the gate, or their coupling. Therefore, it is crucial to distinguish changes in coupling from changes in the function of sensor or gate. One way to do this is by fitting steady-state data over a wide range of voltage and [Ca²⁺] as in Fig. 2 (A and B) to determine all parameters in the HA model. However, a more direct and model-independent approach to measure coupling is to determine the energetic effect on one domain of forcing coupled domains into defined conformations (e.g., all activated or deactivated) under extreme stimulus conditions (see also Chowdhury and Chanda in this issue). For example, the total coupling between all Ca²⁺ sensors and the gate $\left(\Delta \Delta {\text{G}}_{\text{CO}}^{\text{Ca}}=5.0{\hspace{0.17em}\text{kcal mol}}^{-1}\right)$ can be determined by comparing Log(P_o) in 0 Ca²⁺ and saturating 100 µM Ca²⁺ at extreme negative voltages where voltage sensors are in the resting state, and voltage-sensor/gate coupling $\left(\Delta \Delta {\text{G}}_{\text{CO}}^{\text{V}}=7.6{\hspace{0.17em}\text{kcal mol}}^{-1}\right)$ can be determined by comparing Log(P_o) at extreme negative and positive voltages in 0 Ca²⁺ (Fig. 2 B; Horrigan and Aldrich, 2002). In general, the HA model predicts that channels can occupy many different open and closed states, defined by the number of voltage- and Ca²⁺-sensors activated in each channel. But under extreme stimulus conditions, where all voltage- or Ca²⁺-sensors are either activated or deactivated, gating reduces to a single closed and open state. For a two-state process, the free energy difference between closed and open (ΔG_CO) can be defined in terms of the equilibrium constant (P_o/1-P_o) for the C-O transition (i.e., $\Delta {\text{G}}_{\text{CO}}=kT\text{ln}\left[{\text{P}}_{\text{O}}/\left(1-{\text{P}}_{\text{O}}\right)\right]$; Chowdhury and Chanda, 2010, 2012). Thus, changes in Log(P_o) in Fig. 2 B reflect the energetic effects of voltage- and Ca²⁺-sensor activation on the gate. Similarly, a weak coupling between voltage- and Ca²⁺-sensors $\left(\Delta \Delta G_{\mathit{RA}}^{\mathit{Ca}}=0.5{\hspace{0.17em}\text{kcal mol}}^{-1}\right)$ has been measured by comparing the effects of 0 Ca²⁺ and saturating Ca²⁺ on voltage-sensor activation measured with gating currents while the gate is closed (Horrigan and Aldrich, 2002).

Although measurement of Ca²⁺-sensor/gate coupling as in Fig. 2 B is relatively straightforward, measurement of voltage-sensor/gate coupling is subject to several challenges (Fig. 3). The relationship between gating and voltage-sensor/gate coupling is illustrated in Fig. 3 A by expanding the HA model to show the four combinations of states that the gate (C and O) and voltage-sensor (R and A) can assume in a single subunit (RC, RO, AC, and AO) together with the equilibrium constants between them. The equilibrium constant for the C-O transition increases from L when the voltage sensor is in the resting state (Fig. 3 A, #1) to LD when a voltage sensor is activated (Fig. 3 A, #2). Thus the voltage-sensor/gate coupling factor D can be determined by comparing P_o at extreme voltages (Fig. 3 B, #1 and 2), with the expectation that P_o/(1-P_o) will increase by a factor of D⁴ when all four voltage sensors are activated. One challenge is the large dynamic range of these measurements, which span a seven-order-of-magnitude change in P_o and require both macroscopic and unitary current recordings in the same patch and a high level of expression that cannot always be achieved with mutant channels. A related challenge is that P_o in 0 Ca²⁺ approaches saturation near unity at +300 mV as voltage sensors become fully activated (Fig. 2 A). As P_o approaches unity, determination of the equilibrium constant P_o/(1-P_o) becomes problematic and coupling energy can therefore be underestimated, especially in the presence of Ca²⁺ or with mutants that are easier to open than the WT because P_o may saturate before voltage sensors are fully activated. Finally, the C-O conformational change, as in many ion channels, has a weak intrinsic voltage dependence (L(V)) that must be taken into account when comparing P_o at extreme voltages (Figs. 2 B and 3 B, dashed lines).

Figure 3.

The energetics of voltage sensor/gate coupling. (A) Voltage sensor/gate states in a single subunit. Numbers refer to data in B, C, and D used to determine the indicated equilibrium constants. (B) P_O-V determines L (1) and LD⁴ (2). Dashed lines indicate the predicted voltage dependence of P_O with all voltage sensors either in the resting or activated state and z_L = 0.3 e. (C) Normalized Q_C-V for closed channels determined from ON gating currents (inset) is fit by a Boltzmann function with z_J = 0.58 e and defines J (3). (D) Q_O-V relation for open channels defines JD (4). Q_O is estimated by fitting the foot of the q_a-V relation (q_a = kTdln(P_O)/dV) with a Boltzmann function. The shift between Q_O and Q_C relations defines the coupling factor D.

A complementary approach to measure voltage-sensor/gate coupling is to determine the effect of channel opening on voltage-sensor activation. The equilibrium constant for the R-A transition increases from J when channels are closed to JD when channels are open (Fig. 3 A, #3 and 4). The equilibrium constant J is determined from the charge distribution for closed channels (Q_C-V; Fig. 3 C). Q_c can be measured by integrating ON gating currents (Fig. 3 B, inset) because voltage-sensor activation in BK channels is rapid and occurs while most channels remain closed. The equilibrium constant JD is determined from the charge distribution for open channels (Q_O-V; Fig. 3 D). Q_O cannot be determined from gating currents because BK channels close rapidly. However, Q_O can be estimated in a model-independent fashion from the log-slope of the P_o-V relation (q_a = kTdln(P_O)/dV), as shown in Fig. 3 D (Horrigan and Aldrich, 2002). The Q_O-V and Q_C-V relations have the same shape but are shifted relative to each other by a voltage directly proportional to coupling energy for a single voltage sensor ($\Delta \mathrm{V}=\text{kT ln}\left(\mathrm{D}\right)/{\text{z}}_{\mathrm{J}}=\Delta \Delta {\text{G}}_{\text{CO}}^{\mathrm{V}}/4{\text{z}}_{\mathrm{J}}$; Ma et al., 2006). This method yields similar results as in Fig. 3 B and avoids challenges relating to the voltage dependence of L(V), or P_O saturation. However, gating currents are difficult to measure in BK channels and require an even higher level of expression than in Fig. 3 B.

Molecular mechanisms of conformational coupling

Although the energetics and biophysical mechanisms of sensor/gate and sensor/sensor coupling in BK channels are well defined, many fundamental questions remain concerning the molecular basis of these interactions. Where in the channel do they occur? What are the identity and nature of amino acid interactions involved? When do the interactions occur during channel activation? These questions are broad because many potential sites of domain/domain interaction exist, the conformational changes that these domains and their interfaces undergo during gating are not all understood in detail, and insight provided by the structure of BK or homologous channels is in many cases limited. For example, although voltage-sensor/gate coupling is likely to be mediated in large part by interfaces between the VSD and PGD as in Kv channels, there is also a unique interface between the VSD and CTD in BK channels that may contribute to this process. Intracellular Mg²⁺ is a BK channel activator that is coordinated by residues in both VSD and CTD and interacts electrostatically with the voltage sensor, indicating (together with cross-linking experiments) that these domains come in contact (Yang et al., 2007, 2008). The primary functional effect of Mg²⁺ is to enhance voltage-sensor/gate coupling, suggesting that VSD/CTD interaction could provide a basis for this process (Horrigan and Ma, 2008). VSD/CTD interaction must also mediate coupling between voltage and Ca²⁺ sensors. However information about the VSD/CTD interface is incomplete. Structures of BK and MthK channel CTDs and the Kv channel VSD help identifying residues that may lie at this interface. But the complete BK channel structure including the VSD/CTD interface has yet to be determined, and neither MthK nor Kv channels contain a homologous interface.

Because most domain/domain interactions involved in conformational coupling remain to be identified, it is useful to consider what properties such interactions must have. In general, coupling may occur through linkers that directly connect two domains or through noncovalent interactions at domain/domain interfaces. In BK channels, Ca²⁺-sensor/gate coupling is thought to be mediated by the S6-RCK1 linker connecting CTD to PGD (Jiang et al., 2002; Niu et al., 2004). However multiple domain/domain interfaces are also involved in coupling, as noted above. Structural information has helped to identify where these interfaces are and to locate potential interaction partners. But elucidating the basis of conformational coupling is more complex than simply identifying domain/domain interactions. Coupling is necessarily a state-dependent process that depends on the conformations of two coupled domains. To understand the possible interaction mechanisms, it is useful to consider the energetics of coupling in the context of a gating cycle such as that describing voltage-sensor/gate coupling in Fig. 3 A. The coupling energy between a single voltage sensor and gate $\left(\Delta \Delta G_{CO}^{RA}=kT\text{ln}\left(D\right)\right)$ can be expressed in terms of the free energies of the four states involved (AC, AO, RC, and RO):

$$\begin{array}{l}\Delta \Delta {\text{G}}_{\text{CO}}^{\text{RA}}=\left[\Delta {\text{G}}_{\text{CO}}^{\text{A}}-\Delta {\text{G}}_{\text{CO}}^{\text{R}}\right]=\left[\left({\text{G}}_{\text{C}}^{\text{A}}-{\text{G}}_{\text{O}}^{\text{A}}\right)-\left({\text{G}}_{\text{C}}^{\text{R}}-{\text{G}}_{\text{O}}^{\text{R}}\right)\right]=\\ {\text{G}}_{\text{C}}^{\text{A}}-{\text{G}}_{\text{O}}^{\text{A}}-{\text{G}}_{\text{C}}^{\text{R}}+{\text{G}}_{\text{O}}^{\text{R}}\end{array}$$ (1)

Therefore, the change in coupling produced by changes in the free energy of each state is:

$$\Delta \Delta \Delta {\text{G}}_{\text{CO}}^{\text{RA}}=\left[\Delta {\text{G}}_{\text{C}}^{\text{A}}-\Delta {\text{G}}_{\text{O}}^{\text{A}}-\Delta {\text{G}}_{\text{C}}^{\text{R}}+\Delta {\text{G}}_{\text{O}}^{\text{R}}\right]$$ (2)

Eq. 2 indicates that coupling is enhanced ($\Delta \Delta \Delta {\text{G}}_{\text{CO}}^{\text{RA}}>0$) by decreasing ${\text{G}}_{\text{C}}^{\text{R}}$ or ${\text{G}}_{\text{O}}^{\text{A}}$ (stabilizing the RC or AO state) or by increasing ${\text{G}}_{\text{C}}^{\text{A}}$ or ${\text{G}}_{\text{O}}^{\text{R}}$ (destabilizing the AC or RO state). Coupling could also be enhanced by changing the free energy of multiple states, provided the net contribution (Eq. 2) is positive. However, interactions that are state independent or depend on the conformation of only one domain (e.g., $\Delta {\text{G}}_{\text{C}}^{\text{A}}=\Delta {\text{G}}_{\text{C}}^{\text{R}}$ or $\Delta {\text{G}}_0^{\text{R}}=\Delta {\text{G}}_{\text{C}}^{\text{R}}$) will have no effect on coupling (i.e.,$\Delta \Delta {\text{G}}_{\text{CO}}^{\text{RA}}=0$).

This analysis has several important implications for elucidating mechanisms of conformational coupling. First, to identify coupling interactions by structural methods requires that structures be solved in four conformations defined by two domains and have sufficient resolution to observe state-dependent changes in interaction. In practice, because changes in interaction energy may be subtle or difficult to estimate based on structure, coupling interactions would have to be verified and quantified by structure-function analysis. When only one or two structures of a channel are available, as is currently the case for BK and homologous channels, then structure-function analysis is required to determine if observed interactions participate in coupling, and residues that do not interact in an observed structure may still mediate coupling by interacting in other conformations. Second, structure-function analysis involving site-directed mutagenesis and measurements of coupling energy, as in Figs. 2 and 3, should be sufficient to identify residues involved in coupling interactions. However, such experiments must be interpreted cautiously. Allosteric proteins are often sensitive to modulation at domain interfaces by heterotropic ligands that bind and introduce interactions that do not normally exist, and mutations can have similar effects. For example, introduction of a positively charged residue near the BK channel Mg²⁺-binding site (Q397R) mimics the effect of Mg²⁺ by introducing an electrostatic interaction (Yang et al., 2007). Thus, the ability of Q397R to enhance coupling does not indicate that Q397 is normally involved in this process, just that it is located at a sensitive interface where conformational changes associated with voltage-sensor activation and channel opening both occur. Such false positives cannot be avoided simply by restricting analysis to mutations that reduce coupling because, based on Eq. 2, coupling can be reduced by introducing interactions that destabilize the RC or AO states or stabilize the AC or RO states. Intracellular heme, which inhibits voltage-sensor/gate coupling in BK channels, may act in this way (Horrigan et al., 2005). Consequently, whether a mutation increases or decreases coupling is less critical than the use of mutations such as Ala that are least likely to introduce interactions. Finally, to define the mechanism of voltage-sensor/gate coupling we must not only identify mutations that alter coupling but also characterize those changes in terms of the effect on individual states (i.e., RC, RO, AC, and AO) to determine when during activation the interactions occur. Although the change in free energy of any particular state cannot be determined directly, the equilibria between states can be evaluated as in Fig. 3 to define the change in free energy of individual states relative to each other. Such analysis has indicated that Mg²⁺ enhances voltage-sensor/gate coupling by preferentially stabilizing the AO state (Horrigan and Ma, 2008), whereas a stabilization of the RO state is consistent with the inhibitory effect of heme (Horrigan et al., 2005). It is worth noting that, depending on their state dependence, coupling interactions may influence open probability when sensors are in a resting conformation. Thus, the basal activity of BK channels in the absence of sensor activation defined by the equilibrium constant L in the HA model cannot be interpreted simply as the intrinsic stability of the gate because it also reflects any state-dependent interactions between the gate and resting sensors.

Mechanisms of voltage-sensor/gate coupling

Kv channel structures reveal two interfaces between VSD and PGD: intrasubunit contacts between the S4–S5 linker and S6 and intersubunit contacts between S4 and S5 (Long et al., 2005a, 2007). In BK channels, additional intersubunit interactions occur between the VSD and CTD (Yang et al., 2008). All of these interfaces potentially play a role in voltage-sensor/gate coupling in BK channels, but their relative contributions and mechanisms remain unknown. The S4/S5 interface is implicated because a mutation near the top of S4 (R210E) reduces coupling energy by half (Ma et al., 2006). However, we cannot rule out that this is a false positive produced by introducing rather than disrupting an interaction because other mutations at this site (R210C and R210N) appear to constitutively activate the channel preventing measurement of voltage-sensor/gate coupling (Ma et al., 2006). Similarly, the VSD/CTD interface is implicated indirectly based on the ability of Mg²⁺, Q397R, and heme to modulate coupling by introducing interactions at or near this interface.

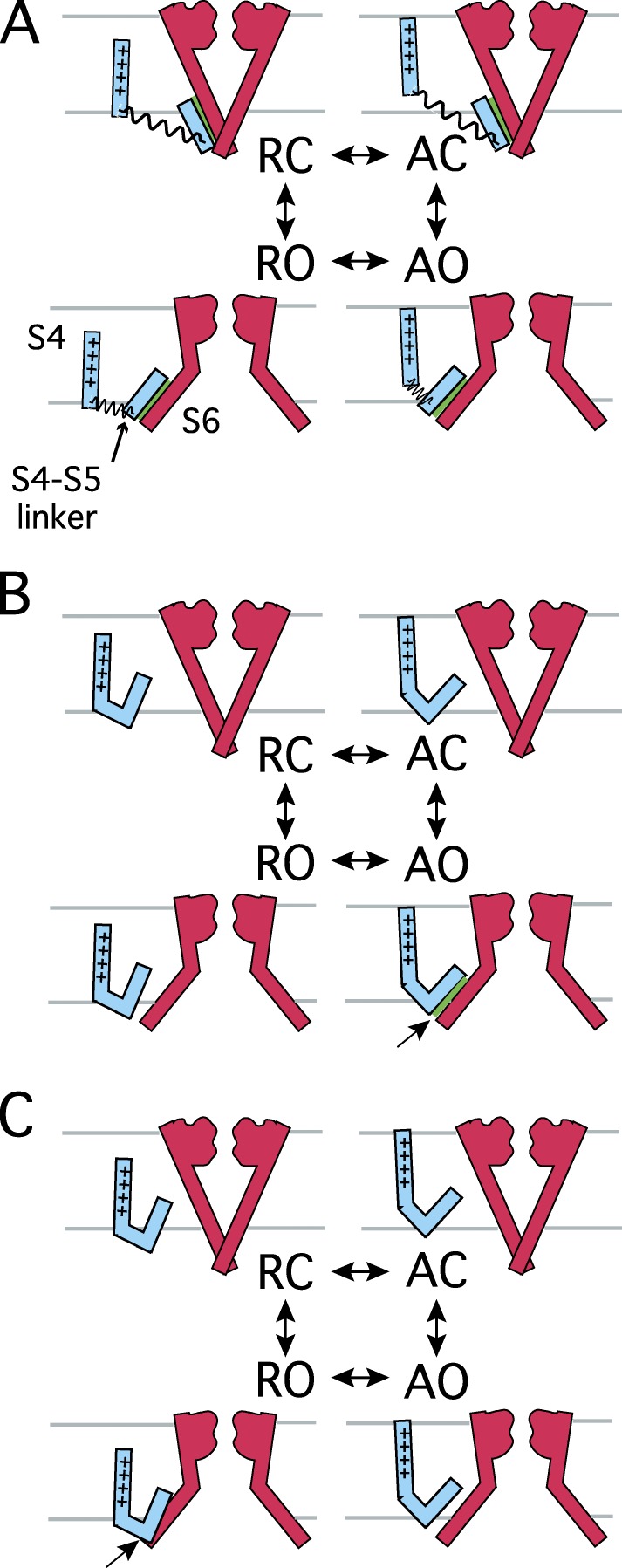
Interactions between the S4–S5 linker and S6 are widely considered to underlie voltage-sensor/gate coupling, also known as electromechanical coupling, in Kv channels (Lu et al., 2002; Tristani-Firouzi et al., 2002; Long et al., 2005b; Chowdhury and Chanda, 2012) and are also likely to be important in BK channels (Sun et al., 2012). However, even in Kv channels many of the questions raised above remain to be answered, such as what are the individual residues and nature of interactions that contribute to coupling and when do they occur during gating? The importance of these questions can be illustrated by comparing three hypothetical mechanisms of voltage-sensor/gate coupling that include S4–S5/S6 interactions and are consistent with the allosteric nature of voltage gating in Slo1 (Fig. 4). Fig. 4 (A–C) depicts the four combinations of states the gate and voltage-sensor can assume in a single subunit. The possibility that S4–S5/S6 forms a rigid connection that forces sensor and gate to move as a unit can be ruled out because voltage sensors can activate while channels remain closed. However, it is conceivable that the S4–S5 linker remains bound to S6 at all times, whereas flexibility in adjoining regions allows sensor and gate to move as if coupled by a spring (Fig. 4 A). Another possibility is the S4–S5 linker binds to the open gate only when the voltage sensor is activated, stabilizing the AO state (Fig. 4 B). Alternatively, the S4–S5 linker of the resting voltage sensor might clash with the open gate to destabilize the RO state (Fig. 4 C). These and other mechanisms could account for the ability of voltage-sensor activation to promote opening but make different predictions concerning the source of coupling and the role of S4–S5/S6 interaction. Fig. 4 A suggests that many parts of the S4–S5 linker could contribute to coupling by influencing the mechanical properties of the linkage. In this case, S4–S5/S6 interaction acts merely as a passive connection that affects coupling only to the extent that it is intact or disrupted. In contrast, Fig. 4 (B and C) predicts that the S4–S5/S6 interaction energy is the main determinant of coupling energy. However, the panels in Fig. 4 differ in the nature of the proposed interaction (Fig. 4 B, binding; Fig. 4 C, steric hindrance) and the state dependence of the interaction. The analysis of coupling energy and equilibria for such gating cycles, as outlined above, should allow such mechanisms and predictions to be distinguished in BK channels.

Figure 4.

Three models of voltage-sensor/gate coupling. Interaction of S4–S5 linker with the S6 gate in a single subunit. The voltage sensor can be in a resting (R) or activated (A) state, and the gate is closed (C) or open (O). (A) Flexible linkage with S4–S5/S6 interacting in all states. (B) S4–S5/S6 binding stabilizes AO state. (C) Steric hindrance destabilizes the RO state.

Despite substantial homology between BK and K_V channels, important differences also exist that could be relevant to voltage-sensor/gate coupling. First, BK channels are weakly voltage dependent compared with Kv channels and exhibit a different pattern and contribution of voltage-sensing residues in the VSD, suggesting that conformational changes associated with voltage-sensor activation may differ (Ma et al., 2006). Second, the ability of intracellular blockers and Cys-modifying reagents to access the inner pore of closed BK channels (Wilkens and Aldrich, 2006; Zhou et al., 2011) suggests that the BK channel gate may be formed by the selectivity filter (Cox and Hoshi, 2011; Thompson and Begenisich, 2012), as in cyclic-nucleotide–gated channels (Contreras et al., 2008), rather than by crossing of S6 segments at the inner mouth of the pore, as in Kv channels (del Camino and Yellen, 2001). These differences do not require that voltage-sensor/gate coupling occurs through fundamentally different mechanisms. For example, if the BK channel gate is in the selectivity filter it is still likely to be strongly coupled to S6 movement, as in CNG channels (Flynn and Zagotta, 2001), and therefore subject to control by S4–S5/S6 interaction. Indeed, there is considerable evidence for S6 movement associated with BK channel opening (Li and Aldrich, 2006; Wu et al., 2009; Chen and Aldrich, 2011). However, the coupling mechanisms for BK and Kv channels may differ in detail, and a selectivity gate in the BK channel could potentially support a larger role for S4/S5 interaction in voltage-sensor/gate coupling. It should also be noted that regulatory β and γ subunits have been reported to modulate voltage-sensor/gate coupling (Bao and Cox, 2005; Yan and Aldrich, 2010); thus, additional state-dependent interactions may form in BK channels between the VSD and regulatory subunits.

Mechanisms of coupling Ca²⁺ sensors to the gate and voltage sensors

Of the three coupling interactions in the HA model, Ca²⁺-sensor/gate coupling is easiest to measure and best understood at a molecular level. Nonetheless, many questions and controversies remain to be resolved concerning the conformational changes that occur upon Ca²⁺ binding and the mechanisms coupling these changes to the gate and voltage sensors.

Ca²⁺-dependent activation is generally consistent with the idea, originally proposed for MthK, that Ca²⁺ binding causes a conformational change in the gating ring that opens the channel by pulling on the RCK1-S6 linker (Jiang et al., 2002). Crystal structures in the presence and absence of Ca²⁺ suggest that MthK and BK channel gating rings expand in diameter by 8 and 12 Å, respectively, upon Ca²⁺ binding (Ye et al., 2006; Wu et al., 2010; Yuan et al., 2012). Experimental evidence in BK channels shows a monotonic relationship between channel activation and linker length, suggesting that the linker is under constant tension in the presence or absence of Ca²⁺, like a spring (Niu et al., 2004). Likewise, effects on Ca²⁺-sensor/gate coupling and Ca² sensitivity of mutations in the N-terminal AC region of the BK channel RCK1 domain suggest that the flexibility of this region is important for transmitting Ca²⁺-dependent conformational changes to the gate (Yang et al., 2010). Although the latter results are consistent with the linker hypothesis, they also have raised the possibility that conformational changes in the AC region could be coupled to the gate through direct contact with the PGD. Consistent with this possibility, the N-terminal half of RCK1 undergoes a substantial reorientation relative to the rest of the BK channel gating ring upon Ca²⁺ binding (Yuan et al., 2012). However, determining whether a CTD/PDG interface exists and contributes to coupling may have to wait until a complete BK channel structure is available.

The BK channel CTD contains two high affinity Ca²⁺-binding sites (one in each RCK domain) that have been identified by site-directed mutagenesis (Bao et al., 2004; Zhang et al., 2010). By using mutations to eliminate each site individually and carefully measuring the effects of Ca²⁺ on P_o at −80 mV (similar to Fig. 2 B), Sweet and Cox (2008) determined that the contribution to Ca²⁺-sensor/gate coupling of the RCK1 site (3.74 kCal mol⁻¹) was slightly greater than that of the RCK2 Ca²⁺ bowl site (3.04 kCal mol⁻¹), but the RCK2 site has a higher affinity for Ca²⁺. In addition, the summed contribution of the individual sites exceeded their combined effect in the WT channel ($\Delta \Delta {\text{G}}_{\text{CO}}^{\text{Ca}}=5.0{\hspace{0.17em}\text{kcal mol}}^{-1}$; Fig. 2 B), consistent with negative cooperativity between sites in the same subunit (Sweet and Cox, 2008). In contrast, another group performing similar experiments at +50 mV concluded that positive cooperativity exists between the two binding sites (Qian et al., 2006). In the latter case, positive cooperativity could potentially be accounted for if both Ca²⁺ sites were coupled to the voltage sensor because the voltage sensor is not held in a resting state at +50 mV. However Sweet and Cox (2008) concluded that the RCK1 site is solely responsible for Ca²⁺-sensor/voltage-sensor coupling. A recent study combining Ca²⁺ site mutations and voltage clamp fluorometry to monitor the effects of Ca²⁺ on steady-state voltage-sensor activation and P_o reached conclusions similar to that of Sweet and Cox (2008) regarding intrasubunit cooperativity and Ca²⁺-sensor/voltage-sensor coupling (Savalli et al., 2012). However, this study also suggested that Ca²⁺ site mutations may have effects other than elimination of Ca²⁺ binding. This caveat, together with the fact that none of the studies mentioned measured Ca²⁺-sensor/voltage-sensor coupling directly, suggests that the extent to which the individual Ca²⁺-binding sites are coupled to the voltage sensor or to each other, as well as the molecular mechanisms mediating such interactions, is still open to question.

Although the CTD contains two high affinity Ca²⁺-binding sites, only the Ca²⁺ bowl is occupied in the Ca²⁺-bound gating-ring structure (Yuan et al., 2012), raising questions of to what extent this structure resembles the Ca²⁺-saturated conformation in the intact channel. In principal, the two Ca²⁺ sites could have independent effects on activation by stabilizing a single Ca²⁺-bound open conformation. However, mutations in the AC region of RCK1 selectively alter the Ca²⁺ sensitivity of the RCK1 site (Yang et al., 2010), suggesting that some conformational changes may be coupled to RCK1 occupancy alone. This, together with the fact that the gating ring of the intact channel is expected to contact the VSD, suggests that significant differences in structure could exist between the crystal structure and intact Ca²⁺-saturated gating ring. A related question is to what extent gating ring expansion is determined by channel opening (i.e., RCK1-S6 linker tension) versus Ca²⁺ binding. Because gating ring expansion is observed upon Ca²⁺ binding in isolated gating rings, it seems reasonable to suppose that expansion and channel opening might not occur simultaneously. If the gating ring could expand into a high-Ca²⁺-affinity conformation while the channel is closed, it could have important implications for gating models and for the possible state dependence of CTD/VSD coupling. However, there is as yet no evidence supporting this possibility. Indeed Sweet and Cox (2008) concluded that their results were best fit by assuming gating-ring expansion is tightly coupled to channel opening, consistent with the HA model.

A final question relates to conformational events that occur in Ca²⁺-binding sites during channel opening. As in any allosteric model of ligand-dependent gating, the HA model predicts that Ca²⁺-binding sites must have a higher affinity for Ca²⁺ in the open than the closed conformation. Therefore, understanding how Ca²⁺ coordination changes upon channel opening is fundamental to the mechanism of Ca²⁺-sensor/gate coupling. In principal, the contribution of individual Ca²⁺-coordinating residues to state-dependent binding can be evaluated by determining the effect on coupling energy of mutating such sites (Purohit et al., 2012). Previous studies have generally identified likely Ca²⁺-coordination sites based on a reduced sensitivity of mutated channels to Ca²⁺ in the physiological range (≤100 µM). However, experiments at higher [Ca²⁺] may be required to saturate mutated sites and determine if Ca²⁺-sensor/gate coupling is altered.

Summary

The BK channel is an important example of a voltage- and ligand-gated channel whose function depends on conformational coupling between multiple domains. Many questions remain about the molecular basis of domain–domain coupling, but this channel represents a favorable system for studying such processes owing to its unique functional properties and methods that have allowed the energetics of coupling to be studied in detail. Combining these methods with emerging structural information about domain/domain interfaces and conformational changes in the channel should provide further insight into coupling mechanisms that are important in BK channels and in other voltage-gated or ligand-gated channels. BK channels also constitute a powerful system for understanding the interplay between ligand- and voltage-dependent gating. Defining the interactions that mediate coupling between voltage and Ca²⁺ sensors in this channel should provide unique insight into processes that may be relevant to other multimodal channels such as HCN or TRP.

This Perspectives series includes articles by Andersen, Colquhoun and Lape, and Chowdury and Chanda.