An emerging consensus on voltage-dependent gating from computational modeling and molecular dynamics simulations

Abstract

Developing an understanding of the mechanism of voltage-gated ion channels in molecular terms requires knowledge of the structure of the active and resting conformations. Although the active-state conformation is known from x-ray structures, an atomic resolution structure of a voltage-dependent ion channel in the resting state is not currently available. This has motivated various efforts at using computational modeling methods and molecular dynamics (MD) simulations to provide the missing information. A comparison of recent computational results reveals an emerging consensus on voltage-dependent gating from computational modeling and MD simulations. This progress is highlighted in the broad context of preexisting work about voltage-gated channels.

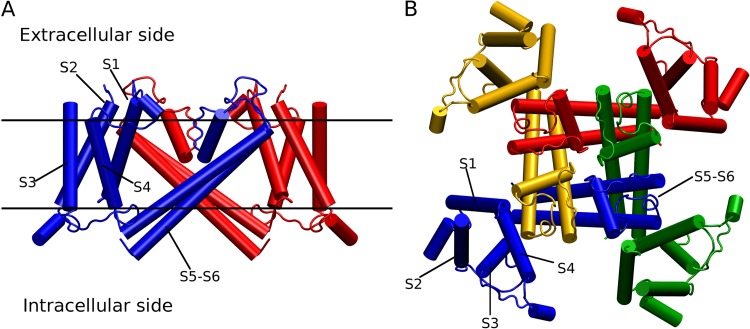
Voltage-gated K⁺ (K_V) channels and prokaryotic voltage-gated Na⁺ (Na_V) channels are formed by four subunits surrounding a central aqueous pore that allows ion permeation. Each subunit consists of six transmembrane α-helical segments called S1 to S6; the first four of these, S1–S4, constitute the voltage-sensor domain (VSD), whereas the S5–S6 segments assemble to form an ion-selective pore domain (see Fig. 1). The VSDs respond to changes in the potential difference across the cell membrane. When the membrane is depolarized, the VSD in each subunit undergoes a conformational transition from a resting to an activated state, and this information is communicated to the ion-conducting pore to promote its opening (Bezanilla et al., 1994; Zagotta et al., 1994). The activation of the VSD and opening of the pore are associated with the transfer of an electric charge ΔQ across the membrane, called the “gating charge” (Sigworth, 1994). Opening of the voltage-gated K⁺ channel Shaker corresponds to the outward translocation of a large positive charge on the order of 12–14 elementary charges (Schoppa et al., 1992). Four highly conserved arginines along S4 (R1, R2, R3, and R4) underlie the dominant contributions to the total gating charge of Shaker and appear to be mainly responsible for the coupling to the membrane voltage (Papazian et al., 1991; Aggarwal and MacKinnon, 1996; Seoh et al., 1996). The overall structure of eukaryotic voltage-gated Na⁺ channels, which are composed of four analogous subunits covalently linked in a single polypeptide, appears to be similar (Catterall, 2012).

Figure 1.

Overall view of the voltage-activated Kv1.2 K⁺ channel (Protein Data Bank accession no. 3LUT). (A) Two of the four subunits of the channel are displayed from a side view. The VSD comprises the transmembrane segments S1–S4, and the pore domain comprises the transmembrane segments S5–S6. (B) The tetramer is displayed from the extracellular side (each subunit is a different color). The two views are related by a 90° rotation.

The nature of the conformational change within the VSD, and how it is communicated to the pore domain, is the key question that must be answered to explain voltage-dependent gating. Ultimately, we need to know the 3-D structure of the multiple resting and activated states of the VSDs and their relationship to the closed and open conformations of the pore at atomic resolution to understand the voltage-dependent gating mechanism in molecular terms. However, although x-ray crystallographic structures of the Kv1.2 channel, Kv1.2/Kv2.1 chimera, and bacterial Na_VAb channels have provided information on the conformation of the active state (Long et al., 2005, 2007; Payandeh et al., 2011), no atomic resolution structure of a K_V or Na_V channel in the resting state is currently available. This has motivated the use of computations to provide the missing information about channel gating (Yarov-Yarovoy et al., 2006, 2012; Pathak et al., 2007; Bjelkmar et al., 2009; Delemotte et al., 2010, 2011; Khalili-Araghi et al., 2010, 2012; Schwaiger et al., 2011; Vargas et al., 2011; Jensen et al., 2012). These computational studies have relied on different approaches, including Rosetta modeling, a protein-folding method using knowledge-based potentials, and molecular dynamics (MD) simulations, consisting of propagating Newton’s classical equation of motion as a function of time using an all-atom force field. Remarkably, despite the considerable variations in computational methodologies and in template x-ray structures used, a highly consistent picture is emerging from these studies. Here we briefly review the most recent results in the broad context of preexisting work about voltage-gated channels.

Computational models of the resting state

Early models of the resting-state conformation of the VSD were obtained using the Rosetta method (Yarov-Yarovoy et al., 2006; Pathak et al., 2007); these initial models were subsequently refined with all-atom MD simulations (Khalili-Araghi et al., 2010) and with high-resolution Rosetta algorithms (Yarov-Yarovoy et al., 2012). Independent studies obtained very similar conformations using a combination of experimentally derived constraints based on engineered cross-links and metal bridges during MD simulations (Delemotte et al., 2010, 2011; Henrion et al., 2012). Moreover, these earliest models (Yarov-Yarovoy et al., 2006; Pathak et al., 2007) predicted pairs of neighboring residues before they were identified experimentally (Campos et al., 2007). Subsequent refinement of structural models of the resting state made it possible to demonstrate the existence of a consensus 3-D conformation of the VSD that satisfied a wide range of experimental data (Vargas et al., 2011). Rosetta models for the bacterial sodium channel NaChBac are very similar to those of K_V channels and have been extensively tested by disulfide cross-linking studies (DeCaen et al., 2008, 2009, 2011; Yarov-Yarovoy et al., 2012).

In practice, the atomic models of the resting state have either been refined by imposing inter-residue distances that are consistent with the experimentally derived constraints (Yarov-Yarovoy et al., 2006, 2012; Delemotte et al., 2010, 2011), or by explicitly modeling the side chains involved in the various cross-links or metal bridges themselves (Vargas et al., 2011; Henrion et al., 2012). Although these various models display high similarity, they all relied to varying degrees on computational “shortcuts” to obtain meaningful results about the VSD conformations within a reasonable computational time. Ultimately, the dream would be to “visualize,” atom-by-atom, how the channel moves as a function of time in response to a realistic membrane potential.

This has now become possible in part by relying on the virtual reality provided by computer simulations. Computer trajectories “simulating” the effect of membrane hyperpolarization on a voltage-gated ion channel were generated by several research groups, with the goal of triggering deactivation to directly observe the conformational response and reorganization of the VSD (Treptow et al., 2004, 2009; Nishizawa and Nishizawa, 2008, 2009; Bjelkmar et al., 2009; Denning et al., 2009; Delemotte et al., 2011; Freites et al., 2012). More recently, Jensen et al. (2012) used long (hundreds of microseconds) MD simulations to visualize a complete spontaneous conformational transition of a voltage-gated K⁺ channel upon changes of the membrane potential. As in the previous simulations, large negative hyperpolarizing membrane potentials were applied (−750 mV) to shorten the time for the voltage-dependent transition toward the resting state within accessible computing time (although some simulations were also generated at −375 mV). The long MD simulations performed by Jensen et al. (2012) led to a computationally derived model of the resting-state conformation of the channel very similar to those deduced previously with different methods (Yarov-Yarovoy et al., 2006, 2012; Pathak et al., 2007; Bjelkmar et al., 2009; Delemotte et al., 2010, 2011; Khalili-Araghi et al., 2010; Schwaiger et al., 2011; Henrion et al., 2012) (Fig. 2). The results confirm and substantially strengthen the consensus from previous computational studies.

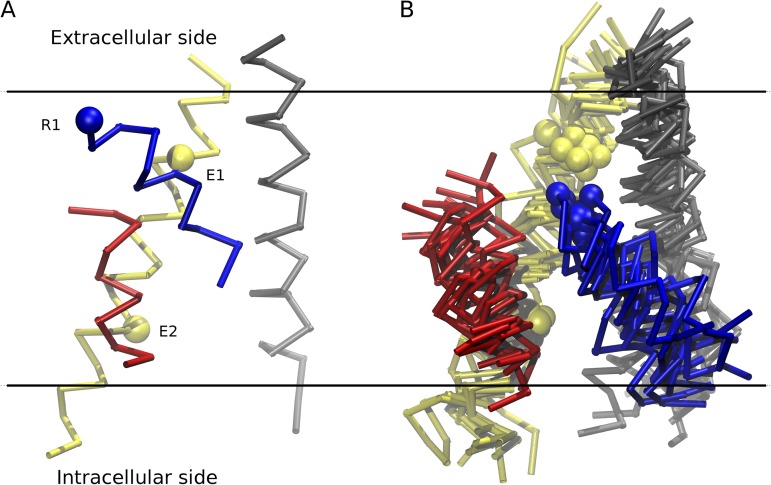
Figure 2.

Main elements of secondary structure of the VSD in the active and resting state. (A) The VSD in the active conformation (taken from the x-ray structure; PDB accession no. 3LUT). (B) A superposition of different models of the resting-state configuration of the VSD obtained by independent research teams (Delemotte et al., 2010; Schwaiger et al., 2011; Vargas et al., 2011; Jensen et al., 2012) using different constraints and methodologies. The four helices, S1 (gray), S2 (yellow), S3 (red), and S4 (blue), are displayed. The spheres correspond to the Cα atoms of E1 (Glu226) and E2 (Glu236) along S2, and R1 (Arg294) along S4.

By several quantitative measures, all the mentioned atomic models of the resting state display a high degree of similarity, indicating that a consensus on the structure of the resting state and the mechanism of VSD function has emerged from the independent computational studies. The backbone Cα carbons of all the models lie within 3–4 Å root mean square deviation (RMSD) of one another (Table S1). This is comparable to the RMSD among the four VSDs of tetrameric structures obtained in various models. The RMSD among the four VSDs of the tetrameric structure of Delemotte et al. (2010, 2011) vary between 2.7 and 3.9 Å, and the RMSD between the four VSDs of the tetrameric structure of Jensen et al. (2012) vary between 1.3 and 3.4 Å. For comparison, the VSDs of the x-ray structures of the Kv1.2 and Kv1.2/Kv2.1 chimera display RMSDs of 1.5 Å for the same region. The largest deviations of any of the resting-state models from a hypothetical average configuration are <3 Å; the two main outliers are one subunit from Delemotte et al. (2010, 2011) and one subunit from Jensen et al. (2012) (Fig. S1).

In all of the resting-state models, the S4 helix is predominantly rotated and translated inward along its main axis relative to the x-ray structures of the activated conformation, whereas the S1 and S2 helices retain their configuration. Averaging over all models, the absolute vertical displacement of S4 at the level of the Cα of the R1 position is ∼10 Å, with a spread of 3–4 Å (Table S1). There is some uncertainty in estimating the vertical translation of S4 because of the large structural fluctuations exhibited by the flexible VSDs. For example, the vertical position of R1 in the two x-ray structures of the active state of the K_V1.2 VSD differs by 2.6 Å (Long et al., 2005, 2007), and the net vertical displacement in the VSDs of the four subunits from Jensen et al. (2012) is 13.2, 16.2, 14.9, and 12.0 Å. All the resting-state models place the Cα of the R1 between the two acidic side chains E1 and E2 along the S2 helix, and R1 is also located above the highly conserved Phe located in the middle of S2. Most importantly, all of the resting-state models show the positive gating charge residues along S4 in position to either form salt bridges with acidic residues in the S1–S3 helices, or interact with the aqueous regions or the polar head groups. Similar conclusions have been obtained from the experiments on Na_V channels that combined structural modeling with disulfide cross-linking experiments (DeCaen et al., 2008, 2009, 2011; Yarov-Yarovoy et al., 2012).

The term “resting state” in the above discussion is used to loosely describe the conformation in which S4 inhabits its most inward position. Upon careful consideration, however, “the” resting state is probably an oversimplified concept because it is likely that S4 does not withdraw to the same position in all channels as result of sequence variations, regardless of the applied membrane potential. Furthermore, several of these resting states of the VSD may favor the nonconducting closed state of the pore. Consistent with this idea, hyperpolarization of the membrane potential slows the activation of voltage-gated channels, a behavior known as the “Cole–Moore effect” (Cole and Moore, 1960), because the VSDs must move through more resting states before activation when they start from a more negative membrane potential. To highlight the structural differences among the various proposed resting-state models shown in Fig. 2 (right), it is useful to realign the different models with respect to the S1–S3 helices, which are the most stable structural elements. The set of models, displayed in Fig. S2, places the S4 helix at various depths relative to S1–S3, with a slight spread in the tilt angle of its main axis. The initial resting-state model of K_V1.2 (Yarov-Yarovoy et al., 2006) captured a resting state in which the S4 segment is not drawn as far inward as the models of Fig. 2 and which, therefore, likely represents an initial step toward activation. Models of a full range of resting states of the VSD extending to quite negative voltages have been developed for both K_V and Na_V channels (DeCaen et al., 2009, 2011; Delemotte et al., 2012; Henrion et al., 2012; Yarov-Yarovoy et al., 2012).

The existence of multiple resting states is supported by a wide range of experiments, including analysis of multiple engineered metal bridges tracking successive states of the VSD (Henrion et al., 2012), noncovalent interactions between R2 and a tryptophan residue inserted in S1 (Lacroix et al., 2012), and disulfide cross-linking results of S4 gating charges with ion pair partners in S2 and S3 (DeCaen et al., 2009, 2011; Yarov-Yarovoy et al., 2012). It is expected that the multiple resting states of the VSDs of K_V and Na_V channels all stabilize the pore in its nonconducting closed conformation over a specific range of negative membrane potentials. Interestingly, a series of such resting states is observed in the long MD simulations of Jensen et al. (2012) as pauses in the inward movement of the VSD after the pore has closed. Thus, the conformations obtained from extremely long MD simulations are consistent with the resting state predicted by several independent studies using various computational approaches including knowledge-based structure prediction algorithms (Yarov-Yarovoy et al., 2006, 2012; Pathak et al., 2007) and MD simulations with experimental constraints (Delemotte et al., 2010; Vargas et al., 2011; Henrion et al., 2012). The final resting state from long MD simulations of Jensen et al. (2012) appears closest to the state reported in Delemotte et al. (2012), with the most inward position of S4. It is very satisfying that the conformational states are visited as the result of spontaneous transitions during long unbiased MD trajectories of the protein submitted to a negative membrane potential. The ability to simulate the spontaneous conformational transitions strengthens confidence in our current understanding of the physical forces and molecular interactions governing the voltage-gating process at the atomic level.

Mechanism of voltage-dependent activation

A consistent mechanistic perspective of voltage gating has emerged from these computational studies. The scenario that most accurately conveys the conformational change occurring within the VSD during activation as observed in these computations is the classical helical screw–sliding helix mechanism in which the S4 segment retains its helical conformation as it moves principally along its long axis (Catterall, 1986a,b; Guy and Seetharamulu, 1986). The gating charges are not directly exposed to the lipid hydrocarbon, and the S3–S4 helix-turn-helix does not move as a highly concerted structural motif across the membrane during voltage gating as proposed in the more recent paddle model (Jiang et al., 2003). Rather, sequential formation of salt bridges involving the gating residues plays an important role as proposed by Clay Armstrong (1981). Lastly, the concept of the “focused electric field” (Islas and Sigworth, 2001; Asamoah et al., 2003; Starace and Bezanilla, 2004), in which the spatial variation in the transmembrane potential affecting the gating charges of the VSD is concentrated over a narrow region that is considerably thinner than the full bilayer membrane, has been clarified by explicit calculations of the gating charge contributions based on all-atom MD simulations following two different approaches (Khalili-Araghi et al., 2010; Delemotte et al., 2011) and further supported by structural modeling studies (Yarov-Yarovoy et al., 2012). The gating charge calculations of Jensen et al. (2012) following the methodology of Khalili-Araghi et al. (2010) provided an additional confirmation of the concept of a focused electric field. Nonetheless, the S4 segment moves outward through the focused field, and the mechanism of voltage gating is not primarily a rearrangement in the transmembrane field as proposed in the transporter model (Chanda et al., 2005).

The MD simulations of Jensen et al. (2012) showed that the ion-conducting pore closes before any of the four VSDs have undergone a transition to the most stable resting-state conformation. This sequence of events is consistent with kinetic models with discrete states developed long ago to describe voltage gating in the Shaker K⁺ channel (Bezanilla et al., 1994; Zagotta et al., 1994; Schoppa and Sigworth, 1998). According to these kinetic models, the first step involved in closing an activated channel is the closing of the pore domain, followed by the independent transitions of the four VSDs toward the resting state. Recent x-ray structures of bacterial Na_V channels provide examples of this intermediate state, showing a closed pore domain associated with VSDs in their activated conformation (Payandeh et al., 2011, 2012; Zhang et al., 2012).

In summary, the major advances are that the resting-state conformation of the VSD reached by the long MD simulations is consistent with the results of numerous previous studies using different computational methods (Yarov-Yarovoy et al., 2006, 2012; Pathak et al., 2007; Bjelkmar et al., 2009; Delemotte et al., 2010, 2011; Khalili-Araghi et al., 2010; Schwaiger et al., 2011; Henrion et al., 2012), and that the sequence of events seen in the long simulations appears to be in qualitative accord with classical kinetic models of the voltage-gating process (Bezanilla et al., 1994; Zagotta et al., 1994; Schoppa and Sigworth, 1998). However, there is no experimental data at the large negative voltages used in the long simulations, and one must be cautious in trying to extrapolate the experimental time constants determined around −100 mV for ionic currents (Rodríguez and Bezanilla, 1996) and gating currents (Rodríguez et al., 1998).

Novel mechanistic hypotheses from MD simulations

Some novel ideas about the mechanism of voltage-dependent gating are suggested by the computational studies but do not yet have direct structural or experimental support. For example, sections of the S4 segment are observed in 3₁₀ helical conformation in x-ray crystal structures (Long et al., 2007; Clayton et al., 2008; Vieira-Pires and Morais-Cabral, 2010; Payandeh et al., 2011, 2012; Zhang et al., 2012). An intriguing suggestion from several simulation studies is the concept of a sequential dynamical transition to a 3₁₀ helical conformation for all or part of the S4 segment as it moves through the most hydrophobic region of the VSD (DeCaen et al., 2009, 2011; Khalili-Araghi et al., 2010; Schwaiger et al., 2011; Yarov-Yarovoy et al., 2012). Although the presence of some amount of 3₁₀ helical conformation is supported by available data (Villalba-Galea et al., 2008), the concept of a dynamic 3₁₀ transition of S4 during the voltage-gating process will require further experimental validation.

Another suggestion from the long MD simulations is that the closure of the pore domain is driven by a rapid de-wetting transition taking place in the intracellular vestibule. A similar de-wetting process was previously found in voltage-driven simulations of an isolated pore domain, in the absence of the VSDs (Jensen et al., 2010). The de-wetting process results in a closed pore with a nearly dry central cavity. However, evidence that ions may be captured in the cavity of a closing Shaker K⁺ channel argues against a complete de-wetting (Baukrowitz and Yellen, 1996a,b; Ray and Deutsch, 2006). We note here also that the structures of the preopen and inactivated states of prokaryotic Na_V channels have closed, water-filled pores (Payandeh et al., 2011, 2012; Zhang et al., 2012). More experimental work is required to determine whether de-wetting drives pore closure or arises only at very negative membrane potentials.

Lastly, the relationship of the voltage-gating transition displayed by the long MD simulations to the three major conformations of a VSD (resting, activated, and relaxed) observed in most of the S4-based VSDs (Villalba-Galea et al., 2008; Lacroix et al., 2011) remains uncertain. Moreover, the transitions observed in long MD simulations do not appear to reproduce all of the early components of the gating current (time constant of ∼10 µs) observed in Shaker K⁺ channels (Sigg et al., 2003). New experiments in which long MD simulations and gating current measurements are made in parallel on the same channel will give more insight into these issues.

Confidence in the computational results

Several models derived from a combination of experimental data and computations, produced from different approaches, have converged to yield a low resolution picture of the resting-state conformation, defined within ∼3–4 Å RMSD (Fig. 2, right). Upon a closer look, fine differences can be noted among the various models (Fig. S2), which points to the concept of multiple resting states in which the segment S4 is drawn to different depths toward the intracellular side. The broad agreement among the various computational methods, most likely, is not fortuitous, and the picture emerging represents a genuine advance in understanding voltage-gated channels. The implication, if the computational results are to be trusted, is that many of the apparently conflicting measures about voltage gating can be resolved. Nevertheless, some might argue that the controversy about the resting-state conformation of the VSD will remain until an experimental x-ray structure becomes available. In this context, it is important to note that all structures are models, even x-ray crystal structures. However, structural models from x-ray crystallography rely on a huge amount of experimental data and are derived from rigorously established procedures that have been extensively tested and cross-validated. It is expected that experimental structure determination will increasingly rely on sophisticated computational modeling to complement low resolution data (Chen et al., 2007; Trabuco et al., 2008; Brunger et al., 2012). In the early 1980s, NMR structures were considered tentative models until it was demonstrated that the results were consistent with x-ray crystallography (Billeter et al., 1989). What ultimately matters is the quantifiable level of confidence that can be attributed to a structural model. As the methodologies become more and more reliable and consistent, computational modeling will play an increasingly important role in structural biology (DiMaio et al., 2011; Lange et al., 2012). The present situation, in which the proposed models of the VSD (Fig. 2) are supported by such a wide range of computational approaches applied by different investigators, is unprecedented to our knowledge. For this reason, our view is that one may be (cautiously) optimistic that the resting-state structures of Fig. 2 and the related structures in other computational papers cited here are close (within ∼3–4 Å RMSD) to reality. Notably, this accuracy can be predicted from the distribution of models themselves (even the early ones).

At this point it is prudent to sound a note of caution. The progress documented in this Viewpoint on understanding structural aspects of a membrane-bound channel protein has been made possible by using novel computational methodologies and an empirical potential energy (force field) that subsumes polarization and nuclear quantum effects in an average fashion. Although MD simulation articles often imply that every in silico detail from the trajectory is real, it is useful to remind ourselves that this is not necessarily the case. Experience indicates that current approximations are more successful in predicting conformational states than transition rates. The reason is that the overall topology of the potential energy surface, with its wells and barriers, is more or less correct, even though the relative depths of the wells and heights of the barriers may be imperfect. As a consequence, the order in which the chain of events takes place in a simulation during a complex conformational transition may not reflect reality, as some parts may undergo transitions that are too slow, whereas other parts undergo transitions that are too fast. Therefore, although a strong consensus is emerging on the nature of the conformation of the resting state, the dynamic properties of the gating process require more scrutiny. This will be challenging notwithstanding the massively increased length of recent MD trajectories.

Conclusion

A clear consensus on the mechanism of voltage-dependent gating is emerging from various studies based on a wide range of computational and experimental methods. This consensus, which is to be celebrated, highlights the increasingly important role of computational modeling in linking molecular structure to biological function by supplementing missing information. It is important, however, to remain prudent in assessing the significance of details and features of the computationally derived models that have not yet been experimentally validated. Even if the resting-state conformation of the VSD reached by the simulations is correct, and the sequence of events is in accord with classical kinetic models of the voltage-gating process, it is possible that the rates of the individual processes is differentially affected by insufficient sampling, force field inaccuracies, and the large membrane potential typically applied so far. Nevertheless, it is encouraging to note that, despite their inherently approximate nature, current computational models can provide meaningful answers to important questions about complex biomolecular systems. Further studies using computational methods in concert with structure–function experiments seem likely to soon reveal the missing details of VSD function.

Online supplemental material

Table S1 provides all the data about minimum global RMSD of the VSDs using best pairwise alignments for all models. Fig. S1 shows the deviation of backbone atom of each model relative to the average. Fig. S2 shows a superposition of all the VSD models in the resting-state configuration aligned with respect to S1–S3 helices. Fig. S3 presents a quantitative structural comparison of all the VSD models with the crystal structures. Video 1 includes an animation showing all the available VSD models rotating in superposition. The online supplemental material is available at http://www.jgp.org/cgi/content/full/jgp.201210873/DC1.